5
Implications of the New Foundations for Assessment Design
This chapter describes features of a new approach to assessment design that is based on a synthesis of the cognitive and measurement foundations set forth in Chapters 3 and 4. Ways in which the three elements of the assessment triangle defined in Chapter 2—cognition, observation, and interpretation—must work together are described and illustrated with examples. This chapter does not aim to describe the entire assessment design process. A number of existing documents, most notably Standards for Educational and Psychological Testing (American Educational Research Association [AERA], American Psychological Association, and National Council of Measurement in Education, 1999), present experts’ consensus guidelines for test design. We have not attempted to repeat here all of the important guidance these sources provide, for instance, about standards for validity, reliability, and fairness in testing. Instead, this chapter focuses on ways in which assessment design and practice could be enhanced by forging stronger connections between advances in the cognitive sciences and new approaches to measurement.
Three important caveats should be borne in mind when reading this chapter. First, the presentation of topics in this chapter corresponds to a general sequence of stages in the design process. Yet to be most effective, those stages must be executed recursively. That is, design decisions about late stages in the assessment process (e.g., reporting) will affect decisions about earlier stages (e.g., task design), causing assessment developers to revisit their choices and refine the design. All aspects of an assessment’s design, from identifying the targets of inference to deciding how results will be reported, must be considered—all within the confines of practical constraints—during the initial conceptualization.
Second, the design principles proposed in this chapter apply to assessments intended to serve a variety of purposes. The different ways in which the principles play out in specific contexts of use and under different sets of constraints are illustrated with a diverse set of examples. In other words, it should not be assumed that the principles proposed in this chapter pertain only to formal, large-scale assessment design. These principles also apply to informal forms of assessment in the classroom, such as when a teacher asks students oral questions or creates homework assignments. All assessments will be more fruitful when based on an understanding of cognition in the domain and on the precept of reasoning from evidence.
Finally, the features of assessment design described here represent an ideal case that is unlikely to be fully attained with any single assessment. The examples provided of actual assessments are approximations of this ideal. They illustrate how advances in the cognitive and measurement sciences have informed the development of many aspects of such an ideal design, and provide evidence that further efforts in this direction could enhance teaching and learning. In turn, these examples point to the limitations of current knowledge and technology and suggest the need for further research and development, addressed in Part IV.
THE IMPORTANCE OF A MODEL OF COGNITION AND LEARNING
Deciding what to assess is not as simple as it might appear. Existing guidelines for assessment design emphasize that the process should begin with a statement of the purpose for the assessment and a definition of the content domain to be measured (AERA et al., 1999; Millman and Greene, 1993). This report expands on current guidelines by emphasizing that the targets of inference should also be largely determined by a model of cognition and learning that describes how people represent knowledge and develop competence in the domain (the cognition element of the assessment triangle). Starting with a model of learning is one of the main features that distinguishes the committee’s proposed approach to assessment design from current approaches. The model suggests the most important aspects of student achievement about which one would want to draw inferences and provides clues about the types of assessment tasks that will elicit evidence to support those inferences.
For example, if the purpose of an assessment is to provide teachers with a tool for determining the most appropriate next steps for arithmetic instruction, the assessment designer should turn to the research on children’s development of number sense (see also Chapter 3). Case, Griffin, and colleagues have produced descriptions of how young children develop understanding in various mathematical areas (Case, 1996; Case, Griffin, and
Kelly, 1999; Griffin and Case, 1997). A summary of their cognitive theory for the development of whole-number sense is presented in Box 5–1. Drawing from their extensive research on how children develop mathematical understanding as well as the work of other cognitive development researchers— such as Gelman, Siegler, Fuson, and Piaget—Case, Griffin and colleagues have constructed a detailed theory of how children develop number sense. This theory describes the understandings that children typically exhibit at various stages of development, the ways they approach problems, and the processes they use to solve them. The theory also describes how children typically progress from the novice state of understanding to expertise.
Case, Griffin, and colleagues have used their model of cognition and learning to design mathematics readiness programs for economically disadvantaged young children. The model has enabled them to (1) specify what knowledge is most crucial for early success in mathematics, (2) assess where any given population stands with regard to this knowledge, and (3) provide children who do not have all this knowledge with the experience they need to construct it (Case et al., 1999). These researchers have implemented their Rightstart program in different communities in Canada and the United States and have consistently found that children in the experimental program perform significantly better on a variety of measures of number sense than those in control groups (Griffin and Case, 1997; Griffin, Case, and Sandieson, 1992; Griffin, Case, and Siegler, 1994). Later in this chapter we present an assessment they have developed to assess student understanding relative to this theory.
Features of the Model of Cognition and Learning
The model of learning that informs assessment design should have several key features. First, it should be based on empirical studies of learners in the domain. Developing a model of learning such as the example in Box 5–1 requires an intensive analysis of the targeted performances, using the types of scientific methods described in Chapter 3. The amount of work requirfsed should not be underestimated. Research on cognition and learning has produced a rich set of descriptions of domain-specific performance that can serve as the basis for assessment design, particularly for certain areas of mathematics and science (e.g., National Research Council [NRC], 2001; American Association for the Advancement of Science, 2001) (see also the discussion of domain-based models of learning and performance in Chapter 3). Yet much more research is needed. The literature contains analyses of children’s thinking conducted by various types of professionals, including teachers, curriculum developers, and research psychologists, for a variety of purposes. Existing descriptions of thinking differ on a number of dimensions: some are highly detailed, whereas others are coarser-grained; some
|
BOX 5–1Example of a Model of Cognition and Learning: How Children Come to Understand the Whole Number System Below is a brief summary of the theory of Case, Griffin, and colleagues of how children gain understanding of the whole-number system, based on empirical study of learners. For a more detailed discussion see Case (1996) or Griffin and Case (1997).
|
focus on procedures, whereas others emphasize conceptual understanding; and some focus on individual aspects of learning, whereas others empha size the social nature of learning. Differing theoretical descriptions of learning should not be viewed as competitive. Rather, aspects of existing theoretical descriptions can often be combined to create a more complete picture of student performance to better achieve the purposes of an assessment.
|
children begin to learn the system of notation that is used for representing numbers on paper, further serving to bind together the elements of the new cognitive structure.
Case and Griffin explain that although most children develop these competencies, there are always some who do not. This usually does not mean that they are incapable of achieving these understandings, but rather that there has not been a heavy emphasis on counting and quantity in their early environment. The researchers have designed educational interventions to help disadvantaged children develop these competencies because they are so important for later mathematical learning. |
Second, the model of cognition and learning should identify performances that differentiate beginning and expert learners in the domain. The nature of subject matter expertise has been the focus of numerous studies in human cognition (see also Chapter 3). From this type of research it is known that experts have acquired extensive knowledge in their disciplines, and that this knowledge affects what they notice and how they organize, represent,
and interpret information. The latter characteristics in turn affect their ability to remember, reason, and solve problems. Most useful for assessment design are descriptions of how characteristics of expertise are manifested in particular school subject domains. Studies of expert performance describe what the results of highly successful learning look like, suggesting targets for instruction and assessment.
It is not, however, the goal of education to make all school children experts in every subject area, and many would argue that “literacy” and “competency” are more appropriate goals. Ideally, then, a model of learning will also provide a developmental perspective, laying out one or more typical progressions from novice levels toward competence and then expertise, identifying milestones or landmark performances along the way. The model of learning might also describe the types of experiences that provoke change or learning. Models of learning for some content areas will depict children as starting out with little or no knowledge in the domain and through instruction gradually building a larger and larger knowledge base. An example is learning to represent large-scale space. Children’s drawings provide a starting point for cartography, but they need to learn how to represent position and direction (e.g., coordinate systems) to create maps of spaces. In other domains, such as physics, students start with a good deal of naive or intuitive knowledge based on observations of the world around them. Some of this knowledge includes deeply entrenched misconceptions or concepts that must be disentangled through instruction. Given a developmental description of learning, assessments can be designed to identify current student thinking, likely antecedent understandings, and next steps to move the student toward more sophisticated understandings. Developmental models are also the starting point for designing assessment systems that can capture growth in competence.
There is no single way in which knowledge is represented by competent performers, and there is no single path to competence. But some paths are traveled more than others. When large samples of learners are studied, a few predominant patterns tend to emerge. For instance, as described in Box 5–2, the majority of students who have problems with subtraction demonstrate one or more of a finite set of common conceptual errors (Brown and Burton, 1978; Brown and VanLehn, 1980).1 The same is true with fractions (Resnick et al., 1989; Hart, 1984) and with physics (diSessa and Minstrell, 1998). Research conducted with populations of children speaking different languages shows that many of the difficulties children experience in comprehending and solving simple mathematics word problems apply consistently across a wide range of languages and instructional settings. The re-
|
BOX 5–2 Manifestations of Some Subtraction Bugs
|
||||||||||||||||||||
search reveals that children’s difficulties are derived from underlying conceptual representation issues that transcend linguistic differences (Verschaffel, Greer, and DeCorte, 2000).
Differences among learners should not be ignored. Thus a third key feature of a model of learning is that it should convey a variety of typical ways in which children come to understand the subject matter of interest. Children are exposed to different content depending on the curriculum and family environment they encounter, and this affects what they learn (see Chapter 3). When developing models of learning, one starting point for capturing such differences is to study a group of learners that reflects the diversity of the population to be instructed and assessed in terms of such factors as age, culture, socioeconomic status, gender, and region.
Fourth, starting with a theory of how people learn the subject matter of interest, the designers of an assessment will need to select a slice or subset of the larger theory of cognition and learning as the assessment targets. That is, any given model of learning underlying an assessment will capture some, but not all, aspects of what is known about how students think and learn in the domain. That selection should depend on the purpose for the assessment. For instance, the purpose of an intelligent tutor is to determine the precise topic or skill area in which a student is struggling at the moment so that the student can be directed to further help. To develop this kind of assessment, a detailed description of how people at different levels of expertise use correct and incorrect rules during problem solving is often needed (such as that illustrated by the model of cognition underlying the Anderson tutor, described below). More typical classroom assessments, such as quizzes administered by teachers to a class several times each week or month, provide individual students with feedback about their learning and areas for improvement. They help the teacher identify the extent of mastery and appropriate next steps for instruction. To design such assessments, an extraction from the theory that is not quite so detailed, but closer to the level at which concepts are discussed in classroom discourse, is most helpful. The model of cognition and learning underlying a classroom assessment might focus on common preconceptions or incomplete understandings that students tend to have and that the teacher can identify and build on (as illustrated by the Facets example described below). If the purpose for the assessment is to provide summative information following a larger chunk of instruction, as is the case with statewide achievement tests, a coarser-grained model of learning that focuses on the development of central conceptual structures in the subject domain may suffice.
Finally, a model of learning will ideally lend itself to being aggregated in a principled way so that it can be used for different assessment purposes. For example, a fine-grained description of cognition underlying an intelligent tutoring system should be structured so the information can be com-
bined to report less detailed summary information for students, parents, and teachers. The model should, in turn, be compatible with a coarse-grained model of learning used as a basis for an end-of-year summative assessment.
To be sure, there will always be school subjects for which models of cognition and learning have not yet been developed. Policies about what topics should be taught and emphasized in school change, and theories of how people learn particular content will evolve over time as understanding of human cognition advances. In such situations, the assessment developer may choose to start from scratch with a cognitive analysis of the domain. But when resources do not allow for that, basic principles of cognition and learning described in Chapter 3—such as the importance of how people organize knowledge, represent problems, and monitor their own learning— can inform the translation of curriculum into instruction and assessment. The principle that learning must start with what students currently understand and know about a topic and build from there will always hold.
Some existing assessments have been built on the types of models of learning described above. The following examples have been chosen to illustrate the variation in theories that underlie assessments for different purposes. First, we use the example of intelligent tutoring systems (used to illustrate a number of points in this volume). Existing intelligent tutoring systems are built on detailed cognitive theories of expert problem solving (Anderson, Boyle, Corbett, and Lewis, 1990; VanLehn and Martin, 1998). The tutors use assessment constantly to (1) provide continuous, individualized feedback to learners as they work problems; (2) offer help when appropriate or when requested by the learner; and (3) select and present appropriate next activities for learning. The second example describes a classroom assessment approach that teachers can use for diagnosing qualitatively different states of student understanding in physics. An important point of this report is that a model of learning can take different forms and encompass different research perspectives. Thus the third example illustrates a model of learning that focuses on the situative and participatory aspects of learning mathematics. The fourth example demonstrates how models of learning can be used as the basis for large-scale as well as classroom assessments.
Underlying Models of Cognition and Learning: Examples
PAT Algebra Tutor
John Anderson’s ACT-R research group has developed intelligent tutoring systems for algebra and geometry that are being used successfully in a number of classrooms (Koedinger, Anderson, Hadley, and Mark, 1997). The cognitive models of learning at the core of their systems are based on the group’s more general theory of human cognition, ACT-R, which has many
features consistent with the cognitive architecture and structure of knowledge as described in Chapter 3. ACT-R theory aims to describe how people acquire and organize knowledge and produce successful performance in a wide range of simple and complex cognitive tasks, and it has been subjected to rigorous scientific testing (Anderson et al., 1990). The model of learning is written as a system of “if-then” production rules that are capable of generating the multitude of solution steps and missteps typical of students. As a simple example, below is a small portion of an ACT-R production system for algebra:
|
Rule: |
IF the goal is to solve a(bx + c) = d THEN rewrite this as bx + c = d/a |
|
Rule: |
IF the goal is to solve a(bx + c) = d THEN rewrite this as abx + ac = d |
|
Bug rule: |
IF the goal is to solve a(bx + c) = d THEN rewrite this as abx + c = d |
The cognitive model consists of many rules—some correct and some flawed—and their inclusion is based on empirical studies of student performance on a wide range of algebra problems. As the student is working, the tutor uses two techniques to monitor his or her activities: model tracing and knowledge tracing. Model tracing is used to monitor the student’s progress through a problem (Anderson et al., 1990). This tracing is done in the background by matching student actions to those the cognitive model might generate; the tutor is mostly silent through this process. However, when the student asks for help, the tutor has an estimate of where he or she is and can provide hints that are tailored to that student’s particular approach to the problem. Knowledge tracing is used to monitor students’ learning from problem to problem (Corbett and Anderson, 1992). A Bayesian estimation procedure, of the type described in Chapter 4, identifies students’ strengths and weaknesses by seeking a match against a subset of the production rules in the cognitive model that best captures what a student knows at that point in time. This information is used to individualize problem selection and pace students optimally through the curriculum.
Facet-Based Instruction and Assessment
The Facets program provides an example of how student performance can be described at a medium level of detail that emphasizes the progression or development toward competence and is highly useful for classroom assessment (Hunt and Minstrell, 1994; Minstrell, 2000). Developed through collaboration between Jim Minstrell (an experienced high school science teacher) and Earl Hunt (a cognitive psychologist), the assessment approach
is based on models of learning termed facets of student thinking. The approach is predicated on the cognitive principle that students come to instruction with initial ideas and preconceptions that the teacher should identify and build on.
The term facets refers to pieces of knowledge or reasoning, processes, beliefs, or constructions of pieces of knowledge that serve as a convenient unit of thought for analysis of student behavior. In many ways they behave like general rules that students have in their knowledge base about how the world works. Facets are derived from research and from teachers’ observations of student learning. For instance, students in introductory physics classes often enter instruction with the belief (or facet) that air pressure has something to do with weight, since air presses down on objects. Another widely held facet is that if two bodies of different sizes and speeds collide, larger, faster bodies exert more force than do smaller, slower bodies. Whereas neither of these facets is consistent with actual physical principles, both are roughly satisfactory explanations for understanding a variety of situations. Facets are gathered in three ways: by examining relevant research when it exists, by consulting experienced teachers, and by examining student responses to open-ended questions intended to reveal the students’ initial ideas about a topic.
Facet clusters are sets of related facets, grouped around a physical situation, such as forces on interacting objects, or some conceptual idea, such as the meaning of average velocity. Within the cluster, facets are sequenced in an approximate order of development, and for recording purposes they are numerically coded. Those ending with 0 or 1 in the units digit tend to be appropriate, acceptable understandings for introductory physics; those ending in 9, 8, or 7 are more problematic facets that should be targeted with remedial instruction. An example of a facets cluster is presented in Box 5–3 (another example was presented earlier in Box 3–10).
Starting with a model of learning expressed in terms of facets, Minstrell and Hunt have carefully crafted assessment tasks and scoring procedures to provide evidence of which facets a student is likely to be using (illustrated later in this chapter).
Middle School Math Through Applications Project
Greeno and colleagues have designed curriculum and assessment practices based on situative theories of cognition and learning (see Chapter 3) (Cole, Coffey, and Goldman, 1999; Greeno, 1991). From a situative perspective, one who knows mathematics is able to participate successfully in the mathematical practices that prevail in one or more of the communities where mathematical knowledge is developed, used, or simply valued. Learning mathematics is a process of becoming more effective, responsible, and au-
|
BOX 5–3 Sample Facets Cluster: Separating Medium Effects from Gravitational Effects A common goal of an introductory physics course is for students to understand the nature of gravity and its effects, as well as the effects of ambient, fluid mediums (e.g., air or water) on objects they contain, whether the objects are at rest or moving them. Below is a facets cluster that corresponds to this domain of understanding. It lays out the pieces of knowledge that studies of learners have shown students apply as they attempt to make sense of such phenomena. The facets of student thinking are ordered along a continuum, from correct to problematic understandings.
|
thoritative in the ways in which an individual participates in mathematical practices. Through participation in a community, such as through interactions with other learners and people who use mathematics in their work and everyday lives, individuals develop identities as learners and knowers of mathematics (Greeno and The Middle-School Mathematics Through Applications Group, 1997).
The Middle School Mathematics Through Applications Program is a collaboration of curriculum developers, teachers, and researchers. They have developed software and print curriculum that present mathematics mainly as a resource for a variety of design activities. They have also developed curriculum-embedded assessment activities.
|
||||||||||||||||||||||||||||||
For example, to assess student learning as part of a seventh-grade unit called the Antarctica Project, students work in groups to design a research station for scientists. Self- and peer-assessment strategies are used. Students are asked to continually consider and discuss four general questions while they work on classroom projects: What are we learning? What is quality work? To whom do we hold ourselves accountable? and How do we use assessment tools to learn more? Assessment activities include journal writing, group design of scoring rubrics (or criteria), and group presentations followed by peer critiques based on the rubrics. The group conversations that define the rubric, together with peer and self-evaluation of how a particular piece of work fares against that rubric, create a shared vocabulary and standards for quality work (Cole, Coffey, and Goldman, 1999).
Australia’s Developmental Assessment
The Australian Council for Educational Research has developed the Developmental Assessment program, which is being used in several states in Australia. As discussed and illustrated in Chapter 4, central to the program are models of learning known as progress maps, intended to serve as a basis for the design of both large-scale and classroom assessments. Progress maps provide a description of skills, understandings, and knowledge in the sequence in which they typically develop—a picture of what it means to improve over time in an area of learning. Australia’s Developmental Assessment is used as an example throughout this report, not because the progress maps are particularly reflective of recent advances in cognitive research, but because the Developmental Assessment approach represents a notable attempt to measure growth in competence and to convey the nature of student achievement in ways that can benefit teaching and learning.
These maps can serve as the basis for assessments for both large-scale and classroom purposes. “Progress is monitored in much the same way as a child’s physical growth is monitored: from time to time an estimate is made of a student’s location on a developmental continuum, and changes in location provide measures of growth over time” (Masters and Forster, 1996, p. 1). Progress maps have been developed for a variety of areas of the curriculum, and several states in Australia use them as a basis for reporting assessment results back to schools and parents (Meiers and Culican, 2000). Box 5–4 presents a sample progress map for counting and ordering (for additional examples of progress maps see Chapter 4).
The progress maps are based on a combination of expert experience and research. Developers talked with teachers and curriculum experts about what kinds of understandings they typically see in children by the end of particular grade levels. They also reviewed available research on learning in the subject domain. Once an initial map had been drafted, it was validated or tested. Teachers were interviewed and probed about whether the map was consistent with their experience and whether it covered the kinds of skills and understandings they viewed as important in the domain.
In addition, more empirical evidence was often collected by constructing tasks designed to tap specific performances on the map, having students respond, analyzing the responses, and looking at whether the statistical analyses produced patterns of performance consistent with the progressions on the maps. Areas of discrepancy were pointed out to the developers so they could refine the maps. This process is a good example of the assessment triangle at work: the process moves back and forth between the cognition, observation, and interpretation corners of the triangle so that each informs the others.
|
BOX 5–4 Progress Map for Counting and Ordering Following (below and on the next two pages) is the lower portion of a counting and ordering progress map. The map shows examples of knowledge, skills, and understandings in the sequence in which they are generally expected to develop from grades one through five. This type of map is useful for tracking the progress of an individual child over time. An evaluation using tasks designed to tap specific performances on the map can provide a “snapshot” showing where a student is located on the map, and a series of such evaluations is useful for assessing a student’s progress over the course of several years.
|
|
THE DESIGN OF OBSERVATIONAL SITUATIONS
Once the purpose for an assessment, the underlying model of cognition in the domain, and the desired types of inferences to be drawn from the results have been specified, observational situations must be designed for collecting evidence to support the targets of inference. This design phase includes the development of tasks and procedures for evaluating students’ responses, the construction of sets of tasks, and the assembly of an assessment instrument. These processes involve both reflection and empirical observation, and require several iterations of the steps described below.
In addition to starting with a model of learning for the subject domain, assessment design should be led by the interpretation element of the assessment triangle, which guides how information from the assessment tasks will be filtered and combined to produce results (that is, how observations will be transformed into measurements). A central message of this report is that
|
||||||||
the interpretation model must be consistent with the underlying model of learning. While there are a variety of ways of achieving this consistency (see Chapter 4), it frequently is not achieved in current practice.
Task Design Guided by Cognitive and Measurement Principles
Many people consider the designing of assessment tasks to be an art. But to produce high-quality information for educational decision making, a more scientific and principled approach is needed. Only through such an approach is it possible to design tasks that precisely tap the intended aspects of learning and provide evidence that can lead to valid, fair, and useful inferences.
Messick (1994) distinguishes between a task-centered and a construct-centered approach to assessment design, the latter being the approach espoused here. With a task-centered approach, the focus is on having students perform meaningful and important tasks, and the target of inference is, implicitly, the tendency to do well on those tasks. Such an approach makes sense under certain circumstances, such as an arts contest or figure-skating competition, when evaluation of the product or performance per se is the focus. But educational decision makers are rarely concerned with one particular performance. They tend to be more interested in the underlying competencies that enable performance on a task, as well as on a range of related activities. In such cases, a construct-centered approach is needed. Such an approach starts with identifying the knowledge, skills, or other attributes that should be assessed (expressed through the model of learning), which then guide the selection or construction of relevant tasks and scoring procedures. Messick notes that the movement toward performance assessment in the last decade has often been task-centered, with an emphasis on creating assessment tasks that are “authentic” and representative of important activities students should be able to perform, but without specification of the underlying constructs that are the targets of inference. Simply because a task is “authentic” does not mean it is a valid observation of a particular construct (Baker, 1997).
A related point is that design should focus on the cognitive demands of tasks (the mental processes required for successful performance), rather than primarily on surface features, such as how tasks are presented to students or the format in which students are asked to respond. For instance, it is commonly believed that multiple-choice items are limited to assessing low-level processes such as recall of facts, whereas performance tasks elicit more complex cognitive processes. However, the relationship between item format and cognitive demands is not so straightforward. Although multiple-choice items are often used to measure low-level skills, a variety of item formats, including carefully constructed multiple-choice questions, can in fact tap complex cognitive processes (as illustrated later in Box 5–7). Similarly, performance tasks, usually intended to assess higher-level cognitive processes, may inadvertently tap low-level ones (Baxter and Glaser, 1998; Hamilton, Nussbaum, and Snow, 1997; Linn, Baker, and Dunbar, 1991).
Linking tasks to the model of cognition and learning forces attention to a central principle of task design—that tasks should emphasize those features relevant to the construct being measured and minimize extraneous features (AERA et al., 1999; Messick, 1993). This means that ideally, a task will not measure aspects of cognition that are irrelevant to the targeted performance. For instance, when assessing students’ mathematical reasoning, one should avoid presenting problems in contexts that might be unfamiliar to a particular population of students. Similarly, mathematics tasks should
not make heavy demands for reading or writing unless one is explicitly aiming to assess students’ abilities to read or communicate about mathematics. Thus surface features of tasks do need to be considered to the extent that they affect or change the cognitive demands of the tasks in unintended ways.
Ideally, task difficulty should be explained in terms of the underlying knowledge and cognitive processes required, rather than simply in terms of statistical item difficulty indices, such as the proportion of respondents answering the item correctly. Beyond knowing that 80 percent of students answered a particular item incorrectly, it would be educationally useful to know why so many did so, that is, to identify the sources of the difficulty so they could be remedied (assuming, of course, that they represented important construct-relevant variance). Cognitive theory and analysis can be helpful here.
For instance, one cognitive principle emphasized in Chapter 3 is that tasks in which children are asked to apply their knowledge in novel situations tend to be more difficult than those in which children apply what they have learned in the context in which they learned it. Similarly, research shows that a mathematics word problem that describes the combining of quantities and seeks the resultant total (e.g., John has 3 marbles and Mary has 5, How many do they have altogether?) is easier to comprehend than one that describes the same actors but expresses a comparison of their respective quantities (e.g., John has 3 marbles. He has 2 less than Mary. How many does she have?). Although the solution to both problems is to add the quantities, the success rate on the first problem is much higher than on the second (Riley and Greeno, 1988). Part of the difficulty for children is the conflict between the relational expression less than, which implies subtraction, and the operation required, which involves addition. No such conflict arises for the first problem, in which the expression clearly implies addition. Cognitive research also shows that in comprehending a portion of narrative or expository text, inferring why an event occurred is more difficult if the causes are widely dispersed in the text and relatively remote from the description of the resultant event (Lorch and van den Broek, 1997).
The point is not that such sources of difficulty should necessarily be avoided. Rather, these kinds of cognitive complexities should be introduced into the assessment tasks in principled ways only in those cases in which one wants to draw inferences about whether students can handle them. For instance, there are many reasons why educators might want to assess students’ abilities to apply integrated sets of skills (e.g., literacy and mathematics capabilities) to complex problems. That is entirely consistent with the approach being set forth here as long as assessment design begins with a model of learning that describes the complex of skills, understandings, and communicative practices about which one is interested in drawing infer-
ences, and tasks are specifically designed to provide evidence to support those inferences.
The most commonly used statistical measures of task difficulty ignore the fact that two tasks with similar surface features can be equally difficult, but for different reasons. For example, two language tasks that require combined reading and writing skills may exhibit the same overall level of difficulty according to the statistical item parameters, even though one task places greater demands on compositional skills and the other on reading comprehension.
There has been some exploration of the cognitive demands of achievement tasks in semantically rich domains, including Marshall’s (1995) work on assessing students’ schemas for story problems and White and Frederiksen’s (1998) exploration of levels of understanding of electrical circuits. As described in Chapter 4, several existing measurement models are able to incorporate and analyze aspects of item difficulty. Yet while some of these models have been available for several years, their use in mainstream assessment has been infrequent (e.g., Wilson and Wang, 1995).
It would also be educationally useful to analyze the difficulty of an assessment task in terms of which students get it wrong, and why it is so problematic for those students. Part of the answer might lie in differences in the communicative practices students bring to the assessment. Some researchers have used the differential item functioning methods described in Chapter 4 to help study such issues.
No existing assessment examples embody all of the principles set forth above. However, some assessments have begun to approximate certain of these features. The following is an example of an assessment composed of tasks that were designed to correspond directly to a model of learning.
Example: Number Knowledge Test
The Number Knowledge Test (Griffin and Case, 1997), presented in Box 5–5, was originally designed by Case and Griffin as a research tool to test out their theory about the development of children’s central conceptual structures for whole numbers (see Box 5–1). Over the past decade, the test has increasingly been used in the United States and Canada as an educational diagnostic tool to determine most appropriate next steps for arithmetic instruction.
Referring back to the model of learning presented in Box 5–1, items at the 4-year-old level, which are presented to students with physical objects, provide evidence of whether children have acquired the initial counting schema. Items at the 6-year-old level, presented without physical objects, assess whether children have acquired the “mental counting line” structure. Items at the 8-year-old level assess whether children have acquired the “double
mental counting line” structure. Finally, items at the 10-year-old level indicate whether children can handle double- and triple-digit numbers in a more fully integrated fashion.
The teacher administers the test orally and individually to children. The few items included at each age level yield a wealth of information about children’s developing understanding. Testing stops when a child does not pass a sufficient number of items to go on to the next level. This is an example of a set of questions for which the interpretation of responses is relatively simple. The strength of the assessment derives from the underlying model of cognition and learning.
The researchers have found that although many teachers express some hesitation about having to administer and score an individual oral test, they usually end up feeling that it was not as difficult as they had feared and that the results are highly worthwhile. Teachers report that the experience reveals differences in children’s thinking that they had not previously noticed, prompts them to listen more actively to each child in their class, and gives them a sense of what developmental instruction entails (Griffin and Case, 1997).
Evaluation of Student Responses
The observation corner of the assessment triangle includes tasks for eliciting student performance in combination with scoring criteria and procedures, or other methods for evaluating student responses to the tasks. For convenience, we often refer to this process simply as “scoring,” while recognizing that in many cases student responses might be evaluated using other means, such as informal evaluation by the teacher during class discussion.
Tasks and the procedures to be used for drawing the relevant evidence from students’ responses to those tasks must be considered together. That is, the ways in which student responses will be scored should be conceptualized during the design of a task. A task may stimulate creative thinking or problem solving, but such rich information will be lost unless the means used to interpret the responses capture the evidence needed to draw inferences about those processes. Like tasks, scoring methods must be carefully constructed to be sensitive to critical differences in levels and types of student understanding identified by the model of learning. At times one may be interested in the quantity of facts a student has learned, for instance, when one is measuring mastery of the alphabet or multiplication table. However, a cognitive approach generally implies that when evaluating students’ responses, the focus should be on the quality or nature of their understanding, rather than simply the quantity of information produced. In many cases, quality can be modeled quantitatively; that is, even in highly qualitative contexts, ideas of order and orderliness will be present (see also Chapter 4).
|
BOX 5–5 Number Knowledge Test Below are the 4-, 6-, 8-, and 10-year-old sections of the Number Knowledge Test. Preliminary Let’s see if you can count from 1 to 10. Go ahead. Level 0 (4-year-old level): Go to Level 1 if 3 or more correct
Level 1 (6-year-old level): Go to Level 2 if 5 or more correct
4a. Which is bigger: 5 or 4? 4b. Which is bigger: 7 or 9? 5a. (This time, I’m going to ask you about smaller numbers.) Which is smaller: 8 or 6? 5b. Which is smaller: 5 or 7? 6a. (Show visual array.) Which number is closer to 5:6 or 2? 6b. (Show visual array.) Which number is closer to 7:4 or 9?
9a. (Show visual array—8, 5, 2, 6—ask child to point to and name each numeral.) When you are counting, which of these numbers do you say first? 9b. When you are counting, which of these numbers do you say last? |
|
Level 2 (8-year-old level): Go to Level 3 if 5 or more correct
3a. Which is bigger: 69 or 71? 3b. Which is bigger: 32 or 28? 4a. (This time I’m going to ask you about smaller numbers.) Which is smaller: 27 or 32? 4b. Which is smaller: 51 or 39? 5a. (Show visual array.) Which number is closer to 21:25 or 18? 5b. (Show visual array.) Which number is closer to 28:31 or 24?
Level 3 (10-year-old level): Go to Level 4 if 4 or more correct
3a. Which difference is bigger: the difference between 9 and 6 or the difference between 8 and 3? 3b. Which difference is bigger: the difference between 6 and 2 or the difference between 8 and 5? 4a. Which difference is smaller: the difference between 99 and 92 or the difference between 25 and 11? 4b. Which difference is smaller: the difference between 48 and 36 or the difference between 84 and 73?
SOURCE: Griffin and Case (1997, pp. 12–13). Used with permission of the authors. |
Silver, Alacaci, and Stylianou (2000) have demonstrated some limitations of scoring methods used by the National Assessment of Educational Progress (NAEP) for capturing the complexities of learning. They reanalyzed a sample of written responses to an NAEP item that asked students to compare two geometric figures and found important differences in the quality of the reasoning demonstrated: some students showed surface-level reasoning (paying attention to the appearance of the figures), others showed analytic reasoning (paying attention to geometric features), and still others demonstrated more sophisticated reasoning (looking at class membership). Despite these qualitative differences, however, the NAEP report simply indicated that 11 percent of students gave satisfactory or better responses—defined as providing at least two reasons why the shapes were alike or different—while revealing little about the nature of the students’ understanding. Whereas the current simple NAEP scoring strategy makes it relatively easy to control variation among raters who are scoring students’ responses, much other information that could have educational value is lost. Needed are enhanced scoring procedures for large-scale assessments that capture more of the complexity of student thinking while still maintaining reliability. When the scoring strategy is based on a strong theory of learning, the interpretation model can exploit the extra information the theory provides to produce a more complex and rich interpretation, such as those presented in Chapter 4.
Task Sets and Assembly of an Assessment Instrument
An assessment should be more than a collection of items that work well individually. The utility of assessment information can be enhanced by carefully selecting tasks and combining the information from those tasks to provide evidence about the nature of student understanding. Sets of tasks should be constructed and selected to discriminate among different levels and kinds of understanding that are identified in the model of learning. To illustrate this point simply, it takes more than one item or a collection of unrelated items to diagnose a procedural error in subtraction. If a student answers three of five separate subtraction questions incorrectly, one can infer only that the student is using some faulty process(es), but a carefully crafted collection of items can be designed to pinpoint the limited concepts or flawed rules the student is using.
In Box 5–6, a typical collection of items designed to work independently to assess a student’s general understanding of subtraction is contrasted with a set of tasks designed to work together to diagnose the common types of subtraction errors presented earlier in Box 5–2. As this example shows, significantly more useful information is gained in the latter case that can be used to provide the student with feedback and determine next steps for instruction. (A similar example of how sets of items can be used to diagnose
|
BOX 5–6 Using Sets of Items to Diagnose Subtraction Bugs The traditional testing approach is to present students with a sample of independent or disconnected items that tap the same general set of skills in order to obtain a reliable estimate of students’ abilities to solve such problems. Thus to assess a student’s understanding of multidigit subtraction, items such as the following might be used: 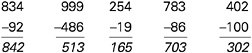 In this case, the student answered three of the five problems incorrectly (the first, third, and fourth items from the left). Typically, the number of correct answers would be summed, and the student would receive a score of 40 percent correct; from this evidence it might be inferred that the student has a poor understanding of subtraction. In contrast, consider the information gained from the following set of five items (Siegler, 1998, p. 294) that are linked to the theory of subtraction errors (Brown and Burton, 1978) presented in Box 5–2. 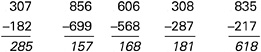 Here the pattern of errors (the first, third, and fourth problems from the left) and the particular answers given suggest the existence of two bugs. First, whenever a problem required subtraction from zero, the student simply flipped the two numbers in the column with the zero. For example, in the problem 307–182, the student treated 0–8 as 8–0 and wrote 8 as the answer. The second bug involved not decrementing the number to the left of the zero (e.g, not reducing the 3 to 2 in 307–182). This lack of decrementing is not surprising because, as indicated by the first bug, the student did not borrow anything from this column. Thus, this particular pattern of correct and incorrect responses can be explained by positing a basically correct subtraction procedure with two particular bugs. Note that in both the traditional and cognitive research-based examples shown here, the student answered three problems incorrectly and two correctly. However, the interpretations afforded by the two approaches are qualitatively quite different. |
student understandings is provided by the balance-scale problems presented in Boxes 2–1, 2–2, and 2–3 in Chapter 2.)
When using such an approach, however, measurement issues arise that must be addressed by the interpretation element of the assessment triangle. Making sense of students’ responses to patterns of items requires an interpretation model that can handle the added complexity. Statistical and informal interpretation models not only serve to make sense of the data after the assessment has been administered, but also play a crucial role in selecting the optimal set of items to include so that one can differentiate among profiles of understanding on the basis of pilot test data. Interpretation models tell the assessment designer how much and what types of tasks and evidence are needed to support the desired inferences and at what point additional assessment tasks will provide unnecessarily redundant information.
The interpretation model also serves as the “glue” that holds together the information gleaned from the items and transforms it into interpretable results. Traditional classical and item response models (as discussed in Chapter 4) would not allow for the diagnostic interpretation afforded by the second set of problems in Box 5–6. But some of the more complex models discussed in Chapter 4 could be used to exploit the model of learning for subtraction to produce a richer interpretation. The validity of these richer interpretations depends on the correctness of the model of learning for the situation at hand, and hence will be somewhat less robust than an interpretation based on the simpler measurement methods. On the other hand, the richer interpretations afforded by the more complex measurement methods and underlying cognitive theory offer hope for making assessments much more educationally useful.
We now return to the Facets program to illustrate how the cognitive and interpretation elements guide the design of observations (tasks, scoring, and sets of tasks) that make it possible to collect instructionally useful information about a student’s understanding.
Example: Facets-Based Assessment
The Facets instructional program begins with various facet clusters (model of learning) of the type shown earlier in Box 5–3. Teachers can use the facet clusters as the basis for crafting questions to initiate class discussion of a topic or to develop a preinstruction quiz. Minstrell (2000) describes one such quiz that he has used to start a physics unit on separating effects of gravity from effects of the ambient medium. In the quiz, students are asked a question carefully designed to provide evidence of facets of student thinking on this topic.
First, suppose we weigh some object on a large spring scale, not unlike the ones we have at the local market. The object apparently weighs 10
pounds, according to the scale. Now we put the same apparatus, scale, object and all, under a very large glass dome, seal the system around the edges, and pump out all the air. That is, we use a vacuum pump to allow all the air to escape out from under the glass dome. What will the scale reading be now? Answer as precisely as you can at this point in time, [pause] And in the space provided, briefly explain how you decided, (p. 50)
Students write their answers and rationales. From their words a facet diagnosis can be made relatively easily using the facets continuum as a scoring guide for locating student understanding. Students who give an answer of zero pounds for the scale reading in a vacuum usually are thinking that air only presses down, and “without air there would be no weight, like in space” (Facet 319). Other students suggest a number “a little less than 10” because “air is very light, so it doesn’t press down very hard, but does press down some, thus, taking the air away will only decrease the scale reading slightly” (Facet 318). Other students suggest there will be no change at all: “Air has absolutely no effect on scale reading.” The explanation could convey a belief that media do not exert any force or pressure on objects in them (Facet 314), or that fluid pressures on the top and bottom of an object are equal (Facet 315). A few students suggest that while there are pressures from above and below, there is a net upward pressure by the fluid: “There is a slight buoyant force” (Facet 310, an acceptable workable idea at this point).
The numbering scheme for the facets enables the teacher to do more than simply mark the answers “right” or “wrong.” When data are coded, the teacher or researcher can scan the class results to identify dominant targets for the focus of instruction, and movement along the continuum from highto low-numbered facets indicates growth.
Multiple-choice questions have also been designed to identify facets of student thinking by having each of the answer choices map back to a particular facet. That is, each “wrong” answer represents a particular naive or unformed conception, while the “right” answer indicates the goal of instruction. In fact, the computerized DIAGNOSER, designed to facilitate facet-based instruction, relies entirely on multiple-choice questions of the sort shown in Box 5–7.
The Facets program also provides an example of how sets of items can be used to diagnose characteristics of student understanding. The set of questions in Box 5–7 was developed to determine whether students’ knowledge is organized theoretically in a coordinated, internally consistent manner, or students have a more fragmentary knowledge-in-pieces understanding. Minstrell (Minstrell, 1992; Minstrell, Stimpson, and Hunt, 1992) gave these questions to 60 students at the end of a high school introductory physics course and developed an informal interpretation model. He determined beforehand that students answering in the pattern of line 1 could be characterized as taking a Newtonian perspective; this ended up being true of
|
BOX 5–7 Use of Multiple-Choice Questions to Test for Theoretical vs. Knowledge-in-Pieces Perspective Problem: In the following situation, two identical steel marbles M1 and M2 are to be launched horizontally off their respective tracks. They each leave the ends of their respective tracks at the same time, but M2 will leave its track travelling twice as fast as M1. The track for M1 can be set at any height in relation to M2.
Now, suppose we have set the track for M1 at an appropriate height so that the marbles will collide in the space between and below the two tracks.
[A for horizontal component in the forward direction] [B for no horizontal component in the forward direction]
Briefly justify your answer.
Briefly justify your answer. |
7 of the 60 students. Students taking an Aristotelian or novice perspective would show the pattern of line 17 (1 student). The rest of the combinations reflect a knowledge-in-pieces understanding. Note that across the four questions, 81 (3 × 3 × 3 × 3) response combinations would have been possible, but students tended to produce certain patterns of responses. For example, line 10 shows that 10 students apparently understood the independence of horizontal and vertical motions (problem parts a and d) without understanding the forces on projectiles (part b) or forces during collisions (part c). (The list of answer combinations in Box 5–7 is not meant to imply a linear progression from novice to Newtonian). Such profiles of student understanding are more instructionally useful than simply knowing that a student answered some combination of half of the test questions correctly.
On a single physics assessment, one could imagine having many such sets of items corresponding to different facet clusters. Interpretation issues could potentially be addressed with the sorts of measurement models presented in Chapter 4. For instance, how many bundles of items are needed for reliable diagnosis? And could the utility of the information produced be enhanced by developing interpretation models that could generate profiles of student performance across numerous topics (facet clusters)? Doing so would require not only cognitive descriptions of developing competence within a topic, but also a model of how various topics are related and which topics are more difficult or build on earlier ones. A statistical interpretation model could articulate these aspects of learning and also help determine how many and which items should be included on the test to optimize the reliability of the inferences drawn.
TASK VALIDATION
Once a preliminary set of tasks and corresponding scoring rubrics have been developed, evidence of their validity must be collected. Traditionally, validity concerns associated with achievement tests have tended to center around test content, that is, the degree to which the test samples the subject matter domain about which inferences are to be drawn. Evidence is typically collected through expert appraisal of the alignment between the content of the assessment tasks and the subject matter framework (e.g., curriculum standards). Sometimes an empirical approach to validation is used, whereby items are included in a test on the basis of data. Test items might be selected primarily according to their empirical relationship with an external criterion, their relationship with one another, or their power to differentiate among groups of individuals. Under such circumstances, it is likely that the selection of some items will be based on chance occurrences in the data (AERA et al., 1999).
There is increasing recognition within the assessment community that traditional forms of validation emphasizing consistency with other measures, as well as the search for indirect indicators that can show this consistency statistically, should be supplemented with evidence of the cognitive or substantive aspect of validity (e.g., Linn et al., 1991; Messick, 1993). That is, the trustworthiness of the interpretation of test scores should rest in part on empirical evidence that the assessment tasks actually tap the intended cognitive processes.
Situative and sociocultural research on learning (see Chapter 3) suggests that validation should be taken a step further. This body of research emphasizes that cognitive processes are embedded in social practices. From this perspective, the performance of students on tests is understood as an activity in the situation presented by the test and success depends on ability to participate in the practices of test taking (Greeno, Pearson, and Schoenfeld, 1996). It follows that validation should include the collection of evidence that test takers have the communicative practices required for their responses to be actual indicators of such abilities as understanding and reasoning. The assumption that students have the necessary communicative skills has been demonstrated to be false in many cases. For instance, Cole, Gay, and Glick (1968) conducted research in Liberia in which they assessed various cognitive capabilities, such as conservation and classification. From a standard assessment perspective, the Liberian test takers appeared to lack the skills being tested. But when assessments were designed that made sense in their practices, a much more positive picture of their competencies emerged.
Approaches to Task Validation
As described by Messick (1993) and summarized by Magone, Cai, Silver and Wang (1994), a variety of techniques can be used to examine the processes examinees use during task performance to evaluate whether prospective items are functioning as intended. One such method is protocol analysis, in which students are asked to think aloud as they solve problems or to describe retrospectively how they solved the problems (see Ericsson and Simon, 1984). Another method is analysis of reasons, in which students are asked to provide rationales for their responses to the tasks. A third method is analysis of errors, in which one draws inferences about processes from incorrect procedures, concepts, or representations of the problems. All of these methods were described earlier in Chapter 3 as part of the scientific reasoning process used by researchers to develop and test theories of the knowledge and processes underlying performance on cognitive tasks.
Baxter and Glaser (1998) used some of these techniques to examine how well test developers’ intentions are realized in performance assessments that purport to measure complex cognitive processes. They devel-
oped a simple framework, a content-process space that depicts tasks’ demands for content knowledge as lying on a continuum from rich to lean. At one extreme are knowledge-rich tasks that require in-depth understanding of subject matter topics; at the other extreme are tasks that depend not on prior knowledge or experience but on information given in the assessment situation. Similarly, tasks’ demands for process skills are arrayed on a continuum from constrained to open. Assessment tasks can involve many possible combinations of content knowledge and process skills. Analyzing a diverse range of science assessments from state and district testing programs, Baxter and Glaser found matches and mismatches between the intentions of test developers and what the tasks actually measured, and varying degrees of correspondence between observed cognitive activity and performance scores. Box 5–8 provides an example of a concept mapping task that was found to overestimate quality of understanding.
In another study, Hamilton et al. (1997) investigated the usefulness of small-scale interview studies as a means of exploring the validity of both multiple-choice and performance-based science achievement tests. Interviews illuminated unanticipated cognitive processes used by test takers. One finding was the importance of distinguishing between the demands of open-ended tasks and the opportunities such tasks provide students. Some open-ended tasks enabled students to reason scientifically but did not explicitly require them to do so. If a task did not explicitly require scientific reasoning, students often chose to construct answers using everyday concepts and language. More-structured multiple-choice items, in contrast, did not offer students this choice and forced them to attend to the scientific principles. Clarifying the directions and stems of the open-ended tasks helped resolve these ambiguities.
Though the research studies described above analyzed tasks after they had already been administered as part of a large-scale assessment, the researchers concluded that cognitive task analysis should not be an after-thought, done only to make sense of the data after the test has been developed and administered to large numbers of students. Rather, such analyses should be an integral part of the test development process to ensure that instructions are clear and that tasks and associated scoring rubrics are functioning as intended. Some developers of large-scale assessments are beginning to heed this advice. For example, as part of the development of the Voluntary National Test, the contractor, American Institutes for Research, used cognitive laboratories to gauge whether students were responding to the items in ways the developers intended. The laboratories were intended to improve the quality of the items in two ways: by providing specific information about items, and by making it possible to generalize the findings to evaluate the quality of other items not tried out in the laboratories (NRC, 1999a).
It should be noted that exploring validity in the ways suggested here could also enhance the quality of informal assessments used in the classroom, such as classroom questioning, and the kinds of assignments teachers give students in class and as homework. The formulation of tasks for class work calls for similar reflection on the cognitive basis and functions of the assignments. The next example describes the design of the QUASAR assessment, which included efforts to collect evidence of the cognitive validity of the assessment tasks. This example also illustrates several of the other features of design proposed in this chapter, such as the central role of a model of learning and the highly recursive nature of the design process, which continually refers back to the model of learning.
Example: QUASAR Cognitive Assessment Instrument
QUASAR is an instructional program developed by Silver and colleagues to improve mathematics instruction for middle school students in economically disadvantaged communities (Silver, Smith, and Nelson, 1995; Silver and Stein, 1996). To evaluate the impact of this program, which emphasizes the abilities to solve problems, reason, and communicate mathematically, assessments were needed that would tap the complex cognitive processes targeted by instruction. In response to this need, the QUASAR Cognitive Assessment Instrument was developed (Lane, 1993; Silver and Lane, 1993).
Assessment design began with the development of a model of learning. Using the Curriculum and Evaluation Standards for School Mathematics (National Council of Teachers of Mathematics, 1989), augmented with findings from cognitive research, the assessment developers specified a number of cognitive processes important to competent performance in the domain: understanding and representing problems; discerning mathematical relations; organizing information; using and discovering strategies, heuristics, and procedures; formulating conjectures; evaluating the reasonableness of answers; generalizing results; justifying an answer or procedures; and communicating. These processes were defined more specifically in each of the content categories covered by the assessment: number and operations; estimation; patterns; algebra, geometry, and measurement; and data analysis, probability, and statistics. Specifications of the targeted content and processes served as the basis for developing preliminary tasks and scoring rubrics that would provide evidence of those processes.
Preliminary tasks were judged by a team of internal reviewers familiar with the QUASAR goals and the curricular and instructional approaches being used across different school sites. After internal review involving much group discussion, tasks were revised and pilot tested with samples of students. In addition to collecting students’ written responses to the tasks, some students were interviewed individually. A student was asked to “think aloud”
|
BOX 5–8 Cognitive Complexity of Science Tasks Baxter and Glaser (1998) studied matches and mismatches between the intentions of test developers and the nature of cognitive activity elicited in an assessment situation. The Connecticut Common Core of Learning Assessment Project developed a number of content-rich, process-constrained tasks around major topics in science. Baxter and Glaser analyzed a task that asked high school students to write an explanation in response to the following: “For what would you want your blood checked if you were having a transfusion?” (Lomask, Baron, Greig, and Harrison, 1992). Concept maps were developed for scoring student explanations. The expert’s (teacher’s) concept map below served as a template against which students’ performances were evaluated. 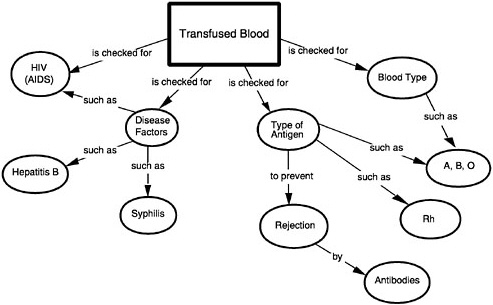 |
|
On the surface, concept maps appear to be an excellent way to showcase the differential quality of student responses for teachers and students because they explicitly attend to the organization and structure of knowledge. However, Baxter and Glaser found that an overestimate of students’ understanding stems from two features of the concept map: (1) the knowledge assumed, with half of the core concepts (e.g., HIV, disease, blood type) being learned in contexts outside science class, and (2) the relations among the concepts, 90 percent of which are at the level of examples or procedural links (such as, is checked for) rather than processes or underlying causal mechanisms. Unless proficient performance displayed by the concept map requires inferences or reasoning about subject matter relations or causal mechanisms reflective of principled knowledge, the concept map serves primarily as a checklist of words and misrepresents (overestimates in this case) students’ understanding. SOURCE: Lomask, Baron, Greig, and Harrison (1992, p. 27). Used with permission of the authors. |
as he or she completed the task, and also to elaborate retrospectively on certain aspects of the solution. Interviews were recorded, transcribed, and analyzed to determine whether the student had interpreted each task as intended and the task had elicited the intended processes.
The judgments of the internal reviewers, along with the pilot data, were used to answer a series of questions related to the quality of the tasks: Does the task assess the skill/content it was designed to assess? Does the task assess the high-level cognitive processes it was designed to assess? Does the task elicit different representations and strategies? What are they, and how often do they occur in the pilot data? If the task asks for an explanation, are the students providing high-level conceptual explanations? If the task requires students to show their work, are they complete in providing the steps involved in their solutions?
On the basis of the answers to these questions, a task was either discarded, revised and pilot tested again, or judged satisfactory and forwarded to the next stage of external review. External review was conducted by teams of outside expert mathematics educators, mathematicians, and psychometricians. This review served as a check on whether important mathematical content and processes were being assessed, and whether the tasks were free from bias and technically sound.
|
BOX 5–9 Revising Tasks The Pattern Task was designed to assess reasoning skills for identifying the underlying regularities of a figural pattern, using these regularities to extend the pattern, and communicating these regularities effectively. The following is the original version of this task: For homework, Allan’s teacher asked him to look at the pattern below and draw the figure that should come next.  Allan doesn’t know how to find the next figure. Write a description for Allan telling him which figure comes next. The pilot data showed that in response to this initial version, many students simply drew a fifth figure rather than providing a description of the pattern regularities, making it difficult to obtain a sense of their solution strategies. The task was therefore revised so it asked students to describe how they knew which figure comes next. This change increased |
The development process for the QUASAR Cognitive Assessment Instrument required continual interplay among the validation procedures of logical analysis, internal review, pilot testing, and external review. Sometimes a task would undergo several iterations of a subset of these procedures before it was considered ready for the next stage of development. An example is given in Box 5–9.
REPORTING OF ASSESSMENT RESULTS
Although reporting of results occurs at the end of an assessment cycle, assessments must be designed from the outset to ensure that reporting of the desired types of information will be possible. As emphasized at the beginning of this chapter, the purpose for the assessment and the kinds of inferences one wants to draw from the results should drive the design, including
|
the cognitive complexity of the students’ responses. On the basis of further pilot testing and expert review, the task was revised to its present form. For homework Miguel’s teacher asked him to look at the pattern below and draw the figure that should come next.  Miguel does not know how to find the next figure. A. Draw the next figure for Miguel. B. Write a description for Miguel telling him how you knew which figure comes next. SOURCE: Magone, Cai, Silver, and Wang (1994, p. 324). Reprinted with permission from Elsevier Science. |
the selection of an appropriate model of learning, the observations, and the interpretation model.
The familiar distinction between norm-referenced and criterion-referenced testing is salient in understanding the central role of a model of learning in the reporting of assessment results. Traditionally, achievement tests have been designed to provide results that compare students’ performance with that of other students. The results are usually norm-referenced since they compare student performance with that of a norm group (that is, a representative sample of students who took the same test). Such information is useful, just as height and weight data are informative when placed in the context of such data on other individuals. Comparative test information can help parents, teachers, and others determine whether students are progressing at the same rate as their peers or whether they are above or below the average. Norm-referenced data are limited, however, because they do not
show what a student actually can or cannot do. A score indicating that a student is in the 40th percentile in mathematics does not reveal what mathematics knowledge the student does or does not have. The student may have answered most items correctly if the norm group was high-performing, or may have answered many questions incorrectly if the norm group performed less well. Nor does the norm-referenced score indicate what a student needs to do to improve. In the 1960s, Glaser (1963) drew attention to the desirability of shifting to criterion-referenced testing so that a student’s performance would be reported in absolute terms, that is, in terms of what the student can or cannot do.
…the specific behaviors implied at each level of proficiency can be identified and used to describe the specific tasks a student must be capable of performing before he achieves one of these knowledge levels…. Measures which assess student achievement in terms of a criterion standard thus provide information as to the degree of competence attained by a particular student which is independent of reference to the performance of others, (pp. 519–520)
The notion of criterion-referenced testing has gained popularity in the last few decades, particularly with the advent of standards-based reforms in the 1990s. As a result of these reforms, many states are implementing tests designed to measure student performance against standards in core content areas. A number of states are combining these measures with more traditional norm-referenced reports to show how students’ performance compares with that of students from other states as well (Council of Chief State School Officers, 2000).
Because criterion-referenced interpretations depend so directly on a clear explication of what students can or cannot do, well-delineated descriptions of learning in the domain are key to their effectiveness in communicating about student performance. Test results should be reported in relation to a model of learning. The ways people learn the subject matter and different states of competence should be displayed and made as recognizable as possible to educators, students, and the public to foster discussion and shared understanding of what constitutes academic achievement. Some examples of enhanced reporting afforded by models of learning (e.g., progress maps) are presented in Chapter 4.
FAIRNESS
Fairness in testing is defined in many ways (see AERA et al., 1999; NRC, 1999b), but at its core is the idea of comparable validity: a fair test is one that yields comparably valid inferences from person to person and group to group. An assessment task is considered biased if construct-irrelevant characteristics of the task result in different meanings for different subgroups.
For example, it is now common wisdom that a task used to observe mathematical reasoning should include words and expressions in general use and not those associated with particular cultures or regions; the latter might result in a lack of comparable score meanings across groups of examinees.
Currently, bias tends to be identified through expert review of items. Such a finding is merely judgmental, however, and in and of itself may not warrant removal of items from an assessment. Also used are statistical differential item functioning (DIF) analyses, which identify items that produce differing results for members of particular groups after the groups have been matched in ability with regard to the attribute being measured (Holland and Thayer, 1988). However, DIF is a statistical finding and again may not warrant removal of items from an assessment. Some researchers have therefore begun to supplement existing bias-detection methods with cognitive analyses designed to uncover the reasons why items are functioning differently across groups in terms of how students think about and approach the problems (e.g., Lane, Wang, and Magone, 1996; Zwick and Ercikan, 1989).
A particular set of fairness issues involves the testing of students with disabilities. A substantial number of children who participate in assessments do so with accommodations intended to permit them to participate meaningfully. For instance, a student with a severe reading and writing disability might be able to take a chemistry test with the assistance of a computer-based reader and dictation system. Unfortunately, little evidence currently exists about the effects of various accommodations on the inferences one might wish to draw about the performance of individuals with disabilities (NRC, 1997), though some researchers have taken initial steps in studying these issues (Abedi, Hofstetter, and Baker, 2001). Therefore, cognitive analyses are also needed to gain insight into how accommodations affect task demands, as well as the validity of inferences drawn from test scores obtained under such circumstances.
In some situations, rather than aiming to design items that are culture-or background-free, a better option may be to take into account learner history in the interpretation of responses to the assessment. The distinction between conditional and unconditional inferences deserves attention because it may provide a key to resolving some of the thorniest issues in assessment today, including equity and student choice of tasks.
Conditional Versus Unconditional Inferences
To some extent in any assessment, given students of similar ability, what is relatively difficult for some students may be relatively easy for others, depending on the degree to which the tasks relate to the knowledge structures students have, each in their own way, constructed (Mislevy, 1996). From the traditional perspective, this is “noise,” or measurement error, and if
excessive leads to low reliability (see Chapter 4). For inferences concerning overall proficiency in this sense, tasks that do not rank individuals in the same order are less informative than ones that do.
Such interactions between tasks and prior knowledge are fully expected from modern perspectives on learning, however, since it is now known that knowledge typically develops first in context, then is extended and decontextualized so it can be applied more broadly to other contexts. An indepth project that dovetails with students’ prior knowledge provides solid information, but becomes a waste of time for students for whom this connection is lacking. The same task can therefore reveal either vital evidence or little at all, depending on the target of inference and the relationship of the information involved to what is known from other sources.
Current approaches to assessment, particularly large-scale testing, rely on unconditional interpretation of student responses. This means that evaluation or interpretation of student responses does not depend on any other information the evaluator might have about the background of the examinee. This approach works reasonably well when there is little unique interaction between students and tasks (less likely for assessments connected with instruction than for those external to the classroom) or when enough tasks can be administered to average over the interactions (thus the SAT has 200 items). The disadvantage of unconditional scoring is that it precludes saying different things about a student’s performance in light of other information that might be known about the student’s instructional history.
An alternative way to interpret evidence from students’ responses to tasks is referred to as conditional interpretation. Here the observer or scorer has additional background information about the student that affects the interpretation. This can be accomplished in one of three ways, each of which is illustrated using the example of all assessment of students’ understanding of control of variables in scientific experimentation (Chen and Klahr, 1999).
Example: Assessment of Control-of-Variables Strategy
In their study, Chen and Klahr (1999) exposed children to three levels of training in how to design simple unconfounded experiments. One group received explicit training and repeated probe questions. Another group received only probe questions and no direct training. Finally, the third group served as a control: they received equal exposure to the materials, but no instruction at all. Three different kinds of materials were used for subgroups of children in each training condition. Some children were initially exposed to ramps and balls, other to springs and weights, and still other to sinking objects.
Children in each training condition were subsequently assessed on how
well they could transfer their knowledge about the control-of-variables procedures. The three assessments were designed to be increasingly “distant” from the materials used during the training.
-
“Very near transfer”: This assessment was in the same domain as was the initial exposure (e.g., children trained on ramps were asked to design additional experiments using ramps).
-
“Near transfer”: In this assessment, children initially exposed to one domain (e.g., springs) were asked to design experiments in a different domain (e.g., ramps).
-
“Far transfer”: Here, children were presented with a task that was amenable to the same control-of-variables strategy but had different surface features (e.g., paper-and-pencil assessments of good and bad experimental designs in domains outside physics).
Two points are central to the present discussion:
-
The targets of assessment were three factors: tendency to subsequently use the control-of-variables strategy in the instructional context, in near-transfer contexts, and in far-transfer contexts. All the tasks were carefully designed to make it possible to determine whether a child used the strategy.
-
Whether a task was an example task, a near-transfer task, or a far-transfer task was not a property of the task, but of the match between the task and the student. Tasks were even counterbalanced within groups with regard to which was the teaching example and which was the near-transfer task.
The results of the study showed clear differences among groups across the different kinds of tasks: negligible differences on the repeat of the task on which a child had been instructed; a larger difference on the near-transfer task, favoring children who had been taught the strategy; and a difference again favoring these children on far-transfer tasks, which turned out to be difficult for almost all the children. What is important here is that no such pattern could have emerged if the researchers had simply administered the post test task to all students without knowing either the training that constituted the first half of the experiment or the match between each child’s post test task and the training he or she had received. The evidence is not in the task performance data, but in the evaluation of those data in light of other information the researchers possessed about the students.
Methods of Conditional Inference
The first method of conditional inference is that the observer influences the observational setting (the assessment task presented to the student) or the conditions that precede the observation in ways that ensure a certain task-examinee matchup. This method is demonstrated by the design of the control-of-variables study just described.
A second way to condition the extraction of information from student performances is to obtain relevant background information about students from which to infer key aspects of the matchups. In the Klahr et al. (in press) example, this approach would be appropriate if the researchers could only give randomly selected post-test tasks to students, but could try to use curriculum guides and teacher interviews to determine how each student’s post-test happened to correspond with his or her past instruction (if at all).
A third method is to let students choose among assessment tasks in light of what they know about themselves—their interests, their strengths, and their backgrounds. In the control-of-variables study, students might be shown several tasks and asked to solve one they encountered in instruction, one a great deal like it, and one quite dissimilar (making sure the student identified which was which). A complication here is that some students will likely be better at making such decisions than others.
The forms of conditional inference described above offer promise for tackling persisting issues of equity and fairness in large-scale assessment. Future assessments could be designed that take into account students’ opportunity to learn what is being tested. Similarly, such approaches could help address issues of curriculum fairness, that is, help protect against external assessments that favor one curriculum over another. Issues of opportunity to learn and the need for alignment among assessment, curriculum, and instruction are taken up further in Chapter 6.
CONCLUSIONS
The design of high-quality classroom and large-scale assessments is a complex process that involves numerous components best characterized as iterative and interdependent, rather than linear and sequential. A design decision made at a later stage can affect one occurring earlier in the process. As a result, assessment developers must often revisit their choices and refine their designs.
One of the main features that distinguishes the committee’s proposed approach to assessment design from current approaches is the central role of a model of cognition and learning, as emphasized above. This model may be fine-grained and very elaborate or more coarsely grained, depending on the purpose of the assessment, but it should always be based on empirical
studies of learners in a domain. Ideally, the model of learning will also provide a developmental perspective, showing typical ways in which learners progress toward competence.
Another essential feature of good assessment design is an interpretation model that fits the model of learning. Just as sophisticated interpretation techniques used with assessment tasks based on impoverished models of learning will produce limited information about student competence, assessments based on a contemporary and detailed understanding of how students learn will not yield all the information they otherwise might if the statistical tools available to interpret the data, or the data themselves, are not sufficient for the task. Observations, which include assessment tasks along with the criteria for evaluating students’ responses, must be carefully designed to elicit the knowledge and cognitive processes that the model of learning suggests are most important for competence in the domain. The interpretation model must incorporate this evidence in the results in a manner consistent with the model of learning.
Validation that tasks tap relevant knowledge and cognitive processes, often lacking in assessment development, is another essential aspect of the development effort. Starting with hypotheses about the cognitive demands of a task, a variety of research techniques, such as interviews, having students think aloud as they work problems, and analysis of errors, can be used to analyze the mental processes of examinees during task performance. Conducting such analyses early in the assessment development process can help ensure that assessments do, in fact, measure what they are intended to measure.
Well-delineated descriptions of learning in the domain are key to being able to communicate effectively about the nature of student performance. Although reporting of results occurs at the end of an assessment cycle, assessments must be designed from the outset to ensure that reporting of the desired types of information will be possible. The ways in which people learn the subject matter, as well as different types or levels of competence, should be displayed and made as recognizable as possible to educators, students, and the public.
Fairness is a key issue in educational assessment. One way of addressing fairness in assessment is to take into account examinees’ histories of instruction—or opportunities to learn the material being tested—when designing assessments and interpreting students’ responses. Ways of drawing such conditional inferences have been tried mainly on a small scale, but hold promise for tackling persistent issues of equity in testing.
Some examples of assessments that approximate the above features already exist. They are illustrative of the new approach to assessment the committee advocates, and they suggest principles for the design of new assessments that can better serve the goals of learning.
|
Four themes guide the discussion in this chapter of how advances in the cognitive sciences and new approaches to measurement have created opportunities, not yet fully realized, for assessments to be used in ways that better serve the goals of learning.
|












































