2
The Nature of Assessment and Reasoning from Evidence
PURPOSES OF ASSESSMENT
This report focuses on the assessment of school learning, also referred to as the assessment of school achievement. The assessment of achievement is often contrasted with the assessment of aptitude (ability), which has the purpose of predicting performance in some future situation. An example is the use of the SAT I to predict college performance. This type of assessment is not the focus of this report, although many of the theoretical underpinnings discussed here apply to assessments used for any purpose.
Assessments of school learning provide information to help educators, policy makers, students, and parents make decisions. The specific purposes for which an assessment will be used are an important consideration in all phases of its design. For example, assessments used by teachers in classrooms to assist learning may need to provide more detailed information than assessments whose results will be used by state policy makers. The following subsections address issues of purpose and use by examining three broad purposes served by assessments in classroom and large-scale contexts: assisting learning, measuring individual student achievement, and evaluating programs.
Assessment to Assist Learning
In the classroom context, effective teachers use various forms of assessment to inform day-to-day and month-to-month decisions about next steps for instruction, to give students feedback about their progress, and to motivate students. One familiar type of classroom assessment is a teacher-made quiz, but assessment also includes more informal methods for determining how students are progressing in their learning, such as classroom projects,
feedback from computer-assisted instruction, classroom observation, written work, homework, and conversations with and among students—all interpreted by the teacher in light of additional information about the students, the schooling context, and the content being studied.
In this report, these situations are referred to as assessment to assist learning, or formative assessment. These assessments provide specific information about students’ strengths and difficulties with learning. For example, statistics teachers need to know more than the fact that a student does not understand probability; they need to know the details of this misunderstanding, such as the student’s tendency to confuse conditional and compound probability. Teachers can use information from these types of assessment to adapt their instruction to meet students’ needs, which may be difficult to anticipate and are likely to vary from one student to another. Students can use this information to determine which skills and knowledge they need to study further and what adjustments in their thinking they need to make.
A recent review (Black and Wiliam, 1998) revealed that classroom-based formative assessment, when appropriately used, can positively affect learning. According to the results of this review, students learn more when they receive feedback about particular qualities of their work, along with advice on what they can do to improve. They also benefit from training in self-assessment, which helps them understand the main goals of the instruction and determine what they need to do to achieve. But these practices are rare, and classroom assessment is often weak. The development of good classroom assessments places significant demands on the teacher. Teachers must have tools and other supports if they are to implement high-quality assessments efficiently and use the resulting information effectively.
Assessment of Individual Achievement
Another type of assessment used to make decisions about individuals is that conducted to help determine whether a student has attained a certain level of competency after completing a particular phase of education, whether it be a classroom unit or 12 years of schooling. In this report, this is referred to as assessment of individual achievement, or summative assessment.1
Some of the most familiar forms of summative assessment are those used by classroom teachers, such as end-of-unit tests and letter grades assigned when a course is finished. Large-scale assessments—which are administered at the direction of users external to the classroom—also provide
information about the attainment of individual students, as well as comparative information about how one individual performs relative to others. This information may be used by state- or district-level administrators, teachers, parents, students, potential employers, and the general public. Because largescale assessments are typically given only once a year and involve a time lag between testing and availability of results, the results seldom provide information that can be used to help teachers or students make day-to-day or month-to-month decisions about teaching and learning.
As described in the National Research Council (NRC) report High Stakes (1999a), policy makers see large-scale assessments of student achievement as one of their most powerful levers for influencing what happens in local schools and classrooms. Increasingly, assessments are viewed as a way not only to measure performance, but also to change it, by encouraging teachers and students to modify their practices. Assessment programs are being used to focus public attention on educational concerns; to change curriculum, instruction, and teaching practices; and to motivate educators and students to work harder and achieve at higher levels (Haertel, 1999; Linn, 2000).
A trend that merits particular attention is the growing use of state assessments to make high-stakes decisions about individual students, teachers, and schools. In 1998, 18 states required students to pass an exam before receiving a high school diploma, and 8 of these states also used assessment results to make decisions about student promotion or retention in grade (Council of Chief State School Officers, 1999). When stakes are high, it is particularly important that the inferences drawn from an assessment be valid, reliable, and fair (American Educational Research Association, American Psychological Association, and National Council on Measurement in Education, 1999; NRC, 1999a). Validity refers to the degree to which evidence and theory support the interpretations of assessment scores. Reliability denotes the consistency of an assessment’s results when the assessment procedure is repeated on a population of individuals or groups. And fairness encompasses a broad range of interconnected issues, including absence of bias in the assessment tasks, equitable treatment of all examinees in the assessment process, opportunity to learn the material being assessed, and comparable validity (if test scores underestimate or overestimate the competencies of members of a particular group, the assessment is considered unfair). Moreover, even when these criteria for assessment are met, care must be taken not to extend the results to reach conclusions not supported by the evidence. For example, a teacher whose students have higher test scores is not necessarily better than one whose students have lower scores. The quality of inputs—such as the entry characteristics of students or educational resources available—must also be considered. Too often, high-stakes assessments are used to make decisions that are inappropriate in light of the limitations discussed above.
Assessment to Evaluate Programs
Another common purpose of assessment is to help policy makers formulate judgments about the quality and effectiveness of educational programs and institutions (these assessments also fall under the category of summative assessment). Assessments are used increasingly to make high-stakes decisions not only about individuals, but also about institutions. For instance, public reporting of state assessment results by school and district can influence the judgments of parents and taxpayers about their schools. In addition, many states provide financial or other rewards to schools in which performance increases and impose sanctions—including closing schools— when performance declines. Just as with individuals, the quality of the measure is of critical importance in the validity of these decisions.
The National Assessment of Educational Progress (NAEP), a national program begun in 1969 to measure broad trends in the achievement of U.S. students, is used for program evaluation in broad terms. Also known as “the nation’s report card,” NAEP is administered periodically in core academic subjects to students at certain ages. The NAEP assessment items are not designed to match any particular curriculum, but rather to reflect national consensus about what students should know and be able to do. Since 1990, NAEP results have also been available for participating states, providing them with an independent source of information about how their students are achieving relative to the nation as a whole.
As with evaluating teachers, care must be taken not to extend the results of assessments at a particular school to reach conclusions not supported by the evidence. For example, a school whose students have higher test scores is not necessarily better than one whose students have lower test scores. As in judging teacher performance, the quality of inputs—such as the entry characteristics of students or educational resources available—must also be considered.
Reflections on the Purposes of Assessment
Several important points should be made about the purposes of assessment. Note that all of the issues introduced briefly below are discussed more fully in Chapter 6.
First, many of the cognitive and measurement principles set forth in this report apply to the design of assessments for all three purposes discussed above. At the same time, it is important to emphasize that one type of assessment does not fit all. The purpose of an assessment determines priorities, and the context of use imposes constraints on the design. Often a single assessment will be used for multiple purposes. For instance, many state tests are used for both individual and program assessment purposes. In general, however, the more purposes a single assessment aims to serve, the more
each purpose will be compromised. This is not necessarily a problem as long as the assessment designers and users recognize the compromises and trade-offs involved.
Second, U.S. society generally places greater value on large-scale than on classroom assessment. A significant industry and an extensive research literature have grown up around large-scale tests; by contrast, teachers have tended to fend for themselves in developing assessments for classroom use. The good news is that researchers are paying more attention to the potential benefits of well-designed classroom assessments for improving learning (e.g., Falk, 2000; NRC, 2001; Niyogi, 1995; Pellegrino, Baxter, and Glaser, 1999; Shepard, 2000; Stiggins, 1997; Wiggins, 1998). Moreover, national standards in science and mathematics recognize this type of assessment as a fundamental part of teaching and learning (National Council of Teachers of Mathematics [NCTM], 2000; NRC, 1996). This report describes ways in which substantially more valid and useful inferences could be drawn from largescale assessments. Also emphasized is the significant potential for advances in the cognitive and measurement sciences to improve classroom assessment. Powerful theories and tools are now available that enable deep and frequent assessment of student understanding during the course of instruction.
Third, there is a need for better alignment among the various purposes of assessment. Ideally, teachers’ goals for learning should be consistent with those of large-scale assessments and vice versa. In reality, however, this is often not the case. Black and Wiliam (1998, p. 59) emphasize that a major problem to be addressed relates to “the possible confusions and tensions, both for teachers and learners, between the formative and summative purposes which their work might have to serve…if an optimum balance is not sought, formative work will always be insecure because of the threat of renewed dominance by the summative.” The contrast between classroom and large-scale assessments arises from the different purposes they serve and contexts in which they are used. To guide instruction and monitor its effects, teachers need information intimately connected to what their students are studying, and they interpret this evidence in light of everything else they know about their students and their instruction. The power of classroom assessment resides in these connections. Yet precisely because they are individualized, neither the rationale nor the results of the typical classroom assessments are easy to communicate beyond the classroom. Standardized assessments do communicate efficiently across time and place— but by so constraining the content and timeliness of the message that they often have little utility in the classroom. Most would agree that there is a need for both classroom and large-scale assessments in the educational system; one challenge is to make stronger connections between the two so they work together to support a common set of learning goals. Needed are systems of assessments, consisting of both classroom and large-scale compo-
nents, that provide a variety of evidence to inform and support educational decision making.
PRECISION AND IMPRECISION IN ASSESSMENT
Assessments serve a vital role in providing information to help students, parents, teachers, administrators, and policy makers reach decisions. Sophisticated statistical methods have been developed to enhance the accuracy of assessments and describe precisely their margins of error. But the heightened, and possibly exaggerated, attention paid to standardized testing in the U.S. educational system can overshadow the essential point that even assessments meeting the highest technical requirements are still, by their nature, imprecise to some degree. As noted earlier, an assessment result is an estimate, based on samples of knowledge and performance from the much larger universe of everything a person knows and can do. Although assessment can provide valuable information about a student’s competence, scores may nevertheless vary for reasons unrelated to achievement, such as the specific content being assessed, the particular format of the assessment items, the timing and conditions for administering the assessment, or the health of the student on that particular day.
Educators assess students to learn about what they know and can do, but assessments do not offer a direct pipeline into a student’s mind. Assessing educational outcomes is not as straightforward as measuring height or weight; the attributes to be measured are mental representations and processes that are not outwardly visible. One must therefore draw inferences about what students know and can do on the basis of what one sees them say, do, or make in a handful of particular situations. What a student knows and what one observes a student doing are not the same thing. The two can be connected only through a chain of inference, which involves reasoning from what one knows and observes to form explanations, conclusions, or predictions, as discussed in the following section. Assessment users always reason in the presence of uncertainty; as a result, the information produced by an assessment is typically incomplete, inconclusive, and amenable to more than one explanation.
ASSESSMENT AS A PROCESS OF REASONING FROM EVIDENCE
An assessment is a tool designed to observe students’ behavior and produce data that can be used to draw reasonable inferences about what students know. In this report, the process of collecting evidence to support the types of inferences one wants to draw is referred to as reasoning from
evidence (Mislevy, 1994, 1996). This chain of reasoning about student learning characterizes all assessments, from classroom quizzes and standardized achievement tests, to computerized tutoring programs, to the conversation a student has with her teacher as they work through an experiment.
People reason from evidence every day about any number of decisions, small and large. When leaving the house in the morning, for example, one does not know with certainty that it is going to rain, but may reasonably decide to take an umbrella on the basis of such evidence as the morning weather report and the clouds in the sky.
The first question in the assessment reasoning process is “evidence about what?” Data become evidence in an analytic problem only when one has established their relevance to a conjecture being considered (Schum, 1987, p. 16). Data do not provide their own meaning; their value as evidence can arise only through some interpretational framework. What a person perceives visually, for example, depends not only on the data she receives as photons of light striking her retinas, but also on what she thinks she might see. In the present context, educational assessments provide data such as written essays, marks on answer sheets, presentations of projects, or students’ explanations of their problem solutions. These data become evidence only with respect to conjectures about how students acquire knowledge and skill.
Assessment comes down to which types of evidence or observations are available to help reason about the examinee’s competence. What one believes about the nature of learning will affect the kinds of assessment data sought and the chain of inferences drawn. Cognitive researchers, for example, would seek evidence about how learners approach problems, including what they understand about why they are being asked to solve these problems, as well as the strategies they then use for solution. Assessment also depends on which tools are available to make sense of the evidence. Measurement science offers various methods for using available evidence to make determinations about the competencies of learners. For example, some assessments use probabilistic models to handle sampling or to communicate uncertainty. The chain of reasoning determines what to look for in what students say, do, or produce and why it constitutes evidence about what they know and can do.
The methods and practices of familiar tests and test theory are special cases of reasoning from evidence. Their evolution has been channeled by the kinds of inferences teachers and other assessment users have wanted to draw, shaped by the ways people have thought about learning and schooling, and constrained by the technologies that have been available to gather and use assessment data. The same underlying principles of reasoning from evidence that led to classical test theory can support inference in a broader universe of assessments, including those based on cognitive theory.
THE ASSESSMENT TRIANGLE
The process of reasoning from evidence can be portrayed as a triad referred to throughout this report as the assessment triangle. As shown in Figure 2–1, the corners of the triangle represent the three key elements underlying any assessment noted earlier: a model of student cognition and learning in the domain, a set of beliefs about the kinds of observations that will provide evidence of students’ competencies, and an interpretation process for making sense of the evidence.
These three elements, which are discussed in detail below, may be explicit or implicit, but an assessment cannot be designed and implemented without some consideration of each. The three are represented as corners of a triangle because each is connected to and dependent on the other two. A major tenet of this report is that for an assessment to be effective, the three elements must be in synchrony. The assessment triangle provides a useful framework for analyzing current assessment or designing future ones.
Cognition
The cognition corner of the triangle refers to a theory or set of beliefs about how students represent knowledge and develop competence in a subject domain (e.g., fractions). In any particular assessment application, a theory of learning in the domain is needed to identify the set of knowledge and skills that is important to measure for the task at hand, whether that be characterizing the competencies students have acquired thus far or guiding instruction to increase learning.
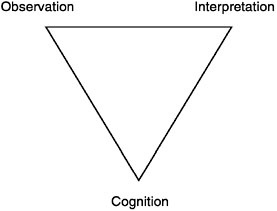
FIGURE 2–1 The assessment triangle
In this report we argue that assessment will be most effective if the designer (in many cases the teacher) starts with such an explicit and clearly conceptualized cognitive model of learning. This model should reflect the most scientifically credible understanding of typical ways in which learners represent knowledge and develop expertise in a domain. These findings should derive from cognitive and educational research about how people learn, as well as the experience of expert teachers (Webb, 1992). As scientific understanding of learning evolves, the cognitive underpinnings of assessment should change accordingly. Our use of the term “cognition” is not meant to imply that the theory must necessarily come from a single cognitive research perspective. As discussed in Chapter 3, theories of student learning and understanding can take different forms and encompass several levels and types of knowledge representation that include social and contextual components.
Depending on the purpose for an assessment, one might distinguish from one to hundreds of aspects of student competence to be sampled. These targets of inference for a given assessment will be a subset of the larger theory of how people learn the subject matter. Targets for assessment could be expressed in terms of numbers, categories, or some mix; they might be conceived as persisting over long periods of time or apt to change at the next problem step. They might concern tendencies in behavior, conceptions of phenomena, available strategies, or levels of development. For instance, at one extreme, verbal and quantitative ability are the only two variables in the cognitive framework that underlies the SAT I. In this case, the purpose is to rank order examinees in relation to their general verbal and quantitative abilities, so a more detailed theory may not be necessary.
More detailed cognitive models of learning can be used by teachers to diagnose particular difficulties students are having in a specific domain of the curriculum. For instance, on the basis of research with learners, developmental psychologist Robert Siegler (1998) has identified rules (both correct and erroneous) learners appear to use to solve problems in various mathematical and scientific domains. The example presented in Box 2–1 is a cognitive model of the rules learners use to solve balance-scale problems.
Below we continue to use the balance-scale problem to illustrate the observation and interpretation elements of the triangle. But first it should be noted that the cognitive model underlying performance on this set of problems is more straightforward than would be the case if one were trying to model performance on less structured problems. Furthermore, additional analyses of children’s reasoning with the balance scale and in other domains of problem solving have provided more dynamic and complex accounts of the understandings children have and develop about these kinds of systems (see, e.g., Goldman, Pellegrino and Mertz, 1988; Schauble, 1990; Siegler and Crowley, 1991). This point raises an issue of practicality. Assessment design
|
BOX 2–1 Example of a Cognitive Model of Learning for Assessing Children’s Problem-Solving Rules Siegler (1976) examined how people develop an understanding of the components underlying the principle of torque in balance-scale problems. He presented children of different ages with the type of balance scale shown below, which includes a fulcrum and an arm that can rotate around it. The arm can tip left or right or remain level, depending on how weights (metal disks with holes in them) are arranged on the pegs on each side of the fulcrum. However, a lever (not shown in the figure) is typically set to hold the arm motionless. The child’s task is to predict which (if either) side would go down if the lever were released.  Two variables influence the outcome: (1) the amount of weight on each side of the fulcrum and (2) the distance of the weight from the fulcrum. Thus the keys to solving such problems are to attend to both of the relevant dimensions and to combine them appropriately by using the multiplicative relationship of weight times distance. On the basis of his research, together with the known tendency of young |
need not take into account every subtlety and complexity about learning in a domain that has been uncovered by cognitive research. Instead, what is being proposed in this report is that assessment design be based on a representation or approximation of cognition that is both consistent with a richer psychological perspective and at a level of detail sufficient to accomplish the job of assessment. Any model of learning underlying an assessment will be a simplification of what is going on in the mind of the examinee and in the social situation within which the assessment takes place. As described and illustrated more fully in Chapter 5, the point of basing assessment on a cognitive model is to focus the assessment on those competencies that are most important to measure in light of the desired inferences about student learning.
Finally, if the goal of basing assessment on an appropriate model of learning is to be realized, cognitive models will need to be developed for a broader range of the curriculum. Currently, cognition and learning are con-
|
children to focus on a single relevant dimension, Siegler developed the following cognitive model, which incorporates four different rules children use to solve such problems: Rule I—If the weight is the same on both sides, predict that the scale will balance. If the weight differs, predict that the side with more weight will go down. Rule II—If one side has more weight, predict that it will go down. If the weights on the two sides are equal, choose the side with the greater distance (i.e., the side that has the weight farther from the fulcrum). Rule III—If both weight and distance are equal, predict that the scale will balance. If one side has more weight or distance, and the two sides are equal on the other dimension, predict that the side with the greater value on the unequal dimension will go down. If one side has more weight and the other side more distance, muddle through or guess. Rule IV—Proceed as in Rule III unless one side has more weight and the other more distance. In that case, calculate torques by multiplying weight times distance on each side. Then predict that the side with the greater torque will go down. SOURCE: Siegler (1976, p. 482). Used by permission of Academic Press. |
siderably better understood in some domains, such as physics and reading, than in others, such as history and chemistry. Moreover, the models developed by cognitive scientists will need to be recast in ways that are easily understood and readily usable by assessment developers and teachers.
Observation
Every assessment is also based on a set of beliefs about the kinds of tasks or situations that will prompt students to say, do, or create something that demonstrates important knowledge and skills. The tasks to which students are asked to respond on an assessment are not arbitrary. They must be carefully designed to provide evidence that is linked to the cognitive model of learning and to support the kinds of inferences and decisions that will be based on the assessment results.
The observation corner of the assessment triangle represents a description or set of specifications for assessment tasks that will elicit illuminating responses from students. In a tutoring session, for example, the observation framework describes what the learner says and does, does not say and do, or says or does with specific kinds of support or scaffolding. In a formal assessment, the observation model describes examinee products, such as written or oral responses or the choice of a distractor for multiple choice items. In assessment, one has the opportunity to structure some small corner of the world to make observations. The assessment designer can use this capability to maximize the value of the data collected, as seen through the lens of the underlying beliefs about how students learn in the domain.
For example, on the basis of the cognitive model presented in Box 2–1, Siegler (1976) designed situations to observe which rules, if any, describe how a child is solving balance-scale problems. Asking children how they solved the problems might appear to be the simplest strategy, but Siegler believed that answers to such questions could either overestimate or underestimate children’s knowledge. The answers would give a misleadingly positive impression if children simply repeated information they had heard at home or in school, whereas the answers would give a misleadingly negative impression if children were too inarticulate to communicate knowledge they in fact possessed. In light of these considerations, Siegler formulated an observation method that he called the rule assessment method to determine which rule a given child is using (see Box 2–2).
The tasks selected for observation should be developed with the purpose of the assessment in mind. The same rich and demanding performance task that provides invaluable information to a teacher about his tenth-grade class—because he knows they have been studying transmission genetics for the past 6 weeks—could prove impenetrable and worthless for assessing the knowledge of the vast majority of students across the nation. Large-scale assessments generally collect the same kind of evidence for all examinees; thus observations cannot be closely tied to the specific instruction a given student has recently experienced.
Interpretation
Every assessment is based on certain assumptions and models for interpreting the evidence collected from observations. The interpretation corner of the triangle encompasses all the methods and tools used to reason from fallible observations. It expresses how the observations derived from a set of assessment tasks constitute evidence about the knowledge and skills being assessed. In the context of large-scale assessment, the interpretation method is usually a statistical model, which is a characterization or summarization of patterns one would expect to see in the data given varying levels of student
|
BOX 2–2 Methods for Observing Children’s Rules for Solving Balance-Scale Problems Below are descriptions of the kinds of problems Siegler (1976) crafted to observe which rules children are using to solve balance-scale problems. Children who use different rules produce different patterns of responses to these six problems:
SOURCE: Siegler (1976). Used by permission of Academic Press. |
competency. In the context of classroom assessment, the interpretation is often made less formally by the teacher, and is usually based on an intuitive or qualitative model rather than a formal statistical one.
Returning to the example of Siegler’s balance-scale problems, one example of an interpretation method is presented in Box 2–3. In this example the interpretation framework specifies patterns of response to the six problems and the corresponding rule, if any, that one can infer a student is using.
Relationships Among the Three Vertices of the Assessment Triangle
A crucial point is that each of the three elements of the assessment triangle not only must make sense on its own, but also must connect to each of the other two elements in a meaningful way to lead to an effective assessment and sound inferences.
|
BOX 2–3 Interpreting Observations of Student Performance on Balance-Scale Problems Siegler (1976) describes how children who use the different rules described in Box 2–1 will produce different patterns of response to the problems presented in Box 2–2. For instance, children using Rule I would be expected to predict correctly on balance, weight, and conflict-weight problems and incorrectly on the other three problem types. Children using Rule II would behave similarly, except that they would answer correctly on distance problems. The figure below shows the predicted percentage of correct answers on each problem type for children using each of the four rules. 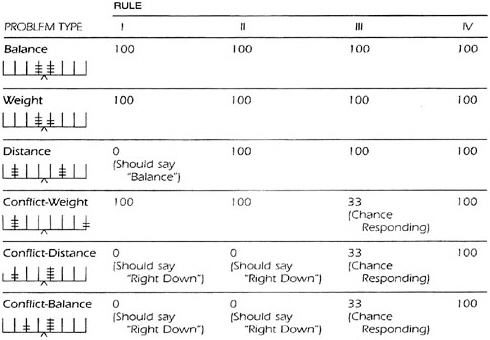 In a study of 5-to 17-year-olds solving balance-scale problems, Siegler found that more than 80 percent used one of the four rules consistently; the other 20 percent produced less consistent patterns of responses that did not match perfectly any of the above profiles. This finding may reflect an intermediate or transitional state of responding, which would not be unexpected in children’s development. SOURCE: Siegler (1976, p. 486). Used by permission of Academic Press. |
Connections Between Cognition and Observation. A cognitive theory of how people develop competence in a domain provides clues about the types of situations that will elicit evidence about that competence. Conversely, a well-developed knowledge base about the properties and affordances of tasks—what does and does not work to reveal what students know and can do—helps the assessment designer anticipate the types of knowledge and skills likely to be elicited by tasks with certain features. When the knowledge derived from both perspectives is combined, relevant information about student performance is more likely to be collected through assessment tasks.
Connections Between Cognition and Interpretation. A cognitive theory of how people develop competence in a domain also provides clues about the types of interpretation methods that are appropriate for transforming the data about student performance into assessment results. The cognitive theory suggests aspects of knowledge and skills by which we want to characterize students. Conversely, a familiarity with available measurement models provides a set of experience-tested methods for handling thorny and often subtle issues of evidence.
Connections Between Observation and Interpretation. Knowing the possibilities and limitations of various interpretation models helps in designing a set of observations that is at once effective and efficient for the task at hand. The interpretation model expresses how the observations from a given task constitute evidence about the performance being assessed as it bears on the targeted knowledge. It is only sensible to look for evidence one knows how to reason from or interpret.
Thus to have an effective assessment, all three vertices of the triangle must work together in synchrony. It will almost certainly be necessary for developers to go around the assessment triangle several times, looking for mismatches and refining the elements to achieve consistency. The interdependent relationships among cognition, observation, and interpretation in the assessment design process are further elaborated and illustrated throughout this report.
ASSESSMENT, CURRICULUM, AND INSTRUCTION: COGNITION AT THE CORE
Assessment is not an isolated part of the education system. What is measured and how the information is used depend to a great extent on the curriculum that is taught and the instructional methods used. Viewed from the other perspective, assessment has a strong effect on both curriculum and instruction.
Curriculum consists of the knowledge and skills in subject areas that teachers teach and students learn. The curriculum generally encompasses a
scope or breadth of content in a given subject area and a sequence for learning. The standards discussed in Chapter 1 outline the goals of learning, whereas curriculum sets forth the more specific means to be used to achieve those ends. Instruction refers to methods of teaching and the learning activities used to help students master the content and objectives specified by a curriculum. Instruction encompasses the activities of both teachers and students. It can be carried out by a variety of methods, sequences of activities, and topic orders. Assessment is the means used to measure the outcomes of education and the achievement of students with regard to important competencies. As discussed earlier, assessment may include both formal methods, such as large-scale state assessments, or less formal classroom-based procedures, such as quizzes, class projects, and teacher questioning.
A precept of educational practice is the need for alignment among curriculum, instruction, and assessment (e.g., NCTM, 1995; Webb, 1997). Alignment, in this sense, means that the three functions are directed toward the same ends and reinforce each other rather than working at cross-purposes. Ideally, an assessment should measure what students are actually being taught, and what is actually being taught should parallel the curriculum one wants students to learn. If any of the functions is not well synchronized, it will disrupt the balance and skew the educational process. Assessment results will be misleading, or instruction will be ineffective. Alignment is difficult to achieve, however. Often what is lacking is a central theory around which the three functions can be coordinated.
Decisions about assessment, curriculum, and instruction are further complicated by actions taken at different levels of the educational system, including the classroom, the school or district, and the state. Each of these levels has different needs, and each uses assessment data in varied ways for somewhat different purposes. Each also plays a role in making decisions and setting policies for assessment, curriculum, and instruction, although the locus of power shifts depending on the type of decision involved. Some of these actions emanate from the top down, while others arise from the bottom up. States generally exert considerable influence over curriculum, while classroom teachers have more latitude in instruction. States tend to determine policies on assessment for program evaluation, while teachers have greater control over assessment for learning. This situation means that adjustments must continually be made among assessment, curriculum, and instruction not only horizontally, within the same level (such as within school districts), but also vertically across levels. For example, a change in state curriculum policy will require adjustments in assessment and instruction at all levels.
Realizing the new approach to assessment set forth in this report will depend on making compatible changes in curriculum and instruction. As with assessment, most current approaches to curriculum and instruction are based on theories that have not kept pace with modern knowledge of how people learn (NRC, 1999b; Shepard, 2000). The committee believes that align-
ment among assessment, curriculum, and instruction could be better achieved if all three were derived from a shared knowledge base about cognition and learning in the subject domain. The model of learning would provide the central bonding principle, serving as a nucleus around which the three functions would revolve. Without such a central core, and under pressure to prepare students for high-stakes accountability tests, teachers may feel compelled to move back and forth between instruction and assessment and teach directly to the items on a test. This approach can result in an undesirable narrowing of the curriculum and a limiting of learning outcomes. Such problems can be ameliorated if, instead, decisions about both instruction and assessment are guided by a model of learning in the domain. Although current curriculum, instruction, and assessment are designed on the basis of implicit conceptions of learning, those conceptions tend to be fragmented, outdated, and not clearly delineated. Instead, the committee contends that the cognitive underpinnings should be made explicit and public, and they should represent the best available scientific understanding of how people learn.
CONCLUSIONS
This report addresses assessments used in both classroom and largescale contexts for three broad purposes: to assist learning, to measure individual achievement, and to evaluate programs. The purpose of an assessment determines priorities, and the context of use imposes constraints on the design. Thus it is essential to recognize that one type of assessment does not fit all
Often a single assessment is used for multiple purposes; in general, however, the more purposes a single assessment aims to serve, the more each purpose will be compromised. For instance, many state tests are used for both individual and program assessment purposes. This is not necessarily a problem, as long as assessment designers and users recognize the compromises and trade-offs such use entails.
Although assessments used in various contexts and for differing purposes often look quite different, they share certain common principles. One such principle is that assessment is always a process of reasoning from evidence. By its very nature, moreover, assessment is imprecise to some degree. Assessment results are only estimates of what a person knows and can do.
Every assessment, regardless of its purpose, rests on three pillars: a model of how students represent knowledge and develop competence in the subject domain, tasks or situations that allow one to observe students’ performance, and an interpretation method for drawing inferences from the performance evidence thus obtained. In the context of large-scale assessment, the interpretation method is usually a statistical model that characterizes expected
data patterns, given varying levels of student competence. In less formal classroom assessment, the interpretation is often made by the teacher using an intuitive or qualitative rather than formal statistical model.
Three foundational elements, comprising what is referred to in this report as the “assessment triangle,” underlie all assessments. These three elements—cognition, observation, and interpretation—must be explicitly connected and designed as a coordinated whole. If not, the meaningfulness of inferences drawn from the assessment will be compromised.
The central problem addressed by this report is that most widely used assessments of academic achievement are based on highly restrictive beliefs about learning and competence not fully in keeping with current knowledge about human cognition and learning. Likewise, the observation and interpretation elements underlying most current assessments were created to fit prior conceptions of learning and need enhancement to support the kinds of inferences people now want to draw about student achievement. A cognitive model of learning should serve as the cornerstone of the assessment design process. This model should be based on the best available understanding of how students represent knowledge and develop competence in the domain.
The model of learning can serve as a unifying element—a nucleus that brings cohesion to curriculum, instruction, and assessment. This cohesive function is a crucial one because educational assessment does not exist in isolation, but must be aligned with curriculum and instruction if it is to support learning.
Finally, aspects of learning that are assessed and emphasized in the classroom should ideally be consistent with (though not necessarily the same as) the aspects of learning targeted by large-scale assessments. In reality, however, these two forms of assessment are often out of alignment. The result can be conflict and frustration for both teachers and learners. Thus there is a need for better alignment among assessments used for different purposes and in different contexts.




















