3
Advances in the Sciences of Thinking and Learning
In the latter part of the 20th century, study of the human mind generated considerable insight into one of the most powerful questions of science: How do people think and learn? Evidence from a variety of disciplines— cognitive psychology, developmental psychology, computer science, anthropology, linguistics, and neuroscience, in particular—has advanced our understanding of such matters as how knowledge is organized in the mind; how children develop conceptual understanding; how people acquire expertise in specific subjects and domains of work; how participation in various forms of practice and community shapes understanding; and what happens in the physical structures of the brain during the processes of learning, storing, and retrieving information. Over the same time period, research in mathematics and science education has advanced greatly. In the 1999 volume How People Learn, the National Research Council (NRC) describes numerous findings from the research on learning and analyzes their implications for instruction. This chapter focuses on those findings that have the greatest implications for improving the assessment of school learning.
EXPANDING VIEWS OF THE NATURE OF KNOWING AND LEARNING
In the quest to understand the human mind, thinkers through the centuries have engaged in reflection and speculation; developed theories and philosophies of elegance and genius; conducted arrays of scientific experiments; and produced great works of art and literature—all testaments to the powers of the very entity they were investigating. Over a century ago, scientists began to study thinking and learning in a more systematic way, taking early steps toward what we now call the cognitive sciences. During the first
few decades of the 20th century, researchers focused on such matters as the nature of general intellectual ability and its distribution in the population. In the 1930s, scholars started emphasizing such issues as the laws governing stimulus-and-response associations in learning. Beginning in the 1960s, advances in fields as diverse as linguistics, computer science, and neuroscience offered provocative new perspectives on human development and powerful new technologies for observing behavior and brain functions. The result during the past 40 years has been an outpouring of scientific research on the mind and brain—a “cognitive revolution” as some have termed it. With richer and more varied evidence in hand, researchers have refined earlier theories or developed new ones to explain the nature of knowing and learning.
As described by Greeno, Pearson and Schoenfeld (1996b), four perspectives are particularly significant in the history of research and theory regarding the nature of the human mind: the differential, behaviorist, cognitive, and situative perspectives. Most current tests, and indeed many aspects of the science of educational measurement, have theoretical roots in the differential and behaviorist traditions. The more recent perspectives—the cognitive and the situative—are not well reflected in traditional assessments but have influenced several recent innovations in the design and use of educational assessments. These four perspectives, summarized below, are not mutually exclusive. Rather, they emphasize different aspects of knowing and learning with differing implications for what should be assessed and how the assessment process should be transacted (see e.g., Greeno, Collins, and Resnick, 1996a; Greeno et al., 1996b).
The Differential Perspective
The differential perspective focuses mainly on the nature of individual differences in what people know and in their potential for learning. The roots of research within this tradition go back to the start of the 20th century. “Mental tests” were developed to discriminate among children who were more or less suited to succeed in the compulsory school environment that had recently been instituted in France (Binet and Simon, 1980). The construction and composition of such tests was a very practical matter: tasks were chosen to represent a variety of basic knowledge and cognitive skills that children of a given age could be expected to have acquired. Inclusion of a task in the assessment was based on the how well it discriminated among children within and across various age ranges. A more abstract approach to theorizing about the capacities of the mind arose, however, from the practice of constructing mental tests and administering them to samples of children and adults. Theories of intelligence and mental ability emerged that were based entirely on analyses of the patterns of correlation among test scores. To pursue such work, elaborate statistical machinery was devel-
oped for determining the separate factors that define the structure of intellect (Carroll, 1993).
At the core of this approach to studying the mind is the concept that individuals differ in their mental capacities and that these differences define stable mental traits—aspects of knowledge, skill, and intellectual competence—that can be measured. It is presumed that different individuals possess these traits in differing amounts, as measured by their performance on sample tasks that make up a test. Specific traits or mental abilities are inferred when the pattern of scores shows consistent relationships across different situations.
The differential perspective was developed largely to assess aspects of intelligence or cognitive ability that were separate from the processes and content of academic learning. However, the methods used in devising aptitude tests and ranking individuals were adopted directly in the design of “standardized” academic achievement tests that were initially developed during the first half of the century. In fact, the logic of measurement was quite compatible with assumptions about knowing and learning that existed within the behaviorist perspective that came to dominate much of research and theory on learning during the middle of the century.
The Behaviorist Perspective
Behaviorist theories became popular during the 1930s (e.g., Hull, 1943; Skinner, 1938), about the same time that theories of individual differences in intellectual abilities and the mental testing movement were maturing. In some ways the two perspectives are complementary. In the behaviorist view, knowledge is the organized accumulation of stimulus-response associations that serve as the components of skills. Learning is the process by which one acquires those associations and skills (Thorndike, 1931). People learn by acquiring simple components of a skill, then acquiring more complicated units that combine or differentiate the simpler ones. Stimulus-response associations can be strengthened by reinforcement or weakened by inattention. When people are motivated by rewards, punishments, or other (mainly extrinsic) factors, they attend to relevant aspects of a situation, and this favors the formation of new associations and skills.
A rich and detailed body of research and theory on learning and performance has arisen within the behaviorist perspective, including important work on the strengthening of stimulus-response associations as a consequence of reinforcement or feedback. Many behavioral laws and principles that apply to human learning and performance are derived from work within this perspective. In fact, many of the elements of current cognitive theories of knowledge and skill acquisition are more elaborate versions of stimulusresponse associative theory. Missing from this perspective, however, is any
treatment of the underlying structures or representations of mental events and processes and the richness of thought and language.
The influence of associationist and behaviorist theories can easily be discerned in curriculum and instructional methods that present tasks in sequence, from simple to complex, and that seek to ensure that students learn prerequisite skills before moving on to more complex ones. Many common assessments of academic achievement have also been shaped by behaviorist theory. Within this perspective, a domain of knowledge can be analyzed in terms of the component information, skills, and procedures to be acquired. One can then construct tests containing samples of items or assessment situations that represent significant knowledge in that domain. A person’s performance on such a test indicates the extent to which he or she has mastered the domain.
The Cognitive Perspective
Cognitive theories focus on how people develop structures of knowledge, including the concepts associated with a subject matter discipline (or domain of knowledge) and procedures for reasoning and solving problems. The field of cognitive psychology has focused on how knowledge is encoded, stored, organized in complex networks, and retrieved, and how different types of internal representations are created as people learn about a domain (NRC, 1999). One major tenet of cognitive theory is that learners actively construct their understanding by trying to connect new information with their prior knowledge.
In cognitive theory, knowing means more than the accumulation of factual information and routine procedures; it means being able to integrate knowledge, skills, and procedures in ways that are useful for interpreting situations and solving problems. Thus, instruction should not emphasize basic information and skills as ends in themselves, but as resources for more meaningful activities. As Wiggins (1989) points out, children learn soccer not just by practicing dribbling, passing, and shooting, but also by actually playing in soccer games.
Whereas the differential and behaviorist approaches focus on how much knowledge someone has, cognitive theory also emphasizes what type of knowledge someone has. An important purpose of assessment is not only to determine what people know, but also to assess how, when, and whether they use what they know. This information is difficult to capture in traditional tests, which typically focus on how many items examinees answer correctly or incorrectly, with no information being provided about how they derive those answers or how well they understand the underlying concepts. Assessment of cognitive structures and reasoning processes generally requires more complex tasks that reveal information about thinking patterns,
reasoning strategies, and growth in understanding over time. As noted later in this chapter and subsequently in this report, researchers and educators have made a start toward developing assessments based on cognitive theories. These assessments rely on detailed models of the goals and processes involved in mental performances such as solving problems, reading, and reasoning.
The Situative Perspective
The situative perspective, also sometimes referred to as the sociocultural perspective, grew out of concerns with the cognitive perspective’s nearly exclusive focus on individual thinking and learning. Instead of viewing thought as individual response to task structures and goals, the situative perspective describes behavior at a different level of analysis, one oriented toward practical activity and context. Context refers to engagement in particular forms of practice and community. The fundamental unit of analysis in these accounts is mediated activity, a person’s or group’s activity mediated by cultural artifacts, such as tools and language (Wertsch, 1998). In this view, one learns to participate in the practices, goals, and habits of mind of a particular community. A community can be any purposeful group, large or small, from the global society of professional physicists, for example, to a local book club or school.
This view encompasses both individual and collective activity. One of its distinguishing characteristics is attention to the artifacts generated and used by people to shape the nature of cognitive activity. Hence, from a traditional cognitive perspective, reading is a series of symbolic manipulations that result in comprehension of text. In both contrast and complement, from the perspective of mediated activity, reading is a social practice rooted in the development of writing as a model for speech (Olson, 1996). So, for example, how parents introduce children to reading or how home language supports language as text can play an important role in helping children view reading as a form of communication and sense making.
The situative perspective proposes that every assessment is at least in part a measure of the degree to which one can participate in a form of practice. Hence, taking a multiple-choice test is a form of practice. Some students, by virtue of their histories, inclinations, or interests, may be better prepared than others to participate effectively in this practice. The implication is that simple assumptions about these or any other forms of assessment as indicators of knowledge-in-the-head seem untenable. Moreover, opportunities to participate in even deceptively simple practices may provide important preparation for current assessments. A good example is dinnertime conversations that encourage children to weave narratives, hold and defend
positions, and otherwise articulate points of view. These forms of cultural capital are not evenly distributed among the population of test takers.
Most current testing practices are not a good match with the situative perspective. Traditional testing presents abstract situations, removed from the actual contexts in which people typically use the knowledge being tested. From a situative perspective, there is no reason to expect that people’s performance in the abstract testing situation adequately reflects how well they would participate in organized, cumulative activities that may hold greater meaning for them.
From the situative standpoint, assessment means observing and analyzing how students use knowledge, skills, and processes to participate in the real work of a community. For example, to assess performance in mathematics, one might look at how productively students find and use information resources; how clearly they formulate and support arguments and hypotheses; how well they initiate, explain, and discuss in a group; and whether they apply their conceptual knowledge and skills according to the standards of the discipline.
Points of Convergence
Although we have emphasized the differences among the four perspectives, there are many ways in which they overlap and are complementary. The remainder of this chapter provides an overview of contemporary understanding of knowing and learning that has resulted from the evolution of these perspectives and that includes components of all four. Aspects of the most recent theoretical perspectives are particularly critical for understanding and assessing what people know. For example, both the individual development of knowledge emphasized by the cognitive approach and the social practices of learning emphasized by the situative approach are important aspects of education (Anderson, Greeno, Reder, and Simon, 2000; Cobb, 1998).
The cognitive perspective can help teachers diagnose an individual student’s level of conceptual understanding, while the situative perspective can orient them toward patterns of participation that are important to knowing in a domain. For example, individuals learn to reason in science by crafting and using forms of notation or inscription that help represent the natural world. Crafting these forms of inscription can be viewed as being situated within a particular (and even peculiar) form of practice—modeling—into which students need to be initiated. But modeling practices can also be profitably viewed within a framework of goals and cognitive processes that govern conceptual development (Lehrer, Schauble, Carpenter and Penner, 2000; Roth and McGinn, 1998).
The cognitive perspective informs the design and development of tasks to promote conceptual development for particular elements of knowledge, whereas the situative perspective informs a view of the larger purposes and practices in which these elements will come to participate. Likewise, the cognitive perspective can help teachers focus on the conceptual structures and modes of reasoning a student still needs to develop, while the situative perspective can aid them in organizing fruitful participatory activities and classroom discourse to support that learning.
Both perspectives imply that assessment practices need to move beyond the focus on individual skills and discrete bits of knowledge that characterizes the earlier associative and behavioral perspectives. They must expand to encompass issues involving the organization and processing of knowledge, including participatory practices that support knowing and understanding and the embedding of knowledge in social contexts.
FUNDAMENTAL COMPONENTS OF COGNITION
How does the human mind process information? What kinds of “units” does it process? How do individuals monitor and direct their own thinking? Major theoretical advances have come from research on these types of questions. As it has developed over time, cognitive theory has dealt with thought at two different levels. The first focuses on the mind’s information processing capabilities, generally considered to comprise capacities independent of specific knowledge. The second level focuses on issues of representation, addressing how people organize the specific knowledge associated with mastering various domains of human endeavor, including academic content. The following subsections deal with each of these levels in turn and their respective implications for educational assessment.
Components of Cognitive Architecture
One of the chief theoretical advances to emerge from cognitive research is the notion of cognitive architecture—the information processing system that determines the flow of information and how it is acquired, stored, represented, revised, and accessed in the mind. The main components of this architecture are working memory and long-term memory. Research has identified the distinguishing characteristics of these two types of memory and the mechanisms by which they interact with each other.
Working Memory
Working memory, sometimes referred to as short-term memory, is what people use to process and act on information immediately before them
(Baddeley, 1986). Working memory is a conscious system that receives input from memory buffers associated with the various sensory systems. There is also considerable evidence that working memory can receive input from the long-term memory system.
The key variable for working memory is capacity—how much information it can hold at any given time. Controlled (also defined as conscious) human thought involves ordering and rearranging ideas in working memory and is consequently restricted by finite capacity. The ubiquitous sign “Do not talk to the bus driver” has good psychological justification.
Working memory has assumed an important role in studies of human intelligence. For example, modern theories of intelligence distinguish between fluid intelligence, which corresponds roughly to the ability to solve new and unusual problems, and crystallized intelligence, or the ability to bring previously acquired information to bear on a current problem (Carroll, 1993; Horn and Noll, 1994; Hunt, 1995). Several studies (e.g., Kyllonen and Christal, 1990) have shown that measures of fluid intelligence are closely related to measures of working memory capacity. Carpenter, Just, and Shell (1990) show why this is the case with their detailed analysis of the information processing demands imposed on examinees by Raven’s Progressive Matrix Test, one of the best examples of tests of fluid intelligence. The authors developed a computer simulation model for item solution and showed that as working memory capacity increased, it was easier to keep track of the solution strategy, as well as elements of the different rules used for specific problems. This led in turn to a higher probability of solving more difficult items containing complex rule structures. Other research on inductive reasoning tasks frequently associated with fluid intelligence has similarly pointed to the importance of working memory capacity in solution accuracy and in age differences in performance (e.g., Holzman, Pellegrino, and Glaser, 1983; Mulholland, Pellegrino, and Glaser, 1980).
This is not to suggest that the needs of educational assessment could be met by the wholesale development of tests of working memory capacity. There is a simple argument against this: the effectiveness of an information system in dealing with a specific problem depends not only on the system’s capacity to handle information in the abstract, but also on how the information has been coded into the system.
Early theories of cognitive architecture viewed working memory as something analogous to a limited physical container that held the items a person was actively thinking about at a given time. The capacity of working memory was thought to form an outer boundary for the human cognitive system, with variations according to task and among individuals. This was the position taken in one of the first papers emerging from the cognitive revolution—George Miller’s (1956) famous “Magic Number Seven” argument, which maintains that people can readily remember seven numbers or unrelated
items (plus or minus two either way), but cannot easily process more than that.
Subsequent research developed an enriched concept of working memory to explain the large variations in capacity that were being measured among different people and different contexts, and that appeared to be caused by the interaction between prior knowledge and encoding. According to this concept, people extend the limits of working memory by organizing disparate bits of information into “chunks” (Simon, 1974), or groupings that make sense to them. Using chunks, working memory can evoke from long-term memory items of highly variable depth and connectivity.
Simply stated, working memory refers to the currently active portion of long-term memory. But there are limits to such activity, and these limits are governed primarily by how information is organized. Although few people can remember a randomly generated string of 16 digits, anyone with a slight knowledge of American history is likely to be able to recall the string 1492– 1776–1865–1945. Similarly, while a child from a village in a developing country would be unlikely to remember all nine letters in the following string— AOL-IBM-USA—most middle-class American children would have no trouble doing so. But to conclude from such a test that the American children had more working memory capacity than their developing-country counterparts would be quite wrong. This is just one example of an important concept: namely, that knowledge stored in long-term memory can have a profound effect on what appears, at first glance, to be the capacity constraint of working memory.
Recent theoretical work has further extended notions about working memory by viewing it not as a “place” in the cognitive system, but as a kind of cognitive energy level that exists in limited amounts, with individual variations (Miyake, Just, and Carpenter, 1994). In this view, people tend to perform worse when they try to do two tasks at once because they must allocate a limited amount of processing capacity to two processes simultaneously. Thus, performance differences on any task may derive not only from individual differences in prior knowledge, but also from individual differences in both the amount and allocation or management of cognitive resources (Just, Carpenter, and Keller, 1996). Moreover, people may vary widely in their conscious or unconscious control of these allocation processes.
Long-Term Memory
Long-term memory contains two distinct types of information—semantic information about “the way the world is” and procedural information about “how things are done.” Several theoretical models have been developed to characterize how information is represented in long-term memory. At present the two leading models are production systems and connectionist
networks (also called parallel distributed processing or PDP systems). Under the production system model, cognitive states are represented in terms of the activation of specific “production rules,” which are stated as condition-action pairs. Under the PDP model, cognitive states are represented as patterns of activation or inhibition in a network of neuronlike elements.
At a global level, these two models share some important common features and processes. Both rely on the association of contexts with actions or facts, and both treat long-term memory as the source of information that not only defines facts and procedures, but also indicates how to access them (see Klahr and MacWhinney, 1998, for a comparison of production and PDP systems). The production system model has the added advantage of being very useful for constructing “intelligent tutors” —computerized learning systems, described later in this chapter, that have promising applications to instruction and assessment in several domains.
Unlike working memory, long-term memory is, for all practical purposes, an effectively limitless store of information. It therefore makes sense to try to move the burden of problem solving from working to long-term memory. What matters most in learning situations is not the capacity of working memory—although that is a factor in speed of processing—but how well one can evoke the knowledge stored in long-term memory and use it to reason efficiently about information and problems in the present.
Cognitive Architecture and Brain Research
In addition to examining the information processing capacities of individuals, studies of human cognition have been broadened to include analysis of mind-brain relations. This topic has become of increasing interest to both scientists and the public, especially with the appearance of powerful new techniques for unobtrusively probing brain function such as positron-emission tomography (PET) scans and functional magnetic resonance imaging (fMRI). Research in cognitive neuroscience has been expanding rapidly and has led to the development and refinement of various brain-based theories of cognitive functioning. These theories deal with the relationships of brain structure and function to various aspects of the cognitive architecture and the processes of reasoning and learning. Brain-based research has convincingly demonstrated that experience can alter brain states, and it is highly likely that, conversely, brain states play an important role in the potential for learning (NRC, 1999).
Several discoveries in cognitive neuroscience are relevant to an understanding of learning, memory, and cognitive processing, and reinforce many of the conclusions about the nature of cognition and thinking derived from behavioral research. Some of the more important topics addressed by this research, such as hemispheric specialization and environmental effects on
brain development, are discussed in Annex 3–1 at the end of this chapter. As noted in that discussion, these discoveries point to the need for caution so as not to overstate and overgeneralize current findings of neuroscience to derive direct implications for educational and assessment practices.
Contents of Memory
Contemporary theories also characterize the types of cognitive content that are processed by the architecture of the mind. The nature of this content is extremely critical for understanding how people answer questions and solve problems, and how they differ in this regard as a function of the conditions of instruction and learning.
There is an important distinction in cognitive content between domain-general knowledge, which is applicable to a range of situations, and domain-specific knowledge, which is relevant to a particular problem area. In science education, for example, the understanding that unconfounded experiments are at the heart of good experimental design is considered domain-general knowledge (Chen and Klahr, 1999) because the logic underlying this idea extends into all realms of experimental science. In contrast, an understanding of the underlying principles of kinetics or inorganic chemistry, for example, constitutes domain-specific knowledge, often accompanied by local theories and particular types of notation. Similarly, in the area of cognitive development, the general understanding that things can be organized according to a hierarchy is a type of domain-general knowledge, while an understanding of how to classify dinosaurs is domain-specific (Chi and Koeske, 1983).
Domain-General Knowledge and Problem-Solving Processes
Cognitive researchers have studied in depth the domain-general procedures for solving problems known as weak methods. Newell and Simon (1972) identify a set of such procedures, including hill climbing; means-ends analysis; analogy; and, as a last resort, trial and error. Problem solvers use these weak methods to constrain what would otherwise be very large search spaces when they are solving novel problems. Because the weak methods, by definition, are not tied to any specific context, they may reveal (and predict) people’s underlying ability to solve problems in a wide range of novel situations. In that sense, they can be viewed as the types of processes that are frequently assessed by general aptitude tests such as the SAT I.
In most domains of instruction, however, learners are expected to use strong methods: relatively specific algorithms, particular to the domain, that will make it possible to solve problems efficiently. Strong methods, when
available, make it possible to find solutions with little or no searching. For example, someone who knows the calculus finds the maximum of a function by applying a known algorithm (taking the derivative and setting it equal to zero). To continue the assessment analogy, strong methods are often measured by such tests as the SAT II. Paradoxically, although one of the hallmarks of expertise is access to a vast store of strong methods in a particular domain, both children and scientists fall back on their repertoire of weak methods when faced with truly novel problems (Klahr and Simon, 1999).
Schemas and the Organization of Knowledge
Although weak methods remain the last resort when one is faced with novel situations, people generally strive to interpret situations so that they can apply schemas—previously learned and somewhat specialized techniques (i.e., strong methods) for organizing knowledge in memory in ways that are useful for solving problems. Schemas help people interpret complex data by weaving them into sensible patterns. A schema may be as simple as “Thirty days hath September” or more complex, such as the structure of a chemical formula. Schemas help move the burden of thinking from working memory to long-term memory. They enable competent performers to recognize situations as instances of problems they already know how to solve; to represent such problems accurately, according to their meaning and underlying principles; and to know which strategies to use to solve them.
This idea has a very old history. In fact, the term schema was introduced more than 50 years ago to describe techniques people use to reconstruct stories from a few, partially remembered cues (Bartlett, 1932). The modern study of problem solving has carried this idea much further. Cheng and Holyoak’s (1985) study of schematic problem solving in logic is a good example. It is well known that people have a good deal of trouble with the implication relationship, often confusing “A implies B” with the biconditional relationship “A implies B, and B implies A” (Wason and Johnson-Laird, 1972). Cheng and Holyoak showed that people are quite capable of solving an implication problem if it is rephrased as a narrative schema that means something to them. An example is the “permission schema,” in which doing A implies that one has received permission to do B; to cite a specific case, “Drinking alcoholic beverages openly implies that one is of a legal age to do so.” Cheng and Holyoak pointed out that college students who have trouble dealing with abstract A implies B relationships have no trouble understanding implication when it is recast in the context of “permission to drink.”
The existence of problem-solving schemas has been demonstrated in a wide variety of contexts. For instance, Siegler and colleagues have shown
that schoolchildren learn progressively more complicated (and more accurate) schemas for dealing with a variety of situations, such as balance-scale problems (Siegler, 1976) (see Boxes 2–1, 2–2, and 2–3 in Chapter 2) and simple addition (Siegler and Crowley, 1991). Marshall (1995) developed a computer-aided instruction program that reinforces correct schematic problem solving in elementary arithmetic. Finally, Lopez, Atran, Coley, and Medin (1997) showed that different cultures differentially encourage certain types of schemas. In reasoning about animals, American college students tend to resort to taxonomic schemas, in which animals are related by dint of possessing common features (and indirectly, having certain genetic relationships). In contrast, the Itzaj Maya, a jungle-dwelling group in Guatemala, are more likely to reason by emphasizing ecological relationships. It is not that the Americans are unaware of ecological relations or the Maya are unaware of feature possession. Rather, each group has adopted its own schema for generalizing from an observed characteristic of one animal to a presumed characteristic of another. In each case, however, the schema has particular value for the individuals operating within a given culture.
Extensive research shows that the ways students represent the information given in a mathematics or science problem or in a text that they read depends on the organization of their existing knowledge. As learning occurs, increasingly well-structured and qualitatively different organizations of knowledge develop. These structures enable individuals to build a representation or mental model that guides problem solution and further learning, avoid trial-and-error solution strategies, and formulate analogies and draw inferences that readily result in new learning and effective problem solving (Glaser and Baxter, 1999). The impact of schematic knowledge is powerfully demonstrated by research on the nature of expertise as described below.
Implications for Assessment
Although we have discussed aspects of cognition at a rather general level thus far, it is possible to draw implications for assessment practice. Most of these implications relate to which memory system one might need to engage to accomplish different purposes, as well as the care needed to disentangle the mutual effects and interactions of the two systems.
For example, it can be argued that estimates of what people have stored in long-term memory and how they have organized that information are likely to be more important than estimates of working memory capacity in most instances of educational assessment. The latter estimates may be useful in two circumstances: first, when the focus of concern is a person’s capacity to deal with new and rapidly occurring situations, and second, when one is assessing individuals below the normal range and is interested in a potential indicator of the limits of a person’s academic learning proficiency. However,
such assessments must be carefully designed to minimize the potential advantages of using knowledge previously stored in long-term memory.
To estimate a person’s knowledge and problem-solving ability in familiar fields, however, it is necessary to know which domain-specific problem-solving schemas people have and when they use them. Assessments should evaluate what information people have and under what circumstances they see that information as relevant. This evaluation should include how a person organizes acquired information, encompassing both strategies for problem solving and ways of chunking relevant information into manageable units. There is a further caveat, however, about such assessments. Assessment results that are intended to measure knowledge and procedures in long-term memory may, in fact, be modulated by individual differences in the processing capacity of working memory. This can occur when testing situations have properties that inadvertently place extra demands on working memory, such as keeping track of response options or large amounts of information while answering a question.
THE NATURE OF SUBJECT-MATTER EXPERTISE
In addition to expanding our understanding of thinking and learning in general, cognitive research conducted over the past four decades has generated a vast body of knowledge about how people learn the content and procedures of specific subject domains. Researchers have probed deeply the nature of expertise and how people acquire large bodies of knowledge over long periods of time. Studies have revealed much about the kinds of mental structures that support problem solving and learning in various domains ranging from chess to physics, what it means to develop expertise in a domain, and how the thinking of experts differs from that of novices.
The notion of expertise is inextricably linked with subject-matter domains: experts must have expertise in something. Research on how people develop expertise has provided considerable insight into the nature of thinking and problem solving. Although every child cannot be expected to become an expert in a given domain, findings from cognitive science about the nature of expertise can shed light on what successful learning looks like and guide the development of effective instruction and assessment.
Knowledge Organization: Expert-Novice Differences
What distinguishes expert from novice performers is not simply general mental abilities, such as memory or fluid intelligence, or general problem-solving strategies. Experts have acquired extensive stores of knowledge and skill in a particular domain. But perhaps most significant, their minds have organized this knowledge in ways that make it more retrievable and useful.
In fields ranging from medicine to music, studies of expertise have shown repeatedly that experts commit to long-term memory large banks of well-organized facts and procedures, particularly deep, specialized knowledge of their subject matter (Chi, Glaser, and Rees, 1982; Chi and Koeske, 1983). Most important, they have efficiently coded and organized this information into well-connected schemas. These methods of encoding and organizing help experts interpret new information and notice features and meaningful patterns of information that might be overlooked by less competent learners. These schemas also enable experts, when confronted with a problem, to retrieve the relevant aspects of their knowledge.
Of particular interest to researchers is the way experts encode, or chunk, information into meaningful units based on common underlying features or functions. Doing so effectively moves the burden of thought from the limited capacity of working memory to long-term memory. Experts can represent problems accurately according to their underlying principles, and they quickly know when to apply various procedures and strategies to solve them. They then go on to derive solutions by manipulating those meaningful units. For example, chess experts encode midgame situations in terms of meaningful clusters of pieces (Chase and Simon, 1973), as illustrated in Box 3–1.
One of the best demonstrations of the differences between expert and novice knowledge structures comes from physics. When presented with problems in mechanics, expert physicists recode them in terms of the basic principles of physics as illustrated in Box 3–2. For example, when presented with a problem involving balancing a cart on an inclined plane, the expert physicist sees the problem as an example of a balance-of-forces problem, while the novice is more likely to view it as being specific to carts and inclined planes (Chi, Feltovich, and Glaser, 1981; Larkin, McDermott, Simon, and Simon, 1980).
The knowledge that experts have cannot be reduced to sets of isolated facts or propositions. Rather, their knowledge has been encoded in a way that closely links it with the contexts and conditions for its use. An example of this observation is provided in Box 3–3 which illustrates the ways in which the physics knowledge of novices and experts is structured. Differences in what is known and how it is represented give rise to the types of responses shown in Box 3–2. Because the knowledge of experts is “conditionalized” in the manner illustrated in Box 3–3, they do not have to search through the vast repertoire of everything they know when confronted with a problem. Instead, they can readily activate and retrieve the subset of their knowledge that is relevant to the task at hand (Glaser, 1992; Larkin et al., 1980). These and other related findings suggest that teachers should place more emphasis on the conditions for applying the facts or procedures being taught, and that assessment should address whether students know when, where, and how to use their knowledge.
|
In one study a chess master, a Class A player (good but not a master), and a novice were given 5 seconds to view a chess board as of the middle of a chess game, as in the examples shown. After 5 seconds the board was covered, and each participant attempted to reconstruct the positions observed on another board. This procedure was repeated for multiple trials until every participant had received a perfect score. On the first trial, the master player correctly placed many more pieces than the Class A player, who in turn placed more than the novice: 16, 8, and 4, respectively. However, these results occurred only when the chess pieces were arranged in configurations that conformed to meaningful games of chess. When the pieces were randomized and presented for 5 seconds, the recall of the chess master and Class A player was the same as that of the novice—all placed from 2 to 3 pieces correctly. Data over trials for valid middle-game positions and random board positions are shown below. 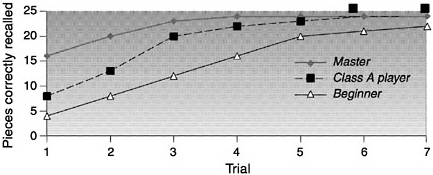
SOURCE: Adapted from Chase and Simon (1973) and NRC (1999). |
|
BOX 3–2 Sorting of Physics Problems Novices’ explanations for their grouping of two problems 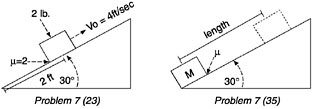
Explanations Novice 1: These deal with blocks on an inclined plane. Novice 5: Inclined plane problems, coefficient of friction. Novice 6: Blocks on inclined planes with angles. Experts’ explanations for their grouping of two problems 
Explanations Expert 2: Conservation of energy. Expert 3: Work-theory theorem. They are all straightforward problems. Expert 4: These can be done from energy considerations. Either you should know the principle of conservation of energy, or work is lost somewhere. Above is an example of the sorting of physics problems performed by novices and experts. Each picture shown represents a diagram that can be drawn from the storyline of a physics problem taken from an introductory physics textbook. The novices and experts in this study were asked to categorize many such problems on the basis of similarity of solution. A marked contrast can be noted in the experts’ and novices’ categorization schemes. Novices tend to categorize physics problems as being solved similarly if they “look the same” (that is, share the same surface features), whereas experts categorize according to the major principle that could be applied to solve the problems. SOURCE: Adapted from Chi, Feltovich, and Glaser (1981, p. 67) and NRC (1999). |
|
BOX 3–3 Novices’ and Experts’ Schemas of Inclined Planes Some studies of experts and novices in physics have explored the organization of their knowledge structures. Chi, Glaser, and Rees (1982) found that novices’ schemas of an inclined plane contain primarily surface features, whereas experts’ schemas connect the notion of an inclined plane with the laws of physics and the conditions under which the laws are applicable. 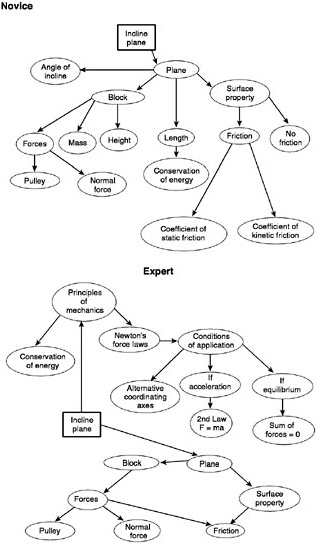
SOURCE: Adapted from Chi, Glaser, and Rees (1982, pp. 57–58). |
The Importance of Metacognition
In his book on unified theories of cognition, Newell (1990) points out that there are two layers of problem solving—applying a strategy to the problem at hand, and selecting and monitoring that strategy. Good problem solving, Newell observed, often depends as much on the selection and monitoring of a strategy as on its execution. The term metacognition (literally “thinking about thinking”) is commonly used to refer to the selection and monitoring processes, as well as to more general activities of reflecting on and directing one’s own thinking.
Experts have strong metacognitive skills (Hatano, 1990). They monitor their problem solving, question limitations in their knowledge, and avoid overly simplistic interpretations of a problem. In the course of learning and problem solving, experts display certain kinds of regulatory performance, such as knowing when to apply a procedure or rule, predicting the correctness or outcomes of an action, planning ahead, and efficiently apportioning cognitive resources and time. This capability for self-regulation and self-instruction enables advanced learners to profit a great deal from work and practice by themselves and in group efforts.
Metacognition depends on two things: knowing one’s mental capabilities and being able to step back from problem-solving activities to evaluate one’s progress. Consider the familiar situation of forgetting the name of a person to whom one was introduced only a few minutes ago. There are simple metacognitive tricks for avoiding this situation, including asking the person for a business card and then reading it immediately instead of putting it in one’s pocket. Metacognition is crucial to effective thinking and competent performance. Studies of metacognition have shown that people who monitor their own understanding during the learning phase of an experiment show better recall performance when their memories are tested (Nelson, 1996). Similar metacognitive strategies distinguish stronger from less competent learners. Strong learners can explain which strategies they used to solve a problem and why, while less competent students monitor their own thinking sporadically and ineffectively and offer incomplete explanations (Chi, Bassok, Lewis, Reiman, and Glaser, 1989; Chi and VanLehn, 1991). Good problem solvers will try another strategy if one is not working, while poor problem solvers will hold to a strategy long after it has failed. Likewise, good writers will think about how a hypothetical audience might read their work and revise parts that do not convey their meaning (Hayes and Flower, 1986).
There is ample evidence that metacognition develops over the school years; for example, older children are better than younger ones at planning for tasks they are asked to do (Karmiloff-Smith, 1979). Metacognitive skills can also be taught. For example, people can learn mental devices that help
them stay on task, monitor their own progress, reflect on their strengths and weaknesses, and self-correct errors. It is important to note, however, that the teaching of metacognitive skills is often best accomplished in specific content areas since the ability to monitor one’s understanding is closely tied to domain-specific knowledge and expertise (NRC, 1999).
Implications for Assessment
Studies of expert-novice differences in subject domains illuminate critical features of proficiency that should be the targets for assessment. The study of expertise reinforces the point made earlier about the importance of assessing the nature of the knowledge that an individual has in long-term memory. Experts in a subject domain have extensive factual and procedural knowledge, and they typically organize that knowledge into schemas that support pattern recognition and the rapid retrieval and application of knowledge.
As noted above, one of the most important aspects of cognition is metacognition—the process of reflecting on and directing one’s own thinking. Metacognition is crucial to effective thinking and problem solving and is one of the hallmarks of expertise in specific areas of knowledge and skill. Experts use metacognitive strategies for monitoring understanding during problem solving and for performing self-correction. Assessment of knowledge and skill in any given academic domain should therefore attempt to determine whether an individual has good metacognitive skills.
THE DEVELOPMENT OF EXPERTISE
Studies of expertise have helped define the characteristics of knowledge and thought at stages of advanced learning and practice. As a complement to such work, considerable effort has also been expended on understanding the characteristics of people and of the learning situations they encounter that foster the development of expertise. Much of what we know about the development of expertise has come from studies of children as they acquire competence in many areas of intellectual endeavor, including the learning of school subject matter.
In this section we consider various critical issues related to learning and the development of expertise. We begin with a consideration of young children’s predisposition to learn, and how this and other characteristics of children and instructional settings impact the development of expertise. We close with a discussion of the important role of social context in defining expertise and supporting its development.
Predisposition to Learn
From a cognitive standpoint, development and learning are not the same thing. Some types of knowledge are universally acquired in the course of normal development, while other types are learned only with the intervention of deliberate teaching (which includes teaching by any means, such as apprenticeship, formal schooling, or self-study). For example, all normal children learn to walk whether or not their caretakers make any special efforts to teach them to do so, but most do not learn to ride a bicycle or play the piano without intervention.
Infants and young children appear to be predisposed to learn rapidly and readily in some domains, including language, number, and notions of physical and biological causality. Infants who are only 3 or 4 months old, for example, have been shown to understand certain concepts about the physical world, such as the idea that inanimate objects need to be propelled in order to move (Massey and Gelman, 1988).
Young children have a natural interest in numbers and will seek out number information. Studies of surprise and searching behaviors among infants suggest that 5-month-olds will react when an item is surreptitiously added to or subtracted from the number of items they expected to see (Starkey, 1992; Wynn, 1990, 1992). By the time children are 3 or 4 years old, they have an implicit understanding of certain rudimentary principles for counting, adding, and subtracting cardinal numbers. Gelman and Gallistel (1978) studied number concepts in preschoolers by making a hand puppet count a row of objects in correct, incorrect, or unusual ways; the majority of 3- and 4-year-olds could detect important counting errors, such as violations of the principles of one-to-one correspondence (only one number tag per item and one item per tag) or cardinality (the last ordinal tag represents the value).
Thus in mathematics, the fundamentals of ordinality and cardinality appear to develop in all normal human infants without instruction. In contrast, however, such concepts as mathematical notation, algebra, and Cartesian graphing representations must be taught. Similarly, the basics of speech and language comprehension emerge naturally from millions of years of evolution, whereas mastery of the alphabetic code necessary for reading typically requires explicit instruction and long periods of practice (Geary, 1995).
Even though young children lack experience and knowledge, they have the ability to reason adeptly with what knowledge they do have. Children are curious and natural problem solvers, and will try to solve problems presented to them and persist in doing so because they want to understand (Gelman and Gallistel, 1978; Piaget, 1978). Children can also be deliberate, self-directed, and strategic about learning things they are not predisposed to attend to, but they need adult guidance to develop strategies of intentional learning. Much of what we want to assess in educational contexts is the product of such deliberate learning.
Multiple Paths of Learning
Not all children come to school ready to learn in the same way, nor do they follow the same avenues of growth and change. Rather, children acquire new procedures slowly and along multiple paths. This contradicts earlier notions, inspired by Piaget’s work (e.g., 1952), that cognitive development progresses in one direction through a rigid set of stages, each involving radically different cognitive schemes. Although children’s strategies for solving problems generally become more effective with age and experience, the growth process is not a simple progression. When presented with the same arithmetic problem two days in a row, for instance, the same child may apply different strategies to solve it (Siegler and Crowley, 1991).
With respect to assessment, one of the most important findings from detailed observations of children’s learning behavior is that children do not move simply and directly from an erroneous to an optimal solution strategy (Kaiser, Proffitt, and McCloskey, 1985). Instead, they may exhibit several different but locally or partially correct strategies (Fay and Klahr, 1996). They also may use less-advanced strategies even after demonstrating that they know more-advanced ones, and the process of acquiring and consolidating robust and efficient strategies may be quite protracted, extending across many weeks and hundreds of problems (Siegler, 1998). These studies have found, moreover, that short-term transition strategies frequently precede more lasting approaches and that generalization of new approaches often occurs very slowly. Studies of computational abilities in children indicate that the processes children use to solve problems change with practice and that some children invent more efficient strategies than those they are taught. Box 3–4 provides examples of the types of strategies children often use for solving simple arithmetic problems and how their use of strategies can be studied.
Development of knowledge not only is variable as noted above, but also is constituted within particular contexts and situations, an observation that reflects an “interactionist” perspective on development (Newcombe and Huttenlocher, 2000). Accordingly, assessment of children’s development in school contexts should include attention to the nature of classroom cultures and the practices they promote, as well as to individual variation. For example, the kinds of expectations established in a classroom for what counts as a mathematical explanation affect the kinds of strategies and explanations children pursue (Ball and Bass, in press; Cobb and McClain, in press). To illustrate, in classrooms where teachers value mathematical generalization, even young children (first and second graders) develop informal proofs and related mathematical means to grapple with the mathematically important idea of “knowing for sure” (Lehrer et al., 1998; Strom, Kemeny, Lehrer and Forman, in press). Given a grounding in what it takes to know “for sure,”
|
BOX 3–4 Studying Children’s Strategies for Simple Addition Children who are learning to add two numbers but no longer count on their fingers often use various mental counting strategies to answer addition problems (Resnick, 1989). Those who have not learned their “number facts” to the point where they can quickly retrieve them typically use the following strategies, which increase in develpmental sophistication and cognitive demands as learning progresses:
To gather evidence about the strategies being used, researchers directly observe children and also measure how long it takes them to solve addition problems that vary systematically across the three important properties of such problems (total sum, size of the first addend, and size of the minimum addend). For example, children might be asked to solve the following three problems: What is 6 + 4? What is 3 + 5? What is 2 + 9? The amount of time it takes children to solve these problems depends on what strategy they are using. Using the sum strategy, the second problem should be solved most rapidly, followed by the first, then the third. Using the count-on strategy, the first problem should solved most quickly, then the second, then the third. Using the min strategy, the third problem should be solved soonest, followed by the second, then the first. Mathematical models of the actual times it takes children to respond are compared with models of predicted times to determine how well the data fit any given strategy. Interestingly, as children become more competent in adding single-digit numbers, they tend to use a mixture of strategies, from counting to direct retrieval. SOURCE: Siegler and Crowley (1991). |
young children can also come to appreciate some of the differences between mathematical and scientific generalization (Lehrer and Schauble, 2000).
It is not likely that children will spontaneously develop appreciation of the epistemic grounds of proof and related forms of mathematical argument in the absence of a classroom culture that values and promotes them. Hence, to assess whether children can or cannot reason about appropriate forms of argument assumes participation in classrooms that support these forms of disciplinary inquiry, as well as individual development of the skills needed to generate and sustain such participation.
Role of Prior Knowledge
Studies such as those referred to in the above discussion of children’s development and learning, as well as many others, have shown that far from being the blank slates theorists once imagined, children have rich intuitive knowledge that undergoes significant change as they grow older (Case, 1992; Case and Okamoto, 1996; Griffin, Case, and Siegler, 1994). A child’s store of knowledge can range from broad knowledge widely shared by people in a society to narrow bodies of knowledge about dinosaurs, vehicles, or anything else in which a child is interested. Long before they enter school, children also develop theories to organize what they see around them. Some of these theories are on the right track, some are only partially correct, while still others contain serious misconceptions.
When children are exposed to new knowledge, they attempt to reconcile it with what they think they already know. Often they will need to reevaluate and perhaps revise their existing understanding. The process works both ways: children also apply prior knowledge to make judgments about the accuracy of new information. From this perspective, learning entails more than simply filling minds with information; it requires the transformation of naive understanding into more complete and accurate comprehension.
In many cases, children’s naive conceptions can provide a good foundation for future learning. For example, background knowledge about the world at large helps early readers comprehend what they are reading; a child can determine whether a word makes sense in terms of his or her existing knowledge of the topic or prior notions of narrative. In other cases, misconceptions can form an impediment to learning that must be directly addressed. For example, some children have been found to reconcile their preconception that the earth is flat with adult claims that it is a sphere by imagining a round earth to be shaped like a pancake (Vosniadou and Brewer, 1992). This construction of a new understanding is guided by a model of the earth that helps the child explain how people can stand or walk on its surface. Similarly, many young children have difficulty giving up the notion
that one-eighth is greater than one-fourth, because 8 is more than 4 (Gelman and Gallistel, 1978). If children were blank slates, telling them that the earth is round or that one-fourth is greater than one-eighth would be adequate. But since they already have ideas about the earth and about numbers, those ideas must be directly addressed if they are to be transformed or expanded.
Drawing out and working with existing understandings is important for learners of all ages. Numerous experiments have demonstrated the persistence of a preexisting naive understanding even after a new model that contradicts it has been taught. Despite training to the contrary, students at a variety of ages persist in their belief that seasons are caused by the earth’s distance from the sun rather than by its tilt (Harvard-Smithsonian Center for Astrophysics, 1987), or that an object that has been tossed in the air is being acted upon by both the force of gravity and the force of the hand that tossed it (Clement, 1982). For the scientific to replace the naive understanding, students must reveal the latter and have the opportunity to see where it falls short.
For the reasons just noted, considerable effort has been expended on characterizing the naive conceptions and partially formed schemas that characterize various stages of learning, from novice through increasing levels of expertise. For instance, there are highly detailed descriptions of the common types of misconceptions held by learners in algebra, geometry, physics, and other fields (e.g., Driver, Squires, Rushworth, and Wood-Robinson, 1994; Gabel, 1994; Minstrell, 2000). Knowing the ways in which students are likely to err in their thinking and problem solving can help teachers structure lessons and provide feedback. Such knowledge has also served as a basis for intelligent tutoring systems (discussed further below). As illustrated in subsequent chapters, there are descriptions as well of typical progressions in student understanding of particular domains, such as number sense, functions, and physics. As we show in Chapter 5, such work demonstrates the value of carefully describing students’ incomplete understandings and of building on them to help students develop a more sophisticated grasp of the domain.
Practice and Feedback
Every domain of knowledge and skill has its own body of concepts, factual content, procedures, and other items that together constitute the knowledge of that field. In many domains, including areas of mathematics and science, this knowledge is complex and multifaceted, requiring sustained effort and focused instruction to master. Developing deep knowledge of a domain such as that exhibited by experts, along with conditions for its use, takes time and focus and requires opportunities for practice with feedback.
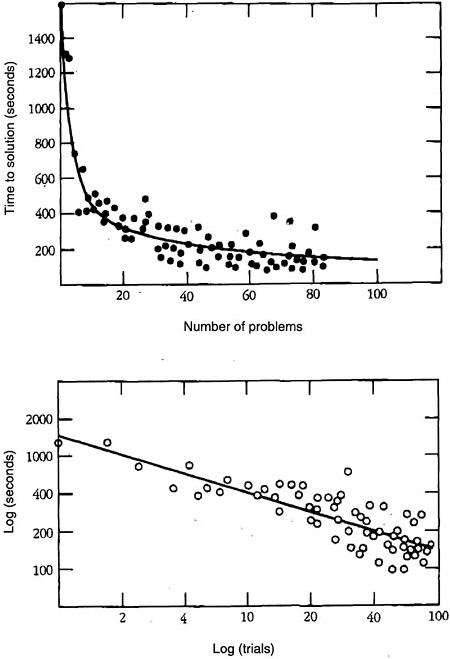
Whether considering the acquisition of some highly specific piece of knowledge or skill, such as the process of adding two numbers, or some larger schema for solving a mathematics or physics problem, certain laws of skill acquisition always apply. The first of these is the power law of practice: acquiring skill takes time, often requiring hundreds or thousands of instances of practice in retrieving a piece of information or executing a procedure. This law operates across a broad range of tasks, from typing on a keyboard to solving geometry problems (Rosenbloom and Newell, 1987). Data consistent with this law are illustrated in Figure 3–1. According to the power law of practice, the speed and accuracy of performing a simple or complex cognitive operation increases in a systematic nonlinear fashion over successive attempts. This pattern is characterized by an initial rapid improvement in performance, followed by subsequent and continuous improvements that accrue at a slower and slower rate. As shown in Figure 3–1, this relationship is linear if plotted in a log-log space.
The power law of practice is fully consistent with theories of cognitive skill acquisition according to which individuals go through different stages in acquiring the specific knowledge associated with a given cognitive skill (e.g., Anderson, 1982). Early on in this process, performance requires effort because it is heavily dependent on the limitations of working memory. Individuals must create a representation of the task they are supposed to perform, and they often verbally mediate or “talk their way through” the task while it is being executed. Once the components of the skill are well represented in long-term memory, the heavy reliance on working memory and the problems associated with its limited capacity can be bypassed. As a consequence, exercise of the skill can become fluent and then automatic. In the latter case, the skill requires very little conscious monitoring, and thus mental capacity is available to focus on other matters. An example of this pattern is the process of learning to read. Children can better focus on the meaning of what they are reading after they have mastered the process of decoding words. Another example is learning multicolumn addition. It is more difficult to metacognitively monitor and keep track of the overall procedure if one must compute sums by counting rather than by directly retrieving a number fact from memory. Evidence indicates that with each repetition of a cognitive skill—as in accessing a concept in long-term memory from a printed word, retrieving an addition fact, or applying a schema for solving differential equations—some additional knowledge strengthening occurs that produces the continual small improvements illustrated in Figure 3–1.
Practice, however, is not enough to ensure that a skill will be acquired. The conditions of practice are also important. The second major law of skill acquisition involves knowledge of results. Individuals acquire a skill much more rapidly if they receive feedback about the correctness of what they
have done. If incorrect, they need to know the nature of their mistake. It was demonstrated long ago that practice without feedback produces little learning (Thorndike, 1931). One of the persistent dilemmas in education is that students often spend time practicing incorrect skills with little or no feedback. Furthermore, the feedback they ultimately receive is often neither timely nor informative. For the less capable student, unguided practice (e.g., homework in mathematics) can be practice in doing tasks incorrectly. As discussed in Chapter 6, one of the most important roles for assessment is the provision of timely and informative feedback to students during instruction and learning so that their practice of a skill and its subsequent acquisition will be effective and efficient.
Transfer of Knowledge
A critical aspect of expertise is the ability to extend the knowledge and skills one has developed beyond the limited contexts in which they were acquired. Yet research suggests that knowledge does not transfer very readily (Bjork and Richardson-Klavhen, 1989; Carraher, 1986; Cognition and Technology Group at Vanderbilt, 1997; Lave, 1988). Contemporary studies have generally discredited the old idea of “mental exercise” —the notion that learning Latin, for example, improves learning in other subjects. More to the point, learning to solve a mathematics problem in school may not mean that the learner can solve a problem of the same type in another context.
Insights about learning and transfer have come from studies of situations in which people have failed to use information that, in some sense, they are known to have. Bassok and Holyoak (1989) showed, for example, that physics students who had studied the use of certain mathematical forms in the context of physics did not recognize that the same equations could be applied to solve problems in economics. On the other hand, mathematics students who had studied the same mathematical forms in several different contexts, but not economics, could apply the equations to economics problems.
A body of literature has clarified the principles for structuring learning so that people will be better able to use what they have learned in new settings. If knowledge is to be transferred successfully, practice and feedback need to take a certain form. Learners must develop an understanding of when (under what conditions) it is appropriate to apply what they have learned. Recognition plays an important role here. Indeed, one of the major differences between novices and experts is that experts can recognize novel situations as minor variants of situations for which they already know how to apply strong methods. Transfer is also more likely to occur when the person understands the underlying principles of what was learned. The models children develop to represent a problem mentally and the fluency with which
they can move back and forth among representations are other important dimensions that can be enhanced through instruction. For example, children need to understand how one problem is both similar to and different from other problems.
The Role of Social Context
Much of what humans learn is acquired through discourse and interactions with others. For example, science, mathematics, and other domains are often shaped by collaborative work among peers. Through such interactions, individuals build communities of practice, test their own theories, and build on the learning of others. For example, those who are still using a naive strategy can learn by observing others who have figured out a more productive one. This situation contrasts with many school situations, in which students are often required to work independently. Yet the display and modeling of cognitive competence through group participation and social interaction is an important mechanism for the internalization of knowledge and skill in individuals.
An example of the importance of social context can be found in the work of Ochs, Jacoby, and Gonzalez (1994). They studied the activities of a physics laboratory research group whose members included a senior physicist, a postdoctoral researcher, technical staff, and predoctoral students. They found that workers’ contributions to the laboratory depended significantly on their participatory skills in a collaborative setting—being able to formulate and understand questions and problems, develop arguments, and contribute to the construction of shared meanings and conclusions.
Even apparently individual cognitive acts, such as classifying colors or trees, are often mediated by tools and practice. Goodwin’s (2000) study of archaeologists suggests that classifying the color of a sample of dirt involves a juxtaposition of tools (the Munsell color chart) and particular practices, such as the sampling scheme. The chart arranges color into an ordered grid that can be scanned repeatedly, and cognitive acts such as these are coordinated with practices such as spraying the dirt with water, which creates a consistent environment for viewing. Tools and activity are coordinated among individuals as well, resulting in an apparently self-evident judgment, but upon closer inspection, it becomes clear that these apparently mundane judgments rely on multiple forms and layers of mediation. Similarly, Medin, Lynch, and Coley (1997) examined the classification of trees by experts from different fields of practice (e.g., university botanists and landscape architects). Here, too, classifications were influenced by the goals and contexts of these different forms of practice, so that there were substantial disagreements about how to characterize some of the specimens observed by the
experts involved in the study. Cognition was again mediated by culturally specific practice.
Studies such as these suggest that much knowledge is embedded within systems of representation, discourse, and physical activity. Moreover, communities of practices are sites for developing identity—one is what one practices, to some extent. This view of knowledge can be compared with that which underlies standard test-taking practice, whereby knowledge is regarded as disembodied and incorporeal. Testing for individual knowledge captures only a small portion of the skills actually used in many learning communities.
School is just one of the many contexts that can support learning. A number of studies have analyzed the use of mathematical reasoning skills in workplace and other everyday contexts (Lave, 1988; Ochs, Jacoby, and Gonzalez, 1994). One such study found that workers who packed crates in a warehouse applied sophisticated mathematical reasoning in their heads to make the most efficient use of storage space, even though they might not have been able to solve the same problem expressed as a standard numerical equation. The rewards and meaning people derive from becoming deeply involved in a community can provide a strong motive to learn.
Hull, Jury, Ziv, and Schultz (1994) studied literacy practices in an electronics assembly plant where work teams were responsible for evaluating and representing their own performance. Although team members had varying fluency in English, the researchers observed that all members actively participated in the evaluation and representation processes, and used texts and graphs to assess and represent their accomplishments. This situation suggests that reading, writing, quantitative reasoning, and other cognitive abilities are strongly integrated in most environments, rather than being separated into discrete aspects of knowledge. Tests that provide separate scores may therefore be inadequate for capturing some kinds of integrated abilities that people need and use on the job.
Studies of the social context of learning show that in a responsive social setting, learners can adopt the criteria for competence they see in others and then use this information to judge and perfect the adequacy of their own performance. Shared performance promotes a sense of goal orientation as learning becomes attuned to the constraints and resources of the environment. In the context of school, students also develop facility in giving and accepting help (and stimulation) from others. Social contexts for learning make the thinking of the learner apparent to teachers and other students so it can be examined, questioned, and built upon as part of constructive learning.
Impact of Cultural Norms and Student Beliefs
It is obvious that children from different backgrounds and cultures bring differing prior knowledge and resources to learning. Strong supports for learning exist in every culture, but some kinds of cultural resources may be better recognized or rewarded in the typical school setting. There are cultural variations in communication styles, for example, that may affect how a child interacts with adults in the typical U.S. school environment (Heath, 1981, 1983; Ochs and Schieffelin, 1984; Rogoff, 1990; Ward, 1971). Similarly, cultural attitudes about cooperation, as opposed to independent work, can affect the degree of support students provide for each other’s learning (Treisman, 1990). It is important for educators and others to take these kinds of differences into account in making judgments about student competence and in facilitating the acquisition of knowledge and skill.
The beliefs students hold about learning are another social dimension that can significantly affect learning and performance (e.g., Dweck and Legitt, 1988). For example, many students believe, on the basis of their typical classroom and homework assignments, that any mathematics problem can be solved in 5 minutes or less, and if they cannot find a solution in that time, they will give up. Many young people and adults also believe that talent in mathematics and science is innate, which gives them little incentive to persist if they do not understand something in these subjects immediately. Conversely, people who believe they are capable of making sense of unfamiliar things often succeed because they invest more sustained effort in doing so.
Box 3–5 lists several common beliefs about mathematics derived from classroom studies, international comparisons, and responses on National Assessment of Educational Progress (NAEP) questionnaires. Experiences at home and school shape students’ beliefs, including many of those shown in Box 3–5. For example, if mathematics is presented by the teacher as a set of rules to be applied, students may come to believe that “knowing” mathematics means remembering which rule to apply when a question is asked (usually the rule the teacher last demonstrated), and that comprehending the concepts that undergird the question is too difficult for ordinary students. In contrast, when teachers structure mathematics lessons so that important principles are apparent as students work through the procedures, students are more likely to develop deeper understanding and become independent and thoughtful problem solvers (Lampert, 1986).
Implications for Assessment
Knowledge of children’s learning and the development of expertise clearly indicates that assessment practices should focus on making students’ thinking visible to themselves and others by drawing out their current under-
|
BOX 3–5 Typical Student Beliefs About the Nature of Mathematics
SOURCE: Greeno, Pearson, and Schoenfeld. (1996b, p. 20). |
standing so that instructional strategies can be selected to support an appropriate course for future learning. In particular, assessment practices should focus on identifying the preconceptions children bring to learning settings, as well as the specific strategies they are using for problem solving. Particular consideration needs to be given to where children’s knowledge and strategies fall on a developmental continuum of sophistication, appropriateness, and efficiency for a particular domain of knowledge and skill.
Practice and feedback are critical aspects of the development of skill and expertise. One of the most important roles for assessment is the provision of timely and informative feedback to students during instruction and learning so that their practice of a skill and its subsequent acquisition will be effective and efficient.
As a function of context, knowledge frequently develops in a highly contextualized and inflexible form, and often does not transfer very effectively. Transfer depends on the development of an explicit understanding of when to apply what has been learned. Assessments of academic achievement need to consider carefully the knowledge and skills required to understand and answer a question or solve a problem, including the context in
which it is presented, and whether an assessment task or situation is functioning as a test of near, far, or zero transfer.
Knowledge is often embedded in particular social and cultural contexts, including the context of the classroom, and it encompasses understandings about the meaning of specific practices such as question asking and answering. Assessments need to examine how well students engage in communicative practices appropriate to a domain of knowledge and skill, what they understand about those practices, and how well they use the tools appropriate to that domain.
By considering context and development as co-emerging, school-based assessment can be directed toward the intersection of classroom contexts and individual cognition. Equitable assessment, then, relies on the creation of opportunities for growth and development. Without systematic attention to opportunity, the results of assessment simply recapitulate existing patterns of distribution of resources, both financial and social. Questions must therefore be raised about the validity of inferences that can be drawn from assessments of individual student achievement, using criteria for reasoning and argumentation defined in mathematics and science standards documents. It is uncertain what can be inferred in the absence of clear documentation of students’ opportunities to participate in forms of practice valued by disciplines such as mathematics and science—an issue that is addressed later in this volume.
INTEGRATION OF MODELS OF COGNITION AND LEARNING WITH INSTRUCTION AND ASSESSMENT
By building on findings about cognition, learning, and the development of expertise, researchers have produced models to describe the thinking processes, reasoning strategies, and conceptual understandings of students at various stages of competency. This work has tended to focus on the nature of knowledge and performance in specific domains of mathematics, science, or history. These models can be used to diagnose student understanding, determine next steps in instruction, and design assessments (Baker, 1997).
Detailed models of cognition and learning in specific curricular areas can be used to formulate a set of criteria that are valuable for evaluating the progress of any individual or group, as well as for informing teaching and learning. In other words, a well-developed and empirically validated model of thinking and learning in an academic domain can be used to design and select assessment tasks that support the analysis of various kinds of student performance. Such a model can also serve as the basis for rubrics for evaluating and scoring pupils’ work, with discriminating features of expertise
defining the specific targets of assessment. Ideally, models will highlight the main determinants of and obstacles to learning and include descriptions of students’ conceptual progressions as they develop competence and expertise.
Selected yet powerful examples of such models currently exist and demonstrate how cognitive theory can be applied to issues of curriculum, instruction, and assessment. Some integrate instruction and assessment and make it possible to assess students continuously as they work on problems. The following are three examples of attempts at such integration.
Intelligent Tutoring
Some of the most productive research in cognitive science comes from efforts to understand thinking in a domain in enough detail to craft computerized systems known as intelligent tutors. These systems show that it is possible to assess components of students’ knowledge while they are working on problems on line. In principle, intelligent tutors could be used for assessment in a wide range of well-structured knowledge domains.
The intelligent tutors developed by Anderson and colleagues (Anderson, Boyle, Corbett, and Lewis, 1990) and VanLehn and Martin (1998) represent a well-developed integration of multiple methods of observation and inference about cognition. To design such tutors, these researchers have developed highly specific descriptions of thinking about school subjects typically taught at the secondary level, such as geometry, algebra, and physics. As further discussed in the next section, their task analysis and model-building efforts incorporate information from reaction-time measures, strategy diagnosis, eye-movement analysis, and knowledge assessment. The importance of their cognitive task analyses cannot be overstated. As Newell and Simon (1972, p. 8) point out, “If performance is not well understood, it is somewhat premature to study learning,” and it would certainly be premature to design complex instructional systems that attempt to integrate instruction and assessment to support student learning.
For instance, the systems designed by Anderson’s group seamlessly integrate specific cognitive objectives, such as being able to solve a certain kind of algebraic equation, with individualized assessment of student errors, or “bugs,” and specific instructional steps to remediate those bugs. When a student makes a mistake, the system provides advice and remediation to correct the error. Studies suggest that when individuals work with these tutors, there is a relatively direct relationship between the assessment of student learning and the research-based model of student thinking. On average, students learn more with the system than with traditional instruction (Koedinger and Anderson, 1999). Intelligent tutoring systems are discussed in more detail in subsequent chapters.
Models of Learning Arithmetic
Researchers have conducted a broad range of inquiries about the cognitive foundations of arithmetic, beginning with infants’ sense of number and culminating in the arithmetic basis of algebra. Particularly intriguing from the standpoint of cognitive theory are children’s skills in reasoning about arithmetic word problems. Researchers generally attempt to account for problem difficulty, transitions in children’s solution strategies, and errors. For example, children find the first of the following two problems easier than the second:
-
Joe has 5 marbles. Then Tom gives him 6 more marbles. How many marbles does he have now?
-
Melissa has 5 pieces of candy. Elaine gives her some more pieces of candy. Now Melissa has 11 pieces of candy. How many pieces of candy did Elaine give her?
Carpenter and Moser (1982) and Steffe (1970) attribute the relative difficulty of these problems to their semantic structure. Both problems involve actions, which makes them generally easier for children to solve than nonaction problems. But the second problem is more difficult than the first because it includes an unknown change quantity, and children have difficulty imagining actions that involve combinations of unspecified quantities. Unlike adults, children perceive the problems not as involving different operators (e.g., 5 + 6 = ? and 11–5 = ?), but as variants of combining sets (e.g., 5 + 6 = ? and 5 + ? = 11). Thus it is somewhat more difficult for them to invoke a simple counting strategy to solve the second problem. In contrast, the first can be solved quite easily by counting all the marbles.
Other researchers have supplemented these accounts by building explicit models of student knowledge and cognitive processes. For example, Riley, Greeno and Heller (1983) accounted for differences in problem difficulty by appealing to problem schemas that differentiate among problem types. Under this theory, certain problem schemas are activated by the semantic structure of word problems. Once activated, the schemas invoke associated strategies, such as finding differences between sets. The Riley, Greeno and Heller (1983) model was subsequently augmented by Kintsch and Greeno (1985) to include natural language processing of the problems. A somewhat different set of assumptions guided Briars and Larkin (1984), who assumed that children would use concrete objects, such as teddy bears or chips, to model the relations evident in the semantic structure of a problem. This model predicted that children could solve a wide range of problems, including those typically thought of as multiplication or division, if they could “directly model” (e.g., represent) sets and their relations with
counters. This prediction was subsequently confirmed (Carpenter, Ansell, Franke, and Fennema, 1993).
Carpenter, Fennema, and Franke (1996) propose that teachers who understand children’s thinking about arithmetic would be in a better position to craft more effective mathematics instruction. Their approach, called cognitively guided instruction, borrows from work in cognitive science to characterize the semantic structure of word problems, as well as the strategies children typically use to solve them. Cognitively guided instruction explicitly recasts this work as a coarse-grained model of student thinking that can easily be understood and used by teachers. The model allows teachers to recognize and react to ongoing events as they unfold during the course of instruction. In a sense, the work of Carpenter and colleagues suggests that teachers use this model to support continuous assessment in the classroom so that instruction can be modified frequently as needed. More detail about how this model is used in classroom practice is provided in Chapter 6.
Debugging of Computer Programs
Klahr and Carver (1988) analyzed the kinds of knowledge and reasoning skills required for students to write and debug a basic graphics design program in LOGO (a simple computer language). Beginning students were asked to write a program for drawing a house with windows and doors. Since first attempts usually involve errors (bugs), students had to learn how to debug their programs. This process involves several steps: (1) noticing and describing the discrepancies between the actual and the intended drawing, (2) considering which commands might have bugs (“buggy commands”), (3) creating a mapping between the descriptions of discrepancies and the potentially buggy commands, and (4) examining specific commands to see whether any of them was the culprit.
The investigators formulated these steps as a series of explicit rules, or “productions,” each consisting of a condition (noting, for example, whether there was a discrepancy in the orientation of the drawing) and an action (checking the values on all of the program’s “turn” commands). They wrote a debugging program, or model, based on these rules, then ran simulations to see how well the model could simulate the performance of students at two different levels of programming knowledge. When the model was set to simulate a student who had a high level of knowledge about the structure of computer programs, it quickly converged on the buggy command; when it simulated a student who lacked this knowledge, the model painstakingly examined a much greater number of possible culprits. The simulation paths followed by these two variants of the model were consistent with the behavior of real students having different levels of programming knowledge.
The model not only provided a rough assessment instrument that could reveal whether students had and used knowledge about program structure, but also served as a set of cognitive objectives in the form of a highly detailed group of productions that could guide instruction and assessment. Klahr and Carver also devised a process for teaching children both the productions and the reasons why they were useful and efficient. The instruction combined explaining to students, posting visual examples of mappings, and engaging children in practice with increasingly subtle bugs. Students achieved the goals of this instruction and were able to transfer these skills to another, nonprogramming procedure, such as written instructions for following a map or recipe. This example shows how characterization of cognitive objectives in the form of productions can provide powerful guidance for instruction and assessment, even when the teaching and assessment methods are fairly conventional.
Implications for Assessment
The preceding three examples are representative of the many cases in which a connection between theories of cognition and learning and the processes of instruction and assessment has been forged. Efforts such as these seek to provide clearer benchmarks of student thinking so that teachers can understand what preceded and is likely to follow the student performance they observe in their classrooms. Having good formative benchmarks helps channel teachers’ attention toward important components and landmarks of thinking. These types of programs therefore emphasize ongoing classroom assessment as an integral part of teaching practice, while still allowing teachers the flexibility to decide which kinds of assistance from their repertoires of informed practice will best achieve the learning goals. Thus the effectiveness of assessment based on cognitive theory rests on a bedrock of informed professional practice.
There are several other examples in the literature in which cognitive principles have been applied to instruction and assessment. Some are not as tightly linked to a highly explicit underlying model of cognition. Marshall’s (1995) schematic problem-solving system for teaching elementary school mathematics is an example. Others, discussed more fully later in this report, include Hunt and Minstrell’s (1996) DIAGNOSER and White and Frederiksen’s (1998) Thinkertools programs for teaching high school and middle school science, respectively. Records of students’ interactions with these programs are a rich source of information about which strategies students use, how well they are able to recognize and repair flawed strategies, and in which situations they see particular knowledge as relevant. As discussed later in this report, efforts such as these provide a foundation for exploring new
methods of assessment that can enhance the processes of learning and teaching.
Without question, important work remains to be done to develop models for areas of the curriculum as it now exists and as it will change with the advent of powerful technology-based learning environments (see Chapter 7). In most domains, including many parts of the science and mathematics curricula, research has not produced descriptions as detailed or robust as some of the examples mentioned in this chapter and elsewhere throughout this report. More extensive research should eventually produce models of progression in learning in many domains beyond mathematics and science. Ultimately, it may be necessary to develop as many models as there are disciplines in the curriculum or domains within a discipline.
METHODS OF OBSERVATION AND INFERENCE
We close this presentation of advances in the sciences of thinking and learning with a discussion of some of the methods of observation and inference that underlie our current understanding of cognition. We describe these methods for two reasons. The first is to illustrate the types of scientific methods on which the findings in this chapter are based. The second is to suggest connections between methods of educational assessment and the methods used by cognitive researchers to uncover students’ content knowledge and cognitive processes.
To accomplish the goal of understanding cognition and learning, cognitive scientists have developed a variety of methods and tools for evaluating people’s knowledge structures and mental processes as they reason and solve problems and for studying what infants and young children know and can do. These methods are linked to a general approach of theory development and testing identical in its overall logic to our earlier discussion in Chapter 2 of the three elements of the assessment triangle—cognition, observation, and interpretation—and their interrelationships. For instance, many detailed studies of human cognition begin with the development of a theoretical model (or models) of the knowledge structures and cognitive processes that characterize people at different levels of competence. Researchers then design tasks for people to perform in order to test the model, carefully selecting those tasks that maximize the possibility of discriminating among competing models or hypotheses. Data from observations of individuals performing various tasks are then evaluated using a logical and/or statistical scheme to determine how well the evidence fits a given model.
This method of reasoning from data about underlying cognitive processes and knowledge structures has been applied to both simple and complex performances. As illustrated earlier in Box 3–4, it is possible to obtain a highly accurate and detailed picture of how children are approaching prob-
lems—using correct or incorrect, taught or invented strategies—by such formal analysis. As the simple addition example in Box 3–4 illustrates, hypothesized models of underlying cognitive activities lead researchers to collect rich data sets that can be used to test hypotheses about both the process and progress of students’ learning. Such models can also provide a foundation for interpreting evidence derived using other data gathering and analysis techniques. Some of the most useful techniques, including reaction-time studies, computational modeling and simulations, analysis of protocols, microgenetic analysis, and ethnographic analysis, are described below.
Reaction-Time Studies
As illustrated for the case of simple addition problems, one method of evaluating cognitive processes is to measure and analyze the amount of time people spend on various phases or components of a given task. Data from these analyses can be highly informative when interpreted according to a model of cognitive processes. With an appropriately chosen set of problems, researchers can determine which of several potential strategies or approaches the problem solver is using. This general approach has been used for a wide variety of tasks, varying in complexity from simple addition and subtraction problems for children (e.g., Siegler, 1998) to complex multimove puzzles (Klahr and Robinson, 1981).
MacLeod, Hunt, and Mathews (1978), for example, used reaction-time profiles to determine whether people used imagery to solve simple verbally presented problems. More recently, Hunt, Streissguth, Kerr, and Olson (1995) used a combined measure of reaction time and accuracy to show that children whose mothers had used alcohol during pregnancy displayed tendencies to be impulsive in problem-solving behavior. This observation, which took less than an hour to make, was consistent with observations made by classroom teachers over a period of months. (It may be noted that the children were 14 years old at the time of testing, so the method may have isolated the effect of a drug taken 15 years prior to testing.)
Eye-movement tracking, a specialized technique for studying reaction times and other key behaviors, has received virtually no attention in the assessment literature. By using what is now relatively inexpensive equipment capable of detecting the direction of a person’s gaze while he or she is engaged in a task, psychologists can gather data about the sequence and duration of eye fixations. This information can then be combined with the results of cognitive analysis to infer—quite precisely, in many cases—which of several strategies is being used. Such analyses can yield insights into differences between experts and novices in a range of domains, from playing chess to operating a modern airliner. This approach provides a “window on the mind” that complements and augments other, more traditional ways
of investigating cognitive and perceptual processes. It has been applied quite effectively in studies ranging from an analysis of strategies used to take well-known intelligence and aptitude tests (e.g., Dillon, 1985; Just and Carpenter, 1992) to analyses of strategies used to process and comprehend sentences (Just and Carpenter, 1992) and even of how students interact with a computer-based cognitive tutor (Anderson and Gluck, 2001).
Computational Modeling and Simulation
For many aspects of cognition that unfold over periods of time greater than a few seconds, methods such as the analysis of reaction-time data are less effective. The processes of cognition may be extremely complex, involving multiple mental operations, and they may be highly dependent on the contents of long-term memory. To study such situations, researchers often develop a detailed model of the knowledge structures and processing steps used to perform a particular task or solve some problem. Many such models are developed as formal computer models that embody a variety of assumptions about the nature of the cognitive architecture and the form in which knowledge is represented in the mind. It is common for these models to be written in the language of production systems containing explicit statements about what people know when they perform a task and the sequence of mental events that occur as the task is performed. Such models are not arbitrary because they are developed from observations and logical analysis of task demands. Most important, they are tested by examining the quality of the fit between results obtained from the simulation and actual human performance. The approach has been used in a wide variety of domains, from young children’s understanding of how balance scales work (Klahr and Siegler, 1978), to high schoolers’ learning of geometry (Anderson and Boyle, 1985), to adults’ performance on text editing (Singley and Anderson, 1988) and spatial navigation (Anderson, Kushmerick, and Lebiere, 1993), to the solution of intelligence test problems such as Raven’s Matrices (Carpenter et al., 1990).
Analysis of Protocols
Rich sources of information about the thinking process are offered by records of what people say as they go about solving a problem. These reports, referred to as concurrent verbal protocols, offer a window on the fleeting contents of working memory. An example is a person’s string of utterances while solving a mental arithmetic problem; these comments might refer to partial and temporary results or to the goals and subgoals the person generates during the episode. What a person says, however, should not be viewed as a reliable description of the underlying cognitive strategies being
used to solve the problem. That information remains to be discovered by researchers who analyze the protocol. (See Ericsson and Simon, 1984, for an elaboration of this fundamental point.)
Verbal reports have been used effectively with a range of age groups, starting as early as kindergarten (Klahr and Robinson, 1981). Inter-rater reliabilities are often in the 0.6–0.7 range, depending on the complexity of the report and the training of the people who interpret it. There is a substantial trade-off between the reliability and richness of the record. Also, the analysis of verbal reports is extremely labor-intensive.
An equally rich but potentially more problematic source of data is the analysis of verbal interactions when two or more people work on a series of problems (Okada and Simon, 1997; Palincsar and Magnusson, 2001; Teasley, 1995). Obvious difficulties arise when these data are used to evaluate individual performance. However, the communicative demands of group problem solving may reveal certain kinds of knowledge that might otherwise not easily be assessed. Although it might be difficult to apply group problem-solving situations to large-scale assessment, it could be informative to ask individuals to respond to—or interpret others’ responses to—such multiple-player contexts. Indeed, several studies of cognitive development have used the technique of asking children to explain why another child responded erroneously to a question (Siegler, in press). These probes often yield highly diagnostic information about how well the child doing the explaining understands a domain.
Microgenetic Analysis
An increasingly refined and popular method of investigating cognitive development is microgenetic analysis.1 In this kind of fine-grained analysis, researchers closely observe people at densely spaced time intervals to view minute processes that could be obscured during less-frequent and less-detailed assessments. The properties of microgenetic analysis include (1) observations that span as much as possible of the period during which rapid change in competence occurs; (2) a density of observations within this period that is high relative to the rate of change in the phenomenon; and (3) observations that are examined on an intensive, trial-by-trial basis, with the goal of understanding the process of change in detail. Microgenetic observations may span weeks or months and hundreds of problems. The process
has been likened to high-speed stroboscopic photography of a drop of water forming and falling from a spigot or the famous photograph of a drop of milk splashing into a shallow dish of milk. The finer temporal grain reveals phenomena that would not be seen at normal speeds, thereby indicating new underlying processes. (See Siegler and Crowley [1991] for an extensive discussion of the method.)
Investigators have examined such issues as a child’s development of concepts, with the goal of identifying when the child first used a new strategy, what the experience was like, what led to its discovery, and how it was generalized beyond its individual use. Research by Alibali and Goldin-Meadow (1993), for instance, suggests that a child’s gestures can be indicators of cognitive change; a mismatch between gesture and speech often indicates a point at which a child is poised to make a transition in understanding. As in the case of reaction-time measures, gestures provide yet another potential window on the mind.
Ethnographic Analysis
Long used by anthropologists and other social scientists to study cultural practices and social patterns, ethnographic analyses have also proven useful for analyzing cognitive processes. These techniques are aimed at gathering rich information about the day-to-day experiences of a community and its individual members. They have been used to study cognitive performance in many different settings, including classrooms, workplaces, and other environments. In the ethnographic approach, researchers immerse themselves in a particular situation to obtain a sense of its characteristics and its people. They make detailed observations and records of people engaging in normal tasks. They may also use interviews, surveys, videotape recordings, or other methods to elicit qualitative information. This approach has been adapted by cognitive scientists to conduct what Dunbar (1999) calls “in vivo” studies of complex, situated, scientific problem solving in contexts such as worldclass research laboratories.
Implications for Assessment
Many highly effective tools exist for probing and modeling a person’s knowledge and for examining the contents and contexts of learning. Some of these methods, such as tracking of eye movements and computational modeling, rely on sophisticated technology, while others, such as close observation of what problem solvers say and do over meaningful periods of time, are outgrowths of more traditional and lower-technology modes of research. Although several of these techniques have been designed for use in laboratory studies with one person at a time, they could potentially be
modified to meet the more demanding constraints of everyday assessment, especially assessment in the context of classrooms.
More generally, the methods used in cognitive science to design tasks linked to underlying models of knowledge and cognitive processing, observe and analyze cognitive performance, and draw inferences about what a person knows are directly applicable to many of the challenges involved in educational assessment. Furthermore, these methods can be used across a variety of assessment contexts and purposes. As developed in subsequent chapters of this report, the crux of the assessment process is the integration of empirically based models of student learning and cognition with methods for designing tasks and carefully observing student performance, and with procedures for interpreting the meaning of those observations. In the next chapter we look at how these three elements come together in the many situations in which a statistical method is needed to help interpret the observational data.
CONCLUSIONS
Contemporary theories of learning and knowing emphasize the way knowledge is represented, organized, and processed in the mind. Emphasis is also given to social dimensions of learning, including social and participatory practices that support knowing and understanding. This body of knowledge strongly implies that assessment practices need to move beyond a focus on component skills and discrete bits of knowledge to encompass the more complex aspects of student achievement.
Among the fundamental elements of cognition is the mind’s cognitive architecture, which includes working or short-term memory, a highly limited system, and long-term memory, a virtually limitless store of knowledge. What matters in most situations is how well one can evoke the knowledge stored in long-term memory and use it to reason efficiently about current information and problems. Therefore, within the normal range of cognitive abilities, estimates of how people organize information in long-term memory are likely to be more important than estimates of working memory capacity.
Understanding the contents of long-term memory is especially critical for determining what people know; how they know it; and how they are able to use that knowledge to answer questions, solve problems, and engage in additional learning. While the contents include both general and specific knowledge, much of what one knows is domain- and task-specific and organized into structures known as schemas. Assessments should evaluate what schemas an individual has and under what circumstances he or she regards the information as relevant. This evaluation should include how a person organizes acquired information, encompassing both strategies for problem solving and ways of chunking relevant information into manageable units.
The importance of evaluating knowledge structures comes from research on expertise. Studies of expert-novice differences in subject domains illuminate critical features of proficiency that should be the targets for assessment. Experts in a subject domain typically organize factual and procedural knowledge into schemas that support pattern recognition and the rapid retrieval and application of knowledge.
One of the most important aspects of cognition is metacognition—the process of reflecting on and directing one’s own thinking. Metacognition is crucial to effective thinking and problem solving and is one of the hallmarks of expertise in specific areas of knowledge and skill. Experts use metacognitive strategies for monitoring understanding during problem solving and for performing self-correction. Assessment should therefore attempt to determine whether an individual has good metacognitive skills.
Not all children learn in the same way and follow the same paths to competence. Children’s problem-solving strategies become more effective over time and with practice, but the growth process is not a simple, uniform progression, nor is there movement directly from erroneous to optimal solution strategies. Assessments should focus on identifying the specific strategies children are using for problem solving, giving particular consideration to where those strategies fall on a developmental continuum of efficiency and appropriateness for a particular domain of knowledge and skill.
Children have rich intuitive knowledge of their world that undergoes significant change as they mature. Learning entails the transformation of naive understanding into more complete and accurate comprehension, and assessment can be used as a tool to facilitate this process. To this end, assessments, especially those conducted in the context of classroom instruction, should focus on making students’ thinking visible to both their teachers and themselves so that instructional strategies can be selected to support an appropriate course for future learning.
Practice and feedback are critical aspects of the development of skill and expertise. One of the most important roles for assessment is the provision of timely and informative feedback to students during instruction and learning so that their practice of a skill and its subsequent acquisition will be effective and efficient.
As a function of context, knowledge frequently develops in a highly contextualized and inflexible form, and often does not transfer very effectively. Transfer depends on the development of an explicit understanding of when to apply what has been learned. Assessments of academic achievement need to consider carefully the knowledge and skills required to understand and answer a question or solve a problem, including the context in which it is presented, and whether an assessment task or situation is functioning as a test of near, far, or zero transfer.
Much of what humans learn is acquired through discourse and interaction with others. Thus, knowledge is often embedded in particular social and cultural contexts, including the context of the classroom, and it encompasses understandings about the meaning of specific practices such as asking and answering questions. Assessments need to examine how well students engage in communicative practices appropriate to a domain of knowledge and skill, what they understand about those practices, and how well they use the tools appropriate to that domain.
Models of cognition and learning provide a basis for the design and implementation of theory-driven instructional and assessment practices. Such programs and practices already exist and have been used productively in certain curricular areas. However, the vast majority of what is known has yet to be applied to the design of assessments for classroom or external evaluation purposes. Further work is therefore needed on translating what is already known in cognitive science to assessment practice, as well as on developing additional cognitive analyses of domain-specific knowledge and expertise.
Many highly effective tools exist for probing and modeling a person’s knowledge and for examining the contents and contexts of learning. The methods used in cognitive science to design tasks, observe and analyze cognition, and draw inferences about what a person knows are applicable to many of the challenges of designing effective educational assessments.
ANNEX 3–1: COGNITION AND BRAIN SCIENCE
There is an ever-increasing amount of information about how the brain develops and processes information and how this is linked to various aspects of cognition, development, and learning. Here we briefly consider two areas of special concern—hemispheric specialization and the effects of enriched environments on brain development—because of the way they have been treated in the popular literature, especially as regards educational practices.
Hemispheric Specialization: Realities and Myths
The notion that the left and right hemispheres of the brain serve specialized functions emerged some years ago from studies of people whose speech was impaired after damage to the left hemisphere. A study by Sperry (1984) of split-brain humans popularized this notion. Essentially, these studies indicated that in most humans, the right hemisphere has become specialized for spatial and synthetic tasks and the left for verbal, analytic, and sequential tasks. Careful laboratory studies of normal humans show clear hemispheric advantages in reaction times when information such as words or spatial
objects is presented to only one hemisphere or the other (Hellige, 1993; Springer and Deutsch, 1993).
Brain imaging studies reveal extraordinary degrees of hemispheric specialization (Thompson, 2000). Spatial navigation involves the right hippocampus; attention shift involves the right parietal lobe; attention processes also involve the right anterior cingulate gyrus and right anterior medial frontal lobe; and visual attention processes also activate areas in the left cerebellum. Verbal short-term memory involves the left parietal and frontal areas; spatial short-term memory involves the right parietal, occipital, and frontal areas and the superior frontal sulcus bilaterally; and face working memory predominantly involves the left precentral sulcus, the left middle frontal gyrus, and the left inferior frontal gyrus. The left prefrontal cortex is more involved in retrieval of information from semantic memory, whereas the right prefrontal cortex is more involved in episodic memory retrieval.
In short, hemispheric specialization is the norm for cognitive processes. But from an educational standpoint, this is of little consequence. While there may be some educational implications, those claimed most often (e.g., that a teacher should address the left and right hemispheres separately) are ill founded. In normal humans, the two hemispheres communicate seamlessly. Information projected to one hemisphere is immediately transferred to the other as needed. During most cognitive operations, both hemispheres are activated.
Enriched Environments and Brain Development: Realities and Myths
Another strand of neuroscientific research has examined the effects of enriched environments on the development of the brain and behavior (Greenough, 1976). Various studies have concluded that rats raised together in a complex environment (“rich” rats) have a significantly thicker cerebral cortex and many more dendritic spines (synapses) on their cortical neurons than rats raised alone in plain cages. Similar results have been found with monkeys. Enhanced cortical development can occur in adult rats, but in rich rats it regresses if the animals are placed in poor environments. Rich rats also perform better than poor rats on learning tasks, but we do not yet know whether the cortical changes relate to learning experiences per se or to other processes, such as arousal.
There is a major problem, however, in the way this literature has been interpreted and applied to humans, such that parents believe they should expose their infants to super-rich environments filled with bells, whistles, and moving objects. A particular example of this phenomenon is the attention given to “the Mozart effect” (see Annex Box 3–1). In fact, the animal literature suggests that the effects of a rich environment on brain develop-
ment are simply the effects of a normal environment; the abnormal condition is isolation, resulting in impaired development, as is seen with children raised in extreme isolation.
Indeed, wild rats and laboratory rats raised in semiwild environments (which may be rich in stress) have the same cortical development as rich rats. Thus, the available evidence suggests that the normal environment provided by caring parents or other caregivers is sufficient for normal brain development.
A common misconception is that the brain grows in spurts and is particularly sensitive to specific educational procedures at these critical growth times. This is not the case. Critical periods—periods in development during which brain systems are especially vulnerable—are indeed real, as demonstrated by the literature on visual deprivation. These periods are important, however, only in abnormal or extreme circumstances. Nor is it true that no new nerve cells form after birth. Studies in rats indicate that particular learn-
|
ANNEX BOX 3–1The Mozart Effect Several years ago, great excitement arose over a report published in Nature that claimed listening to the music of Mozart enhanced intellectual performance, increasing IQ by the equivalent of 8 to 9 points as measured by portions of the Stanford-Binet Intelligence Scale (Rauscher, Shaw, and Ky, 1993). Dubbed “the Mozart effect,” this claim was widely disseminated by the popular media. Articles encouraged parents to play classical music to infants and children and even to listen to such music during pregnancy. Companies responded by selling Mozart effect kits including tapes and players. (An aspect of the Nature account overlooked by the media is that the Mozart effect is reported to last about 10 to 15 minutes.) The authors of the Nature report subsequently offered a neurophysiological rationale for their claim (Rauscher, Shaw, and Ky, 1995). This rationale essentially held that exposure to complex musical compositions excites cortical firing patterns similar to those used in spatial-temporal reasoning, so that performance on spatial-temporal tasks is positively affected. Several groups attempted to replicate the Mozart effect, with consistently negative results (Carstens, Huskins, and Hounshell, 1995; Kenealy and Monsef, 1994; Newman et al., 1995; Steele, Ball, and Runk, 1997;. In a careful study, Steele, Bass and Crook (1999) precisely replicated the conditions described by Rauscher and Shaw as critical. Yet the results were entirely negative, even though subjects were |
ing experiences can enhance the proliferation of new neurons, specifically, the hippocampal dentate gyrus used in hippocampal-dependent tasks.
Implications
In general, applications of brain-based theories to education and assessment are relatively limited at this time, though that may not be the case in the future. As Bruer (1997, 1999) and others have noted, brain research by itself currently provides limited guidance for understanding or modifying complex higher-order cognitive processes. Although neuroimaging or neurophysiological measures may reveal limits to cognitive abilities at the behavioral level, in most cases additional understanding and cognitive theory are necessary to translate these observations into instructional and assessment practices. Rushing to conclusions about the educational implications
|
“significantly happier” listening to silence or Mozart than they were listening to a control piece of postmodern music by Philip Glass. One recent report (Nantais and Schellenberg, 1999) indicates a very slight but significant improvement in performance after listening to music by Mozart and Schubert as compared with silence. When listening to Mozart was compared with listening to a story, however, no effect was observed, a finding that negates the brain model. Mood appeared to be the critical variable in this study. Why did the Mozart effect receive so much media play, particularly when the effect, if it exists at all, lasts only minutes? One might speculate that this was the case in part because the initial positive result was published in Nature, a journal routinely viewed by the media as being highly prestigious in science. Another factor, no doubt, is that exposing one’s child to music appears to be an easy way of making her or him smarter—much easier than reading to the child regularly. Moreover, the so-called neurophysiological rationale provided for the effect probably enhanced its scientific credibility in the eyes of the media. Actually, this rationale is not neurophysiological at all: there is no evidence whatsoever to support the argument that music excites cortical firing patterns similar to those used in spatial-temporal tasks. |
of neuroscientific observations could lead to misguided instructional practices, as illustrated by reactions to press reports of the Mozart effect.
The exceptions are limited to situations in which cognitive capacities are far below the normal range. For example, the design of a rehabilitation program following brain damage may indeed benefit from neuroimaging or neurophysiological measures. A less extreme example is emergent neural imaging research on dyslexia (see Annex Box 3–2, above). At present, however, both the theoretical basis and the methodology for applying these
|
ANNEX BOX 3–2 Neural Bases of Dyslexia Recent studies using brain imaging techniques suggest that dyslexia is in some degree due to specific abnormalities in the way the brain processes visual and verbal language information (see Thompson, 2000). Guenevere Eden and associates at the National Institute of Mental Health used functional magnetic resonance imaging (fMRI) to examine the extent of brain activation in area V5/MT—an area particularly involved in the perception of movement—in response to moving stimuli in dyslexic men and normal control subjects. The control group showed substantial activation in this area, while the dyslexic subjects did not. In contrast, presenting the subjects with stationary patterns resulted in equivalent activations in other visuocortical areas in each group. A key point here is that area V5/MT is a part of the magnocellular visual system, which is critical to normal perception of motion. Perceptual studies suggest that dyslexics are deficient in motion detection. A study at the National Institute on Aging used positron emission tomography (PET) to study the degree of activation of the angular gyrus, relative to occipital regions, during reading in normal and dyslexic men. In the normal subjects, there was a strong correlation between activation (i.e., increased blood flow) in the angular gyrus and occipital regions. In the dyslexic group, by contrast, there appeared to be a disconnection between the angular gyrus and the occipital regions; there was no correlation between changes in blood flow in the two regions. Additional PET studies of reading tasks (Shaywitz et al., 2000) also found striking differences between dyslexic and nondyslexic subjects in the degree of activation of different brain areas. Studies conducted by Merzenich, Tallal, and colleagues showed that |
measures to education or training within the normal range remain to be developed. Even in situations in which methods from neuroscience can be used to diagnose learning needs—for example, in imaging diagnosis of dyslexia—behavioral methods are much simpler to use.
|
children who have trouble understanding spoken language have major deficits in their ability to recognize some rapidly successive phonetic elements in speech and similar impairments in detecting rapid changes in nonspeech sounds. The investigators trained a group of these children in computer “games” designed to cause improvement in auditory temporal processing skills. Following 8 to 16 hours of training over a 20-day period, the children improved markedly in their ability to recognize fast sequences of speech stimuli. In fact, their language was notably enhanced. (See Buonomano and Merzenich [1998] and Fitch, Miller, and Tallal [1997] for extensive discussion of issues of brain plasticity and language, and Merzenich et al. [1996] and Tallal et al. [1996] for initial findings on their procedures for treating language-learning-impaired children.) This appears to be one of the few cases in which basic neuroscience knowledge has led to an effective treatment for a learning disorder.* |
|
Using three themes, this chapter reviews broad categories of formal measurement models and the principles of reasoning from evidence that underlie them:
|