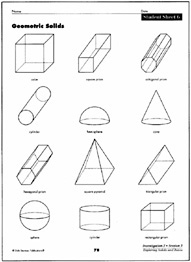
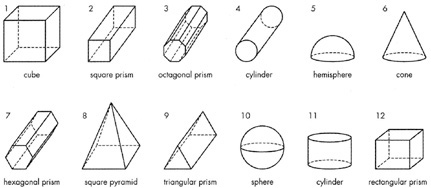
Appendix G: Excerpts from Investigations
ABOUT THE MATHEMATICS IN THIS UNIT
As suggested in the National Council of Teachers of Mathematics Standards, visualization skills are an important part of learning in mathematics and science. In fact, several mathematicians and engineers who reviewed this unit commented that it develops skills they have found essential both in college and in their jobs. The major goal of this unit, therefore, is to develop some basic concepts and the language needed to reflect on and communicate about spatial relationships in three dimensional (3-D) environments.
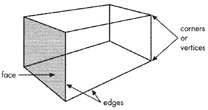
Visualizing a three-dimensional object by looking at a two-dimensional drawing is a critical spatial skill. This task is difficult because a two-dimensional drawing gives us only partial information about the object it represents. For example, the diagram below shows only three sides of the object. Because the picture is two-dimensional, it cannot capture all of the information contained in the actual three-dimensional object it represents.
The next diagram, showing three views of the same objects, presents even less information.

In this type of drawing, not only do students see only three sides, they have no information about how the sides are related or should be put together. To interpret either kind of diagram, students must use the partial information given to form a mental model of the whole object.
Figuring out what the whole object is, given partial information about it, is an important part of problem solving. It requires making inferences, generating and checking possible solutions, and reflecting upon and integrating information gained in previous solution attempts.
Another important notion for both geometry and spatial thinking is that objects look different from different points of view, or perspectives. But students must do more than recognize that this differ ence exists: they must also learn to visualize how objects look from different views. They develop this skill through problems like the three-views task, and problems in which they must figure out what views are possible at different points in given landscapes.
The NCTM Standards also recognize the important role of communication in student learning. This unit encourages students to devise ways to communicate effectively about three-dimensional objects. They explore common graphic methods used to communicate about such objects, for example, isometric and three-views drawings. They also develop suitable vocabulary for describing geometric figures.
To communicate well in writing, students must learn to step into the reader's shoes. In this unit, they see that to write a successful set of building instructions requires that the author see the construction process from the point of view of the reader. Thus, they must learn to read spatial descriptions from the point of view of someone who cannot see the object being described.
Because visualization skills have been neglected by traditional mathematics curricula, many students and adults find such tasks difficult. However, the ability to visualize improves with experience. Through repeated activities with concrete materials, like those provided in this unit, students' visualization skills will gradually increase. Keep in mind, too, that many spatial problems that are difficult to visualize can be easily solved if you build a
INVESTIGATION 1
Making and Visualizing Cube Buildings
What Happens
Session 1: Building with Cubes Students put interlocking cubes together to form cube buildings shown in drawings. They verbalize their strategies for building, and compare the sizes of the different structures.
Session 2: Making Mental Pictures After students are briefly shown a picture of a cube building, they construct it from memory by forming and inspecting a mental image of it. This activity gives students experience with visual organization and analysis of images, and more practice communicating about 3-D drawings and structures.
Mathematical Emphasis
-
Developing concepts and language needed to refleet on and communicate about spatial relationships in 3-D environments
-
Understanding standard drawings of 3-D cube configurations
-
Exploring spatial relationships between components of 3-D figures
-
Developing visualization skills
-
Starting to think about problems related to volume

VOCABULARY SUPPORT FOR SECOND-LANGUAGE LEARNERS
The following activities will help ensure that this unit is comprehensible to students who are acquiring English as a second language. The suggested approach is based on The Natural Approach: Language Acquisition in the Classroom by Stephen D. Krashen and Tracy D. Terrell (Alemany Press, 1983). The intent is for second-language learners to acquire new vocabulary in an active, meaningful context.
Note that acquiring a word is different from learning a word. Depending on their level of proficiency, students may be able to comprehend a word upon hearing it during an investigation, without being able to say it. Other students may be able to use the word orally, but not read or write it. The goal is to help students naturally acquire targeted vocabulary at their present level of proficiency.
We suggest using these activities just before the related investigations. The activities can also be led by English-proficient students.
Investigation 1
cube building
-
As students watch, connect about eight cubes to make a structure of some sort. (It need not resemble a real building.) Explain that you are building with cubes, and that what you are making can be called a cube building.
-
Make two or three more different cube configurations, explaining that cube buildings can have many different shapes.
-
Challenge students to demonstrate comprehension of this term by giving them each about eight cubes and telling them to make a cube building. Have everyone display the finished buildings.
Who has a cube building that looks like mine?
Do you see a cube building made the same way as Luisa's?
Who else has a cube building that is the same as someone else's?
Investigation 2
front, top, side, back
-
Display some small object (a doll, a toy car, an alarm clock) that has a clear front, top, side, and back. Walk around or turn the object as you identify the different views, motioning with a finger from your eyes to the appropriate part.
If I look at it this way, I see the top.
If I look at it this way, I see the front.
From here, I am looking at the side.
-
Make a small, nonsymmetrical cube building. Place it next to the object you have been viewing, and relate the same words (front, top, side, back) to this cube structure.
-
Challenge students to demonstrate comprehension of these words by following action commands.
Stand up when I point to the back of the [clock].
Clap your hands when I point to a side of the building.
Investigation 3
instruction booklet, directions
-
Show and identify instruction booklets from several games, toys, or models. Make sure each booklet is placed on or next to the corresponding
-
Open the booklets and point out that the written text and diagrams are called instructions or directions.
-
Challenge students to demonstrate comprehension of these words by following action commands. Interchange the words directions and instructions.
Pick up the instruction booklet for the model airplane.
Point to the direction booklet for these building blocks.
Point to the first instruction in this booklet.
INVESTIGATION 1
Activity
Discussing Student Strategies
The final activity in this session enables you to more closely observe the strategies students are using to predict the number of cubes that will fit in a box made from a pattern. This should help you better understand how individual students are making sense of the problems.
Show the Discussion Box Pattern transparency, and ask each student to predict how many cubes will fit in the box that it makes. Students write their predictions and a description of how they made the prediction. The Teacher Note, Strategies for Finding the Number of Cubes in a Box (pp. 43–44), includes some examples of students' written descriptions.
• Tip for the Linguistically Diverse Classroom Give each student who may have difficulty describing his or her prediction a copy of the Discussion Box Pattern. Students can mark on this sheet to show how they made their predictions. For example, two students might show their answers as follows:
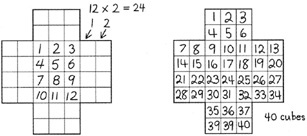
You can easily tell from their markings that one student understands the problem and the other one still does not.
Follow up with a whole-class discussion, asking students to give their predictions and describe their strategies for making them. After all predictions have been discussed, fold a copy of the pattern and fill it with cubes to test the predictions. Ask students how to determine the number of cubes that actually fit in the box. Try the different methods suggested and have the students discuss any discrepancies.