Investigating Teaching Practice: What Mathematical Knowledge, Skills, and Sensibilities Does It Take?
These sessions were designed to focus on looking at practice as a way to identify the mathematical knowledge needed by teachers. Participants took part in two of four concurrent sessions. In each session, they engaged in activities to help them see how teacher knowledge of mathematics is related to investigating tasks that teachers do in the practice of teaching. In each session, the objective was to work through the task as a teacher would, then reflect together about the mathematics teachers need to use in the context of doing the tasks.
SESSIONS
Analyzing Student Thinking
Virginia Bastable, SummerMath for Teachers
Remodeling Mathematical Tasks
Olga G. Torres, Tucson, Arizona Public Schools
Analyzing Student Work
Michaele F. Chappell, University of South Florida
Managing Class Discussion
Erick Smith, University of Illinois-Chicago
Analyzing Student Thinking
Virginia Bastable
SESSION GOALS
This session was designed to allow participants the opportunity to participate in one of the tasks of teaching and to analyze the kind of mathematical understandings, skills, and dispositions this task demands. For this session, the task of teaching being investigated was analyzing students' mathematical thinking.
The overarching questions posed to the participants were as follows:
-
What mathematical knowledge does a teacher need in order to follow, analyze, and evaluate the mathematical thinking of his/her students?
-
What is the nature of the mathematical thinking that teachers must do as they make hypotheses about their students' mathematical ideas?
OVERVIEW
The session was divided into two main components. The first part provided an opportunity for participants to follow the mathematical thinking of students as expressed in a teacher-written narrative. Participants read a five-page case titled “Can you divide 39 into 5? Revisited” and discussed a set of focus questions in both small and large groups. During this part of the discussion, the conversation was designed to allow participants to share and debate their ideas about the mathematical thinking of the students described in the print case.
The second component of the session was an opportunity to reflect on the experience to make more general statements about the kinds of mathematical knowledge required to do this kind of work. After the discussion based on the print case, participants were given five minutes to write about their experience based on this prompt: What kinds of mathematical knowledge, skill, and sensibilities did you call upon as you worked to understand the mathematical thinking of the children in the print case? The session concluded with a discussion of this question.
ACTIVITY CASE STUDY: 39 ÷ 5 OR 5 ÷ 39
The action of sharing provides a context in which children can learn about the meaning of division. It also allows them to
sort out some of the complexities of dividing whole numbers: What happens when the numbers don't divide evenly? Is it even possible to divide a larger number into a smaller? What sense could that possibly have?
In this activity, we visit the same class twice as it explores what 5 ÷ 39 might mean. In the spring of fourth grade, the students think about the question only in terms of whole numbers. What contexts are modeled by 5 ÷ 39 and what would be the result of dividing 5 by 39? When they return to the question several months later as fifth-graders, they are ready to consider their answer in terms of fractions. But their explorations now raise a new set of fascinating questions. The class struggles with the question as described by the teacher.
Participants read the scenario below, “Can You Divide 39 into 5? Revisited.” They were asked to consider these questions:
-
As you read about these students' discussions, what are the ideas about division that are highlighted for you?
-
What new ideas must be entertained as the children extend their work to the realm of fractions?
-
And what ideas are you left to work through for yourself?
|
Can You Divide 39 Into 5? Revisited [A Teacher's Reflection on a Lesson (Schifter, Bastable, & Russell, 1999, pp. 77-82)] This year I am in the fortunate position to have moved up a grade together with my class. The children I had last year in fourth-grade are with me again this year as fifth-graders. I am very pleased. They are delightful children, a pleasure to be with two years in a row. At the beginning of the year, we had much less work to do to establish norms of being in class together; there was already a sense of community among us. The several children who were new needed a couple of weeks to catch on, but they had good models in their classmates. This is especially helpful since we have some difficult circumstances in which to work. For example, I have a class of 28 children that is very unbalanced genderwise: 21 boys and 7 girls! If I had been meeting this group for the first time, we would have had to do a lot of work to make sure that the girls had a voice in the class. I still have to be careful, but in general the girls feel at ease, even if they are in the minority. As far as math class is concerned, most of us already knew what it means to have a mathematical discussion. And it's fascinating to me to have the opportunity to see how ideas develop from one year to the next. In November we were working on division. We had just finished a few sessions in which we looked at remainders in different contexts and saw them expressed as decimals or fractions. We also considered contexts in which it made sense to round up or down to the next whole number. Now I wanted to explore an extension-situation in which there are more sharers than the number of items to be shared. I asked the class to think about 3 kids sharing 2 candy bars. Just as the discussion began, Joe looked puzzled and recalled a conversation that we had last year. He claimed that the class reached the conclusion that we couldn't divide a larger number into a smaller number. As he presented the facts of last year's discussion, others began to nod. They were recalling the conversation and the contexts we used in our 5 ÷ 39 controversy. Now they were looking at me accusingly. How could I be asking them to divide 2 candy bars among 3 kids if we already “knew” that we couldn't do it. From Developing Mathematical Ideas, Number and Operations, part 2: MakingMeaning for Operations Casebook, by Schifter, Bastable, & Russell. © 1999 by Dale Seymour Publications. Used by permission. |
This situation again raised the issue for me of leaving students in the middle of a misunderstanding. Would they have understood any more if last year I had told them that you can divide 39 into 5? Would they have been as invested in today's discussion? Were they now having an intuitive sense that we could do it?
Although it was not my planned entry point into this new division piece—I had intended to work with easier numbers—we stuck with 5 ÷ 39 because the class had an investment in it. I began by writing on the board “5 ÷ 39” and “39 ÷ 5.”
ANTHONY: I think that 39 ÷ 5 will be 7 remainder 4, but I think that 5 ÷ 39 will make a decimal number.
I wonder if he is thinking of a number less than one and I wonder why he went to a decimal rather than a fraction. I was surprised because fractions “look” more like “less than one” than decimals do—at least they do to me.
JACK: I think that you will end up with a fraction of a number because, well, because, 5 and 39—you can't divide 5 by 39 equally. I think it's going to be a number below 0.
I think that Jack is headed in the right direction, especially when he says “a fraction of a number.” I wonder aloud about the answer being a fraction number and then about the idea that it would be below 0. I believe that if I had stuck with my original 2 ÷ 3 problem in the candy-bar context, this might have been easier to visualize. But I don't know if the students would have been so invested; they have a sense of ownership over the 5 and 39 problem.
AL: I agree with Anthony but not with Jack. We had some story problems where the answers were decimals, but they were not below 0. I think we could say that 39 ÷ 5 could be a decimal number. [Al goes to the board and shows how he solved for a quotient of 7.8. I think that this is what Anthony means.]
Anthony says that this is not what he means, but indicates that he doesn't feel ready yet to explain. Al used decimals to solve 39 ÷ 5, but did not try 5 ÷ 39 and did not address the crucial point of using a decimal to name a number smaller than 1. I'm pretty sure that this is where Anthony's going, but I respect his decision to remain quiet for now.
DARREL: I think 39 can't go into 5. I mean it can go into it, but it's going to be a fraction; it's got to be a fraction. A larger number into a smaller number—5 can go into 39, but there's a remainder. No, it's not a remainder; it's not a number.
I really don't get what Darrel is saying. Does he think that fractions or decimals are only remainders? Why does he think that it's not a number?
GONSON: I agree with Anthony and with Jack because 39 divided by 5—5 divided by 39. . . .
Gonson repeats the two problems four or five times. There's something that he's trying to sort out. However, the numbers removed from context clearly have little meaning for him.
JOE: 5 divided by 39 is going to be a smaller number. You got 39 people and 5 candies.
I stop to ask the class which one of the notations—“39 ÷ 5” or “5 ÷ 39”—expresses Joe's story. I want to see if we are at least making a connection between the context and the correct notation. Most of the students didn' t get that last year.
Raymond chooses the correct notation and explains that the answer would be pieces of candy bars. (YES!)
RAYMOND: So, if each kid was going to get equal shares, they would have to cut the 5 candy bars into little equal pieces.
TEACHER: Can you name those equal pieces?
RAYMOND: They might be candy bars.
TEACHER: Can you name the fraction that they might be?
RAYMOND: [After a long pause] They wouldn't be able to do it.
(DARN!)
We stop now to take a class poll. How many people think that you can do the problem 5 ÷ 39 and how many think no, you can't. The results: Yes, 13; No, 15.
After a pause, Joe says that he wants to change his “no” to a “yes.” He starts to explain that you cut each bar into 7 equal pieces and then asks if he can go to the board. He draws circles to show the 39 people and then draws 5 rectangles for the 5 candy bars. He shows that partitioning 2 candy bars into sevenths will yield 14 pieces and then, without making the lines, indicates that partitioning 4 candy bars will produce 28 pieces. He pauses and sees then that the fifth candy bar will give him a total of 35 pieces. He then draws in lines to show that he has cut it into 11 pieces. Now he's satisfied because he has a total of 39 pieces.
Cynthia quickly responds that this representation couldn't be correct because it isn't equal shares. She seems sure of it. There are 4 rectangles with sevenths and only one with elevenths. “That's a problem,” she says.
As Cynthia talks, Valerie goes to the board and points to the elevenths.
VALERIE: Nobody would want one of these small pieces. I think there's something about Joe's solution that feels right, but something also seems wrong.
MARIBEL: I think that Joe is on the right track because each person would only get a really small piece, not anywhere like a whole candy bar. But Valerie is right, too, because the shares that he drew aren' t the same for each person.
LINDA: If I cut each of the 5 candy bars into 39 pieces and then give each kid one piece from each candy bar, you could have each kid have 5/39 of a candy bar.
Linda wants to go to the board and draw hers. She draws 5 rectangles divided up into 39 equal boxes. She is displaying some confidence and some clear mathematical thinking that I have not seen before.
ANTHONY: I think the same thing, that each person will get one piece from the first candy bar and one piece from the second and then from each one after that and will end up with 5 little pieces, so 5/39.
AL: I was thinking that if you wanted you could take 5 from each candy bar over and over again until you were done, but I think that I know that because of the drawing that Linda did.
Al has learned something from the discussion; Linda's work made an impact on him. I'm glad to hear him acknowledge her.
We ended the discussion right there on that day but continued a few days later. Since I happened to have three visitors on that day (three colleagues from the professional development project I'm in), I divided the class into four groups. Each group worked with an adult to come up with a way to show 5 ÷ 39. Time passed very quickly, and we had little time for groups to report back to the whole class.
Joe and Cynthia said that they didn't really have a name for their solution, but they were ready to defend their thinking. Cynthia went to the board and drew the following diagram:
It was time to end class. Time was short but we were clearly not finished yet. Jack looked at Cynthia's diagram and asked what forty fortieths has to do with 5 ÷ 39. 1 asked the students to think about that for their homework.
When we returned to the problem the next day, people were feeling refreshed again, ready to take on Cynthia's diagram. While her drawing helped some of the students picture the problem, it raised even more questions:
-
What is the last piece called? Is it “1/8” or “1/40”?
-
What's the whole?
-
What happens if the last piece is divided into 39 pieces? What if it is divided into 40 pieces?
-
Do we know what 5/39 means?
-
Is “slightly more than 1/8” a better answer than 5/39 because it's clearer even though it's less exact?
-
When we say 1/8, it's 1/8 of what? When we say 1/40, it's 1/40 of what?
-
If we cut the last piece into fortieths, each person gets 1/8 and 1/40 of 1/8. What happens to the extra fortieth? Do we keep on dividing it? (This is where we discussed the “piece,” the “sliver,” and the “crumb.”)
Some of these questions I need to sort out for myself.
FOCUS QUESTIONS
-
Consider the arguments of Anthony, Jack, Al, Darrel, Joe, and Raymond. What might each of them be thinking about division, decimals, about fractions, about what a number is? What is correct about their thinking? What ideas might they be missing?
-
Joe changes his mind from his earlier comments. Explain what it is that Joe now understands? What is he missing?
-
Valerie, Maribel, and Linda offer ideas. Explain the mathematics you see in each case.
-
Joe and Cynthia offer a different kind of representation for the 5 ÷ 39 problem.
-
What is correct about their diagram? What is confusing about it?
-
What is revealed about the students' thinking by the questions that are posed at the end of the text?
DISCUSSION SUMMARY
In the first part of this discussion, participants considered the mathematical thinking of the students represented in the print case. The conversation had several dimensions:
-
clarifying exactly what was said in the print case;
-
making hypotheses about what aspects of mathematics the students understood;
-
making hypotheses concerning the source of the students' confusion;
-
locating the mathematical logic in the student's thinking.
The group also spent part of the time discussing the pedagogical aspects of the case.
The issues raised during this part of the discussion were specifically tied to the mathematics of the case and might not at first glance seem to be relevant to the larger question of what kinds of mathe-
matical knowledge and sensibilities are needed for effective mathematics teaching. However, the groups' responses to the more general question were based on the specific issues raised during the case discussion, and, therefore, they are included in this report.
The list provides a description of the mathematical issues considered by the class described in the print case. For a particular mathematical situation, this list illustrates the range of mathematics and knowledge about the nature of mathematics and mathematical reasoning that a teacher must have to negotiate this kind of classroom conversation. I invite the reader to participate in a second level of conversation while reading the list and to ask what it indicates about the nature of mathematical understanding teachers need to have.
-
Division can be interpreted as partitioning, as repeated subtraction, or as a missing factor.
-
The answer to a division problem can be expressed as a fraction.
-
Interpreting remainders in a division situation is dependent on the context.
-
Fractions can be interpreted as parts of wholes, as answers to division problems, as units of measure, or as missing factors.
-
While
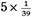 is numerically equivalent to 5/39, these two expressions can represent different ideas.
is numerically equivalent to 5/39, these two expressions can represent different ideas. -
A numerical problem may have multiple representations.
-
Representation is both a tool for expressing ideas and a tool that allows ideas to be manipulated.
-
The transfer from an abstract problem to a concrete situation that exemplifies the problem can be a support for learning.
-
When an abstract problem is related to a concrete situation, there must be consistency between the real life example and the mathematical model.
-
The nature of the inverse relationship between multiplication and division seems more complicated when remainders are expressed as whole numbers.
-
Smaller numbers may have made the problem so easy that the mathematical issue (examining what happens when a smaller number is divided by a larger number) would not have been addressed or even encountered.
-
Analysis of why a particular approach was incorrect was instrumental in developing a correct approach. The students' mathematical arguments examining what was wrong with the first-offered solution provided the means to refine the solution.
It is important to acknowledge that the discussion of issues was rich, energetic, and quite interesting. In fact, with both groups it was hard to turn our attention away from the specifics of the case to the more general question. To provide material for the second part of the discussion, group members were asked to write for a few minutes reflecting on this question, “What mathematical knowledge, disposition towards mathematics, and mathematical understandings, did you call upon in order to participate in this activity of examining children's mathematical reasoning?” The conversation then continued but, because of the participants ' written reflections, with a more general question now on the table: “What kinds of mathematical sensibilities do teachers need to have in order to be able to engage with their students in these ways? ”
In some ways, the second-level conversation was still grounded in the content of the particular set of mathematical ideas that had been discussed earlier; but, even
so, it is still useful to consider some of these statements as particulars of more general principles. As you read the following list of mathematical sensibilities and knowledge needed by teachers compiled by the groups, I again invite the reader to participate in the task we had before us. Use the list as an opportunity to formulate responses to these questions: “What kind of mathematical knowledge is necessary for teachers to be able to engage with their students' mathematical thinking? What understandings about the nature of mathematics and mathematical reasoning must they have?”
-
Have a variety of mental images of 5 ÷ 39; specifically, both a measurement and partitive view of division.
-
Understand the connections (both what is the same and what is different) between the computation 5 ÷ 39 and the number represented by 5/39.
-
Understand the conceptions underlying 5/39 and 5 times 1/39 can be very different, even if these two express the same numerical value.
-
Understand numbers between 0 and 1.
-
Realize that mathematical generalizations are true only for a given domain and that statements that are true for one set of numbers may not be true for another. (For example, “You can't divide a smaller number by a larger number” is in fact true for the domain of whole numbers.)
-
Understand that mathematical generalizations must be revisited (and often revised and extended) as the domain under consideration expands.
-
Take into account one's own (or the teacher's) beliefs about mathematics.
REFLECTIONS
As I examined these lists and reflected on the discussions, I noted that ideas about the nature of mathematics and mathematical reasoning were prominent. While the lists clearly contained significant mathematical content, that content was described within statements of mathematical relationships and mathematical connections. Beliefs about the nature of mathematics were seen as equally important. Expressed in general terms, our discussions implied that to engage effectively with their students' mathematical thinking, teachers must do the following:
-
View mathematics as the development of ideas that are interconnected. For example, as we worked to follow the student thinking, we explored the connections between division and fractions, the inverse relationship between multiplication and division, and the similarities and differences between the set of whole numbers and numbers that are between 0 and 1. This leads to the following implications for teacher preparation: Mathematical content should not be separated into individual topics; the ways preservice teachers encounter mathematics as learners is significant; and understanding how an idea develops over time (and across grade levels) is necessary.
-
Recognize that building mathematical knowledge is an iterative process of making, testing, and revising generalizations. For example, in our discussion we noted that statements, such as “You can't divide a larger number into a smaller number” or “You can't take a larger number from a smaller one” are not absolutely true or false but rather apply over some domains and not
-
others. This leads to the following implications for teacher preparation: Preservice teachers need experiences to identify the mathematical generalizations they hold and to examine them over a variety of number domains; preservice teachers need the opportunity to experience learning mathematics as a series of ever expanding generalizations, understanding the assumptions in each.
-
Recognize the power of mathematical reasoning; that is, have the expectation that mathematics is a coherent field that makes sense and is derivable by reason. One caveat: Some mathematical symbols and forms are agreed on by convention and therefore need to be communicated directly. For instance, in our discussion we noted that the meaning of the division sign is something that is a convention. There are mathematical ideas to be worked through regarding the meaning of division, but there is also a convention by which division calculation is indicated as in 39 ÷ 5 and 5 ÷ 39. For example, in our conversation analyzing the flow of the class discussion in the print case, it was noted the first student solution that was offered was incorrect; however, the mathematical analysis of what was incorrect in the solution moved the class along to a deeper understanding. This leads to the following implications for teacher preparation: preservice teachers need to become aware of and develop their own abilities as mathematical reasoners; preservice teachers need opportunities to sort out which mathematical symbols and forms are conventions and which are amenable to reason; and preservice teachers need opportunities to develop, follow, and critique mathematical arguments.
-
Represent mathematical ideas in a variety of forms: words, diagrams, objects, and symbols. For example, in our discussion we talked about mental images of the operations; we drew diagrams to express mathematical ideas; and we expressed ideas through language. This leads to the following implications for teacher preparation: When preservice teachers encounter mathematics content, they need to have experience with a variety of forms—not only symbolic representations; mathematics class should be a forum for communicating mathematical ideas in both writing and speech.
-
Appreciate that mathematics, while abstract, is often used to model problems that are based in real-world situations and that one operation may model a variety of situations. For example, in our discussion we drew upon a range of meanings for division and for fractions, and we examined the connections between those meanings and a variety of problem contexts. This leads to the following implications for teacher preparation: Preservice teachers need to have experiences linking their current conceptions of the operations to problem contexts and vice versa; mathematics course work should include applications or math modeling components.
Finally, I should note these statements are not unusual to those familiar with the National Council of Teachers of Mathematics Standards. However, it is important to show the way those ideas are connected to the specific discussions that took place at the conference and to highlight the implications of those ideas for preservice teacher preparation.
CONCLUSION
Although the writing of this report and my attendance at the conference has generated many questions for me, there is one in particular that I would like to highlight. It is clear we cannot expect any undergraduate program to include all of the mathematics content that preservice teachers will need to draw on over the course of their careers. This is especially true if we commit ourselves to providing opportunities for preservice teachers to explore mathematical ideas, develop as mathematical reasoners, and deeply engage with a subset of mathematical ideas to determine the ways children make sense of those ideas over time. Even while I expect that once such ideas about mathematics and its nature are understood, teachers would be in a position to continue to learn mathematics through the process of teaching, I am still left asking, “What is the set of ideas around which the undergraduate experience should be built? What set of mathematical ideas offers the most power to the undergraduate students?” These are questions we should continue to ponder.
Schifter, D., Bastable, V., & Russell, S. J. (with Yaffee, L., Lester, J. B., & Cohen, S.) ( 1999). Developing mathematical ideas, number and operations part 2: Making meaning for operations casebook. Parsippany, NJ: Dale Seymour.
National Council of Teachers of Mathematics. ( 1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
Remodeling Mathematical Tasks
Olga G. Torres
SESSION GOALS
This session was designed to allow participants to participate in a task of teaching and to focus on the mathematical knowledge needed to do that task. The task of teaching under investigation was remodeling mathematical tasks. The following question was posed:
-
What mathematical knowledge does a teacher need to remodel a mathematical task to make the task simpler, to broaden student access, to add another dimension to the task to move students forward in their thinking, or to use the same concept in a slightly different form to provide another experience with the idea?
OVERVIEW
The chief activity of the workshop was a variation on a riddle, “Coins in the Purse.” As successive clues were posted on the overhead projector, questions were asked so that the group could deduce the value of the coins in a change purse. To capture their mathematical insights and understandings for later discussions, participants recorded their thinking on paper at every stage.
ACTIVITY
First, participants listened to the sounds the coins made when the coin purse was shaken, then the question, “What coins could I have in the coin purse?” was asked. This began a discussion of what coins were possible, given that the coins were U.S. currency.
Clue 1: There are six coins in my purse.
Question 1: What is the most money I could have?
Clue 2: There are only two different values of coins.
Question 2: What coins are possible and what could be some possible maximum amounts?
Some participants felt there was really only one answer to the question of possible maximum amounts, and some thought it possible to have several maximum amounts. Each was asked to explain their perspective. Some felt confusion
would arise if statements were not clearly stated, and others stated that the maximum amount was relative to the possible combination of coins the student was considering.
It was interesting to observe how one group articulated that it was in the best interest of students to avoid confusion. But, narrowing the possibilities also narrowed student thinking. And from the other perspective, the broader the language, the more opportunity for students to be flexible with number. One choice was for the convenience of the teacher to be precise and get to the answer quickly, and the other choice was to allow the development of mathematical thinking on the students' part as they work at their solutions.
Clue 3: Only dimes and pennies are in my purse.
Question 3: What are the possibilities?
After time was given for participants to record all the possibilities on paper, the combinations were recorded on the overhead.
Clue 4: There are more dimes than pennies.
This clue eliminated some of the combinations that were generated from the previous clue, leaving two combinations, 5 dimes + 1 penny and 4 dimes + 2 pennies.
Clue 5: There is only one penny.
With this last clue, only one possible answer to the original question remained.
Participants were then asked to reflect individually on the mathematical knowledge they used to process the information given in the activity. After five minutes, they began to discuss their thoughts in small groups. The mathematics they identified included computation, value of coins, proportionality, combinations, inequalities, the logic of compared statements (conjunction), decimals, place value, and linear combinations. The mathematical processes included reasoning, systematic listing, and organization of information.
Using Liping Ma's terminology, participants were actually identifying many knowledge packages—a combination of mathematical understandings used in solving the problem. However, the contents of these packages became very difficult to identify. The packages were not made up of distinct parts, and it was more a case of “unraveling” the contents. The ideas were so intricately woven together that it was hard to identify the underlying mathematics embedded in each. At the same time, some of the mathematical ideas applied in the problem-solving experience by the participants were so well known and seemed so intuitive that the participants did not realize that the mathematics they used was once learned, for example, converting the number of coins into amounts of money. In other cases, it was difficult to break down a knowledge package because this is a new way of thinking. Some of us are so far removed from our initial learning of a concept that it is hard to visualize the essential components of the mathematical concept in the activity. The perception often exists that the ideas taught at the elementary level are simple and that it is easy to teach what students need to learn in these grades. The activity helped to make it apparent that anyone involved in teaching mathematics at the elementary level needs to confront the complexity of the apparently simple mathematical ideas these students need to acquire and develop.
A constant series of questions was
asked as knowledge packages were being identified: What are the essential understandings a learner must have to be able to
-
have a sense of place value?
-
count money?
-
use operations? (addition, subtraction, division, and multiplication)
-
represent something symbolically?
-
establish equivalency?
Another way of questioning used to get at the underlying mathematics was, “If the mathematics needed to determine whether two representations are equivalent is a knowledge package, what are the contents of that package. What are its key pieces?”
It was interesting to note that the papers participants used to record their thinking held tremendous information about the reasoning process of the writer. Some made a table listing all the combinations of 6 coins in an orderly sequence and identified all the possible combinations (see Table 1).
Others randomly listed combinations that worked. And still others used different methods of reasoning. The fact that there were different ways to reason was not always immediately obvious to the participants because many pieces of knowledge were being used. Much discussion about the mathematics in the task occurred as participants became
Table 1. Coin Combinations
|
Dimes |
Pennies |
|
0 |
6 |
|
1 |
5 |
|
2 |
4 |
|
3 |
3 |
aware of important “key pieces” contained in such general terms as “place value” or “counting money.” Participants also commented on the danger of assuming that these key concepts are present in student/teacher knowledge bases.
Throughout this exercise, I was conscious of how important it is to know about key number concepts, such as inclusion, 1:1 correspondence, and conservation of number, and of how these concepts contribute to acquiring mathematical understandings. At the elementary level, it is critical to know these key concepts, which help provide the foundation for developing number and operation sense.
Participants were asked to remodel the task, identifying the purpose for the remodeled task. The following were among the suggestions:
-
Make the task simpler to broaden student access. For example, instead of specifying the number of coins, ask how many ways there are to make $0.51.
-
Add another dimension to the task to move students forward in their thinking. For example, specify the number of coins and ask the students to indicate what other information they would need to figure out the amount of money in the purse.
-
Use the same concept in slightly different form to provide another experience with the idea. For example, use pattern blocks to find the number of each block.
The discussion of remodeling reinforced the need to recognize how important it was when engaged in remodeling a task to be cognizant of the key pieces that constitute the original “knowledge package. ” Participants acknowledged that aware
ness of the key mathematical components of a task helps in remodeling the task to build on or extend students' mathematical experiences and to avoid the possibility of creating a “fun” activity devoid of mathematical content.
DISCUSSION SUMMARY
Points raised in the discussion included the following:
Different ways to present the problem
-
The order of clues could be changed.
-
The clues could be presented all at once.
Different ways to change the problem
-
The number of coins could be changed.
-
The problem could use a less abstract form of measurement, such as weight.
Different features of the problem to consider
-
The representation is important, including the role of visual and concrete images.
-
The problem could be seen as involving sets.
-
Language is important.
-
The problem can use inverse relations (numbers of dimes and pennies) and involves algebraic reasoning.
-
The context can be important because the content underlying the task may depend on context.
General observations about the teacher's knowledge base
-
Do all teachers need a rich and varied math background?
-
What knowledge do teachers have at the start?
-
Belief structures should be considered as part of knowledge.
-
Math beliefs are held in the context of some math knowledge.
-
Teachers need to understand what knowledge packages there are to unpack.
As I conclude this summary, I'm cognizant of how very complex it is to teach mathematics. One must be informed about human development, knowledgeable of mathematics content, curious about how mathematical knowledge is constructed, patient with the knowledge that understanding is developed over time, and possess a disposition towards learning and teaching that capitalizes on the dynamics of the learning environment—the people, their ideas and experiences, and the physical materials.
Analyzing Student Work
Michaele F. Chappell
SESSION GOAL
The goal of this session centered on the mathematical knowledge, skills, intuitions, and/or dispositions that matter in order to examine and analyze student work. This goal was positioned within a larger context that dealt with understanding the mathematical knowledge elementary teachers need to teach mathematics well. The session focused on these questions:
-
What mathematical knowledge does a teacher need to analyze student work?
-
What level of mathematical knowledge does a teacher need to respond to varying strategies in ways that will move the entire class forward in their thinking?
OVERVIEW
Forming the basis for the two group discussions were several student responses to the “Mixing Juice” task, which is to determine the relative concentrations of water and juice concentrate in various mixtures (see Figure 1). The exercise is excerpted from the seventh-grade Connected Mathematics Project text, Comparing and Scaling (Lappan, Fey, Fitzgerald, Friel, & Phillips, 1997, p. 27-28).
ACTIVITY
Participants began the session by solving the “Mixing Juice” task. Ensuing dialogue focused on the mathematics entailed in doing the problem. The participants, some individually and some in pairs, critically examined the 12 responses of the student teams (see Figure 2). In the analysis, the participants summarized the responses, noting the strategies used, the differences and similarities between them, and other mathematically related factors that may have contributed to the students' work on the task. At the close of the session, participants recorded their responses to the goal and shared the insights they had related to the focus topic.
DISCUSSION SUMMARY
During both sessions, the discussions focused on three major points: (1) the mathematics embedded in the “Mixing
|
Figure 1. Mixing Juice |
|
Every year, the seventh-grade students at Langston Hughes School go on an outdoor education camping trip. During the week-long trip, the students study nature and participate in recreational activities. Everyone pitches in to help with the cooking and cleanup. Arvind and Mariah are in charge of making orange juice for all the campers. They make the juice by mixing water and orange juice concentrate. To find the mix that tastes best, Arvind and Mariah decided to test some recipes on a few of their friends. Problem Arvind and Mariah tested four juice mixes |
|
|
|
From Comparing and Scaling: Ratio, Proportion, and Percent by Lappan, Fey, Fitzgerald, Friel, & Phillips. © 1997 by Connected Math. Used by permission.
Juice” task; (2) the examination and analysis of the students' work; and (3) the knowledge, skills, and dispositions that matter in analyzing students' mathematics work. An elaboration of each point is provided below.
Mathematics entailed in the task
Participants identified several mathematics content areas embedded in the “Mixing Juice” task. Major topics included the following:
-
understanding proportional reasoning;
-
comparison of different ratios, percentages, and/or fractions;
-
part-to-whole relationships;
-
scaling (e.g., how many “recipes” are needed to make the total amount?);
-
conversions to different units for comparison (e.g., reducing numerator to 1);
-
closeness of the particular numbers—thinking about combining by adding versus multiplying;
-
closeness of the ratios compared to a 1:1 ratio; and
-
distinctions between fractions representing ratios and fractions representing rational numbers.
Other issues surrounding the conversations about the content related to how individual students might think about the task. For instance, one issue pertained to various solution techniques such as “eye-balling ” the ratios of concentrate to water versus finding the percentages of concentrate per cup of mixture. A sliding scale or meter analogy was proposed to illustrate how one might think about the “orangeness ” situation. The ideas of pictures, tables, and graphs were introduced as possible strategies students may use to find a solution. A second issue dealt with the appropriateness of using one approach over another: how one determines the appropriateness of using ratios versus additive differences, for example. Depending on the user, certain approaches may be more efficient and natural to carry out while others require more work.
Another issue highlighted the potential complexity of the situation. The ratios (and proportions) may be thought about as measures (e.g., concentrate-to-concentrate, water-to-water) or as scaling factors. Here, the key idea is keeping track of the unit. A closer examination of the concentrate-to-concentrate or the water-to-water measures indicates that one ratio represents the invariant that measures the mixture while the other represents the invariant of the opposite. Although, to some, one of these ratios may seem intrinsically preferable to the other, both will work in finding a solution.
Examining and analyzing the students' responses
Individually, in pairs, or in trios, the participants examined the 12 responses provided by the student teams (Figure 2). Much of this discussion concerned the mathematics involved and the overall focus question, although comments were made either about the students' work or about the analysis process itself. For example, the groups compared several solutions (e.g., see Teams 1, 5, and 7 or Teams 2, 8, and 11) and examined how they were similar in procedure but different in presentation. Participants discussed the likely choices students made about the division and rounding procedures (e.g., see Teams 2 and 3) and about the estimation used in shading parts of wholes (e.g., see Team 4). They observed how certain teams “produced more work” than seemed necessary. They also noted that the explanations provided vary in detail; whereas some teams (e.g., see Team 1) provided thorough explanations, others (e.g., see Team 9) allowed the mathematics to “do the talking.” Finally, one team's (Team 12) explanation did not seem to match well with the visual solution that appeared, but it was subsequently learned that an error in transcription might explain the disparity.
Participants recognized the process of analyzing the students' work as quite engaging. They reported how the process allowed them to look through a different lens and examine the various contexts from which fractions and ratios may emerge. They commented that because students' work will likely be analyzed within frames of reference, such as teacher expectations or previous lessons, teachers will need to conduct such an activity with open minds. Teachers should recognize their personal values and frames of reference that could lead to certain
evaluations of students' work. Participants discussed how the process and the particular task highlight the need for mathematics instruction that builds on students' understandings to construct a meaningful knowledge of ratios. In addition, because problem solvers all have their own individual methods, teachers must be prepared to think differently in order to understand the various methods students may use in solving a problem of this nature.
Identifying what matters
This discussion pertained to the overall focus questions for the session. Participants shared their thoughts on the mathematical knowledge, skills, intuitions, and dispositions that matter in analyzing students ' work. Their ideas, which encompass thoughts that are both specific to the “Mixing Juice” task and generic to any mathematical activity, are listed below.
Mathematical knowledge that matters:
-
proportional reasoning knowledge package, which, itself, is very complex;
-
role of ratio as expressed in various symbols and situations;
-
arithmetic associated with manipulating ratios (as opposed to rational numbers);
-
flexible understandings of the mathematics (e.g., one could assert that Mix A is the most orange by arguing that the complement of Mix A is the least orange.);
-
different visual representations that are transferable to other contexts;
-
varied solution strategies and how to compare them for correctness, efficiency, and generalizability; how to rank them by sophistication on a developmental continuum;
-
detecting incorrect representations and rationales for such misconceptions (e.g., knowing which aspects of the concept students misunderstand and how to help students see mistakes in their thinking);
-
contextual field (i.e., what mathematics the work supports and where the work fits in the students' broader mathematical experience);
-
linkages between concepts (e.g., the meaning of hierarchy);
-
constructs well beyond the mathematics involved in the task (e.g., does stating 4 cups to 8 cups call upon a different mathematics than stating 1 to 2?).
Skills involved in the process of learning that matter:
-
observe several pieces of data simultaneously;
-
consider problems in terms of relationships, rather than specific techniques;
-
analyze the mathematical terrain of problems with rich potential for learning;
-
recognize valid and invalid concepts (although they may be unfamiliar or have not clearly been expressed);
-
determine how to correct invalid ideas.
Dispositions that matter:
-
look at problems through a different lens;
-
develop interests in and curiosities about students' thinking;
-
invite students to communicate their rationale;
-
appreciate the varied ways to solve problems and recognize that what appears the simplest way for one child may be the least efficient for another;
-
assume that students' work contains valuable mathematical thinking;
-
evaluate students' work as information about instruction;
-
realize that correct answers do not always indicate that students understand the core ideas; likewise, incorrect
-
answers do not always indicate that students lack such understanding;
-
develop a mathematical value system that allows for different choices to be made about reaction to students' work; knowledge of the school mathematics curriculum is important in developing this value system.
Other factors that matter:
-
what the teacher does with all of the information obtained from analyzing students' work;
-
how the teacher plans for the next day once the information is obtained;
-
how to use students' work to generate teacher research questions, such as asking what this child really understands about “x”;
-
the role of the National Council of Teachers of Mathematics (NCTM) Standards (NCTM 1989, 2000) in analyzing students' work;
-
the balance that should be maintained as teachers sort through the many aspects of students' work, considering the numerous demands upon the teacher and the various subjects to be learned.
The ideas outlined above are not intended to serve as a complete list; at best, they represent an attempt to capture the rich dialogue that transpired during both sessions of the workshop. Presenting them in such a format should not imply that a response to the question of what matters can be reduced to a simple “check-off” list of items. Indeed, understanding what matters most when teachers analyze students' mathematical work is a complex phenomenon and undoubtedly will require an integration of several components, some of which have been included here and others yet to be mentioned.
Lappan, G., Fey, J. T., Fitzgerald, W. M., Friel, S. N., & Phillips, E. D. ( 1997). Comparing and scaling: Ratio, proportion, and percent (Connected Mathematics Series). Palo Alto, CA: Dale Seymour.
National Council of Teachers of Mathematics. ( 1989). Curriculum and evaluation standards for school mathematics. Reston, VA: Author.
National Council of Teachers of Mathematics. ( 2000). Principles and standards for school mathematics. Reston, VA: Author.
Managing Class Discussion
Erick Smith
SESSION GOALS
The session was designed to allow participants the opportunity to participate in a task of teaching and focus on the mathematical knowledge needed to do that task. The task of teaching under investigation was managing class discussion. The questions posed were as follows:
-
What mathematical knowledge does a teacher need to orchestrate productive discussions?
-
What is the relation between mathematical understanding and teacher questions?
-
How is what a teacher knows about mathematics reflected in the examples a teacher chooses and the decisions the teacher makes about pursuing discussions about student responses and work?
OVERVIEW
Tony Brown, a math educator from England, tells of being in a professional session where he had to imagine himself as a fly on the wall and describe what the room would look like. He recalls thinking of tabletops as trapezoids and other shapes and figures that arose from his imaginary setting. He realized that the mathematics he was constructing arose not only from the objects he perceived but from his relationship to those objects. Or as he claimed,
Any act of mathematics can be seen as an act of construction where I simultaneously construct in language mathematical notions and the world around me. Meaning is produced as I get to know my relationship to these things. (Brown, 1994, p. 156)
For a mathematics teacher, the “world around me” consists primarily of students, the mathematical language and artifacts they produce, the curriculum, and the norms of schooling. Thus, from Brown's perspective, the mathematical meaning a teacher constructs is in relationship to “these things,” that is, the mathematical world of students.
If we take this contextual view of mathematical meaning seriously, it naturally leads one to wonder how the mathematics of teaching is related to the content of typical mathematics courses. That is: What do we mean when we say teachers do not have enough content knowledge? Another way to ask this is: How do teachers make mathematical meaning within the context of the norms
and goals of schooling as they develop an understanding of their students in general and of the mathematical thoughts of their students in particular?
ACTIVITIES
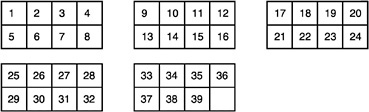
This session addressed these questions by looking in depth at one classroom example where a problem is posed, sixth-grade students work on the problem in small groups, and the small groups make presentations on the board (see Figure 1).
The focus of the discussion was on what kind of knowledge and understandings a teacher would need to manage a classroom discussion around these presentations. An important goal of this session was to focus on teaching “in the moment,” that is, trying to look at what a teacher needs to draw upon in real classroom situations and put less emphasis on general categories of mathematical knowledge.
Participants were given the following instructions:
-
Building on what you have just decided, you look at the clock and see you have 15 minutes to the end of class.
-
What would be your next step?
-
How might you organize a discussion?
-
How would you use what the students have presented?
-
Where would you like to be at the end of class?
-
What would you want the students to learn?
-
How might you characterize your goals for the day in terms of the important math content?
DISCUSSION SUMMARY
After some discussion of these issues, the sessions ended on the more general issue:
Now step out of the role as teacher in the moment to be the reflective teacher. What kinds of knowledge and understandings did you call upon to make the decisions you made as the teacher of the moment?
In the discussion, participants identified several areas of content knowledge that a teacher would presumably need in this situation. These included the following:
-
A broad understanding of operations including appropriate analogies for the operations and the interplay between addition/multiplication and between subtraction/division.
-
An understanding of the role of units, especially in the way units play out in a division problem.
-
An ability to translate symbols into actions (and vice versa).
-
An understanding of equality and of the mathematical use of the “=” sign.
Participants suggested specific ways in which a teacher might start the discussion, such as focus on solutions that are most problematic (the first and sixth solutions) or focus on a solution that is reasonable (the second solution).
In the discussion, we were able to describe the general mathematical knowledge a teacher might draw upon in this situation, and we were able to describe some specific ways to proceed. What was more difficult was to describe what knowing would be supportive for a teacher “ in the moment” and the ways that knowing would be connected to the mathematical worlds of the students. In this particular class, it would be natural

Figure 1. Scenario Presented to Workshop Participants (Adapted from Schifter, Bastable, & Russell, 1999, pp. 120-122)
From Developing Mathematical Ideas, Number and Operations, part 2: Making Meaning for Operations Casebook, by Schifter, Bastable, & Russell. © 1999 by Dale Seymour Publications. Used by permission.
that a group of outsiders would not know the connections and backgrounds that would underlie this connected knowledge. Yet in the group discussion, it was difficult to even decide what it was we were trying to describe.
That this group of experienced professionals did not seem to have language to describe some of the essential kinds of knowledge and ways of knowing that might be important in a particular teaching situation is disquieting. Had there been sufficient time in the sessions, it is likely that more ideas would have been forthcoming and possibly some consensus would have arisen. However, what seems to be a significant conclusion from the session is that we have little readily available language for describing the ways that we want teachers to know subject-matter, that is, language that goes beyond what is typically covered in general mathematics courses.
By focusing on what a teacher needed to know at a particular moment in an actual classroom, this session seemed to highlight a theme that ran through the Workshop sessions. We can make lists of general mathematical topics important to teaching, but understanding how the knowledge of those topics becomes integrated into the actual act of teaching is more difficult. A growing awareness of these issues has led to the development of curricular materials to support teacher learning of mathematics that attempt to connect that learning to the contexts of classrooms by embedding the mathematics into classroom contexts, students' work on mathematics, and teacher interactions about their own classroom mathematizations. As such materials become more widespread, one might expect the development of a language for better describing the mathematical knowledge that supports teaching. As that happens, sessions such as the one described here may offer even stronger insights into the mathematics of teaching.
Brown, T. ( 1994). Describing the mathematics you are part of: A post-structuralist account of mathematical learning. In P. Ernst (Ed.), Mathematics, education and philosophy: An international perspective (pp. 154-162). London: Falmer Press.
Schifter, D., Bastable, V., & Russell, S. J. (with Yaffee, L., Lester, J. B., & Cohen, S.) ( 1999). Developing mathematical ideas, number and operations part 2: Making meaning for operations casebook. Parsippany, NJ: Dale Seymour.





























