Page 23
VISUAL SIMULATION AND ANALYSIS
Physically Based Animation
DAVID BARAFF
Pixar Animation Studios Richmond, California
Animation is a painstaking business. Traditional two-dimensional hand-animated movies require 24 frames of animation per second (or 30, if you animate directly for video), which translates to about 1,500 frames per minute. It was recognized early on that a master animator's time was wasted drawing all those frames; instead, senior animators began drawing characters in key poses at significant points of the action, and more junior animators (“tweeners”) became responsible for drawing the characters in the in-between frames.
Roughly the same process happens in computer animation today. An animator produces what are known as “key frames”—that is, positions for a character at a small number of frames—and the computer interpolates smoothly between them (typically with some sort of spline curve). Additionally, the animator is not responsible for directly drawing the geometric shape of his or her character; this portion of the task, known as “rendering,” is also done by the computer. Instead, the animator is given a relatively small number of controls with which to manipulate the character. A simplistic model of a human might allow the animator to control one or two degrees of freedom per joint in the human (knees, elbow, hips, neck, and so on) and might result in only a couple dozen control knobs. However, a character that needs to convey real emotional content typically will have hundreds of control knobs, allowing the animator to delicately manipulate facial features, breathing, fingers, and the like. As a result, top-quality computer animation is still an expensive proposition.
Physically based animation had its origins in the early 1980s, with the goal of easing an animator's burden. The initial premise was that animators work very hard trying to make realistic animation, and animation is realistic when it conforms to what we see in the real world; hence, realistic animation must have
Page 26
a lot to do with the physics of our world. If we could build animation systems that worked directly from the principles of physics ( Figure 1), then animators clearly could have an easier time animating, and, in many cases, we could dispense with the animators entirely!
INANIMATE ANIMATION?
As it turns out, the initial premise of physically based animation overlooks a key aspect of what animators need to be good at: acting. Consider an action as (seemingly) simple as human walking. Can we use an animation system that understands physics to realistically animate a human walking? The answer, in fact, is yes and no: we can simulate a human walking in some way but not necessarily in the style or manner that we might want for a particular application or scene in a movie. (And walking is, indeed, amazingly complex, both as a movement and as a way of conveying an emotional state—a character's walk can easily convey that he or she is happy, tired, scared, hurt, confused, and so forth.)
Early on, it became obvious that merely running a physical simulation of a system and using the result as animation resulted in “inanimate animation.” That is, if you want to produce animation of models or objects that need to seem “alive,” then the control aspect of your model is as important (or perhaps even more important) that the underlying physics of the model. Coupling physically based animation with requisite control systems is an ongoing and difficult research problem, but it takes us away from our intended topic.
SECONDARY ANIMATION
A much more fruitful niche for physically based animation has turned out to be secondary motion. There are times when the requirements of an animation will overwhelm any animator, and there is no choice but complete automation of the process. An excellent example of this is clothing in computer animation.
While a complex character might have hundreds of degrees of freedom (DOFs) for an animator to manipulate, moderately realistic (or even stylized) clothing has tens of thousands of DOFs, because of the geometric complexity of even the most modest garment ( Figure 2). In addition, there are strong constraints (relationships among the controls of the model) on how clothing behaves under motion in order for it to look like clothing. Using physics to simulate the motion of clothing becomes the obvious (and only) realistic choice. Similarly, automatic physics-based motion of fire, liquids, dust/rain/snow, avalanches, and so on, are all prime targets for physically based animation.
Page 27
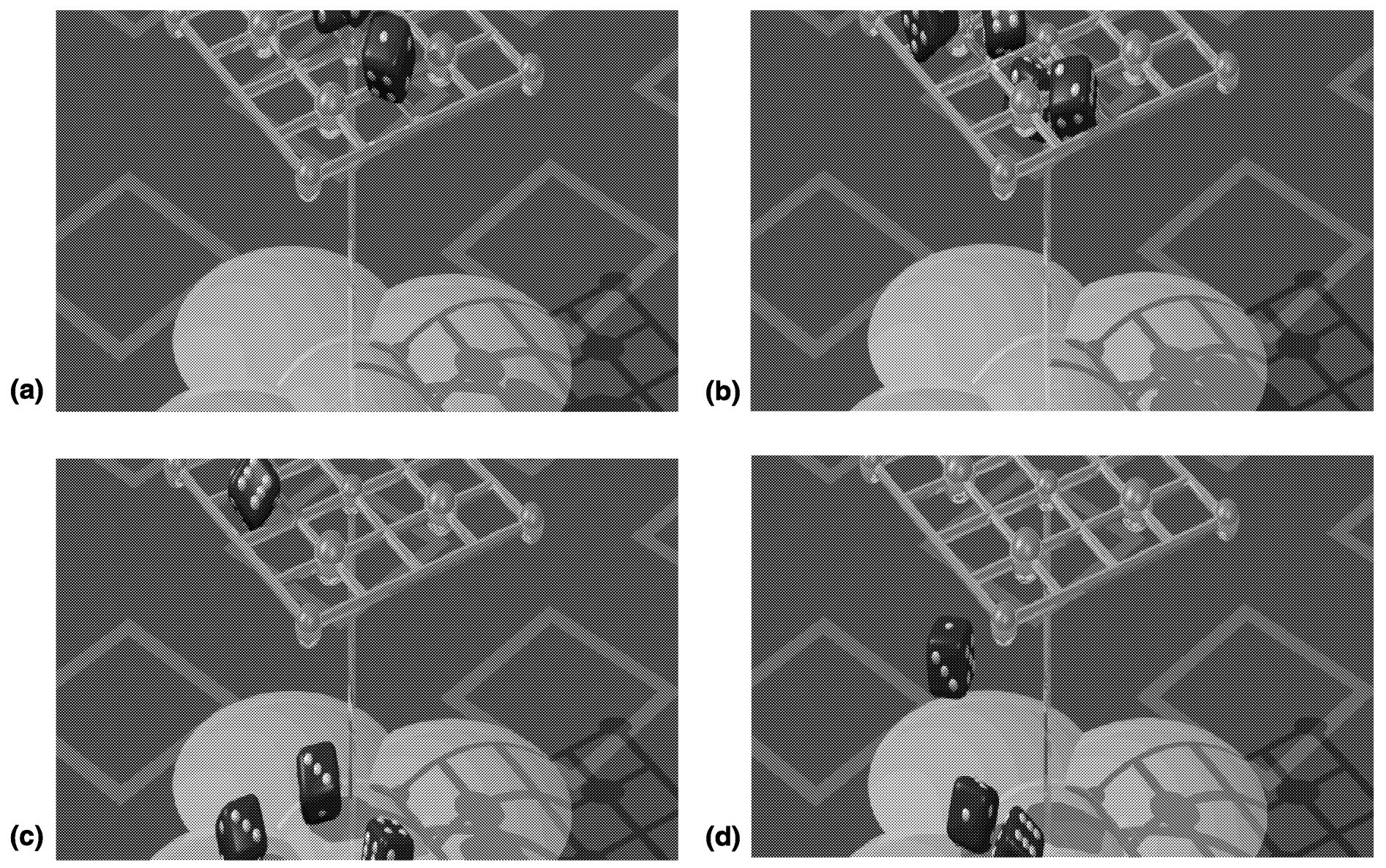
~ enlarge ~
FIGURE 1Simulation as animation. A pure rigid-body simulation of dice falling through a lattice produces realistic animation without the talents of a skilled animator. SOURCE: ©1990 David Baraff.
Page 28

~ enlarge ~
FIGURE 2 Cloth simulation. A single sleeve, simulated as a mesh with more than 14,000 completely independent particles. SOURCE: ©1997 Physical Effects, Inc. Reprinted with permission.
UNDERPINNINGS
It would not be inaccurate to say that physically based animation is, to a large extent, simply physical simulation, provided, however, that one keep in mind that the purpose of the simulation often has a decidedly different flavor from most traditional engineering activities. At a high enough level, physically based animation can be simply described as follows: starting from a description of a system's initial state, and giving a differential equation describing the behavior of the system, we wish to follow the evolution of the system over time. Equivalently, we are solving an initial-valued differential equation. The differential equation, of course, takes its form from the particulars of the world we are trying to animate.
This high-level description obviously hides many details. For example, the differential equation may involve either explicitly or implicitly various constraints on the system over time. The state of the system may be discontinuous (usually not in space, but velocity discontinuities are often fundamental to treatments of rigid bodies in contact). If the number of variables describing the system state is high, we may have to deal with very large systems of coupled equations. In some cases even the inherent computational complexity of the simulation itself may be questionable; for example, some treatments of rigidbody simulation give rise to individual steps for which the solution is NP-
Page 29
complete! Finally, when it comes to animation, strict realism may not be (and often is not) the desired goal; animation, in the end, exists because of the desire to view the world not as it really is but as the artist chooses it to be. Conformance of a simulation to the animator's world often turns out to be a much harder challenge than conformance to the “real” world.







