Appendix B
An Uncertainty Analysis of Neutron Activation Measurements in Hiroshima and Nagasaki
Neutron activation was measured with two fundamentally different types of detection with different types of errors: counting atoms with radiometric methods (beta or gamma counting) and counting atoms with accelerator mass spectroscopy (AMS). The following discussion focuses first on the general approach to error analysis that is used here, and then on each classification of measurement.
The general approach used here is to begin by exhaustively identifying all the quantities that are measured and the formulas by which investigators use the quantities to calculate results in the terms commonly reported in the literature. There must initially be a thorough consideration of the uncertainty in all the measured or assumed values of quantities that are used by investigators to arrive at the final reported result, although some of the quantities may prove to be known with such accuracy and precision that their uncertainty can be ignored in a quantitative treatment. The latter quantities can then be treated as constants. For example, we assume the weighing of samples and standards to be so precise and well calibrated that the associated error is not included in any of the estimates calculated here. But, a volumetric error is typically associated with pipetting microliter quantities of liquids, such as might be used to prepare calibration standards, and this would be a potential contributor to experimental error of some significance if not verified and corrected by weighing.
The objective is to estimate the total uncertainty of each reported result in relation to some presumed true value of interest. For the purposes of this appendix, the true value of interest is the amount of the neutron activation product nuclide per unit mass of the associated stable target element that existed in the sample being measured at the time of the bombing (ATB) in 1945. Depending on the measurement method, this value may be stated in units involving ra-
tios of numbers of atoms or in units of radioactivity per unit mass of the target element.
Sample-specific activity ATB (August 6 or 9, 1945) is related to the dosimetric quantities of interest for survivor dose in a complicated way. The sample-specific activity ATB is a function of the bomb-related thermal-neutron and epithermal-neutron fluences that existed in the sample ATB. Those fluences are in turn related to the free-field neutron fluences at the same location in a way that depends to some extent on local moderation and absorption of the free-field neutron fluences. Local moderation occurs in the terrain and structures close to the sample and in the sample itself. The free-field neutron fluences are of paramount interest because they are the quantities used to calculate doses to survivors and because they constitute a uniform basis for the comparison of measured values. This appendix does not analyze the uncertainty in the free-field neutron fluences calculated by DS86; they are discussed in Chapter 6 of this report. The relationship between free-field and insample neutron fluences is discussed below in connection with the plotting and fitting of measurements.
For analytical purposes, every measured or assumed value is treated here as a random variable. The difference between a true value and an individual measured value has both a systematic and a random component, corresponding to a mean difference and a standard deviation. The former is commonly characterized as a bias and the latter as a random error. Every experiment is based on methods that are intended to minimize systematic and random errors. Although it is difficult for a retrospective analysis as reported here to obtain sufficient information to identify and provide a useful quantitative estimate of a nonzero bias, every reasonable effort is made to do so. More often, the main quantitative result of this type of analysis is to verify the magnitude of an investigator’s estimated random error or provide a more realistic estimate of the true random error. This type of analysis can also help to identify possible sources of error that cannot be quantified with the information at hand but can be addressed in recommendations for future work.
Another way to look at the uncertainty issue is to focus on the limiting case of measurements that approach the limits of detectability by making generic calculations of limits of detection with accepted formulas based on statistics. For radiation-counting methods, such calculations must be based on assumed nominal values for sample and background counting time, counting efficiency, and the amount of the stable target element present in the sample, which are treated as constants for the purpose of the calculation. Those calculations are useful for illustration and for defining limits below which reported measured results should be treated with particular caution. They also help to define the nature of some important relationships for the lowest-level measurements, relating the comparative sizes of counting-system background, sample background, and calculated or measured sample content from the bomb fluence. These issues are addressed in detail below.
PROPAGATION OF ERROR
To estimate the uncertainty in the final reported result, sample-specific activity ATB, a propagation-of-error calculation can be based on the equations by which the measured and assumed values of quantities are used by investigators to calculate reported results, incorporating the uncertainty estimates of the individual values involved. The desired result is an estimate of the total uncertainty in the final reported result that is due to all sources combined. For the purpose of this report, standard formulas based on the first-order terms of Taylor-series expansions are used. It should be noted that these formulas tend to underestimate somewhat the variance in the reported values as a function of the available estimates of component uncertainties. The underestimation might not be negligible. As one indication of the potential inadequacy of first-order approximations, it can be noted that a large majority of the major-component uncertainties given by measurers have fractional standard deviations exceeding 10% in one or both components typically reported. To evaluate and improve the estimates of uncertainty in the specific activity ATB, numerical simulations were performed.1 For any individual result, there is generally no reason to believe that errors in the different components are correlated. The resulting propagation-of-error calculations are therefore relatively simple; the formulas used in spreadsheet calculations based on the first-order approximation are given in the sections below. In general, it is noted that for any set of uncorrelated values and estimated standard deviations, say,
X±a,Y±b,Z±c
and any constants mi, the sum or difference formula gives the result
(1)
|
1 |
When simplified numerical simulations (multivariate normal with zero covariance) are performed to evaluate the combined error of sample-specific activity as calculated from a radiation counting, it is notable that if any term in the divisor of the equation as it is normally formulated (counting efficiency, result of the stable element assay) begins to exceed about 12–15% coefficient of variation, the error distribution of the specific activity becomes badly skewed upward. That is because such a situation involves a nontrivial probability of a small value close to zero in the divisor of the formula for specific activity, with such small values causing arbitrarily large calculated specific activities. Several of the 152Eu measurements of Shizuma and others (1993) have rather large estimated error in the assay of stable europium as reported by the authors. Of these, two cases may deserve review of the determined stable europium content because the calculated specific activity is considerably larger than other nearby measurements: Sorazaya Shrine, 873-m slant range, 15% estimated SD in stable europium, and Enryu Shrine, 1081-m slant range, 14% estimated SD in stable europium. In addition, it should be noted with regard to all the radiometric neutron-activation measurements in the literature that if there are cases in which the author’s estimates of the error in stable europium and cobalt assays are substantially understated, those measurements might be similarly affected. |
and the product or quotient formula gives

(2)
As a matter of nomenclature, the coefficient of variation σ/μ (standard deviation divided by mean) for a variable of interest may be given herein as a fraction and called a fractional standard deviation, or it may be given as a percentage and simply called a % error. Thus, Equation 1 says that for such formulas as sums, differences, and weighted sums the standard deviations themselves sum in quadrature. Equation 2 similarly says that for products and quotients the fractional standard deviations sum in quadrature.
CORRELATED ERRORS
In addition to the possible effect of correlation of the errors in the component quantities on a single result, another type of correlation must be considered in any application based on more than one measured result: correlation of errors among reported results. Various subsets of measured values, classified at various levels (for example, within the same sample, within a given sampling location, within a given investigator’s laboratory, and within a given range of calendar time), can share the same measured or assumed value for some part of the calculated result, such as a calibration factor, and can therefore be correlated with respect to that factor. Such cases will be discussed in detail.
One might ask whether the measurements at a particular site can tend to share a common bias relative to the true value, that is not due to sharing a common value for something, such as a calibration factor. To the extent that such a covariance might exist, it would most likely be due to an unmeasured covariable that affects the true value for the sample, rather than to an error inherent in the measurement process. Nothing about the site should affect the process, and the properties of the sample should have minimal effect on the measurement process. For example, the sample-specific properties that would affect the counting efficiency, such as the effect of the elemental composition of the sample on its self-absorption of the emitted radiation being measured, are likely to have negligible influence.
However, there might be sample-specific variables that appreciably affect the neutron activation level of the sample for a given incident bomb fluence (such as boron content or water content) that have not been measured or have not been properly incorporated in the calculated value for the sample. Such site-correlated errors are not included in the uncertainty analysis reported here, because they are errors in the calculated value and not the measured one as defined here. However, they do
need to be considered in fitting curves to the measurements. They are discussed further in the next section.
COMBINED UNCERTAINTY ESTIMATES: 32P MEASUREMENTS OF FAST NEUTRON FLUENCE
The 32P measurements made by Japanese physicists in 1945 (Yamasaki and others 1987) have often been cited in relation to general source term parameters such as yield and height of burst. Because these measurements are at fairly close distances and are used in this manner, it is of some interest to characterize their uncertainty as an aggregate, as well as individually. Unfortunately, characterizing the uncertainty of these measurements in the aggregate, or using them in fitting a model, is difficult to do correctly, because their errors are highly correlated. Even the calculation of a weighted mean for these measurements, for the reasons discussed below, would require a very careful and somewhat complicated approach to propagation of error.
The 32P measurements were very fortuitous, or very well planned, in several respects, including the facts that the measurements were made on essentially pure elemental sulfur of reliably high purity, and the measurements were originally calibrated with a natural radioactive source of good chemical purity, uranium oxide, whose emission rate of beta particles can therefore be accurately predicted. These factors, along with the preservation of the Lauritsen electroscopes used to perform the measurements, allowed a series of careful retrospective studies of factors related to the measurements’ accuracy by Hamada (1983a,b, 1987) and Shimizu and Saigusa (1987). Hamada (1987) estimates a 2% random error in uniformity of sample preparation that relates to a counting efficiency factor, presumably related primarily to the evenness of spreading the powdered sample on the glass plate for counting and the resulting differences in self-absorption of betas. Based on the accuracy quoted by Hamada (1987) for his 32P reference standard and the likely counting error variance of his calibration measurements, it would seem reasonable to estimate that the calibration error should not exceed 5% or so, where the greater error would likely be the counting error of his calibration measurements rather than the accuracy of his standard reference material.
These numbers can be combined with the counting error given by Hamada (1987) in his Table 2 to provide estimates of the errors in individual measurements considered in isolation, which are shown in Table B-1. (The chemical purity of each sample, as it relates to the accuracy of the estimated weight of pure sulfur present in each sample, appears to be high and to have a fractional standard deviation of only a fraction of a % based on Hamada’s data (1987). It is ignored in this calculation.)
These estimates differ very little from those of Hamada, because the larger counting errors do in fact predominate. The fractional standard deviation (FSD’s) of individual measurements are fairly large, up to 53%. Some measurements with even larger errors are not shown in the table, and some measurements for which the azimuth is unknown are also omitted.
TABLE B-1 Estimates of Errors in Individual Measurements Considered in Isolation
|
Sample |
Counting Interval, min. |
Electroscope Reading, div s−1 |
Activity (Net) dis s−1 Sg−1 |
Total Error, SD dis s−1 Sg−1 |
Total Error % FSDa |
|
background |
200 |
0.00124 |
– |
– |
|
|
A4 |
40 |
0.00200 |
2200 |
434 |
20 |
|
B5 |
38 |
0.00224 |
2940 |
441 |
15 |
|
C6 |
45 |
0.00154 |
880 |
399 |
45 |
|
D12 |
70 |
0.00162 |
1500 |
442 |
29 |
|
D12 |
70 |
0.00178 |
1140 |
247 |
22 |
|
E13 |
95 |
0.00205 |
2430 |
342 |
14 |
|
F14 |
74 |
0.00166 |
1260 |
335 |
27 |
|
G15 |
90 |
0.00167 |
1370 |
337 |
25 |
|
G15 |
90 |
0.00175 |
1620 |
336 |
21 |
|
H7 |
85 |
0.00144 |
630 |
336 |
53 |
|
aFSD=fractional standard deviation. |
|||||
An important caveat is that the errors in these measurements are highly correlated. This is because all measurements appear to share a common determination of background, which is an additive error, and a common determination of counting efficiency, which is a multiplicative error. Background in particular was a rather proportionally large error in this experiment. Any effort to use these error estimates in fitting to calculated values should involve a very careful propagation of error formulation that begins by extracting the common error in background. This would require a careful reestimation based on reworking Hamada’s (1987, actually, Roesch’s and Jablon’s) equations (1) through (8) for calculating error in count rate based on error in time to reach a common electrical charge on the electroscope.
INVESTIGATORS’ ESTIMATES OF UNCERTAINTY BASED ON COUNTING STATISTICS
In radiation-counting applications, investigators have almost universally calculated their estimated errors in the radioactivity content of samples on the basis of Poisson counting statistics. With rare exceptions, these appear to be the sole basis of plotted error bars and published estimates that are intended to suggest the precision of measured values. But the raw data of the measurements are generally not available to allow checking of the calculations. For example, in the case of radiometric methods, one would have to obtain at least the
-
Calendar date(s) when samples were counted.
-
Lengths of the counting intervals (in detector live time) and counts in the region of interest and background subtracted, for all counts of bomb-fluence samples.
-
Blanks for background and calibration standards for counting efficiency.
Although it was the intent of the committee’s questionnaire (see Appendix A) to obtain such information, it was not provided by most investigators.
The most basic aspect of the calculations can be checked in a limited way via a calculation of minimum detectable activity (MDA). If one has estimates of background count rate, counting efficiency, and counting interval for sample and background, an MDA can be calculated and compared to give the sample’s estimated content. Such calculations have the limitation that they assume the counting efficiency and background count rate as fixed constants. The validity of such comparisons is also a function of the extent to which the assumed counting intervals are representative of those used. Calculations of MDA and related quantities are discussed further in later sections.
ESTIMATION OF COMPONENTS OF UNCERTAINTY NOT ESTIMATED BY INVESTIGATORS
Because the method of uncertainty analysis was limited to what could be done with incomplete information, it was necessary that the method be flexible and carefully adapted to each individual situation. In some cases, particular uncertainty components have been estimated on the basis of expert judgment and knowledge of typical standards and practices or by using a carefully considered application of values obtained by other investigators with similar methods. Where such judgments have been made, they are clearly so identified in the following sections, regardless of the magnitude of their effect (sensitivity) on the total uncertainty estimates.
STATISTICAL DISTRIBUTIONS OF ERRORS
A word about statistical distributions is in order. The types of detection methods considered here are counting methods, and their raw results are expected to obey the Poisson distribution. At present it appears that all measurements have sufficient numbers of counts for the Poisson to be well approximated by the Gaussian distribution; therefore, skewness is not a major concern. The counting statistics tend to dominate the uncertainty of the measurements, especially inasmuch as the assays were typically calibrated by comparison with other results of the same (radiation-counting) type applied to standard materials. In the case of radiation measurements, assay of stable-element concentration is another major factor in the reported result. Radiation counting of the activation product radionuclide is a third. Most assays of elemental concentration were also performed with radiation counting after controlled neutron irradiation. Moreover, reported results are usually based on averaging of several measurements, and the central limit theorem supports the distributions of component and overall errors’ being approximately Gaussian.
Statistical distribution does not affect the second-moment properties that define the propagation of error equations, but it does affect the interpretation of a standard deviation in terms of cumulative probability. For example, the construction
of confidence intervals depends on the type of the assumed underlying error distribution and on the estimated value of its standard deviation. Another important consideration in this particular analysis is that the type of error distribution affects decisions about the type of transformation that should be applied to the variable, if any, to fit curves to the data as a function of distance from the epicenter.
ERROR IN THE INDEPENDENT VARIABLE: DISTANCE FROM THE HYPOCENTER
There is appreciable error in the principal independent variable of interest in all analyses of the measurements: the distance from the burst point (epicenter) of the bomb to the location of the sample. That distance is used as a major input for calculating survivor dose. The standard approach in all dose-calculating systems has necessarily been to assume radial symmetry about the hypocenter (ground zero) of the bomb. Therefore, the free-field value calculated by the dosimetry system—the value for an idealized infinitesimal-volume element of air or tissue suspended 1 m above flat ground—depends only on the radial distance from the epicenter (slant distance) or hypocenter (ground distance).
Most investigators have published estimates of uncertainty in distance with their measurements; among neutron measurements, this information is lacking for only a small portion of the data, mainly values reported in the DS86 final report and earlier source documents. The values that are published by measurers are somewhat subjective and have some unusual attributes. For example, because of the geographical context, investigators have tended to think of the “plus-or-minus” values that they estimate as being something like a maximal credible range, rather than a standard deviation. The plus-or-minus uncertainty values tend to fall mostly in a range from about 3 m to about 30 m, but there are a few values as high as 90 m, for samples for which the measurer knew only that a sample came from a particular large building and could obtain no better information from the collector.
The magnitude of the effect of distance error on calculated neutron activation is a function of two factors: geometry and effective attenuation of the radiation fluence. The effective attenuation of the fluence by interactions in air and on the ground predominates: a relaxation length of 125 m, for example, corresponds to a change in fluence of roughly 25% over 30 m at any distance.
In contrast, at distances of interest in connection with survivor dose, the inverse square effect is small: it changes fluence from a point isotropic source by only about 6% over a slant distance of 30 m at 1 km from the epicenter, and 4% at 1.5 km. The effect is larger at shorter distances of interest for fitting the measurements, such as about 10% at 600 m. For a more extended source, such as the fireball, as might apply to delayed radiation to some extent, the geometrical dependence is closer to the inverse of distance than to the inverse square, and the effect is correspondingly smaller.
Efforts are in progress at RERF to provide improved estimates of map location, distance, and related uncertainty by using geographical information system (GIS)
software in combination with the extensive source documents available. Distance uncertainty is discussed below in relation to fitting curves to the data.
GRAPHICAL DEPICTION AND FITTING OF CURVES TO THE DATA
Scaling by the Inverse Square of Distance
For purposes of graphical depiction, measurement results stated ATB are plotted against slant distance from the epicenter on a semilogarithmic plot, which is standard in the literature. To facilitate visual comparisons, all values—those calculated by DS86 and those calculated from measurements—are multiplied by the square of slant distance in kilometers. That removes the inverse-square dependence on distance that is universal for radiation emitted isotropically from a point source. Hence, in the absence of attenuation, radiation fluences from such a source, so scaled, would have a perfectly constant fluence. And the fluences of radiation from such a source if subject to exponential attenuation as a function of distance, would fall on a straight line, whose slope is commonly characterized by its inverse in terms of the natural logarithm; the distance subject to attenuation by a factor of 1/e, is commonly called a relaxation length. Any systematic departure from a straight line indicates a departure from one or both of these assumptions: the source is not isotropic or is not of small extent compared with the distances involved, or the attenuation is not effectively an exponential function of distance.
Appropriate DS86-Calculated Values for Comparison with Specific Measurements
To compare measured values with DS86-calculated values, it is necessary to determine appropriate DS86-calculated values. Samples were chosen by investigators to be near the surface of the sampled material in a location with a direct line of sight to the epicenter, with three exceptions:
-
Samples that were deliberately taken at increasing depths in the material at a given location to measure activities related to depth.
-
In the case of gamma thermoluminescent dosimetry measurements, samples like the pottery shards from the interiors of houses and buildings or underlying roofing tiles that were chosen with foreknowledge that the results would be questionable and that were prominently so identified as “shielded samples.”
-
Steel concrete reinforcement rods (“rebar”) located at depths approximating 8 cm in concrete, that were measured in the 1960’s with a specific plan in mind to evaluate factors related to the spectra of incident neutron fluences (Hashizume and others 1967).
The approach of exclusively measuring surface line-of-sight samples for evaluating neutron activation as related to distance was pursued in the belief that such samples would yield measured values as close as possible to the free-field or free-in-air value at the location in question. That approximation is subject to question. The extent to which a given sample reflects the free-field value at 1 m above flat ground, as a standardized reference value for systematic comparisons of measured values as a function of distance from the bomb, depends on more than its being a surface line-of-sight sample. It also depends on the size, shape, and composition of the structure in which the sample is situated and on the properties of the surrounding terrain.
The situation is further complicated in that DS86 was written to calculate not neutron activation, but rather neutron dose to tissue. Calculating neutron activation, even a free-field value, requires a mathematical convolution of the appropriate neutron-interaction cross-section values with the energy-dependent neutron fluences given by DS86. Such calculations should be done by an expert in any case.
The neutron measurements are in four categories with respect to the DS86-calculated values available for comparison:
-
Measurements for which detailed calculations based on DS86 neutron fluences have used Monte Carlo or Sn simulations with a model of the structure containing the sample, such as the Sn calculations for the Yokogawa Bridge samples by Oak Ridge National Laboratory (Kerr and others 1990) or the calculations done for the Motoyasu Bridge pillar by Hasai and others (1987).
-
Measurements for which relatively simple calculations have been done by Scientific Applications International Corp. (SAIC) to account for the shielding effect of materials overlying the sample.
-
Measurements that have been reviewed by an expert at SAIC (Dr. Egbert) and classified as being well approximated by the free-field value on the basis of expert judgment regarding the nature of the sample location.
-
Measurements, mostly published since 1997, for which no expert evaluation has been performed and the only value available for comparison is the free-field value.
M/C and C/M Plots vs. Plotting M and C Separately
For purposes of comparing measured and DS86-calculated values as a function of distance, some investigators have preferred simply to plot the ratio of measured to calculated (M/C) or the ratio of calculated to measured (C/M) values. However, that gives no information about the behavior of the two individual quantities as a function of distance. When plotting the quantities separately against distance, it is natural to plot the DS86-calculated free-field values rather than the sample-specific in situ calculated values because the former lie on a continuous
curve. If the measured values are plotted without modification, their difference from the DS86-calculated free-field values reflects both
-
The difference between a DS86 free-field value at the indicated distance and a completely calculated DS86-based value for the sample, where the latter includes the effect of local terrain and the shielding due to overlying materials, as would be calculated by a full application of computational methods to the DS86 free-field fluences.
-
Any difference between the measured value and such a completely calculated value for the sample.
To make plots and fitted values that focus on the discrepancies between measured and DS86-calculated values, we made two key decisions:
-
Measurements at subsurface depths in the sample material were omitted to minimize the shielding correction between free-field and sample-specific calculated values, and
-
Plotted and fitted measured values were corrected for the ratio between the DS86 free-field calculated value and the most completely calculated sample-specific DS86 value available. That is, “measured free-field equivalent values” were calculated to remove the effect of shielding and local terrain as much as possible and obtain the free-field value that would presumably be associated with the in situ measured value.
It is emphasized that “measured free-field equivalent values” do not reflect any calculation that is new or different from what has been done before. They merely represent a way of plotting measurements in relation to a continuous curve for the DS86-calculated value as a function of distance for samples that have sample-specific calculated values that differ from the free-field calculated values.
Choice of Functions for Fitting to the Data
The DS86-calculated gamma dose for both cities falls very close to a straight line on a semi-log plot of values scaled by the square of distance: its attenuation is close to exponential, and its effective source size is fairly small relative to all distances on the ground. Some 1/r dependence at shorter distances is to be expected from the distributed nature of such sources as fission products in the fireball and neutron-capture gammas arising from interactions with nitrogen in the air near the explosion. Efforts to estimate coefficients separately for a 1/r dependence and a 1/r2 dependence in fits to the measured values were not successful, apparently because the rate of change in the fitted values due to a 1/r dependence is smaller that due to the exponential attenuation and because of the lack of precision in the measurements. The DS86-calculated neutron activation for both cities shows a small but appre-
ciable upward curvature on such a plot: its relaxation length increases somewhat with distance. For Nagasaki, there is also a substantial departure from a straight line at distances less than about 600 m. For that reason, points representing less than 550-m slant distance in Nagasaki, both DS86-calculated and measured, have not been included in fitted curves. (This peculiarity is related to the source term, and is different for the 1993 suggested modifications to DS86.)
Inherent Assumptions of M/C and C/M Curves
Fitting curves through the data must be done with an understanding of the assumptions on which the fitted curves depend. In no case are such assumptions trivial or beyond question. For example, fitting a line through the ratios of DS86-calculated and measured values on a semilogarithmic plot against distance r is by definition a matter of fitting
(3)
with α and β as fitted parameters. This is a natural result only if M and C are functions of distance that can be separated into a factor, some arbitrary function f(r), that is identical for M and C and a factor that is exponential in r:
(4)
with α=αm−αc and β=βm/βc. It is not a natural result in any more general context. If the fitting is done on logarithms with a simple linear regression and all measurements are given equal weight, there is no consideration of the large variability in the precision of the various measurements. In addition, a subtler but constraining decision is being made regarding the presumed nature of the error distribution: that it is approximately normal in the logarithmic transform, as would be the case for a lognormal distribution of error in the untransformed measured value.
Method of Fitting
To provide a physically meaningful comparison of measured values and DS86-calculated values, some curves must be fitted. Otherwise, there can be no discussion of parameters, such as relaxation length. To provide a basis for such comparisons, a decision was made to fit curves to the scaled DS86 free-field calculated values and scaled measured values corrected for cosmic background and for the ratio of the free-field value to the most completely calculated sample-specific in situ value available. We decided to work in the original space rather than using the logarithms or another transform of the values and to obtain fitted curves by using a nonlinear regression
and weighted least squares. We fitted curves that were based on a simple nonlinear function that gives a good fit to the DS86-calculated values and is consistent with the physics of radiation transport, and we made an important decision to weight each observation by the inverse of its estimated variance as derived from the uncertainty analysis.
Two concerns were recognized in considering how to assign weights to the data to determine the amount of influence that each measurement would have on the fitted result. First, some weighting for the relative uncertainty of each type of measurement is desirable: measurements with greater uncertainty should have less influence. The other concern is related to the fact that the values of interest span a factor of 103–104 in some cases: values measured at the longest distances are sometimes 10−3 or 10−4 of values measured near the hypocenter. A residual of any given absolute size is 103 or 104 times as large in proportion to the average measurements at the longest distances as at the shortest distances. With no weighting, the residuals for the least-squares fit would tend to be that much larger as well in relation to the measured values. If all measurements had been made to an equal relative precision (equal estimated coefficients of variation), this would seem inappropriate.
A simple and natural solution is to use the raw uncertainties reported by the investigators as weights in an inverse-square formulation. This addresses both issues in an intuitively appealing way. That is, if the author reported a value as “x±y” where y is stated in the same units as x, then the weight used for that measurement in the regression would be simply
(5)
Two important relationships are clarified by restating Equation 2 as a product of two implicit factors:
(6)
Weighting by 1/y2 thus amounts to using a weight equal to the product of the inverse of the square of the measurement itself and the inverse of the square of an estimate of the coefficient of variation, σ/μ, of the measurement. Thus, x estimates μ, and y estimates σ.
Inasmuch as the first factor is inversely proportional to the square of the measurement, smaller measurements have higher values of this factor to make up for the lower size that their residuals would tend to have in a proper fit to the correct functional form with the same relative measurement precision. That is, among measurements of the same estimated relative precision, stated as estimated coefficient of variation (same value of y/x), the second factor is constant, and the weights are inversely proportional to the squares of the measured values. Under these
conditions, any discrepancy between fitted and measured values that is some given proportion of the measured value produces a term of the same size in the weighted sum of squares:
(7)
where A(rx) is the fitted curve according to Equation 1 evaluated at the same slant range as x.
Therefore, with constant relative measurement precision, each residual has an influence on the fitted curve equal to the proportion of the measured value that the residual represents, regardless of whether the measured value is a large one or a small one. That seems to be a reasonable approach to giving measurements at greater distances an “equal say” in determining the fitted value.
In addition, inasmuch as each weight has a second factor that is inversely proportional to the square of its estimated coefficient of variation,
(8)
residuals for measurements of a given mean size are weighted in inverse proportion to their estimated variances. The approach has assumptions and limitations, as does any other statistical method, but it is thought to be reasonably straightforward and useful in these circumstances.
Function Used for This Analysis
The function that was chosen for fitting the neutron measurements was
(9)
where A(r) is the activation at slant distance r, and r0 is the slant distance at the hypocenter, that is, r0=burst height. Thus, the scaled values (multiplied by the square of slant distance) are being fitted, and three parameters are estimated:
-
A (r0), the scaled activation at ground zero (hypocenter).
-
λ0, a relaxation length at the hypocenter.
-
δ, a change in relaxation length per unit slant distance.
The function A(r)r2 is consistent with the transport dynamics of the neutron energy groups because the rate of change in the exponent decreases gradually with increasing distance. The function gives a very good fit to the DS86-calculated values, and is flexible enough to accommodate a complete range of curves with dif-
ferent rates of change in relaxation length. But it is simple and requires fitting only one parameter in addition to the slope and intercept of the exponential. Some early attempts were made to fit an equation containing a term for 1/r in addition to 1/r2, but they did not give meaningful results. The effect is too small in comparison with the exponential attenuation to be quantified, especially at the distances for which measurements are made.
Distance Uncertainty
As noted above, the uncertainty in distance, which is the independent variable, is not negligible. A complete and consistent set of distance-uncertainty estimates is not yet available; furthermore, it does not appear feasible to use a statistical method for the fitting that is designed to handle error in the independent variable. In the case of 152Eu, a small subset of four measurements have unusually large distance uncertainties, as estimated by the investigator—50–90 m, compared with less than 30 m for all others. The effect on the fitted curve of removing these measurements was evaluated and found to be negligible. As noted above, RERF is making continuing efforts to reduce this source of error.
Correlated Errors
In producing fitted curves, it would be desirable to take account of all covariance among measurements, especially that known to exist among measurements that share factor or factors, such as a measured value of stable cobalt or europium, a calibration factor for counting efficiency, or a calibration factor for the assay of stable cobalt or europium.
But, it does not appear feasible to identify such sets of measurements exhaustively; it would require minutely detailed information from investigators. However, a major portion of this correlation can be addressed by considering situations that involve multiple measurements by the same investigator at the same site and same distance. First, a weighted mean is calculated for the measurements in the set by using the uncertainty estimates for quantities that are not the same for all measurements in the set, whose identity can normally be established with confidence. Then, the propagation-of-error formulas are used successively to estimate the uncertainty estimate in the weighted mean. Finally, the uncertainty in the weighted mean is combined with the uncertainties in shared factors.
Example of Use of Weighted Means to Address Correlated Errors Among Measurements from a Particular Site
Suppose that independently distributed random variables have estimated variances
with the index identifying the values for the ith measurement. For instance, X might be the radiation count rate of a sample, Y its stable element assay result, and U and V the calibration factors for those two quantities, respectively (U might be the inverse of the calibrated counting efficiency). Those variables would then combine as factors in a formula for the reported result, specific activity=SA, such as
(10)
If one or more of these variables takes on identical values for all measurements in the set, as arises when the same calibration factor is used for more than one measured value—say
—then a weighted mean for the set of measurements from p through q may be calculated for the quantity corresponding to the uncalibrated specific activities, which is designated as follows.
The estimated variance of each individual quotient Xi/Yi is established by application of the quotient rule as
(11)
wherein the weights wi are the inverses of the estimated variances. The variance-weighted mean is
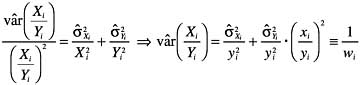
(12)
and the estimated variance of this weighted mean is

(13)
The estimated mean specific activity for the set of measurements is thus
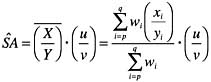
(14)
and its variance is given by
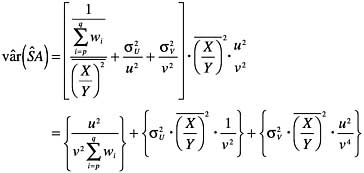
(15)
It appears that some minor variation of this formula is sufficient for all the radiometric results, in that the investigators’ methods are such that subsets of reported values at the same site share either the first, the second and third, or all three of these:
-
The calibration factor for counting efficiency.
-
The calibration factor for the assay of stable cobalt or europium.
-
The measured value of stable cobalt or europium.
In this analysis, the actual values of Xi,Yi, Ui, and Vi are typically not known, because the raw data are not available. Rather, the values of only (XiUi)/(YiVi) or of (XiUi)/(YiVi) and YiVi are known from the source document in which the measurement was reported. Correspondingly, the uncertainty estimates for X, Y, U, and V are typically known or estimated only as fractional standard deviations rather than as raw standard deviations. It is possible to make the necessary calculations with those quantities alone, that is the investigator’s reported result,
and the squares of the related estimated fractional standard deviations,
by using some simple algebraic identities:
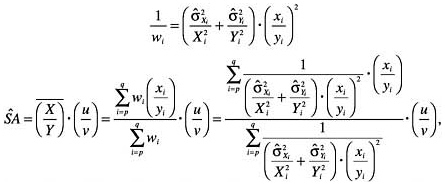
(16)
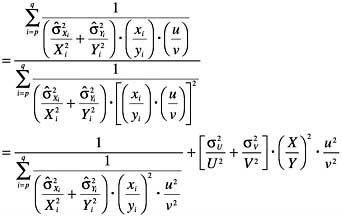
(17)
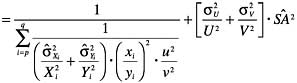
(18)
Apart from that approach of calculating weighted means within sites, some additional analysis might be possible via separate fitting of values for different investigators in cases that involve sufficient numbers of measurements for each investigator. That would serve to quantify any overall systematic difference between investigators that would be due to any combination of the factors above.
Application to Measurements by Radiometric Methods (60Co and 152Eu)
Radiometric methods quantify the neutron activation product nuclide, 60Co or 152Eu, in terms of its radioactive emissions by counting gamma or beta emissions in the sample per unit time. The number of emissions can be corrected by subtracting a background to obtain a net count rate and is then divided by the appli-
cable counting efficiency to obtain a number of atomic disintegrations of the radionuclide in the sample per unit time. That number is divided by the amount (mass) of the target element of the neutron reaction in question that is in the sample, which is determined by a separate measurement, to give a specific activity stated in units of radioactivity per unit mass of the stable element. The result is then backcorrected for decay to the time of the bombing by using the radioactive half-life of the activation product. The equation used for calculating specific activity in the sample ATB is thus
(19)
In Equation 19, ATB is the date of bombing (August 6 or 9, 1945), ATM is the date of the measurement, and the difference (ATM—ATB) is expressed in years. Xnet is the net count rate for the sample in counts s−1. The mass-related value m is the raw result of the assay of the mass of cobalt or europium in the sample in such units as count rate of an activation radionuclide after neutron irradiation or units of absorption in atomic absorption spectroscopy, and mcalib is a calibration factor for that assay; the product of m and mcalib is expressed in milligrams. Finally, eff is the applicable counting efficiency in counts s−1 Bq−1, and HL is the half-life of 60Co (5.2714 yr) or 152Eu (13.54 yr).
All source documents contain an estimate for Am(ATB) or the necessary information to calculate it straightforwardly, and every publication used in this analysis contains an estimated standard deviation for each such measurement. In the case of the 60Co results of Hashizume and others (1967), results are reported as count per milligram of cobalt, and an applicable counting efficiency is given. The date of measurement has been checked (Maruyama 2000) and can be stated with good confidence to be within calendar year 1965, that is, with an uncertainty equating to about 5% standard deviation in the decay factor. Except for the work of Kerr and others (1990) as reported in ORNL 6590, every indication is that the investigators’ estimated standard deviations were based only on the counting statistics involved in the measurement of Xnet(ATM), although other uncertainty estimates were usually published separately for the stable-element assay involved in determining m.
Calibration of Counting Efficiency
With the exception of ORNL 6590, there is no indication that the uncertainty in the calibration of the counting efficiency eff is included in any of the investigators’ estimates. This uncertainty can typically be kept low and is not a major concern among investigators. However, it will be estimated here by using typical values for radiation standard sources and source-detector geometry considerations as detailed below, and it has been added to the estimated total uncertainty calculated herein.
Background and Net Count Rate
A more worrisome issue in these circumstances, particularly because of the significance attributed to measurements at low levels, is the determination of background. In all cases, background has been determined with an empty counting chamber (counting-system background) or has been simultaneously estimated from the spectrum of the sample itself by means of a trapezoidal approximation based on the count rates in channels adjacent to the region of interest for a given photon energy range. Counting of system background was generally not determined with prepared blank samples intended to simulate the radiation-scattering properties of the sample material, but this is not a major concern; in fact, it would have been difficult to simulate the radiation-scattering properties of the samples with materials assured not to contain any detectable sources of radiation in the energy region(s) of interest.
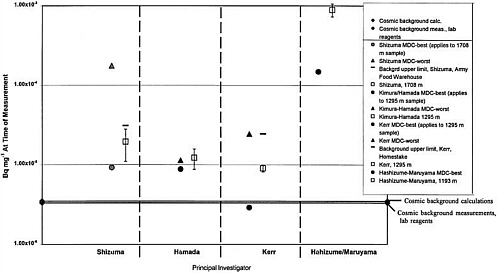
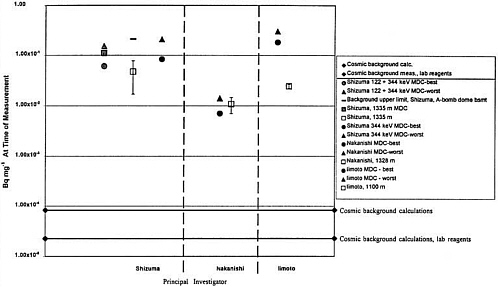
A more serious concern is related to true environmental background samples. These would be samples that are assured to contain, as exactly as possible, the same quantities of 60Co and 152Eu and any potential interfering radionuclides as would exist in the bomb fluence samples, from sources other than activation by the bomb neutrons, including activation by cosmic-ray-generated neutrons. Few samples for either 60Co or 152Eu were at distances sufficient to assure no measurable bomb fluence but made of materials otherwise essentially identical to bomb-fluence samples. The few samples that meet these criteria had poor recovery of stable cobalt or europium, and correspondingly lacked the sensitivity to give a quantitative estimate of true environmental background at the levels that are believed to be attributable to production by cosmic-ray neutrons. As shown in Figures B-1 and B-2, the minimum detectable concentrations in the only apparently suitable samples, which were measured by Shizuma and others (1993, 1998) in the cases of both 60Co and 152Eu, are not at least 1–2 powers of 10 below the lowest reported bomb-fluence sample result, as one would wish them to be. Dr. Shizuma has supplied the spectra of several samples for each nuclide, which he regards as being background samples but for which reported values have not been published. Most of the samples were close enough to the hypocenter for some detectable activation to be normally expected, and it is not clear whether there is sufficiently strong independent information to establish that they were not exposed to the bomb fluence (Shizuma 2000b). A thorough analysis should include strong assurance to establish that these samples do not represent part of the statistical variation that should be included in the range of results from exposed samples.
The best current estimate of cosmic-ray-induced background comes from assays of laboratory reagents (stock chemical compounds). The reagents do not necessarily have the same exposure circumstances as the bomb samples in relation to cosmic rays. Bomb-fluence samples were exposed on the surfaces of various human structures from the time of their removal from the earth—with the possible exception of a sample of granite from a large rock at Shirakami Shrine measured by Shizuma and others (1997), before 1945—until they were removed to a storage area at the time of
sample collection. Laboratory reagents were removed from the earth at some point and were then in various storage situations. The storage areas of both stored bomb-fluence samples and laboratory reagents might or might not have been well shielded from cosmic rays. Although cosmic rays are very penetrating, neutrons generated by cosmic rays in the atmosphere have an attenuation length of about 10 cm or less in rock, and comparable or greater total overlying thicknesses of rock and concrete are certainly present in the deeper portions of some structures. The dates of removal of bomb-fluence specimens from their in situ locations are known in some cases and not in others. As for laboratory reagents, the documentation of their age is not thorough enough to provide firm evidence that they were at saturated levels in their storage location. For all those reasons, considerable uncertainty exists in the comparative saturation levels of bomb-fluence samples and laboratory reagents, but the former are likely to be more saturated overall. A “best currently available” estimate of cosmic-ray background, corrected for decay to reflect investigators’ decay correction to ATB, was subtracted from the measured values for plotting and fitting herein.
These issues are addressed in greater detail below.
Calibration of the Stable Element Assay
As in the case of the assay of sample 60Co and 152Eu, there is no indication that the accuracy in the calibration of the assay of stable cobalt or europium in samples was included by investigators in their estimation of uncertainty in the result of that assay. Again, the estimates appear to have been based only on the counting statistics of neutron activation assays after irradiation in reactors or by other neutron sources, or they were based on similar measures of reproducibility without regard to the accuracy of calibration.
Issues Related to Experimental Design and Data-Quality Assurance
Generally, the assays were well designed to improve sensitivity and reduce the uncertainties in counting statistics, however, their rigor in regard to metrological and administrative issues is unclear.
-
Provenance and storage history of samples, including specific controls to provide assurance of proper labeling and identification and detailed histories of storage locations and conditions, are not well documented, largely because of the practical and social difficulties of obtaining samples.
-
Traceability and guaranteed accuracy of metrological standards seem reasonably well assured in most cases for radioactivity content but much less so for stable-element content.
-
There has been little or no blinding of measurements or other controls that might be used to ensure the integrity of experimental design at various levels, that
-
is, to ensure that the results used for analysis are statistically representative of all results that could have been obtained from the total pool of available samples available to individual investigators or to all investigators combined.
-
There is an absence of quality-assurance procedures of various types that could be used to detect extraneous contamination or cross-contamination of samples with respect to either the radioactive nuclide or the stable target element (for example, prepared blanks in every run). There is no indication of checks on accuracy at low levels of sample activity (such as prepared low-level standards of known activity).
-
Some interlaboratory comparisons have been done, but there was no systematic and comprehensive approach to this issue.
Those observations are based on retrospective evaluation of the entire historical body of available measurements in the context of data-quality standards that have been promulgated in recent years for government and commercial laboratories, which process large numbers of samples according to well-developed methods with commensurate resources. The measurements under analysis here have been performed over some 40 years and necessarily at a research stage of development. They have developed in response to rapidly changing questions and perceived needs that arose as the complex process of modeling and measuring the bomb fluences unfolded while computing and measuring technologies were advancing. Measurements have been given limited funding, which is awarded to individual investigators. In the United States only two funded investigators have been performing measurements since DS86. In Japan, after DS86, a dosimetry group based primarily at Hiroshima University has exerted considerable coordination and control, but not all measurers are in this group, and measurements have not been formally subject to some of the kinds of controls described above. It is not possible to assess the impact of these considerations in the present analysis, but Chapter 3 presents recommendations for future work.
REVISED UNCERTAINTY ESTIMATES (60Co AND 152Eu)
Background and Net Count Rate
As noted above, it was not possible to check investigators’ estimates of uncertainty based on counting statistics, because of the inability to obtain the raw data. One aspect of this issue can be checked in the limiting case by using a different approach: the estimation of minimum detection limits, which will be discussed below.
Measurements have been corrected by subtracting cosmic background, estimated on the basis of measurements in laboratory reagents and other knowledge documented in Appendix C, and back-corrected for decay from the time of the bombing to the time of the measurement, estimated as being 2 years before the year of publication. In addition, the estimates have been given a fairly large uncertainty (such as
25%) because knowledge of such measures as saturation level was sparse, and that uncertainty has been factored into the total estimated uncertainty of the measurement.
Decay Corrections
There is a basis for correcting a small error in the decay calculation for all 152Eu measurements except those published after 1998 by using a new estimate of the half-life, namely, 13.54 y instead of 13.2 y or 13.3 y, as noted by Iimoto (1999).
The investigators’ estimates must be used for the counting error involved in Xnet, and an error in the decay factor to ATB will be assumed insignificant apart from the correction just noted.
Calibration of Counting Efficiency
The best approach to estimating the error in the calibration of counting efficiency eff is to break it down into two components:
-
The error in the radioactivity content of the calibration standard as stated by its supplier and the error in the measured value obtained for that standard material with the investigator’s equipment.
-
The differences caused by differences in the geometry of the bomb-fluence samples and the calibration source.
Those errors are small because of the typically good accuracy and large Bq content of calibration standards in the first instance and because of the care taken by the investigators to devise standards geometrically similar to the bomb samples in the second. On the basis of certificates of analysis and standards of practice, a value of 2% is being used universally for the first factor, pending additional information. A series of experiments reported by Shizuma and others (1993) is extremely helpful in regard to the second factor. A range of error of 1–4% is being used for almost all gamma measurements on the basis of plots in Shizuma and others (1993) and considering the solid angle subtended by the detector, the mass of the sample, and the photon energy being counted.
An exception is the measurements by Okumura and Shimasaki (1997) and Tatsumi-Miyajima (1991). In these cases, a somewhat larger error of 7% has been assumed, pending additional information. It is based on the detector geometry (<2π); the fact that a point source in different source-detector positions was used to simulate the unenriched, intact slices of rock being counted, at least in the work by Tatsumi-Miyajima. It is unclear whether or not investigators measured the sample in different, well-defined positions (such as flipped 180°) to correct for possible inhomogeneities in the bomb-induced radioactivity concentration in different parts of the sample.
Assay of Stable Cobalt or Europium
Most investigators give an estimated uncertainty for the assayed sample content of cobalt or europium, usually stated in percentage by weight or parts per million, rather than weight of cobalt or europium in the sample. In some cases, this uncertainty was estimated by a conventional calculation of the sample standard deviation “s” for a set of replicates. In other cases, such as assay by neutron activation analysis (NAA), the uncertainty was apparently based on the Poisson counting statistics of the radiation from the activation-product nuclide in the irradiated sample. In most cases, it appears that, regardless of which approach was used, the investigator treated the calibration of the assay as a known constant, so the estimated error does not include the error in the cobalt of europium content of the standard solution as given by the supplier, nor the error in the calibration result for that material as measured by the investigator’s equipment. For example, a 1000 ppm standard solution of europium may contain 1000±30 ppm at the 1—σ error level as specified by the supplier, and the irradiation of mcal μg of this solution in a reactor can produce x±√x counts in a given counting interval.
Therefore, for the error in determining the mass m of 60Co or 152Eu in the sample, all the errors stated by investigators were used, but an additional uncertainty in the calibration of the assay was estimated as described in detail below.
Cobalt was generally determined by atomic absorption (AA), although measurements performed in the 1960s used a colorimetric assay (based on o-nitrosore-sorcin monomethyl ether salt) on samples that were highly concentrated in cobalt by electroplating techniques. Concentrations in original sample material cover a wide range, and concentrations in measured samples an even wider range, because chemical enrichment was used in some cases and not in others. Most of the steel samples measured apparently had cobalt concentrations of about 100 ppm to 300 ppm, but a few were about one-tenth as great. Andesite rock has cobalt at about 10–20 ppm (US Geological Survey [USGS] Certificate of Analysis for andesite, AGV-2), and Nakanishi measured about 20 ppm in roof tile (Nakanishi and others 1983), but he measured only about 0.5 ppm in granite and about 5 ppm in concrete (Roesch 1987). The actual milligram amounts of cobalt in samples at greater distances are given in Table B-3 and reflect chemical enrichment in most cases.
There are some reasons to question whether substantial inhomogeneities in stable cobalt concentration could have existed in some of the steel samples. If inhomogeneities in cobalt concentration existed in samples along with positional dependence of neutron fluence, a quotient of the averaged values of becquerals per gram and milligrams per gram obtained from a homogenized extract might not be representative. Kerr and others (1990) obtained such disparate results from a handrail of a smoke-stack of the Chugoku Electric Co. that they concluded that it was made primarily from scrap metal. Shizuma and others (1992) obtained very different results for the same samples in succeeding runs using the same procedure: 21.4 vs. 9.96 mg g−1 for a steel plate at the A-bomb Dome, 41.2 vs. 11.7 mg g−1 for a steel pipe at the Red
Cross Hospital, 37.0 vs. 12.4 mg g−1 for a steel ladder at the Red Cross hospital, and 64.6 vs. 15.1 mg g−1 for a steel ladder at the Hiroshima Bank of Credit (Shizuma 1997; Shizuma and others 1998). In the case of Shizuma and others (1992), there appears to be a pattern in the recovered concentrations of cobalt, but not a similar pattern in the calculated radioactivity concentration. This would tend to support a batch difference in enrichment chemistry rather than inhomogeneities in the original sample matrices.
Europium content, in contrast, was universally determined by NAA with either a reactor or a 252Cf source, except for the work of Kato and others (1990), which is discussed in more detail below. In some cases, it was not the emissions from the decay of the ground-state isomer of 152Eu that were measured, but the emissions from isomeric transition of a short-lived metastable state, namely the 152Eu state with a half-life of 9.311 h (Shizuma and others 1993). The complicated neutron activation production and decay schemes of the europium isotopes and their isomers, including 154Eu and 152Eu, and the related potential interferences in their spectra in various energy regions of interest require careful assay. The relevant data are given in Table B-2 below.
The assay of 152Eu must consider carefully the time-dependent effect of the metastable state with 9.3-h half-life for any measurement within several days of irradiation. Furthermore, any assay of 152Eu that uses the 121.78-keV photon must consider very carefully any possible counts in the region of interest from the 154Eu photon at 123.07 keV, which could vary considerably with the energy calibration of the system. All those considerations deserve further review and analysis.
The actual native concentrations of europium in sample materials are less variable than those of cobalt. All the reported values of Nakanishi and others (1991, 1993, 1998), Roesch (1987), Shizuma (1997), and Shizuma and others (1993) are in the range of about 0.3 to 3 ppm for concrete, granite, and roofing tiles alike, and the USGS Certificate of Analysis for andesite, AGV-2, is about 1.5 ppm. However, some samples were measured without enrichment, some were enriched via a single-step process (Nakanishi and others 1991; Shizuma 1997; Shizuma and others 1993), and others were enriched via a sophisticated
TABLE B-2 Properties of Europium Nuclides of Interest in Assay of Stable Europium by NAA
|
Nuclide |
HL |
Production by N |
|
Photons of Interest |
|
|
152Eu |
13.537 y |
thermal, fast |
~39–49 keV |
~122 keV |
~344 keV |
|
152Eu |
9.3116 h |
thermal, fast |
39.52 (21.1%) |
121.78 (28.58%) |
344.28 (26.5%) |
|
154Eu |
8.593 y |
thermal, fast |
40.12 (38.3%) |
121.78 (7.00%) |
344.28 (2.38%) |
|
|
39.52 (7.40%) |
123.07 (40.79%) |
|
||
|
|
40.12 (13.4%) |
|
|||
multistep process (Nakanishi and others 1991, 1998). The actual amounts recovered in samples, as for cobalt, are given in Tables 3–2a and 3–2b of Chapter 3.
The uncertainty in sample content of stable cobalt or europium is important and differs so much among source documents with regard to the available information and the nature of the assay that a case-by-case discussion is appropriate here. All noted percentage errors given below are 1-SD estimates.
-
Saito (Roesch 1987) and Hashizume and others (1967) measured 60Co in enriched steel samples and assayed stable cobalt by the colorimetric method, and they reported uncertainty estimates that are clearly based on reproducibility among replicate measurements. A reproducibility-based estimate of “<5 %” was given. An additional 3% calibration error for the assay is assumed here.
-
Nakanishi did a few early measurements of 60Co in unenriched samples of a roofing tile (Nakanishi and others 1983) and in the granite and concrete core of the Fukoku Seimei building (Roesch 1987), which were assayed for cobalt by reactor-based NAA. On the basis of recommended value of ±6.25% in the current USGS Certificate of Analysis for andesite (AGV-2), a total calibration error of 7.5% has been assigned to these results.
-
Hoshi and Kato (1987) measured 60Co in unenriched steel samples but do not describe the assay for stable cobalt. A total error of 5% is assumed for stable cobalt, pending further information.
-
Kerr and others (1990) used a unique method to measure 60Co in large, intact steel samples using large-area detectors and cross-calibration done by counting a sample before and after enrichment in the large-area detectors and a well detector, respectively. For cobalt in the intact samples, they give extensive documentation of comparisons with samples supplied by the US National Bureau of Standards (now the National Institute of Standards and Technology [NIST]), and they measured cobalt content by several methods. Their estimate of about 3% overall error in stable cobalt content is included in their error calculations for total measurement error.
-
Kimura (1993) and Kimura and others (1990) measured 60Co in enriched steel samples. In their earlier paper, they state that stable cobalt was measured by NAA. In the later paper, they state that AA was used for the Yokogawa Bridge sample and NAA for the A-bomb Dome sample. A calibration error of 3% is assumed in addition to the error given by the authors. For the A-bomb Dome sample, because no error is given, a total error of 5% is assumed for stable cobalt.
-
Shizuma (1999), and Shizuma and others 1992, 1993, 1998) measured 60Co in unenriched (A-bomb Dome) and enriched steel samples. All stable cobalt assays were done via A A by a commercial laboratory. An error equating to 7.7% is noted for the A-bomb Dome samples, which were unenriched, and an error of 5% is quoted for all the other samples. Given that these estimates are quoted from the results of a commercial laboratory, it is assumed that they include calibration error.
-
Okumura and Shimasaki (1997) measured 60Co in unenriched samples of andesite rock and assayed stable cobalt by NAA. Because no error estimate is given by the authors for stable cobalt and because the samples are unenriched, and considering the substantial uncertainty in the values recommended by USGS for the AGV-2 andesite standard (6.25% SD), a total error of 7.5% is assumed for stable cobalt, pending further information.
-
Nakanishi and others (1983) and Roesch (1987) originally measured 152Eu in unenriched granite, tile, and concrete and later in singly and doubly enriched samples (Nakanishi and others 1991, 1998). Assay of stable europium in unenriched samples was said to have been calibrated with geochemical standard rocks from US and Japanese geological-survey agencies (Nakanishi and others 1983). On the basis of current USGS certificate of analysis for andesite (AGV-2), which gives an error of 6.5% for europium, a calibration error of 7.5% is assumed for the unenriched samples. For enriched samples, 1000 ppm europium solution from a chemical supplier, intended for use in AA assays, was used for calibration. A contemporary certificate of analysis from an international supplier, Sigma-Aldrich, gives a range of ±3% for this type of product. The 1991 paper unfortunately does not give error estimates for stable europium. Pending further information, reproducibility and total calibration errors are assumed at 5% and 3%, respectively for this particular publication. For the 1999 paper, a calibration error of 3% is added to the stated error for stable europium.
-
Hoshi and Kato (1987) measured 152Eu in unenriched granite samples, and Hoshi and others (1989) measured 152Eu in unenriched samples of granite, tile, and concrete. Hoshi and others (1989) give a range of 4–10% for the estimated error in stable europium content, but no estimate is given in Hoshi and Kato (1987). Based on the quoted range and the discussion in Hasai and others (1987), a total uncertainty of 10%, including calibration error, is assumed for all of these measurements, pending additional information.
-
Kato and others (1990) measured 152Eu in enriched granite samples. Stable europium was determined by an electrothermal AA technique (ET-AAS). A calibration error of 3% is assumed to apply in addition to the error estimates given by the authors for stable europium.
-
Shizuma and others (1993, 1998) measured 152Eu in unenriched and enriched granite samples. Stable europium was measured by neutron activation in reactors or with the Geniken 252Cf source and evaluated on the basis of ratios of paired samples to which 50 μg of europium had and had not been added from a standard solution. It is not yet known how the uncertainty calculation was applied to the ratios, and the accuracy and traceability of the standard solution are unknown. Pending additional information, a calibration error of 5% is used here in addition to the error estimates given by the authors for stable europium.
-
Okumura and Shimasaki (1997) and Tatsumi-Miyajima (1991) measured 152Eu in unenriched samples of andesite rock. Stable europium was assayed by reactor-based NAA, but error estimates are not given. Because the samples were
-
unenriched and because of the error suggested by USGS for determinations in andesite by similar methods, a total error of 7.5% is assumed for stable europium in all these measurements.
Combining Estimates of Uncertainty
In summary, errors for calibration were estimated for this analysis for the counting efficiency and the assay of stable cobalt or europium. The calibration error for counting efficiency was estimated in two separate parts, source-detector geometry and other; “other” includes the accuracy of the radioactive solution used as a standard. These errors and the reproducibility-related errors given by the authors for stable cobalt or europium content must be combined with the counting-statistics errors attributed by the authors to count-rate results to obtain a more realistic estimate of total experimental error. All of these errors are in multiplicative factors shown in Equation 6. They were therefore expressed as percentage errors in a spreadsheet and added in quadrature (square root of sum of squares). When weighted means were calculated as described above for measurements at the same location and same distance by the same investigator, the corresponding formulas equivalent to Equations 16 and 17 were used in the spreadsheet.
Results
The fitted values for DS86 calculation and selected subsets of the measurements are given in Table B-3. These estimates do not include any potential error due to cross contamination, sample-selection bias, or failure to account properly for peak interferences. Plots of measurements with their calculated uncertainty estimates depicted as error bars are included in the body of Chapter 3. Details of the RERF database and the uncertainty calculations will be made available on the RERF Web site at rerf.or.jp.
The results shown in Table B-3 include confidence intervals that reflect the actual dispersion in the measured data about the fitted curve, which is considerably greater than would be suggested by the uncertainty estimates for the measurements that are separately calculated by propagation of error in this appendix. Those uncertainty estimates are used as weights in the regression to give more influence to the more precise measurements, but they do not determine the magnitude of the standard errors that the nonlinear least-squares regression routine estimates for the fitted parameters. This total error is estimated by the regression routine based on the properties of the weighted “sum of the squares of residuals” that is being minimized in the least-squares fit.
The results shown in Table B-3 include confidence intervals that reflect the actual dispersion in the measured data about the fitted curve, which is considerably greater than would be suggested by the uncertainty estimates for the measurements that are separately calculated by propagation of the error. For example, simulations performed with the 60Co data suggest that the confidence interval for the relaxation
TABLE B-3 Fitted Neutron Activation Values Using the Total Uncertainty Estimates: Hiroshima
|
60Co |
DS86 |
All Measurements |
Measurements at Slant Range <1000 m |
Measurements at Slant Range <1400m (does not include Yokogawa Bridge) |
Measurements at Slant Range <1500 m (includes Yokogawa Bridge) |
|
A(r0)a, |
18 |
11 |
12 |
12 |
11 |
|
Bq mg-1 |
|
[10,13] |
[10,15] |
[10,14] |
[10,13] |
|
λ0*, m |
119 |
120 |
76 |
93 |
123 |
|
|
|
[95,145] |
[28,124] |
[63,122] |
[99,147] |
|
δ(1000)*, |
11 |
51 |
170 |
130 |
46 |
|
m km−1 |
|
[15,88] |
[49,300] |
[64,190] |
[10,81] |
|
152Eu |
DS86 |
All Measurements |
Measurements at Slant Range <1200 m, All Investigators |
Measurements by Nakanishi et al., All Distances |
Measurements by Shizuma et al. and Hoshi et al., All Distances |
|
A(r0)a, |
169 |
110 |
110 |
113 |
107 |
|
Bq mg-1 |
|
[101,119] |
[101,119] |
[95,131] |
[98,119] |
|
λ0*, m |
119 |
134 |
128 |
137 |
125 |
|
|
|
[116,153] |
[104,152] |
[102,172] |
[97,152] |
|
δ(1000)*, |
11 |
75 |
92 |
64 |
110 |
|
m km−1 |
|
[42,110] |
[31,150] |
[10,120] |
[51,170] |
|
aA(r0) is activation at the hypocenter and λ0 is relaxation length at the hypocenter. δ(1000) is the change in relaxation length, in m per km slant distance. Units for δ(1000) are shown as m per km for clarity although this quantity is technically unitless and could be expressed as a fraction or a percent. NOTE: Values in brackets are approximate 95% confidence limits for the indicated parameter estimates based on asymptotic approximations supplied by the Stata version 6.0 nonlinear least-squares regression procedure “nl.” |
|||||
length at the hypocenter would be less than half as wide as the confidence interval shown in Table B-3. Some of this apparent over-dispersion in the measurements could clearly be reduced by using detailed models of samples and their environs to create more accurate sample-specific calculated values for all of the measurements. Some of this over-dispersion, however, might also reflect sources of random error in the measurement process that are still unknown.
Issues Related to Background, Spurious Signal, and Detection Limits
The presence of background is a sine qua non of radiometric measurements and is of particular interest in the type of low-level measurement that is necessary for neutron activation products from the atomic bombs in Hiroshima and Nagasaki. In
addition to counting-system intrinsic background and the background levels of the radionuclide being measured that might be present in a sample because of sources other than the atomic bombs, this report touches on potential sources of misleading signal (counts) that might more appropriately be denoted as counting “interferences.” Statistically defined limits of detectability are calculated and compared with both the possible naturally occurring background levels and the bomb-induced levels of interest at greater distances from the hypocenter.
Issues related to the detection of 36Cl by accelerator mass spectroscopy are different from those related to the radiometric detection of other thermal-neutron activation products because AMS is a fundamentally different type of measurement process. The available information on it is also different, as explained below.
Quantification of Minimum Detectable Concentrations (MDCs) of Total Sample Radioactivity per Unit Mass of Target Element
The quantification of detection limits is critically important to the elucidation of the background issue. The first question to be asked for a given measurement method is how much total radioactivity in the sample, regardless of how it came to be there, can reliably be distinguished from the counting-system background that applies to nonradioactive samples. This detection limit, which would be based on a count with no sample or a nonradioactive blank sample present in the counting chamber, provides an indication of the level below which no reliable determination can be made regarding the presence or absence of any radioactivity in the sample, whether it might arise from cosmic background, the bomb fluence, some other unidentified source, or any combination of these factors. The MDC that actually applies to a given sample with respect to bomb fluence is defined by the total background count rate that applies to that sample, including background from cosmic-ray activation and other possible sources.
To obtain some generic values for the analysis of the various radiometric methods, it is assumed that sample and background are counted for equal intervals, that type I and type II error rates are set at 5%, and that the following formula is therefore applicable, as defined in NUREG 1507 (1995):
where SB is the standard deviation of the background count (for a nonradioactive sample) in an interval of T seconds. It is further assumed that K is a counting efficiency that has been estimated with good precision, so that a single value may be used for K in illustrative calculations. (The uncertainty in the value of K is discussed further below and in other parts of this appendix.) A practical limiting value for counting time T is defined on a basis that is stated below and is used for calculating the tabulated values. The assumption of Poisson counting statistics is taken to apply uni-
formly to the counting data for radioactivity counting, with no sources of extra Poisson variation at the level of replicate counting measurements on identical samples, and SB may therefore be taken simply as the square root of the total count.
In actual practice, the “background” for a sample is often obtained by a spectral method from the spectrum for the sample itself, by a trapezoidal approximation in which channels near the photon energy of interest are assumed to represent background levels for those adjacent channels. A line is drawn across the channels in which the photon of interest appears, from the channels on one side of the photon energy region of interest to the other, and used to distinguish “peak counts” from “background counts”. The nature of this process is such that the uncertainties of the resulting numbers are not estimable in the same simple way as those of separate counting intervals conforming to Poisson statistics. For the present purpose, it is felt that MDCs derived from the assumption of a separate background count and equal counting intervals, which roughly equate to a trapezoidal approximation using equal numbers of channels in the emitted photon and background regions of interest, are still representative.
For two representative amounts of recovered stable element that might be present in the sample, a minimum detectable specific activity in the form of a concentration, denoted MDCsa, is then calculated in units of becquerals per milligram of the target element present in the sample on the basis of the measures involved (sample weight, elemental composition, and fraction of the element recovered in an enrichment process). That is, MDCsa=MDC/wtele, where wtele is the weight in milligrams of the stable target element in the sample based on the parameters involved (sample weight, elemental composition, and fraction of the element recovered in an enrichment process). These representative amounts are chosen to bracket the amounts that were present in the samples on which a particular set of measurements of interest, typically at longer ranges, was reported by the investigator.
Finally, the quantities are “decayed back” to the time of the bombing by using a specific assumed measurement date of August of a stated year that approximates the date when some measurements of that type were made, for purposes of allowing a comparison with the reported values of measured specific activity. For samples whose radioactivity contents are assumed to be bomb-induced, investigators have uniformly reported Hiroshima and Nagasaki data as of August 6 or 9, 1945, or ATB. Often, the calculated quantity is the only value available; the raw counting data are not available. The MDC stated in terms of specific radioactivity per unit mass of the stable target element, as of the time of the bombing (Bq/mg ATB), is denoted MDCsa,ATB.
Another important quantity is the critical level for a given counting system and method. This is the level that is used for declaring a given measurement to be distinguishably different from background. As with the MDC, a 5% type I error rate for a one-sided test is assumed, and the formula
is therefore used.
The critical level can also be expressed in terms of Bq/mg ATB for the applicable parameters of a specific measurement. That provides a guideline in the sense that any reported value less than this limit would have a probability greater than 0.05 of having arisen by chance alone in a sample containing only background, on the basis of the critical region for a one-tailed test with H0: sample net count rate=0. Furthermore, for measurements below this limit, the type I error rate for a one-tailed test would be at least as great, and in some cases considerably greater than 0.05, if the presence of background plus the DS86-calculated value is taken as the null hypothesis.
For the situations of interest here,
Technically, observed net values stated as numbers of counts that lie between the Lc and the MDC are “significant” in the sense that they have a probability of less than 0.05 of having arisen by chance alone if there is no radioactivity apart from the defined background level in the sample.
However, the experiment is not sufficiently sensitive to detect, with acceptable reliability, amounts of radioactivity in a sample that correspond to a mean count between the Lc and the MDC. Those amounts do not have at least a 95% probability of giving a count exceeding the Lc (that is, the type I error rate might be marginally acceptable, but the type II error rate, where it is of concern, is not acceptable.)
Furthermore, there is additional uncertainty in the calibration of counting efficiency and, more notably, in the assayed value of the sample’s content of the target element. These uncertainties affect the size of the MDCsa,ATB that corresponds to a given MDC.
For all those reasons, and others discussed below, reported results close to or below the nominal MDCs in Table B-4 should be regarded as requiring great care in their interpretation.
a. The counting-system background for nonradioactive samples and the applicable counting efficiency
i. 60Co
1. Detection of the 1173- and 1332-keV gammas by a well-type HPGe detector (Shizuma and others 1992; Kimura and others 1990)
Shizuma and others use a 54-mm-diameter by 60-mm-long detector whose combined efficiency for the two gamma rays of 60Co is stated as being close to 0.08 cps/Bq in Table 2 of the 1998 paper (Shizuma 1998) for samples of the size (about 1 g) of interest here. Background is estimated by the trapezoidal method. For the purposes of the present calculation, the background count rate that is assumed to apply is that obtained in a 1288030-s measurement of the Army Food Storehouse background sample: 230/1288030=0.00018 cps. This sample is assumed to repre-
sent a reasonable approximation of the applicable system background because the “background counts” value was determined by the trapezoidal method and was consistent with the other “background counts” count rates determined by the same method for the other samples.
Kimura and others (1990) used a detector whose efficiency was stated in their paper as being 0.02849 for the 1.33-MeV gamma rays. The combined efficiency for the two gamma rays is therefore assumed to be about 0.06. As a provisional estimate of background for Kimura and others (1990), the value quoted by Kerr and others (1990) in ORNL 6590 is used: about 200 counts per million seconds per 1-keV channel in a 113-cm2, well-shielded HPGe detector. A 6-keV-wide total region for the two gamma rays is assumed. It does not appear that better information will be available; the necessary records have not been retained.
2. Detection of the 1173- and 1332-keV gammas by a large-area NaI (Tl) detector (Kerr and others 1990)
On the basis of a cross calibration involving the counting of a sample before and after chemical enrichment, the applicable counting efficiency was stated as 3.99± 0.24%—that is, 0.040 cps/Bq—for the paired large (300-mm diameter by 200-mm thick) detectors. The calibration method implicitly includes the total self-absorption in a large (for example, 4 kg) intact steel sample. On the basis of the measurement of the Homestake Mine sample, which was used by the investigators as a background sample, the background count rate was 0.000602 cps for detector 9, or 337 counts in an interval of 560460 s, although the rate for the other detector was almost twice that. Those values are assumed to represent good approximations of system background because the sample was heavily shielded from cosmic rays.
3. Detection of the 318-keV Emax beta by GM-plastic scintillation coincidence detector (Hashizume and others 1967)
In both the 1967 paper (Hashizume and others 1967) and the review by Maruyama and Kawamura in the DS86 Final Report, Vol. 2, the counting efficiency is given as 12% and the background as 0.069 cpm.
ii. 152Eu
1. Detection of the 39–40-keV Sm rays by a planar HPGe detector (Nakanishi and others 1998).
The counting efficiency is given in Figure 3 of Dr. Nakanishi’s most recent paper (1998) and varies from about 0.014 cps/Bq for a 200-mg sample to about 0.008 cps/Bq for an 850-mg sample. For the purposes of the present calculation, the value of 0.008 is used for conservatism. Counting-system background does not seem to be documented in any of the available publications except for a spectrum for a roof-tile specimen for the older planar Ge (Li) detector, as shown in Figure 2 of the 1983 letter to Nature (Nakanishi and others 1983). Apparent background numbers for energies near 39–40 keV were read from this plot and used for a crude calculation, pending additional information from Nakanishi.
2. Detection of the 39–40 keV Sm rays by a coaxial SiLi detector (Iimoto 1999).
The counting efficiency is documented in the paper as 0.002938 cps/Bq. On the basis of a background-sample spectrum provided by Iimoto, the background count rate is about 12 counts/channel in 1.8×106 s, or about 227 counts per million seconds in the noted 34-channel region of interest.
3. Detection of the 122 and 344 keV gammas by a well-type HPGe detector (Shizuma and others 1993, 1997).
The counting efficiency is documented in the 1993 Health Physics paper (Figure 5 and related text by Shizuma and others 1998) as being fairly constant at about 0.05 cps/Bq for the 122-keV gamma and 0.04 cps/Bq for the 344-keV gamma, over the range of applicable sample sizes. Background count rates are discussed extensively in the 1992 paper in Nuclear Instruments and Methods (NIM B66 459–464) and are summarized in Table 4 of that paper. The anti-coincidence values for the well-type detector were determined by the trapezoidal method from a sample containing appreciable 152Eu have been adopted here for the present calculation.
b. Available per-sample amounts of the stable element after enrichment
i. 60Co
The recovered amounts of cobalt for the relevant measurements of Shizuma and others (1998) are well described in their paper in Health Physics. They can be calculated unequivocally from Table 1 and range from 2.2 mg for the 4571-m background sample, which was unfortunately the lowest amount of all the samples, to 73 mg for one of the 1481-m samples. Apart from the background sample at 4571 m, however, each of the longer ranges with a measurement of interest (1014 m, 1481 m, 1484 m, and 1703 m) had at least one sample with at least 26 mg of cobalt.
Kimura and others (1990) report values of 239–314 mg for their samples. The former number was calculated from other values given in the 1990 paper and confirmed by writing to the authors; the latter is given explicitly in the 1993 paper (Kimura 1993).
Kerr and others (1990) give extensive data in Table 5 of ORNL 6590 for the stable-cobalt content of the large (about 4 kg) samples that they measured intact in the large-area detector at PNL. These values range from about 120 mg for the Homestake mine sample, which (as in the case of Shizuma) is the lowest of all the samples, to about 1000 mg.
Hashizume and others (1967) do not give the amounts of recovered stable cobalt in their original 1967 paper. The review by Maruyama and Kuramoto (1987) states that not more than 9 mg was recovered but does not give a minimum or sample-specific values.
ii. 152Eu
Shizuma and others (1993) give extensive sample specific information on ppm concentrations in, for example, the 1993 paper. Multiplication by the appar-
ent sample mass of about 3.5 g for all samples resulted in values of 0.02–0.05 mg per sample.
Nakanishi and others (1991) use a more extensive chemical extraction technique and recover comparatively large amounts of europium. Values for extracted specimens were estimated by multiplying the recovery factors, given on page 75 of the 1991 paper, by the range of in situ values recorded in various references beginning with the 1983 letter to Nature (Nakanishi and others 1983). Additional information is found in handouts distributed by Nakanishi at committee meetings.
c. Corresponding MDCs and critical levels
The fundamental MDCs based on counting-system background only are shown in Table B-4. A revision of these MDCs in the case of 60Co to account for natural 60Co from cosmic-ray production, is discussed below:
TABLE B-4 Detection Limits for Thermal Neutron Activation Measurements in Hiroshima and Nagasaki
|
Radionuclide Investigator(s) |
60Co Shizuma |
60Co Kimura/ Hamada |
60Co Kerr- |
60Co Hashizume/ Maruyama |
60Co Okumura/ Shimazaki |
|
Photon Energy Measured |
1173 keV +1332 keV |
1173 keV +1332 keV |
1173 keV +1332 keV |
beta coincidence 0–318 keV (25–250 keV window) |
|
|
T, seconds |
1.00×10–6 |
1.00×10–6 |
1.00×10–6 |
1.00×10–6 |
|
|
B, cts on interval of T sec. |
1.79E+02 |
1200 |
6.02E+02 |
1.15E+03 |
|
|
SB |
13.36291 |
34.64102 |
24.52889 |
33.91164992 |
|
|
counting efficiency, cps/Bq |
0.08 |
0.06 |
0.04 |
0.12 |
|
|
MDC, Bq |
8.14×10−4 |
2.73×10–3 |
2.93×10–3 |
1.34×10–3 |
|
|
lowest mg per sample |
2.19 |
240 |
120 |
|
|
|
highest MDCsa, Bq/mg |
3.72×10–4 |
1.14×10–5 |
2.44×10–5 |
|
|
|
highest mg per sample |
88.1 |
310 |
1000 |
9 |
|
|
lowest MDCsa, Bq/mg |
9.24×10–6 |
8.82×10–6 |
2.93×10–6 |
1.49×10–4 |
|
|
HL |
5.2719 |
5.2719 |
5.2719 |
5.2719 |
|
|
year of measurement |
1995 |
1990 |
1988 |
1965 |
|
|
highest MDCsa,ATB, |
Bq/mg ATB |
0.26628 |
0.00423 |
0.00696 |
|
|
lowest MDCsa,ATB, Bq/mg ATB |
0.00662 |
0.00327 |
0.00083 |
0.00206 |
|
|
Radionuclide |
152Eu |
152Eu |
152Eu |
152Eu |
152Eu |
60Co
Calculated MDC and critical level values are shown in Figure B-1. A value of 1 million seconds for both sample and background is used here as a nominal counting time for comparing results among investigators. Some investigators count for somewhat longer, in which case the MDC would decrease as the inverse of the square root of the counting time if sample and background counting times were increased equally. However, determining background by trapezoidal approximation from the sample spectrum itself introduces additional uncertainty. And if background is determined by a separate count with an empty sample chamber, there should be some
concern about whether the statistical properties of background count rate were adequately evaluated for such factors as drift in the instrument electronics over long periods and periodic variation due to solar activity. Furthermore, in the case of 60Co counted in recent years in samples from locations far from the hypocenter, there is a nontrivial contribution from cosmic-ray neutrons that increases the total background count rate beyond what is evaluated by either of the two methods above and correspondingly increases the MDC.
ii. 152Eu
Calculated MDC and critical level values are shown in Figure B-2. A value of 1 million seconds is used as a nominal counting time for comparing results among investigators. All the considerations cited above for 60Co also apply to 152Eu except that the cosmic-ray-generated background is not expected to make a significant contribution to experimental error.
iii. 36Cl
AMS results intrinsically report the isotope ratio of 36Cl to chlorine (36Cl/Cl). In this case, there is a system background for a condition of no injected sample that consists of electronic noise in the detectors being used for 36Cl and chlorine, but it is not typically reported. Ratios obtained for blank samples involve a source of stable chlorine of some type, which contains 36Cl at a level defined by the long-term (geological) saturation of the cosmic ray activation in the source material from which the chlorine was taken. Published data on the intrinsic detection limits of the method indicate that it is about 1 atom of 36Cl per 1015 atoms of chlorine (Straume and others 1994). Although that value is not precise or clearly stated from a statistical point of view, it is about one-hundredth of the background levels of interest that appear to exist in unexposed samples. Thus, the situation for 36Cl is different from that of 60Co and 152Eu: the MDC is determined completely by the statistical variation in the background due to cosmic-ray activation.
Calculated Estimates of In Situ Cosmic-ray Production
See Appendix C for a detailed discussion of cosmic-ray neutron fluences.
60Co
Komura and Yousef (1998) give a calculated value of 0.2 dpm/g (3.3× 10−6 Bq/mg) at saturation, on the basis of a flux of 0.008 n/cm2 s, in their 1998 abstract of a presentation at the 41st meeting of the Japan Radiation Research Society (December 2–4, 1998, Nagasaki). That value is also cited by Shizuma and others in their 1998 Health Physics paper.
152Eu
Komura and Yousef give a calculated value of 5 dpm/g (8.3×10−5 Bq/mg), based on a flux of 0.008 n/cm2/s in the 1998 abstract just cited.
Measurements of Samples Far from the Hypocenters or Heavily Shielded Samples
60Co
Kerr and others (1990) measured two samples, one from a surface building and one from a mine. Both had rather meager cobalt content, and the MDC is about 2.4×10−5 Bq/mg as measured for the mine sample and 1.5×10−5 Bq/mg for the surface sample. Shizuma and others (1998) measured a sample from the Army Food Warehouse at 4571 m in Hiroshima. It also had little stable cobalt in the extracted sample, and the MDC was about 3.7×10–4 Bq/mg.
152Eu
Shizuma and others (1992) measured a heavily shielded sample from the basement of the A-bomb Dome, but its MDC was about 0.21 Bq/mg as measured, not nearly low enough to be informative. Shizuma also supplied some results from the Hiroshima Commercial High School at a 2870-m ground distance (Shizuma 2000a). It appears that this sample also had a poor recovery of 1.82 ppm in an enriched sample of 6.75 g, equaling about 0.0123 mg, resulting in an MDC of about 0.341 Bq/mg at time of measurement in 2000, or about 5 Bq/mg ATB in 1945.
Trends in Deep Portions of Cored Samples
60Co
Some early attempts were made to measure depth profiles in steel, for example, the work on Aioi Bridge girders reported by Hoshi and Kato (1987) and the work by Shizuma and others (1992) on structural steel of the A-bomb Dome, but these measurements are far too shallow to approach the asymptote.
152Eu
A thorough review indicates that a total of six cores or samples of a similar nature have been measured in granite or concrete. Of these, two (the Saikou-ji gravestone and the Motoyasu Bridge pillar) are of such small cross section that the effective depth of the deepest samples is not what is indicated by the axial distance on the depth profile. Of the others, none is measured at a depth greater than 37 cm, and no apparent approach to an asymptote is seen in the depth profiles. Two of the cores measured by Shizuma and others (1997) are deep enough to allow measurement at somewhat greater depths (Hiroshima Bank, 62 cm; Shirakami Shrine; 81 cm), but indicates that those deeper slices would fall below the MDC.
36Cl
On the basis of material presented by Tore Straume at the workshop on RERF dosimetry held on March 13–14, 2000, in Hiroshima, measurements deep in concrete appear to approach an asymptote in the vicinity of 100 Bq mg–1 at depths greater than 35 cm. That is consistent with background samples measured in a shielded location at 1700 m and that with other background samples reported by Straume and others (1994).
Measurements of Laboratory Reagents
60Co
Komura and Yousef (1998) measured laboratory reagents containing large amounts of stable cobalt in a subterranean laboratory, giving very low detection limits. They reported a measured value of 0.21 dpm/g (3.5×10–6 Bq/mg), comparable with calculated values. Shizuma (1999) also measured 60Co in 4 g of CoO with a well-type Ge detector and obtained a much lower value of 7.2×10–7 Bq/mg. It is possible that this sample was not old enough to have reached saturation at background levels in its storage location or was stored in a heavily shielded location.
152Eu
Komura and Yousef (1998) report a value of 1.37 dpm/g (2.3×10–5 Bq/mg) in their measurements on Eu2O3 that is described as “modern” with respect to age (as opposed to before World War II), which is only about one-fourth of the calculated value. Shizuma (1999) reported an even lower value of 4.6×10–6 in 1 g of Eu2O3 reported to be about 25 years old. Again, there are major unresolved questions about the saturation levels of both Eu2O3 samples.
Potential Counting Interferences
Several potential causes of misleading results have been identified by reviewing the literature and interviewing the investigators. The specific possibilities mentioned here are preliminary and require further investigation. Spectral and radiochemical data were taken from the WWW Table of Radioactive Isotopes by Chu, Ekstrom, and Firestone, of the Lawrence Berkeley National Laboratory in the United States and the University of Lund in Sweden at the Internet address http://nucleardata.nuclear.lu.se/nucleardata/toi/index.asp.
Lanthanum X-rays from Photon Interactions in Stable Lanthanum of Sample Matrix
Nakanishi and others have primarily counted 152Eu via the Kα x-rays of samarium that are emitted at 39.522 keV and 40.118 keV. Because of the chemistry of the europium enrichment process and the natural abundance of lanthanum in the lithosphere, the samples are expected to contain large amounts of lanthanum. Lanthanum has Kβ rays at 37.720 keV, 37.801 keV, 38.804 keV, 38.726 keV, and 38.826 keV. All can be produced by interactions of higher-energy photons, such as background photons and photons from 152Eu, with inner-shell electrons in the lanthanum contained in the sample.
138La and 176Lu Relative to 152Eu in the 39 to 40-keV Region
138La and 176Lu are extremely long-lived (over 1010 y) naturally occurring lanthanides that might be expected to accompany 152Eu in chemical separations. Their
natural isotopic abundances are 0.0902% and 2.59%, respectively. By calculation, natural lanthanum should be about 0.82 Bq/g 138La/La and natural lutetium should be about 52 Bq/g 176Lu/Lu. 138La emits Ba x-rays at 36.304 keV (1.19%), 36.378 keV (3.69%), 37.255 keV (1.16%), and 37.349 keV (0.261%), and five Ce x-rays at 39.17−40.33 keV, all with low spectral abundance under 0.01%. This source of interference is expected to be minor compared with the lanthanum x-rays.
176Lu emits no photons at these precise energies but does emit a number of lower—and higher—energy photons and was specifically identified by Nakanishi as a possible concern, perhaps because of its substantial natural abundance.
212Pb(212Bi) Relative to 152Eu in the 39 to 40-keV Region
212Bi of the thorium series (half-life, 60.55 m) has a 39.9-keV gamma with 1.1% spectral abundance associated with its alpha decay.
223Ra and 234U Relative to 152Eu in the 122 keV Region
223Ra (half-life, 11.435 d), a naturally occurring member of the actinium (4n+3) series, has a gamma ray of 1.2% spectral abundance at 122.319 keV. 234U has a gamma ray of 0.034% spectral abundance at 120.90 keV.
227Ac Relative to 152Eu in the 122-keV Region
227Ac (half-life, 21.773 y) of the actinium series, has a gamma ray of low spectral abundance (0.00213%) at 121.53 keV.
Discussion
In many cases, the uncertainty estimates calculated for this analysis are substantially greater than those published by the authors originally. That is due primarily to the inclusion of terms involving the assay of stable cobalt or europium. Estimates of the precision of the stable cobalt or europium assay based on measures of reproducibility have often been included in publications but have almost never been included in a combined estimate of total uncertainty. The accuracy (as opposed to the precision) of the assays is also of concern, especially in cases involving unenriched samples. The calibration of the assays of stable cobalt or europium in unenriched samples appears to have unexpectedly substantial uncertainty, according to the information that has been obtained to date. Thus, the values estimated here for the uncertainty in the reported values of stable cobalt or europium and the total combined uncertainty of the specific radioactivity per unit mass of stable cobalt or europium, are often considerably larger than might have been suggested previously.
The most important effect of these revised estimates, in a proportional sense, is to increase somewhat the unrealistically low uncertainty that was sometimes estimated for measurements with good counting statistics because of their relatively large radioactivity content.
Table B-3 offers some interesting observations. In all cases, the measurements suggest that the DS86-calculated value is (very roughly) 50% too high at the short-
est ranges. Interestingly, the initial fitted relaxation lengths are not particularly discrepant compared with DS86. But the measurements clearly display substantially greater curvature than DS86, as quantified by the δ parameter for change in relaxation length per unit slant range. Several selected subsets of the data are shown in the table. They serve mainly to illustrate that the trends are not strongly influenced by the less precise data at longer ranges. For 60Co, three subsets show the effect of omitting successively, in order of decreasing range. The highly discrepant measurements at distances beyond the Yokogawa Bridge; the measurements at the Yokogawa Bridge, for which the fully calculated DS86 values involve a large correction from free-field values because of the unusual nature of the structure in which the samples were constituent; the measurements at 1168 and 1330 m that are thought to be above the MDC but are not completely documented with respect to mg cobalt content.
In the case of 152Eu, essentially all measurements beyond 1200 m are suspect with respect to the MDC, at least pending some additional information on several measurements by Nakanishi and others. However, these more distant measurements do not account for the curvature in the fitted values. There is a difference between the fitted values for the two main groups making measurements, the Nakanishi group and the Shizuma group, but the difference does not appear to be statistically significant.
The Nagasaki measurements, in contrast with those in Hiroshima, do not appear to support statistically a discrepancy with DS86, on the basis of the methods described here that have been applied to them thus far. However, the absence of a discrepancy in Nagasaki is not well established. Some trends in the data are suggestive but do not achieve statistical significance, and the 152Eu analysis in particular is very strongly dependent on a few influential observations at the greatest distances. Showing the absence of an effect amounts to “proving a negative.” The relative paucity of measurements in Nagasaki, particularly at greater distances, is problematic. To a great extent, this lack of longer-range measurements in Nagasaki is driven by the lower overall neutron fluences there. One cannot measure as far from the hypocenter in Nagasaki as in Hiroshima, for a given limit of detection, because the values of neutron activation overall are somewhat lower in Nagasaki.
The low-level measurement situation is different among the three main radionuclides that have been measured for thermal-neutron activation. For 36Cl, the detection limit might be some 2 powers of 10 below the apparent natural background level in materials similar to the samples of interest, which presumably is due to cosmic-ray production over geological time. The natural background level has been measured in several types of relevant sample materials and appears to be reasonably consistent overall with the level that is approached in the deeper portions of large concrete cores. Nevertheless, the limit on detectability of 36Cl attributable to the bomb fluence might prove to be determined by the uncertainty in the sample-specific level of 36Cl due to cosmic-ray production, which has some uncertainty in addition to counting statistics. There is substantial potential variation among samples in the saturation level of the chlorine in the sample, which presumably is due to the geological and hydrological history of the chlorine involved. In concrete
cores, although the material was presumably homogenized at the time of construction in very recent geological time, so that cosmic background should be homogeneous throughout a concrete pour, many cores are not deep enough to approach an unequivocal asymptote that clearly applies to the concrete in question. In fact, the situation is even more complicated, in that concrete can contain inclusions in the form of rocks, pebbles, and so on, that could dominate the material in a given slice of a core and have a different background level from the concrete itself.
Another source of measurement error in the case of 36Cl is the possible dilution of the stable-chlorine pool by infiltration of rainwater into the sample matrix in situ, which needs further evaluation.
Several types of possible errors are related to the depth profile of 36Cl activation in a concrete core: physical modifications of the exposed surfaces of concrete structures (adding or removing material), which might affect the depth profile near the surface or cause uncertainty in the effective depth of a slice from a core at the time of sampling versus ATB, and unexpected buildup or other unforeseen effects due to the interactions of incident high-energy neutrons near the exposed surface.
In addition, there is an issue of possible error due to production of 36Cl from a competing neutron reaction on potassium. However, the classifications pertaining to depth profile and competing production by the 39K(n,α)36Cl reaction are related to errors in calculated values rather than measured values.
For 60Co, the background samples that have been measured have rather high detection limits, especially because of relatively small content of stable cobalt in the steel samples that were measured. The only available indications of likely natural background levels of this radionuclide in iron and steel come from calculation and from measurements in laboratory reagents that contain large masses of concentrated stable cobalt. These natural background indications are below the levels of interest in the more distant bomb samples by less than a power of 10, and the situation is degrading with each passing year because of the radioactive decay of the 60Co from the bomb fluence.
Thus, natural background levels due to cosmic-ray neutrons appear to be a small but not negligible source of bias in the more distant 60Co measurements. That effect has been evaluated here and an effort has been made to correct for it, but better in situ measurements of background in true environmental samples would be helpful.
All but perhaps one of the reported 60Co measurements appear to lie above the nominal calculated MDCs reported here. (More detail on specific measurements is given in the body of Chapter 3.) If samples contained naturally occurring 60Co at exactly 3.33×10−6 Bq/mg due to cosmic-ray production, this would increase the applicable background count rate by no more than 5%, except for the larger and more distant samples of Shizuma and others (1992), which would see increases up to about 14%. The actual increase in the MDC would depend on the assumed statistical distribution among samples of true values for 60Co due to cosmic-ray production, but the effect would be minor for most cases of interest.
For 152Eu, there are no relevant background samples at all. Distant samples have not been measured, and the deeper portions of granite cores are too small and too close to some portion of the surface exposed to the bomb fluence to provide an indication of natural background levels in the sample materials of interest. The sample from the basement of the A-bomb Dome building (Shizuma and others 1992) has a detection limit that is insufficient to measure the levels of interest. Again, the only available indications of likely natural background levels of this radionuclide in rocks, concrete, and ceramic tiles come from calculation and from measurements in laboratory reagents that contain large masses of concentrated stable europium. These natural background indications lie below the levels of interest in the more distant bomb samples by at least 2 powers of 10; this suggests that they should not be a significant source of bias in the measurements done to date. However, that has not been confirmed with true background samples of rocks, concrete, and ceramic tiles.
In the case of 152Eu, some of the most distant measurements are close to or below the MDCs calculated here and should be interpreted with caution. That also implies that current methods might not have sufficient precision to provide useful estimates of natural background levels in the sample materials of interest; therefore, it might not be feasible to measure true background levels in sample-type materials. However, it might still be of interest to extract and measure a few large background samples, in order to reduce the MDC for excluding natural background levels further below the range currently being reported in measurements.
There is a possibility that measurements of 152Eu at greater distances are affected by the counting interferences discussed above. It is not yet clear that all the measurements made by Nakanishi and others at 39–40 keV are free of potential bias from these sources. The method described by Shizuma and others (1993) of comparing the results of the 122 and 344-keV regions is intended to address this issue, but it might not have adequate sensitivity to identify all measurements that are affected by the counting interferences in the 122-keV region at these low levels. These issues deserve further attention and clarification.
Finally, substantial issues related to various aspects of quality assurance cannot be quantitatively evaluated here. Any future work should give serious consideration to maximizing the value of this important body of work by following a well-designed program of remeasurements and intercomparisons with stringent data-quality objectives.
SUMMARY AND CONCLUSION
Careful Analysis of the Measurement Data Has Results in Several Important Observations
The uncertainty used to characterize published measurements should be increased somewhat in most cases by calculating a total combined uncertainty for each
measurement to account for all sources of random error that might have affected final reported values.
Statistical simulations indicate that the dispersion among the measurements, even after correcting some of the measurements for sample composition and local environment using the limited sample-specific calculated values that are currently available, is much too large to be consistent with the estimated uncertainties of the measurements, when those uncertainties are calculated based on propagation of error methods applied to the measurement process. Some of this apparent over-dispersion among the measurements could clearly be reduced by using detailed models of samples and their environs to create more accurate sample-specific calculated values for all of the measurements. However, some of this over-dispersion may also reflect sources of random error in the measurement process that are still unknown.
When the estimated uncertainties are increased to the extent that appears appropriate on the basis of the (admittedly sparse) information available for the present analysis, a discrepancy with DS86-calculated values clearly still remains in Hiroshima.
The data for Nagasaki are to some extent suggestive of a discrepancy, but more measurements are necessary to resolve this issue.
The discrepancy with DS86 in Hiroshima is statistically fairly robust and does not appear to be attributable solely to the less precise measurements made at the greatest distances.
When the measurements are fitted with a model that allows the relaxation length to vary, as should be allowed because of physical considerations, it appears that the initial relaxation length near the hypocenter is close to DS86 values, but the relaxation length increases more rapidly with distance than DS86. That might offer a clue to the nature of the discrepancy.
The 36Cl measurements have several significant, recently discovered complications that must be resolved before they can be subjected to useful analysis.
The 60Co and 152Eu measurements are subject to several important concerns that could be addressed by a program of additional measurements or remeasurements and intercomparisons among laboratories.
Fitting a rapidly changing relaxation length involves an effect at the greater distances of interest in the Hiroshima neutron activation measurements (say, 1000–2000-m slant range) that is similar to fitting a finite asymptote, which might correspond to a “background effect” of some kind; and the two models might not be statistically distinguishable from each other in these data.