5
Mathematical Understanding: An Introduction
Karen C. Fuson, Mindy Kalchman, and John D. Bransford
For many people, free association with the word “mathematics” would produce strong, negative images. Gary Larson published a cartoon entitled “Hell’s Library” that consisted of nothing but book after book of math word problems. Many students—and teachers—resonate strongly with this cartoon’s message. It is not just funny to them; it is true.
Why are associations with mathematics so negative for so many people? If we look through the lens of How People Learn, we see a subject that is rarely taught in a way that makes use of the three principles that are the focus of this volume. Instead of connecting with, building on, and refining the mathematical understandings, intuitions, and resourcefulness that students bring to the classroom (Principle 1), mathematics instruction often overrides students’ reasoning processes, replacing them with a set of rules and procedures that disconnects problem solving from meaning making. Instead of organizing the skills and competences required to do mathematics fluently around a set of core mathematical concepts (Principle 2), those skills and competencies are often themselves the center, and sometimes the whole, of instruction. And precisely because the acquisition of procedural knowledge is often divorced from meaning making, students do not use metacognitive strategies (Principle 3) when they engage in solving mathematics problems. Box 5-1 provides a vignette involving a student who gives an answer to a problem that is quite obviously impossible. When quizzed, he can see that his answer does not make sense, but he does not consider it wrong because he believes he followed the rule. Not only did he neglect to use metacognitive strategies to monitor whether his answer made sense, but he believes that sense making is irrelevant.
|
BOX 5-1 One boy, quite a good student, was working on the problem, “If you have 6 jugs, and you want to put 2/3 of a pint of lemonade into each jug, how much lemonade will you need?” His answer was 18 pints. I said, “How much in each jug?” “Two-thirds of a pint.” I said, “Is that more or less that a pint?” “Less.” I said, “How many jugs are there?” “Six.” I said, “But that [the answer of 18 pints] doesn’t make any sense.” He shrugged his shoulders and said, “Well, that’s the way the system worked out.” Holt argues: “He has long since quit expecting school to make sense. They tell you these facts and rules, and your job is to put them down on paper the way they tell you. Never mind whether they mean anything or not.”1 |
A recent report of the National Research Council,2Adding It Up, reviews a broad research base on the teaching and learning of elementary school mathematics. The report argues for an instructional goal of “mathematical proficiency,” a much broader outcome than mastery of procedures. The report argues that five intertwining strands constitute mathematical proficiency:
-
Conceptual understanding—comprehension of mathematical concepts, operations, and relations
-
Procedural fluency—skill in carrying out procedures flexibly, accurately, efficiently, and appropriately
-
Strategic competence—ability to formulate, represent, and solve mathematical problems
-
Adaptive reasoning—capacity for logical thought, reflection, explanation, and justification
-
Productive disposition—habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy
These strands map directly to the principles of How People Learn. Principle 2 argues for a foundation of factual knowledge (procedural fluency), tied to a conceptual framework (conceptual understanding), and organized in a way to facilitate retrieval and problem solving (strategic competence). Metacognition and adaptive reasoning both describe the phenomenon of ongoing sense making, reflection, and explanation to oneself and others. And, as we argue below, the preconceptions students bring to the study of mathematics affect more than their understanding and problem solving; those preconceptions also play a major role in whether students have a productive
disposition toward mathematics, as do, of course, their experiences in learning mathematics.
The chapters that follow on whole number, rational number, and functions look at the principles of How People Learn as they apply to those specific domains. In this introduction, we explore how those principles apply to the subject of mathematics more generally. We draw on examples from the Children’s Math World project, a decade-long research project in urban and suburban English-speaking and Spanish-speaking classrooms.3
PRINCIPLE #1: TEACHERS MUST ENGAGE STUDENTS’ PRECONCEPTIONS
At a very early age, children begin to demonstrate an awareness of number.4 As with language, that awareness appears to be universal in normally developing children, though the rate of development varies at least in part because of environmental influences.5
But it is not only the awareness of quantity that develops without formal training. Both children and adults engage in mathematical problem solving, developing untrained strategies to do so successfully when formal experiences are not provided. For example, it was found that Brazilian street children could perform mathematics when making sales in the street, but were unable to answer similar problems presented in a school context.6 Likewise, a study of housewives in California uncovered an ability to solve mathematical problems when comparison shopping, even though the women could not solve problems presented abstractly in a classroom that required the same mathematics.7 A similar result was found in a study of a group of Weight Watchers, who used strategies for solving mathematical measurement problems related to dieting that they could not solve when the problems were presented more abstractly.8 And men who successfully handicapped horse races could not apply the same skill to securities in the stock market.9
These examples suggest that people possess resources in the form of informal strategy development and mathematical reasoning that can serve as a foundation for learning more abstract mathematics. But they also suggest that the link is not automatic. If there is no bridge between informal and formal mathematics, the two often remain disconnected.
The first principle of How People Learn emphasizes both the need to build on existing knowledge and the need to engage students’ preconceptions—particularly when they interfere with learning. In mathematics, certain preconceptions that are often fostered early on in school settings are in fact counterproductive. Students who believe them can easily conclude that the study of mathematics is “not for them” and should be avoided if at all possible. We discuss these preconceptions below.
Some Common Preconceptions About Mathematics
Preconception #1: Mathematics is about learning to compute.
Many of us who attended school in the United States had mathematics instruction that focused primarily on computation, with little attention to learning with understanding. To illustrate, try to answer the following question:
What, approximately, is the sum of 8/9 plus 12/13?
Many people immediately try to find the lowest common denominator for the two sets of fractions and then add them because that is the procedure they learned in school. Finding the lowest common denominator is not easy in this instance, and the problem seems difficult. A few people take a conceptual rather than a procedural (computational) approach and realize that 8/9 is almost 1, and so is 12/13, so the approximate answer is a little less than 2.
The point of this example is not that computation should not be taught or is unimportant; indeed, it is very often critical to efficient problem solving. But if one believes that mathematics is about problem solving and that computation is a tool for use to that end when it is helpful, then the above problem is viewed not as a “request for a computation,” but as a problem to be solved that may or may not require computation—and in this case, it does not.
If one needs to find the exact answer to the above problem, computation is the way to go. But even in this case, conceptual understanding of the nature of the problem remains central, providing a way to estimate the correctness of a computation. If an answer is computed that is more than 2 or less than 1, it is obvious that some aspect of problem solving has gone awry. If one believes that mathematics is about computation, however, then sense making may never take place.
Preconception #2: Mathematics is about “following rules” to guarantee correct answers.
Related to the conception of mathematics as computation is that of mathematics as a cut-and-dried discipline that specifies rules for finding the right answers. Rule following is more general than performing specific computations. When students learn procedures for keeping track of and canceling units, for example, or learn algebraic procedures for solving equations, many
view use of these procedures only as following the rules. But the “rules” should not be confused with the game itself.
The authors of the chapters in this part of the book provide important suggestions about the much broader nature of mathematical proficiency and about ways to make the involving nature of mathematical inquiry visible to students. Groups such as the National Council of Teachers of Mathematics10 and the National Research Council11 have provided important guidelines for the kinds of mathematics instruction that accord with what is currently known about the principles of How People Learn. The authors of the following chapters have paid careful attention to this work and illustrate some of its important aspects.
In reality, mathematics is a constantly evolving field that is far from cut and dried. It involves systematic pattern finding and continuing invention. As a simple example, consider the selection of units that are relevant to quantify an idea such as the fuel efficiency of a vehicle. If we choose miles per gallon, a two-seater sports car will be more efficient than a large bus. If we choose passenger miles per gallon, the bus will be more fuel efficient (assuming it carries large numbers of passengers). Many disciplines make progress by inventing new units and metrics that provide insights into previously invisible relationships.
Attention to the history of mathematics illustrates that what is taught at one point in time as a set of procedures really was a set of clever inventions designed to solve pervasive problems of everyday life. In Europe in the Middle Ages, for example, people used calculating cloths marked with vertical columns and carried out procedures with counters to perform calculations. Other cultures fastened their counters on a rod to make an abacus. Both of these physical means were at least partially replaced by written methods of calculating with numerals and more recently by methods that involve pushing buttons on a calculator. If mathematics procedures are understood as inventions designed to make common problems more easily solvable, and to facilitate communications involving quantity, those procedures take on a new meaning. Different procedures can be compared for their advantages and disadvantages. Such discussions in the classroom can deepen students’ understanding and skill.
Preconception #3: Some people have the ability to “do math” and some don’t.
This is a serious preconception that is widespread in the United States, but not necessarily in other countries. It can easily become a self-fulfilling prophesy. In many countries, the ability to “do math” is assumed to be attributable to the amount of effort people put into learning it.12 Of course,
some people in these countries do progress further than others, and some appear to have an easier time learning mathematics than others. But effort is still considered to be the key variable in success. In contrast, in the United States we are more likely to assume that ability is much more important than effort, and it is socially acceptable, and often even desirable, not to put forth effort in learning mathematics. This difference is also related to cultural differences in the value attributed to struggle. Teachers in some countries believe it is desirable for students to struggle for a while with problems, whereas teachers in the United States simplify things so that students need not struggle at all.13
This preconception likely shares a common root with the others. If mathematics learning is not grounded in an understanding of the nature of the problem to be solved and does not build on a student’s own reasoning and strategy development, then solving problems successfully will depend on the ability to recall memorized rules. If a student has not reviewed those rules recently (as is the case when a summer has passed), they can easily be forgotten. Without a conceptual understanding of the nature of problems and strategies for solving them, failure to retrieve learned procedures can leave a student completely at a loss.
Yet students can feel lost not only when they have forgotten, but also when they fail to “get it” from the start. Many of the conventions of mathematics have been adopted for the convenience of communicating efficiently in a shared language. If students learn to memorize procedures but do not understand that the procedures are full of such conventions adopted for efficiency, they can be baffled by things that are left unexplained. If students never understand that x and y have no intrinsic meaning, but are conventional notations for labeling unknowns, they will be baffled when a z appears. When an m precedes an x in the equation of a line, students may wonder, Why m? Why not s for slope? If there is no m, then is there no slope? To someone with a secure mathematics understanding, the missing m is simply an unstated m = 1. But to a student who does not understand that the point is to write the equation efficiently, the missing m can be baffling. Unlike language learning, in which new expressions can often be figured out because they are couched in meaningful contexts, there are few clues to help a student who is lost in mathematics. Providing a secure conceptual understanding of the mathematics enterprise that is linked to students’ sense-making capacities is critical so that students can puzzle productively over new material, identify the source of their confusion, and ask questions when they do not understand.
Engaging Students’ Preconceptions and Building on Existing Knowledge
Engaging and building on student preconceptions, then, poses two instructional challenges. First, how can we teach mathematics so students come to appreciate that it is not about computation and following rules, but about solving important and relevant quantitative problems? This perspective includes an understanding that the rules for computation and solution are a set of clever human inventions that in many cases allow us to solve complex problems more easily, and to communicate about those problems with each other effectively and efficiently. Second, how can we link formal mathematics training with students’ informal knowledge and problem-solving capacities?
Many recent research and curriculum development efforts, including those of the authors of the chapters that follow, have addressed these questions. While there is surely no single best instructional approach, it is possible to identify certain features of instruction that support the above goals:
-
Allowing students to use their own informal problem-solving strategies, at least initially, and then guiding their mathematical thinking toward more effective strategies and advanced understandings.
-
Encouraging math talk so that students can clarify their strategies to themselves and others, and compare the benefits and limitations of alternate approaches.
-
Designing instructional activities that can effectively bridge commonly held conceptions and targeted mathematical understandings.
Allowing Multiple Strategies
To illustrate how instruction can be connected to students’ existing knowledge, consider three subtraction methods encountered frequently in urban second-grade classrooms involved in the Children’s Math Worlds Project (see Box 5-2). Maria, Peter, and Manuel’s teacher has invited them to share their methods for solving a problem, and each of them has displayed a different method. Two of the methods are correct, and one is mostly correct but has one error. What the teacher does depends on her conception of what mathematics is.
One approach is to show the students the “right” way to subtract and have them and everyone else practice that procedure. A very different approach is to help students explore their methods and see what is easy and difficult about each. If students are taught that for each kind of math situation or problem, there is one correct method that needs to be taught and learned, the seeds of the disconnection between their reasoning and strategy development and “doing math” are sown. An answer is either wrong or
|
BOX 5-2 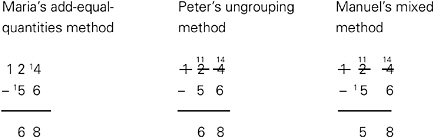 |
right, and one does not need to look at wrong answers more deeply—one needs to look at how to get the right answer. The problem is not that students will fail to solve the problem accurately with this instructional approach; indeed, they may solve it more accurately. But when the nature of the problem changes slightly, or students have not used the taught approach for a while, they may feel completely lost when confronting a novel problem because the approach of developing strategies to grapple with a problem situation has been short-circuited.
If, on the other hand, students believe that for each kind of math situation or problem there can be several correct methods, their engagement in strategy development is kept alive. This does not mean that all strategies are equally good. But students can learn to evaluate different strategies for their advantages and disadvantages. What is more, a wrong answer is usually partially correct and reflects some understanding; finding the part that is wrong and understanding why it is wrong can be a powerful aid to understanding and promotes metacognitive competencies. A vignette of students engaged in the kind of mathematical reasoning that supports active strategy development and evaluation appears in Box 5-3.
It can be initially unsettling for a teacher to open up the classroom to calculation methods that are new to the teacher. But a teacher does not have to understand a new method immediately or alone, as indicated in the description in the vignette of how the class together figured out over time how Maria’s method worked (this method is commonly taught in Latin America and Europe). Understanding a new method can be a worthwhile mathematical project for the class, and others can be involved in trying to figure out why a method works. This illustrates one way in which a classroom community can function. If one relates a calculation method to the quantities involved, one can usually puzzle out what the method is and why it works. This also demonstrates that not all mathematical issues are solved or understood immediately; sometimes sustained work is necessary.
|
BOX 5-3 The following example of a classroom discussion shows how second-grade students can explain their methods rather than simply performing steps in a memorized procedure. It also shows how to make student thinking visible. After several months of teaching and learning, the students reached the point illustrated below. The students’ methods are shown in Box 5-2.
|
|
Manuel’s method combined Maria’s add-equal-quantities method, which he had learned at home, and Peter’s ungrouping method, which he had learned at school. It increases the ones once and decreases the tens twice by subtracting a ten from the top number and adding a ten to the bottom subtracted number. In the Children’s Math Worlds Project, we rarely found children forming such a meaningless combination of methods if they understood tens and ones and had a method of drawing them so they could think about the quantities in a problem (a point discussed more later). Students who transferred into our classes did sometimes initially use Manuel’s mixed approach. But students were eventually helped to understand both the strengths and weaknesses of their existing methods and to find ways of improving their approaches. SOURCE: Karen Fuson, Children’s Math Worlds Project. |
Encouraging Math Talk
One important way to make students’ thinking visible is through math talk—talking about mathematical thinking. This technique may appear obvious, but it is quite different from simply giving lectures or assigning textbook readings and then having students work in isolation on problem sets or homework problems. Instead, students and teachers actively discuss how they approached various problems and why. Such communication about mathematical thinking can help everyone in the classroom understand a given concept or method because it elucidates contrasting approaches, some of which are wrong—but often for interesting reasons. Furthermore, communicating about one’s thinking is an important goal in itself that also facilitates other sorts of learning. In the lower grades, for example, such math talk can provide initial experiences with mathematical justification that culminate in later grades with more formal kinds of mathematical proof.
An emphasis on math talk is also important for helping teachers become more learner focused and make stronger connections with each of their students. When teachers adopt the role of learners who try to understand their students’ methods (rather than just marking the students’ procedures and answers as correct or incorrect), they frequently discover thinking that can provide a springboard for further instruction, enabling them to extend thinking more deeply or understand and correct errors. Note that, when beginning to make student thinking visible, teachers must focus on the community-centered aspects of their instruction. Students need to feel comfortable expressing their ideas and revising their thinking when feedback suggests the need to do so.
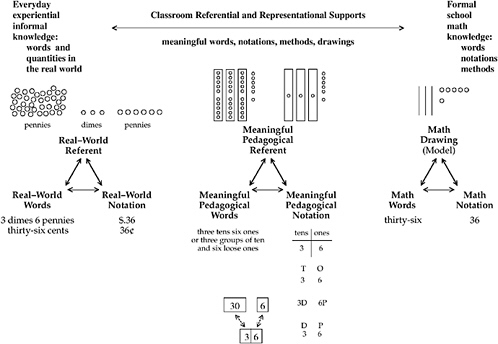
Math talk allows teachers to draw out and work with the preconceptions students bring with them to the classroom and then helps students learn how to do this sort of work for themselves and for others. We have found that it is also helpful for students to make math drawings of their thinking to help themselves in problem solving and to make their thinking more visible (see Figure 5-1). Such drawings also support the classroom math talk because they are a common visual referent for all participants. Students need an effective bridge between their developing understandings and formal mathematics. Teachers need to use carefully designed visual, linguistic, and situational conceptual supports to help students connect their experiences to formal mathematical words, notations, and methods.
The idea of conceptual support for math talk can be further clarified by considering the language students used in the vignette in Box 5-3 when they explained their different multidigit methods. For these explanations to become meaningful in the classroom, it was crucially important that the students explain their multidigit adding or subtracting methods using the meaningful words in the middle pedagogical triangle of Figure 5-2 (e.g., “three
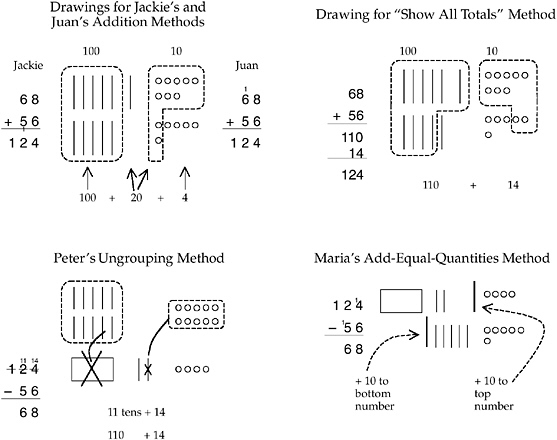
FIGURE 5-1
tens six ones”), as well as the usual math words (e.g., “thirty-six”). It is through such extended connected explanations and use of the quantity words “tens” and “ones” that the students in the Children’s Math Worlds Project came to explain their methods. Their explanations did not begin that way, and the students did not spontaneously use the meaningful language when describing their methods. The teacher needed to model the language and help students use it in their descriptions. More-advanced students also helped less-advanced students learn by modeling, asking questions, and helping others form more complete descriptions.
Initially in the Children’s Math Worlds Project, all students made conceptual support drawings such as those in Figure 5-1. They explicitly linked these drawings to their written methods during explanations. Such drawings linked to the numerical methods facilitated understanding, accuracy, communication, and helping. Students stopped making drawings when they were no longer needed (this varied across students by months). Eventually, most students applied numerical methods without drawings, but these numerical
methods then carried for the members of the classroom the meanings from the conceptual support drawings. If errors crept in, students were asked to think about (or make) a drawing and most errors were then self-corrected.
Designing Bridging Instructional Activities
The first two features of instruction discussed above provide opportunities for students to use their own strategies and to make their thinking visible so it can be built on, revised, and made more formal. This third strategy is more proactive. Research has uncovered common student preconceptions and points of difficulty with learning new mathematical concepts that can be addressed preemptively with carefully designed instructional activities.
This kind of bridging activity is used in the Children’s Math Worlds curriculum to help students relate their everyday, experiential, informal understanding of money to the formal school concepts of multidigit numbers. Real-world money is confusing for many students (e.g., dimes are smaller than pennies but are worth 10 times as much). Also, the formal school math number words and notations are abstract and potentially misleading (e.g., 36 looks like a 3 and a 6, not like 30 and 6) and need to be linked to visual quantities of tens and ones to become meaningful. Fuson designed conceptual “supports” into the curriculum to bridge the two. The middle portion of Figure 5-2 shows an example of the supports that were used to help students build meaning. A teacher or curriculum designer can make a framework like that of Figure 5-2 for any math domain by selecting those conceptual supports that will help students make links among the math words, written notations, and quantities in that domain.
Identifying real-world contexts whose features help direct students’ attention and thinking in mathematically productive ways is particularly helpful in building conceptual bridges between students’ informal experiences and the new formal mathematics they are learning. Examples of such bridging contexts are a key feature of each of the three chapters that follow.
PRINCIPLE #2: UNDERSTANDING REQUIRES FACTUAL KNOWLEDGE AND CONCEPTUAL FRAMEWORKS
The second principle of How People Learn suggests the importance of both conceptual understanding and procedural fluency, as well as an effective organization of knowledge—in this case one that facilitates strategy development and adaptive reasoning. It would be difficult to name a discipline in which the approach to achieving this goal is more hotly debated than mathematics. Recognition of the weakness in the conceptual under-
standing of students in the United States has resulted in increasing attention to the problems involved in teaching mathematics as a set of procedural competences.14 At the same time, students with too little knowledge of procedures do not become competent and efficient problem solvers. When instruction places too little emphasis on factual and procedural knowledge, the problem is not solved; it is only changed. Both are clearly critical.
Equally important, procedural knowledge and conceptual understandings must be closely linked. As the mathematics confronted by students becomes more complex through the school years, new knowledge and competencies require that those already mastered be brought to bear. Box 1-6 in Chapter 1, for example, describes a set of links in procedural and conceptual knowledge required to support the ability to do multidigit subtraction with regrouping—a topic encountered relatively early in elementary school. By the time a student begins algebra years later, the network of knowledge must include many new concepts and procedures (including those for rational number) that must be effectively linked and available to support new algebraic understandings. The teacher’s challenge, then, is to help students build and consolidate prerequisite competencies, understand new concepts in depth, and organize both concepts and competencies in a network of knowledge. Furthermore, teachers must provide sustained and then increasingly spaced opportunities to consolidate new understandings and procedures.
In mathematics, such networks of knowledge often are organized as learning paths from informal concrete methods to abbreviated, more general, and more abstract methods. Discussing multiple methods in the classroom—drawing attention to why different methods work and to the relative efficiency and reliability of each—can help provide a conceptual ladder that helps students move in a connected way from where they are to a more efficient and abstract approach. Students also can adopt or adapt an intermediate method with which they might feel more comfortable. Teachers can help students move at least to intermediate “good-enough” methods that can be understood and explained. Box 5-4 describes such a learning path for single-digit addition and subtraction that is seen worldwide. Teachers in some countries support students in moving through this learning path.
Developing Mathematical Proficiency
Developing mathematical proficiency requires that students master both the concepts and procedural skills needed to reason and solve problems effectively in a particular domain. Deciding which advanced methods all students should learn to attain proficiency is a policy matter involving judgments about how to use scarce instructional time. For example, the level 2 counting-on methods in Box 5-4 may be considered “good-enough” meth-
ods; they are general, rapid, and sufficiently accurate that valuable school time might better be spent on topics other than mastery of the whole network of knowledge required for carrying out the level 3 methods. Decisions about which methods to teach must also take into account that some methods are clearer conceptually and procedurally than the multidigit methods usually taught in the United States (see Box 5-5). The National Research Council’s Adding It Up reviews these and other accessible algorithms in other domains.
This view of mathematics as involving different methods does not imply that a teacher or curriculum must teach multiple methods for every domain. However, alternative methods will frequently arise in a classroom, either because students bring them from home (e.g., Maria’s add-equal-quantities subtraction method, widely taught in other countries) or because students think differently about many mathematical problems. Frequently there are viable alternative methods for solving a problem, and discussing the advantages and disadvantages of each can facilitate flexibility and deep understanding of the mathematics involved. In some countries, teachers emphasize multiple solution methods and purposely give students problems that are conducive to such solutions, and students solve a problem in more than one way.
However, the less-advanced students in a classroom also need to be considered. It can be helpful for either a curriculum or teacher or such less-advanced students to select an accessible method that can be understood and is efficient enough for the future, and for these students to concentrate on learning that method and being able to explain it. Teachers in some countries do this while also facilitating problem solving with alternative methods.
Overall, knowing about student learning paths and knowledge networks helps teachers direct math talk along productive lines toward valued knowledge networks. Research in mathematics learning has uncovered important information on a number of typical learning paths and knowledge networks involved in acquiring knowledge about a variety of concepts in mathematics (see the next three chapters for examples).
Instruction to Support Mathematical Proficiency
To teach in a way that supports both conceptual understanding and procedural fluency requires that the primary concepts underlying an area of mathematics be clear to the teacher or become clear during the process of teaching for mathematical proficiency. Because mathematics has traditionally been taught with an emphasis on procedure, adults who were taught this way may initially have difficulty identifying or using the core conceptual understandings in a mathematics domain.
|
BOX 5-4 Children around the world pass through three levels of increasing sophistication in methods of single-digit addition and subtraction. The first level is direct modeling by counting all of the objects at each step (counting all or taking away). Students can be helped to move rapidly from this first level to counting on, in which counting begins with one addend. For example, 8 + 6 is not solved by counting from 1 to 14 (counting all), but by counting on 6 from 8: counting 8, 9, 10, 11, 12, 13, 14 while keeping track of the 6 counted on. For subtraction, Children’s Math Worlds does what is common in many countries: it helps students see subtraction as involving a mystery addend. Students then solve a subtraction problem by counting on from the known addend to the known total. Earlier we saw how Maria solved 14 - 6 by counting up from 6 to 14, raising 8 fingers while doing so to find that 6 plus 8 more is 14. Many students in the United States instead follow a learning path that moves from drawing little sticks or circles for all of the objects and crossing some out (e.g., drawing 14 sticks, crossing out 6, and counting the rest) to counting down (14, 13, 12, 11, 10, 9, 8, 7, 6). But counting down is difficult and error prone. When first or second graders are helped to move to a different learning path that solves subtraction problems by forward methods, such as counting on or adding on over 10 (see below), subtraction becomes as easy as addition. For many students, this is very empowering. The third level of single-digit addition and subtraction is exemplified by Peter in the vignette in Box 5-2. At this level, students can chunk |
The approaches in the three chapters that follow identify the central conceptual structures in several areas of mathematics. The areas of focus—whole number, rational number, and functions—were identified by Case and his colleagues as requiring major conceptual shifts. In the first, students are required to master the concept of quantity; in the second, the concept of proportion and relative number; and in the third, the concept of dependence in quantitative relationships. Each of these understandings requires that a supporting set of concepts and procedural abilities be put in place. The extensive research done by Griffin and Case on whole number, by Case and Moss on rational number, and by Case and Kalchman on functions provides a strong foundation for identifying the major conceptual challenges students
|
numbers and relate these chunks. The chunking enables them to carry out make-a-ten methods: they give part of one number to the other number to make a ten. These methods are taught in many countries. They are very helpful in multidigit addition and subtraction because a number found in this way is already thought of as 1 ten and some ones. For example, for 8 + 6, 6 gives 2 to 8 to make 10, leaving 4 in the 6, so 10 + 4 = 14. Solving 14–8 is done similarly: with 8, how many make 10 (2), plus the 4 in 14, so the answer is 6. These make-a-ten methods demonstrate the learning paths and network of knowledge required for advanced solution methods. Children may also use a “doubles” strategy for some problems—e.g., 7 + 6 = 6 + 6 + 1= 12 + 1 = 13—because the doubles (for example, 6 + 6 or 8 + 8) are easy to learn. The make-a-ten methods illustrate the importance of a network of knowledge. Students must master three kinds of knowledge to be able to carry out a make-a-ten method fluently: they must (1) for each number below 10, know how much more makes 10; (2) break up any number below 10 into all possible pairs of parts (because 9 + 6 requires knowing 6 = 1 + 5, but 8 + 6 requires knowing 6 = 2 + 4, etc.); and (3) know 10 + 1 = 11, 10 + 2 = 12, 10 + 3 = 13, etc., rapidly without counting. Note that particular methods may be more or less easy for learners from different backgrounds. For example, the make-a-ten methods are easier for East Asian students, whose language says, “Ten plus one is ten one, ten plus two is ten two,” than for English-speaking students, whose language says, “Ten plus one is eleven, ten plus two is twelve, etc.” |
face in mastering these areas. This research program traced developmental/ experiential changes in children’s thinking as they engaged with innovative curriculum. In each area of focus, instructional approaches were developed that enable teachers to help children move through learning paths in productive ways. In doing so, teachers often find that they also build a more extensive knowledge network.
As teachers guide a class through learning paths, a balance must be maintained between learner-centered and knowledge-centered needs. The learning path of the class must also continually relate to individual learner knowledge. Box 5-6 outlines two frameworks that can facilitate such balance.
|
BOX 5-5 In over a decade of working with a range of urban and suburban classrooms in the Children’s Math Worlds Project, we found that one multidigit addition method and one multidigit subtraction method were accessible to all students. The students easily learned, understood, and remembered these methods and learned to draw quantities for and explain them. Both methods are modifications of the usual U.S. methods. The addition method is the write-new-groups-below method, in which the new 1 ten or 1 hundred, etc., is written below the column on the line rather than above the column (see Jackie’s method in Figure 5-1). In the subtraction fix-everything-first method, every column in the top number that needs ungrouping is ungrouped (in any order), and then the subtracting in every column is done (in any order). Because this method can be done from either direction and is only a minor modification of the common U.S. methods, learning-disabled and special-needs students find it especially accessible. Both of these methods stimulate productive discussions in class because they are easily related to the usual U.S. methods that are likely to be brought to class by other students. |
PRINCIPLE #3: A METACOGNITIVE APPROACH ENABLES STUDENT SELF-MONITORING
Learning about oneself as a learner, thinker, and problem solver is an important aspect of metacognition (see Chapter 1). In the area of mathematics, as noted earlier, many people who take mathematics courses “learn” that “they are not mathematical.” This is an unintended, highly unfortunate, consequence of some approaches to teaching mathematics. It is a consequence that can influence people for a lifetime because they continue to avoid anything mathematical, which in turn ensures that their belief about being “nonmathematical” is true.15
An article written in 1940 by Charles Gragg, entitled “Because Wisdom Can’t be Told,” is relevant to issues of metacognition and mathematics learning. Gragg begins with the following quotation from Balzac:
So he had grown rich at last, and thought to transmit to his only son all the cut-and-dried experience which he himself had purchased at the price of his lost illusions; a noble last illusion of age.
Except for the part about growing rich, Balzac’s ideas fit many peoples’ experiences quite well. In our roles as parents, friends, supervisors, and professional educators, we frequently attempt to prepare people for the future by imparting the wisdom gleaned from our own experiences. Some-
|
BOX 5-6 Eliciting and then building on and using students’ mathematical thinking can be challenging. Yet recent research indicates that teachers can move their students through increasingly productive levels of classroom discourse. Hufferd-Ackles and colleagues16 describe four levels of a “math-talk learning community,” beginning with a traditional, teacher-directed format in which the teacher asks short-answer questions, and student responses are directed to the teacher. At the next level, “getting started,” the teacher begins to pursue and assess students’ mathematical thinking, focusing less on answers alone. In response, students provide brief descriptions of their thinking. The third level is called “building.” At this point the teacher elicits and students respond with fuller descriptions of their thinking, and multiple methods are volunteered. The teacher also facilitates student-to-student talk about mathematics. The final level is “math-talk.” Here students share responsibility for discourse with the teacher, justifying their own ideas and asking questions of and helping other students. Key shifts in teacher practice that support a class moving through these levels include asking questions that focus on mathematical thinking rather than just on answers, probing extensively for student thinking, modeling and expanding on explanations when necessary, fading physically from the center of the classroom discourse (e.g., moving to the back of the classroom), and coaching students in their participatory roles in the discourse (“Everyone have a thinker question ready.”). Related research indicates that when building a successful classroom discourse community, it is important to balance the process of discourse, that is, the ways in which student ideas are elicited, with the content of discourse, the substance of the ideas that are discussed. In other words, how does a teacher ensure both that class discussions provide sufficient space for students to share their ideas and that discussions are mathematically productive? Sherin17 describes one model for doing so whereby class discussions begin with a focus on “idea generation,” in which many student ideas are solicited. Next, discussion moves into a “comparison and evaluation” phase, in which the class looks more closely at the ideas that have been raised, but no new ideas are raised. The teacher then “filters” ideas for the class, highlighting a subset of ideas for further pursuit. In this way, student ideas are valued throughout discussion, but the teacher also plays a role in determining the extent to which specific mathematical ideas are considered in detail. A class may proceed through several cycles of these three phases in a single discussion. |
times our efforts are rewarded, but we are often less successful than we would like to be, and we need to understand why.
The idea that “wisdom can’t be told” helps educators rethink the strategy of simply telling students that some topic (e.g., mathematics) is important, and they can master it if they try. There are important differences between simply being told something and being able to experience it for oneself. Students’ experiences have strong effects on their beliefs about themselves, as well as their abilities to remember information and use it spontaneously to solve new problems.18 If their experiences in mathematics classes involve primarily frustration and failure, simply telling them, “trust me, this will be relevant someday” or “believe me, you have the ability to understand this” is a weak intervention. On the other hand, helping students experience their own abilities to find patterns and problems, invent solutions (even if they are not quite as good as expert solutions), and contribute to and learn from discussions with others provides the kinds of experiences that can help them learn with understanding, as well as change their views about the subject matter and themselves.19
However, research on metacognition suggests that an additional instructional step is needed for optimal learning—one that involves helping students reflect on their experiences and begin to see their ideas as instances of larger categories of ideas. For example, students might begin to see their way of showing more ones when subtracting as one of several ways to demonstrate this same important mathematical idea.
One other aspect of metacognition that is nicely illustrated in the context of mathematics involves the claim made in Chapter 1 that metacognition is not simply a knowledge-free ability, but requires relevant knowledge of the topics at hand. At the beginning of this chapter, we noted that many students approach problems such as adding fractions as purely computational (e.g., “What is the approximate sum of 8/9 plus 11/13?”). Ideally, we also want students to monitor the accuracy of their problem solving, just as we want them to monitor their understanding when reading about science, history, or literature.
One way to monitor the accuracy of one’s computation is to go back and recheck each of the steps. Another way is to estimate the answer and see whether there is a discrepancy between one’s computations and the estimate. However, the ability to estimate requires the kind of knowledge that might be called “number sense.” For the above fraction problem, for example, a person with number sense who computes an answer and sees that it is greater than 2 knows that the computation is obviously wrong. But it is “obvious” only if the person has learned ways to think about number that go beyond the ability merely to count and compute.
Instruction That Supports Metacognition
Much of what we have discussed with regard to making student thinking visible can be thought of as ongoing assessment of students. Such assessment can include students so they become involved in thinking about their own mathematical progress and that of their classmates. Such ongoing assessment can then become internalized as metacognitive self-monitoring. Classroom communication about students’ mathematical thinking greatly facilitates both teacher and student assessment of learning. Teachers and students can see difficulties particular students are having and can help those students by providing explanations. Teachers can discern primitive solution methods that need to be advanced to more effective methods. They also can see how students are advancing in their helping and explaining abilities and plan how to foster continued learning in those areas.
Students can also learn some general problem-solving strategies, such as “make a drawing of the situation” or “ask yourself questions” that apply to many different kinds of problems. Drawings and questions are a means of self-monitoring. They also can offer teachers windows into students’ thinking and thus provide information about how better to help students along a learning path to efficient problem-solving methods.
An Emphasis on Debugging
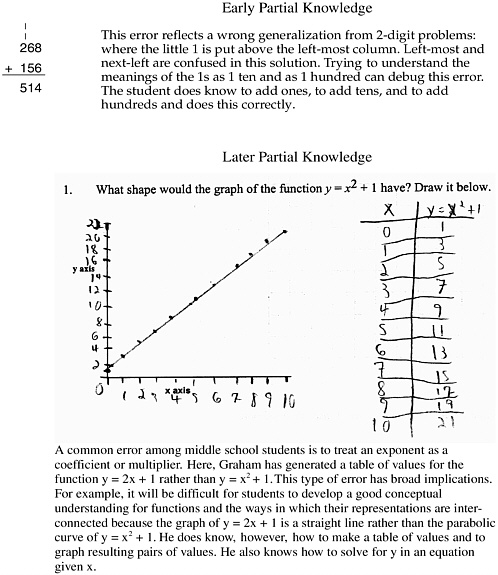
Metacognitive functioning is also facilitated by shifting from a focus on answers as just right or wrong to a more detailed focus on “debugging” a wrong answer, that is, finding where the error is, why it is an error, and correcting it. Of course, good teachers have always done this, but there are now two special reasons for doing so. One is the usefulness of this approach in complex problem solving, such as debugging computer programs. Technological advances mean that more adults will need to do more complex problem solving and error identification throughout their lives, so debugging—locating the source of an error—is a good general skill that can be learned in the math classroom.
The second reason is based on considerable amount of research in the past 30 years concerning student errors. Figure 5-3 illustrates two such typical kinds of errors in early and late school topics. The partial student knowledge reflected in each error is described in the figure. One can also see how a focus on understanding can help students debug their own errors. For example, asking how much the little “1’s” really represent can help students start to see their error in the top example and thus modify the parts of the method that are wrong.
Internal and External Dialogue as Support for Metacognition
The research summarized in How People Learn and Adding It Up and the professional experience summarized in the standards of the National Council of Teachers of Mathematics all emphasize how important it is for students to communicate about mathematics and for teachers to help them learn to do so. Students can learn to reflect on and describe their mathematical thinking. They can learn to compare methods of solving a problem and identify the advantages and disadvantages of each. Peers can learn to ask thoughtful questions about other students’ thinking or help edit such statements to clarify them. Students can learn to help each other, sometimes in informal, spontaneous ways and sometimes in more organized, coaching-partner situations. The vignette in Box 5-3 illustrates such communication about mathematical thinking after it has been developed in a classroom. Experience in the Children’s Math Worlds Project indicates that students from all backgrounds can learn to think critically and ask thoughtful questions, reflect on and evaluate their own achievement, justify their points of view, and understand the perspectives of others. Even first-grade students can learn to interact in these ways.
Of course, teachers must help students learn to interact fruitfully. To this end, teachers can model clear descriptions and supportive questioning or helping techniques. In a classroom situation, some students may solve problems at the board while others solve them at their seats. Students can make drawings or use notations to indicate how they thought about or solved a problem. Selected students can then describe their solution methods, and peers can ask questions to clarify and to give listeners a role. Sometimes, pairs of students may explain their solutions, with the less-advanced partner explaining first and the other partner then expanding and clarifying. Students usually attend better if only two or three of their fellow students explain their solution method for a given problem. More students can solve at the board, but the teacher can select the methods or the students for the class to hear at that time. It is useful to vary the verbal level of such explainers. Doing so assists all students in becoming better explainers by hearing and helping classmates expand upon a range of explanations. The goal in all of this discussion is to advance everyone’s thinking and monitoring of their own understanding and that of other students rather than to conduct simple turn taking, though of course over time, all students can have opportunities to explain.
Seeking and Giving Help
Students must have enough confidence not only to engage with problems and try to solve them, but also to seek help when they are stuck. The
dialogue that occurs in pair or class situations can help generate self-regulating speech that a student can produce while problem solving. Such helping can also increase the metacognitive awareness of the helper as he or she takes into consideration the thinking of the student being helped.
The Framework of How People Learn: Seeking a Balanced Classroom Environment
The framework of How People Learn suggests that classroom environments should at the same time be learner-centered, knowledge-centered, assessment-centered, and community-centered (see Chapter 1). These features map easily to the preceding discussion of the three principles, as well as to the chapters that follow. The instruction described is learner-centered in that it draws out and builds on student thinking. It is also knowledge-centered in that it focuses simultaneously on the conceptual understanding and the procedural knowledge of a topic, which students must master to be proficient, and the learning paths that can lead from existing to more advanced understanding. It is assessment-centered in that there are frequent opportunities for students to reveal their thinking on a topic so the teacher can shape instruction in response to their learning, and students can be made aware of their own progress. And it is community-centered in that the norms of the classroom community value student ideas, encourage productive interchange, and promote collaborative thinking.
Effective teaching and learning depend, however, on balance among these features of the classroom environment. There must be continual connections between the learner-centered focus on student knowledge and the more formal knowledge networks that are the goals of teaching in a domain. Traditional teaching has tended to emphasize the knowledge networks and pay insufficient attention to conceptual supports and the need to build on learner knowledge. Many students learn rote knowledge that cannot be used adequately in solving problems. On the other hand, an overemphasis on learner-centered teaching results in insufficient attention to connections with valued knowledge networks, the crucially important guiding roles of teachers and of learning accessible student methods, and the need to consolidate knowledge. Four such excesses are briefly discussed here.
First, some suggest that students must invent all their mathematical ideas and that we should wait until they do so rather than teach ideas. This view, of course, ignores the fact that all inventions are made within a supportive culture and that providing appropriate supports can speed such inventions. Too much focus on student-invented methods per se can hold students back; those who use time-consuming methods that are not easily generalized need to be helped to move on to more rapid and generalizable “good-enough” methods. A focus on sense making and understanding of the meth-
ods that are used is the balanced focus, rather than an emphasis on whether the method was invented by the student using it.
Second, classroom discussions may not be sufficiently guided by the teacher through the learning path. Students may talk on and on, meandering without much focus. Descriptions of student thinking may have a turn-taking, “every method is equally wonderful” flavor so that other students do not listen carefully or ask questions, but passively await their turn to talk. Different student methods may be described, but their advantages and disadvantages, or at least their similar and different features, are not discussed. There may be no building toward student-to-student talk, but everything said may be directed toward the teacher.
Third, the use of real-world situations and conceptual supports may consist more of a series of activities in which the mathematical ideas are not sufficiently salient and not connected enough to the standard math notations and vocabulary. The result may be a scattershot approach involving many different activities rather than careful choices of core representations or bridging contexts that might guide students through a coherent learning path.
Fourth, learning may not be consolidated enough because of an excessive focus on the initial learning activities. Time for consolidation of learning, with feedback loops should errors arise, is vital for mathematical fluency.
The recent Third International Mathematics and Science Study showed that teaching in the United States is still overwhelmingly traditional. However, the above caveats need to be kept in mind as teachers move forward in implementing the principles of How People Learn.
NEXT STEPS
There are some curricula that implement, at least partially, the principles of How People Learn. Even without extensive curricular support, however, teachers can substantially improve their practice by understanding and using these principles. This is particularly true if they can examine their own teaching practices, supported by a teaching–learning community of like-minded colleagues. Such a community can help teachers create learning paths for themselves that can move them from their present teaching practices to practices that conform more fully to the principles of How People Learn and thereby create more effective classrooms. Two such teacher communities, involving video clubs and lesson study, respectively, are summarized in Boxes 5-7 and 5-8. A third approach to a teacher learning community is to organize teacher discussions around issues that arise from teaching a curriculum that supports conceptual approaches. Box 5-9 describes research summarizing one productive focus for such discussions—the use of openings in the curriculum where teachers can focus on student questions or misunderstandings.
|
BOX 5-7 Research indicates that teachers can develop their ability to attend to and interpret student thinking not only in the midst of class discussions, but also outside of class as they reflect on students’ ideas. One model for doing so is the use of video clubs in which teachers meet together to watch and discuss video excerpts from their classrooms.20 By providing teachers opportunities to examine student thinking without the pressure of having to respond immediately, video clubs can help prompt the development of new techniques for analyzing student thinking among teachers—techniques that teachers can then bring back to their classrooms. |
|
BOX 5-8 Lesson study is “a cycle in which teachers work together to consider their long-term goals for students, bring those goals to life in actual ‘research lessons,’ and collaboratively observe, discuss, and refine the lessons.”21 Lesson study has been a major form of teacher professional development in Japan for many decades, and in recent years has attracted the attention of U.S. teachers, school administrators, and educational researchers.22 It is a simple idea. Teachers collaboratively plan a lesson that is taught by one group member while others observe and carefully collect data on student learning and behavior. The student data are then used to reflect on the lesson and revise it as needed. Lesson study is a teacher-led process in which teachers collaboratively identify a concept that is persistently difficult for students, study the best available curriculum materials in order to rethink their teaching of this topic, and plan and teach one or more “research lessons” that enable them to see student reactions to their redesigned unit. Ideally, a lesson study group allows teachers to share their expertise and knowledge, as well as questions related to both teaching and subject matter. Lesson study groups may also draw on knowledgeable outsiders as resources for content knowledge, group facilitation, and so on. NOTE: Resources, including a handbook, videotapes, listserve, and protocols for teachers who wish to engage in lesson study, can be found at the websites of the Lesson Study Research Group at Teachers College, Columbia University: (http://www.tc.columbia.edu/lessonstudy/) and the Mills College Lesson Study Group (www.lessonresearch.net). See also Lewis (2002). |
|
BOX 5-9 Even when using a prepared curriculum, teachers have an important role as curriculum designers. In a study of two elementary teachers using a new textbook, Remillard23 found that teachers made regular decisions about what parts of the teacher’s guide to read, which suggestions to follow and to what ends, how to structure students’ mathematical activities, and how to respond to students’ questions and ideas. The decisions teachers made had a substantial impact on the curriculum experienced by students. In other words, written curriculum alone does not determine students’ experiences in the classroom; this is the role of the teacher. Remillard and Geist24 use the term “openings in the curriculum” to denote those instances during instruction in which things do not go as described in the preset curriculum. These openings are often prompted by students’ questions or teachers’ observations about student understanding or misunderstanding. The authors argue that teachers must navigate these openings by (1) carefully analyzing student work and thinking, (2) weighing possible options for proceeding against one’s goals for student learning, and (3) taking responsive action that is open to ongoing examination and adjustment. They suggest that teaching with curriculum guides can be improved as teachers recognize and embrace their role while navigating openings in the curriculum to determine learning paths for students. Similarly, Remillard25 found that teachers came to reflect on their beliefs and understandings related to their teaching and its content while involved in the very work of deciding what to do next by interpreting students’ understanding with respect to their goals for the students and particular instructional tasks. Thus, some of the most fruitful opportunities for teacher learning when using a new curriculum occurred when teachers were engaged in the work of navigating openings in the curriculum. |
It will take work by teachers, administrators, researchers, parents, and politicians to bring these new principles and goals to life in classrooms and to create the circumstances in which this can happen. Nonetheless, there are enough examples of the principles in action to offer a vision of the new kinds of learning that can be accessible to all students and to all teachers. Some materials to support teachers in these efforts do exist, and more are being developed. Helpful examples of the three principles in action are given in the chapters that follow. It is important to note, once again, that other projects have generated examples that implement the principles of How People Learn. Some of these examples can be found in the authors’ references to that research and in the suggested teacher reading list. All of
this work indicates that we have begun the crucial journey into mathematical proficiency for all and that the principles of How People Learn can guide us on this journey.
NOTES
REFERENCES
Anghileri, J. (1989). An investigation of young children’s understanding of multiplication. Educational Studies in Mathematics, 20, 367-385.
Ashlock, R.B. (1998). Error patterns in computation. Upper Saddle River, NJ: Prentice-Hall.
Baek, J.-M. (1998). Children’s invented algorithms for multidigit multiplication problems. In L.J. Morrow and M.J. Kenney (Eds.), The teaching and learning of algorithms in school mathematics. Reston, VA: National Council of Teachers of Mathematics.
Baroody, A.J., and Coslick, R.T. (1998). Fostering children’s mathematical power: An investigative approach to k-8 mathematics instruction. Mahwah, NJ: Lawrence Erlbaum Associates.
Baroody, A.J., and Ginsburg, H.P. (1986). The relationship between initial meaningful and mechanical knowledge of arithmetic. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 75-112). Mahwah, NJ: Lawrence Erlbaum Associates.
Beishuizen, M. (1993). Mental strategies and materials or models for addition and subtraction up to 100 in Dutch second grades. Journal for Research in Mathematics Education, 24, 294-323.
Beishuizen, M., Gravemeijer, K.P.E., and van Lieshout, E.C.D.M. (Eds.). (1997). The role of contexts and models in the development of mathematical strategies and procedures. Utretch, The Netherlands: CD-B Press/The Freudenthal Institute.
Bergeron, J.C., and Herscovics, N. (1990). Psychological aspects of learning early arithmetic. In P. Nesher and J. Kilpatrick (Eds.), Mathematics and cognition: A research synthesis by the International Group for the Psychology of Mathematics Education. Cambridge, England: Cambridge University Press.
Bransford, J.D., Franks, J.J., Vye, N.J., and Sherwood, R.D. (1989). New approaches to instruction: Because wisdom can’t be told. In S. Vasniadou and A. Ortony (Eds.), Similarity and analogical reasoning (pp. 470-497). New York: Cambridge University Press.
Brophy, J. (1997). Effective instruction. In H.J. Walberg and G.D. Haertel (Eds.), Psychology and educational practice (pp. 212-232). Berkeley, CA: McCutchan.
Brownell, W.A. (1987). AT Classic: Meaning and skill—maintaining the balance. Arithmetic Teacher, 34(8), 18-25.
Canfield, R.L., and Smith, E.G. (1996). Number-based expectations and sequential enumeration by 5-month-old infants. Developmental Psychology, 32, 269-279.
Carey, S. (2001). Evolutionary and ontogenetic foundations of arithmetic. Mind and Language, 16(1), 37-55.
Carpenter, T.P., and Moser, J.M. (1984). The acquisition of addition and subtraction concepts in grades one through three. Journal for Research in Mathematics Education, 15(3), 179-202.
Carpenter, T.P., Fennema, E., Peterson, P.L., Chiang, C.P., and Loef, M. (1989). Using knowledge of children’s mathematics thinking in classroom teaching: An experimental study. American Educational Research Journal, 26(4), 499-531.
Carpenter, T.P., Franke, M.L., Jacobs, V., and Fennema, E. (1998). A longitudinal study of invention and understanding in children’s multidigit addition and subtraction. Journal for Research in Mathematics Education, 29, 3-20.
Carraher, T.N. (1986). From drawings to buildings: Mathematical scales at work. International Journal of Behavioural Development, 9, 527-544.
Carraher, T.N., Carraher, D.W., and Schliemann, A.D. (1985). Mathematics in the streets and in schools. British Journal of Developmental Psychology, 3, 21-29.
Carroll, W.M. (2001). A longitudinal study of children using the reform curriculum everyday mathematics. Available: http://everydaymath.uchicago.edu/educators/references.shtml [accessed September 2004].
Carroll, W.M., and Fuson, K.C. (1999). Achievement results for fourth graders using the standards-based curriculum everyday mathematics. Unpublished document, University of Chicago, Illinois.
Carroll, W.M., and Porter, D. (1998). Alternative algorithms for whole-number operations. In L.J. Morrow and M.J. Kenney (Eds.), The teaching and learning of algorithms in school mathematics (pp. 106-114). Reston, VA: National Council of Teachers of Mathematics.
Case, R. (1985). Intellectual development: Birth to adulthood. New York: Academic Press.
Case, R. (1992). The mind’s staircase: Exploring the conceptual underpinnings of children’s thought and knowledge. Mahwah, NJ: Lawrence Erlbaum Associates.
Case, R. (1998). A psychological model of number sense and its development. Paper presented at the annual meeting of the American Educational Research Association, April, San Diego, CA.
Case, R., and Sandieson, R. (1988). A developmental approach to the identification and teaching of central conceptual structures in mathematics and science in the middle grades. In M. Behr and J. Hiebert (Eds.), Research agenda in mathematics education: Number concepts and in the middle grades (pp. 136-270). Mahwah, NJ: Lawrence Erlbaum Associates.
Case, R., Griffin, S., and Kelly, W.M. (1999). Socioeconomic gradients in mathematical ability and their responsiveness to intervention during early childhood. In D.P. Keating and C. Hertzman (Eds.), Developmental health and the wealth of nations: Social, biological, and educational dynamics (pp. 125-149). New York: Guilford Press.
Ceci, S.J. (1996). On intelligence: A bioecological treatise on intellectual development. Cambridge, MA: Harvard University Press.
Ceci, S.J., and Liker, J.K. (1986). A day at the races: A study of IQ, expertise, and cognitive complexity. Journal of Experimental Psychology, 115(3), 255-266.
Cotton, K. (1995). Effective schooling practices: A research synthesis. Portland, OR: Northwest Regional Lab.
Davis, R.B. (1984). Learning mathematics: The cognitive science approach to mathematics education. Norwood, NJ: Ablex.
De la Rocha, O.L. (1986). The reorganization of arithmetic practice in the kitchen. Anthropology and Education Quarterly, 16(3), 193-198.
Dixon, R.C., Carnine, S.W., Kameenui, E.J., Simmons, D.C., Lee, D.S., Wallin, J., and Chard, D. (1998). Executive summary. Report to the California State Board of Education, review of high-quality experimental research. Eugene, OR: National Center to Improve the Tools of Educators.
Dossey, J.A., Swafford, J.O., Parmantie, M., and Dossey, A.E. (Eds.). (2003). Multidigit addition and subtraction methods invented in small groups and teacher support of problem solving and reflection. In A. Baroody and A. Dowker (Eds.), The development of arithmetic concepts and skills: Constructing adaptive expertise. Mahwah, NJ: Lawrence Erlbaum Associates.
Fernandez, C. (2002). Learning from Japanese approaches to professional development. The case of lesson study. Journal of Teacher Education, 53(5), 393-405.
Fraivillig, J.L., Murphy, L.A., and Fuson, K.C. (1999). Advancing children’s mathematical thinking in everyday mathematics reform classrooms. Journal for Research in Mathematics Education, 30, 148-170.
Fuson, K.C. (1986a). Roles of representation and verbalization in the teaching of multidigit addition and subtraction. European Journal of Psychology of Education, 1, 35-56.
Fuson, K.C. (1986b). Teaching children to subtract by counting up. Journal for Research in Mathematics Education, 17, 172-189.
Fuson, K.C. (1990). Conceptual structures for multiunit numbers: Implications for learning and teaching multidigit addition, subtraction, and place value. Cognition and Instruction, 7, 343-403.
Fuson, K.C. (1992a). Research on learning and teaching addition and subtraction of whole numbers. In G. Leinhardt, R.T. Putnam, and R.A. Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 53-187). Mahwah, NJ: Lawrence Erlbaum Associates.
Fuson, K.C. (1992b). Research on whole number addition and subtraction. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 243-275). New York: Macmillan.
Fuson, K.C. (2003). Developing mathematical power in whole number operations. In J. Kilpatrick, W.G. Martin, and D. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 68-94). Reston, VA: National Council of Teachers of Mathematics.
Fuson, K.C., and Briars, D.J. (1990). Base-ten blocks as a first- and second-grade learning/teaching approach for multidigit addition and subtraction and place-value concepts. Journal for Research in Mathematics Education, 21, 180-206.
Fuson, K.C., and Burghardt, B.H. (1993). Group case studies of second graders inventing multidigit addition procedures for base-ten blocks and written marks. In J.R. Becker and B.J. Pence (Eds.), Proceedings of the fifteenth annual meeting of the North American chapter of the international group for the psychology of mathematics education (pp. 240-246). San Jose, CA: The Center for Mathematics and Computer Science Education, San Jose State University.
Fuson, K.C., and Burghardt, B.H. (1997). Group case studies of second graders inventing multidigit subtraction methods. In Proceedings of the 19th annual meeting of the North American chapter of the international group for the psychology of mathematics education (pp. 291-298). San Jose, CA: The Center for Mathematics and Computer Science Education, San Jose State University.
Fuson, K.C., and Fuson, A.M. (1992). Instruction to support children’s counting on for addition and counting up for subtraction. Journal for Research in Mathematics Education, 23, 72-78.
Fuson, K.C., and Kwon, Y. (1992). Korean children’s understanding of multidigit addition and subtraction. Child Development, 63(2), 491-506.
Fuson, K.C., and Secada, W.G. (1986). Teaching children to add by counting with finger patterns. Cognition and Instruction, 3, 229-260.
Fuson, K.C., and Smith, T. (1997). Supporting multiple 2-digit conceptual structures and calculation methods in the classroom: Issues of conceptual supports, instructional design, and language. In M. Beishuizen, K.P.E. Gravemeijer, and E.C.D.M. van Lieshout (Eds.), The role of contexts and models in the development of mathematical strategies and procedures (pp. 163-198). Utrecht, The Netherlands: CD-B Press/The Freudenthal Institute.
Fuson, K.C., Stigler, J., and Bartsch, K. (1988). Grade placement of addition and subtraction topics in Japan, mainland China, the Soviet Union, Taiwan, and the United States. Journal for Research in Mathematics Education, 19(5), 449-456.
Fuson, K.C., Perry, T., and Kwon, Y. (1994). Latino, Anglo, and Korean children’s finger addition methods. In J.E.H. van Luit (Ed.), Research on learning and instruction of mathematics in kindergarten and primary school, (pp. 220-228). Doetinchem/Rapallo, The Netherlands: Graviant.
Fuson, K.C., Perry, T., and Ron, P. (1996). Developmental levels in culturally different finger methods: Anglo and Latino children’s finger methods of addition. In E. Jakubowski, D. Watkins, and H. Biske (Eds.), Proceedings of the 18th annual meeting of the North American chapter for the psychology of mathematics education (2nd edition, pp. 347-352). Columbus, OH: ERIC Clearinghouse for Science, Mathematics, and Environmental Education.
Fuson, K.C., Lo Cicero, A., Hudson, K., and Smith, S.T. (1997). Snapshots across two years in the life of an urban Latino classroom. In J. Hiebert, T. Carpenter, E. Fennema, K.C. Fuson, D. Wearne, H. Murray, A. Olivier, and P. Human (Eds.), Making sense: Teaching and learning mathematics with understanding (pp. 129-159). Portsmouth, NH: Heinemann.
Fuson, K.C., Smith, T., and Lo Cicero, A. (1997). Supporting Latino first graders’ ten-structured thinking in urban classrooms. Journal for Research in Mathematics Education, 28, 738-760.
Fuson, K.C., Wearne, D., Hiebert, J., Murray, H., Human, P., Olivier, A., Carpenter, T., and Fennema, E. (1997). Children’s conceptual structures for multidigit numbers and methods of multidigit addition and subtraction. Journal for Research in Mathematics Education, 28, 130-162.
Fuson, K.C., De La Cruz, Y., Smith, S., Lo Cicero, A., Hudson, K., Ron, P., and Steeby, R. (2000). Blending the best of the 20th century to achieve a mathematics equity pedagogy in the 21st century. In M.J. Burke and F.R. Curcio (Eds.), Learning mathematics for a new century (pp. 197-212). Reston, VA: National Council of Teachers of Mathematics.
Geary, D.C. (1994). Children’s mathematical development: Research and practical applications. Washington, DC: American Psychological Association.
Gelman, R. (1990). First principles organize attention to and learning about relevant data: Number and the animate-inanimate distinction as examples. Cognitive Science, 14, 79-106.
Ginsburg, H.P. (1984). Children’s arithmetic: The learning process. New York: Van Nostrand.
Ginsburg, H.P., and Allardice, B.S. (1984). Children’s difficulties with school mathematics. In B. Rogoff and J. Lave (Eds.), Everyday cognition: Its development in social contexts (pp. 194-219). Cambridge, MA: Harvard University Press.
Ginsburg, H.P., and Russell, R.L. (1981). Social class and racial influences on early mathematical thinking. Monographs of the Society for Research in Child Development 44(6, serial #193). Malden, MA: Blackwell.
Goldman, S.R., Pellegrino, J.W., and Mertz, D.L. (1988). Extended practice of basic addition facts: Strategy changes in learning-disabled students. Cognition and Instruction, 5(3), 223-265.
Goldman, S.R., Hasselbring, T.S., and the Cognition and Technology Group at Vanderbilt (1997). Achieving meaningful mathematics literacy for students with learning disabilities. Journal of Learning Disabilities, March 1(2), 198-208.
Greer, B. (1992). Multiplication and division as models of situation. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 276-295). New York: Macmillan.
Griffin, S., and Case, R. (1997). Re-thinking the primary school math curriculum: An approach based on cognitive science. Issues in Education, 3(1), 1-49.
Griffin, S., Case, R., and Siegler, R.S. (1994 ). Rightstart: Providing the central conceptual structures for children at risk of school failure. In K. McGilly (Ed.), Classroom lessons: Integrating cognitive theory and classroom practice (pp. 13-48). Mahwah, NJ: Lawrence Erlbaum Associates.
Grouws, D. (1992). Handbook of research on mathematics teaching and learning. New York: Teachers College Press.
Hamann, M.S., and Ashcraft, M.H. (1986). Textbook presentations of the basic addition facts. Cognition and Instruction, 3, 173-192.
Hart, K.M. (1987). Practical work and formalisation, too great a gap. In J.C. Bergeron, N. Hersovics, and C. Kieren (Eds.), Proceedings from the eleventh international conference for the psychology of mathematics education (vol. 2, pp. 408-415). Montreal, Canada: University of Montreal.
Hatano, G., and Inagaki, K. (1996). Cultural contexts of schooling revisited. A review of the learning gap from a cultural psychology perspective. Paper presented at the Conference on Global Prospects for Education: Development, Culture, and Schooling, University of Michigan.
Hiebert, J. (1986). Conceptual and procedural knowledge: The case of mathematics. Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J. (1992). Mathematical, cognitive, and instructional analyses of decimal fractions. In G. Leinhardt, R. Putnam, and R.A. Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 283-322). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J., and Carpenter, T.P. (1992). Learning and teaching with understanding. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 65-97). New York: Macmillan.
Hiebert, J., and Wearne, D. (1986). Procedures over concepts: The acquisition of decimal number knowledge. In J. Hiebert (Ed.), Conceptual and procedural knowledge: The case of mathematics (pp. 199-223). Mahwah, NJ: Lawrence Erlbaum Associates.
Hiebert, J., Carpenter, T., Fennema, E., Fuson, K.C., Murray, H., Olivier, A., Human, P., and Wearne, D. (1996). Problem solving as a basis for reform in curriculum and instruction: The case of mathematics. Educational Researcher, 25(4), 12-21.
Hiebert, J., Carpenter, T., Fennema, E., Fuson, K.C., Wearne, D., Murray, H., Olivier, A., and Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Holt, J. (1964). How children fail. New York: Dell.
Hufferd-Ackles, K., Fuson, K., and Sherin, M.G. (2004). Describing levels and components of a math-talk community. Journal for Research in Mathematics Education, 35(2), 81-116.
Isaacs, A.C., and Carroll, W.M. (1999). Strategies for basic-facts instruction. Teaching Children Mathematics, 5(9), 508-515.
Kalchman, M., and Case, R. (1999). Diversifying the curriculum in a mathematics classroom streamed for high-ability learners: A necessity unassumed. School Science and Mathematics, 99(6), 320-329.
Kameenui, E.J., and Carnine, D.W. (Eds.). (1998). Effective teaching strategies that accommodate diverse learners. Upper Saddle River, NJ: Prentice-Hall.
Kerkman, D.D., and Siegler, R.S. (1993). Individual differences and adaptive flexibility in lower-income children’s strategy choices. Learning and Individual Differences, 5(2), 113-136.
Kilpatrick, J., Martin, W.G., and Schifter, D. (Eds.). (2003). A research companion to principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
Knapp, M.S. (1995). Teaching for meaning in high-poverty classrooms. New York: Teachers College Press.
Lampert, M. (1986). Knowing, doing, and teaching multiplication. Cognition and Instruction, 3, 305-342.
Lampert, M. (1992). Teaching and learning long division for understanding in school. In G. Leinhardt, R.T. Putnam, and R.A. Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 221-282). Mahwah, NJ: Lawrence Erlbaum Associates.
Lave, J. (1988). Cognition in practice: Mind, mathematics and culture in everyday life. London, England: Cambridge University Press.
LeFevre, J., and Liu, J. (1997). The role of experience in numerical skill: Multiplication performance in adults from Canada and China. Mathematical Cognition, 3(1), 31-62.
LeFevre, J., Kulak, A.G., and Bisantz, J. (1991). Individual differences and developmental change in the associative relations among numbers. Journal of Experimental Child Psychology, 52, 256-274.
Leinhardt, G., Putnam, R.T., and Hattrup, R.A. (Eds.). (1992). The analysis of arithmetic for mathematics teaching. Mahwah, NJ: Lawrence Erlbaum Associates.
Lemaire, P., and Siegler, R.S. (1995). Four aspects of strategic change: Contributions to children’s learning of multiplication. Journal of Experimental Psychology: General, 124(1), 83-97.
Lemaire, P., Barrett, S.E., Fayol, M., and Abdi, H. (1994). Automatic activation of addition and multiplication facts in elementary school children. Journal of Experimental Child Psychology, 57, 224-258.
Lewis, C. (2002). Lesson study: A handbook of teacher-led instructional change. Philadelphia, PA: Research for Better Schools.
Lo Cicero, A., Fuson, K.C., and Allexaht-Snider, M. (1999). Making a difference in Latino children’s math learning: Listening to children, mathematizing their stories, and supporting parents to help children. In L. Ortiz-Franco, N.G. Hernendez, and Y. De La Cruz (Eds.), Changing the faces of mathematics: Perspectives on Latinos (pp. 59-70). Reston, VA: National Council of Teachers of Mathematics.
McClain, K., Cobb, P., and Bowers, J. (1998). A contextual investigation of three-digit addition and subtraction. In L. Morrow (Ed.), Teaching and learning of algorithms in school mathematics (pp. 141-150). Reston, VA: National Council of Teachers of Mathematics.
McKnight, C.C., and Schmidt, W.H. (1998). Facing facts in U.S. science and mathematics education: Where we stand, where we want to go. Journal of Science Education and Technology, 7(1), 57-76.
McKnight, C.C., Crosswhite, F.J., Dossey, J.A., Kifer, E., Swafford, J.O., Travers, K.T., and Cooney, T.J. (1989). The underachieving curriculum: Assessing U.S. school mathematics from an international perspective. Champaign, IL: Stipes.
Miller, K.F., and Paredes, D.R. (1990). Starting to add worse: Effects of learning to multiply on children’s addition. Cognition, 37, 213-242.
Moss, J., and Case, R. (1999). Developing children’s understanding of rational numbers: A new model and experimental curriculum. Journal for Research in Mathematics Education, 30(2), 122-147.
Mulligan, J., and Mitchelmore, M. (1997). Young children’s intuitive models of multiplication and division. Journal for Research in Mathematics Education, 28(3), 309-330.
National Council of Teachers of Mathematics. (1989). Curriculum and evaluation standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: National Council of Teachers of Mathematics.
National Council of Teachers of Mathematics. (2000). Principles and standards for school mathematics. Reston, VA: National Council of Teachers of Mathematics.
National Research Council. (2001). Adding it up: Helping children learn mathematics. Mathematics Learning Study Committee, J. Kilpatrick, J. Swafford, and B. Findell (Eds.). Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
National Research Council. (2002). Helping children learn mathematics. Mathematics Learning Study Committee, J. Kilpatrick, J. Swafford, and B. Findell (Eds.). Center for Education, Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press.
National Research Council. (2004). Learning and instruction: A SERP research agenda. Panel on Learning and Instruction. M.S. Donovan and J.W. Pellegrino (Eds.). Division of Behavioral and Social Sciences and Education. Washington, DC: The National Academies Press.
Nesh, P., and Kilpatrick, J. (Eds.). (1990). Mathematics and cognition: A research synthesis by the International Group for the Psychology of Mathematics Education. Cambridge, MA: Cambridge University Press.
Nesher, P. (1992). Solving multiplication word problems. In G. Leinhardt, R.T. Putnam, and R.A. Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 189-220). Mahwah, NJ: Lawrence Erlbaum Associates.
Peak, L. (1996). Pursuing excellence: A study of the U.S. eighth-grade mathematics and science teaching, learning, curriculum, and achievement in an international context. Washington, DC: National Center for Education Statistics.
Remillard, J.T. (1999). Curriculum materials in mathematics education reform: A framework for examining teachers’ curriculum development. Curriculum Inquiry, 29(3), 315-342.
Remillard, J.T. (2000). Can curriculum materials support teachers’ learning? Elementary School Journal, 100(4), 331-350.
Remillard, J.T., and Geist, P. (2002). Supporting teachers’ professional learning though navigating openings in the curriculum. Journal of Mathematics Teacher Education, 5(1), 7-34.
Resnick, L.B. (1987). Education and learning to think. Committee on Mathematics, Science, and Technology Education, Commission on Behavioral and Social Sciences and Education. Washington, DC: National Academy Press.
Resnick, L.B. (1992). From protoquantities to operators: Building mathematical competence on a foundation of everyday knowledge. In G. Leinhardt, R.T. Putnam, and R.A. Hattrup (Eds.), The analysis of arithmetic for mathematics teaching (pp. 373-429). Mahwah, NJ: Lawrence Erlbaum Associates.
Resnick, L.B., and Omanson, S.F. (1987). Learning to understand arithmetic. In R. Glaser (Ed.), Advances in instructional psychology (vol. 3, pp. 41-95). Mahwah, NJ: Lawrence Erlbaum Associates.
Resnick, L.B., Nesher, P., Leonard, F., Magone, M., Omanson, S., and Peled, I. (1989). Conceptual bases of arithmetic errors: The case of decimal fractions. Journal for Research in Mathematics Education, 20(1), 8-27.
Ron, P. (1998). My family taught me this way. In L.J. Morrow and M.J. Kenney (Eds.), The teaching and learning of algorithms in school mathematics (pp. 115-119). Reston, VA: National Council of Teachers of Mathematics.
Saxe, G.B. (1982). Culture and the development of numerical cognition: Studies among the Oksapmin of Papua New Guinea. In C.J. Brainerd (Ed.), Progress in cognitive development research: Children’s logical and mathematical cognition (vol. 1, pp. 157- 176). New York: Springer-Verlag.
Schmidt, W., McKnight, C.C., and Raizen, S.A. (1997). A splintered vision: An investigation of U.S. science and mathematics education. Dordrecht, The Netherlands: Kluwer.
Schwartz, D.L., and Moore, J.L. (1998). The role of mathematics in explaining the material world: Mental models for proportional reasoning. Cognitive Science, 22, 471-516.
Secada, W.G. (1992). Race, ethnicity, social class, language, and achievement in mathematics. In D. Grouws (Ed.), Handbook of research on mathematics teaching and learning (pp. 623-660). New York: Macmillan.
Sherin, M.G. (2000a). Facilitating meaningful discussions about mathematics. Mathematics Teaching in the Middle School, 6(2), 186-190.
Sherin, M.G. (2000b). Taking a fresh look at teaching through video clubs. Educational Leadership, 57(8), 36-38.
Sherin, M.G. (2001). Developing a professional vision of classroom events. In T. Wood, B.S. Nelson, and J. Warfield (Eds.), Beyond classical pedagogy: Teaching elementary school mathematics (pp. 75-93). Mahwah, NJ: Lawrence Erlbaum Associates.
Sherin, M.G. (2002). A balancing act: Developing a discourse community in a mathematics classroom. Journal of Mathematics Teacher Education, 5, 205-233.
Shuell, T.J. (2001). Teaching and learning in a classroom context. In N.J. Smelser and P.B. Baltes (Eds.), International encyclopedia of the social and behavioral sciences (pp. 15468-15472). Amsterdam: Elsevier.
Siegler, R.S. (1988). Individual differences in strategy choices: Good students, not-so-good students, and perfectionists. Child Development, 59(4), 833-851.
Siegler, R.S. (2003). Implications of cognitive science research for mathematics education. In J. Kilpatrick, W.G. Martin, and D.E. Schifter (Eds.), A research companion to principles and standards for school mathematics (pp. 1289-1303). Reston, VA: National Council of Teachers of Mathematics.
Simon, M.A. (1995). Reconstructing mathematics pedagogy from a constructivist perspective. Journal for Research in Mathematics Education, 26, 114-145.
Starkey, P., Spelke, E.S., and Gelman, R. (1990). Numerical abstraction by human infants. Cognition, 36, 97-127.
Steffe, L.P. (1994). Children’s multiplying schemes. In G. Harel and J. Confrey (Eds.), The development of multiplicative reasoning in the learning of mathematics (pp. 3-39). New York: State University of New York Press.
Steffe, L.P., Cobb, P., and Von Glasersfeld, E. (1988). Construction of arithmetical meanings and strategies. New York: Springer-Verlag.
Sternberg, R.J. (1999). The theory of successful intelligence. Review of General Psychology, 3(4), 292-316.
Stigler, J.W., and Hiebert, J. (1999). Teaching gap. New York: Free Press.
Stigler, J.W., Fuson, K.C., Ham, M., and Kim, M.S. (1986). An analysis of addition and subtraction word problems in American and Soviet elementary mathematics textbooks. Cognition and Instruction, 3(3), 153-171.
Stipek, D., Salmon, J.M., Givvin, K.B., Kazemi, E., Saxe, G., and MacGyvers, V.L. (1998). The value (and convergence) of practices suggested by motivation research and promoted by mathematics education reformers. Journal for Research in Mathematics Education, 29, 465-488.
Thornton, C.A. (1978). Emphasizing thinking in basic fact instruction. Journal for Research in Mathematics Education, 9, 214-227.
Thornton, C.A., Jones, G.A., and Toohey, M.A. (1983). A multisensory approach to thinking strategies for remedial instruction in basic addition facts. Journal for Research in Mathematics Education, 14(3), 198-203.
Tobias, S. (1978). Overcoming math anxiety. New York: W.W. Norton.
Van de Walle, J.A. (1998). Elementary and middle school mathematics: Teaching developmentally, third edition. New York: Longman.
Van de Walle, J.A. (2000). Elementary school mathematics: Teaching developmentally, fourth edition. New York: Longman.
Wynn, K. (1996). Infants’ individuation and enumeration of actions. Psychological Science, 7, 164-169.
Zucker, A.A. (1995). Emphasizing conceptual understanding and breadth of study in mathematics instruction. In M.S. Knapp (Ed.), Teaching for meaning in high-poverty classrooms. New York: Teachers College Press.
SUGGESTED READING LIST FOR TEACHERS
Carpenter, T.P. Fennema, E., Franke, M.L., Empson, S.B., and Levi, L.W. (1999). Children’s mathematics: Cognitively guided instruction. Portsmouth, NH: Heinemann.
Fuson, K.C. (1988). Subtracting by counting up with finger patterns. (Invited paper for the Research into Practice Series.) Arithmetic Teacher, 35(5), 29-31.
Hiebert, J., Carpenter, T., Fennema, E., Fuson, K.C., Wearne, D., Murray, H., Olivier, A., and Human, P. (1997). Making sense: Teaching and learning mathematics with understanding. Portsmouth, NH: Heinemann.
Jensen, R.J. (Ed.). (1993). Research ideas for the classroom: Early childhood mathematics. New York: Macmillan.
Knapp, M.S. (1995). Teaching for meaning in high-poverty classrooms. New York: Teachers College Press.
Leinhardt, G., Putnam, R.T., and Hattrup, R.A. (Eds.). (1992). The analysis of arithmetic for mathematics teaching. Mahwah, NJ: Lawrence Erlbaum Associates.
Lo Cicero, A., De La Cruz, Y., and Fuson, K.C. (1999). Teaching and learning creatively with the Children’s Math Worlds Curriculum: Using children’s narratives and explanations to co-create understandings. Teaching Children Mathematics, 5(9), 544-547.
Owens, D.T. (Ed.). (1993). Research ideas for the classroom: Middle grades mathematics. New York: Macmillan.
Schifter, D. (Ed.). (1996). What’s happening in math class? Envisioning new practices through teacher narratives. New York: Teachers College Press.
Wagner, S. (Ed.). (1993). Research ideas for the classroom: High school mathematics. New York: Macmillan.