8
Teaching and Learning Functions
Mindy Kalchman and Kenneth R. Koedinger
This chapter focuses on teaching and learning mathematical functions.1 Functions are all around us, though students do not always realize this. For example, a functional relationship between quantities is at play when we are paying for gasoline by the gallon or fruit by the pound. We need functions for financial plans so we can calculate such things as accrued income and interest. Functions are important as well to interpretations of local and world demographics and population growth, which are critical for economic planning and development. Functions are even found in such familiar settings as baseball statistics and metric conversions.
Algebraic tools allow us to express these functional relationships very efficiently; find the value of one thing (such as the gas price) when we know the value of the other (the number of gallons); and display a relationship visually in a way that allows us to quickly grasp the direction, magnitude, and rate of change in one variable over a range of values of the other. For simple problems such as determining gas prices, students’ existing knowledge of multiplication will usually allow them to calculate the cost for a specific amount of gas once they know the price per gallon (say, $2) with no problem. Students know that 2 gallons cost $4, 3 gallons cost $6, 4 gallons cost $8, and so on. While we can list each set of values, it is very efficient to say that for all values in gallons (which we call x by convention), the total cost (which we call y by convention), is equal to 2x. Writing y = 2x is a simple way of saying a great deal.
As functional relationships become more complex, as in the growth of a population or the accumulation of interest over time, solutions are not so easily calculated because the base changes each period. In these situations,
algebraic tools allow highly complex problems to be solved and displayed in a way that provides a powerful image of change over time.
Many students would be more than a little surprised at this description. Few students view algebra as a powerful toolkit that allows them to solve complex problems much more easily. Rather, they regard the algebra itself as the problem, and the toolkit as hopelessly complex. This result is not surprising given that algebra is often taught in ways that violate all three principles of learning set forth in How People Learn and highlighted in this volume.
The first principle suggests the importance of building new knowledge on the foundation of students’ existing knowledge and understanding. Because students have many encounters with functional relationships in their everyday lives, they bring a great deal of relevant knowledge to the classroom. That knowledge can help students reason carefully through algebra problems. Box 8-1 suggests that a problem described in its everyday manifestation can be solved by many more students than the same problem presented only as a mathematical equation. Yet if the existing mathematics understandings students bring to the classroom are not linked to formal algebra learning, they will not be available to support new learning.
The second principle of How People Learn argues that students need a strong conceptual understanding of function as well as procedural fluency. The new and very central concept introduced with functions is that of a dependent relationship: the value of one thing depends on, is determined by, or is a function of another. The kinds of problems we are dealing with no longer are focused on determining a specific value (the cost of 5 gallons of gas). They are now focused on the rule or expression that tells us how one thing (cost) is related to another (amount of gas). A “function” is formally defined in mathematics as “a set of ordered pairs of numbers (x, y) such that to each value of the first variable (x) there corresponds a unique value of the second variable (y).”2 Such a definition, while true, does not signal to students that they are beginning to learn about a new class of problems in which the value of one thing is determined by the value of another, and the rule that tells them how they are related.
Within mathematics education, function has come to have a broader interpretation that refers not only to the formal definition, but also to the multiple ways in which functions can be written and described.3 Common ways of describing functions include tables, graphs, algebraic symbols, words, and problem situations. Each of these representations describes how the value of one variable is determined by the value of another. For instance, in a verbal problem situation such as “you get two dollars for every kilometer you walk in a walkathon,” the dollars earned depend on, are determined by, or are a function of the distance walked. Conceptually, students need to understand that these are different ways of describing the same relationship.
Good instruction is not just about developing students’ facility with performing various procedures, such as finding the value of y given x or creating a graph given an equation. Instruction should also help students develop a conceptual understanding of function, the ability to represent a function in a variety of ways, and fluency in moving among multiple representations of functions. The slope of the line as represented in an equation, for example, should have a “meaning” in the verbal description of the relationship between two variables, as well as a visual representation on a graph.
The third principle of How People Learn suggests the importance of students’ engaging in metacognitive processes, monitoring their understanding as they go. Because mathematical relationships are generalized in algebra, students must operate at a higher level of abstraction than is typical of the mathematics they have generally encountered previously. At all levels of mathematics, students need to be engaged in monitoring their problem solving and reflecting on their solutions and strategies. But the metacognitive engagement is particularly important as mathematics becomes more abstract, because students will have few clues even when a solution has gone terribly awry if they are not actively engaged in sense making.
When students’ conceptual understanding and metacognitive monitoring are weak, their efforts to solve even fairly simple algebra problems can, and often do, fail. Consider the problem in Figure 8-1a. How might students approach and respond to this problem? What graph-reading and table-building skills are required? Are such skills sufficient for a correct solution? If students lack a conceptual understanding of linear function, what errors might they make? Figure 8-1b shows an example student solution.
What skills does this student exhibit? What does this student understand and not understand about functions? This student has shown that he knows how to construct a table of values and knows how to record in that table coordinate points he has determined to be on the graph. He also clearly recalls that an algorithm for finding the slope of the function is dividing the change in y(Δy) by the change in x(Δx). There are, however, significant problems with this solution that reveal this student’s weak conceptual understanding of functions.
Problem: Make a table of values that would produce the function seen on page 356.
First, and most superficially, the student (likely carelessly) mislabeled the coordinate for the y-intercept (0, 3) rather than (0, –3). This led him to make an error in calculating Δy by subtracting 0 from 3 rather than from –3. In so doing, he arrived at a value for the slope of the function that was negative—an impossible solution given that the graph is of an increasing linear function. This slip, by itself, is of less concern than the fact that the
|
BOX 8-1 Which of these problems is most difficult for a beginning algebra student? Story Problem When Ted got home from his waiter job, he multiplied his hourly wage by the 6 hours he worked that day. Then he added the $66 he made in tips and found he had earned $81.90. How much does Ted make per hour? Word Problem Starting with some number, if I multiply it by 6 and then add 66, I get 81.9. What number did I start with? Equation Solve for x: x * 6 + 66 = 81.90 Most teachers and researchers predict that students will have more difficulty correctly solving the story or word problem than the equation.4 They might explain this expectation by saying that a student needs to read the verbal problems (story and word) and then translate them into the equation. In fact, research investigating urban high school students’ performance on such problems found that on average, they scored 66 percent on the story problem, 62 percent on the word problem, and only 43 percent on the equation.5 In other words, students were more likely to solve the verbal problems correctly than the equation. Investigating students’ written work helps explain why. Students often solved the verbal problems without using the equation. For instance, some students used a generate-and-test strategy: They estimated a value for the hourly rate (e.g., $4/hour), computed the corresponding pay (e.g., $90), compared it against the given value ($81.90), |
|
and repeated as needed. Other students used a more efficient unwind or working backwards strategy. They started with the final value of 81.9 and subtracted 66 to undo the last step of adding 66. Then they took the resulting 15.9 and divided by 6 to undo the first step of multiplying by 6. These strategies made the verbal problems easier than expected. But why were the equations difficult for students? Although experts in algebra may believe no reading is involved in equation solving, students do in fact need to learn how to read equations. The majority of student errors on equations can be attributed to difficulties in correctly comprehending the meaning of the equation.6 In the above equation, for example, many students added 6 and 66, but no student did so on the verbal problems. Besides providing some insight into how students think about algebraic problem solving, these studies illustrate how experts in an area such as algebra may have an “expert blind spot” for learning challenges beginners may experience. An expert blind spot occurs when someone skilled in an area overestimates the ease of learning its formalisms or jargon and underestimates learners’ informal understanding of its key ideas. As a result, too little attention is paid to linking formal mathematical understanding to informal reasoning. Looking closely at students’ work, the strategies they employ, and the errors they make, and even comparing their performance on similar kinds of problems, are some of the ways we can get past such blind spots and our natural tendency to think students think as we do. Such studies of student thinking contributed to the creation of a technology-enhanced algebra course, originally Pump Algebra Tutor and now Cognitive Tutor Algebra.7 That course includes an intelligent tutor that provides students with individualized assistance as they use multiple representations (words, tables, graphs, and equations) to analyze real-world problem situations. Numerous classroom studies have shown that this course significantly improves student achievement relative to alternative algebra courses (see www.carnegielearning.com/research). The course, which was based on basic research on learning science, is now in use in over 1,500 schools. |
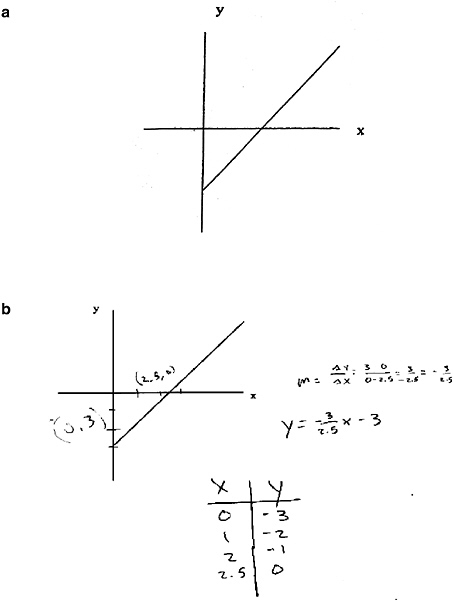
FIGURE 8-1
student did not recognize the inconsistency between the positive slope of the line and the negative slope in the equation. Even good mathematicians could make such a mistake, but they would likely monitor their work as they went along or reflect on the plausibility of the answer and detect the inconsistency. This student could have caught and corrected his error had he
acquired both fluency in interpreting the slope of a function from its equation (i.e., to see that it represents a decreasing function) and a reflective strategy for comparing features of different representations.
A second, more fundamental error in the student’s solution was that the table of values does not represent a linear function. That is, there is not a constant change in y for every unit change in x. The first three coordinates in the student’s table were linear, but he then recorded (2.5, 0) as the fourth coordinate pair rather than (3, 0), which would have made the function linear. He appears to have estimated and recorded coordinate points by visually reading them off the graph without regard for whether the final table embodied linearity. Furthermore, the student did not realize that the equation he produced, ![]() , translates not only into a decreasing line, but also into a table of numbers that decreases by
, translates not only into a decreasing line, but also into a table of numbers that decreases by ![]() for every positive unit change in x.
for every positive unit change in x.
At a surface level, this student’s solution reflects some weaknesses in procedural knowledge, namely, getting the sign wrong on the y-intercept and imprecisely reading x-y coordinates off the graph. More important, however, these surface errors reflect a deeper weakness in the student’s conceptual understanding of function. The student either did not have or did not apply knowledge for interpreting key features (e.g., increasing or decreasing) of different function representations (e.g., graph, equation, table) and for using strategies for checking the consistency of these interpretations (e.g., all should be increasing). In general, the student’s work on this problem reflects an incomplete conceptual framework for linear functions, one that does not provide a solid foundation for fluid and flexible movement among a function’s representations.
This student’s work is representative of the difficulties many secondary-level students have with such a problem after completing a traditional textbook unit on functions. In a study of learning and teaching functions, about 25 percent of students taking ninth- and eleventh-grade advanced mathematics courses made errors of this type—that is, providing a table of values that does not reflect a constant slope—following instruction on functions.8 This performance contrasts with that of ninth- and eleventh-grade mathematics students who solved this same problem after receiving instruction based on the curriculum described in this chapter. This group of students had an 88 percent success rate on the problem. Because these students had developed a deeper understanding of the concept of function, they knew that the y-values in a table must change by the same amount for every unit change in x for the function to be linear. The example in Figure 8-1c shows such thinking.
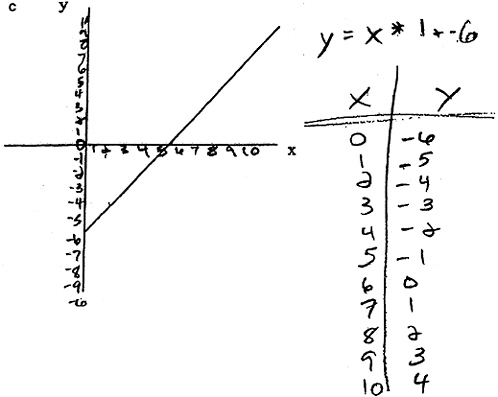
FIGURE 8-1
Problem: Make a table of values that would produce the function seen above.
This student identified a possible y-intercept based on a reasonable scale for the y-axis. She then labeled the x- and y-axes, from which she determined coordinate pairs from the graph and recorded them in a table of values. She determined and recorded values that show a constant increase in y for every positive unit change in x. She also derived an equation for the function that not only corresponds to both the graph and the table, but also represents a linear relationship between x and y.
How might one teach to achieve this kind of understanding? The goal of this chapter is to illustrate approaches to teaching functions that foster deep understanding and mathematical fluency. We emphasize the importance of designing thoughtful instructional approaches and curricula
that reflect the principles of How People Learn (as outlined in Chapter 1), as well as recent research on what it means to learn and understand functions in particular. We first describe our approach to addressing each of the three principles. We then provide three sample lessons that emphasize those principles in sequence. We hope that these examples provide interesting activi ties to try with students. More important, these activities incorporate important discoveries about student learning that teachers can use to design other instructional activities to achieve the same goals.
ADDRESSING THE THREE PRINCIPLES
Principle #1: Building on Prior Knowledge
Principle 1 emphasizes the importance of students and teachers continually making links between students’ experiences outside the mathematics classroom and their school learning experiences. The understandings students bring to the classroom can be viewed in two ways: as their everyday, informal, experiential, out-of-school knowledge, and as their school-based or “instructional” knowledge. In the instructional approach illustrated here, students are introduced to function and its multiple representations by having their prior experiences and knowledge engaged in the context of a walkathon. This particular context was chosen because (1) students are familiar with money and distance as variable quantities, (2) they understand the contingency relationship between the variables, and (3) they are interested in and motivated by the rate at which money is earned.
The use of a powerful instructional context, which we call a “bridging context,” is crucial here. We use this term because the context serves to bridge students’ numeric (equations) and spatial (graphic) understandings and to link their everyday experiences to lessons in the mathematics classroom. Following is an example of a classroom interaction that occurred during students’ first lesson on functions, showing how use of the walkathon context as an introduction to functions in multiple forms—real-world situation (walkathon), table, graph, verbal (“$1.00 for each kilometer”), situation-specific symbols ($ = 1 * km), and generic symbolic (y = x * 1)—accomplishes these bridging goals. Figures 8-2a through 8-2c show changes in the whiteboard as the lesson proceeded.
|
Teacher |
What we’re looking at is, we’re looking at what we do to numbers, to one set of numbers, to get other numbers…. So how many of you have done something like a walkathon? A readathon? A swimathon? A bikeathon? |
|
|
[Students raise their hands or nod.] So most of you… So I would say “Hi Tom [talking to a student in class], I’m going to raise money for such and such a charity and I’m going to walk ten kilometers.” |
|
Tom |
OK. |
|
Teacher |
Say you’re gonna sponsor me one dollar for every kilometer that I walk. So that’s sort of the first way that we can think about a function. It’s a rule. One dollar for every kilometer walked. So you have one dollar for each kilometer [writing “$1.00 for each kilometer” on the board while saying it]. So then what I do is I need to calculate how much money I’m gonna earn. And I have to start somewhere. So at zero kilometers how much money do I have Tom? How much are you gonna pay me if I collapse at the starting line? [Fills in the number 0 in the left-hand column of a table labeled “km”; the right-hand column is labeled “$”.] |
|
Tom |
None. |
|
Teacher |
So Tom, I managed to walk one kilometer [putting a “1” in the “km” column of the table of values below the “0”]…. |
|
Tom |
One dollar. |
|
Teacher |
One dollar [moving to the graph]. So I’m going to go over one kilometer and up one dollar [see Figure 8-2a]. |
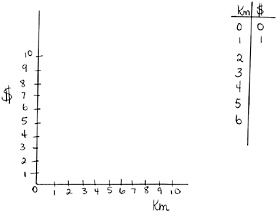
FIGURE 8-2a Graphing a point from the table: “Over by one kilometer and up by one dollar.” The teacher uses everyday English (“up by”) and maintains connection with the situation by incorporating the units “kilometer” and “dollar.”
FIGURE 8-2b The teacher and students construct the table and graph point by point, and a line is then drawn.
|
|
[Students continue to provide the dollar amounts for each of the successive kilometer values. Simple as it is, students are encouraged to describe the computation—”I multiply two kilometers by one to get two dollars.” The teacher fills in the table and graphs each coordinate pair. [The board is now as shown in Figure 8-2b.] |
|
Teacher |
Now, what I want you to try and do, first I want you to look at this [pointing to the table that goes from x = 0 to x = 10 for y = x] and tell me what’s happening here. |
|
Melissa |
You, like, earn one dollar every time you go up. Like it gets bigger by one every time. |
|
Teacher |
So every time you walk one kilometer you get one more dollar, right? [Makes “> 1” marks between successive “$” values in the table—see Figure 8-2c.] And if you look on the graph, every time I walk one kilometer I get one more dollar. [Makes “step” marks on the graph.] So now I want to come up with an equation, I want to come up with some way of using this symbol [pointing to the “km” header in the left-hand column of the table] and this symbol [pointing to the “$” header in the right-hand column of the table] to say the same thing, that for every kilometer I walk, let’s put it this way, the money I earn is gonna be equal to one times the number of kilometers I walk. Someone want to try that? |
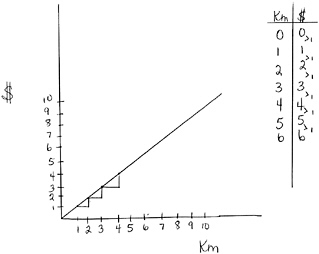
FIGURE 8-2c The teacher highlights the “up by” amount in the table (“>1” marks), graph (over and up “step” marks), and symbolic equation (pointing at “*1”).
|
Alana |
Um, kilometers times one equals money. [The teacher writes “km x 1 = $” and “y = x * 1”; see Figure 8-2c.] |
|
Teacher |
So this equation, this table, and this graph are all the same function. They all mean the same thing. They all mean that you’re multiplying each of these numbers (pointing to the values along the x-axis of the graph) by one to get new numbers. |
Another way of building on students’ prior knowledge is to engage everyday experiential knowledge. Students frequently know things through experience that they have not been taught explicitly. They can often solve problems in ways we do not teach them or expect if, and this is an important qualification, the problems are described using words, drawings, or notations they understand. For example, the topic of slope is typically reserved for ninth-grade mathematics, and is a part of students’ introduction to relations and functions in general and to linear functions in particular. It is generally defined as the ratio of vertical distance to horizontal distance, or “rise to run.” The rise is the change in the vertical distance, and the run is the change in the horizontal distance so that ![]() . Once the equation for a straight line,
. Once the equation for a straight line, ![]() , has been introduced, m is defined as the slope of that line and is calculated using the formula
, has been introduced, m is defined as the slope of that line and is calculated using the formula ![]() .
.
For students to understand slope in these definitional and symbolic ways, they must already have in place a great deal of formal knowledge, including
the meaning of ratio, coordinate graphing, variables, and subscripts, and such skills as solving equations in two variables and combining arithmetic operations. Knowing algorithms for finding the slope of a function, however, does not ensure that the general meaning of slope will be understood. As illustrated in Figure 8-1a, a student can know the algorithm for finding the slope, but not understand that the slope of a line characterizes its relative steepness on a graph and tells something about the rate of change in covarying, dependent quantities.
We have found that younger students have intuitive and experiential understandings of slope that can be used to underpin the formal learning that involves conventional notations, algorithms, and definitions. To illustrate, we gave a class of fifth and sixth graders the following situation:
Jane is in a walkathon. A rule or “function” tells us how much Jane will earn depending on how many kilometers she walks. We don’t know what the function is. It is a mystery. We do know that if Jane walks 1 kilometer she will earn 4 dollars and if she walks 3 kilometers she will earn 8 dollars.
Students were asked to figure out the slope of the function that tells how much Jane will earn. Half of the students were provided with the formal rise-over-run ratio definition of slope; the other half were given a definition of slope that reflected more familiar, student language, being told that the slope of a function is the amount by which the answer goes up for every change of one in the start value.
We found that many of these younger students were able to describe informally the slope of the function given in the story problem by figuring out how much Jane’s earnings go up by for every kilometer she walks. They noticed that when Jane walks three kilometers instead of one, she earns four more dollars; thus she earns two more dollars for every extra kilometer she walks. In this way, these prealgebra students identified the slope of the mystery function as 2 without receiving instruction on formal definitions or procedures. In contrast, students who were given the textbook definition of slope were not able to determine the slope in this example.
Our point is not that all problems should be phrased in “student language.” It is important for students to learn formal mathematics terminology and abstract algebraic symbolism. Our point, instead, is that using student language is one way of first assessing what knowledge students are bringing to a particular topic at hand, and then linking to and building on what they already know to guide them toward a deeper understanding of formal mathematical terms, algorithms, and symbols.
In sum, students’ prior knowledge acts as a building block for the development of more sophisticated ways of thinking mathematically. In some cases, we may underestimate the knowledge and skills students bring to the learning of functions. Topics and activities we presume to be challenging
and difficult for students may in fact have intuitive or experiential underpinnings, and it is important to discover these and use them for formalizing students’ thinking.
Principle #2: Building Conceptual Understanding, Procedural Fluency, and Connected Knowledge
The focus of Principle 2 is on simultaneously developing conceptual understanding and procedural fluency, and helping students connect and organize knowledge in its various forms. Students can develop surface facility with the notations, words, and methods of a domain of study (e.g., functions) without having a foundation of understanding. For students to understand such mathematical formalisms, we must help them connect these formalisms with other forms of knowledge, including everyday experience, concrete examples, and visual representations. Such connections form a conceptual framework that holds mathematical knowledge together and facilitates its retrieval and application.
As described previously, we want students to understand the core concept of a fuctional relationship: that the value of one variable is dependent on the value of another. And we want them to understand that the relationship between two variables can be expressed in a variety of ways—in words, equations, graphs, tables—all of which have the same meaning or use the same “rule” for the relationship. Ultimately, we want students’ conceptual understanding to be sufficiently secure, and their facility with representing functions in a variety of ways and solving for unknown variables sufficiently fluid, that they can tackle sophisticated problems with confidence. To this end, we need an instructional plan that deliberately builds and secures that knowledge. Good teaching requires not only a solid understanding of the content domain, but also specific knowledge of student development of these conceptual understandings and procedural competencies. The developmental model of function learning that provides the foundation for our instructional approach encompasses four levels—0 to 3—as summarized in Table 8-1. Each level describes what students can typically do at a given developmental stage. The instructional program is then designed to build those competences.
Level 0
Level 0 characterizes the kinds of numeric/symbolic and spatial understandings students typically bring to learning functions. Initially, the numeric and spatial understandings are separate. The initial numeric understanding is one whereby students can iteratively compute within a single string of whole numbers. That is, given a string of positive, whole numbers such as 0,
TABLE 8-1 A Developmental Model for Learning Functions
|
Level |
General Description |
Example Tasks and Understandings |
|
0 |
Students have separate numeric and spatial understandings. • Initial numeric understanding: students iteratively compute (e.g., “add 4”) within a string of positive whole numbers. • Initial spatial understanding: students represent the relative sizes of quantities as bars on a graph and perceive patterns of qualitative changes in amount by a left-to-right visual scan of the graph, but cannot quantify those changes. |
Extend the pattern 3, 7, 11, 15, ___, ____, ____. Notice in a bar graph of yearly population figures that each bar is taller than the previous bar. |
|
1 |
Spatial and numeric understandings are elaborated and integrated, forming a central conceptual structure. • Elaboration of numeric understanding: —Iteratively apply a single operation to, rather than within, a string of numbers to generate a second string of numbers. —Construct an algebraic expression for this repeated operation. • Elaboration of spatial understanding: —Use continuous quantities along the horizontal axis. —Perceive emergent properties, such as linear or increasing, in the shape of the line drawn between points. • Integration of elaborated understandings: |
Multiply each number in the sequence 0, 1, 2, … by 2 to get a set of pairs: 0-0, 1-2, 2-4,…. Generalize the pattern and express it as y = 2x. Notice that a graph of daily plant growth must leave spaces for unmeasured Saturday and Sunday values. For every 1 km, a constant “up by” $2 in both the y-column of a table and the y-axis in a graph generates a linear pattern (spatial) with a slope of 2 (numeric). y = 2x can be read |
|
Level |
General Description |
Example Tasks and Understandings |
|
|
—See the relationship between the differences in the y-column in a table and the size of the step from one point to the next in the associated graph. • Interpret algebraic representations both numerically and spatially. |
from, or produced in, both a table and a graph. |
|
2 |
• Elaborate initial integrated numeric and spatial understandings to create more sophisticated variations. • Integrate understanding of y = x and y = x + b to form a mental structure for linear functions. • Integrate rational numbers and negative integers. • Form mental structures for other families of functions, such as y = xn + b. |
Look at the function below. Could it represent y = x – 10? Why or why not? 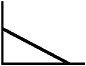 If you think it could not, sketch what you think it looks like. |
|
3 |
• Integrate variant (e.g., linear and nonlinear) structures developed at level 2 to create higher-order structures for understanding more-complex functions, such as polynomials and exponential and reciprocal functions. • Elaborate understanding of graphs and negative integers to differentiate the four quadrants of the Cartesian plane. • Understand the relationship of these quadrants to each other. |
At what points would the function y = 10x – x2 cross the x axis? Please show all of your work. |
2, 4, 6, 8, …, students are able to see the pattern of adding 2 to each successive number. The initial spatial understanding is one whereby students can represent the relative sizes of quantities as bars on a graph. Students can easily see differences in the sizes of bars (how tall they are) and can use this spatial information to draw inferences about associated quantities. Students can read bar graphs that, for instance, show daily measurements of the growth of a plant in the classroom. They can see that each bar is taller than the previous one, that the plant is taller on Friday than on Thursday, but cannot easily quantify those changes.
Level 1
At level 1, students begin to elaborate and integrate their initial numeric and spatial understandings of functions. They elaborate their numeric understanding in two steps. First, whereas students at level 0 can extend a single sequence of numbers such as 0, 2, 4, 6, …, at level 1 they can operate on one sequence of numbers to produce a second sequence. For example, students can multiply each number in the sequence 0, 1, 2, 3, … by 2 and form the resulting pairs of values: 0-0, 1-2, 2-4, 3-6, …. Students learn to record these pairs of values in a table and to construct an algebraic equation for this repeated operation by generalizing the pattern into an equation such as y = 2x.
Students’ spatial understanding is also improving. They come to understand that maintaining equal distances between values on the x-axis is critical to having a meaningful graph of a function. They also progress from understanding graphs with verbal or categorical values along the x-axis, such as cities (with their populations on the y-axis), to understanding graphs with quantitative values along the x-axis, such as time quantified as days (with the height of a plant on each successive day on the y-axis). The example of graphing plant growth is an interesting one because it is an activity at the cusp of this transition. Students initially view values on the x-axis as categorical, not sequenced (so that Thursday, Friday, Monday is okay). Later they come to view these values as quantitative, in a sequence with a fixed distance between the values (such that Thursday, Friday, Monday is not okay because Saturday and Sunday must be accounted for).
Without being able to view the x-axis as quantitative, students cannot see graphs as representing the relationship between two changing quantities. Drawing a line to join the points provides a visual representation of the relationship between the quantities. The line offers a way of packaging key properties of the function or pattern of change that can be perceived quickly and easily. For example, students can see how much earnings change per kilometer by looking at the steepness of the line.
As their initial numeric and spatial understandings are elaborated, students at level 1 also begin to connect, or integrate, these understandings. They make connections between tables and graphs of x-y pairs, using one representation to generate inferences that can be checked by the other. The overall pattern of a function can be understood both in the size of the increments in the y-column of the table and in the steepness of the line moving from one point to another in the graph. The constant “up-by” 1 seen, for example, in Figure 8-2c in the right-hand column of a table is the same as the constant “up-by” 1 in a line of a graph (see the same figure). As these views become integrated, students develop a deeper and more flexible understanding of functions, in this case, a linear pattern with a rise of 1. With this new integrated mental structure for functions, students can support numeric and spatial understandings of algebraic representations such as y = 1x.
Grasping why and how the line on a graph maps onto the relationship described in a word problem or an equation is a core conceptual understanding. If students’ understanding is only procedural, they will not be well prepared for the next level (see Box 8-2). To ensure that students master the concepts at this level, complex content is avoided. Students are not required to operate with negative or rational numbers or carry out more than one operation in a single function (such as multiplying x by any value and adding or subtracting a constant, as in the general y = mx + b form). Such limiting of these complicating factors is intended to minimize loads on processing and working memory, thus enabling students to focus on the essence of the integration of numeric and spatial understandings of function. Students learn more complex content during levels 2 and 3.
Level 2
As students progress to level 2, they begin to elaborate their initial integrated numeric and spatial understandings. In doing so, they begin to combine operations and develop fluency with functions in the form y = mx + b, where m and b can be positive or negative rational numbers. They also work with y = xn + b, where n is a positive whole number, and b is any positive or negative rational number. For a full elaboration to occur, it is necessary for students to understand integers and rational numbers and have facility in computing with both of these number systems. Finally, students differentiate families of functions to see differences in the shapes and characteristics of linear, quadratic, and cubic functions.
Level 3
At level 3, students learn how linear and nonlinear terms can be related and understand the properties and behaviors of the resulting entities by analyzing these relations. To achieve this understanding, students must have well-constructed and differentiated models of different sorts of functions, such as quadratics in the form y = ax2 + bx + c or y = a(x – p)2 + q; polynomials; and reciprocal, exponential, and growth functions. They must also have the necessary facility with computational, algebraic, and graphing operations to interrelate the numeric/symbolic and spatial representations of these complex functions. Furthermore, students must elaborate their understanding of graphs so they differentiate the four quadrants of the Cartesian plane, understand the relationship of these quadrants to each other, and relate these quadrants to negative numbers.
Recall Figure 8-1a and the difficulties the student had in producing a table of values for an increasing linear function with a negative y-intercept. This student did not recognize, or at least did not acknowledge, why it is impossible for the given function to have a negative slope and to have a table of values without a constant rate of change. These are the sorts of problems that occur when students experience instruction that fails to promote the development of a sound conceptual framework for functions. Now consider the solution to the problem in Box 8-3, in which a student introduces a table (without prompting) to help solve a problem about interpreting a graph in terms of an equation.
This student exhibited an integrated concept of function. He generated a response that showed consistency between the spatial (graph) and numeric (table and equation) representations of the function. He explained why the function has a slope of –2 as per its numeric (tabular) and spatial (graphic) representations and correctly symbolized that rationale in the equation.
Such integration can be supported in the classroom. For example, throughout the walkathon classroom exchange reported earlier, the teacher is moving fluidly and rapidly between numeric and spatial representations of a function (the table and equation and the graph, respectively). Such movement helps students simultaneously build understandings of each of these representations in isolation, and of the integrated nature of the representations in particular and the concept in general. This integration helps students begin to understand and organize their knowledge in ways that facilitate the retrieval and application of relevant mathematical concepts and procedures.
If students’ numeric and spatial understandings are not integrated, they may not notice when a conclusion drawn from one understanding is inconsistent with a conclusion drawn from another. The inconsistencies found in the student’s work in Figure 8-1a illustrate such a lack of reflective recognition.
|
BOX 8-2 What students glean from instruction is often very different from what we as teachers intend. This observation is nicely illustrated by the research of Schoenfeld and colleagues.9 They detail the surprising misunderstandings of a 16-year old advanced algebra student who is grappling with conceptual questions about equations and graphs of linear functions. Most standard algebra instruction is intended to guide students toward developing what Schoenfeld and colleagues10 call the “2-slot schema” for understanding and graphing an equation for a line. This schema says that knowing the slope of a line and its y-intercept enables one to obtain a complete description of the line, both graphically and algebraically. Call the line L; let its slope be m and its y-intercept b. Algebraically, the line L has equation y = mx + b if and only if the line has slope m and y-intercept b. Graphically, the line L passes through the point (0, b) and rises m units vertically for each unit it traverses horizontally. The student in Schoenfeld’s study, called IN, was relatively sophisticated in understanding aspects of the above schema. However, IN’s knowledge was not fully integrated, and she exhibited a surprising misunderstanding. She initially believed that three quantities must be known to graph an equation of a line: (1) slope, (2) y-intercept, and (3) x-intercept. After having solved the equation 2 = 4x + 1 to get x = 1/4, she was asked to the graph the function 4x + 1 on the right side of this equation. She responded as follows: “the slope, which is 4, … the y-intercept, which is 1, … and … the x-intercept, which is 1/4, so we’ve found everything.” Note that IN said that to find “everything,” she needed the slope, y-intercept, and x-intercept. In other words, she appeared to have a 3-slot schema for understanding and graphing a linear equation instead of the 2-slot schema described above. Clearly this student had received extensive instruction in linear functions. For instance, in an earlier exchange, when asked for an equation of |
Principle #3: Building Resourceful, Self-Regulating Problem Solvers
As discussed above, teaching aimed at developing robust and fluent mathematical knowledge of functions should build on students’ existing real-world and school knowledge (Principle 1) and should integrate procedural
|
a straight line, she immediately said, “y = mx + b.” However, IN lacked a well-integrated understanding of the relationships between the features of the equation and graphical forms of a line. Schoenfeld and colleagues11 explain: When a person knowledgeable about the domain determines that the slope of a particular line is some value (say, 1…) and that its intercept is some other value (say, 3), then the job is done. The equation of the line must be y = (1)x + 3. IN had no such procedure. Although she believed that the slope, x-intercept, and y-intercept were all important (and she could read the values of the slope and y-intercept off equations of the form y = mx + b), she did not have a stable procedure for determining the values of those entities from a graph and did not know what to do with the values when she had them. As other researchers have shown,12 learners often struggle to tell the difference between the surface features of a subject, which are easy to see but can be misleading, and the deep features, which are difficult to see but are needed for understanding and accurate performance. In this case, three “entities” or aspects of the graph of a line stood out when IN looked at a graph: namely, where it crossed the x-axis, where it crossed the y-axis, and the steepness of the line. All three are important, but IN had the surface understanding that all three are necessary. She appeared to lack the deeper understanding that only two of these three are needed to draw a line. She did not understand how using the y-intercept and slope, in particular, facilitate an efficient graphing strategy because they can be read immediately off the standard form of an equation. Schoenfeld and colleagues’ fine-grained analysis of learning nicely illustrates how subtle and easily overlooked misconceptions can be—even among our best students.13 |
skill and conceptual understanding (Principle 2). However, instruction should assist students not only in thinking with mathematical procedures and concepts, but also in thinking about procedures and concepts and in reflecting on and articulating their own thinking and learning. This kind of thinking about thinking, or metacognition, is the focus of Principle 3. Encouraging students to reflect on and communicate their ideas about functions supports
|
BOX 8-3 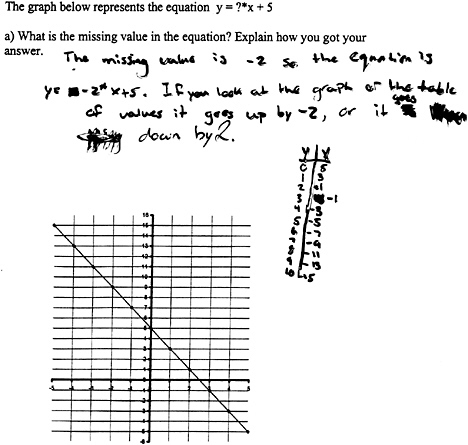 |
them in making the connections among representations that are necessary for flexible, fluent, and reliable performance.
A particularly important type of metacognitive thinking in mathematics is coordinating conclusions drawn from alternative mathematical representations or strategies. Teachers will recognize one form of such coordination in the well-known recommendation that students solve problems in more than one way (e.g., add up and add down) to check whether the same answer is found. A more subtle form of such coordination was exemplified in the earlier discussion of desired student performance on the assessment item shown in Figure 8-1a. In this example, good metacognitive thinking was not about checking the consistency of numeric answers obtained using different strategies, but about checking the consistency of verbal interpretations (e.g., increasing vs. decreasing) of different representations. In other words, we want to encourage students to think about problems not only in
multiple ways (strategies), but also with multiple tools (representations), and to draw conclusions that are not only quantitative (numeric answers), but also qualitative (verbal interpretations).
Supporting metacognitive thinking and attitudes goes beyond reflection and coordination of alternative mathematical representations and strategies. It includes creating a classroom atmosphere in which students feel comfortable to explore, experiment, and take risks in problem solving and learning. It also includes helping students develop a tolerance for the difficulties mathematics sometimes presents and a will to persevere when, for example, they are unable to detect the pattern in the table of values that identifies the relationship between x and y in a particular function. Yet another type of instructional support for metacognitive thinking involves helping students become better help seekers. Students need to learn to recognize when they have reached the limits of their understanding and to know how to obtain the support they need, including asking the teacher or a fellow student; consulting reference materials; and using such tools as computer software, the Internet, or a graphing calculator.
TEACHING FUNCTIONS FOR UNDERSTANDING
Good teaching requires more than knowledge of the content to be taught and of a developmental model for how students acquire an understanding of that content. It also requires a set of instructional strategies for moving students along that developmental pathway and for addressing the obstacles and opportunities that appear most frequently along the way. Below we describe a unit of instruction, based on the developmental model described above, that has been shown experimentally to be more effective than traditional instruction in increasing understanding of functions for eighth and tenth graders.14 In fact, sixth-grade students taught with this instructional approach were more successful on a functions test than eighth and tenth graders who had learned functions through conventional instruction. At the secondary level, tenth graders learning with this approach demonstrated a deeper understanding of complex nonlinear functions. For instance, they performed significantly better on a test item requiring them to draw a “qualitative” graph (no scale on the axes) of the function y = x3 in relation to a given graph of y = x4.
Curriculum for Moving Students Through the Model
This section summarizes the key features and activities of a curriculum that was developed for moving students through the four-level learning sequence described above. We believe such theory-based instruction encourages students (1) to build on and apply their prior knowledge (Principle 1),
(2) to construct an integrated conceptual framework for understanding functions (principle 2), and (3) to apply metacognitive skills to their learning (principle 3). An overview of this curriculum is presented in Table 8-2, followed by a more detailed description. Example lessons are provided in the next section.
The curricular sequence we suggest has been used effectively with students in sixth, eighth, tenth, and eleventh grades. Because timetables and scheduling vary from school to school and from grade to grade, the amount of material per lesson will also vary depending on the available class time. This unit requires approximately 650 minutes of class time to complete. We recommend that it be taught as a whole and in the sequence suggested, even if students are in an upper secondary-level grade and require the more advanced level 3 material. We emphasize implementing the full sequence of topics because the concepts addressed in the level 3 material are supported by a deep and flexible understanding of the ideas found in the level 1 and 2 material, an understanding that is often insufficiently developed in earlier grades. Students in the senior grades will likely move more quickly through the beginning part of the unit than will junior students, and the extra time allotted for the unit can then be used for working through more-advanced ideas that are likely beyond younger students’ capabilities.
The instructional approach we are suggesting is different from some more traditional approaches in many ways. First, the latter approaches often use different contexts or situations for introducing the individual topics within the domain, rather than the single bridging context of the walkathon we use. Within one curriculum, for example, the gradient of a hill may be used for introducing slope, and fixed cost in production may be used for introducing y-intercept. Mixing contexts can make understanding y = mx + b as an integrated concept more difficult than is the case if slope and y-intercept are introduced within the same context.
The use of multiple representations is another significant feature of the suggested curriculum, one that again distinguishes it from more traditional approaches. In many traditional approaches, instruction may be focused on a single representation (e.g., equation or graph) for weeks before multiple representations are related. In our curricular approach, tables, graphs, equations, and verbal rules are copresented within seconds, and students are encouraged to see them as equivalent representations of the same mathematical relationship. Emphasis is placed on moving among these representations and on working to understand how they relate to each other.
Our approach also engages students in the construction of functional notation, and thus helps them build notations and meanings for such constructs as slope and y-intercept into equations. This approach contrasts with many existing curricula, which give students the formal notation and then
focus on introducing them to procedures for finding, for example, the slope of a linear function or the vertex of a quadratic function. Over the course of our instruction, students progressively formalize their own initial notations until those notations correspond with conventional general equations, such as y = mx + b or y = ax2 + bx + c.
Finally, the kinds of follow-up activities we suggest may differ from those of more traditional approaches. We suggest activities that allow students to remain situated in the context of instruction for the first part of the unit (that is, related to a walkathon) until they are confident and competent with the concepts on a more abstract basis. Then, when students move to the computer environment, they engage in activities in which no new concepts are introduced at first. Rather, students have time to consolidate the individual concepts addressed in the first part of the unit, and then move on to more challenging activities that advance their thinking and understanding in the domain. These more challenging activities involve the addition of new features to familiar structures. For example, the left-hand quadrants of the Cartesian plane are eventually included in activities, and linear terms are added to y = x2 + b to generate equations in the form y = ax2 + bx + c. Students also give presentations on a particular kind of function (e.g., linear, quadratic, reciprocal, cubic) to their classmates. In these presentations, students share their understanding of and expertise in key characteristics and behaviors of these functions.
Example Lessons
In the following sections, we elaborate on three specific lessons that highlight the role of the three principles of How People Learn in the curriculum described in Table 8-2. Although we do not provide a complete description of these lessons, the example activities should be sufficient to suggest how the lessons might be used in other classrooms. The three lessons and their companion activities illustrate the principles of How People Learn in three key topic areas: slope, y-intercept, and quadratic functions. Example lesson 1, “Learning Slope,” illustrates principle 1, building on students’ prior knowledge. Example lesson 2, “Learning y-intercept,” illustrates principle 2, connecting students’ factual/procedural and conceptual knowledge. Example lesson 3, “Operating on y = x2,” illustrates principle 3, fostering reflective thinking or metacognition in students. Although each of the selected lessons is used to highlight one of the principles in particular, the reader should keep in mind that all three principles interact simultaneously throughout each lesson.
TABLE 8-2 Suggested Curricular Sequence
|
Topic |
Description |
Activities |
|
Level 1 |
||
|
Introduction |
The walkathon bridging context is introduced. Students record in tables the money earned for each kilometer walked and plot each pair of values for a variety of rules. Using kilometers and dollars, an equation is constructed based on the rule of sponsorship. |
Student partners each invent at least two of their own sponsorship arrangements, for which their partner constructs tables, graphs, and equations. |
|
Slope |
Slope is introduced as the constant numeric up-by (or down-by) amount between successive dollar values in a table or a graph. It is a relative measure of the steepness of a function. It is the amount by which each kilometer (x – value) is multiplied. |
Students are asked to find the slope of several different functions expressed in tables, graphs, and equations. |
|
y-Intercept |
y-Intercept is introduced as the “starter offer,” that is, a fixed starting bonus students receive before the walkathon begins. It affects only the vertical starting point of the numeric sequence and graph. It does not affect the steepness or shape of the line. |
Students invent two linear functions that allow them to earn exactly $153.00 after walking 10 kilometers. Students record the slope and y-intercept of each function and explain how the y-intercept of each function can be found in its table, graph, and equation. |
|
Curving functions |
Nonlinear functions are introduced as those having up-by amounts that increase (or decrease) after each kilometer walked. They are |
Students are asked to decide which of four functions expressed in tables are nonlinear and to explain their reasoning. They are also |
|
Topic |
Description |
Activities |
|
|
derived by multiplying the kilometers (x) by itself at least . once The more times x is multiplied by itself, the greater is the difference between dollar values and thus the steeper the curve. |
asked to write an equation for and to sketch and label the graph of each function. Students are asked to come up with a curved-line function for earning $153.00 over 10 kilometers. |
|
Levels 2 and 3 |
||
|
Computer activities |
Level 2 students use spreadsheet technology and prepared files and activity sheets to consolidate and extend the understandings they constructed about slope, y-intercept, and linearity in the first part of the curriculum. Level 3 extensions include working in all four quadrants to transform quadratic and cubic functions and to explore the properties, behaviors, and characteristics of exponential, reciprocal, and other polynomial functions. |
Students change the steepness, y-intercept, and direction of y = x and y = x2 to make the function go through preplotted points. They record the numeric, algebraic, and graphic effects of their changes. They also invent functions with specific attributes, such as parallel to y = 4x and a y-intercept below the x-axis, or an inverted parabola that is compressed and in the lower left-hand quadrant. |
|
Presentations |
Groups of students investigate and then prepare a presentation about a particular type of function. Presentations stimulate discussion and summarizing of key concepts and serve as a partial teacher assessment for evaluating students’ postinstruction understanding about functions. |
Groups of students use computer-generated output of graphs, equations, and tables to illustrate a particular type of function’s general properties and behaviors. Students give presentations about their function and share their expertise with classmates. |
Example Lesson 1: Learning Slope
The classroom interaction recounted below took place during students’ first lesson on slope. The students had already worked through the construction of representations for the introductory rule of the walkathon—earning one dollar for every kilometer walked. In this interaction we can see how Katya quickly grasps the idea of slope as relative steepness, as defined by the variable relationship between two quantities (distance walked and money earned in this case):
|
Teacher |
I want to think of a way, let’s see, Katya, how might you sponsor me that would make a line that is steeper than this [y = x is already drawn on graph, as in Figure 8-2b]? |
|
Katya |
Steeper? Alright … every kilometer you walk you get two dollars. |
|
Teacher |
Two dollars. So let’s try that. So at zero kilometers how much am I going to have? |
|
Katya |
At zero kilometers you’ll have zero. |
|
Teacher |
At one? |
|
Katya |
You’ll have two. |
|
Teacher |
And what happens at ten? |
|
Katya |
At ten you’ll have twenty. |
|
Teacher |
So Katya, what have you done each time? |
|
Katya: |
I’ve just multiplied by two. |
|
Teacher |
You’ve multiplied each one of these [pointing to the numbers in the left column of the table] by two, right? Zero times two, one times two [moving finger back and forth between columns]. If I graph that, where’s it going to start, Katya? |
|
Katya |
It’s going to start at zero. |
|
Teacher |
So at zero kilometers, zero money. At one? |
|
Katya |
At one it’s going to go to two. |
|
Teacher |
At two it’s going to go to? |
|
Katya |
Four. |
|
Teacher |
Over two up to four. At three? |
|
Katya |
It’s going to go to six. |
|
Teacher |
What do you see on the graph? What do you see happening? |
|
Katya |
It’s going higher. It’s steeper than the other one. |
|
Teacher |
So it’s steeper and it’s going up by how much? |
|
Katya |
Two. |
|
Teacher |
So Katya, since this is your function, what would the equation for this function be? |
|
Katya |
Kilometers times two equals money. |
|
Teacher |
That’s absolutely right. And what do you notice about these values [pointing to dollar values in the table and making “>“ marks between successive values]? |
|
Katya |
They’re going up by 2. |
The Lesson. The lesson on slope is the second lesson suggested in the overall sequence of instruction, after the walkathon has been introduced. It requires about two class periods, or 90 minutes. We introduce slope as the constant numeric up-by amount that is found between successive y-values for every unit change in x. This up-by amount can be seen in a function’s table or its graph. The up-by terminology was invented by students who were asked to describe the meaning of slope using their own words. When introducing this up-by idea to students, we suggest beginning with the graph and the table for the rule of earning one dollar for every kilometer walked ($ = 1 x km) and having students see that in each of these representations, the dollar amount goes up by one for each kilometer walked. To show this on the graph, the teacher may draw a staircase-like path from point to point that goes over one and then up one (see Figure 8-2c). In the table, a third column may be created to show the constant up-by difference between successive y-values, as also illustrated in Figure 8-2c. We then suggest drawing students’ attention to the facts that this up-by amount corresponds to the mathematical concept of slope and that slope is a relative measure of a function’s steepness. That is, the greater the up-by amount, the steeper is the function. From this point on, y = x (y = 1 • x with a slope of 1) may be employed as a landmark function for students to use in qualitative reasoning, by comparison, about the slopes (and later the y-intercepts) of other functions. Conceptual landmarks are crucial tools to support learners in making sense of, catching, and correcting their own and others’ errors.
After having created tables and graphs for the one dollar per kilometer context, we challenge students such as Katya to provide sponsorship rules (or functions) having slopes that are steeper and less steep than y = x. To facilitate the comparison of graphs of functions with different slopes, we encourage students to plot functions on the same set of axes. Before each rule is graphed, we ask the students to predict the steepness of the line
relative to y = x. We also have them invent other rules and make tables and graphs for those rules. These explorations in multiple contexts and representations develop students’ deeper understanding of slope. After all, the essence of understanding is being able to apply a concept flexibly in different contexts and with different representations. After having worked with functions having varying degrees of steepness, we ask the students to summarize their findings about slope and to explain that steeper lines are the result of functions having bigger up-by amounts.
In our instruction, we do not provide students at the outset with an algorithm for finding the slope of a function. However, we do suggest that students be asked for their ideas about how the steepness, or slope, of a function can be quantified—that is, represented as a number—and how they can obtain that number from any of the representations of a function they have seen. This is illustrated by the following teacher–student exchange from a ninth-grade class:
|
Teacher |
This line [pointing to a graph of y = x] has a certain steepness to it…. If you had to give a number to this steepness, what would you give it? Look at these numbers (pointing to the corresponding table of values). |
|
Aaron |
One. |
|
Teacher |
Why one? |
|
Aaron |
‘Cause they all go up by one. |
Introducing and working with functions having negative slopes is also important to show that the way the students have been constructing slope as the up-by amount is applicable to all straight-line functions, whether they increase or decrease. We generally introduce negative values along the y-axis by asking students to think about how the negative values along the y-axis can be used. One situation we employ is from the perspective of the donor or sponsor, who loses money as the participant walks. In our experience, students generally recognize that these lines have a down-by amount when a fixed amount of money is given away for each kilometer walked.
Summary of Principle #1 in the Context of Learning Slope. We have used a lesson on slope to illustrate how students’ initial knowledge of a topic can be used for building formal or conventional mathematical knowledge and notation structures. In this case, we draw on three sorts of prior knowledge. First, students’ prior knowledge of familiar situations such as earning money in a walkathon can be used to elicit and extend the students’ informal, intuitive ideas about a difficult topic such as slope. Second, students’ prior knowledge of natural language, such as “up-by,” can be used to
build a sound foundation of understanding for explaining and working with more formal concepts and procedures, such as finding slope from a graph. Third, prior knowledge with respect to initial numeric and spatial understandings can be integrated through instruction to help students construct a conceptual understanding of slope within a broader framework for understanding functions in general.
Example Lesson 2: Learning y-Intercept
This example lesson focuses on learning and teaching y-intercept. It illustrates the effect of theory-based instructional design in connecting students’ factual/procedural and conceptual knowledge (principle 2).
A commonly taught procedure for finding the y-intercept of a function is to substitute x = 0 into the function’s equation, with the result being the y-intercept. Instead of starting by formally introducing this method, this lesson begins by having students explore situations in which a nonzero starting amount is used. This approach appears to do a better job of helping students learn the formal procedure in the context of a robust conceptual understanding.
The Lesson. The lesson on y-intercept follows that on slope in the overall curricular sequence. Two class periods of about 90 minutes are suggested for working with y-intercept. We introduce the y-intercept by suggesting the idea of a starting bonus or an initial amount of money that may be contributed before the walkathon even begins. Students have termed this starting amount the “starter offer” or “starter upper.” These phrases have repeatedly been shown to be simple for students to understand first in the walkathon context and then in more abstract situations.
We again begin this lesson with a sponsorship arrangement of earning one dollar for every kilometer walked. We then have students graph this function, construct a table of values, and write a symbolic representation for the function. We then tell students they will be given a five-dollar starter offer just for participating in the walkathon. That is, before they have walked at all, they will already have earned five dollars. In addition to this starting bonus, they will still be earning one dollar for every kilometer walked. Students are then asked to construct a table for this function and to calculate how much money they will have earned at zero kilometers, one kilometer, two kilometers, and so on. After the table has been constructed, students are asked to graph the function and to make an equation for it. Having students verbally describe the relationship between the kilometers and dollars helps them formulate an equation. For example, a student might say, “I think it would be five plus the kilometers equals money.” That description could then be translated into the situation-specific symbolic ex-
pression 5 + km = $, and that expression, in turn, formalized into the general expression, y = x + 5.
As the lesson proceeds, we suggest other rules whereby students earn one dollar per kilometer but have different starter offer amounts, such as two dollars, ten dollars, and three and a half dollars. We ask the students first to predict where on a graph each new function will be relative to the first example given (y = x + 5) and then to construct tables, graphs, and equations for each new function. Students are asked to describe any patterns or salient characteristics they see in this group of functions. What we want students to see, both literally and figuratively, is that all of the functions are parallel, with a slope of 1, but their starting point on the graph changes in accordance with the starting bonus offered. Furthermore, the distance between points on any two graphs is equal to the difference in starting bonuses. For example, the functions 5 + km = $ and 10 + km = $ are five units apart at every point along the line of each function. Likewise, in examining the tables for each of the functions, we want students to see that all of the functions go up by one (accounting for the parallel lines), but the first value in the dollar column of each of the tables is equal to the starting bonus. We then connect the “starting points” of the graphs and tables with the structure of the equations to show that the starting bonus is indeed added to each x-value.
Emphasizing that the only effect of changing the starter offer is a vertical shift in a function is crucial because a number of researchers have found that students regularly confuse the values for slope and y-intercept in equations. That is, in an equation such as y = 2x + 7, many students are unsure of which “number” is the y-intercept and which is the slope. Initially, students of all ages and grades in our program often predict that changing the starter offer will also change the steepness (slope) of a function. However, working through many examples for which the amount earned per kilometer (the slope) is held constant will help students see, in context, that changing the starting bonus does not affect the amount being earned per kilometer, which is how the steepness or slope of the function is determined. Ultimately, by establishing the meaning of y-intercept in the context of the walkathon and by applying that meaning to the different representations of a function, the confusion of slope and y-intercept is significantly minimized for students.
Negative y-intercepts are introduced using the idea of debt. In this case, students have to pay off a starter offer amount. For example, a student in one of our studies suggested that if she owed ten dollars on her credit card and paid off one dollar every time she walked a kilometer, she would have to start at minus ten dollars. Then after one kilometer, she would pay off one dollar and still be nine dollars in debt, then eight, then seven, etc. Students can construct tables, graphs, and equations for such situations that they invent and perhaps share with a partner or the class. The writing of the
equations for these functions may take different forms at first. Many students choose to adhere to the notion that the starter offer is “added” in the equation. Thus an equation for a function such as that described above would look like $ = 1 • km + –10. While students are consolidating the concept of y-intercept and distinguishing it from slope, we recommend that they be allowed to write equations in this way. An alternative, more conventional format may be suggested by repeating the function and writing it in conventional notation alongside the student-constructed expression. Again, we stress the importance of students’ developing a conceptual framework for these difficult concepts, which can be formalized over time once the ideas are firmly in place.
Following is a short classroom exchange between a teacher and a student. The context of earning five dollars per day for a paper route had already been developed by the teacher for an earlier teaching example. The teacher continued with this context in introducing linear functions with negative y-intercepts and positive slopes.
|
Teacher |
We owe 90 dollars, so think of it as a negative amount we have and over time we’re coming up toward zero. We’re coming toward breaking even; towards no longer being in debt. So every day that goes 5 dollars toward zero [referring to and constructing both a graph and a table]. So up by 5, up by 5, up by 5, and so on. What are these differences [referring to the y values in the table]? |
|
Justin |
Positive 5. |
|
Teacher |
Ya, we’re going up by 5 so as we go across 1 we go up by 5. |
In the lessons on nonlinear functions, the starter offer idea is also applied. Generally, students quickly see that including the starter offer in a curved-line function has the same effect as it does on straight-line functions. That is, the steepness of the line (or curve) is not altered by changing the starter offer, only the place at which the function meets the vertical axis in a graph. The result is that each point on the curve is shifted up (or down) by the starter offer amount.
A suggested follow-up activity that addresses both slope and y-intercept is to have students, either individually or in pairs, invent two functions that will allow them to earn exactly $153 upon completing a ten-kilometer walkathon. Both strategies must produce straight lines. We ask students to construct tables, graphs, and equations to show their work, and also ask them to identify the slope and y-intercept of each function. Individuals or
pairs of students then show their functions to the whole group. Samples of student work are shown in Box 8-4. We also challenge students to work “backwards,” that is, to find what the starter offer would have to be if the slope were 10, or what the slope would have to be if the starter offer were 20.
Summary of Principle #2 in the Context of Learning y-Intercept. We have used a lesson on y-intercept to illustrate how students connect their factual/procedural and conceptual knowledge within the instructional bridging context of a walkathon. The walkathon context is intended to help students relate their new and existing knowledge within an organized conceptual framework in ways that facilitate efficient retrieval of that knowledge. The idea of a “starter offer” gives students a reasonably familiar situation that provides a context for learning y-intercept—ordinarily a relatively abstract and difficult mathematical topic that is often confused with slope in students’ understanding of linear function. In our approach, students still learn the notations, symbols, words, and methods necessary for identifying the y-intercept of a function (linear or nonlinear). However, they acquire that knowledge in context and initially without algorithms, and with a depth of understanding and attribution of meaning that minimize the procedural and conceptual difficulties many students experience with the topic.
Example Lesson 3: Operating on y = x2
After the first four lessons, which take place in the classroom, students move to a computer environment where they work with spreadsheet technology to consolidate and apply the concepts introduced in the classroom instruction and to extend their understandings to new situations. The particular lesson we use for illustrating principle 3, developing metacognitive skills, is the fourth in the series of computer activities.
The Lesson. Pairs of students use prepared spreadsheet files to work with a computer screen such as that seen in Figure 8-3. Students are asked to change specific parameters in the function y = ax2 + b to move the graph through preplotted colored points. The file is designed so the students can change the value of just the exponent, the coefficient of x2, the y-intercept, or any combination of these. With each change, the graph and table of values change instantly and automatically to reflect the numeric (tabular) and graphic (spatial) implications of that change. For example, students are asked to describe and record what happens to the graph and the “Y” column of the table of values when the exponent in y = x2 is changed to 3, to 4, and then more generally to any number greater than 2. Students are then asked to describe and record what happens to the curve when x2 is multiplied by
|
BOX 8-4 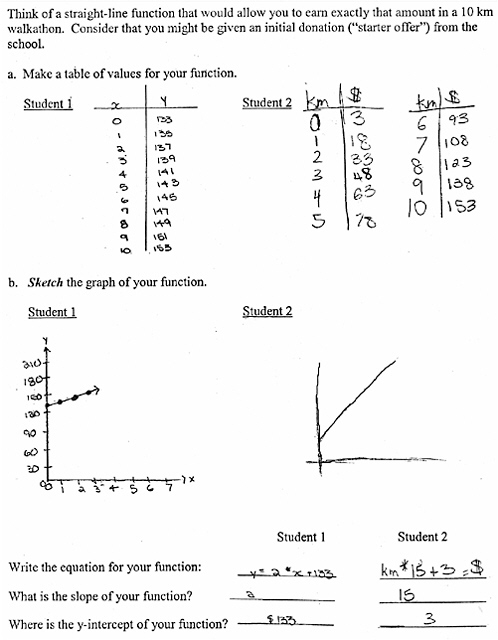 |
a value larger than 1, smaller than 1 but greater than 0, and less than 0. They are then asked to compare the tables and graphs for y = x2, y = 2 * x2, y = 3 * x2, y = 4 * x2, etc. and to describe in words what patterns they find. Finally, students are asked to compare the table of values for y = 2 * x2 and y = -2 * x2 and describe what they notice.
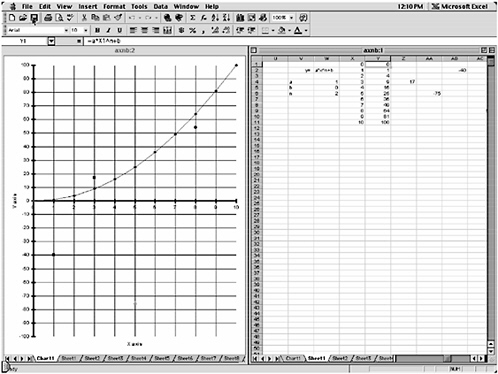
FIGURE 8-3 Sample computer screen. In this configuration, students can change the value of a, n, or b to effect immediate and automatic changes in the graph and the table. For example, if students change the value of b, just the y-intercept of the curve will change. If students change a or n to a positive value other than 1, the degree of steepness of the curve will change. If students change the value of a to a negative value, the curve will come down. All graphic patterns will be reflected in the table of values.
Students must employ effective metacognitive strategies to negotiate and complete these computer activities. Opportunities for exploring, persevering, and knowing when and how to obtain help are abundant. Metacognitive activity is illustrated in the following situation, which has occurred among students from middle school through high school who have worked through these activities.
When students are asked to change the parameters of y = x2 to make it curve down and go through a colored point that is in the lower right quadrant, their first intuition is often to make the exponent rather than the coefficient negative. When they make that change, they are surprised to find that the graph changes shape entirely and that a negative exponent will not
satisfy their needs. By trying a number of other possible alterations (persevering), some students discover that they need to change the coefficient of x2 rather than the exponent to a negative number to make the function curve down. It is then a matter of further exploration and discovery to find the correct value that will make the graph pass through the point in question. Some students, however, require support to discover this solution. Some try to subtract a value from x2 but are then reminded by the result they see on the computer screen that subtracting an amount from x2 causes a downward vertical shift of the graph. Drawing students’ attention to earlier exercises in which they multiplied the x in y = x by a negative number to make the numeric pattern and the graph go down encourages them to apply that same notion to y = x2. To follow up, we suggest emphasizing for students the numeric pattern in the tables of values for decreasing curves to show how the number pattern decreases with a negative coefficient but not with a negative exponent.
Following is a typical exchange between the circulating teacher and a pair of students struggling with flipping the function y = x2 (i.e., reflecting it in the x-axis). This exchange illustrates the use of metacognitive prompting to help students supervise their own learning by suggesting the coordination of conclusions drawn from one representation (e.g., slope in linear functions) with those drawn from another (e.g., slope in power functions).
|
Teacher |
How did you make a straight line come down or change direction? |
|
John |
We used minus. |
|
Teacher |
How did you use “minus”? |
|
Pete |
Oh yeah, we times it by minus something. |
|
Teacher |
So … how about here [pointing at the x2]? |
|
John |
We could times it by minus 2 [typing in x2 • -2]. There! It worked. |
Without metacognitive awareness and skills, students are at risk of missing important inconsistencies in their work and will not be in a position to self-correct or to move on to more advanced problem solving. The example shown earlier in Figure 8-1a involves a student not reflecting on the inconsistency between a negative slope in his equation and a positive slope in his graph. Another sort of difficulty may arise when students attempt to apply “rules” or algorithms they have been taught for simplifying a solution to a situation that in fact does not warrant such simplification or efficiency.
For example, many high school mathematics students are taught that “you only really need two points to graph a straight line” or “if you know it’s a straight line, you only need two points.” The key phrase here is “if you know it’s a straight line.” In our research, we have found students applying

FIGURE 8-4
that two-point rule for graphing straight lines to the graphing of curved-line functions. In the example shown in Figure 8-4, an eleventh-grade advanced mathematics student who had been learning functions primarily from a textbook unit decided to calculate and plot only two points of the function y = x2 +1 and then to join them incorrectly with a straight line. This student had just finished a unit that included transformations of quadratic functions and thus presumably knew that y = x2 makes a parabola rather than a straight line. What this student did not know to perform, or at least exercise, was a metacognitive analysis of the problem that would have ruled out the application of the two-points rule for graphing this particular function.
Summary of Principle #3 in the Context of Operating on y = x2. The general metacognitive opportunities for the computer activities in our curriculum are extensive. Students must develop and engage their skills involving prediction, error detection, and correction, as well as strategies for scientific inquiry such as hypothesis generating and testing. For instance, because there are innumerable combinations of y-intercept, coefficient, and exponent that will move y = x2 through each of the colored points, students must recognize and acknowledge alternative solution paths. Some students may fixate on the steepness of the curve and get as close to the colored points as possible by adjusting just the steepness of the curve (by changing either the exponent or the coefficient of x2) and then changing the y-intercept. Others may begin by selecting a manageable y-intercept and then adjust the steepness of the curve by changing the exponent or the coefficient. Others may use both strategies equally. Furthermore, students must constantly be pre-
dicting the shapes and behaviors of the functions with which they are working and adjusting and readjusting their expectations with respect to the mathematical properties and characteristics of linear and nonlinear functions.
SUMMARY
Sometimes mathematics instruction can lead to what we refer to as “ungrounded competence.” A student with ungrounded competence will display elements of sophisticated procedural or quantitative skills in some contexts, but in other contexts will make errors indicating a lack of conceptual or qualitative understanding underpinning these skills. The student solution shown earlier in Figure 8-1a illustrates such ungrounded competence. On the one hand, the student displays elements of sophisticated skills, including the slope formula and negative and fractional coefficients. On the other hand, the student displays a lack of coordinated conceptual understanding of linear functions and how they appear in graphical, tabular, and symbolic representations. In particular, he does not appear to be able to extract qualitative features such as linearity and the sign of the slope and to check that all three representations share these qualitative features.
The curricular approach described in this chapter is based on cognitive principles and a detailed developmental model of student learning. It was designed to produce grounded competence whereby students can reason with and about multiple representations of mathematical functions flexibly and fluently. Experimental studies have shown that this curriculum is effective in improving student learning beyond that achieved by the same teachers using a more traditional curriculum. We hope that teachers will find the principles, developmental model, and instructional examples provided here useful in guiding their curriculum and teaching choices.
We have presented three example lessons that were designed within one possible unifying context. Other lessons and contexts are possible and desirable, but these three examples illustrate some key points. For instance, students may learn more effectively when given a gradual introduction to ideas. Our curriculum employs three strategies for creating such a gradual introduction to ideas:
-
Starting with a familiar context: Contexts that are familiar to students, such as the walkathon, allow them to draw on prior knowledge to think through a mathematical process or idea using a concrete example.
-
Starting with simple content: To get at the essence of the idea while avoiding other, distracting difficulties, our curriculum starts with mathematical content that is as simple as possible—the function “you get one dollar for every kilometer you walk” (y = x).
-
Focusing on having students express concepts in their own language before learning and using conventional terminology: To the extent that a curriculum initially illustrates an idea in an unfamiliar context or with more-complex content, students may be less likely to be able to construct or invent their own language for the idea. Students may better understand and explain new ideas when they progress from thinking about those ideas using their own invented or natural language to thinking about them using formal conventional terms.
A risk of simplicity and familiarity is that students may not acquire the full generality of relevant ideas and concepts. Our curriculum helps students acquire correct generalizations by constructing multiple representations for the same idea for the same problem at the same time. Students make comparisons and contrasts across representations. For example, they may compare the functions y = .5x, y = 2x, and y = 10x in different representations and consider how the change in slope looks in the graph and how the table and symbolic formula change from function to function. We also emphasize the use of multiple representations because it facilitates the necessary bridging between the spatial and numerical aspects of functions. Each representation has both spatial and numerical components, and students need experience with identifying and constructing how they are linked.
As illustrated earlier in Figure 8-1a, a curriculum that does not take this multiple-representation approach can lead students to acquire shallow ideas about functions, slope, and linearity. The student whose response is shown in that figure had a superficial understanding of how tables and graphs are linked: he could read off points from the graph, but he lacked a deep understanding of the relationship between tables and graphs and the underlying idea of linearity. He did not see or “encode” the fact that because the graph is linear, equal changes in x must yield equal changes in y, and the values in the table must represent this critical characteristic of linearity.
The curriculum presented in this chapter attempts to focus limited instructional time on core conceptual understanding by using multiple representations and generalizing from variations on just a few familiar contexts. The goal is to develop robust, generalizable knowledge, and there may be multiple pathways to this end. Because instructional time is limited, we decided to experiment with a primary emphasis on a single simple, real-world context for introducing function concepts instead of using multiple contexts or a single complex context. This is not to say that students would not benefit from a greater variety of contexts and some experience with rich, complex, real-world contexts. Other contexts that are relevant to students’ current real-world experience could help them build further on prior knowledge. Moreover, contexts that are relevant to students’ future real-world experiences, such as fixed and variable costs of production, could help them
in their later work life. Since our lessons can be accomplished in anywhere from 3 to 6 weeks (650 minutes), there is sufficient time for other activities to supplement and extend students’ experience.
In addition to providing a gradual introduction to complex ideas, a key point illustrated by our lessons is that curriculum should be mathematically sound and targeted toward high standards. Although the lessons described here start gradually, they quickly progress to the point at which students work with and learn about sophisticated mathematical functions at or beyond what is typical for their grade level. For instance, students progress from functions such as y = x to y = 10 – .4x in their study of linear functions across lessons 1 to 3, and from y = x2 to y = (x – 2)2 + 4 in their study of nonlinear functions across lessons 4 to 8.
We do not mean to suggest that this is the only curriculum that promotes a deep conceptual understanding of functions or that illustrates the principles of How People Learn. Indeed, it has important similarities, as well as differences, with other successful innovations in algebra instruction, such as the Jasper Woodbury series and Cognitive Tutor Algebra (previously called PUMP), both described in How People Learn. All of these programs build on students’ prior knowledge by using problem situations and making connections among multiple representations of function. However, whereas the Jasper Woodbury series emphasizes rich, complex, real-world contexts, the approach described in this chapter keeps the context simple to help students perceive and understand the richness and complexity of the underlying mathematical functions. And whereas Cognitive Tutor Algebra uses a wide variety of real-world contexts and provides intelligent computer tutor support, the approach described here uses spreadsheet technology and focuses on a single context within which a wide variety of content is illustrated.
All of these curricula, however, stand in contrast to more traditional textbook-based curricula, which have focused on developing the numeric/ symbolic and spatial aspects of functions in isolation and without particular attention to the out-of-school knowledge that students bring to the classroom. Furthermore, these traditional approaches do not endeavor to connect the two sorts of understandings, which we have tried to show is an essential part of building a conceptual framework that underpins students’ learning of functions and ultimately their learning in related areas.
ACKNOWLEDGMENTS
Thanks to Ryan Baker, Brad Stephens, and Eric Knuth for helpful comments. Thanks to the McDonnell Foundation for funding.
NOTES
REFERENCES
Chi, M.T.H., Feltovich, P.J., and Glaser, R. (1981). Categorization and representation of physics problems by experts and novices. Cognitive Science, 5, 121-152.
Goldenberg, E.P. (1995). Multiple representations: A vehicle for understanding. In D. Perkins, J. Schwartz, M. West, and M. Wiske (Eds.), Software goes to school: Teaching for understanding with new technologies (pp. 155-171). New York: Oxford University Press.
Kalchman, M. (2001). Using a neo-Piagetian framework for learning and teaching mathematical functions. Doctoral Dissertation, Toronto, Ontario, University of Toronto.
Koedinger, K.R., and Nathan, M.J. (2004). The real story behind story problems: Effects of representations on quantitative reasoning. Journal of the Learning Sciences, 13(2).
Koedinger, K.R., Anderson, J.R., Hadley, W.H., and Mark, M.A. (1997). Intelligent tutoring goes to school in the big city. International Journal of Artificial Intelligence in Education, 8, 30-43.
Leinhardt, G., Zaslavsky, O., and Stein, M. (1990). Functions, graphs, and graphing: Tasks, learning, and teaching. Review of Educational Research, 60(1), 1-64.
Nathan, M.J., and Koedinger, K.R. (2000). Teachers’ and researchers’ beliefs of early algebra development. Journal for Research in Mathematics Education, 31(2), 168-190.
Romberg, T., Fennema, E., and Carpenter, T.P. (1993). Integrating research on the graphical representation of functions. Mahwah, NJ: Lawrence Erlbaum Associates.
Schoenfeld, A.H. (1987). Cognitive science and mathematics education. Mahwah, NJ: Lawrence Erlbaum Associates.
Schoenfeld, A.H. (1998). Reflections on a course in mathematical problem solving. In A.H. Schoenfeld, J. Kaput, and E. Dubinsky (Eds.), CBMS issues in mathematics education (vol. 7, pp. 81-99.) Washington, DC: Conference Board of the Mathematical Sciences.
Schoenfeld, A.H., Smith J., and Arcavi A. (1993). Learning: The microgenetic analysis of one student’s evolving understanding of a complex subject matter. In R. Glaser (Ed.), Advances in Instructional Psychology (vol. 4, pp. 55-175). Mahwah, NJ: Lawrence Erlbaum Associates.
Thomas, G.B. (1972). Calculus and analytic geometry. Reading, MA: Addison-Wesley.
OTHER RELEVANT READINGS
Bednarz, N., Kieran, C., and Lee, L. (1996). Approaches to algebra. Perspectives for research and teaching. Dordrecht, The Netherlands: Kluwer Academic Press.
Confrey, J., and Smith, E. (1995). Splitting, co-variation, and their role in the development of exponential functions. Journal for Research in Mathematics Education, 26(1), 66-86.
Janvier, C. (1987). Problems of representation in the teaching and learning of mathematics. Mahwah, NJ: Lawrence Erlbaum Associates.
Kaput, J.J. (1989). Linking representations in the symbol systems of algebra. In S. Wagner and C. Kieran (Eds.), Research issues in the learning and teaching of algebra (pp. 167-181). Reston, VA: National Council of Teachers of Mathematics.
