4
Social Interactions and Fertility Transitions
STEVEN N.DURLAUF AND JAMES R.WALKER
INTRODUCTION
No topic in demography has received as much theoretical and empirical attention as the study of fertility transitions. Yet, as Mason (1997) notes in her presidential address to the Population Association of America (PAA), no single extant theory explains the historical record on transitions in a sufficiently comprehensive way so as to dominate its competitors. The empirical evidence is too varied and too rich to admit any of the current explanations: for every existing theory, there is a striking counterexample. For example, Coale (1986) documents one pattern exhibited by Western European countries whereas Bongaarts and Watkins (1996) show that Asia and Latin America follow quite a different one and the African countries yet another. Although conventional economic explanations play an important role in several of the primary theories, the historical experiences appear to be too disparate for fertility transitions to have been generated solely in this way. Cultural explanations thus appear to be a natural complement to the economic explanations. Yet, it also is true that “culture,” unless defined so broadly as to render the explanation tautological, is insufficient to place the full range of transitions in a common framework.
Within demography, it seems fair to conclude that a consensus view of fertility transitions is slowly emerging through the combination of several traditional competing explanations—economic and cultural. This new
Steven N.Durlauf and James R.Walker are professors of economics at the University of Wisconsin, Madison.
literature finds a parallel within economic theory with the emergence of a theory of social interactions.1 As described below, social interactions models apply neoclassical economic reasoning to environments that embody richer sociological structures than have been traditionally studied by economists. In this way, the core ideas of both economics and sociology are preserved as the role of individual incentives emphasized by economists is integrated with the social norms stressed by sociologists.
This paper is designed to introduce demographers to the social interactions approach in economics. We do this through the development of an analytical framework that shows how the rational-choice approach of neoclassical economics can be combined with social factors. We present models that are sufficiently rich (or at least complicated) to provide some qualitative insights into fertility transitions. We leave the actual task of formally implementing these models empirically to future research. Our goal in this paper is to communicate the basic ideas of social interactions models in a way that demographers can use in subsequent research.
The models we describe are complementary to that strand of the demography literature based on contextual effects in fertility. For example, Entwisle et al. (1986), and Entwisle and Mason (1985) provide analyses of how socioeconomic development levels within a society affect individual fertility decisions; Entwisle et al. (1989) provide complementary evidence on village-level influences. Further, Pollak and Watkins (1993) provide an interpretation of the role of interactions in demography, which is complementary to ours. We hope to add to this literature by emphasizing how these approaches can be embedded in a structural model of choices that embodies both contextual effects as well as feedbacks from the actual decisions of group members. This structural modeling approach will in turn have implications for statistical analysis.2
The second section of this paper provides a survey of the empirical evidence on fertility transitions that the social interactions model can help to explain. The third section provides some basic ideas concerning interactions. The fourth section develops a discrete-choice approach to interactions (due to Brock and Durlauf, 1999a, b), which seems useful for demographic analysis. The fifth section comments on the statistical obstacles that challenge the empirical implementation of these models. The sixth and final section concludes with implications for demographic research.
EMPIRICAL EVIDENCE ON FERTILITY TRANSITIONS
There are several recent summaries of the empirical descriptions of fertility transitions and we draw liberally on these.3 We focus our discussion on a set of empirical observations, which suggest social interactions may be important.
With so many descriptions available in the literature, it is difficult to
concisely characterize the fertility transitions experienced by countries during the last couple of hundred years. Nevertheless, we use two tables modified from Schultz (1997) to focus our discussion. Table 4–1 reports birth and death rates and natural rates of growth for high- and low-income countries for a 250-year period from 1750 to 2000. Definitions of high- and low-income countries are based on income levels in the second half of the twentieth century.
Europe experienced its demographic transition during the 60-year period from 1870 to 1930, with considerable variation in the timing of the transition for individual countries. All countries in Europe (including Russia and the other countries of the former Soviet Union) completed the transition by 1960.4 European countries comprise an important share of the high-income countries of Table 4–1, and the influence of the European experience on the overall features of the table is in some respects evident. One such respect is the relative stability of the natural rate of population growth through the nineteenth century. By the end of the demographic transition in Europe (conventionally dated around 1960), the natural rate of population growth for high-income countries is only slightly higher than that reported a century earlier. Since 1960, the rate of natural population growth for high-income countries fell, and the medium variant forecast of the United Nations for 2000 suggests that it will fall further. Interestingly, the crude birth and death rates imply that the decline in the
TABLE 4–1 Birth, Death, and Natural Growth Rate By Income Group, 1750–2000
|
|
High-Income Countries |
Low-Income Countries |
||||
|
|
Birth |
Death |
Growth |
Birth |
Death |
Growth |
|
1750 |
|
6.5 |
|
4.0 |
||
|
1850 |
|
10.6 |
|
4.9 |
||
|
1900 |
|
9.9 |
|
6.7 |
||
|
1950 |
22.6 |
10.1 |
12.5 |
44.6 |
24.3 |
20.3 |
|
1960 |
20.1 |
9.0 |
11.1 |
41.9 |
18.3 |
23.6 |
|
1970 |
16.7 |
9.3 |
7.4 |
37.1 |
13.2 |
23.9 |
|
1980 |
15.2 |
9.6 |
5.6 |
31.7 |
10.6 |
21.1 |
|
1990 |
13.9 |
9.6 |
4.3 |
30.0 |
9.1 |
20.9 |
|
2000 |
13.1 |
9.7 |
3.4 |
25.3 |
7.8 |
17.5 |
|
NOTES: High-income countries include industrially advanced countries, such as Europe, North America, Asiatic USSR, Australia, New Zealand and Japan. Low-income countries include all other countries. Crude birth, death, and natural population growth rates in annual growth per 1,000 population in the 5-year period following the year reported from 1950 to 2000, for the 50-year period following the year reported in 1750, 1850, and 20-year period after 1900. SOURCE: Schultz (1997:352–353). Reprinted with permission from Elsevier Science. |
||||||
natural population growth rate for high-income countries stems from falling birth rates.
Consistent with the European transition, the population growth rate for the currently high-income countries increased in the initial stages of the demographic transition (around 1850) and then declined as a new equilibrium was reached. Admittedly, the highly time-aggregated nature of Table 4–1 and the baby boom following World War II make this difficult to see. The detailed analysis of the European Fertility Projects supports this claim. The common explanation for the surge in population is that mortality rates decline initially and then stimulate a decline in fertility rates. Table 4–1 does not, of course, report birth and death rates during the period of the demographic transition and so we rely on the extensive analysis of the European Fertility Project to support this conclusion.
The demographic rates of the low-income countries also are informative. Unsurprisingly, the rates of natural population increase for low- and high-income countries are low (about 1/2 percent) and close in magnitude (differing by only 2.5 per 1,000) at the onset of the Industrial Revolution (around 1750). Yet during the first half of the twentieth century, the natural rate of increase jumps by threefold for the low-income countries (from 6.7 to 20.3 per 1,000). Although Table 4–1 does not give a decomposition of the demographic components, it indicates that the huge increase in natural population growth rates for these countries stems from the reduction in mortality rates. These gains in life expectancy continued through the second half of the 1900s, so that by 1990 there is no difference in crude death rates between high- and low-income countries.5 Notice, however, that while death rates fell by 67 percent, fertility rates only fell by 40 percent among low-income countries. If the currently developing countries had followed a demographic pattern even roughly consistent with the European demographic transition, birth rates among low-income countries would have fallen much more rapidly and be much lower than are actually observed. So, even the highly aggregated statistics of Table 4–1 illustrate the diversity of fertility transitions.
Grouping all low- and high-income countries together masks important differences among these countries. Table 4–2 reports (age-adjusted) period measures of fertility, mortality, and life expectancy as well as rates of change of these measures during 1950–2000. We separately report rates for various regions to highlight differences among developing countries.
Notice that all countries experienced large relative improvements in infant mortality rates—even Africa more than halved its rate of infant mortality, although the projected absolute level for 2000 exceeds that of the higher income countries in 1950. Gains in life expectancy mirror the improvements in infant mortality rates. The smallest relative gain occurred among the higher income countries (16 percent) while the lower
TABLE 4–2 Period Rates 1950–2000 by Region
|
|
1950 |
2000 |
Percent Change |
|
Higher Income |
|||
|
TFR |
2.84 |
1.91 |
–32.7 |
|
Infant Morality Rate |
56.0 |
9.0 |
–83.9 |
|
Life Expectation |
66.0 |
76.6 |
16.1 |
|
Lower Income |
|||
|
TFR |
6.19 |
3.20 |
–48.3 |
|
Infant Mortality Rate |
180.0 |
57.0 |
–68.3 |
|
Life Expectation |
42.2 |
66.5 |
57.6 |
|
Latin America |
|||
|
TFR |
5.87 |
2.81 |
–52.1 |
|
Infant Mortality Rate |
126.0 |
37.0 |
–73.0 |
|
Life Expectation |
51.9 |
70.4 |
35.6 |
|
South East and East Asia |
|||
|
TFR |
5.78 |
2.33 |
–59.7 |
|
Infant Mortality Rate |
175.0 |
24.0 |
–86.2 |
|
Life Expectation |
44.1 |
72.1 |
63.5 |
|
South and West Asia |
|||
|
TFR |
6.17 |
3.61 |
–41.5 |
|
Infant Mortality Rate |
190.0 |
68.0 |
–64.2 |
|
Life Expectation |
39.6 |
64.4 |
62.6 |
|
Africa |
|||
|
TFR |
6.65 |
5.31 |
–20.2 |
|
Infant Mortality Rate |
188.0 |
77.0 |
–59.0 |
|
Life Expectation |
37.7 |
58.1 |
54.1 |
|
NOTES: Rates refer to the 5-year period following the year reported. South East and East Asia extends from Myanmar to Mongolia excluding Japan and Asiatic USSR. Southern and Western Asia extends from Bangladesh to Turkey. SOURCE: Schultz (1997:355). Reprinted with permission from Elsevier Science. |
|||
income countries as a group increased life expectancy by 58 percent. These relative increases translate into quite different absolute gains, from 10 years for the higher income countries to 20 and 25 years for the lower income countries. There is, however, only a weak relationship between reductions in infant mortality and reduced fertility. By this measure, Africa looks more like the high-income countries than other low-income countries. That is, in Africa fertility rates fell only 20 percent, about one-third the decline of infant mortality rates, while in the other regions the ratio of percent change of fertility rates to percent change in the infant mortality rate is closer to 2/3 to 3/4. Thus, as we know from other studies, the fertility transition in African countries is distinct.
Yet, it is still the case that fertility and infant mortality rates are linked. The relationship, as Mason (1997) notes, is that declines in infant mortal-
ity are necessary but not sufficient for fertility transitions. Indeed, the conceptual link between the two is at the very core of some theories of fertility transitions. To Notestein and other practitioners of classical demographic transition theory, modernization (development in modern parlance) and modern technology first decreased infant mortality rates, which as families realized that survivorship had improved, were translated into lower fertility rates. The direct causal link between mortality and fertility rates is based on the relative costs and benefits of children. Families are seen as caring about the surviving number of children. With lower infant mortality, fewer births are necessary to obtain the desired stock of surviving children. Moreover, modernization also is assumed to have shifted the relative costs of children; the net benefit of children declines through the increased housing prices in urban areas and restrictions on child labor reduce children’s productivity.
It is interesting to note that in her presidential address to the PAA, Mason lists six theories of fertility transitions, four of which are premised on the economic costs and benefits of children. Thus, although the exact mechanism characterizing the role of individual (household) incentives is often disputed, there is general agreement on the importance of these types of incentives. However, if households were responding solely to economic conditions, it is difficult to understand why fertility transitions have been initiated at such different levels of development. Similarly, it is difficult to see why later transitions have occurred at much lower development levels than observed in the case of Europe. Although we fully accept that economic conditions are important, they do not appear to be the only determinant of transitions.
Indeed, as Bongaarts and Watkins (1996) neatly summarize in their review of the literature and their findings from an analysis of 62 developing countries during the period from 1960 to 1990, there is a “highly significant” negative correlation between fertility (as measured by the total fertility rate) and development (as measured by the Human Development Index6). A central feature of this analysis is that there is no tight link between development and fertility:
The main implication of these findings, is that, as in Europe, at the onset of a fertility decline the level of development as measured by conventional socioeconomic indicators is highly variable and has very limited power to predict a country’s transition timing… There is apparently no fixed threshold of development for entry into the transition. In this respect, the contemporary record is a continuation of the historical one. (1996:647)
The weakness of this link is one factor that motivates our belief that social interactions may be an important component of a successful theory of demographic transition.
Bongaarts and Watkins (1996:651) also find that the relationship between fertility and development is both nonlinear and shifting over time, “[there] is a clear reduction over time in the level of development associated with transition onset. Transitions are observed first among the most developed countries within each macro-region, and later transitions are initiated at much lower development levels.”
Indeed, various nonlinearities are an important feature of the historical record of Europe. A primary finding of the European Fertility Project was a dynamic threshold effect in fertility decline; “once marital fertility had fallen by at least 10 percent—the decline is not reversed until marital fertility had fallen very far, by 50 percent or more” (Coale, 1986:21). Threshold effects (while not impossible) are difficult to generate from independent households. In contrast, this kind of threshold effect, that is, a situation where a change in a variable above or below some level produces a qualitative change in the properties of a system, is one which social interactions models commonly generate.
The simple tabulation of aggregate statistics considered so far misses the spatial dimension of fertility transitions. The beautiful maps at the back of the Coale and Watkins (1986) monograph document a number of interesting patterns of spatial diffusion of fertility control across modern Europe. Bongaarts and Watkins (1996) summarize the literature:
Examination of the historical evidence in Europe shows that regions (geographically proximate provinces with a common language and elements of a common culture) tend to experience fertility decline at more or less the same time, largely independently of the level of development … (1996:647)
The link with language and a common culture, noneconomic factors, again highlights the importance of noneconomic factors and particularly a role for social interactions. As our discussion will illustrate, social interactions models, through social multipliers and multiple equilibria, have the feature that small differences in the initial conditions between two populations can lead to very large differences between the populations’ respective behaviors. Our argument is that it is precisely these features that allow social interactions models to usefully complement monocausal explanations of fertility transition in a way to accommodate the heterogeneous experiences observed historically.
BASIC IDEAS
Before describing various formal models of social interactions, it is useful to define the basic notions of social interactions that underlie the algebra. Social interactions arise when actions by one or more individu-
als, which are not mediated through the market, affect the propensity of decisions made by another. Similar definitions of social interactions or diffusion in the context of fertility behavior have appeared in Montgomery and Casterline (1993), Chung (1994), and Bongaarts and Watkins (1996) among others.7 The distinction between market and nonmarket influences is important. Market influences operate only through the price system and affect the resources and opportunities available to households. Social exchanges that occur in markets have long been studied by economists. Indeed, until recently this was the only form of social interactions studied by neoclassical economists who adopted independent and atomistic households as its unit of analysis. Alternatively, sociologists have seen social groups as the basic unit of society and have an equally long history of considering a wider range of social interactions. Some of the mechanisms giving rise to social interactions considered by sociologists include sanctions, social learning, and conformity.
The key feature of the social interactions of interest is that they are endogenous: the choices made by one individual depend on actions taken by others. It is important to note that not all social effects are endogenous, though we wish to reserve the term social interactions for endogenous effects. Manski (1993) classifies three types of social effects. The first type is an endogenous social effect, which we have labeled as social interactions. The classic example of an endogenous effect is a pure contagion effect from epidemiology whereby the probability of infection increases with the proportion of the population infected (Feller, 1971). The second type of effect, contextual, occurs when an individual’s behavior is affected by exogenous characteristics of the group of which he is a member. So, the distribution of fertility choices within a community can affect the future behavior of children growing up there. Alternatively, contextual effects appear if fertility rates vary with the socioeconomic composition of the reference group. Finally, correlated effects occur when “individuals in the same group tend to behave similarly because they face similar institutional environments or have similar individual characteristics.” A correlated effect would be present if households within the same group face the same costs and benefits of childbearing and therefore have similar fertility profiles.
The following example illustrates some of the subtleties involved in distinguishing these different explanations of inter-group differences in behavior. Consider a family planning program that successfully reduces fertility for a given group. Whether there is a social interaction depends on the mechanism involved. If the program operated solely through the direct cost or benefits of children, (e.g., distributing free contraceptives) then according to Manski’s scheme there is a correlated effect but not a social interaction. However, if a woman’s use of the modern contracep-
tive devices depends on the prevalence of use by her neighbors or village members, then a social interaction exists. Several mechanisms could give rise to the social interaction. It could be that social learning occurs as women communicate their experiences to one another on the effectiveness of the new technology. As more women adopt the new technology, each succeeding woman faces less uncertainty on the technology thereby lowering the cost of adopting and increasing the adoption rate. Alternatively, greater use by community members signals its acceptance and the lowering of social sanctions against the new technology. These conjectures are of course not exhaustive as yet other mechanisms may occur.
The distinction between endogenous and exogenous forms of social effects is important. Why? The answer is embedded in the family planning example above. Social interactions generate social multipliers,8 which exogenous social effects do not. By social multipliers, we refer to the idea that the total change in individual incentives in a population leads, through interactions, to an effect in excess to that generated directly by the change in incentives. Stated differently, social multipliers exist when the cumulative social effect of an individual’s decision on a population’s behavior is larger than simply the direct effect of her choice. Consider the family planning example above. In the presence of social interactions, a woman’s decision to reduce her fertility will, through one of the mechanisms described above, increase the likelihood of reductions by others. The size of the spillover effect depends on the timing of the decision, decisions by individuals early in the process may have large social multipliers (e.g., the decision by leaders); in some cases, their actions can even generate a new equilibrium, in a sense we formalize below. To understand the dynamics of the system, we need to distinguish between endogenous and exogenous effects because their dynamic paths will be different.
The difference between endogenous and exogenous effects also is important for evaluating the effects of public policies. As may be obvious from the family planning example, a program that spawns social interactions will have very different consequences than does a program that changes only the exogenous determinants. The exact nature of the effect will depend on the nature of the social interaction, but the presence of social interactions dramatically changes the policy landscape.
Within demography, there has been criticism of the use of social diffusion models to explain fertility patterns (see the summary in Bongaarts and Watkins, 1996) on the grounds that the diffusion process is not simply a mechanical “carrier” as occurs in models of this type. However, this criticism does not apply to the social interactions approach. The behavior or factors giving rise to the social interaction is an integral part of the theory that makes it impossible to separate the diffusion process from its sources. To study the process is to study behavior. The old criticisms of
social diffusion processes do not apply to the economic models of social interactions.
To fix the basic ideas associated with social interactions models, we discuss two simple examples. Although the examples are extremely stylized, they are illustrative of issues that arise in observed behavior. We select these examples to capture the features of different equilibrium outcomes that arise when considering population issues.
Social Interactions as a Coordination Problem
For our first example, we make use of a standard example from noncooperative game theory.9 Consider a 2 by 2 game in which each player chooses between the action low and high, which we denote by 1 and 2 respectively. In the payoff matrix describing outcomes, the pair pi,j denotes the payoffs to players 1 and 2 when 1 chooses i and 2 chooses j. We focus on a particular payoff structure, which can be represented by a matrix whose elements (i, j) correspond to the pi, js we have defined.
(1)
To see how to read this matrix, consider the (1,2) element. This says that if player 1 chooses low and player 2 chooses high, each receives a payoff of zero. For concreteness, we can think of the possible actions as levels of effort in using contraception. This payoff structure reveals that if both players exert low contraceptive effort, then each receives a payoff (e.g., in “utils”) of 1. We can interpret the payoff as meaning that birth rates remain high and per-capita income low. If both exert a high effort (e.g., birth rates decline, per-capita income increases and welfare increases), then both players receive a payoff of 2.
Notice that the choice pairs high-high and low-low are both Nash equilibria, which means that at this pair of choices, neither player has an incentive to deviate from his respective choice. Therefore, when players act noncooperatively, they can each choose an individually rational strategy which leads everyone off track. That is to say, once individuals axe making low-low choices, they will continue to do so, unless there is some coordinating mechanism (e.g., a government intervention) that can induce individuals to change their behavior.
At the same time, the collectively efficient set of choices (in this case both players choosing high) is also sustainable as a Nash equilibrium. Therefore, the absence of any mechanism to coordinate individual decisions does not preclude the achievement of a first-best outcome. This
feature is different from a Prisoner’s Dilemma game. In that game, the payoff matrix has a form such as
(2)
Here, the choice of high by both agents is not a Nash equilibrium, since each person has an incentive to deviate and choose low given that the other agent chooses high.
Social Interactions as Complementarities
The basic ideas of our two-person game with multiple equilibria have been elaborated in an important paper by Cooper and John (1988). In this model, they consider how each of a group of I individuals chooses an effort level e, which is constrained to lie in the interval [0, ē]. Each of the individuals makes this choice so as to maximize a payoff function
ui=ϕi (e1,…,eI) (3)
What is important about this function is that the individual’s payoff depends not just on his own effort level, but on the effort levels of others. Cooper and John distinguish between two types of such dependence. First, there is the property of positive spillovers, which means that ∂ϕi/∂ϕj> 0 for; j≠i. The second is that of complementarities, which means that, ∂2ϕi/ ∂ei∂ej>0. Notice that positive spillovers is an assumption about payoff levels whereas complementarities is an assumption about marginal payoffs. Intuitively, complementarities are relevant for individual behavior in a noncooperative environment as an individual’s maximal payoff is implicitly characterized by a first-order condition (see equation 6).
Without loss of any important ideas, we assume that the payoff function for each individual is identical and that the payoff for each individual does not depend on the identities of the others, only the set of effort levels. This means that we can restrict ourselves to considering symmetric Nash equilibria, that is, equilibria where each person makes the same effort choice. Hence we can rewrite the payoff function for individual i as
ϕ(ei, ē–i) (4)
where ē–i denotes the average choice of everyone other than i in the population.
The first-order condition for payoff maximization by individual i is that
(5)
Given concavity, this will be sufficient as well. A symmetric Nash equilibrium will exist if there is an e*∈[0, ē] such that
(6)
There are two features of this model of interest to us. First, the Nash equilibrium can be inefficient. To see this, we can ask what common effort level would be agreed upon if individuals could coordinate their decisions. A common effort level e** will represent a symmetric cooperative equilibrium if
(7)
Since ∂ϕ(e*,e*)/∂ē–i>0 in the presence of positive spillovers, it must be the case that at the cooperative effort level, ∂ϕ(e**,e**)/∂ei. must be negative. Contrasting this with the first-order condition for a Nash equilibrium and recalling that ϕ is concave with respect to ei, we can conclude that e**>e* and everyone is worse off at a noncooperative equilibrium. Thus, as one expects in a model with externalities, there is a gap between the private and social benefits of individual behavior.
Second, there is a relationship between complementarities and the number of Nash or noncooperative equilibria. To see this, notice that from the perspective of an individual, there is an optimal response function of the form ei=r(ē–i) that describes his optimal-effort level given the average-effort level of others. If one were to graph the function r in (ei, ē–j) space, then it is clear that the intersection of this function in (ē, ei) space with the 45° line will define a Nash equilibrium. Equally clearly, multiple intersections, and multiple Nash equilibria, can only occur if the function is upward sloping somewhere.
We can compute the slope of this function as follows. Rewrite the noncooperative first-order condition (6) as
(8)
and differentiate with respect to ē–i. This yields
(9)
which implies that
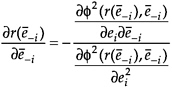
Because ![]() the right-hand side of this equation implies that the function r (·) can be upward sloping over some region of ē–i values if and only if the model exhibits strategic complementarities, as we have assumed the denominator is negative. This condition is of course necessary rather than sufficient for multiple equilibria to actually exist.
the right-hand side of this equation implies that the function r (·) can be upward sloping over some region of ē–i values if and only if the model exhibits strategic complementarities, as we have assumed the denominator is negative. This condition is of course necessary rather than sufficient for multiple equilibria to actually exist.
Both this and the two-player game example illustrate key ideas in the social interactions literature. The first idea is that there is a deep relationship between multiple equilibria and the condition that the optimal decision of one agent is increasing in the choice levels of others. The potential for multiple equilibria gives scope for social norms to combine with individual incentives to determine aggregate population behavior, in the sense that these norms can act to coordinate behavior on one of the possible equilibria. The second idea is that there may be some sort of social welfare ranking between equilibria. This is important in considering policies which are designed to alter which equilibria characterizes a population, as it facilitates resolving the difficult issue of adjudicating benefits and losses.
In the presence of multiple equilibria, which one is selected? Dasgupta (1993, 1995) argues that selection occurs through one of two basic sources, either through the expectations that individuals have of one another or through history (i.e., evolutionary selection). Under the expectations mechanism, each equilibrium is self-consistent in that the beliefs of each actor are validated by actual behavior. Perhaps it is not surprising that the empirical evidence on fertility control suggests that the perception of others’ behavior is more important than the actual behavior of others (Chung, 1994).
DISCRETE CHOICE WITH SOCIAL INTERACTIONS
This section develops a model of choice, which captures the basic intuitions of the simpler models of the previous section, and simultaneously seems appropriate for considering demographic issues. In our analysis, we follow a framework for studying social interactions, which is developed in Brock and Durlauf (1999a). This particular version of social interactions models has the advantage that the equilibria are in a form
that corresponds to the various logistic likelihood functions, which are standard in discrete choice analysis. In fact, when social interactions do not exist, the equilibria and the standard likelihood functions are identical. Therefore, the econometric formulation of these types of social interactions can draw on a substantial existing literature. In addition, Durlauf (1997) shows how many social interactions models can be placed in our discrete choice framework without any reduction of the economic logic driving their main features, so we believe this analysis can be generalized to have wide application in demography.
As we have noted, one of the most important features of social interactions models is their capacity to generate multiple steady states and this feature will reappear in our stochastic model. In this case, multiplicity occurs because the probability that one person makes a choice is an increasing function of whether members of his reference group make the same choice. Mathematically, this multiplicity occurs because the models are nonergodic, so that the conditional probability measures describing individual decisions conditional on their information sets do not generate a unique joint probability measure over all choices. One difficulty in identifying nonergodicity in a data set is that there may be types of behavior that are consistent with the decisions of agents (or the conditional probability measures describing the decisions), yet are never observed in the history of the process. It is for this reason that some types of nonergodicity are not identifiable. However, our estimation strategy allows us to identify those parameters of individual decisions that are consistent with multiple equilibria and thereby infer their presence or absence. Specifically, the use of individual-level data allows one to identify the sensitivity of individual choices to aggregate behavior, from which one can calculate the number of equilibria for the population.
We consider a population of I individuals, indexed by i who each make a binary choice wi whose support is {–1,1}. In its most general form, this choice is the solution to maximizing a payoff function V(.,.,.,.)
(10)
In this payoff function, Z̰i denotes a vector of individual specific characteristics which are known to the modeller. The variable ![]() is agent i’s expectation of the value of the average choice of the population. Thus we modify the interactions studied in the previous section in that social interactions in this model are mediated by the beliefs individuals have about one another’s choices. This assumption seems intuitively appealing when groups are large, such as those defined by ethnicity, gender, or age, so that the total behavior of one’s reference group is not directly observable. (It also is of great mathematical convenience.) Finally, εi(ωi)
is agent i’s expectation of the value of the average choice of the population. Thus we modify the interactions studied in the previous section in that social interactions in this model are mediated by the beliefs individuals have about one another’s choices. This assumption seems intuitively appealing when groups are large, such as those defined by ethnicity, gender, or age, so that the total behavior of one’s reference group is not directly observable. (It also is of great mathematical convenience.) Finally, εi(ωi)
denotes payoff shocks, which are observable to agent i but are unknown to the modeler. As is standard, we assume that εi(1) and εi(–1) are distinct shocks. We will further assume that these innovations are independent across individuals.
To render the model amenable to formal analysis, a number of assumptions are placed on the structure of the payoff function. First, the payoff function is assumed to possess the linear structure
(11)
This formulation allows us to refer to u(ωi, Z̰i) as deterministic private utility, ![]() as deterministic social utility and εi(ωi) as random private utility. Notice that if J=0, V reduces to a standard discrete choice payoff function (compare Anderson, dePalma, and Thisse, 1992). This feature means that our social interactions model nests the standard model of choice as a special case, and so the logic of the analysis in no way deviates from standard economic reasoning.
as deterministic social utility and εi(ωi) as random private utility. Notice that if J=0, V reduces to a standard discrete choice payoff function (compare Anderson, dePalma, and Thisse, 1992). This feature means that our social interactions model nests the standard model of choice as a special case, and so the logic of the analysis in no way deviates from standard economic reasoning.
Second, we assume that the random private utility terms are extreme-value distributed, so that their difference has the standard logistic distribution.
(12)
To solve the equilibrium mean-choice level of the model, we proceed as follows. The probability of a particular choice, given an individual’s observable characteristics and beliefs, equals the probability that his payoff given the choice exceeds the payoff given the other choice,
(13)
Equations (13) and (12) together imply that
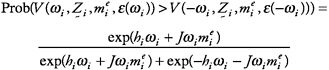
(14)
where ![]() Observe that hi measures the difference
Observe that hi measures the difference
in private deterministic utility between the two choices and is the only aspect of that utility term that is relevant to the decision problems. Each choice is of course Bernoulli distributed, (14) gives the probability in terms of the relevant structural parameters of the model, the hi’s and J.
A rational expectations solution to the model corresponds to any m* which solves
(15)
where dFh denotes the empirical probability measure of h’s within the population.10
The uniqueness or multiplicity of equilibrium average choice levels will depend upon dFh. In the special case where hi=h∀i, it is possible to explicitly characterize the relationship between the structural parameters of the model, since the expected choice level is any solution to
m*=tanh(h+Jm*). (16)
Brock and Durlauf (1999b) verify the following theorem.
Proposition 1. (Brock and Durlauf, 1999b). Existence of multiple average-choice levels in equilibrium
-
If J>1 and h=0, there exist three roots to equation (16). One of these roots is positive, one root is zero, and one root is negative.
-
If J>1 and h=0, there exists a threshold H (which depends on J), such that
-
for |h|<H, there exist three roots to equation (16), one of which has the same sign as h, and the others possessing opposite sign.
-
for |h|>H, there exists a unique root to equation (16) with the same sign as h.
-
Intuitively, this theorem says the following. If the strength of social interactions, as measured by J is below 1, these interactions will be too weak to generate multiple equilibria. If the strength is such that J>1, then the presence or absence of multiplicity will depend on the private incentives for one choice or another as measured by h. If these private incentives are strong enough, as measured by the magnitude of h, they will swamp the interactions effect and produce one equilibria. Observe that this theorem provides an example of threshold effects in group behavior. Small changes in private incentives, h, can alter the qualitative features of group behavior in the sense of altering the number of equilibrium expected average choice levels. By implication, in a dynamic model where h evolves, it is possible to generate a highly nonlinear path for the expected average choice.
Issues in Empirical Implementation
Estimating models with social interactions poses new challenges, challenges that for the most part are only beginning to be understood. This section highlights a few of the problems and offers some observations. The basic theme of this section is that models with social interactions require a tight integration of theory and application; in turn, empirical specifications motivated by loose appeals to theory will be largely uninformative.
We start our discussion of empirical implementation of social interactions models by considering the conditions under which the binary choice model of the previous section is identified. Therefore, we assume that the model is a correct specification of the structural determinants of individual and group behavior and consider whether the model parameters can be recovered from behavioral data. To do this, we take our original Z̰i vector and split it into an r-length vector of individual-specific observables X̰i and an s-length vector of exogenously determined neighborhood observables Y̰n(i) associated with each individual in the sample. The subscript n(i) maps individuals into groups, so two people in the same group n must have the same Y̰n(i). Relative to the Manski classification we described in Section 2, the Y̰n(i) variables are contextual effects. Finally, we assume the errors εi(ωi) are independent of the regressors.
For identification, we consider the likelihood function implied by the model, that is,
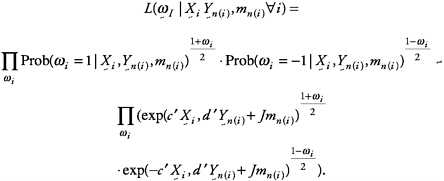
(17)
We take the expectation mn(i) as observable without loss of generality; Brock and Durlauf (1999b) discuss ways to construct instruments for this variable.
Identification of the baseline model therefore is a specific case of the general (and well studied) question of the identifiability of logistic likeli-
hood coefficients for the regressor set (X̰i, Y̰n(i), mn(i)). Following the treatment in Manski (1988:730), the necessary and sufficient condition for identification in a logit model such as this one is that the covariance matrix of these regressors is nonsingular. To discuss this, we need some additional notation. For any r length vector A̰ and s-length vector B̰, let V(A̰, B̰) denote the variance-covariance matrix of the random variables {a1,…,ar, b1,…,bs}. Finally, let ρ(V(A̰, B̰)) denote the rank of V(A̰, B̰). Thus, identification will require that ρ(V(X̰i, Y̰n(i),mn(i)))r+s+1
To see what is necessary to produce identification in the binary-choice model, notice that there is a functional relationship between the distribution of the X̰i’s, Y̰n(i) and mn(i) for each neighborhood, the form of which is determined by the theoretical model. At first glance, one might think that this means the model is not identified. However, notice as well that this relationship is nonlinear, since by our theoretical model
(18)
where FX is the within-neighborhood n(i) distribution of X̰i ’s. Nonidentification would require special restrictions on the cross-neighborhood distribution of the X̰i’s and Y̰n(i)’s to reduce the dimensionality of H(X̰i, Y̰n(i), mn(i)) below r+s+1. Stated differently, so long as X̰i and Y̰n(i) possess a joint variance covariance matrix of full rank, the addition of the regressor mn(i) cannot affect nonsingularity except for pathological cases. Therefore, we can state the following theorem.
Theorem. Identification in the binary-choice model with interactions (Brock and Durlauf, 1999a, b)
In the logistic binary-choice model with interactions, if ρ(V(X̰i, Y̰n(i)))= r+s, then the model’s parameters are identified.
Taking this model as a baseline, one can isolate several key features that are essential in empirical work. First, nonlinearity plays a key role. Manski’s (1993) nonidentification results for social interaction models were obtained in the context of a linear model; as shown by Brock and Durlauf (1999a,b), nonidentification in the context can be overcome through a certain exclusion restriction concerning the X̰i and Y̰n(i) variables, which is not necessary for the binary-choice case.
Second, it is necessary that with respect to the individual-level determinants of behavior, X̰i, neighborhoods are not perfectly segregated. To see this, notice that a violation of the rank condition means that there is a
combination of individual characteristics which is perfectly collinear with some linear combination of group characteristics, that is,
(19)
One can interpret the left-hand side of this equation as a composite individual characteristic and the right-hand side as a composite neighborhood characteristic. Therefore, a violation of the rank condition would require that there is a composite individual characteristic that perfectly predicts a composite neighborhood characteristic. This is equivalent to saying that with respect to that composite individual characteristic, there is perfect segregation of neighborhoods. Partial segregation will affect standard errors, but not identification per se.
Alternatively, the assumption that the errors Ei(ωi)’s are independent of the regressors is not critical per se, in the sense that one can relax it to something, such as independence of the median from the regressors in order for identification to hold (Manski, 1985; Horowitz, 1998).
Turning from identification to specification, what is critical in empirical analysis of interactions is that the errors are uncorrelated with the regressors. A violation of this condition is a form of misspecification. This will only be plausible if one is confident that the individual and contextual regressor sets are rich enough to incorporate the full range of factors that determine individual behavior within the group.
At first glance, this would appear to be a standard problem with any statistical analysis, in that the omission of relevant variables will render estimates of a structural model inconsistent. However, it is particularly salient for interactions models when groups are endogenously formed. Because the factors that cause individuals to form a common group are plausibly correlated across the individuals and with the errors in the behavioral equation that describes what they will do once they are in the group. Although Brock and Durlauf (1999a) suggest ways of dealing with this problem, it is clear that empirical analysis of interactions will require careful specification of the determination of the sources of individual behavior as well as an understanding of the process of group formation to provide compelling empirical support for interactions. This in turn will, we believe, require attention to ethnographic and historical studies.
CONCLUSIONS
The “new economic demography” initiated by Gary Becker in 1960 focused on the choices of individual households. Much of our understanding of the determinants of the costs and benefits for childbearing
and the tradeoffs that households face by having and raising children stem from this literature. It is a literature that focuses on individual decision making at the household level. Less is known about the aggregate consequences of these individual decisions. Indeed, in a real sense, until Boserup, economists had to look back to Malthus for a model of endogenous population and economic growth. Interest in the environment and an increasing recognition of the finiteness of the world’s natural resources stimulated public debate on population growth. Spawned from this debate was an appreciation of the negative externalities generated by excessive population growth and the insight that understanding the determinants of individual decision making is not enough. As Paul Demeny stated in his 1986 presidential address to the PAA, “We must bear in mind that the workings of the invisible hand are not necessarily always for the better, not necessarily for improvement” (1986:477). In the presence of externalities, there can be substantial divergence between the individual’s welfare and that of the society. To evaluate the consequences of population growth requires consideration of the whole not solely the individual.
The emerging literature on the economics of social interactions identifies other aggregate mechanisms that complement the negative externalities noted by Demeny. Unlike the literature on the population problem, the new models in economics concentrate on positive feedback mechanisms, including coordination failure, social learning, and social preferences. However, a commonality between these literatures is that both develop frameworks that generate multiple equilibria. The multiplicity of equilibria is central because it permits the same analytical framework to represent both the pre-and post-transition equilibria and thus provides a causal interpretation for a transition. An important implication of the new economic models on social interactions is that (in the presence of social interactions) small changes in individual behavior can have large changes on the observed equilibrium outcome. Behavior by interacting agents can reinforce one another that may serve to destabilize the system. Thresholds and rapid social change are common occurrences in these models as social processes may appear to “jump” from one equilibrium to another.
And yet, social interactions by themselves are not enough. A compelling causal interpretation requires some exogenous forcing variable or variables to generate change. Our perspective is that the economic conditions drive the process, which are then amplified by social interactions. Applied to fertility transitions, the insight of the social multiplier is that economic conditions need only change enough to get a few “leaders” to switch behavior. Then once in play, endogenous exchanges among agents (i.e., social interactions) ultimately drive the fertility transition. The context, characterized by the level and relative importance of economic and
cultural factors, will vary from society to society (and across time) so there is no reason why a common level of economic development will initiate a fertility transition. Some cultures may possess strong proscriptions against fertility control or the economic benefit of children may be so large to mandate high levels of economic development to induce even a few individuals to change their behavior. The interplay between economic conditions and social interactions is important, if not obvious. In isolation of one another the empirical literature reveals that economic and cultural factors are unable to explain fertility transitions. However, when combined and employed in a structured way, economic determinants and social interactions offer a rich set of mechanisms by which to explain the process of fertility transitions. The daunting task for researchers is to harness the theoretical insights from these models and implement empirical representations that will help us understand sometimes elusive and always complex fertility behavior.
NOTES
|
1. |
Important precursors to this new literature include Schelling (1971) on the emergence of racial segregation and Föllmer (1974) and Pollak (1976) on interdependent preferences; Brock and Durlauf (1999b) provide an extensive survey of the recent research in this broad area. |
|
2. |
As will become apparent, the statistical concerns that have arisen in the economics literature on interactions are quite different from those that have arisen in other social sciences. In particular, hierarchical linear models, which have become a standard approach to modeling interactions in sociology, education, and demography, have had no impact as far as we know on economics. Our guess is that this has occurred because of the interest economists have in structural modeling, which makes the random coefficient assumption, and is the hallmark of linear hierarchical models, relatively unnatural. See Bryk and Raudenbusch (1992) for an excellent discussion of the statistical issues that have arisen outside of economics. |
|
3. |
For example, Coale (1986) (Introduction) and Watkins (1986) (Conclusion) summarize the findings of the European Fertility Project. Bongaarts and Watkins (1996) summarize the experience of currently developing countries. Schultz (1997) and Kohler (1997) take a longer view and attempt to synthesize the literature. Each summary also includes a particular interpretation of the processes generating the observed patterns. As Bongaarts and Watkins (1996) note, it is the interpretation of the observed patterns, not the facts that are in dispute. |
|
4. |
As clearly described by Coale (1986), European societies moved from one locally stable (in time) equilibrium of moderate fertility and moderate mortality to another characterized by low fertility and low mortality. Pretransition fertility rates were maintained through changes in marriage rates and not primarily by changes in marital fertility per se. |
|
5. |
Indeed, the rates reported in Table 4–1 suggest that death rates are forecasted to be higher among high-income than low-income countries. This may reflect substantive differences in the mortality experiences between high- and low-income countries. More likely, the discrepancy reflects differences in the age composition of the two populations—the percentage of the aged in the populations of high-income countries is higher than that of other countries. |
|
6. |
The Human Development Index was proposed by UNDP (1990). The index is a linear combination of life expectancy, literacy, and real per capita Gross Domestic Product. |
REFERENCES
Anderson, S., A.de Palma, and J.F.Thisse 1992 Discrete Choice Theory of Product Differentiation. Cambridge: MIT Press.
Bongaarts, J., and S.Watkins 1996 Social interactions and contemporary fertility transitions. Population and Development Review 22:639–682.
Brock, W., and S.Durlauf 1999a Discrete Choice with Social Interactions. Unpublished internal document, University of Wisconsin at Madison.
1999b Interactions-based models. In Handbook of Econometrics, Volume 5, J.Heckman and E.Learner, eds. Amsterdam: North-Holland.
Bryk, A., and S.Raudenbusch 1992 Hierarchical Linear Models. Newbury Park: Sage Publications.
Chung, W. 1994 Effects of Social Leadership on the Diffusion of Fertility Control: An Analysis of Social Network Data. Working Paper no. 94–03, University of North Carolina at Chapel Hill.
Coale, A. 1986 The decline of fertility in Europe since the eighteenth century as a chapter in demographic history. In The Decline of Fertility in Europe. A.Coale and S.Watkins, eds. Princeton: Princeton University Press.
Coale, A., and S.Watkins, eds. 1986 The Decline of Fertility in Europe. Princeton: Princeton University Press.
Cooper, R., and A.John 1988 Coordinating coordination failures in Keynesian models. Quarterly Journal of Economics CIII:441–464.
Dasgupta, P. 1993 An Inquiry into Well-Being and Destitution. Oxford: Clarendon Press.
1995 The population problem: Theory and evidence. Journal of Economic Literature 33: 1879–1902.
Demeny, P. 1986 Population and the invisible hand. Demography 23:473–487.
Durlauf, S. 1997 Statistical mechanics approaches to socioeconomic behavior. In The Economy as an Evolving Complex System II. W.B.Arthur, S.Durlauf, and D.Lane, eds. Menlo Park, CA: Addison-Wesley.
Entwisle, B., J.Casterline, and H.Sayed 1989 Villages as contexts for contraceptive behavior in rural Egypt. American Sociological Review 54:1019–1034.
Entwisle, B.J., and W.Mason 1985 Multilevel effects of socioeconomic development and family planning programs on children ever born. American Journal of Sociology 91:3, 616–649.
Entwisle, B.J., W.Mason, and A.Hermalin 1986 The multilevel dependence of contraceptive use on socioeconomic development and family planning program strength. Demography 23:2, 199–216.
Feller, W. 1971 An Introduction to Probability Theory and Its Applications, Volume I. New York: John Wiley.
Föllmer H. 1974 Random economies with many interacting agents. Journal of Mathematical Economics 1:51–62.
Horowitz, J. 1998 Semiparametric Methods in Econometrics. New York: Springer-Verlag.
Kohler, H.P. 1997 Fertility and Social Interaction: An Economic Approach. Unpublished P.h.D dissertation, University of California at Berkeley.
Manski, C. 1988 Identification of binary response models. Journal of the American Statistical Association 83:729–738.
1993 Identification of endogenous social effects: The reflection problem. Review of Economic Studies 60:531–542.
Mason, K. 1997 Explaining fertility transitions. Demography 34:443–454.
Montgomery, M., and J.Casterline 1993 The diffusion of fertility control in Taiwan: Evidence from pooled cross-section time-series models. Population Studies 47:457–479.
Pollak, R. 1976 Interdependent preferences. American Economic Review 66:309–320.
Pollak, R., and S.Watkins 1993 Cultural and economic approaches to fertility: Proper marriage or Mésalliance? Population and Development Review 19:3, 467–496.
Schelling, T. 1971 Dynamic models of segregation. Journal of Mathematical Sociology 1:143–186.
Schultz, T.P. 1997 Demand for children in low-income countries. In Handbook of Population Economics, Volume 1A, M.Rosenzweig and O.Stark, eds. New York: North-Holland. United Nations Development Programme (UNDP) 1990 Human Development Report. New York: Oxford University Press.
Watkins, S. 1986 Conclusions. In The Decline of Fertility in Europe, A.Coale and S.Watkins, eds. Princeton: Princeton University Press.























