5
Appropriating the Commons: A Theoretical Explanation
Armin Falk, Ernst Fehr, and Urs Fischbacher
In his classic account of social dilemma situations, Hardin (1968) develops his pessimistic view of the “tragedy of the commons.” Given the incentive structure of social dilemmas, he predicts inefficient excess appropriation of common-pool resources. Hardin’s view has been challenged by the insights of numerous field studies reported in the seminal book by Ostrom (1990). In this book the metaphor of a tragedy is replaced by the emphasis that people are able to govern the commons. Ostrom shows that in many situations people are able to cooperate and improve their joint outcomes. Moreover, the reported field studies point to the importance of behavioral factors, institutions, and motivations. However, although it has been shown that these factors collectively influence behavior, it is of course nearly impossible to isolate the impact of individual factors.
This is why we need controlled laboratory experiments: Only in an experiment is it possible to study the role of each factor in isolation. In carefully varying the institutional environment, the experimenter is able to disentangle the importance of different institutions and motivations. The regularities discovered in the lab then can be used to better understand the behavior in the field. In this paper we concentrate on three such empirical regularities, which are reported in Walker et al., (1990), and Ostrom et al. (1992).1 They first study a baseline situation that captures the central feature of all common-pool resource problems: Because of negative externalities, individually rational decisions and socially optimal outcomes do not coincide. In a next step, the baseline treatment is enriched with two institutional features, the possibility of informal sanctions and the possibility to communicate. The empirical findings can be summarized as follows: In the baseline common-pool resource experiment, aggregate behavior is best described by the Nash equilibrium of selfish money maximizers. People excessively appro-
priate the common-pool resource and thereby give rise to the “tragedy” predicted by Hardin (1968). Giving subjects the possibility to sanction each other, however, strongly improves the prospects for cooperative behavior. The reason is that many people sanction defectors. This is surprising because sanctioning is costly and therefore not consistent with the assumptions that provide the basis for Hardin’s pessimistic view, that is, that subjects are selfish and rational. A similar observation holds for the communication environment. Allowing for communication also increases cooperative behavior. The resulting efficiency improvement is again inconsistent with the behavioral assumptions underlying Hardin’s analysis because communication does not alter the material incentives.
Taken together, therefore, we have the following puzzle: In a sparse institutional environment, people tend to overharvest common-pool resources. In this sense the pessimistic predictions by Gordon (1954) and Hardin (1968), which are based on the assumptions of selfish preferences, are supported. At the same time, however, we find the efficiency-enhancing effect of informal sanctions and communication. This is in clear contradiction to the standard rational choice view, because why should a rational and selfish individual sacrifice money in order to sanction the behavior of another subject? And why should a money-maximizing subject reduce his or her appropriation level following some cheap talk? The question is more general: Why is the rational choice conception correct in one setting and wrong in another?
In this paper we suggest an integrated theoretical framework that is capable of explaining this puzzle. We argue that the reported regularities are compatible with a model of human behavior that extends the standard rational choice approach and incorporates preferences for reciprocity and equity. The basic behavioral principle that is formalized in our model is that a substantial fraction of the subjects act conditionally on what other subjects do. If others are nice or cooperative, they act cooperatively as well, but if others are hostile, they retaliate.2 Our model also accounts for the fact that there are selfish subjects who behave in the way predicted by standard rational choice theory. We formally show that the interaction of these two diverse motivations (reciprocity and selfishness) and the institutional setup is responsible for the observed experimental outcomes. In the absence of an institution that externally enforces efficient appropriation levels, the selfish players are pivotal for the aggregate outcome. However, if there is an institutional setup that enables people to impose informal sanctions or allows for communication, the reciprocal subjects discipline selfish players and thus shape the aggregate outcome. Moreover, our model shows that when the members of a group have a preference for reciprocity or equity, the common-pool resource problem is transformed into a coordination game with efficient and inefficient equilibria. If subjects are given the opportunity to communicate, they can, therefore, ensure that the equilibrium with the efficient appropriation level is reached.
In the presence of a preference for reciprocity and equity, communication is a coordination device that helps subjects to coordinate their behavior on the low—
appropriation equilibrium. Thus, if the institutional setup allows for sanctions or for communication, there is less appropriation in common-pool resource problems and higher voluntary contributions in public goods situations. Even though it is our main purpose in this chapter to show that the approach is able to account for the seemingly contradictory evidence of common-pool resource experiments, we believe the developed arguments are very general and likely to extend beyond the lab.
In the next section, we briefly outline the basic structure of our approach and recently developed fairness models. Then we apply our model to the standard common-pool resource game and discuss the theoretical predictions in light of empirical findings. We also provide propositions for a common-pool resource game with sanctioning opportunities as well as a discussion on the role of communication in the presence of reciprocal preferences. The subsequent section contains a comparison of common-pool resource results to those arrived in public goods games. The final section provides the conclusion.
THEORETICAL MODELS OF RECIPROCITY AND FAIRNESS
A large body of evidence indicates that fairness and reciprocity are powerful determinants of human behavior (for an overview, see e.g., Fehr and Gächter, 2000b). As a response to this evidence, various theories of reciprocity and fairness have been developed (Rabin, 1993; Levine, 1998; Bolton and Ockenfels, 2000; Fehr and Schmidt, 1999; Falk and Fischbacher, 1999; Dufwenberg and Kirchsteiger, 1998; Charness and Rabin, 2000). These models assume that—in addition to their material self-interest—people also have a concern for fair outcomes or fair treatments. The impressive feature of several of these models is that they are capable of correctly predicting experimental outcomes in a wide variety of experimental games. Common to all of these models is the premise that the players’ utility depends not only on their own payoff but also on the payoff(s) of the other player(s). This assumption stands in sharp contrast to the standard economic model according to which subjects’ utility is based solely on their own absolute payoff.
Some of the models mentioned are based on the notion that people care for fair outcomes (Bolton and Ockenfels, 2000; Fehr and Schmidt, 1999). Other models are based on the assumption that people evaluate the fairness of others’ action in terms of the kindness of the intentions that triggered the action (Rabin, 1993; Dufwenberg and Kirchsteiger, 1999). Intention-based fairness models capture an important aspect of what has been called procedural fairness by some authors (e.g., Lind and Tyler, 1988). A third class of models combines outcome-based and intention-based notions of fairness (Falk and Fischbacher, 1998; Charness and Rabin, 2000). The experimental evidence (see, e.g., Blount, 1995; Falk et al., 2000a) indicates that subjects do not only sanction because they want to achieve fair outcomes but that the motive to punish unfair intentions is also a major deter-
minant of sanctioning behavior. Therefore, approaches that rely on distributional concerns and on rewarding and sanctioning of intentions (as, e.g., in Falk and Fischbacher, 1998) best capture the experimental regularities.
All mentioned fairness theories are rational choice theories in the sense that they allow for interdependent preferences but assume rational individuals. This assumption may be criticized because often people act not fully rational but boundedly rational (e.g., Selten, 1998; Dietz and Stern, 1995). Although we are generally sympathetic with this view, we would like to point out that so far there is no formal model of bounded rationality that is able to predict the experimental results presented in this chapter in a rigorous way.
In the games analyzed in this chapter, the Falk and Fischbacher model and the Fehr and Schmidt model yield similar predictions. We therefore restrict our attention to the latter model because it is relatively easy to apply in our context. The Bolton and Ockenfels model also yields similar predictions in the baseline common-pool resource environment, but predicts a wrong punishment pattern in the common-pool resource game with punishment opportunities. The reason is that in their model, each player does not evaluate fairness toward each other player (as in the Falk and Fischbacher and the Fehr and Schmidt models), but rather toward the group average. This basically means that people are indifferent between punishing defectors or punishing cooperators, a prediction that is at odds with the experimental data. Finally, the Dufwenberg and Kirchsteiger model and the Charness and Rabin model are extremely complicated and often do not generate precise predictions. Both models often predict many equilibria. Finally, we do not apply altruism models (see, e.g., Palfrey and Prisbrey, 1997) because these models are not compatible with sanctions, nor with the fact that people cooperate conditionally.
In the Fehr and Schmidt model, fairness is modeled as “inequity aversion.” An individual is inequity averse if he or she dislikes outcomes that are perceived as inequitable. This definition raises, of course, the difficult question of how individuals measure or perceive the fairness of outcomes. Fairness judgments inevitably are based on a kind of neutral reference outcome. The reference outcome that is used to evaluate a given situation is itself the product of complicated social comparison processes. In social psychology (Adams, 1963; Festinger, 1954; Homans, 1961) and sociology (Davis, 1959; Pollis, 1968; Runciman, 1966), the relevance of social comparison processes has been emphasized for a long time. One key insight of this literature is that relative material payoffs affect people’s well-being and behavior. As we will see, without the assumption that relative payoffs matter at least to some people, it is difficult, if not impossible, to make sense of the empirical regularities observed in common-pool resource experiments. There is, moreover, direct empirical evidence suggesting the importance of relative payoffs. The results in Agell and Lundborg (1995) and Bewley (1998), for example, indicate that relative payoff considerations constitute an important constraint for the internal wage structure of firms. In addition, Clark and Oswald
(1996) show that comparison incomes have a significant impact on overall job satisfaction. Strong evidence for the importance of relative payoffs also is provided by Loewenstein et al. (1989). These authors asked subjects to ordinally rank outcomes that differ in the distribution of payoffs between the subject and a comparison person. On the basis of these ordinal rankings, the authors estimate how relative material payoffs enter the person’s utility function. The results show that subjects exhibit a strong and robust aversion against disadvantageous inequality: For a given own income xi subjects rank outcomes in which a comparison person earns more than xi substantially lower than an outcome with equal material payoffs. Many subjects also exhibit an aversion against advantageous inequality, although this effect seems to be significantly weaker than the aversion against disadvantageous inequality.
The determination of the relevant reference group and the relevant reference outcome for a given class of individuals ultimately is an empirical question. The social context, the saliency of particular agents, and the social proximity among individuals are all likely to influence reference groups and outcomes.3 Because in the following discussion we restrict attention to individual behavior in economic experiments, we have to make assumptions about reference groups and outcomes that are likely to prevail in this context. In the laboratory it is usually much simpler to define what is perceived as an equitable allocation by the subjects. The subjects enter the laboratory as equals, they don’t know anything about each other, and they are allocated to different roles in the experiment at random. Thus, it is natural to assume that the reference group is simply the set of subjects playing against each other and that the reference point, that is, the equitable outcome, is given by the egalitarian outcome.
So far we have stressed the importance of the concern for relative payoffs. This does not mean, however, that the absolute payoff should be viewed as a quantité negliable. Moreover, we do not claim that all people share a (similar) concern for an equitable share. In fact, many experiments have demonstrated the heterogeneity of subjects and the importance of absolute payoffs. A discussion on the heterogeneity of individual preferences is given, for example, in Parks (1994), Van Lange et al. (1997), and Kopelman et al. (this volume:Chapter 4). In this literature different types are discussed, such as cooperators, individualists, and competitors. In a similar vein, we assume that there are selfish people who care only for their material payoff and fair-minded people who reward fair and punish unfair behavior. As we will see, the interaction between these two types explains much of the observed data.
To be precise, in the Fehr and Schmidt model it is assumed that in addition to purely selfish subjects, there are subjects who dislike inequitable outcomes. They experience inequity if they are worse off in material terms than the other players in the experiment and they also feel inequity if they are better off. Moreover, it is assumed that, in general, subjects suffer more from inequity that is to their material disadvantage than from inequity that is to their material advantage. Formally,
consider a set of n players indexed by i ![]() {1,…, n} and let π = (π1,…,πn) denote the vector of monetary payoffs. The utility function of player i is given by
{1,…, n} and let π = (π1,…,πn) denote the vector of monetary payoffs. The utility function of player i is given by
(5-1)
where αi ≥ βi ≥ 0 and βi < 1.
The first term in Equation 5-1, πi, is the material payoff of player i. The second term in Equation 5-1 measures the utility loss from disadvantageous inequality, and the third term measures the loss from advantageous inequality. Figure 5-1 illustrates the utility of player i as a function of xj for a given income xi. Given his own monetary payoff xi, player i’s utility function obtains a maximum at xj = xi. The utility loss from disadvantageous inequality (xj > xi) is larger than the utility loss if player i is better off than player j (xj < xi).
To evaluate the implications of this utility function, let us start with the two player case. For simplicity the model assumes that the utility function is linear in inequality aversion as well as in xi. Furthermore, the assumption αi ≥ βi captures the idea that a player suffers more from inequality that is to his disadvantage. The paper mentioned by Loewenstein et al. (1989) provides strong evidence that this assumption is, in general, valid. Note that αi ≥ βi essentially means that a subject is loss averse in social comparisons: Negative deviations from the reference outcome count more than positive deviations. The model also assumes that 0 ≤
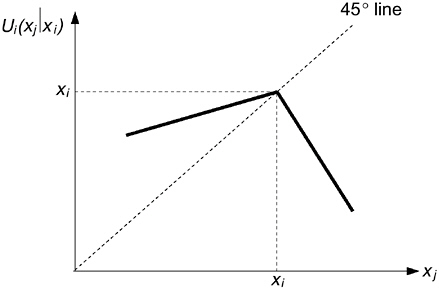
FIGURE 5-1 Preferences of inequity aversion.
βi < 1. βi ≥ 0 means that the model rules out the existence of subjects who like to be better off than others. To interpret the restriction βi < 1, suppose that player i has a higher monetary payoff than player j. In this case βi = 0.5 implies that player i is just indifferent between keeping $1 to himself and giving this dollar to player j. If β = 1, then player i is prepared to throw away $1 in order to reduce his advantage relative to player j which seems very implausible. This is why we do not consider the case βi ≥ 1. On the other hand, there is no justification to put an upper bound on αi. To see this, suppose that player i has a lower monetary payoff than player j. In this case player i is prepared to give up $1 of his own monetary payoff if this reduces the payoff of his opponent by (1 + αi) / α i dollars. For example, if αi = 4, then player i is willing to give up $1 if this reduces the payoff of his opponent by $1.25.
If there are n > 2 players, player i compares his income to all other n – 1 players. In this case the disutility from inequality has been normalized by dividing the second and third term by n – 1. This normalization is necessary to make sure that the relative impact of inequality aversion on player i’s total payoff is independent of the number of players. Furthermore, we assume for simplicity that the disutility from inequality is self-centered in the sense that player i compares himself to each of the other players, but does not care per se about inequalities within the group of his opponents.
THEORETICAL PREDICTIONS
In the following text we discuss the impact of inequity aversion in typical common-pool resource games. The first game we analyze is a standard common-pool resource game without communication and sanctioning opportunities. We proceed by analyzing games that add the possibilities of costly sanctioning and communication, respectively. For all games we first derive the standard economic prediction, that is, the Nash equilibrium assuming that everybody is selfish and rational. We contrast this prediction with experimental results and the prediction derived by our fairness model. In presenting the experimental results, we restrict our attention to behavior of subjects in the final period because in that period, nonselfish behavior cannot be rationalized by the expectation of rewards in future periods. Furthermore, in the final period, we have more confidence that the players fully understand the game being played. The reason we do not analyze one-shot data (as, e.g., in Rutte and Wilke, 1985) is simple: To our knowledge there are no one-shot experiments where the same common-pool resource game has been studied in various environments. Only the repeated game data by Walker and colleagues (1990) allows this type of analysis because they studied the same game in various institutional setups. Of course the final period of a repeated interaction may be different in some way from a pure one-shot game. It has been argued, for example, that people might not sanction if they interact only once. This conjecture, however, clearly is refuted by recent experimental evidence
showing that even in a pure one-shot game, many people engage in costly sanctions and punish defectors (Falk et al. 2000b).
The Standard Common-Pool Resource Game
In a standard common-pool resource game, each player is endowed with an endowment e. All n players in the group decide independently and simultaneously how much they want to appropriate from a common-pool resource. Individual i’s appropriation decision is denoted by xi. The appropriation decision causes a cost c per unit of appropriation but also yields a revenue. Although the cost is assumed to be independent of the decisions of the other group members, the revenue depends on the appropriation decisions of all players. More specifically, the total revenue of all players from the common-pool resource is given by ƒ(Σxj) where Σxj is the amount of total appropriation. For low levels of total appropriation ƒ(Σxj) is increasing in Σxj, but beyond a certain level ƒ(Σxj) is decreasing in Σxj. An individual subject i receives a fraction of ƒ(Σxj) according to the individual’s share in total appropriation ![]() Thus the total material payoff of i is given by:
Thus the total material payoff of i is given by:
In the experiments of Walker and colleagues (1990), e = 10 (or 25) and c = 5. The total revenue is given by ƒ(Σxj) = 23 Σxj – .25(Σxj)2. Thus in this experiment, material payoffs are:
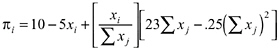
Intuitively this is a social dilemma problem because individual i’s appropriation decision xi does not only affect player i’s payoff, but also that of all other players. Beyond a certain level of total appropriations, an increase in the appropriation of player i lowers the other players’ revenue from the common-pool resource. Because selfish players are concerned only with their own well-being, they do not care about the negative externalities they impose on others. As we will discuss, this leads to the typical inefficiencies that are characteristic for this type of dilemma games.
The above payoff function from Walker and colleagues can be transformed into πi = 10 + 18xi – 0.25xi Σxj or more abstractly as πi =: e + α xi– bxi Σxj. As we will see this notation will be useful in the following discussion.
In this common-pool resource game, the standard economic prediction (assuming completely selfish and rational subjects) is as stated in Proposition 1:4
Proposition 1 (Selfish Nash Equilibrium)
If all players have purely selfish preferences, the unique Nash equilibrium is symmetric and individual appropriation levels are given by ![]()
In the following we denote this equilibrium as SNE (Selfish Nash Equilibrium) and the corresponding individual appropriation levels as xSNE. As can be seen from Proposition 1, the individual contribution is independent of the endowment and it is decreasing in the number of players. In the specification of Ostrom et al., groups of eight players participated in the experiment. Thus in their experiment the predicted individual contribution amounts to ![]() Given the group size, total appropriation is 64. Compared to the social optimum of 36, this equilibrium yields substantial inefficiencies.5 The point is that in their decisions, subjects ignore the negative externality imposed on the other players. Because players are assumed to care only about their own material payoff, they simply don’t care about such externalities.
Given the group size, total appropriation is 64. Compared to the social optimum of 36, this equilibrium yields substantial inefficiencies.5 The point is that in their decisions, subjects ignore the negative externality imposed on the other players. Because players are assumed to care only about their own material payoff, they simply don’t care about such externalities.
How does the presence of inequity-averse or reciprocally motivated subjects alter the standard economic prediction? To answer this question, we will discuss two propositions. The first proposition considers symmetric equilibria whereas the second deals with asymmetric equilibria.
It is useful to start our discussion of the properties of symmetric equilibria with the nature of the best response function of an inequity-averse subject. The best response function indicates the optimal appropriation response of an inequity-averse player to the average appropriation of all other players. Figure 5-2 shows the best response of an inequity-averse subject (with positive α and β ) and compares it to that of a selfish subject. The thin line represents the optimal appropriation of a selfish subject given the average appropriation level of the other group members.6 As can be seen in Figure 5-2, a selfish player appropriates less, the more the other group members appropriate. At the point where the best response function intersects the diagonal, the SNE prevails. At this point the average appropriation level of the other n – 1 players is 8 from the viewpoint of each individual player. Moreover, it is in the self-interest of each player to respond to this average appropriation of the n – 1 other players with an own appropriation level of 8. Now look at the bold line in Figure 5-2. This line shows the best response behavior of an inequity averse subject. Four aspects of this function are important to emphasize.
First, in the area above the diagonal, that is, where the other players appropriate less than in the SNE, the best response curve of an inequity-averse player lies below that of a selfish player. This means that if the other players are “nice” in the sense that they appropriate less than what is in their material self-interest, an inequity-averse subject also appropriates less. Because inequity-averse players dislike being in a too favorable position, they do not exploit the kindness of the
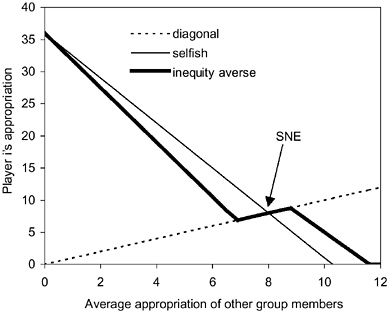
FIGURE 5-2 Best response behavior in a standard common-pool resource game (alpha = 4, beta = 0.6).
other players but instead voluntarily sacrifice some of their resources in favor of the other players.
Second, there is an area below the diagonal. In this area the other group members appropriate more than in the SNE. The best response behavior of an inequity-averse subject dictates to appropriate more than is compatible with pure self-interest in this case. Here, the intuition is that because the other players appropriate more than in the SNE, the inequity-averse player takes revenge by imposing negative externalities on the other players. The desire to take revenge results from the fact that the large appropriation levels of the others cause disadvantageous inequality for the inequity-averse subject. Because appropriating in this area reduces the payoff of the others more than their own payoff, an inequityaverse player can reduce the payoff differences. The selfish player, on the other hand, does not care about payoff differences and therefore appropriates less in this situation.
Third, a part of the inequity-averse player’s best response lies right on the diagonal. This is the area in which symmetric equilibria may exist. There may be equilibria in which subjects appropriate less than in the SNE as well as equilibria in which they appropriate more. Of particular interest are the equilibria to the left of the SNE because in this direction efficiency is increasing (up to the optimal appropriation level of 36). Whether such equilibria do exist depends on the distribution of the parameters α and β (see our discussion on Proposition 2).
Fourth, notice that in case the others do not appropriate at all the best re-
sponses of selfish and inequity-averse players coincide. At first glance, this seems counterintuitive, because in a certain sense appropriating nothing is the most friendly choice of the other group members. However, the coincidence of the two best response functions at that point is quite sensible. The reason is that if the other group members do not appropriate at all, the appropriation decisions of a player do not affect the other players’ payoffs at all. This is because the other players’ share of the total revenue ![]() is zero. So why should an inequity averse-player not choose the money-maximizing appropriation level of 36 units? Remember that the utility function specified in equation 5-1 combines a concern for absolute income and for payoff differences. In case the other players do appropriate nothing, utility is equal to Ui = πi – βi (πi – π–i) = πi(1 – βi ) + βi π–i, where π–i is the individual payoff of each of the n – 1 other players who appropriate zero. Because π–i is equal to e, it does not depend on the choice of player i, and because βi < 1, it is clear that even for a highly inequity-averse subject, money-maximizing behavior and utility-maximizing behavior coincide.
is zero. So why should an inequity averse-player not choose the money-maximizing appropriation level of 36 units? Remember that the utility function specified in equation 5-1 combines a concern for absolute income and for payoff differences. In case the other players do appropriate nothing, utility is equal to Ui = πi – βi (πi – π–i) = πi(1 – βi ) + βi π–i, where π–i is the individual payoff of each of the n – 1 other players who appropriate zero. Because π–i is equal to e, it does not depend on the choice of player i, and because βi < 1, it is clear that even for a highly inequity-averse subject, money-maximizing behavior and utility-maximizing behavior coincide.
Given the best response behavior of inequity-averse subjects, the existence conditions and the nature of symmetric equilibria are described in the next proposition. Note that in this proposition, min(βi ) denotes the smallest βi among all n players and min(α i) denotes the smallest α i.
Proposition 2 (Symmetric Equilibria with Inequity-Averse Subjects)
There is a symmetric equilibrium in which each subject chooses
The intuition of Proposition 2 is as follows: If both the smallest α i and the smallest βi are equal to zero, the only equilibrium is the SNE, that is, ![]() This means that the presence of only one egoistic player in the group (with α i = βi = 0) suffices to induce all other players to act in a selfish manner, regardless of how inequity averse they are. Put differently, a single egoist rules out any efficiency improvement compared to the SNE even if all other n – 1 players are highly inequity averse.
This means that the presence of only one egoistic player in the group (with α i = βi = 0) suffices to induce all other players to act in a selfish manner, regardless of how inequity averse they are. Put differently, a single egoist rules out any efficiency improvement compared to the SNE even if all other n – 1 players are highly inequity averse.
Proposition 2 entails a very strong result. It states that the subject with the “weakest preferences” for an equitable outcome dictates the outcome for the whole group. Only if the lowest α i or the lowest βi are greater than zero do asymmetric equilibria that differ from the SNE exist. Of particular interest are equilibria where the smallest βi is greater than zero. In this case the lower bound of the interval given in Proposition 2 is smaller than xSNE, that is, there are equilibria “to the left” of the SNE. In these equilibria subjects appropriate less than in the SNE. Similarly, if the smallest αi is larger than zero, there exist equilibria in
which subjects appropriate more than in the SNE. If all players in a group are inequity averse and given the parameters of the Ostrom et al. experiment, the range of possible Nash equilibria is ![]() where
where ![]() is always an equilibrium independent of αi and βi .7
is always an equilibrium independent of αi and βi .7
So far we have concentrated on symmetric equilibria. However, there are also asymmetric equilibria. The following proposition provides the details.8
Proposition 3 (Asymmetric Equilibria with Inequity-Averse Subjects)
(i) If there are at least k players with ![]() then there is an equilibrium with less appropriation than in the SNE. In this equilibrium at least k players choose the same appropriation
then there is an equilibrium with less appropriation than in the SNE. In this equilibrium at least k players choose the same appropriation ![]() the other players j choose higher appropriation levels. (ii) If there is no k such that there are at least k players with
the other players j choose higher appropriation levels. (ii) If there is no k such that there are at least k players with ![]() then there is no equilibrium with less appropriation than in the SNE.
then there is no equilibrium with less appropriation than in the SNE.
Corollary 1: If there are ![]() or more selfish players, then there is no equilibrium with less appropriation than in the SNE.
or more selfish players, then there is no equilibrium with less appropriation than in the SNE.
The intuition of Proposition 3 is straightforward. To get more efficient equilibria than the SNE requires that a relatively large fraction of subjects have rather high ![]() combinations. Notice that because 0 < βi < 1 and αi > βi , the expression
combinations. Notice that because 0 < βi < 1 and αi > βi , the expression ![]() is between zero and one. This means that for
is between zero and one. This means that for ![]() the only equilibrium is the SNE. Only if k is higher than n/2 there are
the only equilibrium is the SNE. Only if k is higher than n/2 there are ![]() combinations to ensure a more efficient equilibrium. For example, if the group size is 8, it takes at least 5 nonegoistic players to reach such an equilibrium. In this case the
combinations to ensure a more efficient equilibrium. For example, if the group size is 8, it takes at least 5 nonegoistic players to reach such an equilibrium. In this case the ![]() combinations of these 5 subjects must be at least
combinations of these 5 subjects must be at least ![]() The more people who are nonselfish, the weaker is the requirement for
The more people who are nonselfish, the weaker is the requirement for ![]() Thus, to reach a more efficient outcome, it takes either many subjects with moderate
Thus, to reach a more efficient outcome, it takes either many subjects with moderate ![]() combinations or it takes fewer subjects (but still more than n/2) with very high
combinations or it takes fewer subjects (but still more than n/2) with very high ![]() combinations. Notice that the expression
combinations. Notice that the expression ![]() rises in βi and decreases in αi. It is therefore more likely to reach more efficient outcomes if subjects have a rather large utility loss from advantageous inequality, and a rather small utility loss from disadvantageous inequality.
rises in βi and decreases in αi. It is therefore more likely to reach more efficient outcomes if subjects have a rather large utility loss from advantageous inequality, and a rather small utility loss from disadvantageous inequality.
To summarize the results of this section: What are the prospects for an outcome that is “better” than that of the SNE? If we look at the requirements of Propositions 2 and 3, some skepticism is in place. The requirements are rather tough. In the symmetric case, it takes only one selfish subject to ensure that the only equilibrium is SNE. Of course, more efficient equilibria are possible. However, we expect that this is the exception rather than the rule. For example, if we assume that there are about 25 percent purely selfish people (a rather optimistic guess), the chance to have no egoist in a randomly drawn group of 8 subjects is about 10 percent. This means that on average in 1 out of 10 groups, we would possibly expect less appropriation than in the SNE.
What about the asymmetric case? On first sight, requirements seem weaker. There are more efficient outcomes even in the presence of a selfish player. However, it takes again more than half of the players who are (i) nonselfish and (ii) who have a rather high utility loss from advantageous inequality compared to their loss in utility that derives from disadvantageous inequality. We have strong doubts that this type of preference is sufficiently frequent. As we have pointed out, we expect that the aversion with respect to disadvantageous inequality is usually much stronger than that arising from advantageous inequality (see also Loewenstein et al., 1989).
Our conclusion, therefore, is that even in the presence of many inequityaverse and reciprocal subjects, the prospects for achieving a more efficient equilibrium than the SNE are rather weak in the standard common-pool resource game. This is consistent with much of the reported data, according to which—on average—the SNE describes aggregate behavior quite well. In their repeated common-pool resource game, Ostrom et al. (1994) report that average final period appropriation levels in three different groups were 63, 64, and 78 (in case the endowment was 25 tokens) and 60, 63, and 70 (in case the endowment was 10 tokens).9 These numbers are very close to the standard prediction of 64.
A Common-Pool Resource Game With Sanctioning Opportunities
In this section we discuss a variant of the standard common-pool resource game. Again, we follow the experimental setup of Ostrom et al., (1992).10 Their sanctioning institution is built on the standard common-pool resource game discussed earlier. Subjects now first play the standard game, and after each round of play, all subjects receive data on all individual appropriation decisions. Each subject then can decide to sanction any other group member at a certain cost. Technically, any player i can deduct pij points from player j’s payoff at cost cpij where c is a positive constant smaller than 1. In the reported experiments, different parameter constellations were used where pij varied from 10 to 80 cents and cpij varied from 5 to 20 cents.
Because sanctioning is costly in this type of experiments, the standard game theoretic prediction (assuming selfish preferences) is exactly as stated in Proposi-
tion 1. The rationale for this prediction is straightforward. Why should a rational and selfish person spend resources to sanction another person in the final stage? Because sanctioning is costly and utility depends only on their own material payoff, sanctioning is equivalent to throwing away money. Rational subjects are able to perform the necessary backward induction, so everybody knows that nobody will sanction, no matter how egoistical the appropriation behavior on the first stage actually is. Thus appropriation is totally unaffected by the presence of a sanctioning stage.
Contrary to this prediction, Ostrom et al. (1994:176), report the following stylized facts:11
-
Significantly more sanctioning occurs than according to the standard prediction.
-
Sanctioning is inversely related to the cost of sanctioning (c).
-
Sanctioning is focused primarily on subjects who appropriate the most from the common-pool resource.
-
Sanctioning has a modest efficiency-enhancing impact on appropriation behavior (i.e., there is less appropriation than in the SNE).
-
There is some sanctioning behavior that can be classified as “error, lagged punishment, or ‘blind’ revenge.”
-
Taking into account the cost of sanctioning, overall efficiency is similar to the standard common-pool resource without sanctioning opportunities.
This evidence is largely at odds with the homo economicus perspective. Assuming interdependent preferences, however, this evidence can be explained. In particular, our model predicts that defectors will be punished by those players who have sufficiently strong preferences for equity and reciprocity. This punishment serves as a discipline device for the selfish players. As a consequence selfish players have an incentive to act more cooperatively compared to a situation where there is no sanctioning institution. Thus, for a given population (of selfish and inequity-averse subjects), the prospects for more efficient appropriation levels are clearly improved in a common-pool resource environment with sanctioning possibilities. Precise conditions for the existence of equilibria with appropriation levels below the SNE are given in the following proposition.
Proposition 4 (Equilibria with Sanctioning Possibilities)
Suppose there is a number k ≤ n such that for all players i ≤ k, the utility parameters αiand βisatisfy ![]() We call the players who satisfy this condition “conditionally cooperative enforc-
We call the players who satisfy this condition “conditionally cooperative enforc-
ers” (CCEs). Suppose further that all players i > k obey the condition αi= βi= 0, that is they are selfish. We define βmin= mini≤kβias the smallest βiamong the CCEs. Then there is an equilibrium that can be characterized as follows: (i) All players choose ![]() (ii) If each player does so, there is no sanctioning in the second stage. (iii) If one player chooses a higher appropriation level, then this player is sanctioned equally by all CCEs. The sanctioning equalizes the payoffs of those who sanction and the player who deviates from x. (iv) If more than one player does not play x, an equilibrium of the sanctioning subgame is played.
(ii) If each player does so, there is no sanctioning in the second stage. (iii) If one player chooses a higher appropriation level, then this player is sanctioned equally by all CCEs. The sanctioning equalizes the payoffs of those who sanction and the player who deviates from x. (iv) If more than one player does not play x, an equilibrium of the sanctioning subgame is played.
Proposition 4 determines the critical condition for an equilibrium in which all players appropriate less than xSNE. It states that the cost of sanctioning c must be lower than a certain threshold cost ĉ level, which is defined by the preference parameters of the CCEs. The threshold ĉ, increases in αi, βi , and k.
The intuition for the positive relation between ĉ and αi is the following: A player with a high αi experiences a great disutility from disadvantageous inequity. This player is therefore willing to punish a selfish player who appropriates more than x (and therefore earns more than player i), even if the sanctioning costs are high.
Why does the critical cost ĉ increase in βi? Remember that a person with a high βi has a strong aversion against advantageous inequality. Therefore, such a player i will experience a strong disutility from the advantageous inequity toward the other CCEs when he, himself, does not sanction a selfish player. Put differently, given that the others spend resources in order to sanction a defector, a person with a high βi will feel solidarity toward these punishers. Thus, although a high αi leads to punishment because of the inequity toward the deviating person, a high βi leads to punishment in order to reduce the inequity toward those who actually punish.
Finally, why is ĉ increasing in k? A higher k means there are more subjects who are willing to punish the players who deviate from x. Therefore, the desire to be in solidarity with those who punish increases as well, that is, ceteris paribus there will be more punishment.12
Notice that when there is a sanctioning opportunity, it is much easier to meet the conditions that sustain a cooperative outcome compared to the standard common-pool resource game. The conditions that αi and βi have to meet are tougher when sanctioning is ruled out. Put differently, for a given distribution of inequityaverse and selfish players, it may be impossible to reach an equilibrium with a cooperative outcome when sanctioning is impossible, while there are equilibria with a cooperative outcome when sanctioning is possible. Thus, the model does explain why appropriation is more efficient with a sanctioning device than without. It also correctly predicts that those subjects who deviate from the “agreed” appropriation level x will be punished. This is a very important point. Because it
is exactly the defectors who get punished, the group can discipline the selfish players. As long as there are enough “norm enforcers,” cooperation will be high and stable because the potential deviators face the credible threat of being punished if they behave selfishly. This pattern of punishment behavior can therefore be understood as a norm enforcement device (see Fehr and Gächter, 2000a). We would like to add that the Fehr and Schmidt model as well as the Falk and Fischbacher (1998) model share this feature.13 Finally, the model does explain why sanctioning activities are inversely related to the cost of sanctioning. This follows immediately from Proposition 4. For a given set of preferences, the equilibria with cooperative outcomes will be the more likely the lower the cost of punishment.
In the experiments analyzed so far, the possibility to sanction clearly improves the prospects of cooperation. It has been argued, however, that the implementation of explicit incentive devices such as incentive contracts (which also punish noncompliance) may be counterproductive. In the presence of fairness preferences incentive devices may “crowd out” voluntary cooperation if they are perceived as unfair (see, e.g., Andreoni and Varian, 1999).
In our view, it depends very much on the precise nature of explicit incentives whether they are counterproductive or not. Although reciprocity-based punishments (as observed in the experiment already discussed) and repeated game incentives seem to be compatible with a cooperative atmosphere (Gächter and Falk, 2000), explicit incentive contracts may not always be. If a cooperative atmosphere is important for managing the commons, it is therefore important to balance the potential advantages and disadvantages of explicit incentives.
The Impact of Communication
In all games discussed so far, subjects interact anonymously and without communication. In reality, however, people often communicate. They discuss problems like “overfishing,” make (non)binding agreements on how to behave, and express approval or disapproval through (face-to-face) communication. Unless agreements are binding in a strict sense, however, the standard prediction with respect to behavior remains unchanged. When all people are completely selfish, there is no hope that after the promise not to appropriate excessively, a subject will actually stick to a promise. When it comes down to giving up money just to keep one’s promise, standard theory predicts that subjects won’t hesitate to pursue their material self-interest. In this sense, the opportunity to communicate is irrelevant for the predicted outcomes just as it was the case with the sanctioning opportunity.
The experimental evidence reported in Ostrom et al. (1994) casts serious doubts at this prediction.14 They report that subjects “with one and only one opportunity to communicate, obtained an average percentage of net yield above that which was obtained in baseline experiments…without communication (55 per-
cent compared to 21 percent)” (1994:198). Allowing subjects to communicate repeatedly increases efficiency even more (73 percent).15
In a meta-study by Sally (1995) on the determinants of cooperative behavior in more than 100 public goods experiments, communication has a significant and positive influence. In one-shot games, cooperation is raised by about 45 percent on average, whereas in repeated games the increase is 40 percent. Communication, however, is an elusive term. In some experiments, subjects really talk to each other, that is they exchange verbal and facial expressions. In other experiments, subjects do not communicate face to face but rather via computer or written notes. In yet other experiments, subjects do not actually talk but simply identify each other, that is, they do not exchange any verbal information. As diverse as the experiments is the discussion on why communication has a positive impact. Kerr and Kaufman-Gilliland (1994), for example, discuss nine different effects communication may have. It is not our aim to address these issues at length. The purpose of this section is to discuss how communication affects decisions when fairness concerns play a role. The two main effects we consider as relevant from this perspective are coordination and the expression of approval and disapproval. Both effects were possible in the common-pool resource communication treatment outlined earlier because subjects could not only exchange information, but also did see and talk to each other.
Coordination
Remember that in the standard common-pool resource game with inequityaverse or reciprocal preferences, there may be multiple equilibria. The SNE is always one of these equilibria, among others that are more (or less) efficient. To emphasize our point, let us abstract from all details and assume a two-player common-pool resource game. In terms of material payoffs, the game could look like the one expressed in Table 5-1a, that is, the common-pool resource game is similar to a prisoners’ dilemma game. Even though it is in their common interest to choose the low appropriation level, both players can individually improve their material payoffs if they choose the high appropriation strategy. This yields the unique equilibrium where both players choose the high appropriation. If both
TABLE 5-1a A Simple CPR Game without Reciprocal Preferences
|
|
|
Player 2 |
|
|
|
|
Low appropriation |
High appropriation |
|
Player 1 |
Low appropriation |
10,10 |
0,15 |
|
|
High appropriation |
15,0 |
5,5 |
players have purely selfish preferences, this is the end of the story (and communication has no impact).
In the presence of reciprocal preferences, however, the common-pool resource game is no longer a prisoners’ dilemma (see Table 5-1b). The reason is that if both players are sufficiently reciprocally motivated, they don’t like to cheat on the other player. If, for example, player 1 chooses the low appropriation strategy, player 2 with reciprocal preferences is better off choosing the low instead of the high appropriation level and vice versa. Even though players forgo some material payoffs, they have a higher utility if they reciprocate the nice behavior of the other player. If player 1 chooses the high appropriation level, however, player 2 has no desire to choose the low level (neither if he is a selfish nor a reciprocal player). Instead, player 2 will in this case also play the high appropriation strategy. As a consequence, there are two (pure) equilibria now, the efficient equilibrium with low appropriations and the inefficient one with high appropriations. Put differently, the prisoners’ dilemma game in Table 5-1a with a unique and inefficient equilibrium has turned into a coordination game with one efficient and one inefficient equilibrium. Game theory does not help much in this situation. It simply predicts that some Nash equilibrium will be played, but not which one.16
In the presence of multiple equilibria, subjects face a tremendous strategic uncertainty. How shall a person know which strategy the other player will select? It is obvious that communication can have a positive impact in a situation of strategic uncertainty. In fact it has been shown experimentally that communication can help players to coordinate on better equilibria.17 As an example, take Cooper et al. (1992), who study different coordination games with and without communication. They find that, depending on the precise structure of the coordination game, communication may improve efficiency. This holds even though all announcements are nonbinding. They also show, however, that communication does not always improve coordination. The prospects for improved cooperation depend both on the nature of the game and the nature of the communication process.
In the common-pool resource experiments with communication mentioned earlier, players had intensive opportunities for communication because they could actually talk to each other and were (with some restrictions) allowed to discuss anything they wanted. As reported in Ostrom et al. (1994), subjects usually came
TABLE 5-1b A Simple CPR Game in the Presence of Reciprocal Preferences
|
|
|
Player 2 |
|
|
|
|
Low appropriation |
High appropriation |
|
Player 1 |
Low appropriation |
10,10 |
0,9 |
|
|
High appropriation |
9,0 |
5,5 |
to the agreement to appropriate a particular amount (e.g., 5 tokens). If this is the case, coordination on “good” equilibria seems possible. Given these extensive communication opportunities and the fact that there is usually a substantial fraction of reciprocal subjects, it seems quite likely that communication raised efficiency because subjects could coordinate their choices on more efficient equilibria.
Communication as a Sanctioning Device
Social interactions frequently are associated with social approval or disapproval. The anticipation of such social rewards and punishments may have important economic consequences. For example, it may affect the efficiency of team production and the decisions in diverse areas such as tax evasion, the exploitation of the welfare state, criminal activities, union membership, and voting behavior. The behavioral role of social rewards and punishments is stressed in social exchange theory (Blau, 1964). In contrast to pure economic exchanges, social exchanges involve not only the exchange of economic rewards but also the exchange of social rewards. The admiration or the contempt that is sometimes expressed by parents, teachers, professional colleagues, and spectators are prime examples of a social reward. In general social rewards are not based on explicit contractual arrangements but are triggered by spontaneous positive or negative emotions that can be interpreted as approval and disapproval, respectively.
Of course, approval as well as disapproval can be communicated and can have an important impact on individual behavior in a common-pool resource game. People who talk to each other enter a social relationship. Within this relationship, exchange of approval and disapproval is possible. Two assumptions must be met in order to observe more cooperative behavior compared to SNE, however. First, there must be subjects who actually care about approval or disapproval and who change their behavior in the expectation of such approval or disapproval. Second, there must be subjects who actually express approval or disapproval. The first condition is obvious. The second condition is important because it is usually not costless to express approval and in particular disapproval. Our point is that reciprocally motivated subjects are willing to bear the cost and are willing to reciprocate the cooperative or noncooperative actions by others. Thus, preferences as assumed in our model may explain why communication in combination with the expression of approval and disapproval can have a positive impact on cooperative behavior.
Taken together, we have described two potential channels through which communication may elicit cooperative behavior in the presence of reciprocal preferences. Although the first rests only on the exchange of information, the second is built on the possibility of communication face to face. We would expect, therefore, that communication effects are particularly strong if face-to-face communication is possible (as it is the case in the treatment already discussed).
This is also the conclusion of Rocco and Warglien (1995), who report a study showing that it is the communication face to face that makes the big difference (on this point, see also Frey and Bohnet, 1995; Bohnet and Frey, 1999a; Bohnet and Frey, 1999b; and Ostrom, 1998).
PUBLIC GOODS: A COMPARISON
So far we have analyzed common-pool resource games. However, many of the arguments apply also to public goods games. In fact, public goods games and common-pool resource games are very similar. Whereas in a common-pool resource game, subjects’ decisions impose negative externalities on other subjects, subjects in a public goods game produce positive externalities. In a common-pool resource game, it is nice or kind not to appropriate too much, while in a public goods game it is kind not to contribute too little to the public good. Public goods situations are very important and very frequent in reality.18 Moreover, there exists a huge experimental literature on public goods games. As we will show, many of the findings reported on common-pool resource problems carry over to those of public goods. In this section we discuss a one-stage public goods game (similar to the standard common-pool resource game) and a two-stage public goods game, where after the first stage, subjects have a sanctioning opportunity (similar to the common-pool resource with sanctioning opportunities).
We start with the following linear public goods game. There are n ≥ 2 players who decide simultaneously on their contribution levels ![]() to the public good. Each player has an endowment of y. The monetary payoff of player i is given by
to the public good. Each player has an endowment of y. The monetary payoff of player i is given by ![]() where 1 / n < a < 1. Because a < 1, a marginal investment into G causes a monetary loss of (1 – a), that is, the dominant strategy of a completely selfish player is to choose gi = 0. However, because a > 1/n, the aggregate monetary payoff is maximized if each player chooses gi= y.
where 1 / n < a < 1. Because a < 1, a marginal investment into G causes a monetary loss of (1 – a), that is, the dominant strategy of a completely selfish player is to choose gi = 0. However, because a > 1/n, the aggregate monetary payoff is maximized if each player chooses gi= y.
Consider now a slightly different public goods game that consists of two stages. At stage 1 the game is identical to the previous game. At stage 2 each player i is informed about the contributions of all other players and can simultaneously impose a costly punishment on the other players, just as in the sanctioning common-pool resource game discussed.
What does the standard model predict for the two-stage game? Because punishments are costly, players’ dominant strategy at stage 2 is to not punish. Therefore, if selfishness and rationality are common knowledge, each player knows that the second stage is completely irrelevant. As a consequence, players have exactly the same incentives at stage I as they have in the one-stage game without punishments, that is, each player’s optimal strategy is to contribute nothing.
To what extent are these predictions of the standard model consistent with the data from public goods experiments? For the one-stage game there are, fortunately, a large number of experimental studies. In a meta-study of 12 experimen-
tal studies (with a total of 1,042 subjects participating), Fehr and Schmidt (1999) report that in the final period of public goods games without punishment, the vast majority of subjects play the equilibrium strategy of complete free riding. On average, 73 percent of all subjects choose gi= 0 in the final period. It is also worth mentioning that in addition to those subjects who play exactly the equilibrium strategy, there is often a nonnegligible fraction of subjects who play “close” to the equilibrium.19 In view of the facts, it seems fair to say that the standard model “approximates” the choices of a big majority of subjects rather well. However, if we turn to the public goods game with punishment, a radically different picture emerges although the standard model predicts the same outcome as in the one-stage game. Figure 5-3 shows the distribution of contributions in the final period of the two-stage game conducted by Fehr and Gächter (2000a). Note that the same subjects generated the distribution in the game without and in the game with punishment. Whereas in the game without punishment, most subjects play close to complete defection, a strikingly large fraction of 82.5 percent cooperates fully in the game with punishment. Fehr and Gächter report that the vast majority of punishments are imposed by cooperators on the defectors and that lower contribution levels are associated with higher received punishments. Thus, defectors do not gain from free riding because they are being punished.
When these results are compared with the evidence from common-pool re-
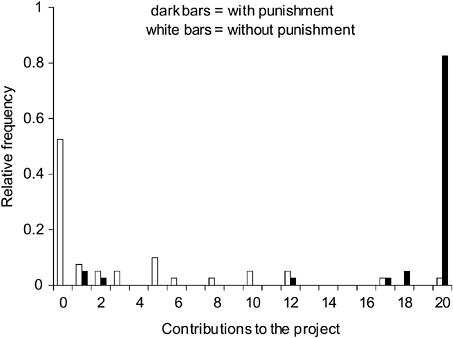
FIGURE 5-3 Contributions to the public good with and without punishment.
source games, a striking similarity arises. In the standard common-pool resource game, average behavior (in final periods) is fairly consistent with the standard prediction. However, if subjects have the opportunity to sanction each other, behavior becomes much more cooperative—even though the standard prediction yields the same outcome. As we have seen in our discussion, our fairness model can explain the evidence in both common-pool resource games. This holds also for the public goods games. The intuition for the one-stage public goods game is straightforward. Only if sufficiently many players have a dislike for an advantageous inequity can they possibly reach some cooperative outcome. As long as only a few players are willing to contribute if others contribute as well, they would suffer too much from the disadvantageous inequality caused by the free riders. Thus, inequity-averse players prefer to defect if they know there are selfish players. To put it differently: The greater the aversion against being the “sucker” the more difficult it is to sustain cooperation in the one-stage game.
Consider now the public goods game with punishment. To what extent is our model capable of accounting for the very high cooperation in this treatment? The crucial point is that free riding generates a material payoff advantage relative to those who cooperate. Because c < 1, cooperators can reduce this payoff disadvantage by punishing the free riders. Therefore, if those who cooperate are sufficiently upset by the inequality to their disadvantage, that is, if they have sufficiently high α ’s, then they are willing to punish the defectors even though this is costly to themselves. Thus, the threat to punish free riders may be credible, which may induce potential defectors to contribute at the first stage of the game.
Notice that according to the present model (and the inequity-aversion approach in general), a person will punish another person if and only if this reduces the inequity between the person and his opponent(s). Therefore, as long as c < 1 (as is the case in the common-pool resource problem and the public goods game analyzed previously), the model predicts punishments for sufficiently inequity-averse subjects. If, on the other hand, c ≥ 1, the Fehr-Schmidt model predicts no punishment at all. This holds regardless of whether we look at public goods games or at the common-pool resource problems. Experimental evidence suggests, however, that many subjects in fact punish others even if punishment does not reduce inequity (as is the case if c ≥ 1). Falk and colleagues (2000b) present several experiments that address this question in more detail. As it turns out, a substantial amount of punishment occurs even in situations where inequity cannot be reduced. For example, in one of their public goods games with punishment, they implemented a punishment cost of c = 1. Nevertheless, 46.8 percent of the subjects who cooperated in this game punished defectors. The conclusion from Falk et al. (2000b) is, therefore, that the desire to reduce inequity cannot be the only motivation to punish unkind acts. An alternative interpretation is offered in Falk and Fischbacher (1998), who model punishment as the desire to reduce the unkind players’ payoff(s). Their model also correctly predicts punishments in those situations where punishment is costly and cannot reduce inequity.
DISCUSSION
In the preceding sections, we have demonstrated that with the help of a simple fairness theory, many stylized facts of common-pool resource or public goods experiments can be explained. In fact, the range of experiments that have been successfully analyzed with the help of our fairness theories is even wider. Both the model by Fehr and Schmidt (1999) and that of Falk and Fischbacher (1998) are capable of predicting correctly a wide variety of seemingly contradictory experimental facts. They are, in particular, capable of reconciling the puzzling evidence that in competitive experimental markets with complete contracts, very unfair outcomes that are compatible with the predictions of the pure self-interest model can emerge, while in bilateral bargaining situations or in markets with incomplete contracts, stable deviations from the predictions of the self-interest model, in the direction of more fair and equitable outcomes, are the rule.
The basic behavioral principle that is formalized in the models is that a substantial fraction of the subjects act conditionally on what other subjects do. If others are nice or cooperative, they act cooperatively as well, but if others are hostile, they retaliate. The models also pay attention to the fact that there are large individual differences between subjects. In particular, it is assumed that there are selfish subjects who behave in the way predicted by standard economic theory and reciprocal subjects who exhibit the type of conditional behavior just mentioned. The interaction of these diverse motivations and the institutional setup is responsible for the observed experimental outcomes. If there is no institutional rule that externally enforces cooperation or that allows for sanctioning possibilities, the interaction of selfish and conditional subjects frequently leads to noncooperative outcomes. If, on the other hand, subjects dispose of sanctioning possibilities, the reciprocal subjects are able to discipline selfish players. As a consequence, more cooperative outcomes will emerge. This approach goes beyond the standard economic conception, not least because it assigns institutions a much more important role. In the presence of reciprocal and selfish subjects, institutions determine which type of preference is pivotal for the equilibrium outcome. In a sense institutions select the type of player that shapes the final result.
Of course there are several important behavioral factors that we have not addressed or that cannot be explained with the help of the presented theoretical framework. For example, there is a long tradition in social-psychological research that points to the importance of values and altruism as mechanisms to overcome the free-rider incentives inherent to social dilemma situations. Some of the literature associated with concepts of “social motives” or “social value orientation” is discussed in the Kopelman et al. paper (this volume:Chapter 4). Another alternative explanation to the one presented in the current paper comes from the literature on altruism rooted in theories of moral norm activation (Schwartz, 1977) and research on the structure of human values (Schwartz, 1992). This research has been tied to environmental resource management through studies of individual
behavior in field situations, mainly measured by attitudinal and self-report indicators in surveys. In Stern et al. (1999), it is shown, for example, that people who accept a movement’s values, who believe that things important to those values are threatened and who believe that their actions may help to alleviate the threat, experience a personal norm to support the movement.
The latter explanations as well as the fairness models presented in this paper assume different prosocial motives that mitigate free-rider incentives as suggested by the empirical findings. The theories do not, however, ask about possible evolutionary roots of such prosocial behavior. This important question is addressed in Richerson et al. (this volume:Chapter 12).20
Yet another remark is in place. We have emphasized the importance of reciprocity and inequity aversion but have not mentioned the impact of reputation and repeated game effects. Many of the real life common-pool resource or public goods problems are in fact “played” repeatedly. In such repeated interaction, players usually can condition their behavior on past behavior of others. This allows players to build up reputations and to ensure cooperative outcomes, even among selfish players. In the parlance of game theory, this kind of cooperation may be supported as an equilibrium in infinitely repeated games (folk theorems) or in finitely repeated games with incomplete information (see Kreps et al., 1982).21 Many experiments have demonstrated the efficiency-enhancing effect of repeated versus one-shot interactions. Moreover, it has been shown that reciprocity and repeated game effects interact in a complementary way (Gächter and Falk, in press). In Gächter and Falk’s experimental study of a bilateral labor relation, the reciprocal relationship between workers and firms is increased significantly in a repeated interaction compared to one-shot encounters. The driving force behind this “crowding in” of reciprocal behavior is the fact that people who behave selfishly in the one-shot game have an incentive to imitate reciprocity in the repeated game.22 Thus, in the presence of repeated game incentives, the prospects for cooperative outcomes are expected to be better than according to the one-shot analysis undertaken in this paper.
NOTES
|
1 |
We also refer to the book by Ostrom et al. (1994) that summarizes and discusses the experimental findings. For an overview on experimental results, see also Kopelman et al. (this volume:Chapter 4). |
|
2 |
The importance of reciprocity has been established in dozens, if not hundreds, of experiments. For rewarding behavior in response to kind acts, see Fehr et al. (1993) or Berg et al. (1995). For punishing behavior in response to hostile acts, see Güth et al. (1982). Recent overviews are provided in Ostrom (1998) and Fehr and Gächter (2000b). |
|
3 |
For a first attempt to endogenize the choice of refernce agents or standards in a formal model, see Falk and Knell (2000). |
|
4 |
All propositions are proved in the Appendix to this chapter. |
|
5 |
The derivation of the social optimum is given in the Appendix to this chapter. |
|
6 |
Note that Figure 5-2 shows the symmetric case, where the other players’ appropriation decisions are equal. |
|
7 |
Because there is a whole range of equilibria, the question of equilibrium selection arises. This issue is discussed in the later section on coordination. |
|
8 |
We restrict attention to the cases wherein equilibrium appropriation is less than in SNE. |
|
9 |
We concentrate on the behavior of subjects in the final periods to exclude the possible confound of repeated games effects and to make behvior comparable to our one-shot predictions. |
|
10 |
A sanctioning institution was first studied by Yamagishi (1986). |
|
11 |
Moir (1999) studies the impact of monitoring additional to sanctioning. He points out that pure monitoring does not help to overcome excess appropriation. Institutions with a high level of monitoring but a low level of sanctioning may even lead to more apprpriation than institutions without any monitoring. A different design is suggsted by Casari and Plott (1999) in which monitoring and punishment are compacted in a single decision. In their treatment, efficiency is also higher compared to a baseline treatment without monitoring/punishment. |
|
12 |
Notice that according to Proposition 4, the reason for c to increase in k is not because the costs of punishment can be shared between more punishers. |
|
13 |
Other models predict a very different pattern of punishment. In Bolton and Ockenfels (2000), for example, punishment is not addressed individually, but directed toward a group average. This could imply, for example, that those who deviate are not punished whereas those who cooperate are punished. This is at odds with the experimental findings. Moreover, it does not take account of the ptential of reciprocal or equity preferences to establish and enforce social norms. For a detailed discussion of this point, see Falk et al. (2000b). |
|
14 |
See also Ostrom and Walker (1991). |
|
15 |
On communication, also see the paper by Kopelman et al. (this volume:Chapter 4). |
|
16 |
See, however, the literature on equilbrium selection in, for example, Harsanyi and Selten (1988). |
|
17 |
On coordination game experiments, see Ochs (1995). |
|
18 |
For an overview on public goods experiments, see Ledyard (1995). |
|
19 |
The results of the meta-study refer to public goods games where the group size is smaller than 10. There is also an experiment where the group size is substantially higher (40 and 100). In this experiment, contributions in the final period(s) are higher compared to small groups (Isaac et al., 1994). |
|
20 |
See also Gintis (2000), Sethi and Somananthan (2000), and Huck and Oechssler (1999). See also de Waal (1996), who shows that conditional behavior is observed among chimpanzees. Their food-sharing behavior exhibits some reciprocal pattern: A chimpanzee is ceteris paribus more willing to share food with another champanzee if the latter has shared with the former in the past. |
|
21 |
Notice that the latter model is built on the assumption that there exist selfish and reciprocal (tit-for-tat) types. |
|
22 |
On the complementary relationship between reputation and reciprocity, also see the paper by Ostrom (1998). |
REFERENCES
Adams, J.S. 1963 Toward an understanding of inequity. Journal of Abnormal and Social Psychology 62:422-436.
Agell, J., and P. Lundborg 1995 Theories of pay and unemployment: Survey evidence from Swedish manufacturing firms. Scandinavian Journal Of Economics 97:295-307.
Andreoni, J., and H. Varian 1999 Preplay contracting in the prisoner’s dilemma. Proceedings of the National Academy of Sciences 96:10933-10938.
Berg, J., J. Dickhaut, and K. McCabe 1995 Trust, reciprocity and social history. Games and Economic Behavior 10:122-142.
Bewley, T. 1998 Why not cut pay? European Economic Review 42:459-490.
Blau, P. 1964 Exchange and Power in Social Life. New York: Wiley.
Blount, S. 1995 When social outcomes aren’t fair: The effect of causal attributions on preferences. Organizational Behavior and Human Decision Processes 63(2):131-144.
Bohnet, I., and B.S. Frey 1999a The sound of silence in prisoner’s dilemma games. Journal of Economic Behavior and Organization 38:43-57.
1999b Social distance and other rewarding behavior in dictator games: Comment. American Economic Review 89:335-339.
Bolton, G.E., and A. Ockenfels 2000 A theory of equity, reciprocity and competition. American Economic Review 90:166-193.
Casari, M., and C. Plott 1999 Agents Monitoring Each Other in a Common-Pool Resource Environment. Working paper, California Institute of Technology, Pasadena.
Chamess, G., and M. Rabin 2000 Social Preferences: Some Simple Tests and a New Model. Working paper, University of California Berkeley.
Clark, A.E., and A.J. Oswald 1996 Satisfaction and comparison income. Journal of Public Economics 61:359-381.
Cooper, R., D. DeJong, R. Forsythe, and T. Ross 1992 Communication in coordination games. Quarterly Journal of Economics 107:739-771.
Davis, J.A. 1959 A formal interpretation of the theory of relative deprivation. Sociometry 102:280-296.
Dietz, T., and P.C. Stern 1995 Toward a theory of choice: Socially embedded preference construction. Journal of Socio-Economics 24(2):261-279.
Dufwenberg, M., and G. Kirchsteiger 1998 A Theory of Sequential Reciprocity. Discussion paper, Center for Economic Research, Tilburg University.
Falk, A., E. Fehr, and U. Fischbacher 2000a Testing Theories of Fairness: Intentions Matter. Working paper, Institute for Empirical Research, University of Zurich.
2000b Informal Sanctions. Working paper, Institute for Empirical Research, University of Zurich.
Falk, A., and U. Fischbacher 1998 A Theory of Reciprocity. Working paper 6, Institute for Empirical Research, University of Zurich.
Fehr, E., and S. Gächter 2000a Cooperation and punishment in public good experiments—An experimental analysis of norm formation and norm enforcement. American Economic Review 90:980-994.
2000b Fairness and retaliation: The economics of reciprocity. Journal of Economic Perspectives 14:159-181.
Fehr, E., G. Kirchsteiger, and A. Riedl 1993 Does fairness prevent market clearing? An experimental investigation. Quarterly Journal of Economics 108:437-460.
Falk, A., and M. Knell 2000 Choosing the Joneses: On the Endogeneity of Reference Groups? Working paper 53, Institute for Empirical Research, University of Zurich.
Fehr, E., and K. Schmidt 1999 A theory of fairness, competition, and cooperation. Quarterly Journal of Economics 114:817-851.
Festinger, L. 1954 A theory of social comparison processes. Human Relations 7:117-140.
Frey, B.S., and I. Bohnet 1995 Institutions affect fairness: Experimental investigations. Journal of Institutional and Theoretical Economics 151:286-303.
Gächter, S., and A. Falk 2000 Work motivation, institutions, and performance. In Advances in Experimental Business Research, R. Zwick and A. Rapoport, eds. Kluwer Academic Publishers. in press Reputation or Reciprocity—Consequences for the Labour Market. Submitted to Scandinavian Journal of Economics.
Gintis, H. 2000 Strong reciprocity and human sociality. Journal of Theoretical Biology.
Gordon, S. 1954 The economic theory of common-property resource: The fishery. Journal of Political Economy 62:124-142.
Güth, W., R. Schmittberger, and B. Schwarze 1982 An experimental analysis of ultimatum bargaining. Journal of Economic Behavior and Organization 3(3):367-388.
Hardin, G. 1968 The tragedy of the commons. Science 162:1243-1248.
Harsanyi, J., and R. Selten 1988 A General 7heory of Equilibrium Selection in Games. Cambridge, MA: MIT Press.
Homans, G.C. 1961 Social Behavior: Its Elementary Forms. New York: Harcourt, Brace & World.
Huck, S., and J. Oechssler 1996 The indirect evolutionary approach to explaining fair allocations. Games and Economic Behavior 28:13 -24.
Isaac, M.R., J.M. Walker, and A.M. Williams 1994 Group size and the voluntary provision of public goods. Journal of Public Economics 54:1-36.
Kerr, N., and C. Kaufmann-Gilliland 1994 Communication, commitment and coordination in social dilemmas. Journal of Personality and Social Psychology 66:513-529.
Kreps, D., P. Milgrom, J. oberts, and R. Wilson 1982 Rational cooperation in the finitely repeated Prisoners’ Dilemma. Journal of Economic Theory 27:245-252.
Ledyard, J. 1995 Public goods: A survey of experimental research. In Handbook of Experimental Economics, J. Kagel and A. Roth, eds. Princeton: Princeton University Press.
Levine, D. 1998 Modeling altruism and spitefulness in experiments. Review of Economic Dynamics 1:593-622.
Lind, E.A., and T.R. Tyler 1988 The Social Psychology of Procedural Justice. New York: Plenum Press.
Loewenstein, G.F., L. Thompson, and M.H. Bazerman 1989 Social utility and decision making in interpersonal contexts. Journal of Personality and Social Psychology 57:426-44 1.
Moir, R. 1999 Spies and Swords: Behavior in Environments with Costly Monitoring and Sanctioning. Working paper, University of New Brunswick.
Ochs, J. 1995 Coordination problems. In Handbook of Experimental Economics, J. Kagel and A. Roth, eds. Princeton: Princeton University Press.
Ostrom E. 1990 Governing the Commons: The Evolution of Institutions for Collective Action. New York: Cambridge University Press.
1998 A behavioral approach to the rational choice theory of collective action—Presidential address of the American Political Science Association 1997. American Political Science Review 92:1-22.
Ostrom, E., R. Gardner, and J. Walker 1994 Rules, Games, and Common Pool Resources. Ann Arbor: University of Michigan Press.
Ostrom, E., and J. Walker 1991 Communication in a commons: Cooperation without external enforcement. Pp. 287-322 in Laboratory Research in Political Economy, T. Palfrey, ed. Ann Arbor: University of Michigan.
Ostrom, E., J. Walker, and R. Gardner 1992 Covenants with and without a sword: Self-governance is possible. American Political Science Review 40:309-317.
Palfrey, T., and J. Prisbrey 1997 Anomalous behavior in public goods experiments: How much and why? American Economic Review 87:829-846.
Parks, C.D. 1994 The predictive ability of social values in resource dilemmas and public goods games. Personality and Social Psychology Bulletin 20(4):431-438.
Pollis, N.P. 1968 Reference groups re-examined. British Journal of Sociology 19:300-307.
Rabin, M. 1993 Incorporating fairness into game theory and economics. American Economic Review 83(5):1281-1302.
Rocco, E., and M. Warglien 1995 Computer Mediated Communication and the Emergence of Electronic Opportunism. Working paper RCC 13659, Universita degli Studi di Venezia.
Runciman, W.G. 1966 Relative Deprivation and Social Justice. New York: Penguin.
Rutte, C.G., and H.A.M. Wilke 1985 Preference for decision structures in a social dilemma situation. European Journal of Social Psychology 15:367-370.
Sally, D. 1995 Conversation and Cooperation in Social Dilemmas: A Meta-Analysis of Experiments from 1958 to 1992. Rationality and Society 7(1):58-92.
Schwartz, S.H. 1977 Normative Influences on Altruism. Pp. 221-279 in Advances in Experimental Social Psychology Volume 10, L. Berkowitz, ed. New York: Academic Press.
1992 Universals in the content and structure of values: Theoretical advances and empirical tests in 20 countries. Pp. 1-65 in Advances in Experimental Social Psychology Volume 25, L. Berkowitz, ed. New York: Academic Press.
Selten, R. 1998 Features of experimentally observed bounded rationality. European Economic Review 42:413-436.
Sethi, R., and E. Somananthan 2000 Preference evolution and reciprocity. Journal of Economic Theory.
Stem, P.C., T. Dietz, G.A. Guagnano, and L. Kalof 1999 A Value-belief-norm theory of support for social movements: The case of environmentalism. Human Ecology Review 6(2):81-97
Van Lange, P.A.M., W. Otten, E.M.N. De Bruin, and J.A. Joireman 1997 Development of prosocial, individualistic, and competitive orientations: Theory and preliminary evidence. Journal of Personality and Social Psychology, 73:733-746.
de Waal, F. 1996 Good Natured. The Origins of Right and Wrong in Humans and Other Animals. Cambridge, MA: Harvard University Press.
Walker, J., R. Gardner, and E. Ostrom 1990 Rent dissipation in a limited access common-pool resource: experimental evidence. Journal of Environmental Economics and Management 19:203-211.
Yamagishi, T. 1986 The provision of a sanctioning system as a public good. Journal of Personality and Social Psychology 51:110-116.
APPENDIX TO CHAPTER 5
Proof Proposition 1 (Selfish Nash Equilibrium)
The standard common-pool resource game we look at has the following form:
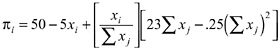
Defining e=50, a=18 and b=0.25, we get:
πi = 50 + 18xi – 0.25xiΣxj
πi =:e + axi– bxi∑xj
To find the selfish best reply for xi,we calculate
Setting it equal to zero, we get as best reply
First suppose that all ![]() In this case
In this case ![]()
Summing up the terms for all i, we get ![]()
Hence ![]()
Entering the sum into ![]() we get
we get ![]() Now consider that there are some players who choose 0. Let n0 be the number of players who choose xi equal to zero. Then all values above zero must be equal to
Now consider that there are some players who choose 0. Let n0 be the number of players who choose xi equal to zero. Then all values above zero must be equal to ![]() Calculating the best reply for one of the n0 players who originally played 0 now yields a contradiction. QED
Calculating the best reply for one of the n0 players who originally played 0 now yields a contradiction. QED
Social optimum: To find the social optimum, we calculate
Hence, in the social optimum, we get ![]()
Proof of Proposition 2 (Symmetric Equilibria with Inequity-Averse Subjects)
First note that if ![]() the players who choose the higher appropriation level also have higher payoffs:
the players who choose the higher appropriation level also have higher payoffs:
So let us first consider this case.
Suppose all players j ≠ i choose ![]() . Because Ui is concave in xi, the best reply is unique. So, to show that
. Because Ui is concave in xi, the best reply is unique. So, to show that ![]() is the best reply, it is sufficient to show that it is a local optimum. It is clear that
is the best reply, it is sufficient to show that it is a local optimum. It is clear that ![]() because otherwise player i could improve his material payoff as well as he could reduce inequity by increasing xi. It remains to check that there is no incentive for i to increase xi above
because otherwise player i could improve his material payoff as well as he could reduce inequity by increasing xi. It remains to check that there is no incentive for i to increase xi above ![]() . As the following calculation shows, the derivative from above
. As the following calculation shows, the derivative from above ![]() is a linear function in x. So, player i has no incentive to increase
is a linear function in x. So, player i has no incentive to increase ![]() above
above ![]() if this derivative equals at least zero.
if this derivative equals at least zero.
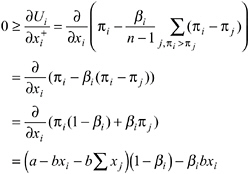
Thus, we get a critical condition for ![]()
(5-A)
The right-hand side of this inequality is decreasing in βi . Thus, the left inequality of the proposition is satisfied, if and only if (5-A) is satisfied for all i.
Assume now all other players j ≠ i choose ![]() Now, the critical condition is
Now, the critical condition is ![]()
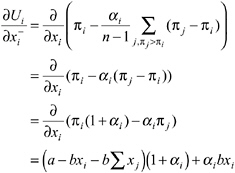
Thus, we get a critical condition for
5-A(1)
The righthand side of this inequality is increasing in αi. Thus, the left inequality of the proposition is satisfied, if and only if 5-A(1) is satisfied for all i and we get the right inequality in the proposition.
It remains to show that there is no equilibrium with appropriation decisions above ![]() We fix
We fix ![]() The critical condition is
The critical condition is ![]() Because a decrease of the appropriation level now generates inequity in favor of player i, we get the following condition:
Because a decrease of the appropriation level now generates inequity in favor of player i, we get the following condition:
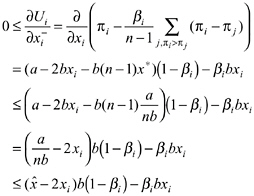
Because βi < 1, the last term is negative if xi is close to ![]() . Hence, there are no equilibria with
. Hence, there are no equilibria with ![]()
Proof of Proposition 3 (Asymmetric Equilibria with Inequity-Averse Subjects)
We first show (ii): Let us assume there is an equilibrium with some ![]() By reordering the players, we can assume that we have
By reordering the players, we can assume that we have ![]() Furthermore, let k be the highest index for which
Furthermore, let k be the highest index for which ![]() Now let’s consider i ≤ k. Because we are in an equilibrium, we have
Now let’s consider i ≤ k. Because we are in an equilibrium, we have ![]() Remember that πj– πi= (a – bΣxk) (xj- xi). So
Remember that πj– πi= (a – bΣxk) (xj- xi). So
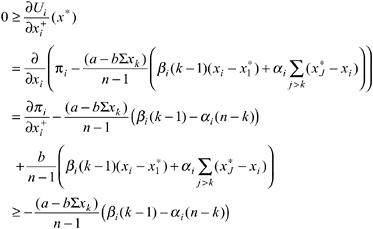
Hence
βi(k – 1) – αi(n – k) ≥ 0
or
which proves (ii).
Let us now come to the proof of (i). Assume without loss of generality that for i between 1 and k, we have![]() This implies
This implies ![]() because
because ![]() We will show that there is an equilibrium with x1, = x2=…= xk< xSNE. For x
We will show that there is an equilibrium with x1, = x2=…= xk< xSNE. For x ![]() [0, xSNE] we define the strategy combination s(x) as follows: We fix s(x)i = x for i ≤ k and choose s(x)j for j > k as the joint best reply. That means that s(x)j is a part of a Nash equilibrium in the (n – k)-player game induced by the fixes choice of x by the first k players. Because at least half of the players choose x, the best reply can never be smaller than x (by increasing the appropriation level below x, the material payoff could be increased and the inequity disutility could be decreased as well). If we find
[0, xSNE] we define the strategy combination s(x) as follows: We fix s(x)i = x for i ≤ k and choose s(x)j for j > k as the joint best reply. That means that s(x)j is a part of a Nash equilibrium in the (n – k)-player game induced by the fixes choice of x by the first k players. Because at least half of the players choose x, the best reply can never be smaller than x (by increasing the appropriation level below x, the material payoff could be increased and the inequity disutility could be decreased as well). If we find ![]() , such that
, such that ![]() for i ≤ k, then
for i ≤ k, then ![]() is the desired equilibrium.
is the desired equilibrium.
Now
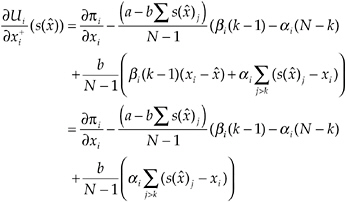
We then get
Hence, for some ![]() near enough to xSNE, we get
near enough to xSNE, we get ![]() The strategy combination s(
The strategy combination s(![]() ) is the desired equilibrium. QED
) is the desired equilibrium. QED
Proof of Proposition 4 (Equilibria with Sanctioning Possibilities)
Proof: We note:
(A) The condition ![]() guarantees that x maximizes the utility for the CCEs if all other players choose x.
guarantees that x maximizes the utility for the CCEs if all other players choose x.
We call a player a deviator who chooses an appropriation x’ that results in a higher payoff in the first stage compared to choosing x.
(B) If there is a single deviator, then the payoffs for the other players are smaller compared to the situation where there is no deviator.
First, if punishment is executed, the selfish players have no incentive to deviate. Because punishment results in equal payoffs for the CCEs and for the deviator, this payoff is smaller than the payoff in the first stage of the CCE. Hence, a selfish deviator has no incentive to deviate if he risks being punished.
Let us now prove that no CCE has an incentive to change the punishment strategy if a selfish player has not chosen x. Let πp be the payoff after punishment for the CCEs and for the deviator. Let πs be the payoff of the selfish players. A CCE player never has an incentive to choose a higher punishment than the equi
librium punishment. This only increases inequity with respect to all players and reduces the material payoff. So let w be a positive number and assume CCE player i chooses a punishment of p – w instead of p. We get:
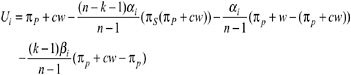
This is a linear function in w. Player i has no incentive to deviate iff the derivative with respect to w is negative, so iff
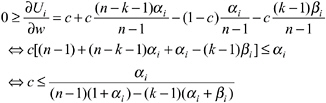
QED.




































