Page 1
Chapter 1
Unmasking Constructs Through New Technology, Measurement Theory, and Cognitive Science
Drew H. Gitomer and Randy Elliot Bennett
Educational Testing Service
Knowing What Students Know provides us with a compelling view of the future of educational assessment, a future that includes better information about student learning and performance consistent with our understandings of cognitive domains and of how students learn. That future also promises a much tighter integration of instruction and assessment. Realizing these ambitions depends on progress in the fields of cognition, technology, and assessment, as well as significant changes in educational policy at local and national levels.
The challenges to attaining the vision should not be underestimated. Key examples of cognitive models go back a quarter of a century or more (e.g., Brown & Burton, 1978; Siegler, 1976). Similarly, technology research efforts have demonstrated complex tasks that appear to assess problem solving in particular domains much more authentically than traditional methods (Steinberg & Gitomer, 1996). And our psychometric models are clearly up to characterizing human performance on these more complex tasks (e.g., Almond & Mislevy, 1999). Why, then, are we still very much in the early formative stages of a new generation of educational assessment (Bennett, 1998)?
One of the major obstacles is scale. Representing cognition in large domains remains a mammoth undertaking. We do not yet have the technology to rapidly and cost-effectively map the structure of knowledge for broad cognitive domains like the K-12 curriculum, for example. Designing tasks closely linked to these cognitive-domain structures is still a time-intensive enterprise reserved for a relatively small cadre of experts. The interpretation of evidence does not appear to face the same scaling limitations. If we can adequately scale the cognition and observation legs of the assessment triangle, we believe that the interpretation leg will not provide as great an obstacle.
Even if we can build assessments that scale cost effectively, we are still left with important policy questions. Will there be the political support for more textured assessments, or is there a comfort and familiarity with single summary scores, no matter how oversimplifying they may be? Will there be the willingness to give greater time, and funding, for assessments that provide better information? Time and economic constraints have had a major influence on the kinds of assessments that we currently practice. And will policy makers and educators give adequate attention to more formative assessments as a way of describing both student learning and the conditions affecting that learning? The more revealing an assessment, the more
Page 2
threatening it can be, for it can uncover issues around opportunities to learn that can be fairly well hidden with our traditional test structures.
In considering these significant challenges, at Educational Testing Service (ETS) we are trying to reconceptualize assessment at a number of levels. We'd like to share with you some of our colleagues' efforts that vary on a host of dimensions; some of these efforts represent incremental improvements in our most traditional assessments, while others involve radically new approaches to assessment consistent with the most ambitious visions of Knowing What Students Know. What these efforts have in common, though, is that they have used technology to help unmask the constructs that are the targets of assessment.
What do we mean by the unmasking of constructs and why is this important? Standardized assessments have often been characterized as irrelevant and arcane to the test taker. The recent characterizations of the Scholastic Aptitude Test (SAT) by Richard Atkinson, president of the University of California S ystem, are a striking example. Atkinson argues that the SAT is problematic, in part, because task types such as analogies are puzzle-like, limited in scope, and not directly linked to any California curricular frameworks. Thus, he contends that preparing for such tests distracts students and teachers from focusing on the important learning goals articulated in the state's K-12 content standards. Atkinson also makes the point that access to the secrets of these tests is not equitably distributed in our society.
Such criticisms are not unique, and they point to a historical problem with traditional tests—the masking of constructs, that is, a lack of clarity of the meaning associated with performance. On high stakes tests, such ambiguity causes overwhelming attention to particular task types and to test questions themselves. In attending so nearsightedly to these test components, we lose sight of the constructs underlying the measures and why the original designers thought those components might be useful indicators of important knowledge and skills. For example, while some might argue that verbal analogy items are irrelevant to content standards, most educators, including cognitive scientists, would agree that analogical reasoning is critical to learning and performance in virtually any discipline. Similarly, although reading comprehension items might be criticized for a lack of surrounding context, few would argue that the comprehension of written text is anything but essential.
The kinds of assessments envisioned in Knowing What Students Know are clearly designed to unmask the constructs by making the link between learning goals and assessment practices much more explicit. It is worth noting that much of the emphasis in this report is on providing rich, instructionally relevant assessment feedback to students. We would argue that the unmasking must begin far earlier. Students and teachers should have a much clearer sense of what is valued (i.e., the construct) through engagement with tasks more tightly coupled with content standards and instructional activities. The assessment tasks should facilitate, rather than interfere with, an understanding of what is important.
We will briefly discuss three efforts that attempt to further unmask important constructs. Recognizing the dominance of standardized assessments and the important issues that must be addressed before the promise of a new generation of assessments is realized, we begin with two efforts focused on our more traditional tests. In these projects, we investigate how we can help
Page 3
to make the constructs underlying standardized assessments more transparent to students and teachers, with the goal of altering the focus from the tasks themselves to the constructs they measure. Indeed, the unmasking of constructs was not the primary goal of either of these efforts but the unintended, and fortunate, consequence of attempts to improve traditional assessments.
Our third example is a prototype that illustrates the kind of purposefully designed assessment/instruction system that we believe represents the future of educational measurement. All three efforts have been made possible through advances in technology and assessment, as well as attention to the cognitive aspects of performance.
Our first project focuses on the production of greater diagnostic information for a test that was never designed to be diagnostic but to provide a summative judgment of a student's overall academic preparedness for college-level work: the Preliminary Scholastic Aptitude Test/National Merit Scholarship Qualifying Test (PSAT/NMSQT). This project confronted two questions: (1) What skills are necessary for success on the PSAT/NMSQT (and in college)? and (2) How can we communicate these skills, and ways to improve them, to students, teachers, parents, and counselors? To answer the first question, ETS staff conducted cognitive analyses to identify the skills required to solve test items. For the second question, they assembled three panels of math and English teachers who refined the report language, provided suggested activities for skill development, and prioritized the skills.
The essence of the approach was to extract, via psychometric modeling, diagnostic information from the pattern of item responses provided by the examinee. Solving each item requires some small subset of the skills tapped by the test section. The psychometric modeling allows the skill information to be aggregated across items so that meaningful statements can be made from what is essentially an item-by-skill patchwork. Uncertainty in that response pattern is accounted for by generating a mastery probability for each of the skills represented in the test. The basic psychometric machinery used is derived from the rule-space method of Tatsuoka (1995).
For the verbal section, 31 skills were identified. Examples are understanding difficult vocabulary, recognizing a definition when it is presented in a sentence, comprehending long sentences, understanding negation in sentences, choosing an answer based on the meaning of the entire sentence, and understanding writing that deals with abstract ideas. Sixteen mathematical skills were defined, including using basic concepts in arithmetic problem solving; creating figures to help solve problems; recognizing patterns and equivalent forms; understanding geometry and coordinate geometry; using basic algebra; making connections among math topics; dealing with probability, basic statistics, charts, and graphs; and applying rules and algorithms in algebra and geometry. Finally, the writing section was thought to tap 10 skills, such as using verbs correctly; recognizing improper pronoun use; following the conventions of word choice, phrases, and sentence construction; understanding the structure of sentences that contain abstract ideas; and understanding complicated sentences.
As a result of each individual's pattern of item performance, an enhanced score report is generated. An example of such a report is given in Figure 1-1. The report lists the three most promising skills for the student to work on and gives suggestions for improvement. For a diagnosis of understanding difficult vocabulary, the suggestion is:
Page 4
Figure 1-1 Sample enhanced score report for the PSAT. Note the bottom third of the report in which the specific instructional recommendations are provided. SOURCE:
http://www.collegeboard.com/psat/student/html/indx001.html [March 6, 2002] 
~ enlarge ~
Page 5
Broaden your reading to include newspapers and magazines, as well as fiction and nonfiction from before the 1900s. Include reading material that is a bit outside your comfort zone. Improve your knowledge of word roots to help determine the meaning of unfamiliar words.
For a diagnosis of applying rules and algorithms in algebra and geometry, the suggestion is:
Review algebra rules (such as exponents, solving equations and inequalities) and geometry rules (such as angles associated with parallel lines). Become familiar with geometric formulas at the beginning of math sections, and practice problems that use them.
There are several issues associated with the provision of such diagnostic feedback that can be informed by empirical analysis. One key concern is whether the skills identified for students explain test performance. Regressing PSAT/NMSQT scaled scores on mastery probabilities is a preliminary means of exploring this question. Such regression produced multiple correlations of .82 for math and .92 for writing on one test form, and .97 for each section on a second form. This initial finding suggests that the probabilities do a reasonable job of explaining test scores and, thus, making more visible the constructs underlying the PSAT/NMSQT. Another issue is whether the same set of skills would be identified for an examinee as needing improvement on other forms of the same test. Preliminary analyses across two forms for the mathematical and writing sections suggest that the proportion of students who would receive the same “needs improvement/doesn't need improvement” designation exceeds chance levels (.50) for the vast majority of skills. However, these results also imply significant variability in the consistency of skill profiles. Such variability is to be expected because the PSAT/NMSQT was not designed with the requisite numbers of items to support fine-grained, highly reliable diagnostics. Some variability in this context may be acceptable, though, because the decisions based on the diagnostics—which concern what to study next—are relatively limited in import and easily reversible. What appears to be highly valued, though, is that the mystery of the PSAT/NMSQT (and SAT I) for many users is revealed by more effective communication of the underlying constructs and by reasonable guidance that moves from test preparation to more construct-relevant instruction. Ultimately, the value of this approach will be determined by the extent to which students successfully engage in learning activities that develop these competencies.
To be sure, the PSAT/NMSQT project represents only a first step. This test was neither designed from a construct definition that would be meaningful to examinees nor intended to be diagnostic. Given those facts, we are limited in how meaningful we can make the construct or how usefully we can guide instruction. The challenge for the future is to design tests from inception so that examinees can understand both what is being measured and how to improve their performance on that underlying construct.
Our second example derives from a pragmatic need to generate many assessment tasks efficiently and effectively, which we have begun doing through the use of Test Creation
Page 6
Assistants (Singley & Bennett, 2002). Not only do we need to generate many assessment tasks, but we also want to be able to design tasks that have prespecified characteristics, including difficulty. To do this, we need to have a better understanding of the cognitive demands associated with particular tasks and task features. Again, the focus here is on our traditional assessments, though the basic approach can be generalized to other types of assessment tasks. The immediate goal is to automatically generate calibrated items so that costs can be reduced and validation is built into test development. Items are generated from templates that describe a content class. Each template contains both fixed and variable elements. The variable elements can be numeric or linguistic. Replacing the template's variables with values results in a new item.
The concept of automatic item generation goes back to the criterion-referenced testing movement of the 1960s-1970s, which introduced the notion of generating items to satisfy content specifications and psychometric requirements (Hively, Patterson, & Page, 1968). Further progress was made through research on intelligent tutoring in which generation proceeded from cognitive but not psychometric principles (e.g., Burton, 1982). More recent work has merged the cognitive and psychometric perspectives and demonstrated successful, though still experimental, applications (e.g., Bejar, 1993; Embretson, 1998).
The intent of these more recent efforts is to model both content and responses. This modeling can be done from strong or weak theory. Strong theory posits the cognitive mechanisms required to solve items and the features of items that cause difficulty. These approaches use design principles in manipulating item content to produce questions of desired difficulty levels. Variation in difficulty may be obtained by creating different templates, each intended to produce items in a particular target range, or by creating a single template to generate items spanning the desired range.
We use both weak and strong theories of performance within this general approach. Weak theory is used when strong theory does not exist, which is true especially in the broad domains covered by most admissions tests, where the intensive cognitive analysis needed to develop strong theory is not practical. Weak-theory approaches also attempt to generate calibrated items automatically, but do so from design guidelines. These guidelines constitute a theory of “invariance” which, in addition to indicating which features affect difficulty, suggests which ones do not. Empirically calibrated items spanning the target range are used as the basis for developing templates. Each template is then written to generate items of the same difficulty by varying the incidental features. Figure 1-2 is a template—essentially an abstracted representation—for a mathematics problem, while Figure 1-3 illustrates an item generated from that representation.
At ETS we have begun a research initiative to introduce automatic item generation into our large-scale testing programs. The studies cover the mathematical, analytical, verbal, and logical reasoning domains. The issues touch psychometrics (e.g., how does one calibrate items without empirical data?), security (e.g., at what point does a template become overexposed?), and operations (e.g., what tools might be constructed to help test developers create and test item templates?).
Page 7
Figure 1-2 An abstracted representation of a mathematics task or item template. SOURCE: ETS Mathematics Test Creation Assistant (TCA) 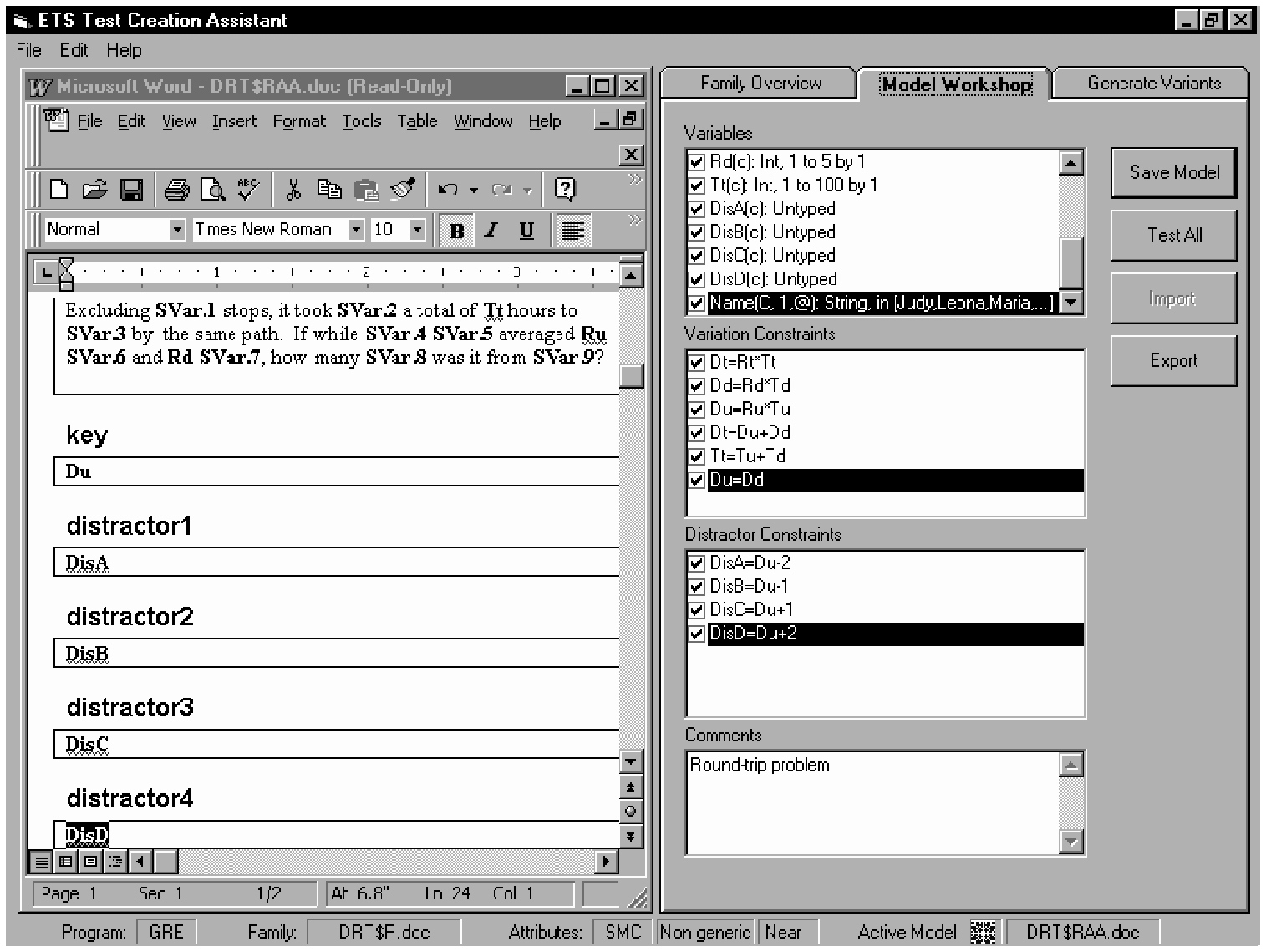
~ enlarge ~
Figure 1-3 A specific task generated automatically from the template. SOURCE: ETS Mathematics Test Creation Assistant (TCA) 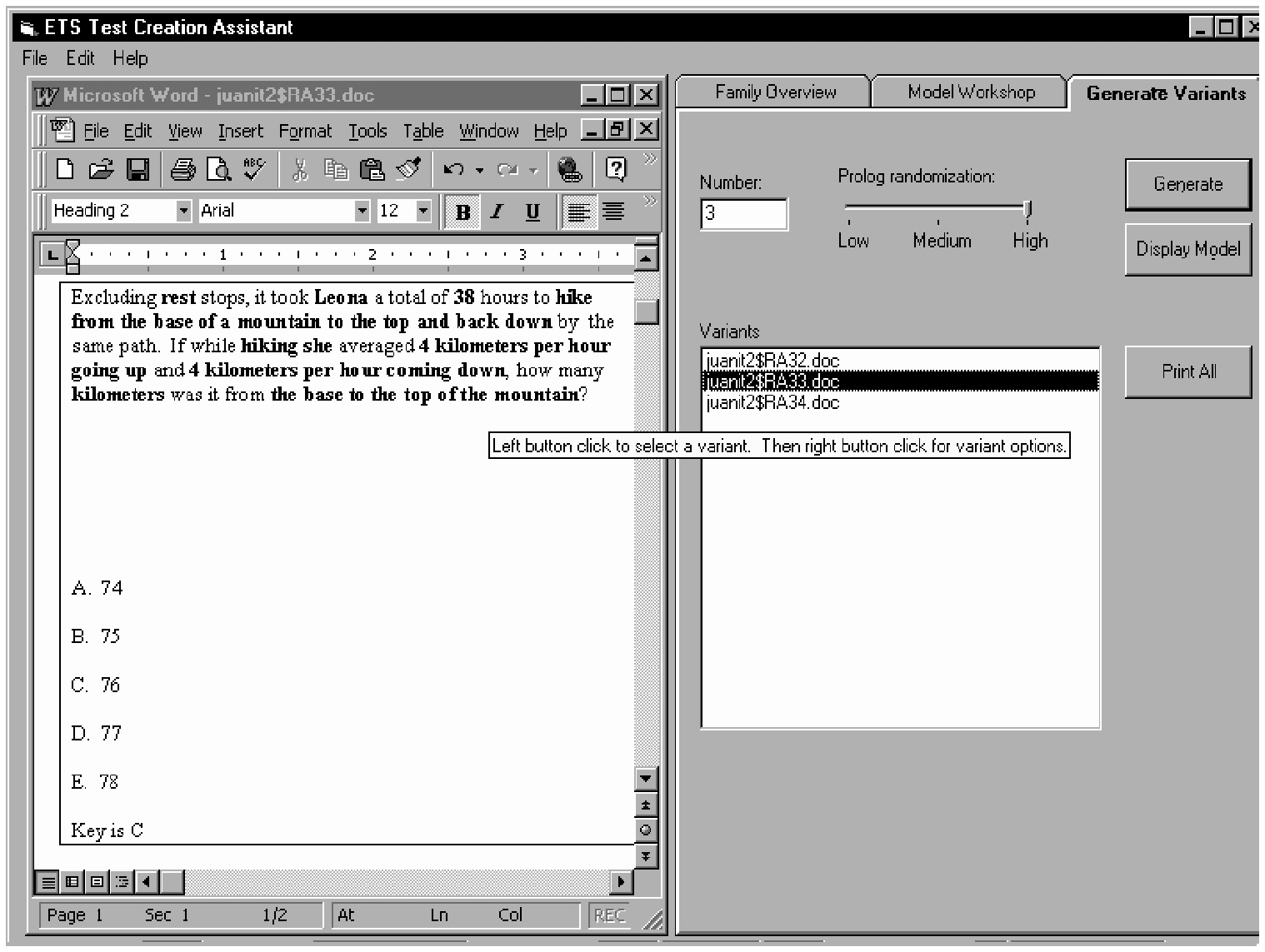
~ enlarge ~
Page 8
How does automatic item generation help to unmask the underlying construct? Generation from strong theory is most helpful in this regard because item content is modeled in terms of the demands it places on the cognitive apparatus abstracted from the particulars of any item. Thus, the structures and processes that underlie item performance must be made explicit. Otherwise, item parameters will not be accurately predicted, and the calibration goal will fail. But generation from weak theory may also be revealing because it allows tests to be described, designed, and implemented not as a large collection of unrelated problems but, rather, as a smaller set of more general problem classes with which we want students to be proficient. Designing tests in this way encourages instruction to focus on developing problem schemas that, according to cognitive theory, constitute the units into which all knowledge is packaged (Marshall, 1995; Rumelhart, 1980).
As an end state, what we would hope to do one day in the not too distant future is to make available to all assessment candidates an entire library of task models for all types of assessments. Based on the item templates, each task model would define in a more understandable way an important mathematical problem class. We would aspire to the goal that a full understanding of all task models constitutes a thorough understanding of the relevant domain. Thus, memorizing task models would not be seen as beating the test, but as a legitimate way of learning the domain. This, of course, implies that the set of task models must adequately represent the domain of interest.
Finally, we turn to our work that has the potential to help us develop a fundamentally new generation of assessments. The Evidence-Centered Design Framework (ECD) of Bob Mislevy, Linda Steinberg, Russell Almond, and others (e.g., Mislevy, Almond, Yan, & Steinberg, in press) provides tools and principles for developing assessments that, through every step of the design and delivery process, force a detailed thinking of the constructs to be assessed.
While the two previous examples involve some significant retrofitting and elaboration of existing tests, ECD pushes us into thinking of assessment development as an integrated design process. While ECD doesn't prescribe any particular cognitive-domain model, type of evidence, tasks, or scoring models, it does force designers into considering these aspects of assessment design very explicitly. We will illustrate our points by referring to BIOMASS, a prototype system developed by Mislevy, Almond, Yan, and Steinberg (in press) to assess understanding of transmission genetics. By adhering to a disciplined design process, the developer of an assessment must explicitly consider and represent the following:
The Domain—What concepts and skills constitute the domain, how are the various components related, and how are they represented? The domain representation becomes the vehicle to communicate, through the assessment process, the valued nature of understanding. One of the continuing criticisms of standardized assessments is that the domain representations that one would infer from looking at tests is often at odds with more robust conceptualizations of these domains. Therefore, if a domain is represented as a rich and integrated conceptual network, it would not be consistent to have an assessment that queried students about isolated facts. An abstracted representation of the science domain can be viewed in Figure 1-4. This representation highlights the interplay of domain-specific conceptual structures, unifying
Page 9
concepts, and scientific inquiry understanding as all contributing to an integrated understanding of science.
Figure 1-4 An abstracted representation of science understanding SOURCE: Mislevey et al., in press. 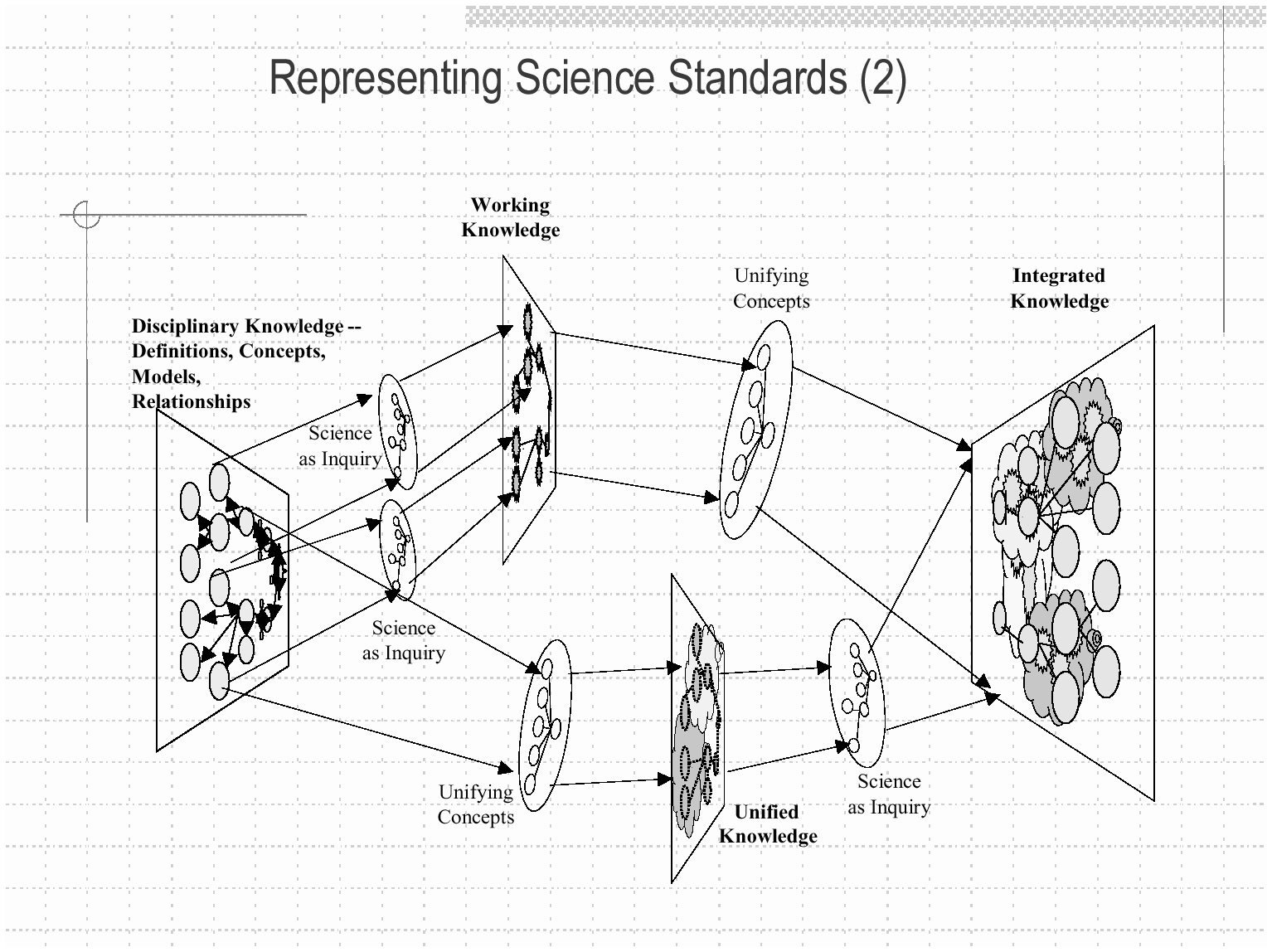
~ enlarge ~
It is also important to use the appropriate communicative methods and symbols for a given domain. Certainly, we wouldn't expect an assessment of musical skill that was strictly verbal, and we wouldn't expect an assessment of mathematics that did not require the use of numbers. Transmission genetics includes a complex conceptual structure as well as a set of domain-specific reasoning skills that are interleaved with genetics concepts. In addition, there are symbolic formalisms that scientists use to represent concepts within the domain.
The Evidence—What are the data that would lead one to believe that a student did, in fact, understand some portion of the domain model? What would a student have to demonstrate to show that he or she could perform at a designated level of accomplishment? Clarifying what the evidence should be is important, not only for the shaping of tasks but also to help students understand in very clear ways what is expected. For a richly represented domain, evidence would likely involve demonstrations of the ability to explain complex relationships. In the case of transmission genetics, evidence of understanding can be gauged, in part, by the ability to explain generational patterns for a variety of plausible conditions.
The Tasks—In light of domain and evidence requirements, assessment tasks can be developed. If the tasks are driven by such requirements, there is a much greater likelihood that the tasks will be focused, relevant, and representative. Note that the path of moving from domain, to evidence, to task is quite different from many traditional test-development practices
Page 10
in which the availability and constraints of particular tasks shape the assessment development. Note, too, that with an ECD approach, the tasks are more visibly construed as vehicles to elicit evidence, not as the definition of the assessment itself. (It is this same conceptual hurdle that must occur among teachers and students generally if assessment tasks are not to be the overwhelming focus of instruction.) In BIOMASS, a small set of complex scenarios with multiple layers have been designed to elicit evidence about students' understanding of transmission genetics. These scenarios, quite compatible with effective biology instruction, provide pieces of evidence relevant to different aspects of science understanding, e.g., disciplinary knowledge, model revision, investigation, etc. For example, one scenario provides evidence of student understanding of investigations and disciplinary knowledge, a second offers evidence of both these aspects together with evidence of understanding of how students revise their working mental models of phenomena (model revision) with new data, and a third is designed to give evidence of model revision only.
ECD also considers the interplay between these and other assessment components. How are tasks selected from an array of potential tasks? How are tasks presented amidst a set of constraints, including delivery options and time available? How are complex responses evaluated? How are response evaluations aggregated so that we can make statements about student performance with respect to the larger domain? Each of these considerations, in conjunction with explicit representations of the domain, the evidence, and the tasks, can give students insight into what matters and how a person can demonstrate specific levels of accomplishment.
CONCLUSION
We believe that each of the three above efforts—enhanced score reporting, automatic item generation, and evidence-centered design—is consistent with the vision espoused in Knowing What Students Know of forging a tighter integration of assessment and instruction. Our particular tactic has been to unmask the constructs we measure so that students can more easily improve their standing on them. By forcing a clarification of the domain and a consistent set of representations that govern what students see and how they are evaluated, ECD gives us a methodology for doing exactly that. A logical extension to ECD, automatic item generation, permits us to efficiently instantiate ECD's domain representations in terms of higher order task classes, which can themselves become a legitimate way of learning the domain. Finally, the technology of enhanced score reporting can be used to make clear the specifics of what a student needs to work on to improve. Clearly, these design, item creation, and reporting tools do not guarantee good assessment. But they can help reduce, if not eventually eliminate, the mystery associated with traditional tests, as well as improve the outlook for future assessments.
ACKNOWLEDGMENTS
We are grateful to the following individuals for their reviews of this paper (although the authors are solely responsible for the contents): Russell Almond, Isaac Bejar, Lou DiBello, Dan Eignor, and Linda Steinberg.
Page 11
REFERENCES
, & ( 1999 ). Graphical models and computerized adaptive testing. Applied Psychological Measurement , 23 223-238 .
( 1993 ). A generative approach to psychological and educational measurement. In N. Frederiksen, R.J. Mislevy, & I.I. Bejar (Eds.), Test theory for a new generation of tests ( pp. 323-357 ). Hillsdale, NJ : Erlbaum .
( 1998 ). Reinventing assessment: Speculations on the future of large-scale educational testing . Princeton, NJ : Policy Information Center, Educational Testing Service. Also as RR-97-14. Also available: ( http://www.ets.org/research/pic/bennett.html ).
, & ( 1978 ). Diagnostic models for procedural bugs in basic mathematics skills. Cognitive Science , 2 , 155-192 .
( 1982 ). Diagnosing bugs in a simple procedural skill. In D.H. Sleeman & J.S. Brown (Eds.), Intelligent tutoring systems ( pp. 157-183). London : Academic Press .
( 1998 ). A cognitive design system approach to generating valid tests: Application to abstract reasoning. Psychological Methods , 3 , 380-396 .
, , & ( 1968 ). A “universe-defined” system of arithmetic achievement tests. Journal of Educational Measurement , 5 , 275-290 .
( 1995 ). Schemas in problem solving . New York : Cambridge University Press .
, , , & (in press). On the roles of task model variables in assessment design. In S. Irvine & P. Kyllonen (Eds.). Generating items for cognitive tests: Theory and practice . Hillsdale, NJ : Erlbaum .
( 1980 ). Schemata: The building blocks of cognition. In R.J. Spiro, B.C. Bruce, & W.F. Brewer (Eds.), Theoretical issues in reading comprehension ( pp. 33-58 ). Hillsdale, NJ : Erlbaum .
( 1976 ). Three aspects of cognitive development. Cognitive Psychology , 8 , 481-520 .
, & ( 2002 ). Item generation and beyond: Applications of schema theory to mathematics assessment. In S. Irvine & P. Kyllonen (Eds.), Item generation for test development . Hillsdale, NJ : Erlbaum .
, & ( 1996 ). Intelligent tutoring and assessment built on an understanding of a technical problem-solving task. Instructional Science , 24 , 223-258
( 1995 ). Architecture of knowledge structures and cognitive diagnosis: A statistical pattern recognition and classification approach. In P. Nichols, S.F. Chipman, et al. (Eds.), Cognitively diagnostic assessment ( pp. 327-359 ). Hillsdale, NJ : Erlbaum .











