Page 50
Chapter 5
Cognitive Tutor Algebra I: Adaptive Student Modeling in Widespread Classroom Use
Albert Corbett
Human-Computer Interaction Institute Carnegie Mellon University
Individual human tutoring is perhaps the oldest form of instruction, and countless millennia since its introduction, it remains the most effective and most expensive form of instruction. Studies show that students working with the best human tutors attain achievement levels that are two standard deviations higher than students in conventional classroom instruction (Bloom, 1984; Cohen, Kulik, & Kulik, 1982). Over the past 15 years the Carnegie Mellon Pittsburgh Area Cognitive Tutor (PACT) Center has been developing an educational technology called cognitive tutors that provides some of the advantages of individual human tutoring. Cognitive tutors are rich problem-solving environments. Each cognitive tutor is constructed around a cognitive model of the problem-solving knowledge students are acquiring. The cognitive model is employed to provide two types of adaptive student support. In model tracing the cognitive model is used to interpret and respond to each of the student's problem-solving actions. In knowledge tracing, the tutor monitors the student's growing problem-solving knowledge and individualizes the problem sequencing accordingly.
This paper briefly describes three related topics. First, it introduces the Algebra I Cognitive Tutor and describes the project that brought this successful educational technology out of the research lab and into widespread classroom use. Next, the paper describes the cognitive theory underlying cognitive tutors and reports studies that assess the validity of knowledge tracing and its effectiveness in individualizing each student's problem-solving sequence. The paper concludes by suggesting future research directions.
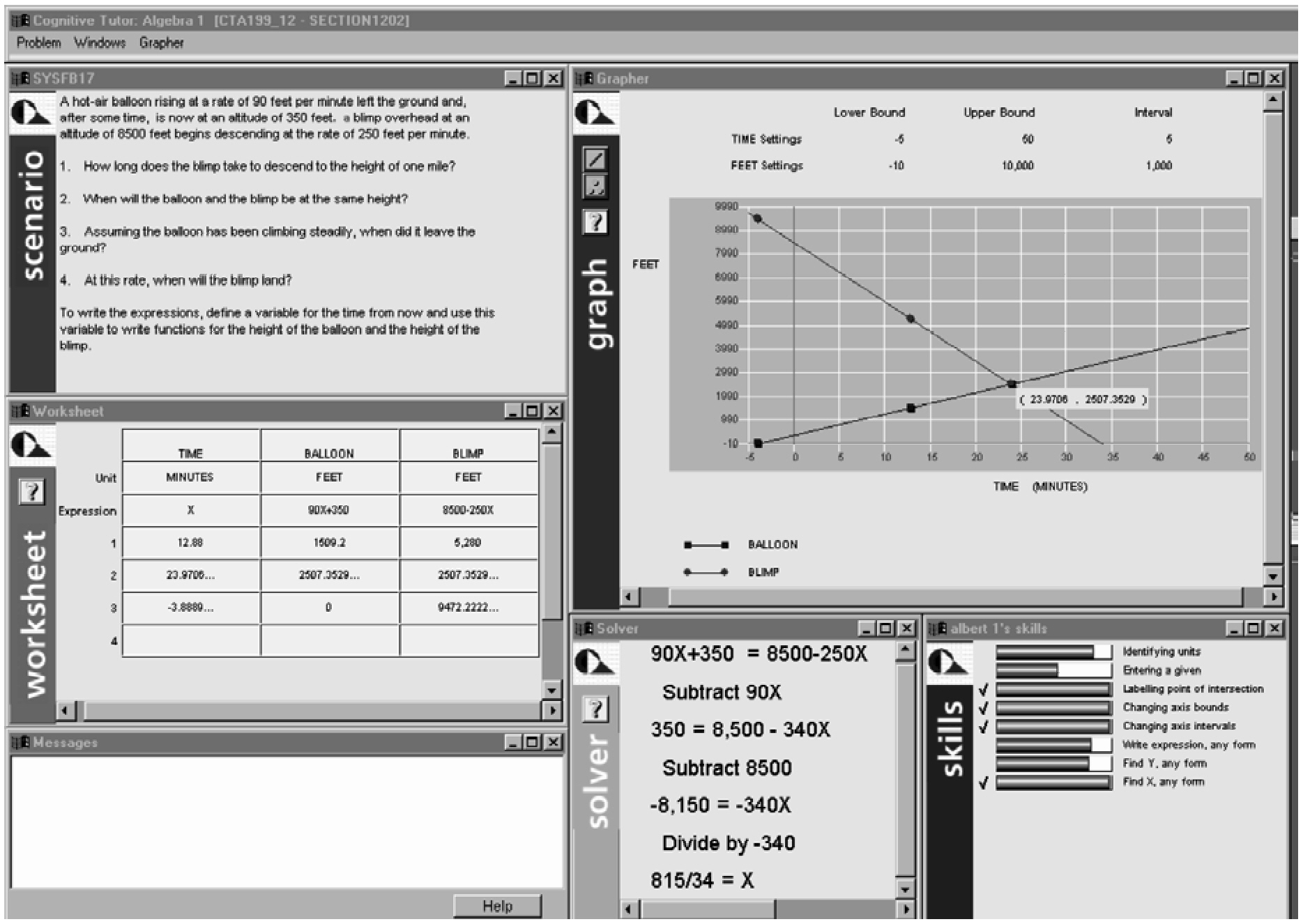
Figure 5-1 displays the Algebra I Cognitive Tutor near the completion of a problem. The problem situation is presented in the scenario window in the upper left corner of the screen:
A hot-air balloon rising at a rate of 90 feet per minute left the ground and, after some time, is now at an altitude of 350 feet. A blimp overhead at an altitude of 8500 begins descending at the rate of 250 feet per minute.
Four questions are posed for the student to answer:
- 1) How long does the blimp take to descend to the height of one mile?
- 2) When will the balloon and the blimp be at the same height?
- 3) Assuming the balloon has been climbing steadily, when did it leave the ground?
- 4) At this rate, when will the blimp land?
Page 51
The student answers the questions by filling in the worksheet immediately below the scenario window. The cells in the worksheet are blank initially. The student analyzes the problem situation, identifies the relevant quantities that are varying (in this situation, time and height of the airships), and labels the worksheet columns accordingly (“TIME,” “BALLOON,” and “BLIMP”). The student enters the appropriate units for measuring these quantities in the second row of the table and enters a symbolic model relating the three quantities in the third row. In the figure, the student has represented the quantity of time with the variable X, related the height of the balloon to time with the algebraic expression 90X + 350, and similarly related the blimp's height to time with the expression 8500 - 250X. Early in the curriculum, the student enters algebraic expressions near the end of the problem, and the individual questions are intended to help scaffold this algebraic modeling. By the time the student has reached the linear systems unit represented by the current problem, he or she tends to enter the algebraic expressions early in the problem. The emphasis in these problems is on using the expressions as problem-solving tools, both in symbol manipulation and to automatically generate values in the worksheet (as described below).
Figure 5-1 The Algebra I Cognitive Tutor.
~ enlarge ~
SOURCE: Carnegie Learning, Inc., 2000
The student answers the questions by filling in the corresponding rows in the worksheet. To answer the first question, “How long does the blimp take to descend to the height of one mile?” the student needs to perform a unit conversion on the given value, “one mile,” and enter 5280 in the question-1 cell of the BLIMP column, immediately below the formula. To compute
Page 52
the solution, the student can set up the equation 5280 = 8500 - 250X in the solver window in the lower center of the screen, solve it in the window, and type the answer, 12.88, into the question-1 cell of the TIME column. Or the student can type an arithmetic expression that unwinds the equation, (5280-8500)/ -250, directly into the question-1 cell of the TIME column, where it will be converted to 12.88. Once the value of X has been typed in this cell, the worksheet automatically generates the corresponding height of the balloon, 1509.2 feet at 12.88 minutes, employing the algebraic expression for balloon height typed by the student.
In completing the problem, the student also graphs the two linear functions in the graph window in the upper right corner of Figure 5-1. The student labels the axes, adjusts the upper and lower bounds on the axes, and sets the scales so that the data points in the table can be displayed. Note that in question 2, “When will the balloon and the blimp be at the same height?” the student is asked to solve for the intersection of the two functions, and in questions 3 and 4, the student is asked to find the x-intercept of the two functions. The student can answer these questions by finding the relevant points on the graph or by setting up and solving equations in the solver window. In Figure 5-1, the student has set up an equation to solve for the intersection of the two functions, 90X + 350 = 8500 – 250X, and proceeded to solve the equation by isolating X.
ADAPTIVE STUDENT MODELING
A central claim of Knowing What Students Know, the recent National Research Council report on educational assessment (NRC, 2001), is that three essential pillars support scientific assessment: a general model of student cognition, tasks in which to observe student behavior, and a method for drawing inferences about student knowledge from students' behaviors. Cognitive tutors embody this framework. Each cognitive tutor is constructed around a cognitive model of the knowledge students are acquiring. As a student performs problem-solving tasks such as that displayed in Figure 5-1, the cognitive model is employed to interpret the student's behavior, and simple learning and performance assumptions are incorporated to draw inferences about the student's growing knowledge.
Model Tracing
In model tracing, the underlying cognitive model is employed to interpret each student action and follow the student's individual solution path through the problem space, providing just the support necessary for the student to complete the problem successfully. The cognitive model is run forward step-by-step along with the student, and each student action is matched to the actions that the model can generate in the same context. As with effective human tutors, the cognitive tutor's feedback is brief and focused on the student's problem-solving context. If the student's action is correct, it is simply accepted. If the student makes a mistake, it is rejected and flagged (in red font). If the student's mistake matches a common misconception, the tutor also displays a brief just-in-time error message (in the window in the lower left corner of Figure 5-1). The tutor does not provide detailed explanations of mistakes, but instead allows the student to reflect on mistakes. Finally, the student can ask for problem-solving advice at any step. The tutor generally provides three levels of advice. The first level advises on a goal to be
Page 53
accomplished, the second level provides general advice on achieving the goal, and the third level provides concrete advice on how to solve the goal in the current context.
Knowledge Tracing
The cognitive model is also employed to monitor the student's growing knowledge in problem solving, in a process we call knowledge tracing. At each opportunity for the student to employ a cognitive rule in problem solving, simple learning and performance assumptions are employed to calculate an updated estimate of the probability that the student has learned the rule (Corbett & Anderson, 1995). These probability estimates are displayed in the skillmeter in the lower right corner of Figure 5-1. Each bar represents a rule, and the shading reflects the probability that the student knows the rule. As advocated by NRC (2001), the goal of knowledge tracing is to improve learning outcomes. It is employed to implement cognitive mastery. Within each curriculum section, successive problems are selected to provide the student the greatest opportunity to apply rules that he or she has not yet mastered. The tutor continues presenting problems in a section until the student has “mastered” each of the applicable rules in the curriculum section. (Mastery is indicated by a checkmark in the skill meter).
TRANSFORMING EDUCATIONAL PRACTICE
I believe that cognitive tutors for mathematics are the first intelligent tutoring systems that are beginning to have a widespread impact on educational practice. In the 2001-2002 school year, Cognitive Tutor Algebra and Geometry courses are in use at about 700 sites and by more than 125,000 students in 38 states. This includes urban, suburban, and rural middle and high schools, both public and private. This success in moving from the research lab into widespread classroom use depends on several factors, including project design, research-based development, demonstrated impact, and classroom support.
Project Design
Several project design features were essential to the success of the dissemination project (Corbett, Koedinger, & Hadley, 2001).
Opportunity: Targeting a National Need
National assessments such as the NAEP and international assessments such as the TIMSS have raised awareness of the need to improve mathematics education. Cities and states have increasingly mandated that all students need to master academic mathematics, and virtually every state has defined high-stakes academic mathematics assessments that are employed to evaluate schools and/or govern student graduation. For more than a decade, the National Council of Teachers of Mathematics (NCTM, 1989) has been recommending that academic mathematics for all students should place a greater emphasis on problem solving, reasoning among different mathematical representations, and communication of mathematical results. As a result of these trends, school districts actively look for, and are open to trying, new solutions to mathematics education, and Cognitive Tutor Algebra I aligns well with the NCTM-recommended objectives.
Page 54
Integrating Technology into a Comprehensive Solution
Teachers face a major “usability” challenge when they are trying to integrate educational technology into a course. It may be difficult to align course curriculum objectives and technology curriculum objectives and to make time for the technology activities. In our cognitive tutor mathematics project, cognitive tutors are fully integrated into yearlong courses. We develop both the paper text that is employed in 60 percent of class periods and the cognitive tutor that is employed in 40 percent of class periods. This coordinated development helps ensure that the problem-solving activities presented two days a week by the cognitive tutors address and develop the same curriculum objectives that students explore in small-group problem solving and whole-class instruction the other three days a week.
Interdisciplinary Research Team
The research team is a collaboration of cognitive psychologists, computer scientists, and practicing classroom teachers throughout the process of developing, piloting, evaluating, and disseminating a cognitive tutor course.
Research-Based Development
Cognitive tutor design is guided by multiple research strands, including cognitive psychology of student thinking (Heffernan & Koedinger, 1997; 1998), research in student learning (Koedinger & Anderson, 1998), and research in effective interactive learning support (Aleven, Koedinger, & Cross, 1999; Corbett & Trask, 2000; Corbett & Anderson, 2001). Formative evaluations of tutor lessons are employed to guide iterative design improvements, including studies of learning rate, validity of the underlying student model, and pre-test to post-test learning gains (Corbett, McLaughlin, & Scarpinatto, 2000).
Demonstrated Impact
Cognitive tutor courses have a demonstrable impact on the classroom, student motivation, and student achievement.
Substantial Achievement Gains
Beginning with our two earliest cognitive tutors, the ACT Programming Tutor (APT) and the Geometry Proof Tutor (GPT), cognitive tutor technology has an established history of yielding substantial achievement gains compared to conventional learning environments (Anderson, Corbett, Koedinger & Pelletier, 1995). College students working with APT completed a problem set three times faster and scored 25 percent higher on tests than students completing the same problems in a conventional programming environment. High school students in geometry classes that employed GPT for in-class problem solving scored about a letter grade higher on a subsequent test than students in other geometry classes who engaged in conventional classroom problem-solving activities. Koedinger, Anderson, Hadley, and Mark (1997) demonstrated that the Cognitive Tutor Algebra I course yields similar achievement gains.
Page 55
High school students in the Cognitive Tutor Algebra I course scored about 100 percent higher on tests of algebra problem solving and reasoning among multiple representations, and about 15 percent higher on standardized assessments than similar students in traditional Algebra I classes.
Student-Centered Learning-by-Doing
In cognitive tutor courses, students actively learn-by-doing, both in the cognitive tutor lab and in small-group problem solving in the classroom. Schofield (1995) formally documented the impact of cognitive tutors on the student-teacher relationship in a field study of the Geometry Proof Tutor in the mid-1980s. This was the first cognitive tutor deployed in high school classrooms. She found that teachers in the cognitive tutor lab serve as collaborators in learning. Teachers shift their attention to the students who need more help, and they can engage in more extended interactions with an individual student while other students in the class make substantial progress as they work with the cognitive tutor.
Increased Student Motivation
In the same study, Schofield (1995) documented that students are highly motivated and highly engaged in mathematics in the cognitive tutor lab. Teachers are excited about student attitudes and about engaging students in individualized discussions of mathematics. Letters from some of our Cognitive Tutor Algebra I teachers include such comments as “Gone are the phrases ‘this is too hard—I can't do this,' instead I hear ‘how do you do this? why is this wrong?'” and “Students now love coming to class. They also spend time during their study halls, lunch, before and after school working on the computers. Self-confidence in mathematics is at an all time high.”
Classroom Support
When a school adopts a cognitive tutor mathematics course, we also provide comprehensive classroom support that includes pre-service and in-service professional development, both on the cognitive tutor technology and on small-group problem solving in class. We also provide software installation, hotline support (both email and telephone) for pedagogical questions and technical problems, and email user groups and teacher focus group meetings.
U.S. Department of Education Exemplary Curriculum
In 1999 Cognitive Tutor Algebra I was designated an “exemplary” curriculum by the U.S. Department of Education. Sixty-one K-12 mathematics curricula were reviewed on three criteria: the program's quality, usefulness to others, and educational significance. Of these 61 curricula, five were awarded the highest, “exemplary,” designation.
Comments on Continued Scaling Up
Perhaps two key issues arise in considering the future growth in impact of cognitive tutor courses: the cost of developing new cognitive tutor courses and the need to provide high-quality site support.
Page 56
Cognitive Tutor Course Development
Our best current estimate of the development cost for a cognitive tutor course comes from our current Cognitive Tutor Middle School Mathematics Project in which we are developing three full-year courses. In this project, just over 100 hours of effort yields one hour of classroom activity. It should be emphasized that this estimate includes all aspects of design, development, piloting support, and evaluation including: developing the cognitive task analysis that underlies text and cognitive tutor design: writing the text: programming the cognitive model; programming the tutor interface; writing and coding the tutor problems; installing and maintaining the tutor; conducting teacher training; and designing, conducting, and analyzing formative and summative evaluations.
We believe that this cost level is already economically competitive, given the substantial impact of cognitive tutor courses on achievement outcomes and the demonstrable impact on student motivation. Evaluations of the mathematics and programming cognitive tutors indicate that model tracing alone can yield a one-standard deviation effect size, which is about half the benefit of the best human tutors (Anderson et al., 1995). Our estimations, based on evaluations of knowledge tracing and cognitive mastery in the programming tutor, suggest that this method of dynamic assessment and curriculum individualization can add as much as another half-standard deviation effect size (Corbett, 2001). We believe that the cost/benefit ratio will continue to improve as new research leads to improvements in tutor effectiveness. Perhaps the more important limiting factor in cognitive tutor course development is not the cost, but the availability of trained professionals to conduct cognitive task analyses and develop cognitive models.
Site Support
The single greatest challenge in site support is teacher training. As the Algebra and Geometry Cognitive Tutors become more robust, technical support is not a problematic issue. Teachers and students need little training in the use of the cognitive tutor software. Instead, the greatest need is to help students become not just “active problem solvers” but “active learners,” who view problem solving not as an end in itself, but as a vehicle for learning. Teachers need professional development to help students make use of the learning opportunities that arise in problem solving, not just in the cognitive tutor lab but also in small-group problem-solving activities during other class periods. As the deployment of cognitive tutor mathematics courses has grown, we have relied on a growing number of experienced cognitive tutor mathematics teachers to offer professional development. But this need for effective teacher development is not limited to our project. Research is needed to define effective teaching methods that support active student learning, and this knowledge needs to become integrated into pre-service teacher education.
COGNITIVE THEORY AND DYNAMIC ASSESSMENT
Cognitive tutors are grounded in cognitive psychology. The cognitive model underlying each tutor reflects the ACT-R theory of skill knowledge (Anderson, 1993). ACT-R assumes a fundamental distinction between declarative knowledge and procedural knowledge. Declarative
Page 57
knowledge is factual or experiential and goal-independent, while procedural knowledge is goal-related. For example, the following sentence and example in an algebra text would be encoded declaratively:
If the same amount is subtracted from the quantities on both sides of an equation, the resulting quantities are equal. For example, if we have the equation X + 4 = 20, then we can subtract 4 from both sides of the equation and the two resulting expressions X and 16 are equal, X = 16.
ACT-R assumes that skill knowledge is initially encoded in declarative form when the student reads or listens to a lecture. Initially the student employs general problem-solving rules to apply this declarative knowledge in problem solving, but with practice, domain-specific procedural knowledge is formed. ACT-R assumes that procedural knowledge can be represented as production rules—if-then rules that associate problem-solving goals and problem states with actions and consequent state changes. The following production rule may emerge when the student applies the declarative knowledge above to equation-solving problems:
If the goal is to solve an equation of the form X + a = b for the variable X, Then subtract a from both sides of the equation.
Substantial cognitive tutor research has validated production rules as the unit of procedural knowledge (Anderson, Conrad, & Corbett, 1989; Anderson, 1993).
Evaluating Knowledge Tracing and Cognitive Mastery
As the student works, the tutor estimates the probability that he or she has learned each of the rules in the cognitive model. The tutor makes some simple learning and performance assumptions for this purpose (Corbett & Anderson, 1995). At each opportunity to apply a problem-solving rule, the tutor
-
uses a Bayesian computational procedure to update the probability that the student already knew the rule, given the evidence provided by the student's response (whether the student's action is correct or incorrect), and
-
adds to this updated estimate the probability that the student learns the rule at this opportunity if it has not already been learned.
The goal of knowledge tracing is to promote efficient learning and enable cognitive mastery of the problem-solving knowledge introduced in the curriculum. Within each curriculum section, the tutor presents an individualized set of problems to each student, until the student has “mastered” the rule (typically defined as a 0.95 probability of knowing the rule).
Validating Knowledge Tracing: Predicting Tutor Performance
The same learning and performance assumptions that allow us to infer the student's knowledge state from his or her performance also allow us to predict student performance from the student's hypothesized knowledge state. A series of studies validated knowledge tracing in
Page 58
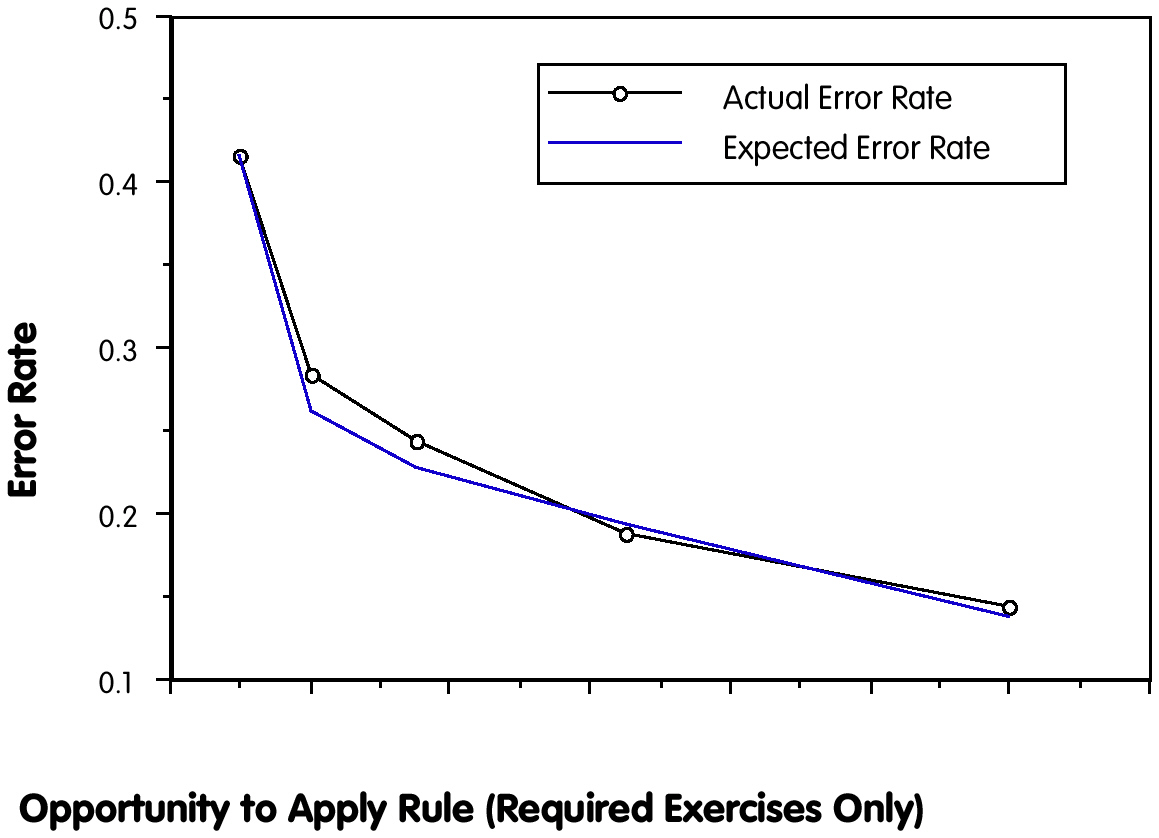
the ACT Programming Tutor by predicting student problem-solving performance, both in the tutor environment and in subsequent tests (Corbett & Anderson, 1995; Corbett, Anderson, & O'Brien, 1995). Figure 5-2 displays the mean learning curve, both actual and predicted, for a set of problem-solving rules in an early section of the ACT Programming Tutor. The first point in the empirical curve indicates that students had an average error rate of 42 percent in applying each of the rules in the set for the first time. Average error rate declined to under 30 percent across the second application of all the rules, and it continued to decline monotonically over successive applications of the rules. As can be seen, the knowledge-tracing model very accurately predicts students' mean production-application error rate in solving tutor problems.
Figure 5-2 Actual error rate and predicted error rate for successive applications of problem-solving rules in the ACT Programming Tutor.
SOURCE: Corbett, Anderson, & O'Brien, 1995, p. 26.
Validating Knowledge Tracing: Individual Differences in Post-test Performance
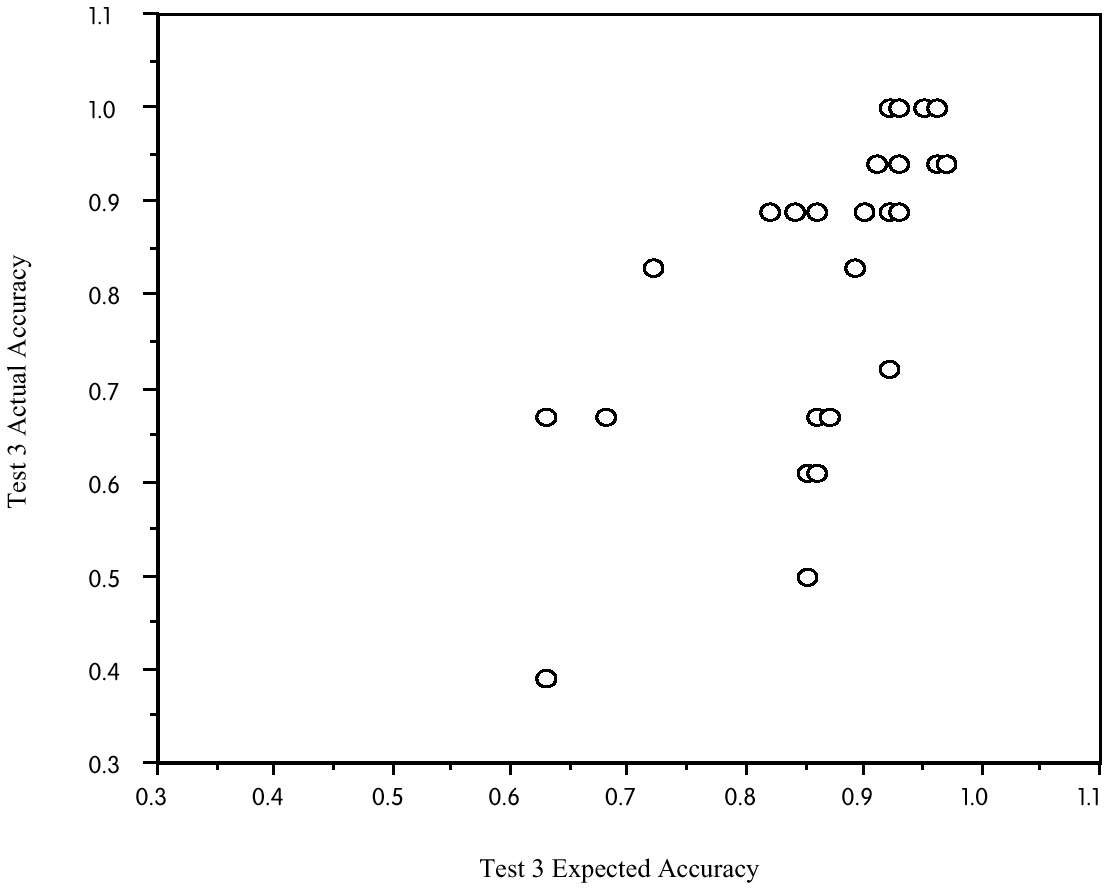
The more important issue is whether knowledge tracing accurately predicts students' performance when they are working on their own. A sequence of studies (Corbett & Anderson, 1995) examined the accuracy of the knowledge-tracing model in predicting students' post-test performance after they had completed work in the ACT Programming Tutor. Figure 5-3 displays quiz results for 25 students in the final study of the series. The figure displays each student's actual post-test accuracy (proportion of problems completed correctly), plotted as a function of the knowledge-tracing model's accuracy prediction for the student. As can be seen, the model predicted individual differences in test performance quite accurately. The model predicted that this group of students would average 86 percent correct, and they actually averaged 81 percent. The correlation of actual and expected performance across the 25 students is 0.66.
Page 59
Figure 5-3 Student post-test accuracy plotted as a function of accuracy predicted by the ACT Programming Tutor knowledge-tracing model. SOURCE: Corbett & Anderson, 1995, p. 274.
Cognitive Mastery Effectiveness
A recent study examined the efficiency of cognitive mastery learning (Corbett, 2001). In this study 10 students in a fixed-curriculum condition worked through a set of 30 ACT Programming Tutor problems. Twelve students in a cognitive mastery condition completed the fixed set of 30 problems and an additional, individually tailored sequence of problems as needed to reach mastery. On a subsequent test, students in the mastery condition averaged 85 percent correct on the test, while students in the fixed-curriculum condition averaged 68 percent correct. This difference is reliable, t(20) = 2.31, p < .05. Of the cognitive mastery students, 67 percent reached a high mastery criterion on the test (90 percent correct), while only 10 percent of students in the fixed-curriculum condition reached this high level of performance. Students in the cognitive-mastery condition completed an average of 42 tutor problems—40 percent more problems than students in the fixed-curriculum condition—and they only required 15 percent more time to do so. This investment of 15 percent more time yielded a high payoff in achievement gains.
Future Research
Three lines of research can be identified to enhance the educational effectiveness and broaden the impact of cognitive tutors in classrooms around the country:
-
We need to develop cognitive tutor interventions that will help students become more active learners and develop a deeper, conceptual knowledge of the problem-solving domain.
-
We also need to better understand how teacher interventions can help students become more active learners.
-
We need to develop authoring systems that can make cognitive tutor development faster.
Page 60
Students working with cognitive tutors are active problem solvers. The principal strength of cognitive tutors is that they expose learning opportunities in detail. They reveal students' missing knowledge and misconceptions step-by-step and afford students the opportunity to construct knowledge. However, the tutors' feedback and advice capabilities are limited. Both take the form of short written messages, with multiple levels of help available upon request at each problem-solving step. Studies show that students do not always make effective use of the assistance available. Eye-tracking studies of students working with the Algebra I cognitive tutor show that they often do not read or even notice the error feedback message (Gluck, 1999). Other studies with the Geometry Cognitive Tutor show that students often make poor use of the help that is available (Aleven & Koedinger, 2000). The knowledge-tracing validation research in the ACT Programming Tutor reveals a related point. The knowledge-tracing model consistently overestimates students' test performance by a small amount, about 10 percent. Studies suggest that this happens because some students are learning some shallow rules in the tutor that do not transfer to the test (Corbett & Knapp, 1996; Corbett & Bhatnagar, 1997).
Cognitive tutors are already at least half as effective as the best human tutors and two or three times as successful as conventional computer-based instruction (Corbett, 2001). They can become far more effective if they provide scaffolding to help students become not just active problem solvers, but active learners when learning opportunities are exposed. We have already had some success in engendering deeper learning with graphical feedback (Corbett & Trask, 2000) and student explanations of problem-solving steps (Aleven & Koedinger, in press), but we need to develop a more general framework for understanding effective tutorial scaffolding for student knowledge. Recent research is continuing to develop our understanding of effective human tutor tactics (e.g., Chi, Siler, Jeong, Yamauchi & Hausmann, 2001). We need to integrate these results into a general theory and to implement effective scaffolding in cognitive tutors.
Similarly, we need to better understand how the teacher in a cognitive tutor class can effectively scaffold active student learning. In the cognitive tutor lab, the teacher has the opportunity to interact with individual student tutors on an extended basis (Schofield, 1995), and there is preliminary evidence that the benefits of cognitive tutors can depend on the teacher's activities in the lab (Koedinger & Anderson, 1993). Research on effective human tutor tactics is relevant, but the classroom teacher needs some additional skills: recognizing when a “teachable moment” arises for one student in a classroom of 20-30 students and being able to jump into the student's problem-solving context to provide effective scaffolding. We also need to understand how teachers can best support small-group problem solving in cognitive tutor courses and integrate these group-paced classroom activities with the individually paced cognitive tutor activities. And we need to develop effective professional development based on this research in effective teacher strategies.
Finally, to broaden the impact of cognitive tutor technology, we need to develop authoring tools that can speed its design and implementation. These tools need to make cognitive tutor development more accessible to domain experts who do not have computer science or cognitive science backgrounds. At minimum, these tools should facilitate curriculum (problem situation) authoring. At best, these can be intelligent tools that make cognitive modeling more accessible to domain experts. In conjunction with this tool development, we need to begin designing cognitive tutors for other domains to examine how well the lessons
Page 61
learned in mathematics generalize. Middle school science would be an opportune domain, both for research and for purposes of educational impact.
In 1984 Bloom issued a challenge to develop educational interventions that are as effective as human tutors, but affordable enough for widespread dissemination. We believe that the research outlined here can make it possible to meet and even exceed Bloom's goal.
REFERENCES
, & (in press). An effective metacognitive strategy: Learning by doing and explaining with a computer-based Cognitive Tutor. Cognitive Science .
, & ( 2000 ). Limitations of student control: Do students know when they need help? In G. Gauthier, C. Frasson, & K. VanLehn (Eds.), Intelligent tutoring systems: Fifth International Conference, ITS 2000 ( pp. 292-303 ). New York : Springer .
, , and ( 1999 ). Tutoring answer explanation fosters learning with understanding. In S. Lajoie & M. Vivet (Eds.), Proceedings of the Artificial Intelligence and Education 1999 Conference ( pp. 199-206 ). Washington, DC : IOS Press .
( 1993 ). Rules of the mind . Mahwah, NJ : Lawrence Erlbaum Associates .
, , & ( 1989 ). Skill acquisition and the LISP Tutor. Cognitive Science , 13 , 467-505 .
, , , & ( 1995 ). Cognitive tutors: Lessons learned. The Journal of the Learning Sciences , 4 , 167-207 .
( 1984 ). The 2-sigma problem: The search for methods of group instruction as effective as one-to-one tutoring. Educational Researcher , 13 , 4-15 .
, , , , and ( 2001 ). Learning from human tutoring. Cognitive Science , 25 , 471-533 .
, , & ( 1982 ). Educational outcomes of tutoring: A meta analysis of findings. American Educational Research Journa l, 19 , 237-248 .
( 2001 ). Cognitive computer tutors: Solving the two-sigma problem. User Modeling: Proceedings of the Eighth International Conference, UM 2001 , 137-147 .
, & ( 1995 ). Knowledge tracing: Modeling the acquisition of procedural knowledge. User Modeling and User-Adapted Interaction , 4 , 253-278 .
, & ( 2001 ). Locus of feedback control in computer-based tutoring: Impact of learning rate, achievement and attitudes. In Proceedings of ACM CHI'2001 Conference on Human Factors in Computing Systems ( pp. 245-252 ).
, , & O'Brien, A.T. ( 1995 ). Student modeling in the ACT Programming Tutor. In P. Nichols, S. Chipman, & R. Brennan (Eds.), Cognitively Diagnostic Assessment ( pp. 19-41 ). Mahwah, NJ : Lawrence Erlbaum Associates .
, & ( 1997 ). Student modeling in the ACT Programming Tutor: Adjusting a procedural learning model with declarative knowledge. Proceedings of the Sixth International Conference on User Modeling . New York : Springer-Verlag Wein .
Page 62
, & ( 1996 ). Plan scaffolding: Impact on the process and product of learning. In C. Frasson, G. Gauthier, & A. Lesgold (Eds.), Intelligent tutoring systems: Third international conference , ITS ‘96 . New York : Springer .
, , & ( 2001 ). Cognitive Tutors: From the research classroom to all classrooms. In P. Goodman (Ed.), Technology enhanced learning: Opportunities for change ( pp. 235-263 ). Mahwah, NJ : Lawrence Erlbaum Associates .
, , & ( 2000 ). Modeling student knowledge: Cognitive Tutors in High School and College. User Modeling and User-Adapted Interaction , 10 , 81-108 .
, & ( 2000 ). Instructional interventions in computer-based tutoring: Differential impact on learning time and accuracy.
( 1999 ). Eye movements and algebra tutoring. Doctoral dissertation. Psychology Department, Carnegie Mellon University
, & ( 1997 ). The composition effect in symbolizing: The role of symbol production vs. text comprehension. In Proceedings of the Nineteenth Annual Conference of the Cognitive Science Society ( pp. 307-312 ). Mahwah, NJ : Lawrence Erlbaum Associates .
, & ( 1998 ). A developmental model for algebra symbolization: The results of a difficulty factors assessment. In Proceedings of the Twentieth Annual Conference of the Cognitive Science Society ( pp. 484-489 ). Mahwah, NJ : Lawrence Erlbaum Associates .
, & ( 1993 ). Effective use of intelligent software in high schoolmath classrooms. In P. Brna, S. Ohlsson, & H. Pain (Eds.), Proceedings of AIED 93 World Conference on Artificial Intelligence in Education ( pp. 241-248 ). Charlottesville, VA : Association for the Advancement of Computing in Education .
, & ( 1998 ). Illustrating principled design: The early evolution of a cognitive tutor for algebra symbolization. Interactive Learning Environments , 5 , 161-180.
, , , & ( 1997 ). Intelligent tutoring goes to school in the big city. International Journal of Artificial Intelligence in Education , 8 , 30-43 .
( 1989 ). Curriculum and evaluation standards for school mathematics . Reston, VA : Author .
. ( 2001 ). Knowing what students know: The science and design of educational assessment . Committee on the Foundations of Assessment. J. Pellegrino, N. Chudowsky, & R. Glaser (Eds). Board on Testing and Assessment, Center for Education. Division of Behavioral and Social Sciences and Education. Washington, DC : National Academ y Press .
( 1995 ). Computers and classroom culture . Cambridge, England : Cambridge University Press .