Appendix A
Comments on the Questionnaires and the Protocol
The questionnaires and other information provided to the study subjects or their parents (or parental surrogates) contain obvious inconsistencies between each other and with the study protocol presented. Examples follow (the references in parentheses, such as Tab 1 or Box 2, refer to the location in the documents the committee received from the investigators).
-
Consent form, page 1 (Tab 1): Specifies two purposes of the study—"if being exposed to fallout relates to changes in being able to have children or thyroid disease in families"— that are not among the stated objectives given in the protocol.
-
Consent form, page 2 (Tab 1) Item A6: Notes that “less than 5% of subjects will be chosen", but the proposal says 10% (on page 29, under "data management").
-
Consent form for fine-needle biopsy, page 2 (Tab 1): Says "treated, if needed, free of charge", but the original consent form says that costs will be borne by insurance if the subject is insured. Such treatment would not be free of charge even if only copayments are required.
-
Refusal Script, page 1 (Tab 6): States that the person would receive a visit from "two medical doctors who specialize in thyroid disease", but the protocol (page 20) states that the team would consist of a nurse practitioner or physician's assistant and a certified sonographer. Neither of the latter is necessarily a medical doctor, and neither necessarily specializes in thyroid disease.
-
New Subject Location Script, page I (Tab 7): States as eligibility criteria “born 1946 through 1958 Lived 1 year in Washington or Lincoln counties in period 1951 through 1958", whereas the eligibility criteria given in the protocol (page 10) states “born 1947 through 1953 Lived in Washington county May1953 through June 1953, or Lincoln county May 1952 through May 1953.” The two sets of criteria are substantially different.
-
Questionnaire Preparation Booklet (Tab 13, page 5 of 14): Asks the subject about medical history after age 17, but the Interview Booklet (for the parent) (Tab 14, page 21 of 31) asks only about the child's medical history up to age 15, and the Exposure Questionnaire (Tab 15, page 79) asks about the child's medical history up to age 18.
-
Questionnaire Preparation Booklet, page 11 (Tab 13): Requests information about "you/your spouse" pregnancies. But more is needed to obtain accurate reproductive histories such as information on pregnancies in all sex partners-and the response could be misleading if the spouse has been pregnant with parties other than the respondent.
-
Exposure Questionnaire, page 4 (Tab 15): Gives incorrect instructions: they cover a much longer period and wider geographic area than contemplated in the protocol.
-
Radiation Dose Determination: Protocol gives no real information on the model to be used for radiation-dose determination. It states that the model is shown in Figure 5 on page 18, but that diagram is meaningless without further description. Figure 5 should be replaced with a
-
figure that shows clearly the steps involved in the dose-estimation process to be used in Phase III. The current Figure 5 is extremely confusing: What does "environmental transport" (Box 8) contain, given that it has inputs of "source term", "animals", "cows/goats", and “commercial milk producers pooled”? How does "radiation released and transported" (Box 2) get to "animals ate contaminated vegetation" (Box 4) without going through "environmental transport" (Box 8)? No reference is provided for either the proposed model or any predecessors.
-
The effort required, or the time required, appears to have been substantially underestimated. Field work is said to require 2 years (page 20). Having two teams examine 5000 subjects means 1250 examinations per team per year, or about six examinations per team per working day. That is impossible, given that examinations are expected to take 60-90 minutes each.
The study protocol does not appear to have been adequately assessed with respect to potential sources of bias. In view of the likely marginal statistical power of the study, a thorough discussion, and preferably a quantitative evaluation, of potential sources of bias is essential, even for small potential biases. Examples follow:
-
Page 20: To minimize the possibility of bias in the review of ultrasound images, it is important that survey locations not be identifiable to reviewers on the basis of characteristics of the images. Will random study identification designation be used, and how will care be taken to avoid minor instrumentation or operator variation that could identify survey subjects in high- vs low-dose regions?
-
Page 22: The contact diagram shown on page 22 has the examiners interpreting the questionnaire. If a nodule is found, the subject is told and schedules fine-needle biopsy before completing the questionnaire. Subjects with immediately detected nodules thus have a potentially traumatic event thrust on them before they complete the questionnaire. That could bias their answers. Moreover, the examiners themselves will know the nodule status of the subject before they perform the review of the questionnaire with the subject—another potential source of bias.
-
Page 43: It seems that the "control" group will be substantially different from the "dosed" groups because of the inclusion of all the late movers. What will be done to evaluate whether that introduces a bias?
-
Page 48, Table 13: The table gives insufficient information to make any judgment about recall bias. In particular, there is no indication of the standard deviations. The table contains information on only 1528 subjects. Why so few, and was the method of selection determined to minimize the introducing of bias?
-
Page 49: The examiners are supposed to be unaware of exposure status, but they are going to start administering the questionnaire before they do the physical examination, and they are presumably going to talk to the subject and so might be made aware of the exposure status from the information so gained. There are instructions to the examiners to avoid such small talk, but it appears that it would be difficult or impossible to control or prevent it.
Appendix B
Power and Uncertainty Analysis of Epidemiologic Studies of Radiation-Related Disease Risk in which Dose Estimates are Based on a Complex Dosimetry System: Some Observations.
Daniel O. Stram, Department of Preventive Medicine, School of Medicine, University of Southern California, Los Angeles, California.
ABSTRACT
This paper discusses practical effects of dosimetry error relevant to the design and analysis of an epidemiologic study of disease risk and exposure. It focuses on shared error in radiation-dose estimates for such studies as the Hanford Thyroid Disease Study or the Utah Thyroid Cohort Study, which use a complex dosimetry system that produces multiple replications of possible dose for the cohort. I argue that a simple estimation of shared multiplicative error components via direct examination of the replications of dose for each person provides information useful for estimating the power of a study to detect a radiation effect. Uncertainty analysis (construction of confidence intervals) can be approached in the same way in simple cases. I also offer some suggestions for Monte Carlo-based confidence intervals.
1. INTRODUCTION
Several recent epidemiologic studies have used a complex dosimetry to estimate radiation-related health effects of exposures to fallout or nuclear-plant releases. Two examples are the Utah Thyroid Cohort Study [1] [2] and the Hanford Thyroid Disease Study (Draft Report). In both, individual doses of radioactive iodine (131I) to the thyroid gland were estimated decades after exposure. In this report, I make a number of observations concerning analysis of study power to detect a simple dose-response relationship and analysis of the uncertainty in estimated dose-response relationships. Those issues involve the uncertainty of dose itself in the study. The setting differs from the traditional measurement-error problem in that errors in dosimetry are not independent from subject to subject. For example, in the 131I setting, the basic approach (cf [3]) is to estimate total deposition of 131I onto grass, uptake by cows on pasture, transfer of iodine into cow’s milk, milk consumption by children, and uptake to the thyroid gland. For each subject, i, in the study, a set of personal data, Wi, regarding age and location of residence during the exposure period, source (backyard cow vs local dairy) and amount of milk consumed, and so on, is collected. The dosimetry system uses those data to impute a dose estimate. Shared uncertainties result, obviously, if such quantities as the total deposition onto grass or the average fraction of 131I that is excreted into cow’s milk are misidentified. Other uncertainties can be regarded as independent from person to person (for example, differences between true and reported milk consumption).
Increasingly, the approach to uncertainty in dose in such studies seems to be to develop a dosimetry system that gives not just one estimate of dose, but rather many replications (100 in the case of the Hanford study) of possible dose for each subject. Moreover, the estimates are not generated independently for each subject; instead, each run of the dosimetry system provides a new realization of possible dose for the entire study population, and the uncertainties in shared
characteristics result in a complex correlation between the dose estimates from subject to subject.
2. AN IDEALIZED DOSIMETRY SYSTEM
Let us pretend that this type of dosimetry system has evolved to the state where we can regard, in a Bayesian framework, each replication of dose to be a sample from the distribution, f(X1, X2,…, XN | W), for true dose, given the full set of input data, W, for all N subjects in the study. Because many replications, r, are available, we can calculate for each subject, i, the expected value of the unknown true dose, Xi, given the input data, Wi, available for the subject simply as the average of that subjects simulated Xi. We will call the expected value, Zi = E(Xi | Wi), the estimated dose for each subject. We assume that the data, Wi, are available for each subject (and the dosimetry system is in place) before the collection of outcome data, Di, for each subject (for example, as in the Hanford study). Finally we assume that Di is independent of Wi, given Xi (so that Wi consists of only “surrogate” variables).
3. FURTHER SIMPLIFICATIONS
I will now make some observations regarding the use of estimated dose, Zi, rather than true dose in the analysis of the dose-response relationship Di | Xi. We assume that E(Di | Xi) is of simple linear form, that is,
E(Di | Xi) = a + b Xi (3.1)
For now, to simplify discussion further, we assume that Di is a continuous outcome distributed symmetrically around its expected value, given true Xi. In addition, we can adopt a simple model for the joint distribution of the true doses, Xi, around the expected true doses, Zi, that incorporates both shared and unshared dosimetry errors. Suppose that we have
Xi = εSMεMiZi + εSA + εAi (3.2)
where εSM is shared multiplicative error, εMi is unshared multiplicative error, and εSA and εAi are shared and unshared additive error, respectively. Assume that the are all independent with E(εSM) = E(εMi) = 1 and E(εSA) = E(εAi) = 0. Let us first consider the situation when the shared multiplicative and additive error components are both fixed but unknown quantities. We can use standard regression techniques to fit
E(Di | Zi) = a* + b*Zi (3.3)
There will be a bias in estimating b using b* of size equal to εSM. Specifically, the estimate of b* obtained by fitting Equation 3.3 will be consistent for b × εSM. Now consider Var (![]() *), still treating εSM and εSA as fixed. For continuous Di and small b*, this will be approximately equal to
*), still treating εSM and εSA as fixed. For continuous Di and small b*, this will be approximately equal to
(3.4)
and we term this quantity the naïve estimate of variance of ![]() because it neglects the effects of shared error in the dose estimates. Finally, consider the total variance of
because it neglects the effects of shared error in the dose estimates. Finally, consider the total variance of ![]() * over the distribution of εSM and εSA. We will have
* over the distribution of εSM and εSA. We will have
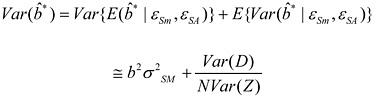
(3.5)
This expression implies that under the null hypothesis that b = 0, the expectation (over the shared error components) of the naïve estimate of the variance of ![]() * is equal to the true variance. However, if |b| > 0, the naïve variance estimate (3.4) is in fact biased downward by the amount
* is equal to the true variance. However, if |b| > 0, the naïve variance estimate (3.4) is in fact biased downward by the amount ![]() compared with the true variance. From that, we may conclude the following:
compared with the true variance. From that, we may conclude the following:
-
Ignoring shared error in the dosimetry system does not affect the asymptotic size of the test of the null hypothesis that b = 0.
-
However, sample sizes or the power of a test calculated under a specific alternative hypothesis, |b| > 0, will, if they ignore shared dosimetry error, be incorrect. Power will be overstated or, equivalently, the necessary sample size will be understated.
-
Confidence intervals will also be affected. Ignoring shared dosimetry error while constructing confidence intervals based on either the Wald or Score test will result in confidence intervals that are too narrow.
-
However, it is the upper bounds of |b|, and not the lower bounds, that are most affected; in particular, a confidence interval ignoring dosimetry error that does not overlap 0 will not overlap 0 once the shared errors in the dosimetry are properly handled. That follows because the validity of a test of the value b = 0 does not depend on shared dosimetry error, because the variance estimate of
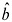 under the null hypothesis is correct.
under the null hypothesis is correct.
Estimation of all the variance parameters in the model of equation (3.2) can be achieved by consideration of the relationship between the variances and covariances between subjects across the replications of the dosimetry. In this model, the covariance of Xir with Xjr over the simulations is equal to
(3.6)
Let Cij for each subject i and j denote the sample covariances between Xir and Xjr over the replications, r. If we fit by OLS regression the model
E(Cij | Zj) = α + βZiZj (3.7)
for all i ≠ j, the intercept and slope estimates will provide estimates of ![]() and
and ![]() respectively. Similarly, the variance of Xir over the replications is equal to
respectively. Similarly, the variance of Xir over the replications is equal to
(3.8)
Linear regression of the sample variance estimates ![]() on
on ![]() will allow the estimation of
will allow the estimation of ![]() (intercept term) and
(intercept term) and ![]() (slope term in the regression). We now have two simple equations to solve for the two remaining unknowns
(slope term in the regression). We now have two simple equations to solve for the two remaining unknowns ![]() and
and ![]()
Such an analysis will give some useful information about the additional variation in ![]() expected because of shared error, and this can be directly incorporated into the power calculations if the model of equation (3.1) is correct. However, the most direct approach to calculating power under specific alternative hypotheses is undoubtedly by simulation. The logical approach is as follows. If we run the dosimetry system many times, the Zi values are computed as E(Xi | Wi) for each subject. Next, for each of the random replications, Xr, new random values of outcome variable Dir are generated under the model of interest, assuming that each Xir is true dose (so that Dir is taken as independent given Xir). For each set of outcome data, Dir is regressed upon the values Zi (which remain fixed over the simulations) to obtain a new estimate,
expected because of shared error, and this can be directly incorporated into the power calculations if the model of equation (3.1) is correct. However, the most direct approach to calculating power under specific alternative hypotheses is undoubtedly by simulation. The logical approach is as follows. If we run the dosimetry system many times, the Zi values are computed as E(Xi | Wi) for each subject. Next, for each of the random replications, Xr, new random values of outcome variable Dir are generated under the model of interest, assuming that each Xir is true dose (so that Dir is taken as independent given Xir). For each set of outcome data, Dir is regressed upon the values Zi (which remain fixed over the simulations) to obtain a new estimate, ![]() r, of b. The usual test statistic,
r, of b. The usual test statistic, ![]() 2/Var(
2/Var(![]() ), for testing the null hypothesis b = 0, here approximated as N
), for testing the null hypothesis b = 0, here approximated as N![]() r2Var (Z)/Var (D) , is computed and compared with the naïve critical value from the χ12 distribution. The naïve critical value may be used here because of observation 1 above. The number of times that the test statistic falls into the critical region is tabulated and used to compute an approximate power of the test.
r2Var (Z)/Var (D) , is computed and compared with the naïve critical value from the χ12 distribution. The naïve critical value may be used here because of observation 1 above. The number of times that the test statistic falls into the critical region is tabulated and used to compute an approximate power of the test.
4. UNCERTAINTY ANALYSIS
We first restrict our attention to simple models, such as that of equation (3.1), where unbiased estimates, ![]() , of b can be obtained by regression of Di on the Zi. Consider the construction of confidence intervals as the set of b for which the test statistic
, of b can be obtained by regression of Di on the Zi. Consider the construction of confidence intervals as the set of b for which the test statistic
(4.1)
takes values less than the chi-square critical value ![]() By the use of the notation Var(
By the use of the notation Var(![]() | b), we are explicitly expressing, as in Equation 3.5, the dependence of the variance of the estimator on the test value of b. If we think that the model of equation (3.2) holds and can estimate
| b), we are explicitly expressing, as in Equation 3.5, the dependence of the variance of the estimator on the test value of b. If we think that the model of equation (3.2) holds and can estimate ![]() we may consider approximating the test statistic as
we may consider approximating the test statistic as
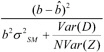
(4.2)
However, this approximation works only for small values of b. Note, for example, that this value approaches ![]() implying infinite upper bounds for small enough values of type I error α, which, of course, is unrealistic. A better approximation replaces Var(D) with
implying infinite upper bounds for small enough values of type I error α, which, of course, is unrealistic. A better approximation replaces Var(D) with
E{Var(D|Z)}, which is actually a function of b and the variances of the random-error terms. The simple constraint that Var(D|Z) ≥ Var(D|X) ≥ 0 will in combination with the variance parameters, impose an upper bound on possible values of b less than infinity. Of course this dependence greatly complicates the calculation of the criteria even under the simple model for dosimetry error given in equation (3.2).
Let us consider estimating the denominator of Expression 4.1 directly by simulation. This will require a series of simulations, one for each test value of b considered. Throughout the simulations, the observed value, ![]() , of the dose-response relation obtained by using Zi is held fixed. For each complete set, Xr, of replications of the dosimetry, a new set of responses, Dri, are simulated according to the dose-response model, using the test value, b. The outcomes are analyzed by using Zi to obtain a new dose-response estimate
, of the dose-response relation obtained by using Zi is held fixed. For each complete set, Xr, of replications of the dosimetry, a new set of responses, Dri, are simulated according to the dose-response model, using the test value, b. The outcomes are analyzed by using Zi to obtain a new dose-response estimate ![]() r . The variance, Var(
r . The variance, Var(![]() r | b), over the simulations is computed and used in Equation 4.1, to determine whether the test value of b is inside or outside the critical region.
r | b), over the simulations is computed and used in Equation 4.1, to determine whether the test value of b is inside or outside the critical region.
This brute-force simulation approach will work only for relatively simple models. In particular, we have assumed that the sampling variance of ![]() does not depend on the intercept parameter, a, and this will generally not hold for binary or counted data. If the intercept parameter markedly affects the variance of
does not depend on the intercept parameter, a, and this will generally not hold for binary or counted data. If the intercept parameter markedly affects the variance of ![]() r we will need a two-dimensional search that requires simulations for each possible pair of values of (a,b) to determine whether they jointly satisfy the equation
r we will need a two-dimensional search that requires simulations for each possible pair of values of (a,b) to determine whether they jointly satisfy the equation
Here, the variance term is the variance-covariance matrix of ![]() r and
r and ![]() r estimated by simulation at the test values (a,b).
r estimated by simulation at the test values (a,b).
5. MONTE CARLO MAXIMAL LIKELIHOOD
For models that are nonlinear in X (so that directly regressing Di on Zi produces biased estimates) or for models with many background risk parameters or many interactions between dose-response relation and other factors, it might be infeasible to consider construction of confidence intervals in the manner described above. We outline briefly here a simulation-based approach for maximal likelihood that in principle can be used both to approximate maximal likelihood estimates and to construct approximations to full likelihood-based confidence limits (based on the change in the log-likelihood). This discussion is based on Geyer 1996 [4]. Let l(a,b), be the log-likelihood ratio for testing the null hypothesis that (a,b) = (a0,b0). Because the full likelihood, f(D,W) is equal to the integral ∫f(D,X | W)dX, we have
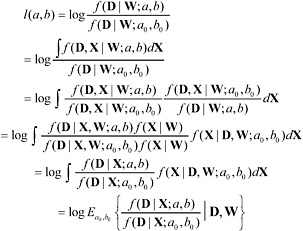
(5.1)
If there is a way of generating a total of n samples, Xr, from the distribution
f(X | D,W;a0,b0) (5.2)
of true dose, X, given both disease, D, and input data, W, we can approximate Equation 5.1 as
(5.3)
Notice that in principle the choice of a0 and b0 in 5.2 is arbitrary and that the change in log-likelihood for any two choices of the parameters (a1, b1) vs (a2, b2) can be written as l(a2,b2)-l(a1,b1). Thus, it appears that we can remove the conditioning on D in Equation 5.1 by choosing b0 = 0, so that Di is independent of Xi. That implies that we can contemplate the calculation of confidence limits for the dose-response parameter b by using the samples, Xr, from f(X|W) provided by the dosimetry system in Equation 5.3.
In general, this simple approach will work well only for b near 0 because as |b| > 0 the ratio in the summand of Equation 5.3 becomes extremely variable, requiring a prohibitive amount of computer time to evaluate the expectation numerically. In general, it is best, numerically, to perform the simulation by using the maximal likelihood estimate of a and b as a0 and b0 in Expression 5.2. Thus, if the dose-response relation is strongly significant, it will be important to provide a means of sampling from the conditional distribution of X, given both W and D. Rejection techniques, such as the Metropolis Hastings algorithm, can in principle be used to transform samples from the conditional distribution given only W to the appropriate distribution, thereby allowing implementation of the relatively complex simulation-based schemes. The basic idea is as follows. An initial Xr is sampled, and then a new Xr+1 is sampled. For each element i, the Hastings criteria are computed
and Xr,i is replaced with Xi with probability pi; otherwise, Xr,i is reused. It is unclear, however, whether the convergence properties of the Monte Carlo EM is based on rejection sampling or of other Monte Carlo methods, such as Gibbs sampling, will be adequate to allow for routine use.
6. DISCUSSION
The techniques described here are based on accepting the notion that the dosimetry system does indeed provide samples from the full joint conditional distribution of true Xi, given the measured input data, Wi, for each subject. In most cases, the uncertainty in dose reflected in the dosimetry system is due to lack of knowledge of parameters (such as true deposition or milk-transfer factors) or data (such as errors in questionnaire data), and the randomness between replications of the dosimetry system represents, at best, a consensus of expert opinion about the likely values of each of the unknown parameters or data. We have simply carried this exercise one step forward; using these approaches is designed to yield a consensus view of the power and uncertainty of a study based on the uncertain dosimetry available.
The simple shared-error model in equation (3.2) clearly may be a vast oversimplification of the error structure of a complicated dosimetry system. It may be useful to expand further on this model to introduce additional terms. For example, subjects whose milk source is the backyard cow will share the uncertainty in the (herd average) values of milk-transfer factors for these animals, not the uncertainty in the (herd average) values of milk-transfer factors for commercial animals. Restricting the estimation of the shared components of variance, using equation (3.7), to similar subjects will allow estimation of separate shared and unshared variance components to reflect this sort of additional complication. Power and uncertainty can be discussed more fully with such an expanded model. The simulation approaches described above, for power and uncertainty, do not depend on the validity of the simple shared-error model given in equation (3.2), however, and are appropriate as long as we can regard each replication from the dosimetry system as representing a sample from the conditional distribution of true dose.
REFERENCES
1. Till, J. E., Simon, S. L., Kerber, R., Lloyd, R. D., Stevens, W., Thomas, D. C., Lyon, J. L., et al. The Utah Thyroid Cohort Study: Analysis of the Dosimetry Results. Health Phys. 68:472-83, 1995.
2. Kerber, R. A., Till, J. E., Simon, S. L., Lyon, J. L., Thomas, D. C., Preston-Martin, S., Rallison, M. L., et al. A Cohort Study of Thyroid Disease in Relation to Fallout from Nuclear Weapons Testing. JAMA. 270:2076-82, 1993.
3. NCI (National Cancer Institute). Estimated Exposures and Thyroid Doses Received by the American People from Iodine-131 in Fallout Following Nevada Atmospheric Nuclear Bomb Tests: A Report from the National Cancer Institute. Bethesda, MD: National Cancer Institute. 1997.
4. Geyer, C. Estimation and Optimization of Functions. In Markov Chain Monte Carlo in Practice Chapman and Hall . W.R. Gilks, S.T. Richardson, and D.J. Spiegelhalter, Editors. Chapman and Hall. p. 241-258, 1996.









