8
The Measurement of Opportunity to Learn1
Robert E. Floden*
Sometimes it seems as though, in the United States at least, the attention to student opportunity to learn (OTL) is even greater than the attention to achievement results. For the Third International Mathematics and Science Study (TIMSS), the finding that the U.S. curriculum is “a mile wide and an inch deep” may be better remembered than whether U.S. students performed relatively better on fourth-grade mathematics or on eighth-grade science. To be sure, the interest in what students have a chance to learn is motivated by a presumed link to achievement, but it is nonetheless striking how prominent OTL has become. As McDonnell says, OTL is one of a small set of generative concepts that “has changed how researchers, educators, and policy makers think about the determinants of student learning” (McDonnell, 1995, p. 305).
Over more than three decades of international comparative studies, OTL has come to occupy a greater part of data collection, analysis, and reporting, at least in studies of mathematics and science learning. The weight of evidence in those studies has shown positive association between OTL and student achievement, adding to interest in ways to use OTL data to deepen understanding of the relationships between schooling and student learning. In the broader realm of education research, its use has been extended to frame questions about the learning opportunities for others in education systems, including teachers, administrators,
and policy makers. In education policy, the concept is used to frame questions about quality of schooling, equal treatment, and fairness of high-stakes accountability. It seems certain to play a continuing part in international studies, with a shift toward use as an analytic tool now that the general facts of connections to achievement and large between-country variations have been repeatedly documented.
Given its importance, it is worth considering what hopes have been attached to OTL, how it has been measured, how it has actually been used, and what might be done to improve its measurement and productive use. This chapter will address these several areas by looking at the role of OTL in international comparative studies and at its use in selected U.S. studies of teaching, learning, and education policy. Most attention will fall on studies of mathematics and science learning because those are the content areas where the use of OTL has been most prominent, in part because it has seemed easier to conceptualize and measure OTL in those subject areas.
WHAT IS OTL?
The most quoted definition of OTL comes from Husen’s report of the First International Mathematics Study (FIMS): “whether or not . . . students have had the opportunity to study a particular topic or learn how to solve a particular type of problem presented by the test” (Husen, 1967a, pp. 162-163, cited in Burstein, 1993). (The formulation, with its mention of both “topic” and “problem presented by the test,” hints at some of the ambiguity found both in definition and in measurement of OTL.) Husen notes that OTL is one of the factors that may influence test performance, asserting that “If they have not had such an opportunity, they might in some cases transfer learning from related topics to produce a solution, but certainly their chance of responding correctly to the test item would be reduced” (Husen, 1967a, pp. 162-163, cited in Burstein, 1993).
The conviction that opportunity to learn is an important determinant of learning was incorporated in Carroll’s (1963) seminal model of school learning, which also extended the idea of opportunity from a simple “whether or not” dichotomy to a continuum, expressed as amount of time allowed for learning. By treating other key factors, including aptitude and ability as well as opportunity to learn, as variables expressed in the metric of time, Carroll’s model created a new platform for the study of learning. One important consequence was that the question became no longer “What can this student learn?” but “How long will it take this student to learn?” Questions of instructional improvement have, as a result, been reshaped to give greater prominence to how much time each student is given to work on topics to be mastered. In the United States, this new
view of aptitude contributed to the shift from identifying which students could learn advanced content to working from the premise that all students could, given sufficient time, learn such content. That shift supports the interest in opportunity to learn as a potentially modifiable characteristic of school that could significantly affect student learning.
Carroll posits that the degree of student learning is a function of five factors:
-
Aptitude—the amount of time an individual needs to learn a given task under optimal instructional conditions.
-
Ability—[a multiplicative factor representing the student’s ability] to understand instruction.
-
Perseverance—the amount of time the individual is willing to engage actively in learning.
-
Opportunity to learn—the time allowed for learning.
-
Quality of instruction—the degree to which instruction is presented so as not to require additional time for mastery beyond that required by the aptitude of the learner.
(Model as presented in Borg, 1980, pp. 34-35)
Of these factors, the first three are characteristics of the student; the last two are external to the child, under direct control of the teacher, but potentially influenced by other aspects of the education system. The model specifies the functional form of the relationship, starting with the general formulation that the degree of learning is a function of the ratio between time spent learning and time needed to learn:
The model elaborates on this function, expressing “time spent learning” as the product of “opportunity to learn” and “perseverance,” and “time needed to learn” as a product of “aptitude,” “quality of instruction,” and “ability to understand instruction” (see Figure 8-1). (The last three variables are scaled counterintuitively, so that a low numerical value is associated with what one would typically think of as “high” aptitude or “high” quality of instruction.)
Carroll’s model, with its general emphasis on the importance of instructional time, was elaborated by Bloom (1976) and Wiley and Harnischfeger (1974). The concept of OTL has been differentiated so that it involves more than a simple time metric. One set of distinctions has separated the intentions for what students will study from the degree to which students actually encounter the content to be mastered. Imagine a
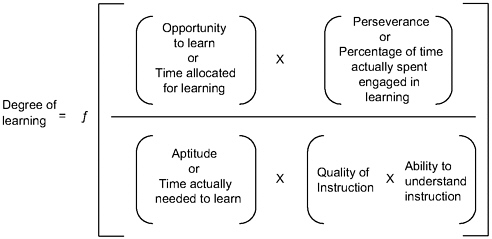
FIGURE 8-1 The Carroll model.
SOURCE: Berliner (1990). Reprinted with permission of Teachers College Press.
progression that starts at a distance from the student—say with a national policy maker—and goes through successive steps, nearer and nearer to the student, ending with content to which the student actually attends. At each step in this chain, a form of OTL exists if the content is present to some degree and does not exist if the content is absent.
Studies could attempt to measure the degree of any of these types of OTL: To what extent is the topic emphasized in the national curriculum? In the state curriculum? In the district curriculum? In the school curriculum? How much time does the teacher plan to spend teaching the content to this class? How much time does the teacher actually spend teaching the topic? How much of that time is the student present? To what degree does the student engage in the corresponding instructional activities? (In Carroll’s model, the latter may be part of “perserverance.”) For each level, common sense and, in some cases, empirical evidence suggest that OTL will be related to whether or how well students learn the content.
International comparative studies, and the International Association for the Evaluation of Educational Achievement (IEA) studies in particular, have divided this chain of opportunities into two segments, or “faces” of the curriculum: the intended curriculum and the implemented curriculum. (A third “face” of the curriculum, the “attained curriculum,” is what students learned. That represents learning itself, rather than an opportunity to learn.) For each link in this chain, a study could measure opportunity to learn as a simple presence or absence or as having some degree of emphasis, usually measured by an amount of time intended to be, or
actually, devoted to the topic. At the level of national goals, for example, one could record whether or not a topic was included, or could record some measure of the relative emphasis given to a topic by noting how many other topics are mentioned at the same level of generality, by examining how many items on a national assessment are devoted to the topic, or by constructing some other measure of relative importance. For the implemented curriculum, emphasis on a topic could be measured by the amount of time spent on the topic (probably the most common measure), by counting the number of textbook pages read on the topic, by asking the teacher about emphasis given to the topic, and so on.
Early studies that used time metrics for opportunity to learn2 looked at several ways of deciding what time to count. These studies looked for formulations that would be highly predictive of student achievement and that could be used to make recommendations for changes in teaching policy and practice. Wiley and Harnischfeger (1974) began by looking at rough measures of the amount of time allocated in the school day, finding a strong relationship between the number of hours scheduled in a school year and student achievement. The Beginning Teacher Evaluation Study (BTES) (Berliner, Fisher, Filby, & Marliave, 1978) also found that allocated time, in this case the time allocated by individual teachers, was related to student achievement. To obtain an even stronger connection to student achievement, the investigators refined the conception of opportunity to learn, adding information about student engagement in instructional tasks and about the content and difficulty of the instructional tasks to their measurement instruments.
Following the work of Bloom (1976), Berliner and his colleagues argued that student achievement would be more accurately predicted by shifting from allocated time to “engaged” time. That is, students are more likely to learn if they not only have time that is supposed to be devoted to learning content, but also are paying attention during that time, if they are “engaged.” Pushing the conception even further, they argued that the student should not only be engaged, but should be engaged in some task that is relevant to the content to be learned. That is, the opportunity that counts is one in which the student is paying attention, and paying attention to material related to the intended learning. Finally, the research group studied what level of difficulty was most related to student learning, asking whether it was more productive for students to work on tasks where the chance of successfully completing the task was high, moderate, or low. They found that student achievement was most highly associated with high success rate.3 Therefore, the version of opportunity to learn that they found to be tied most closely to student learning is what they dubbed “Academic Learning Time” (ALT), defined as “the amount of time a stu-
dent spends engaged in an academic task [related to the intended learning] that s/he can perform with high success” (Fisher et al., 1980, p. 8).
Measuring this succession of conceptions of OTL—allocated time, engaged time, time on task, Academic Learning Time—requires increasing amounts of data collection. Allocated time can be measured by asking teachers to report their intentions, through interview, questionnaire, or log. Measuring engaged time requires an estimate of the proportion of allocated time that students were actually paying attention.4 Measuring time on task requires a judgment about the topical relevance of what is capturing the students’ attention. Measuring Academic Learning Time requires an estimate of the degree to which students are completing the tasks successfully.
In their study of the influence of schooling on learning to read, Barr and Dreeben (1983) supplemented data on amount of time spent with data on the number of vocabulary words and phonics concepts students studied. Building on their own analysis of the literature growing out of Carroll’s model, they investigated how the social organization of schools, especially the placement of students into reading groups, worked to influence learning, both directly and through the mediating factor of content coverage by instructional groups. They argue that Carroll’s model is a model for individual learning, rather than school learning, in the sense that it describes learning as a function of factors as they influence the student, without reference to how those factors are produced within the social settings of the school or classroom.
For large-scale international comparative studies, these conceptions of OTL suggest a continuum of tradeoffs in study design. Each conception of OTL has shown some connection to student achievement. The progression of conceptions from system intension to individual time spent on a topic moves successively closer to the experiences that seem most likely to influence student learning. But the problems of cost and feasibility also increase with the progression. The model of learning suggests that the link will be stronger if OTL is measured closer to the student; policy makers, however, are more likely to have control of the opportunities more distant from students.
Questionnaires have been used in international studies to gather information on allocated time, tied to specific content. Such questionnaires give information on time allocation and the nature of the task, but shed little light on student engagement in the tasks, or on students’ success rate. Ball and her colleagues’ pilot study of teacher logs (Ball, Camburn, Correnti, Phelps, & Wallace, 1999) raises questions about teachers’ ability to estimate the degree of student engagement. (Nearly a century ago, Dewey [1904/1965] claimed that it is difficult for anyone to determine when a student is paying attention. The difficulty probably increases with
the age of students.) Teachers might be able to report on the students’ success rate at a task, but that success rate probably varies across tasks, suggesting that measurement at a single time (e.g., with a questionnaire) would be unlikely to capture difficulty for the school year as a whole. Given the ambiguity about whether engagement is a part of OTL or of a student’s perseverance, it is probably best for large-scale international studies to leave student engagement out of the measurement of OTL.
It should be clear the OTL is a concept that can have a variety of specific interpretations, each consistent with the general conception of students having had the opportunity to study or learn the topic or type of problem. Past international studies have chosen to include measurements of more than one of these conceptions, which may be associated with one another, yet remain conceptually distinct.
WHY IS OTL IMPORTANT?
For international comparative work, OTL is significant in two ways: as an explanation of differences in achievement and as a cross-national variable of interest in its own right. In the first case, scholars and policy makers wish to take OTL into account or “adjust” for it in interpreting differences in achievement, within or across countries. If a country’s low performance on a subarea of geometry, for example, is associated with little opportunity for students to learn the content of that subarea, there is no need to hunt for an explanation of the low score in teaching technique or poorly designed curriculum materials: The students did not know the content because they had never been taught it. In the second case, scholars and policy makers take an interest in which topics are included in a country’s curriculum (as implemented at a particular grade level, with a particular population) and which are excluded or given minimal attention. Policy makers in a country might, for example, be interested to see that some countries have included algebra content for all students in middle school, contrary to a belief in their own country that such content is appropriate for only a select group, or only for older students.
The language of the FIMS reports suggests that the reason for asking whether students had an opportunity to learn content was to determine whether the tests used would be “appropriate” for the students: “Teachers assisting in the IEA investigation were asked to indicate to what extent the test items were appropriate for their students. This information is based on the perception of the teacher as to the appropriateness of the items” (Husen, 1967b, p. 163). The implication suggested is that if a student had not had the opportunity to learn material, testing the student on the material would be inappropriate, in the sense that the student could not be expected to answer the questions. At the level of a country, taking
results for content that students had not had the opportunity to learn at face value also would be inappropriate. Information about OTL has value because it gives a way of deciding whether it is appropriate to look at national achievement results for particular content.
In the same spirit, reports on the Second International Mathematics Study (SIMS) warn against comparing the performance of two countries unless both countries had given students the opportunity to learn the content.
It is interesting to note that students in Belgium (Flemish), France, and Luxembourg were among those who had their poorest performance on the geometry subtest. In those three systems, the study of geometry constitutes a significant portion of the mathematics curriculum, and these results are an indication of the lack-of-fit between the geometry curriculum in those systems and geometry as defined by the set of items used in this study. These findings underscore the importance of interpreting these achievement results cautiously. They are a valid basis for drawing comparisons only insofar as the items which defined the subtests are equally appropriate to the curricula of the countries being compared. (Robitaille & Garden, 1989, p. 123)
Although some scholars deny that comparative studies should be taken as some sort of “cognitive Olympics,” many news reports treat them as such.5 Information on OTL provides a basis for deciding whether a country’s poor performance should be attributed to a decision not to compete.
Adjustments for OTL are also of interest for those scholars who see comparative research as a search for insights into processes of teaching and learning, rather than a way to determine winners and losers. Because of the variation in national education systems, information on the achievement in other countries can be a source of ideas for how teaching processes, school organization, and other aspects of the education system affect student achievement. Comparative research can help countries learn from the experiences of others. To the extent that research is able to untangle the various influences on student achievement, it can help in developing models of teaching and learning that can be drawn on in various national contexts, avoiding some of the pitfalls that come from simply trying to copy the education practices of countries with high student achievement.
The issue . . . is not borrowing versus understanding. Borrowing is likely to take place. The question is whether it will take place with or without understanding.... Understanding . . . is a prerequisite to borrowing with satisfactory results. (Schwille & Burstein, 1987, p. 607)
OTL can be an important determinant of student achievement. If OTL is not taken into account, its effects may be mistakenly attributed to some other attribute of the education system. A general rule in developing and testing models of schooling is that misspecification of the model, such as omitting an important variable like OTL, can lead to mistaken estimates of the effects of other factors.
In addition to its uses for understanding achievement results and their links to education systems, OTL is of interest in its own right. One of the insights from early comparative studies was a picture of the commonalities and differences in what students in varying countries had the opportunity to learn. As one of the SIMS reports puts it: “A major finding of this volume is that while there is a common body of mathematics that comprises a significant part of the school curriculum for the two SIMS target populations . . . , there is substantial variation from system to system in the mathematics content of the curriculum” (Travers & Westbury, 1989, p. 203). An understanding of similarities and differences across countries gives each nation a context for considering the learning opportunities it offers. A look at the within-country variation in OTL also provides a basis for considering current practice and possible alternatives. What variation in OTL occurs across geographic regions in a country? Across social classes? Between boys and girls? The variation found in other countries is a basis for reflecting on the variation in one’s own country.
HOW HAS OTL BEEN MEASURED IN INTERNATIONAL COMPARISONS?
I will focus on FIMS, SIMS, and TIMSS, the three international comparative studies in which OTL has played the most significant role. The First International Mathematics Study (Husen, 1967a, 1967b) included the definition of OTL quoted earlier, as “whether or not . . . students have had the opportunity to study a particular topic or learn how to solve a particular type of problem presented by the test.” The FIMS report describes the questions asked about OTL as “based on the perception of the teacher as to the appropriateness of the items” (Husen, 1967a, p. 163). The choice of the word “appropriate” suggests that the intent in measuring OTL was to prevent interpreting low scores due to lack of OTL as indicative of some deficiency in teachers or students. If the item was not taught to students, then it would be “inappropriate” for those students.
The actual question put to teachers to measure OTL was as follows:
To have information available concerning the appropriateness of each item for your students, you are now asked to rate the questions as to
whether or not the topic any particular question deals with has been covered by the students to whom you teach mathematics and who are taking this set of tests. Even if you are not sure, please make an estimate according to the scale given below.
Please examine each question in turn and indicate in the way described below, whether, in your opinion
-
All or most (at least 75 percent) of this group of students have had an opportunity to learn this type of problem.
-
Some (25–75 percent) of this group of students have had an opportunity to learn this type of problem.
-
Few or none (under 25 percent) of this group of students have had an opportunity to learn this type of problem.
The FIMS investigators used the responses to these questions to create an OTL scale score for each item, assigning the center of the percentage interval in the response as the numeric value for the scale:
These ratings were scaled by assigning the value 87.5 (midway between 75 and 100) to rating A, 50 to rating B, and 12.5 to rating C. The ratings given by a teacher to each of the items in the tests taken by his students were averaged, unrated items being excluded from the calculations. For each teacher there was thus a mean rating and the mean score made by his pupils on the tests rated. (Husen, 1967a, pp. 167-168)
A criticism of this approach to measuring OTL is that it left unclear whether an opportunity to learn “this type of problem” referred to the topic that the item was intended to represent or something specific about the way the problem was formulated. Teachers might be interpreting the question as asking whether they expected students to be able to get the problem right, rather than whether they had worked on the corresponding topic.
For SIMS, the single question was replaced by a pair of questions, in an attempt to disentangle OTL from teacher judgments about students’ likelihood for being able to solve a particular problem. Thus, teachers were asked both about whether the mathematics related to the test item has been taught or reviewed (the OTL question) and about the percentage of students in the class who would get the problem correct.
Specifically, teachers responded to the following pair of questions for each item on the SIMS test:
-
What percentage of the students from the target class do you estimate will get the item correct without guessing?
-
During this school year, did you teach or review the mathematics needed to answer the item correctly? (Flanders, 1994, p. 66)
Asking this pair of questions allows the teacher to indicate that students had studied the topic independently of whether they learned it well enough to answer the test item correctly. OTL might not lead to success because they had not studied the topic in the particular formulation used in the test item or they had not put enough effort into learning the topic. In at least some SIMS analyses, the two items were simply combined into a single scale, which seems difficult to interpret, at least in terms of appropriateness. Is it inappropriate to give a difficult test item on a topic that students did study? Does the teachers’ prediction that students would have a difficult time answering the item correctly (given that they had the opportunity to learn it) mean that teaching had disappointing success, or that the item is somehow not really a test of the topic, perhaps because it seems “tricky” or tangential to the topic? This aspect of OTL measurement was changed again in TIMSS (to using multiple items to illustrate a topic), suggesting that researchers were not satisfied with combining opportunity to learn with predicted student success on the item.
The FIMS approach to the OTL question also leaves unspecified when students had the opportunity to learn the type of problem. That omission reduces information about the country’s mathematics curriculum. It also might be important, for the appropriateness of the item for the test, to know whether the content was studied recently or some time further in the past.6
For SIMS, teachers also were asked OTL questions for each item. Unlike FIMS, the presumption was that OTL was the same for all students in the class: All either had or had not received the opportunity to learn how to answer the item. For content covered, teachers were asked whether the content was covered during the year of the study or earlier. For content not covered, teachers were asked whether students would learn the content later, or not at all. (In either case, the item would be “inappropriate” for these students.) Teachers also predicted what proportion of their students would get the item right.
This SIMS approach still confounds opportunity to learn the mathematical topic with information about students’ familiarity with specific features of the test item that are either irrelevant or tangential to the mathematics topic. The measurement of OTL in TIMSS gets more separation between topic and item by naming a topic, giving more than one item to illustrate the topic, then asking the teacher about opportunity to learn how to “complete similar exercises that address this topic.” Thus teachers are encouraged to think about OTL at a topic, rather than specific item, level. Having multiple illustrations of a topic should clarify what is the core of a topic and what is peripheral. (Information on each illustrative item is collected by asking the teachers to indicate, for each item, whether it is “appropriate” for a test on this topic.)
The SIMS questions about when a topic is taught are expanded from the FIMS questions. For topics taught during the year of the study, the teacher is asked to specify whether the topics already have been taught, are currently being taught, or will be taught later in the year. For topics not taught during the year of the study, TIMSS added two new options to those included in SIMS. The new possibilities are: “Although the topic is in the curriculum for THIS grade, I will not cover it,” and “I DO NOT KNOW whether this topic is covered in any other grade.”
TIMSS also asked teachers whether they think “students are likely to encounter this topic outside of school this year.” This question could shed some light on items where students performed well despite lack of opportunity to learn in school. If students were likely to encounter the topic outside school, the item might be considered inappropriate as an indicator of the success of the education system because mastery of topic should be credited to either institutions or experiences outside the system. No question is asked about whether students might study the topic elsewhere in school (e.g., in science), which would give further understanding of student success despite lack of opportunity to learn in the target class. In this case, the item still might be appropriate if the intent was to understand the performance of the education system as a whole.
OTHER APPROACHES TO MEASURING OTL
Measurement of OTL has not been restricted to international comparisons. As noted, the conceptualization of OTL used in international studies drew on studies of U.S. education, and vice versa. Just as methods of measuring OTL have been changing in international studies, U.S. domestic research has included changing approaches to measurement, which can be drawn on in planning for future measurement of OTL in international comparisons.
Using Teacher Logs to Gather Information on Instruction
One line of OTL work in the United States was initiated by Porter and his colleagues at Michigan State University in the Content Determinants Project (Porter, Floden, Freeman, Schmidt, & Schwille, 1988). As part of the instrumentation for a study of teachers’ decisions about what to teach, the project developed a system for classifying elementary school mathematics content. Classification began with analysis of tests and textbooks. The classification served as the basis for a system in which teachers reported on the content of their mathematics instruction, either through a questionnaire or through logs completed over the course of the school year. Like the TIMSS OTL questions, teachers were asked to list the topics
they covered, rather than to say something about how well their students would do in responding to particular test items. This teacher log approach has been adapted by other researchers, including Knapp (Knapp & Associates, 1995; Knapp & Marder, 1992) and Ball (Ball et al., 1999), as well as being used in Porter’s subsequent research.7
In a recent study of mathematics courses taken in the first year of high school, Gamoran, Porter, Smithson, and White (1997) compared several approaches to the measurement of OTL, looking for the representation that would have the highest association with differences in student achievement. They found the largest correlation with an index that represented content at a fine level of detail and included information both about the amount of time (actually, proportion of class time) spent on tested material and the distribution of that time across the topics tested. The highest correlations came when emphasis was distributed in a pattern similar to the distribution of content coverage on the achievement test.
This research team used teacher questionnaires to gather information on the content coverage in high school mathematics courses intended to provide a bridge between elementary and college preparatory mathematics. The questionnaires focused specifically on the content on which students would be tested in this study. They asked both about which mathematics topics were covered (from among 93 topics that might be covered in such mathematics courses) and what sort of “cognitive demand” the instruction made on students. Cognitive demand
was defined according to six levels: (1) memorize facts, (2) understand concepts, (3) perform procedures/solve equations, (4) collect/interpret data, (5) solve word problems, and (6) solve novel problems. (Gamoran et al., 1997, p. 329)
Content was classified according to both topic and cognitive demand, yielding 558 different topic/demand possibilities. Teachers used this scheme to record the content they taught; test items were classified using the same scheme. Gamoran and his colleagues (1997) found that correlations with achievement were highest when the analysis used the combination of topics and cognitive demand, rather than looking only at topic or demand. Using the intersection, the correlations were 0.451 with class gains and 0.259 with student gains. “Using topics only, the correlations with student achievement gains were –0.205 at the class level and 0.103 at the student level. For cognitive demand only, the correlations were 0.112 at the class level and 0.069 at the student level” (p. 331).
Gamoran also tried different approaches to using the information on coverage. He looked at both the proportion of instructional time spent on the tested topics and at how the pattern of time spent on tested topics
matched the distribution of topic coverage on the test. He labeled the first “level of coverage,” and computed it by dividing the total amount of time teachers reported spending on the 19 topics covered on the test by the total amount of time spent in these mathematics classes. Because the test covered only 19 of the 558 possible mathematics topics, values of this index are small, with averages across different types of mathematics classes ranging from 0.046 to 0.086.
Gamoran labels the match of distribution to the pattern of topics on the test “configuration of coverage.” The configuration is a measure of the match between the relative time spent on each tested topic and the number of test items on that topic. The index of configuration would be reduced, for example, if a large proportion of time were spent on one tested topic, at the expense of time on other tested topics. The index used is created so that 1.0 represents a perfect match in configuration, with lower values occurring as the pattern of time departs from that perfect match.
Gamoran and colleagues tried several different ways and found that the effect on achievement of these two indicators—level and configuration of coverage—was most stable when they were combined as a product, rather than added together or used as two separate variables. Based on these results, they use a model that assumes that
level and configuration are ineffective alone and matter only in combination. This assumption seems reasonable: Great range with shallow depth and great depth in a narrow range of coverage both seem unlikely to result in substantial achievement. (Gamoran et al., 1997, p. 331)8
Elsewhere, Porter characterizes the correlations obtained by this combination of level and configuration, using content recorded as the intersection of topic and cognitive demand, as indicating that the connection between content of instruction and student achievement is high: “From these results, it is possible to conclude that the content of instruction may be the single most powerful predictor of gains in student achievement under the direct control of schools” (Porter, 1998, p. 129).
The high correlations with student achievement gains make it appealing to use a similar approach to measurement of OTL in future international comparisons. The fact that the measure has a strong empirical relationship to achievement gains is strong evidence that the measure has adequate reliability and predictive validity. Two factors raise questions about the adoption of this approach, however.
The first is a practical concern. The level of detail found to be most highly correlated with student outcomes goes beyond information collected in international studies. TIMSS asked OTL questions at a detailed level of content, but when the study asked teachers to report on the amount of time spent on different topics, the content categories were
collapsed into a smaller set. Would the burden on teachers of having to report such specific content, with the amount of time (e.g., number of class periods) spent on the content, be tolerable for a large-scale study? (Gamoran’s study collected information on 56 classrooms in 7 schools.) To date, the burden of international assessments has not led to problems with data collection, but the question deserves attention.
A second concern is a question about the interpretation of an approach to measuring content coverage that gives credit for a pattern of content emphasis, among tested topics, that most closely matched the distribution of emphasis on the achievement test used. Gamoran found that using this information gives a higher correlation with student achievement gains. But what does that match with the pattern of topics included on the test mean for students’ opportunity to learn? Somehow it seems strange to have OTL depend on the relative emphasis of topics on the test; on the other hand, if the purpose of measuring OTL is to take account of the effects of OTL when trying to understand educational processes, perhaps it is best to use the representation that yields the strongest link to learning.
Perhaps the key to thinking about whether to adjust OTL information according to emphasis on the test is to ask whether the distribution of items on the test represents an ideal or standard. As the standards movement in the United States has evolved, assessments sometimes match adopted curriculum standards, but at other times the different schedules for development of standards and assessments results in a misalignment. If the pattern of topic coverage on the test represents agreement about relative value, then it seems sensible to adjust aggregate indices of OTL according to the distribution of test items. If the pattern of coverage does not represent such agreement, that creates a problem for interpreting any aggregate score.9
Web-Based Approaches to Teacher Logs
Ball and her colleagues have been pilot testing the use of Web-based technology to gather detailed information from teachers about their classroom instruction. They have been exploring this approach because they also have concerns about the feasibility of trying to collect detailed information on instructional content and processes. They focused on elementary school mathematics and reading. The scope of desired information includes length of lesson, grouping of students, nature of student activity, topics and materials used, and level of student engagement. In their pilot test (Ball et al., 1999), they were able to get teachers to use the logs regularly, but they report that further work is needed to gather trustworthy data about the topics and other characteristics of instruction. Still, their
work is suggestive of an approach that might, in the future, increase the feasibility of collecting more detailed information about students’ opportunity to learn.
As part of the pilot test for this data collection, researchers observed 24 lessons for which the teacher also entered a report on the instruction. A comparison of teacher and researcher reports on these lessons gave information on the validity of the teacher reports. For reports of length of lesson, the reports differed by an average of more than eight minutes per lesson, where lessons averaged around a total of 50 minutes. For questions about student activity, teachers chose from about six options (in both reading and mathematics), with the possibility of multiple options chosen in one lesson. The options included “students read trade books,” “worked in textbooks,” “worksheets,” and “teacher-led activity.” Agreement between researchers and teacher reports was about 75 percent for both reading and mathematics.
Ball indicated that the pilot test results were encouraging for the ability of the Web-based instrument to capture number and duration of lessons, but that more work was needed to get valid information about topic, instructional task, student and teacher activity, and student engagement. She saw validity problems arising from ambiguity of the meanings of the topic and activity descriptions. She also suggested that teachers may have difficulty remembering details of the lesson between the time the lesson is finished and the time, later in the same day, when teachers would record it. Note that she is concerned by a gap of a few hours, raising even more serious questions about surveys that ask teachers to report on instruction for an entire year.
We need to have confidence about what the items mean to teachers. Central here is understanding how teachers interpret items and how they represent their teaching through their responses in the log. Thus, there are threats to validity that deal with teachers’ understanding of the log’s questions, language, and conceptualization of instruction. Other researchers have found that the validity of items related to instruction is weaker with respect to instructional practices most associated with current reforms (e.g., everyone is likely to report that they hold discussions in class, engage children in literature, or teach problem solving). Another potential problem entails teachers’ ability to recall details of a lesson many hours after that lesson occurred. (Ball et al., 1999, p. 31)
Ball and her colleagues have decided not to use the Web-based approach because of the concerns about teachers’ access to the necessary computer equipment (Ball, personal communication, February 2001). Such concerns seem likely to be even more salient in any international studies conducted in the near future.
Measuring Content Coverage in Reading Instruction
Barr and Dreeben (1983) conceptualized the content of early reading instruction as the vocabulary words and phonics elements that students encountered. Because the teachers in their study taught reading by having students work sequentially through basal reading materials, the investigators were able to use progress through the materials to determine the amount of content covered. The first-grade teachers in the study were asked during the year and at the end of the year to indicate how far each of the reading groups had made it through the materials. An analysis of those materials was used to determine how many basal vocabulary words and how many phonics concepts would be covered at each location in the basal. This use of progress through the curriculum as a way to measure content coverage places low demands on the teacher’s memory of what has or has not been taught, but it will only be appropriate when teachers stick closely to the curriculum materials, without omitting or reordering sections.
Concerns About the Reliability and Validity of Teacher Logs and Surveys
Mayer (1999) recently has argued that little is known about the reliability and validity of teacher surveys used to collect information about instructional practice. His particular focus is on the use of “reform” practices, such as those recommended in the National Council of Teachers of Mathematics (NCTM) teaching standards. He identifies two pieces of prior research: Smithson and Porter’s (1994) look at the instruments used in Reform Up Close (1994) and Burstein and colleagues’ investigation (Burstein et al., 1995) of instruments used to study secondary school mathematics.
Smithson and Porter asked teachers to keep logs over the course of a school year, recording information both on content and on instructional practices. They also asked the teachers to complete a survey, asking for similar information about either the prior half-year or the half-year to come. A comparison between the survey and the logs was used to understand how much information would be lost by using only a survey, which is a less expensive data collection strategy, but one that might suffer from difficulty in recalling what happened many weeks ago, or in predicting how the year is going to run. According to Mayer’s summary, the correlations between teacher practices reported on the survey and those reported on the logs ranged from 0.21 (for “write report/paper”) to 0.65 (for “lab or field report”). Smithson and Porter found these correlations encouraging, but Mayer takes them as evidence of the unreliability of survey reports of such practices.
Burstein also compared teacher logs and surveys, but his research added a second administration of the survey, allowing for a look at the consistency in survey responses over time, as well as comparison of survey results to reports on logs. The comparison of surveys to logs found agreement of 60 percent or less for all types of instructional activities, a result that both Burstein and Mayer view as discouraging. The readministration of the survey yielded perfect agreement for 60 percent of all responses. Again, Mayer views this degree of agreement as low, concluding that “surveys and logs do not appear to overlap enough to prove with any degree of confidence that the surveys are reliable” (Mayer, 1999, p. 33).
Mayer makes an additional contribution by conducting a study of Algebra I teachers that compares teacher survey reports to classroom observations. The categories of practice for the study were chosen to permit a contrast between “traditional” teaching practices (e.g., lecturing) and the types of practices advocated in the NCTM teaching standards (National Council of Teachers of Mathematics, 1991). The traditional approaches were ones in which students
-
listen to lectures,
-
work from a textbook,
-
take computational tests, or
-
practice computational skills.
The NCTM approaches were ones in which students
-
use calculators,
-
work in small groups,
-
use manipulatives,
-
make conjectures,
-
engage in teacher-led discussion,
-
engage in student-led discussion,
-
work on group investigations,
-
write about problems,
-
solve problems with more than one correct answer,
-
work on individual projects,
-
orally explain problems,
-
use computers, or
-
discuss different ways to solve problems.
Results are based on 19 teachers in one school district who vary considerably in instructional practice. Each teacher was asked to complete a survey at the beginning and end of a four-month period, and was observed three times during this period. The survey asked teachers to say how often they used each practice (“never,” “a few times a year,” “once or
twice a month,” “once or twice a week,” “nearly every day,” or “daily”) and how much time was spent in the practice on days they did use it (“none,” “a few minutes in the period,” “less than half,” “about half,” “more than half,” or “almost all of the period”). These two pieces of information were converted to numbers of days per year and minutes per day respectively.10 The product of the two numbers was then an estimate of the number of minutes spent using the practice during the year.
Mayer found that the correlation of the time estimates between the responses on the two survey administrations (four months apart) ranged from 0.66 to a negative 0.09. Although Mayer found these results consistent with his earlier conclusion that surveys give unreliable reports of instructional practice, he also reported that aggregating the reports to form a composite index of NCTM practice produced a measure with “encouraging” reliability (0.69). Comparison of this composite index with the classroom observations showed that teachers had some tendency to report more use of NCTM practices than were observed. But he also found that correlation between the composite index from the survey and the observations was strong (0.85). His overall conclusion is that existing survey instruments give unreliable information on individual instructional practices (e.g., amount of time spent listening to lectures), but that acceptable reliability can be obtained by forming composites, or perhaps by refining the questions teachers are asked.
Mayer’s results suggest that logs could be used to measure instructional practices at a fairly high level of generality (e.g., NCTM-like practice versus traditional practice). That is a caution worth attending to, but it does not have direct consequences for the measurement of OTL. The measures Mayer studied asked teachers to describe their practices, rather than asking them to report on the topics they covered. Mayer’s study does, however, stand as a reminder that the reliability of teacher reports, whether in logs or in surveys, is an issue that deserves attention when developing OTL measures. Achievement tests are developed over several iterations, taking care that the measures used for research have high reliability. Measures of OTL require a similar process of development to attain levels of reliability that will allow for fruitful uses of the measure. As noted already, when measures have shown high associations with student achievement and achievement gains, those associations are themselves strong evidence of the reliability of the measures, because unreliability attenuates the observed relationship with other variables.
Timing of the Measurement of OTL
Over the sequence of international science and mathematics studies, the amount of information collected about when students had opportunity
to learn content has increased. As noted previously, FIMS did not ask for any information about when students had the opportunity; SIMS asked, for topics taught during the year of the study, whether the topic already has been taught, is currently being taught, or will be taught later in the year; TIMSS added the possibilities that the topic is a part of the curriculum that the teacher will omit and that the teacher does not know whether the topic is taught at another grade.
What are the possible advantages of gathering information about OTL at various points in time? How feasible is measurement at different points in time? For the purpose of describing OTL (the second of the two major purposes discussed early in this paper), the most accurate description would come from asking teachers what students have an opportunity to learn at the grade they teach. Information gathered cross-sectionally (e.g., by asking sixth-grade teachers what they cover, as information for what opportunities eighth graders have had) would be useful if the curriculum has been stable for several years; that information would be less useful in times of curriculum change. Asking teachers to report about opportunities to learn at other grades would reduce the number of teachers who would have to give information, but the information would likely be less accurate.
What about the timing of OTL measures when the purpose is to adjust for differences in OTL in interpreting achievement results or in understanding relationships within the education system? Accurate information about opportunities prior to the test could be used much as information about opportunities during the tested year: Low achievement on topics students had never been taught should not be taken as an indication of poor instruction or poor student motivation; low achievement on topics that were taught in prior years suggests either that students do not review material often enough to retain it or that the material was not mastered initially.
Information about opportunities to learn at a later time do not call for a shift in thinking about what the achievement results indicate about the school system’s effectiveness in teaching the topic. Data on later teaching of the topic would, however, affect the overall picture of a country’s mathematics instruction. It would help to distinguish, for example, between countries that teach a topic later in the curriculum (perhaps because of judgments about difficulty for younger students) and countries that have decided not to include the topic in their curriculum.
The difficulties of determining what content students have studied in prior years would be avoided if studies included information about achievement in the previous year, that is, if data were available on achievement gains, rather than merely on achievement attained. It would be unnecessary to adjust for opportunities to learn in prior years if gains, rather
than attainment, were the learning outcome under consideration, because the effects of the prior opportunities to learn would be represented in the initial achievement measure.
HOW HAS OTL BEEN USED?
In the series of international comparative studies of mathematics and science, the OTL data have been used in both the intended ways described at the beginning of this chapter: as a basis for “appropriately” interpreting the achievement results and as a description of the curricula actually implemented within and across the participating countries. Data on OTL have been presented alongside achievement data, as well as being presented on their own. For the most part, the use of the data in the comparative reports has been as commentary on patterns of performance on particular topic areas, rather than attempting any overall adjustment of achievement in light of OTL. That is probably wise, given imprecision of the OTL measures and the inevitable debates that would ensue about the technical details of any adjustment procedure.
Burstein’s analysis of the SIMS longitudinal study (Burstein, 1993) is an exception that could serve as a starting point for developing this approach to adjustment. For the eight education systems that participated in the longitudinal study, Burstein looked at the effect of adjusting the results by creating subtests of items based on OTL data. Data from the question about teaching or reviewing the topic were combined with data from the question asking whether the topic had been taught previously to create an index of whether a teacher reported “teaching, reviewing, or assuming [because it had been taught earlier] the content necessary to answer the test item had been taught” (p. xxxvi). Burstein created subtests by selecting those items that 80 percent of the teachers reported “teaching, reviewing, or assuming.” For each of the resulting eight subtests (one for each education system), he then computed the achievement results for all eight systems. The result was a series of tables, each representing the items that students had the opportunity to learn in a particular system. Each table presented, for that subtest, the pretest, posttest, and gain results for each country, plus the corresponding OTL data—the number of items on the subtest that at least 80 percent of the country’s teachers reported teaching, reviewing, or assuming.
These tables showed both the broad range of OTL across systems and the effects on absolute and comparative performance of varying the test to match the OTL for system. Of the 157 test items common to all these eight systems, the number of items reaching the 80 percent OTL threshold ranged from 48 to 103. In this analysis, the general result was that systems tended to have higher pretest, posttest, and gain scores on their own
system-specific test. The between-system rankings remained about the same, though there were some differences in the magnitude of differences. This analysis demonstrates the possibility for using OTL data to make overall adjustments, which go some way toward making comparisons more plausible. The study also demonstrates the possibility and value of looking at gain scores, rather than simply examining attained achievement. Burstein notes, however, that overall rankings are still problematic in SIMS because the overall item pool did not capture the curricula of all countries, and because the mix of items in the overall pool unevenly represented the various system curricula.
The OTL data also have been used as a basis for noting that a conclusion of comparative research is that OTL is related to achievement, a finding that should no longer be news, but somehow continues to be striking. In the following paragraphs, I will look more closely at the OTL-based conclusions drawn in the series of mathematics and science assessments, with particular attention to Westbury and Baker’s exchange about how looking at OTL shapes interpretation of differences in TIMSS between Japanese and U.S. achievement.
Husen’s report on FIMS (1967b) noted that OTL was correlated with achievement, with modest results within countries (because of little within-country OTL variation) but substantial correlations between countries.
Within countries the correlations between achievement scores and teachers’ perceptions of students’ opportunities to learn the mathematics involved in the test items were always positive and usually substantial. Between countries they were large (0.62 and 0.90 for 1 a and 3 a). The conclusion is that a considerable amount of the variation between countries in mathematics scores can be attributed to the difference between students’ opportunities to learn the material tested. (p. 195)
Husen’s report (1967b) treats this attribution of difference as a rationale for looking at countries’ achievement in light of how “appropriate” the tests were for what was taught in the country. The report seems to consider the differences in OTL as a given context, rather than a basis for possible shifts in national curriculum policy. In the report, these large correlations were not listed among the findings about relations between mathematics achievement and curriculum variables. OTL is apparently seen as a control variable, not a curriculum variable. The report states:
One of the most striking features of the results is the paucity of general . . . relationships between mathematics achievement and curriculum variables investigated. The correlations between achievement scores and these curriculum variables, when based on the pooled data from all countries, were usually quite low. The weakness of many of the relation-
ships that were found limits their usefulness in curriculum planning. (p. 197)
It seems from this statement that, for FIMS, OTL was not seen as a curriculum variable and did not seem to be considered useful in curriculum planning.
In interpretation of the SIMS results, however, OTL began to be seen as a policy relevant curriculum variable. The OTL data continued to be used as a basis for interpreting achievement data, giving a basis for deciding whether test items were appropriate for particular countries, but commentators also began to argue that a country’s pattern of OTL was an appropriate topic for policy discussion, rather than a given part of the context. That is, the discussions began to suggest that the conclusion that might be drawn from seeing low achievement on an item with low OTL was that the country should consider giving students more opportunities to learn how to solve the item, rather than that the low achievement was simply the result of use of an item inappropriate for that country.
To be sure, the OTL results in SIMS continued to be used as a basis for pointing out that some tests results reflected the fact that a set of items was inappropriate for a country. In the main report of SIMS (Robitaille, 1989), achievement results were presented in great detail, with graphic displays that combined each country’s achievement results with its OTL results, and with commentary on specific items that pointed out that some low results reflected a mismatch between what was taught in a country and the items used on the SIMS test.
But SIMS reporting also began to shift discussion to questions about whether a country’s combined pattern of achievement and OTL might suggest that policies should seek to change OTL, rather than treating it as a given. In an exchange published in Educational Researcher, Westbury and Baker (Baker, 1993a, 1993b; Westbury, 1992, 1993) debated how to interpret the U.S.-Japanese difference on SIMS mathematics achievement. They agreed that OTL needs to be taken into account in interpreting the achievement differences. In the analysis that opens the exchange, Westbury uses different course types as a way to describe curricular differences. For example, Westbury notes that the U.S. eighth graders may be in any of four course types: remedial, typical, enriched, or algebra, while Japanese students at that age are all in the single course type. Westbury uses OTL data to describe differences among the U.S. course types, noting that “it is only the U.S. algebra course type that has a profile similar to Japan’s course” (Westbury, 1992, p. 20). He then compares achievement for that course type to the Japanese achievement, trying to equate for OTL. He finds that the achievement difference disappears, even in a further analysis that tries to account for any selectivity of the U.S. algebra courses.
Baker responds with an analysis that uses OTL data to restrict analysis, class by class, to the material teachers report they taught during the year, finding that Japanese students learned 60 percent of the content taught, as contrasted with only 40 percent for the U.S. students. In his rejoinder, Westbury contends that he was trying to ground the comparison in “a notion of intentional curricula,” which includes a wider range of factors, for which looking at courses as a whole was more appropriate.
The debate illustrates some of the detailed analytic choices that can be made about how the OTL data are used in interpreting achievement data. Perhaps more important is that the debate illustrates the shift in the discussion from seeing OTL as a background variable to seeing the connections between OTL and achievement as the grounds for national reconsideration of curricular coverage. Westbury’s argument is that the ways in which OTL information shifts interpretation are grounds for changing the opportunities. Rather than seeing the SIMS results as a reason for emulating Japanese schooling practices, the results are a reason for making different decisions about what students should have a chance to learn. Westbury’s initial argument (modified somewhat in light of Baker’s response) is that the differences in achievement are explained entirely by differences in curriculum coverage. Thus OTL data are used as a basis for shifting discussions about how to make U.S. education more effective from organizational and teaching variables to curricular choices.
In the TIMSS reporting, particularly reporting about curriculum and OTL in the United States, the emphasis has shifted even further toward the problems with existing patterns of OTL. The implemented curriculum in the United States is no longer a given part of the context; it has become the problem to be faced. The stress to be put on differences in learning opportunities was foreshadowed in the extensive cross-national curriculum analysis done as an early part of TIMSS (Schmidt, McKnight, & Raizen, 1997; Schmidt, McKnight, Valverde, Houang, & Wiley, 1997). The description of the U.S. curriculum as “a mile wide and an inch deep” may be the TIMSS result that has been most widely repeated.
The importance assigned to OTL in interpretation of the achievement data can be readily seen in the chapter titles of Facing the Consequences (Schmidt, McKnight, Cogan, Jakwerth, & Houang, 1999): “Curriculum does matter” and “Access to curriculum matters.” The argument in these chapters follows those made in earlier studies by identifying topic areas within a subject area and comparing relative performance in those areas to corresponding data on OTL.
One of the assumptions in this argument is that transfer of learning across topics is limited, so that additional time spent on measurement, for example, will not be of much help in learning how to work problems on relations of fractions. That is, opportunity to learn is important for each
topic area, not just for mathematics or science as a whole. If mathematics or science learning were simply increasing mastery of a single skill, then it would not matter what topics were studied. Students who learned more mathematics would do better on all topics. A look at the relative performance of different countries on different topics reveals that students differ in their knowledge of mathematics across topics. U.S. eighth graders, for example, do relatively well at rounding, but are at the bottom of the pack in measurement units. So test performance is, to some extent, topic specific.
The next step in the OTL analysis would be comparing the results by topic area to the differences in OTL for those topic areas. In Facing the Consequences, however, OTL information was only included as part of general claims about the diffuse nature of the U.S. curriculum, in comparison to the curricula from other countries.11 That diffuseness is given as an explanation of the moderate gains in U.S. student learning between adjoining years. The degree to which OTL differences explain the varying topic-level performance in the United States (or any other country) will need to be determined from OTL analyses like those of Westbury and Baker. That earlier exchange illustrates both that the effects found could be substantial (as when Westbury’s analysis erased the differences in achievement) and that more than one strategy for analysis may be used, and may yield substantially different interpretations. Analyses like these should be pursued in future studies, as OTL data are used as part of the process of modeling the determinants of student achievement.
SOCIAL SUPPORTS AS OTL
Adding to the possibilities for analysis and interpretation, opportunity to learn could be construed more broadly to include factors beyond classroom instructional time, however defined. Students, for example, might have a better opportunity to learn instructional content because they receive help outside of school. Such help might be participation in formal educational programs, such as the often-mentioned Japanese tutoring programs, or they might be experiences that look less like school-away-from-school, perhaps help with homework from a parent, or even practice with a skill in a work or recreational activity. Students who are encouraged to read at home, for example, have more opportunity to learn the skills of reading than students who read only during class time.
Differences in this more broadly defined OTL are substantial, both within countries and across countries. In acquisition of written literacy, for example, children with literate parents have out-of-school opportunities to learn that are not available to illiterate parents. Thus what appears as an effect of schooling may sometimes come from out-of-school learn-
ing, but the importance of out-of-school learning will vary by content area and by country.
In most industrialized countries the path to early literacy begins in the home and continues through formal instruction in school. There is an interdependence between the two sources, since formal instruction gains its full effectiveness on the foundation established and maintained by parents and family members. In many developing countries, however, high rates of parental illiteracy make it impossible for parents to enter directly into the process of helping their children learn how to read. In these societies, instruction in reading depends primarily on what the child encounters in school. (Stevenson, Lee, & Schweingruber, 1999, p. 251)
Such differences in family-based opportunities to learn may account for some of the well-documented associations between family background (including social class, income, levels of mother’s and father’s education) and achievement. Such associations have been found within countries, in the United States most famously in the Coleman report (Coleman et al., 1966). Effects of family background on achievement also have been found in cross-national studies such as SIMS. “Just like its IEA predecessors, the SIMS results of the analyses of the effects of background characteristics on achievement (status) at either pretest or posttest occasions showed the strong relationships of such variables as the pupil’s mother’s education, father’s education, mother’s occupation, and father’s occupation with cognitive outcomes,” note Kifer and Burstein (1992, p. 329). “The immediate evidence and external evidence agree in attributing more variation in student achievement to the family background than to school factors. The reason is not far to seek. It is that parents vary much more than schools,” adds Peaker (1975, p. 22).12
Such family background variables are like OTL in that they may provide an explanation for achievement differences that otherwise might be attributed to differences in the education system. To understand the connections between schooling and achievement, some of the effects of family background can be statistically “controlled,” either by including measures of the background variables in statistical models used to estimate links between schooling and achievement or by including measures of prior achievement, which would themselves be highly associated with family background.
SIMS investigators concluded that including prior achievement was a necessary approach for controlling both the effects of experiences prior to the school year and the effects of differences in curriculum based on those prior experiences (Schmidt & Burstein, 1992). They also found that including prior achievement in the analysis—looking at learning across the
year rather than merely at achievement—greatly reduced the influence of such background variables. “The background characteristics of students are not strongly related to growth because the pretest removes an unknown but large portion of the relationship between those characteristics and the posttest,” note Kifer and Burstein (1992, p. 340, emphasis added).
The strategy of focusing on achievement gains as a way of controlling for differences in background factors seems implicit in the arguments for importance of curriculum in the TIMSS publication, Facing the Consequences (Schmidt et al., 1999). Using items that appear on tests at more than one level, and taking advantage of the fact that tested populations include students at more than one grade level, Schmidt and his colleagues are able to estimate gains in achievement across grades. While acknowledging that gains across grades could be due in part to “life experience” (i.e., opportunities to learn outside school), they argue that the associations of the gains with curriculum content at the corresponding grade levels indicate that curriculum, that is, OTL within schools, is an important factor in learning the content of these items.
The general purport of all specific items discussed above is that, while developmental and life experience factors may be involved in accounting for achievement changes, curricular factors undoubtedly are.... The main evidentiary value of examining these link items is that their differences rule out explanations based on factors such as maturation, life experience, or some general measure of mathematics or science achievement. (Schmidt et al., 1999, pp. 158-159)
In summary, connections between OTL and student achievement typically are conceived as within-school phenomena. Students do, however, sometimes have other opportunities to learn outside the classroom, opportunities that are often linked to differences in family background. The significance of these outside opportunities will vary by content area: Families differ substantially in the opportunities young children have to acquire basic literacy; families likely will vary much less in the opportunities they provide for learning how to compute the perimeter of a rectangle (because such knowledge is less likely to be part of the ordinary lives of any families). Thus, evidence about the connection between OTL and student achievement may be easier to interpret for topics that are more “academic,” that is, more distinctively school knowledge. Although differences in how “academic” that content is will vary by school subject (e.g., chemistry is more academic than reading), looking at individual items can make it easier to identify content that is unlikely to be learned outside school. Looking at measures of gain, rather than status, is another way to simplify interpretation of the effects of school OTL.
WHAT HAS RESEARCH SHOWN ABOUT THE STRENGTH OF OTL EFFECTS?
Empirical support for the influence of time spent engaged in learning on student achievement was provided by the Beginning Teacher Evaluation Study (BTES), which used a combination of teacher logs and classroom observations to record how much time a sample of elementary school teachers “allocated to reading and mathematics curriculum content categories (e.g., decoding consonant blends, inferential comprehension, addition and subtraction with no regrouping, mathematics speed tests, etc.)” (Fisher et al., 1980). (Classroom observations also were used to estimate the fraction of allocated time that students actually engaged in the learning opportunities.) BTES found substantial differences in the time teachers allocated (i.e., in OTL) and found statistically significant associations between time allocated and student achievement. These are samples of the early empirical evidence that if students spend more time working on a topic, they will learn more about the topic. Or, conversely, and perhaps more important in the context of international comparative studies, if students spend little or no time working on a topic, they will learn little about it. As the quote from Husen (p. 232) suggests, the exceptions come either when the student is able to transfer learning from another topic or when the student spends time outside of school on the topic (e.g., learning from parents or independent reading, even though the topic is not studied as part of formal education).
The BTES research found positive associations between student achievement and each of these measures of OTL. For the full set of Academic Learning Time variables, the effects on student achievement were statistically significant for some, but not all, of the specific content areas tested in grades two and five reading and mathematics. Overall, about a third of the statistical tests were significant at the 0.10 level. The magnitudes of the effects are indicated by the residual variance explained by the ALT variables, after the effect of prior achievement has been taken into account. Those residual effects ranged in magnitude from 0.01 to 0.30, with an average on the order of 0.10 (Borg, 1980, p. 67).
Barr and Dreeben (1983) found a high correlation (0.93) between the number of basal vocabulary words covered and a test of vocabulary knowledge, accounting for 86 percent of the variance on that test. The correlation was also high with a broader test of reading at the end of first grade (0.75) and even with a reading test given a year later (0.71). For phonics, the correlations with content coverage were somewhat lower, 0.62 with a test of phonics knowledge, 0.57 with first-grade achievement, and 0.51 with second-grade achievement.
Barr and Dreeben’s attention to the social organization of schooling led them to examine whether the correlation between coverage and
achievement comes because students with higher aptitude cover more content. They found that groups with higher mean aptitude do cover more content, but that the correlation between individual student aptitude and achievement was close to zero. Thus the investigators conclude that student aptitude affects how much content they cover through affecting assignment to group, but, given assignment to group, it is content coverage, not aptitude, that is the major determinant of learning, especially for vocabulary.
In FIMS, the within-country relationship between OTL and achievement was positive, but varied. As Husen (1967a, pp. 167-168) wrote, “There was a small but statistically significant positive correlation between the scores and the teachers’ ratings of opportunity to learn the topics. There was, however, much variation between countries and between population within countries in the size of these coefficients.” The small magnitude of the relationship in some countries may have been due to limited variation in OTL within those countries, that is, in the uniformity of curriculum in those countries. The between-country association between OTL and student achievement, however, was substantial, with correlations of 0.4 to 0.8 for the different populations. “In other words, students have scored higher marks in countries where the tests have been considered by the teachers to be more appropriate to the experience of their students” (p. 168).
For SIMS, the Westbury-Baker exchange mentioned earlier shows that the relationship between OTL and achievement was, at least in Westbury’s initial analysis, strong enough to explain all of the Japan-U.S. differences in achievement. Thus OTL can be a powerful explanatory variable when looking at particular, fairly narrow comparisons.
The more general analysis of OTL data for SIMS, however, did not yield results that were striking enough to be given attention in general conclusions of the study. An overall OTL variable was included in a broader search for patterns in the data (Schmidt & Kifer, 1989). The within-country analysis used a hierarchical model with predictive variables that included student gender, language of the home, family help, hours of mathematics homework, proportion of class in top one-third nationally, class size, school size, and teacher’s age. The model was estimated for each country by achievement topic area (i.e., arithmetic, algebra, geometry, measurement, statistics, total). The frequency of the importance of each variable was reported in a table of the number of statistically significant betas for each topic area over the 20 countries. What is striking about the table (Schmidt & Kifer, 1989, p. 217) is that none of the between-class or between-school variables has more than 4 (out of a possible 20) significant betas for any topic area. The OTL variable has one significant beta over countries for each of the five subtests and one for the total test.
Among the between-class or between-school variables, that puts it below class size, proportion of class in top third nationally, class hours of mathematics per week, and about the same as teacher age. This is, at best, a modest effect within countries. That is consistent with the FIMS results, where within-country associations between OTL and achievement were positive, but weak to modest. Perhaps these modest associations were due, as in the case of FIMS, to relatively small within-country variation in OTL in most countries. (The United States is unusual in the extent of within-country OTL variation.) For FIMS, between-country associations were substantial. Beyond the Westbury-Baker exchange, I did not locate any reports of the between-country OTL-achievement associations from SIMS.
As noted, the TIMSS reports document the cross-country variation in the content of curricular materials, but I did not locate reports on the variation in teachers’ reported OTL.13 Given the important role the differences in national curriculum differences have played in policy discussions, the TIMSS curriculum analysis deserves further attention by scholars within and outside the community that has carried out the TIMSS studies.
CONCLUSION
The sequence of international comparative studies of mathematics and science has given increasing attention to variation in OTL, both in data collection and in reporting. OTL information has obvious importance for the interpretation of achievement differences within and across countries. OTL’s link to curricular intentions has become a major spur for discussions about an individual country’s curriculum, at least in the United States. The positive association between OTL and student learning has been documented in a number of studies, although the measured association between OTL and achievement or achievement gains has been quite varied. Some analyses show a weak connection; Westbury’s analysis produced a dramatic effect of taking OTL into account. Some of the variation in strength of association can be attributed to the amount of variation in OTL; some can be attributed to reliance on teachers’ memories of content coverage; some may be due to learning outside school or to transfer of learning from one topic to another.
The number of reports making extensive use of the currently collected OTL data seems small. The complexities of analysis are likely daunting. The dramatic results in Westbury and Baker should make further analyses attractive. Their focus on a single pair of countries undoubtedly contributed to their ability to find clear (though somewhat contradictory) results.
What does this review suggest for future comparative studies? The importance of continuing to collect some OTL information is evident. Now, as before, interpretation of achievement or learning comparisons requires some understanding of what learning was intended and how much these intentions were realized, by nations and by teachers. Looking at specific topics, rather than general content areas, is more likely to yield measurable differences in OTL and stronger relationships to achievement. But finer grained work also places greater burdens on respondents and analysts.
Choices about what sort of OTL data to collect, and how, must be considered in light of the questions to be answered. Surely no further evidence is needed to support the conclusion that OTL has some positive effect on achievement. Attention now should turn to understanding the processes of teaching and learning, using information on OTL to help construct analytic models that can do a better job of identifying the separate, though perhaps interacting, effects of student aptitude, perseverance, quality of instruction, and opportunity to learn.
The work done to date with OTL suggests several principles that should be used in continuing to refine measures:
-
The questions asked should allow for analyses that separate OTL from related variables, such as teachers’ judgments about whether students have learned (as opposed to having the opportunity to learn) and student perseverance in working on a topic.
-
Questions should also allow for separation of information about classroom processes from information about content coverage. The Carroll model separates OTL from quality of instruction. Keeping these distinct is important for building more accurate models of the influences on student learning. Moreover, methodological studies suggest that teachers are less reliable in giving retrospective information about time spent using different methods of instruction than they are in giving information about time spent on specific topics.
-
Information about opportunities to learn in grades other than those tested is important for understanding a system’s curriculum and for understanding connections between school practices and student learning. Information can be collected from teachers in the tested grades, but their reports may contain inaccuracies because of lack of communication within the system or because of changes in the curriculum over time. Information about student achievement in the prior year can give a better indication of prior learning. In past studies, some countries have seen such longitudinal designs as difficult to implement, but the added information they provide strongly suggests that they should be considered.
-
Information also should be gathered about opportunities to learn topics outside the classrooms in the tested subject. The interpretation of achievement results will be influenced by whether students had opportunities to learn content outside school or in other subject areas (e.g., learning how to write reports in social studies classes or learning about measurement in science classes).
-
Development of measures of OTL deserves the same care given to development of cognitive achievement measures. The reliability of OTL measures can be used as the basis for successive refinements, just as it is in selection and revision of test items. Ambiguous wordings of content descriptions should be detected and eliminated. In mathematics, the wording and organization of topic categories have benefited from decades of research; topic categories in other subject areas would benefit from similar cycles of testing and revision. Studies of the associations between student learning and various OTL variables can be used to determine what combinations and functional forms have the greatest predictive validity. Further work could be done to investigate the construct validity of OTL measures.
In short, researchers and policy makers have come to agree that OTL should be an important part of international comparative studies of achievement, in large part because OTL has been shown to have a link to student learning. In future studies, attention should shift from producing further evidence to support the existence of that link, toward using measures of OTL to build better models of the sources of student learning. Such models should give insight into the reasons students receive differing opportunities to learn and the reasons that student learning varies, given the same opportunities to learn. To make that shift, investments should be made, as they have begun to be in mathematics, into improving OTL measures so that they can better support fruitful research. Carroll’s model of school learning remains a helpful general framework for such research, but should be supplemented to include the factors—system policies, classroom organization, teacher knowledge—that influence the opportunity to learn and the quality of instruction students experience.
NOTES
|
13. |
These may appear in TIMSS reports that were in preparation at the time this paper went to press. |
REFERENCES
Baker, D. P. (1993a). Compared to Japan, the U.S. is a low achiever . . . really: New evidence and comment on Westbury. Educational Researcher, 22(3), 18-20.
Baker, D. P. (1993b). A rejoinder. Educational Researcher, 22(3), 25-26.
Ball, D. L., Camburn, E., Correnti, R., Phelps, G., & Wallace, R. (1999). New tools for research on instruction and instructional policy: A Web-based teacher log (Document W-99-2). Seattle: University of Washington, Center for the Study of Teaching and Policy.
Barr, R., & Dreeben, R. (1983). How schools work. Chicago: University of Chicago Press.
Berliner, D. C. (1990). What’s all the fuss about instructional time? In M. Ben-Peretz & R. Bromme (Eds.), The nature of time in school (pp. 3-35). New York: Teachers College Press.
Berliner, D. C., Fisher, C. W., Filby, N., & Marliave, R. (1978). Executive summary of Beginning Teacher Evaluation Study. San Francisco: Far West Regional Laboratory for Educational Research and Development.
Blank, R. K., Kim, J. J., & Smithson, J. L. (2000). Survey results of urban school classroom practices in mathematics and science: 1999 report. Norwood, MA: Systemic Research.
Bloom, B. S. (1976). Human characteristics and school learning. New York: McGraw-Hill.
Borg, W. R. (1980). Time and school learning. In C. Denham & A. Lieberman (Eds.), Time to learn (pp. 33-72). Washington, DC: U.S. Department of Health, Education, and Welfare, National Institute of Education.
Burstein, L. (1993). Prologue: Studying learning, growth, and instruction cross-nationally: Lessons learned about why and why not engage in cross-national studies. In L. Burstein (Ed.), The IEA Study of Mathematics III: Student growth and classroom processes. New York: Pergamon Press.
Burstein, L., McDonnell, L. M., Van Winkle, J., Ormseth, T., Mirocha, J., & Guitton, G. (1995). Validating national curriculum indicators. Santa Monica, CA: RAND.
Carroll, J. (1963). A model for school learning. Teachers College Record, 64, 723-733.
Coleman, J. S., Campbell, E. Q., Hobson, C. J., McPartland, J., Mood, A. M., Weinfeld, F. D., & York, R. L. (1966). Equality of educational opportunity. Washington, DC: U.S. Department of Health, Education, and Welfare.
Council of Chief State School Officers. (2000). Using data on enacted curriculum in mathematics and science: Sample results from a study of classroom practices and subject content. Washington, DC: Author.
Dewey, J. (1904/1965). The relation of theory to practice in education. In M. L. Borrowman (Ed.), Teacher education in America: A documentary history (pp. 140-171). New York: Teachers College Press.
Fisher, C. W., Berliner, D. C., Filby, N. N., Marliave, R., Cahn, L. S., & Dishaw, M. M. (1980). Teaching behaviors, academic learning time, and student achievement: An overview. In C. Denham & A. Lieberman (Eds.), Time to learn (pp. 7-32). Washington, DC: U.S. Department of Health, Education, and Welfare, National Institute of Education.
Flanders, J. (1994). Student opportunities in grade 8 mathematics: Textbook coverage of the SIMS test. In I. Westbury, C. A. Ethington, L. A. Sosniak, & D. P. Baker (Eds.), In search of more effective mathematics education (pp. 61-93). Norwood, NJ: Ablex.
Gamoran, A., Porter, A. C., Smithson, J., & White, P. A. (1997). Upgrading high school mathematics instruction: Improving learning opportunities for low-achieving, low income youth. Educational Evaluation and Policy Analysis, 19(4), 325-338.
Husen, T. (Ed.). (1967a). International Study of Achievement in Mathematics: A comparison of twelve countries (Vol. I). New York: John Wiley & Sons.
Husen, T. (Ed.). (1967b). International Study of Achievement in Mathematics: A comparison of twelve countries (Vol. II). New York: John Wiley & Sons.
Kifer, E., & Burstein, L. (1992). Concluding thoughts: What we know, what it means. In L. Burstein (Ed.), The IEA Study of Mathematics III: Student growth and classroom processes (pp. 329-341). New York: Pergamon Press.
Knapp, M., with others. (1995). Teaching for meaning in high-poverty classrooms. New York: Teachers College Press.
Knapp, M. S., & Marder, C. (1992). Academic challenge for the children of poverty, Vol. 2: Study design and technical notes. Washington, DC: U.S. Department of Education, Planning and Evaluation Service.
Mayer, D. P. (1999). Measuring instructional practice: Can policymakers trust survey data? Educational Evaluation and Policy Analysis, 21(1), 29-45.
McDonnell, L. M. (1995). Opportunity to learn as a research concept and a policy instrument. Educational Evaluation and Policy Analysis, 17(3), 305-322.
National Council of Teachers of Mathematics. (1991). Professional standards for teaching mathematics. Reston, VA: Author.
Peaker, G. F. (1975). An empirical study of education in twenty-one systems: A technical report (Vol. 8). Stockholm: Almqvist and Wiksell International.
Porter, A., Floden, R., Freeman, D., Schmidt, W., & Schwille, J. (1988). Content determinants in elementary school mathematics. In D. A. Grouws, T. J. Cooney, & D. Jones (Eds.), Effective mathematics teaching (pp. 96-113). Reston, VA: National Council of Teachers of Mathematics.
Porter, A. C. (1998). The effects of upgrading policies on high school mathematics and science. In D. Ravitch (Ed.), Brookings papers on education policy (pp. 123-164). Washington, DC: Brookings Institution Press.
Porter, A. C., & Smithson, J. L. (2001). Are content standards being implemented in the classroom? A methodology and some tentative answers. In S. H. Fuhrman (Ed.), From the capitol to the classroom: Standards-based reform in the states. One hundredth Yearbook of the National Society for the Study of Education. Part II (pp. 60-80). Chicago: University of Chicago Press .
Robitaille, D. F. (1989). Students’ achievements: Population A. In D. F. Robitaille & R. A. Garden (Eds.), The IEA Study of Mathematics II: Context and outcomes of school mathematics (pp. 102-125). New York: Pergamon Press.
Robitaille, D. F., & Garden, R. A. (1989). The IEA study of Mathematics II: Contexts and outcomes of school mathematics. Oxford, England: Pergamon Press.
Schmidt, W. H., & Burstein, L. (1992). Concomitants of growth in mathematics achievement during the population a school year. In L. Burstein (Ed.), The IEA Study of Mathematics III: Student growth and classroom processes (pp. 309-327). New York: Pergamon Press.
Schmidt, W. H., & Kifer, E. (1989). Exploring relationships across Population A systems: A search for patterns. In F. D. Robitaille & R. A. Garden (Eds.), The IEA Study of Mathematics II: Contexts and outcomes of school mathematics (pp. 209-231). New York: Pergamon Press.
Schmidt, W. H., McKnight, C. C., Cogan, L. S., Jakwerth, P. M., & Houang, R. T. (1999). Facing the consequences: Using TIMSS for a closer look at U.S. mathematics and science education. Boston: Kluwer Academic Press.
Schmidt, W. H., McKnight, C. C., & Raizen, S. A. (1997). A splintered vision: An investigation of U.S. science and mathematics education. Boston: Kluwer Academic Press.
Schmidt, W. H., McKnight, C. C., Valverde, G. A., Houang, R. T., & Wiley, D. E. (1997). Many visions, many aims, Vol. 1.: A cross-national investigation of curricular intentions in school mathematics. Boston: Kluwer Academic Press.
Schwille, J., & Burstein, L. (1987). The necessity of trade-offs and coalition building in cross-national research: A critique of Theisen, Achola, and Boakari. Comparative Education Review, 31, 602-611.
Smithson, J. L., & Porter, A. C. (1994). Measuring classroom practice: Lessons learned from the efforts to describe the enacted curriculum — The Reform Up Close Study. Madison: University of Wisconsin-Madison, Consortium for Policy Research in Education.
Stevenson, H. W., Lee, S., & Schweingruber, H. (1999). Home influences on early literacy. In D. A. Wagner, R. L. Venezky, & B. V. Street (Eds.), Literacy: An international handbook (pp. 251-257). Boulder, CO: Westview Press.
Travers, K. J., & Westbury, I. (1989). The IEA Study of Mathematics I: Analysis of mathematics curriculum. Oxford, England: Pergamon Press.
Ware, M., Richardson, L., & Kim, J. (2000). What matters in urban school reform. Norwood, MA: Systemic Research.
Westbury, I. (1992). Comparing American and Japanese achievement: Is the United States really a low achiever? Educational Researcher, 21(5), 18-24.
Westbury, I. (1993). American and Japanese achievement . . . again: A response to Baker. Educational Researcher, 22(3), 21-25.
Wiley, D. E., & Harnischfeger, A. (1974). Explosion of a myth: Quantity of schooling and exposure to instruction, major educational vehicles. Educational Researcher, 3(4), 7-12.






































