9
Statistical Issues in Analysis of International Comparisons of Educational Achievement
Stephen W. Raudenbush and Ji-Soo Kim*
International comparisons of educational achievement have become influential in debates over school reform in the United States and other countries. Such studies provide evidence on how countries compare at a given time with respect to various cognitive skills; on how the average achievement in a society is changing over time; on the magnitude of inequalities in skill levels between subgroups within a society; and on differences in such inequalities between societies. Policy makers in countries that rank low in achievement can cite these data in urgent calls for reform. Researchers use such findings to develop explanations for why certain countries outperform other countries, why certain countries seem to be improving over time faster than others, and why inequality in outcomes appears more egregious in some societies than others. By motivating reform and generating new reform strategies, international comparative studies provoke public concern, heated controversy, and new lines of research.
This chapter considers statistical issues that arise in drawing conclusions from international studies of achievement. It is organized around two distinct but related uses of the data these studies yield.
The first use involves description and comparison: description of the average level of achievement within a society and comparison of such
achievement averages across societies; description of changes in achievement over time for each society and the comparison of such change trends across societies; description of inequality within a society and comparison of inequality between societies. Such description and comparison require statistical inferences and lead inevitably to substantive interpretations. This chapter will consider the statistical issues underlying the validity of such inferences and interpretations.
The second use of international comparative data involves causal explanation. Although such nonexperimental data cannot justify causal inference (Mislevy, 1995), the data are highly relevant to the development of causal explanations. When combined with collateral information on cross-national differences in curriculum and instruction and when viewed in light of the expert judgment of researchers and educators, comparative achievement data can help generate promising new explanations for why children are learning more in one nation than another (Schmidt, McKnight, & Raizen, 1997). Such explanations are central to policy formation and to the design of new research. Promising new explanations tend to be based on statistical inferences about associations among several variables. This chapter will consider the statistical issues underlying the validity of inferences about such multivariate associations.
The Third International Mathematics and Science Study (TIMSS) provides a prominent and useful example. That study aimed to describe the intended curriculum, the implemented curriculum, and the attained curriculum (that is, student achievement) in each of about 50 countries. Each of these three tasks involves description, but the aim is obviously to generate explanations for how curriculum, instructional practice, and student achievement are connected. Indeed, some coherent explanations for the connections between these three domains have emerged and now serve as a focus for new research and debate.
TIMSS is not alone in this regard. The International Adult Literacy Study (IALS) describes the social origins (e.g., parental education) of adults in each of many societies as well as those adults’ educational attainment, level of literacy in each of several domains, current occupational status, and income. One purpose of that study is to describe levels of adult literacy in each country and to compare countries on their levels of adult literacy. But the design of the study points toward explanation of how social origins, education, and, especially, adult literacy are linked to economic outcomes. The rationale for such a design relies on a strong hypothesis that cognitive skill is ever more important to economic success in a global economy and that cross-national differences in literacy are highly salient to cross-national differences in economic success. The goal of causal explanation at least implicitly underlies the design of IALS even
though IALS, as a cross-sectional survey, can never strongly test the many empirical connections implied by any theory for how social origins, education, and literacy are connected to individual and national economic outcomes. Hence this chapter will consider statistical issues underlying valid descriptions while also considering how statistical analysis can best contribute to the larger goal of causal explanation.
The problem of making valid comparisons across societies is multifaceted. Any comparison is founded on the assumption that the outcome variables have the same meaning in every society and that the items designed to measure these variables relate similarly in each society (Mislevy, 1995). The task of translation of the tests into many languages— and of back translation to ensure that the translations are functionally equivalent—is daunting. The task of statistically equating the tests to ensure that they have equal difficulty across countries is also enormous. Yet these challenges are well beyond the scope of this chapter. We shall assume that the outcome variables are measured equivalently in every society in order to focus on the statistical issues of central interest. Of course, any shortcomings in outcome measurement and scaling will amplify the statistical problems discussed here.
We shall also assume that the sampling designs in each study are adequate to ensure that a sample that fits the specifications of the design will represent the intended population. This requires, for example, that sample design weights are available that adjust adequately for unequal probabilities of selection of persons in the target population.
This chapter also assumes that demographic variables and other explanatory variables (such as gender, ethnicity, parental education, books in the home) are sensibly measured within each society. But we cannot avoid a problem that inevitably arises in cross-national research: that some of these explanatory variables will have different meanings in different countries. For example, ethnic and language minority groups that appear in some societies are not present in others, and parental educational attainment is conceived and assessed differently in different countries.
With these constraints in mind, this chapter begins with the problem of description and comparison of national differences. It then turns to the role that statistical analyses of comparative data might play in causal explanations.
DESCRIPTION AND COMPARISON OF NATIONAL OUTCOMES
Accurate description of a nation’s outcomes is a necessary but not sufficient condition for meaningful comparison. We consider three kinds of description as well as the comparison each informs: cross-sectional
description for one cohort, between-cohort descriptions, and descriptions of change over time. Throughout this chapter we define a cohort as a birth cohort, that is, persons born during a given interval of time.
Cross-Sectional Description and Comparison
A valid description should be no more complex than is necessary to capture the key features of the data. It should apply to a well-defined population, and it should be estimated from a sample that represents that population well. We now consider the complexity of a description, the target population being described, and the realized sample as a basis for cross-sectional description.
Complexity of Description
A description is a summary of evidence. Such a summary must be complex enough to capture the essential features of the evidence, but it should be as simple as is justifiable to avoid fastening attention on irrelevancies. A one-number summary, typically the mean, is likely to provide an inadequate basis for comparison. If the nations being compared vary in dispersion, presenting means alone will omit important information about how the countries compare. Two nations with the same mean and varying dispersion would vary in the number of students who are especially low or high. If the outcome displays a skewed distribution, presenting the mean alone will mislead: Presenting the median may add useful information.
Interpreting national means is difficult without knowing how much of the variation in the outcome lies within countries. Outcomes such as achievement and literacy typically are measured on an arbitrary scale. Mean differences between nations might look big, but there is no way of assessing their magnitude without knowing how much variation lies within societies. Thus, for example, figures 1 through 3 of Pursuing Excellence (Takahira, Gonzales, Frase, & Salganik, 1998) give national means on mathematic achievement for “Population 1” (roughly, fourth graders according to the U.S. definition). These numbers seem to vary a lot: Singapore’s mean is about 100 points higher than the international average. But without knowing something about the scale of this variable, we cannot discern whether this difference represents a big or small difference in mathematics proficiency. Figure 4 displays, for each country, the percentage of students who are above the 10th percentile internationally. This conveys some sense of how big the national differences are (e.g., 39 percent of Singapore’s students score above the international 90th percen-
tile). However, it conveys the size of national differences only for the upper end of the distribution.
One-number summaries fail to convey information about uncertainty. Figure 2 of Pursuing Excellence shows a U.S. mean of 565 on science achievement, while the mean for Japan is 574. This information alone does not help us decide whether the nations really differ. However, the figure also puts the nations in “blocks” according to whether they are “significantly different” from the United States. Japan is in the same block as the United States, so these two nations are not significantly different. In contrast, England, which scored 551, is significantly lower than the United States. This dichotomous approach encourages us to conclude that the United States and Japan, which differ by nine points, are similar, but the United States and England, which differ by 14 points, are different. Displaying confidence intervals is more informative because it allows the reader to gauge how much weight to put on an observed mean difference.
Mean differences will be misleading when statistical interactions are present. In the comparative context, an interaction occurs when the magnitude of the difference between countries depends on some background characteristic of the population (rural versus urban or male versus female). Two nations that look similar on average, for example, could differ dramatically if subgroups were compared. For example, to say that a given nation is at the international mean would convey no useful information by itself if boys in that nation were doing very well and girls were doing very poorly.
Mean differences also will be misleading in the presence of confounding. A confounding variable is a background characteristic that is related to achievement but is more prevalent in one country than another. To ignore such variables can lead to an error known as “Simpson’s paradox.” It is possible, in principle, that Nation A can have a higher mean than Nation B even though every subgroup in Nation A does worse than the corresponding subgroup in Nation B! This can occur when the more advantaged subgroups have larger relative frequency in the lower performing nation.
A salient confounding variable in the TIMSS design is student age. Much of the controversy around Population 3 (defined as students in their final year of secondary school or, for short, “school leavers,” including U.S. seniors) focuses on national differences in age. However, even in the less controversial studies of Populations 1 and 2, age as a confounding variable becomes a potential concern. Population 1 includes, in each nation, the pair of adjacent school grades that contain the most nine-year-olds. This rule defines Population 1 as third and fourth graders in the United States, but this definition yields different grade sets in different
countries. Yet TIMSS publications refer to Population 1 as “fourth graders.” Now age is likely to be quite strongly related to achievement. If nations also differ with respect to the mean age of their samples, then age is a confounding variable. Although these national differences in age are likely to be small, one must keep in mind that most national differences in achievement also may be small (relative to differences within nations). Small differences in age might then contribute to nontrivial distortion in between-country comparisons. Moreover, as we shall see in the following example, grade-level comparisons between countries may be subject to misinterpretation as a result of selection bias.
By using TIMSS as an example, we do not mean to imply that TIMSS analyses are incorrect, that TIMSS reports are flawed, or that one should never report mean differences. Rather, our intent is to emphasize that analysts working on international comparative studies have several substantial responsibilities: (a) to explore aspects of the distribution of achievement other than the mean; (b) to report mean differences (or median differences) in the context of within-country variation; (c) to associate mean differences with confidence intervals; (d) to study interactions and report those that are especially salient; and (e) to study confounding variables and take necessary precautions that readers not misinterpret mean differences.
Just how much complexity must be reported must be decided on a case-by-case basis. A useful preliminary step is a graphical display that compares the cumulative distributions of an outcome between two countries. This leads to a pair of “S” curves. If the distance between these curves is essentially invariant and approximately equal to the mean difference, then the data lend some support to the reporting of mean differences as a partial summary of evidence. But if these S curves are nonparallel, the mean difference by itself is misleading. Such a display will not, of course, detect interactions or confounding. We will illustrate this idea in an example.
Defining the Target Population
Statistical inference requires a precise definition of the target population. Subtle differences between studies in this definition can lead to spurious differences in findings. International comparative research poses special challenges in this regard.
We have already referred to the cross-national differences in schooling systems that may lead to differences in mean age between societies, thus distorting comparisons between countries. TIMSS Population 3 entails a much more serious conceptual problem. Population 3 is defined as the population of those about to leave secondary school. Such a definition
leaves great doubt about the meaning of the population in a given country and, hence, about the meaning of any comparisons between countries. First, many students will leave school before the time designated as the “school-leaving” time. In the United States, about 3–5 percent of all students drop out of school before 10th grade (Rumberger, 1995), and a larger number leave prior to high school graduation. Those students are not part of the TIMSS definition of Population 3. This is problematic. If such dropout rates vary by country, comparisons between countries will be biased, such that countries with the highest dropout rates will experience positive biases in their means. Even more problematic, distinctions between secondary and postsecondary school historically have become blurred. In the United States, persons failing to obtain a high school diploma may show up later in community colleges, where many will obtain GEDs (high school equivalency diplomas); some of these will go on to obtain bachelor’s degrees. In reality, the designation of 12th grade as the “school-leaving age” has become quite arbitrary. Similar ambiguities will arise in other societies. For example, in some societies, students leave formal school earlier and obtain significant education in on-the-job-training programs.
In the ideal world, our international studies would define a population as all members of a fairly wide age interval (e.g., all persons between the ages of 5 and 25). We might then obtain a household sample of this age group, assess each participant, and estimate, for each society (and each subgroup), an age-outcome curve. Such a design would create an equated age metric and would include in the sampling frame persons who are dropouts and dropins and who receive various kinds of formal and informal schooling. Although such an ideal may be impossible to obtain, it would be worthwhile to explore better approximations to it. The designation of a population of “school leavers” or students in the final year of secondary school appears to produce serious and insoluble analytic problems.
Similar concerns arise in other studies. In IALS, adult earnings becomes an important outcome variable. It can be quite misleading to include young adults, say from 18 to 25, in such analyses because many of these young adults are in postsecondary school. Indeed, university students, who have high potential earnings, will have low earnings at these ages. Similarly, one does not wish to include retirees in the population definition when adult earnings is the outcome. One strategy is to include in the analysis only those adults between ages 25 and 59. However, the age at which postsecondary schooling terminates—and the age of retirement—may vary significantly from country to country. In a society with an early age of completion of a bachelor’s-level education, 25 year olds will have more work experience than will those in a society where school-
ing takes longer. These differences may produce between-country differences in the outcomes that are misinterpreted.
The Realized Sample
No matter how well a survey is designed and administered, response rates will be less than 100 percent and they will vary from country to country. Nonresponse can therefore bias description for a given country and bias comparisons between countries. Three conditions are possible: nonresponse leading to data missing completely at random (MCAR), missing at random (MAR), or nonignorable missingness. Little and Rubin (1987) and Schafer (1997) describe strategies for minimizing bias that arises from nonresponse.
Example: U.S. and Japanese Science and Mathematics Achievement in Population 2
We use data from TIMSS to illustrate some key points raised in the previous discussion.
Comparing Distributions
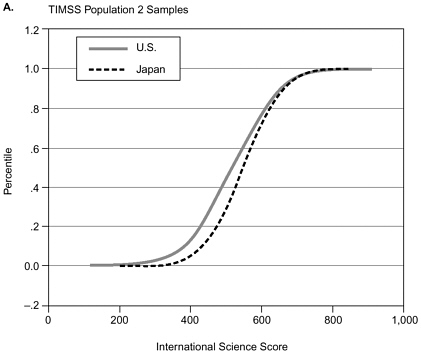
Consider first the problem of using a single number to summarize national differences. Some have objected to this practice, arguing, for example, that students at the top of the U.S. distribution achieve similarly to students at the top of the Japanese distribution, while students at the bottom of the two distributions achieve very differently (c.f., Westbury, 1993). If so, the differences between the two distributions would not be captured by a single number such as an overall mean difference. As a first check on such an assertion, we compare the cumulative distributions of the two countries. Figure 9-1a does so for science achievement. The vertical axis is the percentile, and the horizontal axis is the overall science achievement score. In general, the Japanese distribution (curve furthest to the right) is higher on the achievement scale than is the U.S. distribution. However, the mean difference between the two societies is much larger at low percentiles than at higher percentiles. Indeed, the two countries appear to differ very little at the highest percentiles. Clearly, to summarize the differences between the two countries with a single number such as a mean difference would be misleading in this case. Of course, these national differences may not achieve statistical significance at any percentile, so more investigation is required.
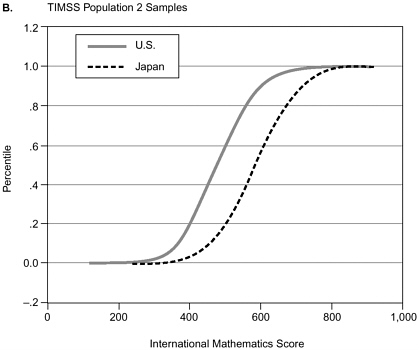
When we turn to mathematics achievement (Figure 9-1b), the story
changes. The large mean difference between the two distributions appears roughly invariant across the percentiles (if anything, the differences are smallest at the lowest percentiles). Here a single mean difference does appear to capture the key feature of the difference in distributions. (Of course, we would go further to characterize the uncertainty about this mean difference by a confidence interval.) Note that Figure 9-1 does not provide a confidence interval for differences between the countries at any given percentile and is therefore appropriate only as a first check on how the distributions differ.
Age and Grade Effects
As mentioned earlier, country comparisons may be confounded by age even after controlling for grade. Even more perplexing, grade may be viewed as an outcome variable as well as a predictor of achievement because substantial numbers of students who fare poorly are likely to be retained in grade in some societies. This policy of grade retention may distort cross-national comparisons.
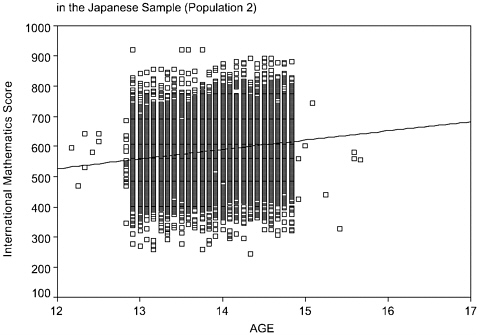
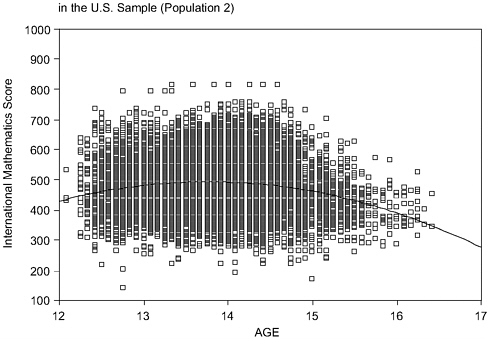
Figures 9-2a and 9-2b illustrate these difficulties. The figures provide scatterplots that display overall mathematics achievement (vertical axis) as a function of age (horizontal axis) for Population 2 (seventh and eighth graders). Figure 9-2a displays this association for Japan and Figure 9-2b does so for the United States. The figures reveal considerably more variability in age for the United States than for Japan. Moreover, the association between age and achievement differs in the two countries. Age and achievement are positively associated, as one might expect, in Japan. In contrast, the association between age and achievement in the United States, although curvilinear, is on average negative. Technically, there is an interaction effect between country and age. Thus, country comparisons will differ at different ages. What accounts for this interaction?1
This U.S. scatterplot seems to suggest that grade retention in the United States is affecting both the distribution of age and the age-outcome association. U.S. students who are older than expected, given their grade, plausibly have been retained in grade, and achieve at lower levels than their grade-level peers.2
The issue of confounding variables often arises in discussion of causal inference, and the reader may wonder whether we are criticizing TIMSS here for not supporting a causal inference. Indeed, the presence of confounding variables would certainly challenge the validity of causal inferences regarding national education systems as causes of national achievement differences. But our concern here simply involves accurate interpretation of descriptive statistics, not causal inference. The implied purpose of cross-national comparisons controlling for grade, as all TIMSS
comparisons do, is to examine how students who are similar in exposure to schooling compare on outcomes. However, U.S. students who have been retained in grade have had more exposure to schooling than their younger, same-grade peers. This creates ambiguity about the meaning of cross-national comparisons and suggests that the mean differences between Japan and the United States, holding constant exposure to schooling, is larger than suggested by grade-specific comparisons.
The statistical problems of confounding (different age distribution in the two societies) and interaction (positive age effects in Japan, negative age effects in the United States) combine to raise questions about the conception of the target population. Students in the same grade in the two countries appear to vary in exposure to schooling as a function of grade retention, casting doubt on the meaning of country comparisons for Population 2, even after adjusting for age.3 One might argue that the mean differences between the United States and Japan in mathematics are large in any case for Population 2, but comparisons between the United States and other countries may be quite sensitive to the differential selection of students into seventh and eighth grades.
Describing Differences Between Cohorts and Comparing Those Differences
Analysts will often wish to describe cohort differences within societies and compare societies with respect to those differences. For example, in TIMSS, the mean difference between Populations 1 and 2 is of interest. Some analysts have interpreted this mean difference as the average gain students make between the ages of nine and 13 (Schmidt & McKnight, 1998). The aim is then to compare countries with respect to their gain scores and to view national differences in gains as evidence of national differences in the effectiveness of the educational system operating for those between ages nine and 13. In interpreting such cohort differences as gains, the concerns mentioned are relevant and new concerns arise.
Applying our Framework for Sound Description
Using the framework developed earlier, it is clear that a comparison between cohorts within a society depends on principles of sound description. Thus, a description of cohort differences must be appropriately complex: Reporting a mean difference alone may omit important cohort differences in dispersion; reporting uncertainty (confidence intervals) associated with cohort differences is essential; statistical interactions between cohort and student background may be relevant; and certain confounding variables may give rise to misleading comparisons. A potentially confound-
ing variable in TIMSS is, once again, student age. If, for any cohort, nations vary in the mean age of their populations, differences in mean age between cohorts will vary as well, and these differences are likely related to mean differences in achievement. Thus, age differences can masquerade as differences in “gains.” In particular, if nations vary in the fraction of students retained in grade between grades four and eight, such differences will bias estimates of the “gains” of interest.4
Again using the framework already described, a description of cohort differences requires a viable definition of the target population for each cohort. Earlier, in the case of TIMSS, we concluded that the definition of Population 3 as “school leavers” is problematic, rendering problematic any cross-national comparison of cohort differences between, say, Population 2 and Population 3.
Finally, we have discussed the problem of response bias. The population for each cohort in each society may be well defined and the sample well designed, but the realized sample will be imperfect. Some degree of nonignorable missingness seems likely. Using statistical methods that are maximally robust to nonrandom sources of nonresponse is essential in any sound comparison of cohorts within a society and in any comparison between societies of these differences
In sum, any error in the description of the outcome for a single cohort in a single country is propagated in the comparison of two cohorts within a country and further propagated in the comparison between countries of such cohort differences.
Additional Challenges
Although all of the principles of sound statistical description apply in constructing cohort comparisons, three new concerns arise: the metric of the outcome, cohort differences in demographic composition, and historical changes in the causes of achievement.
The computation of cohort differences assumes, first, that the outcome is measured on a common metric across ages. A true equating requires that the same underlying construct be measured on each cohort and that the items in the tests for the separate cohorts be calibrated to lie on a common scale. This kind of equating seems unlikely when the cohorts are substantially different in age and the outcome involves math or science. When it is impossible to construct such a common metric, cohort comparisons must rely on some “relative standing” metric. For example, one might assign each person in each country a standard normal equivalent score defined as a distance of that person’s achievement from the international mean for that person’s cohort. This might be called “within-cohort” standardization. Cohort differences are then interpreted as differ-
ences in relative standing from one age to another. Some cohorts will display negative changes even though all children in that cohort are likely growing in math achievement. Moreover, the change in constructs assessed between cohorts can give rise to misleading results.
Suppose, for example, that Construct A is measured for grade four while Construct B is measured for grade eight. Assume for a moment that the target populations for the two grades are well-defined cohorts (persons born during a specified interval of time) and that no historical changes have occurred in the education system. Even then a cohort difference in relative standing confounds change over time with a difference between constructs. Consider the example depicted in Figure 9-3. A hypothetical nation is very proficient at teaching Construct A but very poor at teaching Construct B prior to grade four. Suppose that between grade four and grade eight, that nation promotes very substantial growth in both Constructs A and B. However, that nation’s eighth graders are still comparatively low on Construct B given their low starting point. A distance between cohorts that describes change in relative standing will be, in fact, the distance between Construct A for grade four and Construct B for grade eight. This will be a small change for our hypothetical nation even though, in reality, that nation made substantial positive gains on both constructs.
Let us consider further the mean difference between two cohorts, say Cohort 4 (fourth graders) and Cohort 8 (eighth graders). Suppose the outcome is measured equivalently for both cohorts. Can we interpret a
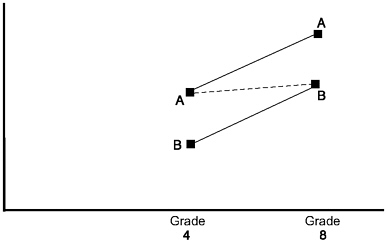
FIGURE 9-3 Construct A is assessed at Grade 4 while Construct B is assessed at Grade 8. The slope of the dotted line represents the estimated gain. Grade Grade
mean difference between these two cohorts as a measure of how much Cohort 8 learned between fourth and eighth grades? There is a substantial literature on inferences of this type (Nesselroade & Baltes, 1979). It is well known that a cross-sectional study of an age-outcome relationship confounds cohort and age. Only if cohort differences other than age are controlled can we interpret this mean difference as an age effect.
More specifically, the interpretation of a cohort mean difference as a mean gain assumes that Cohort 4’s mean is equal to the mean of Cohort 8 when Cohort 8’s members were in grade four. Of course, Cohort 8’s status at grade four is missing. In essence, the logic is to use Cohort 4’s mean as an imputation for this missing value of Cohort 8’s mean at grade four. This imputation will be biased if Cohort 4 and Cohort 8 differ on variables other than age that are related to the outcome. For example, Cohort 4 may differ demographically from Cohort 8. This would occur, for example, if immigrants to a society tend to have younger children than natives of the society. As another example, suppose that the curriculum prior to grade four has changed since Cohort 8 was in the fourth grade. Then Cohort 4’s observed status would not simulate Cohort 8’s missing status at grade four. The first example (demographic differences between cohorts) can be addressed through statistical adjustment if the relevant demographic data are collected as part of the survey. But it is unlikely that data will be available on curricular change in the society because the data on the curriculum experienced by Cohort 8 during and after grade four but before grade eight will be missing. Thus, some uncertainty will remain about the veracity of interpreting cohort differences as age effects.
Now suppose that outcomes measured at the two grades are equated and that we know that cohort differences truly reflect age differences. Thus, according to the logic described, we can interpret cohort differences as age-related gains in achievement. Can we conclude further that international differences in such gains reflect differences in the effectiveness of the schooling systems in the countries compared? We shall consider this issue later under “The Role of International Comparative Data in Causal Explanation.” That section will reveal substantial threats to the inference that age-related differences reflect the differential effectiveness of educational systems.
Describing National Changes Over Time Based on Repeated Cross-Sections
An important goal of international studies of educational achievement is to describe the improvements in a nation’s achievement over time and to compare nations with respect to their rates of improvement. A
natural design for this goal is the repeated cross-section. Two alternative versions of the repeated cross-section come to mind:
-
Hold age constant, let cohort vary. TIMSS-R (“TIMSS Repeat”) assessed eighth graders in 1995 and again in 1999. The idea is to treat differences in achievement between these two cohorts as reflecting changes in the operation of the educational system between 1995 and 1999.
-
Hold cohort constant, let age vary. TIMSS-R also assessed fourth graders in 1995 and eighth graders in 1999. This may be viewed as repeated observation of the same birth cohort (but see following discussion). Age-related differences between 1994 and 1999 are viewed as average learning gains for this cohort.
Advantages of the Repeated Cross-Section That Holds Age Constant
Recall that when nations were compared by comparing cohort differences (e.g., cross-sectional differences between Population 1 and Population 2 in TIMSS), age emerged as a potentially important confounding variable. In a repeated cross-sectional design, age reasonably might be viewed as fully controlled, provided the education system has not changed in its basic structure. If, for example, eighth graders in the United States in 1999 had the same age composition as eighth graders did in 1995, then the mean difference between time 1995 and 1999 in the United States will be unconfounded with age. If the population definition remains invariant in other nations as well, comparisons between nations in rates of change also will be unconfounded with age.5
Furthermore, recall that comparisons between cohorts in a cross-sectional study were likely confounded with differences in what outcomes were of interest. We noted, in particular, that it would be unlikely that outcome measures would be equated between cohorts within a cross-sectional study. In contrast, it should to be possible to equate assessments in a repeated cross-sectional study. The outcomes relevant to eighth graders in 1995 are likely to be quite similar to the constructs of interest for eighth graders in 1999. Thus, it should to be possible to “unconfound” outcome constructs with cohorts in this repeated cross-sectional study.
Threats to the Validity of the Repeated Cross-Sectional Design That Holds Age Constant
Nonresponse rates may differ over time. If they do, and if nonresponse is nonignorable, the effects of varying nonresponse can masquerade as historical change. However, the biggest threat to the repeated cross-sec-
tional comparison is demographic change. A nation’s population at a given age will change over time as a function of immigration, outmigration, and differential fertility of subgroups. If the demographic characteristics that are changing are also associated with achievement, trends in achievement will reflect, in part, this changing demography. Then it will be essential to measure and statistically control such demographic change if one hopes to interpret achievement trends as representing historical effects rather than demographic differences between cohorts. See Willms and Raudenbush (1989) for how such an analysis might proceed using a hierarchical model.
Advantages and Disadvantages of the Repeated Cross-Section That Holds Cohort Constant While Allowing Age to Vary
Suppose we sample fourth graders in 1995 and then sample eighth graders in 1999. We compute the mean difference and interpret it as an age-related gain. We then compare countries by their gains. This is a strong design to the extent that the 1995 and 1999 samples really represent the same birth cohort. Two threats to validity come to mind. First, immigration and outmigration may change the demographic composition of those sampled between the two years. Second, grade retention may censor the sample by excluding those who are retained between fourth and eighth grades, while adding fifth graders retained prior to ninth grade. Cross-national differences in immigration and grade retention would then bias inferences about natural differences in age-related gain.
THE ROLE OF INTERNATIONAL COMPARATIVE DATA IN CAUSAL EXPLANATION
The foregoing discussion reveals that sound explanations of national achievement differences require sound descriptions and sound comparisons: descriptions of achievement within a nation at a given time and comparisons between nations at a given time; description of cohort differences at a given time and comparison between nations on cohort differences; description of achievement trends over historical time and comparison between countries in terms of their achievement trends. We have considered the conditions required for such accurate description and comparison. However, even the soundest descriptions of nations and comparisons between nations do not justify causal inferences. Sound causal inferences require designs and analyses that can cope with the counterfactual character of causal questions.
When we claim that “Educational System 1 is more effective than
Educational System 2” for a given child, we imagine the following scenario: A child has two potential outcomes. The first potential outcome, Outcome 1, is the outcome that child would display if exposed to System 1. The second potential outcome, Outcome 2, is the outcome that child would display if exposed to System 2. To say that System 1 is more effective for the given child is to say that Outcome 1 is greater than Outcome 2 for that child. The counterfactual character of causal inference arises because it will not be possible to observe both Outcome 1 and Outcome 2 for a given child because that child will experience only one of the two systems. Thus the causal effect Outcome 1-Outcome 2 cannot be computed because either Outcome 1 or Outcome 2 will be missing. However, it is possible to estimate the average causal effect, for example, by randomly assigning children to System 1 or System 2. In this case, the population mean of the effect Outcome 1-Outcome 2 is equal to the population mean of System 1 minus the population mean of those in System 2. In the case of a randomized experiment, we can say that the mean of System 2 is a fair estimate of how those in System 1 would have fared, on average, had they received System 2 instead of System 1. (See Holland, 1986, for a clear exposition of the logic of causal inference.)
When random assignment is impossible, various quasi-experimental approximations to a randomized experiment are possible. How might cross-national researchers approach this problem? Four strategies appear prominent: comparing cohort differences, comparing historical trends, isolating plausible causal mechanisms, and comparing students within the same society who experience different systems of schooling. We consider each in turn.
1. Comparing cohort differences. The first approach to causal inference is to compute cross-sectional cohort differences for each society (e.g., differences between those in grade eight and those in grade four) and to compare those differences. Earlier, we considered difficulties in describing cohort differences as “gains.” Cohort and age are confounded, so cohort differences might reflect differences other than age. Moreover, we saw that the U.S. eighth-grade sample was really a mixture of cohorts because of grade retention. Let us presume, however, that grades really do constitute cohorts and that cohort differences also in fact reflect age-related gains. Can we conclude that differences between nations in their gains reflect differences in the effectiveness of the educational systems?
To answer this question, we must reflect on a large literature that considers the adequacy of nonexperimental designs for drawing causal inferences. Our international survey can be likened to a pre-post quasi-experiment. In such a study, nonrandomly formed comparison groups (countries) are assessed prior to the introduction of a treatment. Next,
different educational treatments are administered to each comparison group. Finally, a posttreatment assessment is administered. Differences between the gains of comparison groups are then taken to reflect differences in the effectiveness of the treatments being compared. This scenario is depicted in Figure 9-4. Here the treatments are the education systems of Country 1 and Country 2, as enacted between grades four and eight. The aim is to discern which country has the best educational system between those two grades. Country 1 makes a gain from A to B, while Country 2 makes a gain from C to D between grades four and eight. The magnitude of the quantity in curly braces (B-A)-(D-C) is the difference between mean gains of the two groups and is commonly regarded as a measure of difference in the effectiveness of the education systems as they operate between grades.
A substantial literature emerged during the late 1960s and 1970s on difficulties with this design and the interpretations it produces (Blumberg & Porter, 1983; Bryk & Weisberg, 1977; Campbell & Erlebacher, 1970). The problem with this design is that it requires that Point E be the expected status of children in Country 1 if the children in Country 1 instead had been educated in Country 2. That scenario is somewhat plausible if the scenario described in Figure 9-5 represented reality. Figure 9-5 shows achievement trends for the two groups of children based on two pretests, and then on posttest. In effect, Figure 9-5 tells us where the two countries’ children were on a “pre-pretest.” We see that, between this pre-pretest and the pretest, children of Countries 1 and 2 were growing at the same rate, on average. Then the children of Country 1 received a positive “de
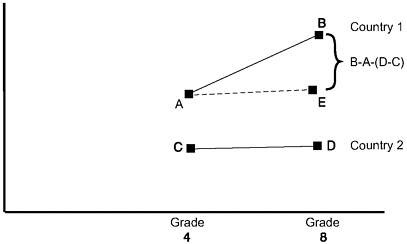
FIGURE 9-4 Causal inference based on two age groups.
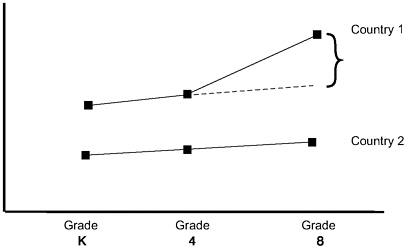
FIGURE 9-5 Scenario 1: Parallel growth prior to grade 4.
flection” by virtue of the educational system they experienced between grades four and eight in Country 1, creating a more rapid rate of growth than that experienced by children in Country 2. This deflection is taken as evidence of the causal effect of Country 1’s educational system relative to that of Country 2 between grades four and eight.
Suppose, however, that the true scenario were that depicted in Figure 9-6. Under that scenario, children in Countries 1 and 2 were growing at different rates prior to fourth grade. Between fourth and eighth grades, their

FIGURE 9-6 Scenario 2: Unequal growth prior to grade 4.
rates of growth remained unchanged. Thus, no deflection is discernible between grades four and eight. The data thus give no evidence that the two systems operated differently between grades four and eight. In both cases, the children grew along trajectories that were already in place prior to grade eight. (Moreover, the differences in trajectories prior to grade four may not reflect the contribution of formal schooling prior to grade four.)
The key problem with the two-point, pre-post quasi-experimental design is that the data provide no information about which scenario— Scenario 1 (Figure 9-5) or Scenario 2 (Figure 9-6)—is more plausible. Unless other data can be brought to bear or strong prior theory is available to rule out some of the possible scenarios, a pre-post design provides essentially no information about the relative effectiveness of the two systems between grades four and eight. The design forces the researcher to make an untestable assumption about where students in Country 1 would have been by grade 8 if those students had experienced the education system of Country 2.
2. Comparing historical trends. Earlier, we noted that historical trend data can eliminate confounding with age, but create a confounding between cohort and historical time (or “period”). Suppose we could adjust completely for cohort differences. Would differences in trends between societies then reveal differences in educational system effectiveness?
The problem in this case is that the changing effectiveness of the schooling system constitutes but one possible historical change that might account for the historical change in achievement. For example, as societies achieve higher and higher levels of educational attainment, parents are increasingly literate. Highly literate parents are better equipped than less literate parents to provide early experiences in the home that support literacy. Other secular trends—such as the increasing number of children in daycare, increasing nutrition, increasing survival rates of premature babies, changes in poverty rates, and changes in access to television and the Internet—can contribute to achievement trends even if the schooling system remained invariant in its effectiveness.
In sum, repeated cross-sections control age in allowing description of historical changes in achievement and comparison of countries in their achievement trends. And they facilitate comparisons over time with respect to a common outcome. However, historical time and cohort are confounded: Demographic differences between cohorts resulting from population change may masquerade as historical change. Moreover, changes in the operation of the schooling system will tend to be confounded with other secular trends that also may affect trends in achievement.
The repeated cross-section that controls cohort while allowing age to vary confronts a different problem: the confounding of age and historical time. Large age-related gains in achievement in a given country might be correlated with historical changes in that society other than changes in the operation of the education system.
3. Isolating plausible causal mechanisms. Researchers using TIMSS data have sought not only to make causal inferences about the impact of educational systems on student learning; they have also sought to identify specific causal mechanisms that would explain these national effects. Not only are such explanations potentially important for policy and theory, they also may compensate for lack of methodological controls. In particular, if one can identify specific educational processes that are strongly theoretically linked with higher achievement, and if those processes are also strongly associated empirically with country differences in achievement, the case for causation would be strengthened. Using this kind of logic, Westbury (1993, p. 24) wrote:
It is, for instance, a curriculum-driven pattern of content coverage that determines algebra achievement and the distribution of opportunity to learn algebra at the eighth-grade level, and it is the way algebra is distributed in the United States that, in turn, plays a major role in determining America’s aggregate standing on grade 8 math achievement in studies like [the Second International Mathematics Study] SIMS.
A common practice in research on TIMSS is to assess associations between a country’s implemented curriculum or “opportunity to learn” (OTL) and student achievement and to view those associations as causal. A large and growing literature in statistics on time-varying treatments, however, reveals the serious perils in such inferences (Robins, Greenland, & Hu, 1999). The OTL that a teacher affords students must be viewed, at least in part, as a response to students’ prior success in learning. OTL is then an outcome of prior learning as well as a predictor of later learning. A nation’s curriculum represents not only an externally imposed “treatment,” but also a historically conditioned set of expectations about how much students will know at any age. The curriculum is thus an endogenous variable. Standard methods of statistical analysis generally cannot reveal the causal impact of such endogenous treatment effects. Indeed, serious biases commonly accompany any attempt to do so. Control for prior achievement in a longitudinal study should reduce the bias, but one cannot rule out unmeasured causes of why OTL is greater for some students than for others.
4. Comparing students within societies who experience different
kinds of schooling. The strategies described for causal inference use data from other nations to estimate counterfactuals for U.S. children. More specifically, the strategy of comparing “gains” between Population 1 and Population 2 claims, in effect, that U.S. children would make gains similar to children in, say, Japan, if Japanese instructional approaches had been adopted in the United States. This chapter has criticized this kind of inference on somewhat technical grounds. Essentially, such inferences require extrapolations across societies: (a) that it is feasible to implement Japanese instructional methods in U.S. schools and (b) that if these methods were implemented, U.S. students would respond similarly to Japanese students. Causal inferences based on comparing trend data between nations require similar cross-national extrapolations. Such extrapolations, although intriguing, should not be confused with reasonable causal inferences.
Instead of basing causal inference on between-nation extrapolations, it makes more sense to develop hypotheses based on between-nation comparisons, but to test such hypotheses by conducting experiments within nations. In essence, we cannot really know how feasible it is to implement a new policy or how children in the United States will respond without actually trying to implement the policy in the United States.
While awaiting truly definitive experiments, it makes sense to contemplate within-nation analyses that approximate the experiment of interest. Consider the hypothesis that the U.S. math curriculum, in comparison to the curricula of other nations, lacks coherence, focus, and rigor, and that this curricular difference explains the observed national difference in math achievement (Schmidt et al., 1997). One might test this hypothesis within nations by identifying variation on coherence, focus, and rigor between schools within nations. One then would formulate a multilevel model of the association between curricular quality and outcomes.6 The model would be constructed such that the difference between a child’s outcome and the expected outcome for that child under the “typical” U.S. curriculum is a function of how far that child’s experienced curriculum deviates from the U.S. average. The beauty of this model is that the causal inference is no longer just a large extrapolation. Rather than imagining how a student would do under a different nation’s curriculum, we are imagining how the student would do under a curriculum actually observed in a U.S. school. The key challenge, however, is to estimate the “expected” outcome for each child under a typical U.S. curriculum. Surely it is true that a child’s exposure to curricular quality depends on a variety of child and family characteristics, including but not limited to social background, ethnicity, and mathematics aptitude. To the extent that these characteristics also are related to achievement, they must be included in the model for “expected achievement” under the typical U.S. curriculum. Past research strongly suggests that prior aptitude, as measured by a
pretest, is the most powerful confounding influence, as it tends to be most strongly related to curricular exposure and to mathematics achievement. Failure to include aptitude in the model will cast doubt on the validity of any causal inferences based on the within-country model. Unfortunately, TIMSS, unlike SIMS, for example, does not include a measure of prior aptitude. This fact seriously limits the utility of TIMSS for approximating the experiment that we wish we could conduct: one in which curricular practices suggested as potentially important in between-nation comparisons are selectively implemented within nations to study their causal effects.
Even if prior achievement were controlled and even if the analysis compared curriculum differences within societies as well as between societies, the potential endogeneity of these curricular variables would remain a concern. Certainly a good pretest would help control selectivity bias. However, teachers generally know much more than researchers do, even in the presence of a pretest, about the children they are assigned to educate. To the extent teachers use this knowledge to shape their instructional strategies, the concern will remain that OTL effects on achievement will be estimated with bias. Only a true experiment can fully resolve this issue, while within-country surveys can attempt to approximate the true experiment.
CONCLUSIONS
The ultimate utility of cross-national surveys is to support the improvement of public policy. Public policy inevitably is based on causal inferences because policy makers must make assumptions about what will happen if regulations or incentives or curricula change. Thus it is tempting to use available data to make strong causal claims. However, cross-sectional survey data generally provide a poor basis for causal inference.
If international surveys of achievement cannot support sound causal inference, of what value are they in thinking about how to improve schooling? We take the view that such data play a significant role in causal thinking by suggesting promising new causal explanations. For example, connections between the intended curriculum, the implemented curriculum, and the achieved curriculum in various countries participating in TIMSS have suggested a provocative explanation for shortcomings in U.S. math and science achievement (Schmidt et al., 1997). That explanation begins with a description of the intended curriculum in the United States as lacking in focus, rigor, and coherence within grades and across grades. These weaknesses are consistent with observable shortcomings in how teachers teach and with cross-national comparisons of achievement
between the United States and other nations, nations whose intended and implemented curricula, by comparison, display high levels of focus, rigor, and coherence. This explanation thus suggests hypotheses about how very detailed changes in the curriculum would translate into changes in teaching and learning.
The explanation that Schmidt and colleagues have suggested appears consistent with the data from the curriculum study and achievement study of TIMSS and also may be well grounded in sound thinking about how mathematics education can best be organized to produce mathematical understanding and proficiency. However, other explanations can be constructed that will be equally consistent with the data from studies like TIMSS. Unfortunately, studies like TIMSS can supply no decisive evidence to arbitrate between such explanations. To test these explanations requires, instead, experimental trials of instructional approaches that embody the explanations of interest. We take the position that one cannot know how well an alternative intended and implemented curriculum would work in a given society without actually putting such a curriculum in place in that society and seeing what happens.
The essential utility of international studies of achievement, we believe, is to suggest causal explanations that can be translated into interventions that can be tested in experimental trials. We recommend analyses pointed toward such explanations and such interventions.
-
One might find data sets collected strictly within the United States or other countries, data sets that are longitudinal at the student level. Possible examples include the National Educational Longitudinal Study of 1988 (NELS) or The Early Childhood Longitudinal Study (ECLS). Such data sets would have to be scrutinized to determine if the key explanatory variables of interest (e.g., variables that capture curriculum and instruction) are available. The key explanatory variables are those suggested by cross-national work such as TIMSS.
-
One might design a new longitudinal study within a nation for the express purpose of testing hypotheses arising from TIMSS or other international comparative studies.
-
One might design a sequel to TIMSS that would collect longitudinal data at the student level in many countries. Multilevel analyses of such data could test hypotheses suggested by between-country comparisons within a number of societies, a powerful design indeed.
Difficulties with the third option include the high cost and managerial complexity of carrying on multiple longitudinal studies in varied nations. Moreover, the decision to “become longitudinal” must be integrated with other design options raised in this chapter. These include
broadening the age range within countries and using a household survey rather than a school survey for older students.
Hybrid proposals might be considered. For example, one might encourage the United States to collaborate with a small number of carefully selected countries to design parallel longitudinal studies having the ambitious aim of linking curricular experiences with trajectories of student growth.
None of these suggestions is intended to undermine the utility of surveys of curriculum and achievement in many societies. Such surveys have proven their worth in generating important hypotheses for educational improvement within societies. Rather, the question is how to test those hypotheses. A combined program of longitudinal studies and experiments seems in order for this purpose.
Over the past several decades, statistical methods have greatly enhanced the capacity of researchers to summarize evidence from largescale, multilevel surveys such as TIMSS and IALS. Our comparatively new understanding of missing data has allowed these studies to compare countries on many cognitive skills even though each examinee is tested on a comparatively small subset of items. Item response models create metrics for achievement and methods for discerning cross-national item bias. Improved graphical procedures enable us to visualize distributions of outcomes in complex and interesting ways. Hierarchical models enable us to study variation within and between countries and to compute sound standard errors for effects at each level.
More could be done to capitalize on these advances. For example, the magnitude of country-level differences could be assessed more sensibly in relation to differences between schools within countries and differences between children within schools using Bayesian inference for hierarchical models (Raudenbush, Cheong, & Fotiu, 1994).
However, upon reflection, our judgment is that the most important shortcoming in the analysis of cross-national international data is the lack of attention to recent advances in our understanding of sources of bias in analyses that suggest, implicitly or explicitly, causal interpretation. We have emphasized a need for greater sensitivity to biases that arise in how populations are defined (e.g., by the meaning of “grade” in the presence of retention or selective dropout), in how cross-national differences are interpreted, and in how we think about curriculum and opportunity to learn as causal mechanisms. These deep issues of design and interpretation cannot be resolved by sophisticated statistical analytic methods. Rather, attention to foundational logical issues is a basis of sound analyses and warranted substantive interpretations.
NOTES
REFERENCES
Blumberg, C., & Porter, A. (1983). Analyzing quasi-experiments: Some implications of assuming continuous growth models. Journal of Experimental Education, 51, 150-159.
Bryk, A., & Weisberg, H. (1977). Use of the non-equivalent control group design when subjects are growing. Psychological Bulletin, 84, 950-962.
Campbell, D., & Erlebacher, A. (1970). How regression artifacts in quasi-experimental evaluations can mistakenly make compensatory education look harmful. In J. Hellmuth (Ed.), Compensatory education: A national debate, volume 3: The disadvantaged child (pp. 185-210). New York: Brunner/Mazel.
Gamoran, A. (1991). Schooling and achievement: Additive versus interactive models. In S. W. Raudenbush & J. D. Willms (Eds.), Schools, pupils, and classrooms: International studies of schooling from a multilevel perspective (pp. 37-52). San Diego, CA: Academic Press.
Holland, P. (1986). Statistics and causal inference. Journal of the American Statistical Association, 81(396), 945-960.
Little, R., & Rubin, D. (1987). Statistical analysis with missing data. New York: John Wiley & Sons.
Mislevy, R. J. (1995). What can we learn from international assessments? Educational Evaluation and Policy Analysis, 17(4), 419-437.
Nesselroade, J., & Baltes, P. (1979). Longitudinal research in the study of behavior and development. New York: Academic Press.
Raudenbush, S. W., Cheong, Y. F., & Fotiu, R. (1994). Synthesizing cross-national classroom effect data: Alternative models and methods. In K. R. M. Binkley & M. Winglee (Eds.), Methodological issues in comparative international studies: The case of reading literacy (pp. 243-286). Washington, DC: National Center for Education Statistics.
Robins, J. M., Greenland, S., & Hu, F.-C. (1999). Estimation of the causal effect of a time-varying exposure on the marginal mean of repeated binary outcome. Journal of the American Statistical Association, 94(447), 687-700.
Rumberger, R. W. (1995). Dropping out of middle schools: A multilevel analysis of students and schools. American Educational Research Journal, 32(3), 583-625.
Schafer, J. (1997). Analysis of incomplete multivariate data. London: Chapman & Hall.
Schmidt, W. H., & McKnight, C. C. (1998). What can we really learn from TIMSS? Science, 282(5395), 1830-1831.
Schmidt, W. H., McKnight, C. C., & Raizen, S. A. (1997). A splintered vision: An investigation of U.S. science and mathematics education. Boston: Kluwer Academic.
Takahira, S., Gonzales, P., Frase, M., & Salganik, L. H. (1998). Pursuing excellence: A study of U.S. twelfth-grade mathematics and science achievement in international context. Washington, DC: National Center for Education Statistics.
Westbury, I. (1993). American and Japanese achievement . . . Again: A response to Baker. Educational Researcher, 22(3), 21-25.
Willms, J., & Raudenbush, S. (1989). A longitudinal hierarchical linear model for estimating school effects and their stability. Journal of Educational Measurement, 26(3), 209-232.