PREDICTABILITY OF REGIONAL HYDROLOGIC SYSTEMS ASSOCIATED WITH TERRESTRIAL COUPLING
Randy Koster
NASA Goddard Space Flight Center
Seasonal Prediction: Recent Results From NSIPP
Seasonal prediction of meteorological conditions cannot rely on the initialization and modeling of the atmosphere alone, since the timescales over which atmospheric anomalies dissipate are much too short. Seasonal forecasting must instead rely on the modeling of slower components of the earth system—namely, the oceans and the land surface. Although the ocean has the longer memory of the two, various studies (e.g., Kumar and Hoerling, 1995; Trenberth et al., 1998; Shukla, 1998; Koster et al., 2000) suggest that ocean conditions have only a limited impact on predictability over midlatitude continents. Thus, the memory associated with land surface soil moisture may turn out to be the chief source of midlatitude forecast skill.
The accurate initialization and modeling of soil moisture can contribute to a seasonal forecast only if two conditions are met: (1) the soil moisture has adequate “memory” (i.e., an anomaly lasts well into the forecast period) and (2) the atmosphere responds in a predictable way to the soil moisture anomaly. Various studies in the literature have addressed soil moisture memory and atmospheric response, both in the real world and in the modeling environment (Delworth and Manabe, 1988; Vinnikov et al., 1996; Huang et al., 1996; Liu and Avissar, 1999). In this paper, in place of a comprehensive literature review, we illustrate some key issues with recent research performed under the National Aeronautics and
Space Administration (NASA) Seasonal-to-Interannual Prediction Project (NSIPP).
Soil Moisture Memory
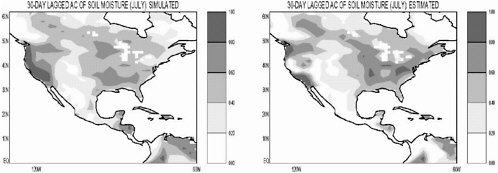
We recently manipulated the water balance equation at the soil surface into a relationship between the autocorrelation of soil moisture and the statistics of the atmospheric forcing, the variance of soil moisture at the beginning of the time period in question, and the structure of the land surface scheme used (Koster and Suarez, in prep.). The equation, despite its various approximations, successfully reproduces, to first order, the spatial distribution of soil moisture autocorrelation produced by the NSIPP modeling system. Figure 1, for example, shows that although many fine-scale details are missed, the equation captures the large-scale structure of the simulated 30-day-lagged autocorrelation for July. The equation works far better than the more traditional “water holding capacity divided by atmospheric demand” approach.
Further manipulation of the equation reveals four distinct physical controls on soil moisture memory: (1) temporal memory in the precipitation and radiation forcing fields, as perhaps induced by land–atmosphere feedback, (2) nonstationarity in the statistics of the forcing, as induced by seasonality, (3) reduction in anomaly size through the functional dependence of runoff on soil moisture, and (4) reduction in anomaly size through the functional dependence of evaporation on soil moisture. The relative importance of each control can be established through analysis of climate model data; thus, the equation can be used to characterize and explain geographical variations in simulated soil moisture memory. For example, the main physical control on memory loss in the eastern United States is seasonality of precipitation, and its impact is not large. Memory is reduced much more to the West because of the evaporation effect, which is influenced in part by low water holding capacities there. Autocorrelations in the far West increase again because of precipitation seasonality (acting in the opposite direction) and precipitation persistence.
Atmospheric Response to Soil Moisture Anomalies
A recent study of the atmosphere's responsiveness to soil moisture anomalies focused on two ensembles of simulations with the NSIPP modeling system (Koster et al., 2000). Ensemble 1 consisted of 16 45-year simulations with interannually varying sea surface temperatures (SSTs) and interactive land surface processes. Ensemble 2 was similar except that land–atmosphere feedback was effectively deactivated; interannually varying land surface evaporation efficiencies (derived from a single member of Ensemble 1) were prescribed in each simulation of Ensemble 2.
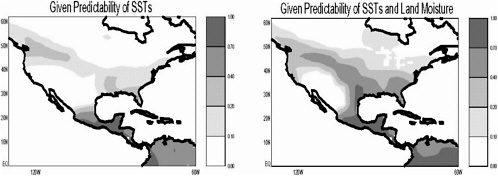
Figure 2 shows the main result. The precipitation statistics from each ensemble were transformed into an index that describes the robustness of precipitation response to the specified boundary conditions. If, at a given point, all members of an ensemble produce basically the same time series of precipitation, then this index has a value close to 1, and we say that precipitation at that point is tied strongly to the surface boundary conditions—precipitation is predictable if the surface boundary conditions are themselves predictable (at least for the general circulation model (GCM) climate). If, on the other hand, the different ensemble members produce very different time series of precipitation, then the index is close to zero, and the potential for predictability is low. In this case, chaotic atmospheric dynamics overwhelm any control on precipitation imposed by the boundary conditions.
The left plot shows this “robustness” index over North America, as computed from boreal summer data (JJA) from Ensemble 1. Notice that foreknowledge of SSTs contributes to the predictability of precipitation only in the tropical areas. The right plot shows this index as computed from Ensemble 2. Foreknowledge of land surface moisture conditions leads to enhanced predictability over a significant part of midlatitude North America.
The land's contribution to precipitation predictability can be isolated by subtracting the values in the left plot from those in the right plot. Over North America, and in fact across the globe, the land contributions are highest in the transition zones between humid and dry areas.
The low contribution in dry areas appears to reflect the low flux of evaporated moisture into the lower atmosphere. Contributions are low in humid areas partly because evaporation there is controlled more by atmospheric demand than by variations in soil moisture.
Unfortunately, Figures 1 and 2 cannot easily be compared, since the underlying simulations were performed at different resolutions—Figure 1 is based on runs with the 2X2.5 GCM, whereas Figure 2 is based on runs with the 4X5 version, with a correspondingly different climatology. Nevertheless, the figures suggest that land contributions can be high where they need to be—namely in regions with significant soil moisture memory. Indeed, soil moisture memory is fostered by land–atmosphere feedback that promotes precipitation persistence.
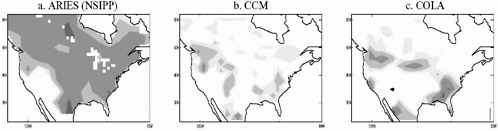
Two more results, though preliminary, are included here. The first comes from an idealized experiment in which all surface boundary conditions, including temperatures, are assumed to be perfectly known into the future. The NSIPP atmospheric GCM was first run for a specific July, using climatological SSTs. At each time step in the simulation, the values of all land surface model prognostic variables were written out to a special file. Then, an ensemble of 16 Julys using the same SSTs was run. At each time step of each member simulation, the updated values of all land surface prognostic variables were discarded and replaced by values read in from the special file. Thus, although the members of the ensemble differed because of their different atmospheric initial conditions, each was forced to maintain the same time series of (geographically varying) land surface prognostic variables. By quantifying the variations of atmospheric variables (precipitation, air temperature, etc.) seen between the ensemble members, using techniques similar to those used to generate Figure 2, we generate the estimates of land–atmosphere feedback strength shown in Figure 3a.
Note that this experiment is basically a simple, computationally cheap version of that which produced Figure 2. The idea is to promote an intercomparison of coupling strength among different models. Shown in Figures 3b and 3c are corresponding results for two other GCMs (Andrea Hahmann and Paul Dirmeyer,
personal communication., 2000). The distinction between the GCMs is obvious; the NSIPP general circulation model (GCM) clearly shows a higher land–atmosphere feedback strength than either the CCM or COLA GCMs.
How do we know which level of feedback strength is most realistic? An additional experiment addresses this, though the results are currently inconclusive. The “control” in this experiment is an ensemble of Atmospheric Model Intercomparison Project (AMIP)-type simulations in which prescribed, realistic SSTs are used to force the GCM over the time period 1996–1999. The corresponding “experiment” ensemble is identical to the control ensemble except for one thing—at every time step in a member simulation, the precipitation generated by the GCM over the United States is replaced by observed precipitation (from a special hourly dataset generated by Wayne Higgins at National Centers for Environment Prediction (NCEP)) just before it hits the ground. Only the land surface feels this more realistic precipitation; the GCM's water vapor fields and the latent heating of the atmosphere are not replaced. The land surface presumably develops more realistic soil moisture states in response to the more realistic precipitation forcing.
Three global precipitation datasets are then compared: (1) the observed precipitation; (2) the precipitation from the AMIP-style runs (i.e., precipitation guided only by SST variability), and (3) the (constantly replaced) precipitation generated by the GCM in the experiment ensemble (i.e., precipitation guided by both SST variability and the presumably more realistic soil moistures). If the precipitation generated in the experiment ensemble is significantly closer to the observations than that generated in the AMIP ensemble, then we will have demonstrated a positive impact of more realistic soil moisture on precipitation in the GCM, and we will have also shown that land–atmosphere feedback is operating in the real world. Some improvement is indeed seen in our preliminary runs—Figure 4 shows significant reductions in precipitation error over the United States, especially in summer.
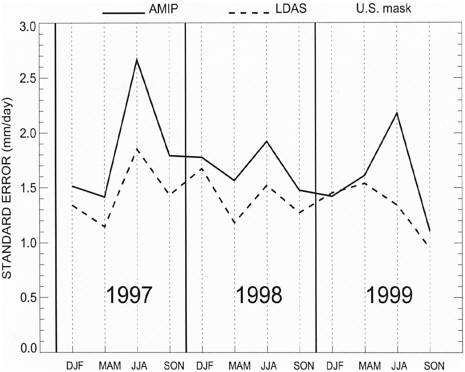
FIGURE 4
Seasonal Prediction: Science Questions and Research Needs
The results above serve as background for three science questions related to seasonal prediction.
-
Over what timescales can soil moisture be predicted in the real world? How well can these timescales be simulated in a modeling system? The analysis leading to Figure 1 shows that several factors can influence soil moisture memory. How relevant is each factor in the real world, and do GCMs simulate their relative importance correctly? Can we specify regions and seasons for which useful soil moisture memory is essentially unattainable?
-
To what degree is the atmosphere “coupled”' to the land surface in the real world? How does the degree of coupling differ among modeling systems, and how do we evaluate the realism of this coupling? The differences seen between modeling systems in Figure 3 are significant and disturbing. Because modeling systems are key to long-term hydrological prediction, differences in their coupling strength must be quantified, understood, and evaluated against observations.
-
Are some hydrologic states more prone to long-term memory than others? Why? The analysis of soil moisture memory (beyond what is presented above) suggests that some hydrologic anomalies, such as drought, may have potential for added persistence. In addition, some meteorological regimes may be more conducive to land–atmosphere feedback and thus may promote persistence. If we find that predictability in a region is generally poor, can we at least hope to predict the occurrence and/or longevity of certain extremes in the region?
Some New and Relevant Initiatives
Although quantifying land–atmosphere feedback strength from a strictly observational analysis is very difficult, a combination of modeling and observations can provide essential insight. Two scientific panels, namely the Global Energy and Water Cycle Experiment (GEWEX) Global Land-Atmosphere System Study (GLASS) panel and the U.S. Climate Variability and Predictability (CLIVAR) Seasonal-to-Interannual Modeling and Prediction (SIMAP) panel, are now promoting a model intercomparison experiment similar to the one that produced Figure 4. The experiment, which would be global in scope and would cover additional years, would have two phases. The first phase, the “maintained soil moisture” phase, is designed to quantify the impact of realistic soil moisture contents on precipitation. In this phase, the coupled land–atmosphere model is forced to maintain realistic soil moistures at all times, so that the focus is mainly on atmospheric response to land conditions (i.e., on the strength of the coupling). The second phase, the “initialization” phase, is similar except that
the artificial replacement of precipitation is halted at some prearranged time. The second phase specifically addresses persistence, being designed to establish the impact of a realistic land surface moisture initialization on precipitation forecasts.
The first phase should address the second question above regarding the degree to which the atmosphere is coupled to the land surface.. An improvement in simulated precipitation due to more realistic soil moistures, if it occurs, would serve both to demonstrate the existence of coupling in the real world and to validate the coupling strength in the modeling system. The second phase, in which soil moistures are initialized at realistic values and then allowed to evolve, will help address the first question regarding the modeling of soil moisture timescales and will, more generally, quantify predictability in the participating models.
Such a modeling effort should be supplemented, of course, by observational studies. The initialization phase of the above experiment could be improved through application of superior initial conditions, as obtained through a land data assimilation system (LDAS) approach. Also, observational analysis of soil moisture and meteorological data outside the modeling context will help establish the real world's prevailing timescales. Currently, such observational analyses are limited by the paucity of historical data; efforts to expand and maintain the observational database are needed.
The modeling experiment that led to Figure 3 is also being promoted by the two science panels, though to a lesser degree. The experiment is highly idealized but at least has the advantage of being easy and computationally inexpensive to perform. It thus can shed light quickly on intermodel differences in coupling.
Role of Federal Agencies
Demonstrating the effectiveness of earth science models for hydrologic prediction, either through the experiment described in 2.2 above or through some other well-structured model intercomparison study, requires substantial computer resources, particularly because such studies will require ensembles of long-term simula-
tions to produce the data needed for statistical analysis. Funding agencies should be ready to support these needs. In addition, maintenance and continuation of observational programs, particularly for soil moisture and meteorological data, are critical for providing a basis for the evaluation of prediction systems.
HYDROLOGIC INITIALIZATION AND FORECAST IN NUMERICAL WEATHER PREDICTION
Dag Lohmann
National Centers for Environmental Prediction (NCEP)
Uncertainty and systematic errors in the prediction of hydrologic states and fluxes, such as soil moisture, evapotranspiration, and runoff, are introduced into the forecast system by three different factors. This paper will concentrate on the third factor and how it is addressed in numerical weather prediction, but will mention the other two as well. The modeling strategy is highlighted in an NCEP-modified “Shukla staircase” (see GAPP science plan), with the model hierarchy on the outside, covering the various spatial scales, and the data assimilation system in the inside, for determining the proper initial conditions for the models.
Hydrologic Model Physics and Problems in Parameter Estimation
Once the physical knowledge about the system is expressed in a mathematical model, one has to find optimal parameters for the model. Hydrological models use many different equations for their model formulation. The hydrologic models, which are currently coupled to atmospheric models, are rather simplistic in the description of horizontal and vertical water fluxes in the soil, while they often have a detailed description of vegetation processes. The reason is that most of these models originate from atmospheric modelers, who traditionally place a greater emphasis on the energy
side of hydrologic processes (turbulent fluxes and ground heat flux), while hydrologists are more concerned with the water balance, especially runoff and streamflow. This led to the development of many based on Richards equation 1-dimensional land-surface models (LSMs), which are used on the scale where hydrologists would use conceptual lumped models like the Sacramento model. Only a few LSMs have incorporated “hydrologic knowledge,” which makes their use for hydrological predictions promising. All LSMs and traditional hydrologic models have parameters, such as hydraulic conductivity and root depth, which can only be inferred indirectly from modeling exercises or interpolated from sparse point measurements.
Resolution of the Atmospheric and the Hydrological Models
Doubling the horizontal resolution of atmospheric models (such as the NCEP estimated time of arrival (ETA) model) increases the execution time roughly by a factor of eight. It therefore will take some time before atmospheric models have a horizontal resolution of well known “as physical as possible” hydrologic models; (on the order of 100 meters). Numerical weather prediction can be shown to benefit from both higher resolution and a physics upgrade for example the coupled LSM.
Uncertainty in the Initialization of the Models
State variables in many of the models have to be initialized. This has led to the development of sophisticated variational methods in atmospheric and ocean sciences, while for operational purposes, methods to initialize land surface models are still in the early stages of development. The soil moisture data from the 4-dimensional data assimilation systems (4DDA) of coupled land–atmosphere models often suffer substantial errors and drift owing to precipitation, temperature, and radiation biases in the land-surface forcing of the coupled system. To constrain such er-
rors and drift, some developers apply soil moisture nudging techniques in coupled 4DDA, but such nudging can introduce other undesirable behavior such as over amplified annual cycles of soil moisture and lack of water conservation.
As an appealing alternative to coupled land-surface 4DDA, a consortium of Continental-Scale International Experiment (GCIP)-supported groups has undertaken the development and execution of an uncoupled Land Data Assimilation System (LDAS). The LDAS execution is hosted on an NCEP developmental computing platform and is supported by NCEP in collaboration with NASA/ Goddard Space Flight Center (GSFC), National Weather Service Office of Hydrology, National Environmental Satellite, Data, and Information Service/Office of Research and applications (NESDIS/ORA), Princeton and Rutgers Universities, the University of Washington and the University of Maryland.
Specifically, these partners are developing, executing, and validating a prototype national, realtime, hourly, 1/8-th degree, distributed, uncoupled, land-surface simulation system. This system consists of several land-surface models (LSMs) running in tandem on a common grid and driven by common surface forcing fields. The hallmarks of the forcing fields are observed, hourly, gage/radar precipitation and observed Geostationary Operational Environmental Satellite (GOES)-based satellite-derived surface solar insolation. Additionally, a common streamflow routing model is being applied to each LSM's gridded runoff on the shared common grid. Finally, the "DA" for "data assimilation" in LDAS denotes a later "Phase II" thrust that will include the assimilation of satellite-derived land-surface fields, such as skin temperature, soil moisture, snowpack, and vegetation density and greenness. Another future but central LDAS phase will be a forecast component, wherein LDAS will be integrated days, weeks, and months into the future using ensemble surface forcing (including ensemble quantitative precipitation forecasting (QPF)) from the weather and seasonal prediction models of NCEP.
With this setup, which is currently under construction, it is hoped that the state variables will be initialized as well as possible; first results look promising.
A number of important questions and discussion points emerge from the preceeding text.
Priority science questions in predictability of hydrologic systems:
-
How do we estimate model parameters in hydrologic models?
-
What is the required complexity / structure for hydrologic models?
Required modeling and analysis initiatives and data collection programs:
-
There is not enough analysis done with the data already produced.
-
More cross-validation is needed to decide about needed model complexity.
Roles of federal agencies that fund research and support monitoring:
-
Federal agencies should be funded to implement operative test-beds for research. This would enable researches of the academic world and federal and state agencies to bridge the gap between research and day-to-day operations.
OPERATIONAL SEASONAL PREDICTION OF HYDROCLIMATE OVER THE UNITED STATES
Huug van den Dool
National Centers for Environmental Prediction
INTRODUCTION
The Climate Prediction Center (CPC/NCEP) has developed a physically based soil moisture data set for the United States for the period 1932 to the present. This data set is the result of integrating the so-called “leaky” bucket of Huang et al. (1996) for nearly 70 years with observed forcing, most notably observed precipitation at 344 Climate Division, but also temperature. The soil moisture data set, with daily updates through yesterday 12Z, thanks to daily precipitation analysis by Higgins and Shi, has been widely applied for drought and wetness monitoring, the launching of monthly/seasonal prediction tools, and many research projects. Other outputs of the model include evaporation, runoff, etc., for all data from 1932 to the present (lower 48 states only), allowing a judgment of present conditions in historical perspective, forming anomalies, etc.
CPC is the organization that issues the official monthly and seasonal forecasts for the U.S. Traditionally, the predictands were time averaged temperature (T) and precipitation (P). Recently, antecedent soil moisture conditions have been used in several emerging systematic methods to improve T and P forecasts, especially in summer. Experimental forecasts for soil moisture itself are also emerging and the possibility of some kind of probabilistic
monthly/seasonal runoff prediction is being considered jointly with Office of Hydrology/National Weather Service (OH/NWS).
Note that in this paper, we are not discussing major NCEP activities in data assimilation for the shorter-range forecasts. The soil plays an important role in these shorter-range forecasts, one main problem being drift of the data assimilation system due to biased precipitation input. We will only mention below the LDAS activity, which is a modern data assimilation, but observed precipitation is used to avoid such drifts.
As time permits we will present/discuss some or all of the following:
-
Monitoring of the current situation. The United States as a whole is and has been very dry. This will be discussed by looking at soil moisture anomalies as of mid-September 2000. Recent changes will be presented as well.
-
Incorporation of short-term forecasts. Taking the medium-range forecast (MRF) ensembles at face value, the bucket model can be integrated 1 and 2 weeks ahead for short-term forecasts.
-
The most recent soil moisture anomalies, after recasting the units where necessary, are used as the initial lower boundary condition in NCEP’s ensemble of “coupled model” runs for multiseasonal forecasts.
-
Likewise, the most recent soil moisture anomalies are used to launch empirical forecast tools. An example Constructed Analogue on Soil (CAS) moisture method for JJA2000. The CAS method can also be used for process studies on academic initial conditions in soil moisture.
-
The aftermath of a La Niña in 2000. This too was a consideration in forecasts made in early 2000. Some La Niña composites of soil moisture will be shown.
-
Some comments on empirical evidence of interactive soil moisture over the United States. Further analysis: comparing model runs with and without interactive soil moisture, in terms of tempera-ture persistence, lagged precipitation–temperature correlation, etc.
-
The latest Atmospheric GCM used at NCEP for ocean–l and “coupled” runs. Analyses of monthly mean temperature, soil moisture, evaporation, and precipitation in 11 Atmospheric Model Intercomparison Project (AMIP) global SST forced runs by this model reveal both strengths and weaknesses. We briefly discuss (for the United States only) the mean state, the interannual variability, spatial degrees of freedom, and various lagged correlation, prediction skill (model vs. observation) and predictability (model vs. model).
The Huang et al. (1996) model has also been run for all other continents, resulting in a global soil moisture data set. This data set for 1979–1999 is updated only about once a year, not as religiously as the U.S. data set, which has operational application. The global data sets are mainly used for two kinds of applications: one where soil moisture is a prescribed lower boundary condition, and the other for various geodetic research activities such as investigation of the feasibility of detecting soil moisture anomalies by measuring gravity from satellite and determinations of the annual cycle of the geoid etc.
Near Future (2-3 years)
The Environmental Modeling Center (EMC) of the NCEP, as a participant in the multi-agency GCIP Land Data Assimilation System (LDAS) project, has started to run its model, the NOAH LSM, in stand-alone mode with observed forcing functions including observed rainfall, from spring 1999 forward. The NOAH model is physically far more complete than the CPC leaky bucket, and it has much higher spatial (1/8th of a degree) and temporal (hourly) resolution. By using observed forcing, one avoids some of the usual biases of coupled data assimilation. In this sense, the philosophy is the same as Huang et al. (1996) model, but LDAS is far more comprehensive. The LDAS data set (currently no more than 2 years) would be extremely useful for climate application if it covered a multidecadal period. We think it is feasible to integrate the NOAH LSM from 1948 to the present. A 1998 pilot, in concert with Regional Reanalysis, is being prepared. This would
require the assembly of many forcing data sets at high resolution for a very long period. The pay-off of this endeavor would be (1) improved soil moisture data for the various CPC prediction and monitoring tools as well as for the community, (2)superior model consistent initial conditions for numerical prediction on time scales ranging from hours to seasons, and (3) model consistent prescribed lower boundary conditions in AMIP-like experiments to determine predictability due to soil moisture anomalies.
Priority science questions in predictability are first and foremost the design of experiments that could give us pertinent information about hydrology and atmospheric predictability. Which one is first—the atmosphere or the soil? If the soil itself is the prediction target, much depends on the precipitation forecast (a very weak link in the chain). If the atmosphere is the forecast target, the characterization of the lower boundary down to some depth is allimportant. Taking the latter point of view, issues are the mixing of SST (global or otherwise) and initial soil moisture, the challenging formulation of lower boundary conditions vs. initial value predictability (is soil moisture the initial value?), and the question of what we can learn from flawed models (which have overactive land– atmosphere interaction). We advocate the design of data studies as a sanity check on numerical models.
In physics, observations are normally all-important. Note that the land surface hydrology is plagued by a lack of data. In spite of its name, LDAS does not assimilate any data. Precipitation observations are difficult, precipitation analysis is a challenge, (especially near orography), soil moisture observations scarce and problematic, and evaporation observation (over any length of time) are almost nonexistent. We need to take a comprehensive look at what data we have, what we ideally want to try to accomplish, and how further observations would help.
PREDICTABILITY OF HYDROLOGIC SYSTEMS IN THE CONTEXT OF A NEW INTERDISCIPLINARY FRAMEWORK LINKING WATER, EARTH, BIOTA (WEB)
Vijay K. Gupta
University of Colorado, Boulder
WEB Vision
Water, Earth, Biota (WEB) is a new interdisciplinary research and education framework that addresses the central role of water in linking landscapes, atmosphere and oceans, geochemistry, and biota in spatial scales from the molecular to the planetary, and in temporal scales from instantaneous to geologic. The perspective of interconnectedness at multiple scales is fundamental for gaining a holistic understanding of the complexity of nature and of changes over space and time through interactions with humans. Increasing threats to natural environments make this broad vision critical for the management of water and other natural resources to sustain growing human populations and modernizing economies. The WEB vision does not stop with the importance of the topic and the definition of science goals; it identifies a path for moving forward.
Key Issues Driving the WEB Imperative
Key issues driving the WEB imperative include the following:
-
Water is the life-blood of the planet. The water cycle comes together at the planetary scale and must be studied as a planetary process to gain holistic understanding.
-
Regional interests, agency missions, disciplinary training, and the institutionalization of field experiments have intellectually partitioned water studies into domains.
-
Scientists working in each domain increasingly recognize that their findings depend highly on boundary conditions at the interfaces with the other domains.
-
As demands on a fixed quantity of water increase and adversely impact the environ-ment, water managers are driven to greater efforts to contain floods, droughts, and contamination while being increasingly stymied by an inadequate science framework for quantifying feedbacks among the domains.
-
Research is needed to assess and extend the predictability of a wide diversity of interconnected hydrologic systems within the broad framework of WEB at many scales to allow better risk and vulnerability assessments that support resource management decisions.
-
Progress toward this WEB ideal will require an observation system that compiles and freely distributes coordinated data on WEB-related processes at a variety of space and time scales. Research and measurement must be planned together.
-
Continued progress will also require an interdisciplinary initiative for education and public outreach that will enable students and the general public to think about water issues from both planetary and local perspectives.
Societal Rationale
Our limited understanding of major couplings of water, energy, and biota leaves policy makers poorly positioned to guide natural resource development and management to serve growing human populations while sustaining environmental quality. Stakes are high, as society is making critical decisions on water supply, floods, and pollution from a fragmented understanding that could prove to be quite dangerous over time.
Science Challenges
The WEB framework identifies four main methodological steps—scaling, coupling, diagnosing, and modeling—to reach consistent conclusions in the face of space–time variability and dynamic nonlinearities that confound cross-scale computations and understanding. These methodological steps are a key to advancing predictability and to understanding the limits-to-prediction of a wide diversity of interconnected hydrologic systems. The WEB framework identifies four separate domains—water cycling, energy, earth structure, and ecology—and the need to understand the ties among them. The WEB report (http://cires.colorado.edu/hydrology) lists multiple scales for research. Each scale has its own level of complexity. A key scientific challenge is to be able to cascade across scales and levels of complexity in a self-consistent manner. Some examples are offered to explain what this means at the global scale, continental scale, drainage basin/aquifer scale, and hillslope scale. For illustration, we list below an example of a science challenge at the global scale. Examples of sciences challenges at other scales are given in the full WEB report.
Example of a Science Challenge at the Global Scale
Global climate varies over time as a result of complex, nonlinear couplings involving the water cycle in ocean, atmosphere, and land. The maintenance of a stable environment by the world's biota is perhaps the most significant phenomenon in ecology (Reiners, 1988). Atmospheric water vapor and the conflicting effects of clouds on radiation (Webster, 1994) are linked to the hydrologic cycle via cloud formation, precipitation, and evapotranspiration. We are far from a quantitative understanding of (1) the role of the water cycle and biota in critical relationships that govern natural quasi-oscillatory climate variability at interannual, interdecadal, and longer time scales, (2) the combined effects of these interactions, and (3) the robustness of world climate to anthropogenic impacts. Large-scale organized components of the
hydrologic cycle, such as monsoonal systems, significantly influence seasonal and longer variations in vegetation and may in turn be influenced by large-scale land use changes. These issues need to be investigated to asses the predictability, risks, and vulnerability of the hydrologic cycle in the context of the hypothesis that global climate is a self-regulating emergent phenomena due to nonlinear coupling between biota and the rest of the earth’s climate system (Lovelock, 1995).
WEB in River Basins as an Illustrative Theme
River basins integrate physical, chemical, and biological processes in the spatial and temporal organizations of fluxes and structures. Science issues that require focused data collection, hypothesis development, and tests and that have the potential for significant cross-disciplinary theoretical advances are identified in a river-basin context as an illustrative example. A number of other settings should be similarly examined. For the river-basin example, major contributions to science could be made through a better understanding of (1) earth-related processes, (2) atmosphere-related processes, (3) climate-related processes, (4) geochemical processes, and (5) ecological processes. It is argued that we need to focus on the dynamics of how these processes integrate in the evolution of planetary structure and life environment.
Suggestive Hypotheses as Examples of Research Challenges
The following list presents some of the working hypotheses, identified by the WEB activities which provide an important framework for future research.
-
The river basin is a self-organizing system. The space/time distributions of water, chemicals, and biota guide the evolution of land structure, drainage networks, habitats, and life itself.
-
River basin-scale processes modulate local processes and thereby alter weather, geochemical fluxes, habitats, and biodiversity—impacts to be captured in downscaling.
-
River basin-scale processes also impact global climate by the way they partition land–atmosphere–ocean fluxes and recharge to/discharge from aquifers—impacts to be captured in upscaling.
-
The water and energy fluxes through ocean, atmosphere, and land at multiple scales in space and time interact through strongly nonlinear connections. These connections must be defined and quantified to simulate planetary environmental dynamics.
-
Human modification to a river basin alters local structure and fluxes in ways that have significant impacts on both upscaling and downscaling.
An Interdisciplinary Initiative for Education and Public Outreach
An interdisciplinary initiative for education and public outreach will enable students and the general public to understand the unique role of the planetary water cycle in the co-evolution of life and of a habitable climate on Earth for 3.8 billion years and also to understand and solve the water problems facing society.
WEB Infrastructure
We propose moving ahead by establishing “Natural Laboratories” and a “National Hydrologic Facility” to organize and analyze comprehensive data sets, both existing and new. We are seeking an administrative mechanism to facilitate the deployment of instrumentation; to coordinate data collection, archiving, and access for integrative large-scale research; and to facilitate education and technology transfer. A multistage approach is necessary to develop infrastructure over time. The procedures will take continuing discussion, and we set forth here a strawman to get thinking going. Our idea is for Phase I to be a pilot project focused on a
science theme at the river-basin scale. A WEB Office for Science Support (WOSS) would be established to reach out to additional themes and to facilitate mechanisms for cross-coordination. Some generic issues related to the selection and management of a network of natural laboratories are described in the full WEB report, and a brief description of Phase II is given.
IDENTIFYING AND EVALUATING PREDICTABILITY FOR LAND–ATMOSPHERE AND HYDROLOGIC PREDICTION SYSTEMS
C. Adam Schlosser
NASA Goddard Space Flight Center
Where’s the Predictability?
Historically, the term “predictability” has been separated into two categories (e.g., Lorenz, 1975) and has been applied to the framework of ensemble predictions (of a physical system that is inherently chaotic). What is commonly referred to as the “initial value problem” is one aspect of predictability. Given hypothetically “perfect” information with which to initialize an ensemble forecast, how can we determine how long that “perfect” information will persist into the forecast in the presence of propagating errors that exist in the prediction system? The other aspect of predictability is associated with an externally forced response that is, to a quantitative degree, ubiquitous among the forecast members of an ensemble prediction (e.g., all forecast members predict consistent soil-water variations in response to a precipitation anomaly).
To identify predictability within “coupled land–atmosphere prediction systems” (e.g., operational weather forecast models and global climate models), previous research has aimed to show which elements of the land–surface system are central to this coupled mechanism. It has been exhaustively shown that soil moisture, and its persistence, play a critical role in coupled land– atmosphere variations. Generally speaking, however, it is the liquid and frozen storage of water on the ground (i.e., snow cover and interception storage) and in the ground (i.e., soil water that is
available for exchange processes between the land–surface and overlying atmosphere) that are central to coupled land–atmosphere variations. These coupled variations result from the fact that the aforementioned terrestrial water storages have a persistence timescale that is comparable to or longer than the characteristic timescales of the interacting atmospheric processes. Therefore, it follows that regions of strong persistence of “active” water storage (i.e., terrestrial water storage available to exchange processes between the land and the atmosphere) will lead to predictability of these water storages and potentially impact atmospheric predictability (as shown by Schlosser and Milly, 2000), which can in turn lead to enhanced land predictability (i.e., predictability via a forced response).
An important additional source of predictability that is external to local land–atmosphere coupling is the impact of sea surface temperature (SST) variations on remote responses of the atmosphere. Certainly, if a given SST pattern (e.g., El Niño) can impose a forced, and predictable, response of the atmosphere over a continental region (e.g., a precipitation anomaly), this could, in turn, produce a predictable signal in the land-surface (i.e., predictability of water storage). However, the ability to which the modified land-surface then imposes a predictable effect on the local land-atmosphere coupling will be largely dependent on land-surface persistence. In other words, when the remotely forced SST response of the atmosphere abates, to what degree will the resulting land anomaly impact subsequent hydroclimatic variability? Here then, we return to the importance of continental water– storage persistence and of its impact on coupled land–atmosphere variability and predictability.
With regard to “hydrologic prediction” (i.e., streamflow, river discharge, and flood/ drought prediction), the challenge lies in translating the predictable information of a (presumably) fully coupled ocean–land–atmosphere (i.e., climate/weather) prediction system (which, in practice, has not explicitly incorporated hydrologic networks) to hydrologic prediction/operational systems, and in assuring that those quantities that are relevant to the information transfer are predictable. For example, for a river–routing scheme to produce a predictable hydrograph, the scheme should receive
surface and subsurface runoff rates (which could be provided by gridded land–surface outputs of the climate prediction system) that are predictable. This requires that to a large degree, the relevant simulated quantities of the ocean–land–atmosphere prediction system (i.e., precipitation, soil moisture) are predictable in order to produce predictable runoff rates. Even still, we must verify that the resulting runoff rates provided to the hydrologic prediction system are predictable.
Is the Predictability for Real?
Continuing with our discussion of predictability through persistence, if we were to find a region within a modeled climate that contains a strong potential for predictability (i.e., strong persistence), can we be assured that the persistence of the model is realistic and therefore is, in a sense, reflecting a “true” potential for predictability? For example, if a persistent (and therefore predictable) anomaly of soil moisture then creates a predictable response of the atmosphere (e.g., a corresponding precipitation and/or temperature anomaly), can we be assured that these predictable signals are real within the coupled model prediction system? In order to answer this question in the context of coupled land–atmosphere modes of predictability, it is necessary to identify whether or not the relevant components of the prediction system (e.g., the soil moisture scheme and/or the precipitation scheme) are behaving in a manner that is consistent to realistic/ observed modes of variability.
To that end, we should identify and verify the sources and controls of the persistence (and therefore the predictability) of terrestrial water storage. The landmark study by Delworth and Manabe (1988) presented a direct relation between simulated soil moisture persistence in a “bucket hydrology” scheme to a first-order Markov process. This direct comparison was possible due, in part, to the linear relationship between soil moisture and evaporative stress in the bucket model (among other simplifying assumptions). However, the more complex “big leaf” models that have been developed within the past decade contain highly nonlinear
relations between soil water storage and runoff and evaporation processes. As a result, an analytical description of the controls of soil moisture persistence becomes more complex. However, a recent study by Koster and Milly (1997) was able to effectively explain the disparity of the simulated annual water budgets of the participating models of the Project for the Intercomparison of Landsurface Parameterizations Schemes (PILPS) through linear approximations of evaporation and runoff controls as a function of soil moisture. The results underscore the potential to effectively summarize and verify the degree and controls of soil-water persistence for the variety of models used to represent the continental surfaces in weather and climate models. More importantly however, we must apply these techniques with corresponding observed quantities in order to verify that our model-based assessments of predictability are reflective of what would (hypothetically) occur in nature.
Similarly for hydrologic prediction, it is crucial that we evaluate the sources of predictability that contribute to the predictability of a hydrologic prediction system. For example, if a climate model were able to provide a predictable forecast of total runoff rates for grid points that span a hydrologic basin, inputted into a river routing prediction system, we must be assured that not only the predictable signal of runoff is robust and realistic, but that also the partitioning of the runoff rates (between surface and subsurface flow) are realistic. Otherwise, the resulting hydrograph prediction, while being predictable, could result in low prediction skill due to the impact of inaccurate runoff partitioning on the resulting streamflow estimates. The impact of the disparity in runoff partitioning for streamflow prediction has been demonstrated in the PILPS 2c simulations by Lohmann et al. (1998).
Therefore, it is important that evaluation of current models used in hydroclimatological prediction are rigorously continued and that the diagnostics used in the evaluation not only aim to identify systematic biases/errors, but also to assess the impacts of the errors/biases on predictability. This will ensure that the predictability that is identified is realistic, and it will build our confidence in the predictive ability of our hydroclimatological prediction systems.
ENSEMBLES AND PREDICTABILITY IN CLIMATE AND HYDROLOGIC SYSTEMS
Joseph J. Tribbia
National Center for Atmospheric Research
Ensembles on the Synoptic Scale
The use of ensembles in weather forecasting is an idea going back to the early attempts to perform stochastic-dynamic forecasts. The moment prediction technique proposed by Epstein (1969) was seen to be computationally infeasible, so Leith (1974) proposed a Monte-Carlo method (i.e., a randomly perturbed ensemble of weather forecasts) in order to provide the two major benefits afforded in the stochastic-dynamic approach. The beneficial attributes to be gained are the improved skill (in a statistical sense) of the mean forecast, which is gained through the nonlinear filtering of the uncertain forecast degrees of freedom/ variables, and an estimate of the uncertainty or reliability of the forecast through the prediction of the variance/ covariance.
Ensemble prediction is now an everyday part of operational short- and medium-range weather forecasting at European Center for Medium Range Weather Forecasts (ECMWF) and National Centers for Environmental Prediction (NCEP), the major global weather centers. The professed goal of the ensemble prediction systems at both centers is more ambitious than that stated above; the aim is to predict the probabilities of event occurrences at forecast locations. This elevated goal is not merely desirable but partly necessitated by the requirement that ensemble predictions be objectively verifiable. Because the number of forecasts within an
ensemble is proportional to computational costs, to date, ensemble size has been limited to at most 50 members. Because of these limitations, elaborate techniques of ensemble member initialization, using methods imported from dynamic systems theory, have been used to maximize the information content of the small-sized ensemble—small, that is, when compared to the phase space dimension of an operational forecast model (106). These methods of initialization are primarily designed to capture the most uncertain aspects of the dynamic meteorology within a forecast, with little or no concern for the uncertainty in the physical processes (e.g., moist processes) and the skill with which precipitation can be forecasted. Nonetheless, these techniques can often give reasonable estimates of the uncertainty of synoptic scale precipitation.
The situation is somewhat different on both the very short range (<24 hours) and long range (one month to a season). Because of the high sensitivity of precipitating mesoscale phenomena to variations in model formulation and low-level moisture, uncertainty in these aspects will likely require a different approach than the one taken on the synoptic scale. At long range, the initial conditions of an ensemble are not treated as elaborately as in the short and medium range, since at these time scales initial conditions are nearly completely forgotten, and anomalous boundary forcing is the sole residual memory driving predictability. The applications of ensemble methods in these two forecast problems, with particular attention to precipitation, are discussed individually below.
Mesoscale Ensemble Prediction
The use of ensemble methods for mesoscale prediction is in its infancy and should properly be considered a research problem. The goals of ensemble prediction on this scale include the prediction of probability of precipitation and the probability of extreme events. Recent research by Crook (1996) and Errico and Stensrud (2000) demonstrates the extreme sensitivity of predicted precipitation coverage and amount to variations in low-level moisture and to changes in convection parameterization. This latter uncertainty reflects both the real lack of scientific consensus and understand-
ing in the current generation of convective parameterizations and the stochastic nature of the relationships between convection and the larger-scale environ-ment. This being the state of affairs on the mesoscale, the most rational methodology may be one in which ensembles include both variations in initial conditions and variations in formulations. Such a strategy might be the most accurate manner of providing threat probabilities, probability of precipitation, and ranges of precipitation amount.
Long-Range Ensemble Prediction
For extended range prediction, the use of ensemble methods is a necessity since weather systems, and characterizing their effect on the large-scale, low-frequency patterns for long-range prediction, are not predictable beyond two weeks. At the present time, there is still active research concerning the statistically optimal method of utilizing ensemble forecasting for long-range predictions. Operationally, at centers like the International Research Institute for Climate Predictions (IRI) and European Center for Medium Range Weather Forecasts, the main use of the ensemble is as a nonlinear filter to generate the most reproducible components of a forecast and to determine a signal-to-noise ratio from the ensemble mean and (ensemble) standard deviation. With respect to precipitation, global prediction and climate models have significant mean climate errors in both the location and magnitude of precipitation. Because the targeted forecast problem is the response to boundary anomalies, (frequently tropical ocean sea surface temperature anomalies), both the climate mean and the anomalous response are subject to a climate drift. The presence of systematic errors and climate drift once again suggests that the most rational strategy for ensemble prediction will be a multimodel, multi-initial condition ensemble method.
Concluding Remarks
Because the current generation of global models and mesoscale models have strong systematic biases in the monthly to seasonal timeframe for global models and 3- to 12-hour range for mesoscale models, the optimal ensemble strategies for precipitation prediction in these time and space scales will include a multimodel ensemble. There remains a great need to analyze and rectify the errors in current methods of parameterization of moist processes.
PEDICTABILITY OF FLASH FLOODS USING DISTRIBUTED PARAMETER PHYSICS-BASED MODELS
Baxter E. Vieux
University of Oklahoma
Why Distributed Parameter Modeling?
Historical climate modeling practice has been to use lumped representations of physical processes because of computational limitations or because sufficient data were not available to populate a distributed model database. How one represents the process in the mathematical analogy and implements it in the hydrologic model determines the degree to which we classify a model as lumped or distributed. Several distinctions on the degree of lumping can be made in order to better characterize a mathematical model, the parameters/input, and the model implementation.
The main advantage of distributed modeling is that the spatial variability of parameters and rainfall input is incorporated into the model response. Each parameter and rainfall input has its own spatial variability, which can be characterized by informational entropy (Vieux, 1993). Incorporating spatial variability of a particular parameter related to vegetative cover, soil infiltration rates, rainfall, or topographic characteristics may or may not have important conse-quences on the hydrograph response of the model. If the parameter has a narrow range of variation or if the parameter has only a few values represented in the basin, then its spatial variability may have little effect on simulated hydrographs.
Mathematical Analogy
A numeric solution of the governing equations in a physics-based model employs discrete elements. The three representative types are finite difference, finite element, and stream tubes. At the level of a computational element, a parameter is regarded as being representative of an average process. Thus, some average property is valid over the computational element used to represent the process of flow. For example, porosity is a property of the soil medium, but it has no meaning at the level of the pore space itself. Physics-based models solve governing equations derived from conservation of mass, momentum, and energy. Unlike empirically based models, differential equations are used to describe the flow of water over the land surface or through porous media to describe, or energy balance in the exchange of water vapor through evapotranspiration.
If the physical character of the hydrologic process is not supported by a particular analogy, then errors result in the physical representation. Difficulties also arise from the simplifications because the terms discarded may have afforded a complete solution while their absence causes mathematical discontinuities. This is particularly true in the kinematic wave analogy, in which changes in parameter values can cause discontinuities, sometimes referred to as shock in the equation solution. Special treatment is required to achieve solution to the kinematic wave analogy of runoff over a spatially variable surface. Vieux et al. (1990) and Vieux (1991) presented such a solution using nodal values of parameters in a finite element solution. This method effectively treats changes in parameter values by interpolating their values across finite elements. The advantage of this approach is that the kinematic wave analogy can be applied to a spatially variable surface without numerical difficulty introduced by the shocks. Vieux and Gaur (1994) presented a distributed watershed model based on this nodal solution using finite elements to represent the drainage network.
A detailed description of the solution methodology used by r.water.fea may be found in Vieux (2000). The naming convention stems from the original concept of a geographic information systems (GIS) tool resident within the Geographic Resources
Analysis Support System (GRASS) GIS for simulating surface runoff in watershed.
Research Questions
Research questions related to parameter modeling are the following:
-
Parameterizing a distributed hydrologic model requires adequate spatial variability. Improved understanding is needed of the influence on reliability, on calibration, and on prediction biases caused by data characteristics related to resolution, surrogate measures, and temporal resolution of input and parameters.
-
New digital elevation datasets are becoming available. Soon, the Shuttle Radar Topography Mission (SRTM) elevation data will provide 30-meter resolution digital elevation models (DEMs) of over 80 percent of the inhabited earth. DEM resolution affects the model responsiveness and flow routing properties. Understanding the influence of resolution and vertical/horizontal precision on hydrologic modeling is needed for efficient model prediction.
-
Distributed model calibration is resolution-dependent. Methods are needed for easily moving from one resolution used in model calibration/validation to a greater resolution in the operation of the model.
-
Effects of using parameters and inputs at various resolutions on model uncertainty and reliability need investigation, particularly when coarse-resolution rainfall is input to a fine-resolution, distributed-parameter hydrologic model.
Lead-Time and Accuracy of Flood Forecasts in Small Basins
Radar is a key source of spatially and temporally distributed rainfall data for hydrologic modeling. Vieux (2000) describes the use of weather radar in hydrology with primary emphasis at the
river basin scale. Interest in using radar estimates of rainfall in distributed modeling comes from the desire to reduce errors associated with imprecise knowledge of the amount and distribution of rainfall input to models.
Radar and satellite sensors offer improved spatial pattern definition to fill in between rain gauges. However, this source of data has limitations as well. Having access to real-time fusion of rain gauge, satellite, and radar estimates of precipitation would advance hydrologic prediction. Algorithms and systems that can ingest multiple-sensor platforms and produce high-resolution rainfall estimates in space and time are needed to make flood forecasts.
Research Questions:
Research questions related to flood forecasts in small basins include the following:
-
How can multisensor rainfall estimates be best fused together given the range of spatial/temporal scales and inherent uncertainties?
-
What errors are inherent in each data source, and how do these data characteristics influence flood prediction?
-
Considering the rainfall estimation errors over a river basin, what are the considerations necessary to relate space–time scales of the storm in relation to the spatial extent of the basin?
-
How do basin characteristics combine and interact with each other to transform rainfall into runoff?
The efficiency of providing warnings in a timely manner must be considered in relation to the time necessary to measure the rainfall, compute the response, and issue the warning. To be of value, there is a limit to the basin size for which forecasts may be made in a timely manner. As the basin becomes smaller, the response time decreases. In order to perform real-time flood forecasting, the rainfall must be estimated by the radar or other sensors, ingested into a hydrologic, model and then compared to some flood stage threshold. Once it is determined that the flood stage is
likely to be exceeded, then a warning must be issued to residents and/or emergency personnel. Feasibility of a real-time flood warning system based on radar and model results is highly influenced by the basin size and characteristics coupled with rainfall intensities, duration, and storm track over the basin.
Research on the relationship between storm and basin scale and the time necessary to issue warnings that are reliable and of value is needed so that action can be taken to mitigate flood damages.
Specific Research Questions:
Specific research questions related to flood forecasts in small basins are the following:
-
Computational time may be limited when forecasting small basins. Can simplified predictive relationships replace physics-based models in predicting basin response?
-
How can a deterministic model be used to forecast flooding when quantitative precipi-tation forecasts are probabilistic?
-
What is the limit of predictability in terms of uncertainty in parameters, in model input, and in the resulting model predictions?
-
What is the practicable or feasible limit to issuing warnings for small upland basins?
-
How does DEM resolution affect the model’s predictive capabilities in relationship to various basin sizes ranging from 1 or 2 km2 to 10, 100, or 1,000 km2?
Interdependence of Atmospheric, Soil Moisture and Basin Runoff Components
Transforming intense rainfall into runoff depends on the initial state of the soil. The degree to which the basin hydrologic response is affected depends on soil properties, antecedent storm events, and meteorological factors. Some basins may produce
about the same amount of runoff whether the soil is wet or dry if clayey or impervious soil conditions prevail. Such basins transform nearly all the rainfall into runoff regardless of initial soil moisture content. Other basins can respond very differently depending on soil moisture. Hydrograph response is also nonlinear to soil moisture contents less than some threshold. At soil moisture contents of greater than 50 percent, a greatly amplified response to soil moisture conditions results.
Research Questions
Research questions related to the interdependence of components include the following:
-
Can adjoint methods used in atmospheric models be exploited in physics-based hydrologic models to automate calibration or make real-time adjustments to flood forecasts?
-
Do unique values exist for a river basin and a series of storm events?
-
What basin characteristics combine to make the adjoint solution ill-conditioned? Can regularization of the cost function improve retrieval of optimal parameters?
-
How can we most efficiently couple atmosphere, soil moisture, and basin runoff models to provide flood forecasts for small basins?
-
Using global data sets for elevation, soils, and vegetation, can specific basin charac-teristics be identified that will improve model formulations, guide selection of spatial/temporal resolution, and indicate the existence of weak/strong coupling of hydrologic cycle components?
CURRENT STATUS AND OPPORTUNITIES IN QUANTITATIVE PRECIPITATION ESTIMATION AND FORECAST (QPE AND QPF)
W. F. Krajewski
University of Iowa
Methods and systems for QPE
Rain Gauge Based Methods
Research continues on the interpolation methods of spatial patterns but the quantitative differences between different approaches do not seem to be substantial. This is because the error of these approaches is dominated by the spatial sampling error. The geostatistical methods seem to be gaining popularity probably due to their ability to quantify the associated errors. Surprisingly, the Thiessen method (essentially a nearest neighbor method) is still in use although it has been demonstrated many times that its performance is poor.
Much research focused recently on the problem of rain gauge measurement accuracy, in particular the wind effect causing underestimation of rainfall quantities. Both experimental (intercomparison, Legates and DeLiberty 1993; Yang et al. 1998) and numerical (computational fluid dynamics, Ne_por and Sevruk 1999; Habib et al., 1999) approaches are used to investigate the problem. The conclusion is that the underestimation of the long term totals rarely exceed 5 percent for rainfall while snowfall estimates maybe underestimated by as much as 50 percent. However, there are numerous other problems with rain gauge measurements. All gauge designs require frequent maintenance and are subject to
mechanical failures while the very popular tipping bucket suffer from their inability to accurately measure lower rainfall amounts (Steiner et al. 2000; Habib et al. 1999). To help in early detection of these problems Ciach and Krajewski (1999a) proposed to use a dual-sensor design. This configuration has been implemented at a number of experimental sites with great success.
Weather Radar Based Methods
The technology has been in use for almost 50 years, yet only recently it found its way into operational use. Currently, the single radar observable used in quantitative estimation of rainfall (operationally) is radar reflectivity. Its conversion to rainfall requires the use of a Z-R relationship. Much of the published research focused on the problem of Z-R selection ignoring numerous and often more significant sources of uncertainty. Relatively little has been reported on the problem of real-time anomalous propagation echo detection (Grecu and Krajewski, 2000c, the effects of the vertical reflectivity profile and their correction, and the effect of the spatial and temporal gradients in the rainfall processes (Kitchen et al., 1994; Andrieu and Creutin, 1995; Joss and Lee, 1995; Anagnostou and Krajewski, 1998; Anagnostou and Krajewski, 1999; Seo et al., 2000).
However, the single most important problem is lack of the rigorous assessment method-ologies. There is no system in place that would systematically monitor progress in the field allowing quantitative comparison of improvements in algorithms in a statistically rigorous and hydrologically relevant way (Ciach and Krajewski, 1999a,b; Ciach et al., 2000). Young et al. (2000) attempted such an evaluation of the hourly product used operationally by the National Weather Service as input to hydrologic models and concluded that they could not find indepen-dent information.
Another important problem is that for proper assessment of radar-rainfall errors we need to know the spatial variability of point rainfall at scales below that of the typical resolution of radar-based products (i.e., 2 km by 2 km). Operational networks have inadequate spacing and past experimental studies (in the 40s, 50s, 60s,
and 70s) did not cover such small scales either. Small-scale clusters of rain gauges should be established operationally to collect the relevant information for different rainfall regimes.
The upcoming technology of multiple parameter radar has been demonstrated to be promising but a systematic system for its evaluation is needed otherwise there is a potential that significant investments will be wasted. An experiment Joint Polarization Experiment (JPOLE) planned for 2003 is a major opportunity in this respect.
Extensive use of radar observation in research (e.g., in the context of WEB) has been hampered by difficult and costly access to data. The National Climatological Data Center (NCDC) that archives both the data and the products is not set up for efficient and convenient data distribution. It takes a considerable effort and expertise to assemble a radar-rainfall data set for research on other applications.
Satellite-Based Methods
The research community in the field of rainfall estimation has been very active in the past 10 years (e.g., see Petty and Krajewski, 1996; Petty, 1995). The culmination of their efforts was the Tropical Rainfall Measurement Mission (TRMM) launched in November 1997 (Simpson et al., 1996; Kummerow et al., 1998). The mission continues stimulating much of rainfall research, including research on new rainfall estimation algorithms and their validation. Perhaps the most mature satellite-based rainfall estimation product is the 10 year data set of monthly rainfall produced by the Global Precipitation Climatology Project (GPCP) with resolution of 2.5° by 2.5° (Huffman et al. 1997). An important aspect of the project continues to be the validation of its results. Several algorithm intercomparison projects (AIPs) were conducted and a center for surface reference data has been established to pursue the validation activities (e.g., Arkin and Xie 1994; PIP-1, 1994; Krajewski et al., 2000). The GPCP is being reorganized towards producing a higher resolution global data set (daily accumulations at 1° by 1° spatial resolution).
There are many algorithms documented in the literature and the previous inter-comparison projects do not indicate a clear “winner.” To establish the accuracy of the space-based products rigorous framework is needed together with adequate reference data. Depending on the space/time scale of the products the requirements for the type and accuracy of the reference data may vary considerably.
The international research community is planning a successor to TRMM called Global Precipitation Mission (GPM), a constellation of eight orbiting satellites equipped with the same passive suite of sensors calibrated with a space-borne radar. The mission is a major opportunity for studies of global processes and integrated management of water resources.
Methods and Systems for QPF
Classification of the QPF methods is less obvious. For the purpose of this presentation one can distinguish statistical methods and physically-based methods. The focus in the discussion below is on short-term (hours) forecasting methods. The statistical methods are based on empirical data for a variety of observing systems. The methods seek a relation between observed data and the future precipitation quantities. A recent review of the methods based on radar observations was given by Wilson et al. (1998). Also Grecu and Krajewski (2000b) conducted a large-sample study of such methods.
The statistical methods can be (and are) used in operational environment (Zawadzki et al., 1999; Wilson et al., 1998). The main challenge here is to design an experiment that would allow consistent, statistically sound, long-term evaluation of the performance of these methods. Also, as follows from the discussion above on the rainfall estimation methods, it is important to figure out a way to separate the forecasting error that is due to the method from that of the observation that serve as the forecast verification.
The second group of methods is mathematical models of the physical processes involved in generation of precipitation. These models range from detailed cloud physics models to mesos-
cale models with parameterized cloud physics to simplified vertically integrated models that focus on the precipitation processes. The main challenge here is data assimilation. Major opportunity exists if the difficulty of assimilating radar data can be overcome (e.g., Sun and Crook, 1997; Grecu and Krajewski, 2000a). The approaches currently being explored focus on variational methods. In addition to the issues of computational efficiency, these methods do not explicitly account for the model error. Kalman filter type methods provide a framework in which both the modeling error and the observational error can be acknowledged and quantitatively accounted for. However, at this time feasibility of such methods is questionable and the potential benefits difficult to assess. Filtering methods can be used (Georgakakos, 2000) with a simpler class of physically-based models such as those proposed by Lee and Georgakakos (1996) and French and Krajewski (1994). Again, well design comparative experiments are needed to properly assess the performance of the complex and simple models.
Recommendations: QPE
-
Deploy dual-sensor rain gauge designs in the operational environment.
-
Establish clusters of rain gauges for observations of small-scale rainfall variability.
-
Develop benchmarks of radar-rainfall estimation performance for monitoring progress in algorithm development and assessment of new technologies.
-
Develop methodologies of using rain gauge data based reference standards for evalua-tion of radar-rainfall estimates.
-
Develop new sensors and technologies that would provide a better reference standard than the gauges.
-
Improve access to radar-rainfall data for the research community.
ISSUES OF SCALE ON PRECIPITATION PREDICTABILITY
E. Foufoula-Georgiou
University of Minnesota
INTRODUCTION
It is well known that some factors affecting predictability of atmospheric and hydrologic variables are related to: uncertainty in the initial conditions, uncertainty in the boundary conditions, and inadequate knowledge of the system dynamics and multiscale interactions of the involved variables. Efforts aimed at quantitatively determining the range of predictability in the atmospheric-hydrologic system have been based either on idealized systems of dynamic equations or in model predictability studies employing more elaborate numerical models. In the first case, methods of nolinear dynamics (e.g., Lyapunov exponents) or methods of stochastic propagation of uncertainty have been used to assess predictability. In the second case, predictability is assessed by quantitative comparison of model forecasts with observations (assuming that the model is completely known and true). In both cases, several issues arise that are far from resolved and need a focused research program to systematically address them.
In this talk, the following questions will be tackled both conceptually and via examples. Results are mostly restricted to those obtained in our group and thus this note is far from comprehensive even in the questions that it tries to address.
Question 1: How do the feedback characteristics of two-way coupled land-atmosphere models impact predictability?
Answer: The feedback characteristics amplify uncertainties (due to initial conditions, boundary conditions, and incomplete knowledge of small-scale structure) and thus limit predictability.
Supporting Evidence:
It has been found that the nonlinear feedback dynamics of the coupled land-atmosphere system amplify the small-scale (1-5km) variability of the forcing variables to create larger-scale variability on other predicted water and energy fluxes (Nykanen et al., 2000). Such an effect imposes limits on the predictive power of numerical hydrometeorological models even if the interest is at larger scales (see also the discussion in Lorenz, 1969). These results suggest that the small-scale variability of precipitation and its nonlinear propagation through the land-atmosphere system cannot be ignored if accurate predictions are desired. Variability of precipitation at scales less than 5km can be incorporated in coupled models in three ways: (a) explicitly running the models at resolution of less than 5 km over the whole domain of interest even if larger scale predictions are requiredd; (b) run nested models which have lower resolution at the outer domain and less than 5 km resolution in the inner domain which represents the area of interest; and (c) run the models at a resolution that can account for the mesoscale atmospheric dynamics (20-30 km) and statistically enhance the variability and resolution of precipitation while preserving large-scale averages and explicitly propagating this enhanced variability (via fine scale two-way feedbacks) through the land-atmosphere system. Option (a) is computa-tionally infeasible in most of today’s computers and for most researchers and is certainly prohibiting in operational forecasts. Option (b) has its own problems, which remain mostly unresearched to date. A main problem is the propagation of boundary conditions (e.g., see Chu, 1999), which manifests itself by giving different predictions depending on the resolution of the outer domain, the convective prameterization of the outer domain, and the size and position of
the inner nested domain. This forms one open problem in which research has to be accelerated.
It has been found that the small-scale variability of cloud hydrometeors and precipitation (down to less than 1 km scale) considerably affects the radiative trasfer through simulated clouds (see Harris and Foufoula-Georgiou, 2000) and thus precipitation retrievals from microwave sensors. Typical algorithms for microwave retrieval of precipitation are based on inversion of a data base obtained from cloud model simulations (typically run at 3 km resolution) and simulated brightness temperature computed via radiative transfer. It has been found that cloud models run at 3 km resolution miss the proper variability at scales up to five times the model resolution (see Harris et al, 2000). Not accounting for this variability affects the computed brightness temperature and the estimated precipitation at large scales (10 to 50 km estimates depending on the channel frequency). This in turn has an impact on climate studies which use these tropical rain estimates for data assimilation or climate model verification.
Question 2: How can the predictive power of models (which remains one practical tool for assessing system predictability) be assessed based on observations?
Answer: QPF verification methodologies, currently in use, present problems and new methodologies that account for scale issues must be developed for an accurate assessment of the predictive power of models.
Supporting Evidence:
Typical measures of performance, such as threat score (TS) and root mean square error (RMSE) have been shown to be of limited power to depict important differences between the forecasted and observed precipitation. A suite of multiscale methods for comparison of forecasted precipitation to observed precipitation has been developed and has shed some light into shortcomings of numerical weather prediction models in terms of capturing statisti-
cal properties of precipitation which are considered important in the prediction of other fluxes in the land-atmosphere system (Zepeda-Arce et al., 2000). Some new measures of forecast verification which are more appropriate for highly variable fields have been explored, such as the Hausdorff distance between two images and have been found to have potential for further study (Dodov and Foufoula-Georgiou, unpublished manuscript, 2000).
A popular method of QPF verification based on RMSE between the outputs of the model and point observations by transforming the areal averages to point values (area to point) or the point values to areal averages (point to area) has been critically assessed and has been found to suffer from scale problems. In particular, changing the scale of the observations to match the scale of the model output (point to area) or vice versa (area to point) imposes a “representa-tiveness error” which is nonzero even in the case of a perfect model (i.e., a model whose predictions are indeed the true averages of the underlying field) and moreover is dependent on scale. It has been shown that the magnitude of the representativeness error is significant (it can be up to 50 percent of the spatial average of the precipitation filed) and has considerable scale dependency within the typical mesoscale range of 5 to 50 km (Tustison et al, 2000). In verification studies in which model performance is assessed as a function of model resolution, ignoring or mischaracterizing the scale dependent representativeness error can significantly affect inferences about the model performance as a function of scale. This is because the total error is composed on the observational error, the representativeness error, and the model error, and thus misspecifying the representativeness error directly mispecifies the model error and any inferences about the model performance as a function of resolution and thus predictability inferences in general. Some new methodologies are under exploration, which are based on multiscale filtering and can explicitly account for scale effects.
Question 3: Theoretical studies of predictability and uncertainty propagation across scales require that semi-empirical parameter-
izations are appropriately scaled such that fluxes are preserved. How is this to be accomplished?
Answer: Commonly used relationships must be studied to establish “scaling’’ relationships, which depend on the form of the nonlinear relationship and the spatial variability of the involved variables.
Supporting Evidence:
Through the analysis of a commonly used relationship that parameterizes surface runoff as a function of soil moisture, it has been demonstrated how the parameters of the relationship must change with scale such that spatially averaged predicted fluxes can be preserved at any scale of interest (Nykanen and Foufoula-Georgiou, 2000). Similar analyses can be performed for other relationships such that the parameters are directly related to the scale-dependent variance of the underlying field and the form of the parameterization. In our analysis, data from the 1997 Southern Great Plains Hydrology Experiment (SGP97) have been used to quantify the spatial variability of soil moisture and it was shown that changing the scale (resolution) at which the model is applied within reasonable ranges (5 km to 50 km) while keeping the parameterization the same can result in biases up to 30 percent in predicted runoff. These issues are not only of practical importance for more accurate predictions but of theoretical importance too in studies that will attempt addressing predictability questions based on the dynamical equations of the land-atmosphere system.
WHY AND HOW DOES PRECIPITATION CHANGE?
K. E. Trenberth
National Center for Atmospheric Research
INTRODUCTION
Why does it rain? If a parcel of air rises, it expands in the lower pressure, cools, and therefore condenses moisture in the parcel, producing rainfall—or perhaps snowfall. So key ingredients are certainly the many and varied mechanisms for causing air to rise. These range from orographically uplifted air as air flows over mountain ranges to a host of instabilities in the atmosphere that arise from unequal heating of the atmosphere, to potential vorticity dynamics. The instabilities include those that result directly in vertical mixing such as convective instabil-ities, to those associated with the meridional heating disparities that give rise to baroclinic instabilities and the ubiquitous weather systems. Thus cold air pushing underneath warmer air (advancing cold front) or warm air gliding over colder air (advancing warm front), and so on, can all provide opportunities for air to rise. These mechanisms for causing air to rise presumably do not in of themselves change. They need to be better understood and modeled, but from a societal standpoint the fact that their relative importance can change with time is of more consequence. These aspects have been the focus of a lot of meteorological research and are only briefly addressed here.
The other main ingredient in the opening statement about why it rains is the assumption that there is moisture present.
Where exactly does the moisture come from? It is argued here that this aspect of precipitation is one that has been under appreciated and is worthy of more attention. After all it will not rain at all unless there is a supply of moisture.
Questions and Issues
-
Better documentation and processing of all aspects of precipitation. The needs include frequency, intensity, and amount. Trenberth (1998) has argued for the creation of a data base of these quantities using hourly precipitation amounts. This time interval averages over individual cells within a storm but typically allows the evolution of a storm to be grossly captured. It is compatible with the time steps in global models, which are typically two or three per hour. It is viable from a data management standpoint. It is also viable from many observations, from recording rain gauges and from radar (e.g., NEXRAD) and satellite (e.g., TRMM, GOES) estimates. In fact, remote sensing measures the instantaneous rain rate, not amount over time, and this has to be converted into a daily amount (e.g., by fitting of log-normal distributions; Short et al., 1993a,b, also Shimizu et al., 1993). Instead it would be better converted into an hourly rate, and histograms of the rate then provide the basic information database.
-
Increased understanding of the efficiency of precipitation and how it changes with environmental conditions. “Precipitation efficiency”' is defined as the ratio of the water mass precipitated to the mass of water vapor entering the storm through its base (e.g., Fankhauser 1988) or the ratio of total rainfall to total condensation in modeling studies (e.g., Ferrier et al. 1996). These studies show that in typical storms the precipitation efficiency varies from about 20 to 50 percent, and 30 percent seems a typical value. In one cloud/thunderstorm model, greater moisture content in the atmosphere produced more condensation and greater precipitation efficiency (Ferrier et al., 1996). However, warmer conditions, which might accompany greater moister content could also imply that more moisture might remain if relative humidity is a key factor, as is likely. Therefore the rainfall may not increase in direct
-
proportion to the moisture convergence because more moisture is left behind. The efficiency of precipitation in climate models is implicit and has not been addressed. Pollution and aerosols may influence the microphysics of precipitation processes and also influence the efficiency of precipitation.
-
Improved parameterization of convection in large-scale models. Parameterization of convection needs to be improved to appropriately allow Convective Available Potential Energy (CAPE) build up as observed and may involve “triggers” and thresholds to initiate convection. This seems to be a scale interaction problem in part, as larger scale motions may suppress or enhance the release of CAPE. As well as the diurnal cycle it may also be a key in the Madden-Julian Oscillation in the tropics which has been difficult for models to get right.
-
Improved observations and modeling of sources and sinks of moisture for the atmosphere, especially over land. This relates to recycling and the disposition of moisture at the surface in models, and whether the moisture is or is not available for subsequent evapotranspira-tion. It relates to improved and validated treatment of runoff, soil infiltration and surface hydrology in models as well as vegetation models.
-
Improved analysis of precipitation rates. We have argued (Trenberth, 1998, 1999a) that increasing the moisture content of the atmosphere should increase the rate of precipitation locally by invigorating the storm through latent heat release and further by supplying more moisture, although what happens to the amount is less clear, as the duration of a storm may also be shortened. Some analysis of model results supports this view but most analyses have used daily and not hourly or higher frequency data, so they also highlight the need for more attention to the nature of the analysis of both models and observational datasets.
-
Improved analysis of the frequency of precipitation and changes in weather systems. Changes occur in large-scale atmospheric circulation, extratropical storms and the overall baroclinicity, from year to year and especially as the climate changes. Held (1993) notes that extratropical storms are greatly influenced by moisture in the atmosphere and that one effect of increased moisture content in the atmosphere is to enhance the latent heating in
-
such storms and thereby increase their intensity. On the other hand, he also notes that more moist air would be transported polewards by transient eddies, reducing the required poleward energy transports normally accomplished by baroclinically unstable eddies and the associated poleward down-gradient heat transports. He therefore argues that this would contribute to “smaller eddies” and suggests that this means a decrease in eddy amplitudes. While recognizing that both effects are important, Held suspects that the latter is dominant. There are other possibilities not considered by Held. In particular, individual storms could be more intense from the latent heat enhancement, but fewer and farther between (Trenberth, 1998), and so this relates to the frequency of storms and precipitation. Changes in the vertical temperature structure (the lapse rate) will also play a role in such storms. Therefore another major factor worth considering in more detail is the frequency and nature of precipitation events. CLIVAR is designed to address other aspects of changes and variability in atmospheric circulation.
-
Improved simulation of the diurnal cycle of precipitation in models. This probably also requires improved simulation of the diurnal cycle of temperature, cloud amount and atmospheric circulation, as well, and especially the build up and release of CAPE.
-
Improved ocean modeling. Rainfall amounts over the oceans are also important because of its contribution to the fresh water budget for the ocean—or equivalently salinity. It is a key in the potential changes in the thermohaline circulation as the climate changes (Gent 2000). Part of this also relates to runoff from land, but it is evaporation and precipitation over the oceans, that is most important along with mass transports and mixing within the ocean.
-
Moisture sources for storms. The above back-of-the-envelope calculations on how far afield the storm-scale circulation reaches out to gather in the moisture that fuels the storm and provides the precipitation probably vary greatly with synoptic situation, with season, and with the nature of the storm and mechanism for producing the precipitation. Can, these numbers be consolidated and refined, and it is worthwhile?
EVOLUTION OF REGIONAL HYDROLOGIC PROCESSES WITHIN THE CLIMATE SYSTEM AS AN INITIAL VALUE PROBLEM: AN OVERVIEW
R. A. Pielke Sr.
Colorado State University
The "hydrologic system" is an intimately coupled component of the Earth's climate system. It is more appropriate, therefore, to discuss hydrologic processes as a component of the climate, rather than as "a hydrologic system". Interactions within the climate system occur at a wide range of temporal and spatial scales, as discussed, for example, in Pielke (1998). In the context of prediction, the interactions that involve water with other components of the climate results in an initial value problem, if the feedbacks are sufficiently large and nonlinear, and occur within the time period which the forecasts are made for. A consequence of these nonlinear interactions is that the climate system is inherently chaotic. In my talk, the concept of climate as an initial value problem will be illustrated with respect to land-atmosphere feedbacks, first with simple models (Zeng et al., 1990; Pielke and Zeng, 1994), and then with several more physically realistic coupled regional and global models of the Earth system (Chase et al., 1999; Pielke et al., 1999; Eastman et al., 2000; Lu et al., 2000). In the context of land-atmosphere interactions, these feedbacks range from short term biophysical, to medium range biogeochemical, to long-term biogeographical interactions. Hydrologic processes are involved on each of these time scales. These conclusions are being confirmed by other investigators as reported, for example, in Pitman et al. (1999), Chen et al. (2000), and the numerous reference
citations in Pielke (2000). Among the major conclusions thus far are:
-
Hydrologic processes must be coupled with carbon and nitrogen processes (and those of other trace gases and aerosols) in order to develop a realistic understanding of the climate. The concept of WEB (Water-Earth-Biota; Gupta et al. 2000: http://cires.colorado.edu/hydrology), which has been initiated by the Hydrology Division of the NSF is an initiative to integrate these processes within a research framework.
As an example of this need, with respect to the concept of carbon sequestration (which is designed to reduce the net input of the radiatively active gas carbon dioxide into the atmosphere), there has been no assessment of whether water vapor, another radiatively active gas, would have increased input into the air as a result of this carbon mitigation approach. The net result of a carbon sequestration program that does not also consider the associated effect on hydrologic processes could be a greater net flux of radiatively active gases into the atmosphere (as well as a change of the net radiation at the surface by altering its albedo) than would occur without carbon sequestration!
-
The biological effect of CO2 on ecosystem function and feedback into atmospheric dynamics and thermodynamics must be included in the assessment of climate and weather prediction. In the short time period, for example, locally increased carbon dioxide associated with urban pollution can alter the stomatal resistance to transpiration loss. This reduction in water flux can influence convective available potential energy (CAPE), and thus subsequent rainfall. On long time scales, the transient evolution to increased carbon dioxide can affect vegetation species composition (more C3 plants at the expense of C4 plants, for example), which subsequently feedbacks to alter rainfall amounts and patterns, as shown by Eastman et al. (2000).
-
Human caused landscape disturbance is a major perturber of the Earth's climate system on the global scale. Indeed, it appears to already have had an effect on the Earth's climate system
-
that is as large or larger than claimed for the radiative effect of doubled CO2. Landscape change has been accelerating and our largest alterations have occurred in recent years (Leemans 1999; O'Brien 2000). This conclusion requires that we must include landscape as an initial value within models of the climate.
-
The success of seasonal weather forecasts has primarily been a result of the treatment of the sea surface temperatures as a static lower boundary condition (Landsea and Knaff 2000). These seasonal "nowcasts" work because the dominant atmospheric-ocean feedbacks occur over a relatively long time (i.e., longer than a season). Similarly, antecedent soil moisture provides a long enough memory for useful seasonal nowcasts (such an inertia within the climate system can help explain the persistent of the Texas drought and heat this summer, since the vegetation in the region is not transpiring due to poor soil moisture). The lack of skilled multi-year SST predictions apparently results because the forecasts on this time period are no longer nowcasts, but true initial value problems with the inherent limitation on the ability to forecast the future.
For these reasons, the concept of weather prediction as an "initial value problem" while "climate is a boundary problem" is being replaced with the new paradigm that weather occurs over a short enough time period so that many of the feedbacks within the climate system do not occur. Both weather and climate are, in fact, initial value problems. "Weather" should be viewed as one subset of the "climate" system.
REFERENCES FOR PRESENTED PAPERS
Anagnostou, E. N., and W. F. Krajewski. 1998. Calibration of the NEXRAD precipitation processing subsystem. Weather and Forecasting 13:396-406.
Anagnostou, E. N., and W. F. Krajewski. 1999. Real-time radar rainfall estimation. Part 1: algorithm formulation. Journal of Atmospheric and Oceanic Technology 16:189-197.
Andrieu H., and J. D. Creutin. 1995. Identification of vertical profiles of reflectivities for hydrological applications using an inverse method. Part I: formulation. J. Appl. Meteor. 34:225-239.
Arkin, P. A., and P. Xie. 1994. The global precipitation climatology project: First algorithm intercomparison project. Bull. Am. Meteorol. Soc. 75:401-419.
Chen, F., R. A. Pielke, Sr., and K. Mitchell. 2000. Development and application of land-surface models for mesoscale atmospheric models: Problems and promises. AMS Monograph.
Chu, P. 1999. Two kinds of predictability in the Lorenz system. J. Atmos. Sciences 56:1427-1432.
Ciach, J. G., and W. F. Krajewski. 1999a. On the estimation of radar rainfall error variance. Advances in Water Resources 22:585-595.
Ciach, G. J., and W. F. Krajewski. 1999b. Conceptualization of radar-raingage comparisons under observational uncertainties. Journal of Applied Meteorology 38:519-1525.
Ciach, G. J., M. L. Morrissey, and W. F. Krajewski. 2000. Conditional bias in radar rainfall estimation. Journal of Applied Meteorology.
Crook, N. A. 1996. Sensitivity of moist convection forced by boundary layer processes to low-level thermodynamic fields. Mon. Wea. Rev. 124:1767-1785.
Delworth, T., and S. Manabe. 1988. The influence of potential evaporation on the variabilities of simulated soil wetness and climate. J. Climate 1:523-547.
Eastman, J. L., M. B. Coughenour, and R. A. Pielke. 2000. The effects of CO2 and landscape change using a coupled plant and meteorological model. Global Change Biology.
Epstein, E. S. 1969. Stochastic dynamic prediction. Tellus 21:739-759.
Errico, R., and D. Stensrud. 2000. Estimation of Error Statistics of Precipitation Produced by Convective Parameterization Schemes for Application to the Variational Assimilation of Precipitation Observations. Draft Manuscript.
Fankhauser, J. C. 1998. Estimates of thunderstorm precipitation efficiency from field measurements in CCOPE. Monthly Weath. Rev. 116:663-684.
Ferrier, B. S., J. Simpson, and W-K Tao. 1996. Factors responsible for precipitation efficiencies in midlatitude and tropical squall simulations. Monthly Weath. Rev. 124:2100-2125.
French, M. N., and W. F. Krajewski. 1994. A model for real-time quantitative rainfall forecasting using remote-sensing, 1, formulation. Water Resources Research 30:1075-1083.
Gent, P. R. 2000. Will the North Atlantic Ocean Thermohaline Circulation Weaken During the Next Century?
Georgakakos, K. P. 2000. Covariance propagation and updating in the context of real-time radar data assimilation by quantitative precipitation forecast models. Journal of Hydrology.
Grecu, M., and W. F. Krajewski. 2000a. Rainfall forecasting using variational assimilation of radar data in numerical cloud models. Advances in Water Resources.
Grecu, M., and W. F. Krajewski. 2000b. A Comprehensive investigation of statistical procedures for radar-based shortterm, quantitative precipitation forecasting, Journal of Hydrology.
Grecu, M., and W. F. Krajewski. 2000c. An efficient methodology for detection of anomalous propagation echoes in radar reflectivity data using neural networks. Journal of Oceanic and Atmospheric Technology 17:121-129.
Habib, E., W. F. Krajewski, V. Ne_por, and A. Kruger. 1999. Numerical simulation studies of raingage data correction due to wind effect. Journal of Geophysical Research-Atmospheres Research 104:(19)723-734.
Harris, D., and E. Foufoula-Georgiou. 2000. Subgrid variability and stochastic downscaling of modeled precipitation and its effects on radiative transfer computations. J. Geophys. Res.
Harris, D., E. Foufoula-Georgiou, K. Droegemeir and J. Levit. 2000. Multiscale statistical properties of a high resolution precipitation forecast. J. Hydrometeorology.
Held, I. M. 1993. Large-scale dynamics and global warming. BAMS 74:228-241.
Huang, J., and H. M. van den Dool. 1993. Monthly precipitation-temperature relation and temperature prediction over the U.S. J. Climate 6:1111-1132.
Huang, J., H. M. van den Dool, and K. G. Georgakakos. 1996. Analysis of model-calculated soil moisture over the U.S. (1931-1993) and applications to long range temperature forecasts. J Climate. 9:1350-1362.
Huffman, G. J., R. F. Adler, P. Arkin, A. Chang, R. Ferraro, A. Gruber, J. Janowiak, A. McNab, B. Rudolf, and U. Schneider. 1997. The global precipitation climatology product (GPCP) combined precipitation data set. Bull. Am. Meteorol. Soc. 78:5-20.
Joss, J., and R. Lee. 1995. The application of radar-gauge comparisons to operational profile corrections. J. Appl. Meteor. 34:2612-2630.
Kitchen M., R. Brown, A. G. Davis. 1994. Real time correction of weather radar for effects of bright band, range and orographic growth in widespread precipitation. Q.J.R. Meteorol. Soc. 120:1231-1254.
Koster, R. D., and P. C. D. Milly. 1997. The interplay between transpiration and runoff formulations in land surface schemes used with atmospheric models. J . Climate. 10:1578-1591.
Koster, R. D., M. J. Suarez, and M. Heiser. 2000. Variance and predictability of precipitation at seasonal-to-interannual timescales. J. Hydrometeor. 26-46.
Krajewski, W. F., G. J. Ciach, J. R. McCollum, and C. Bacotiu. 2000. Initial validation of the global precipitation climatology project over the United States. Journal of Applied Meteorology 39:1071-1086.
Kumar, A., and M. P. Hoerling. 1995. Prospects and limitations of seasonal atmospheric GCM predictions. Bull. Amer. Met. Soc. 335-345.
Kummerow, C., W. Barnes, T. Kozu, J. Shiue, and J. Simpson. 1998. The tropical rainfall measuring mission (TRMM) sensor package. Journal of Atmospheric and Oceanic Technology 15:809–817.
Landsea, C. W., and J. A. Knaff. 2000. How much skill was there in forecasting the very strong 1997-98 El Nino? Bull. Amer. Meteor. Soc. 81:2107-2119.
Lee, T.-H., and K. P. Georgakakos. 1996. Operational rainfall prediction on meso-gamma scales for hydrologic applications. Water Resources Research 32:987-1003.
Leemans, R. 1999. Land-use change and the terrestrial carbon cycle. IGBP Global Change Newsletter 37:24-26.
Legates, D. R., and T. L. DeLiberty. 1993. Precipitation measurement biases in the United States. Water Resources Bulletin 29:855-861.
Leith, C. E. 1974. Theoretical skill of Monte-Carlo forecasts. Mon. Wea. Rev. 102:409-418.
Liu, Y., and R. Avissar. 1999. A study of persistence in the land-atmosphere system using a general circulation model and observations. J. Clim. 2139-2153.
Lohmann, D., and co-authors. 1998. The project for the intercomparison of land-surface parameterization schemes (PILPS) phase 2c Red Arkansas river basin experiment: 3. spatial and temporal analysis of water fluxes. Glob. and Planet. Change 19:161-180.
Lorenz, E. N. 1975. Climate predictability. The physical basis of climate modeling. WMO GARP Publication Series 16:132-136.
Lorenz, E. 1969. The predictability of a flow, which possesses many scales of motion. Tellus 3:289-307.
Lovelock, J. 1995. The Ages of Gaia. Oxford University Press, Oxford, UK.
Lu, L., R. A. Pielke, G. E. Liston, W. J. Parton, D. Ojima, and M. Hartman. 2000. Imple-mentation of a two-way interactive atmospheric and ecological model and its application to the central United States. J. Climate.
Ne_por, V., and B. Sevruk. 1999. Estimation of wind-induced error of rainfall gauge measurements using a numerical simulation. Journal of Atmospheric and Oceanic Technology 16:450-464.
Nykanen D, E. Foufoula-Georgiou, and W. Lapenta. 2000. Impact of small-scale precipitation variability on larger-scale spatial organization of land-atmosphere fluxes. J. of Hydro-meteorology.
Nykanen D., and E. Foufoula-Georgiou. 2000. Soil moisture variability and its effect on scale-dependency of nonlinear parameterizations on coupled land-atmosphere models. Advances in Water Resources.
O'Brien, K. L. 2000. Upscaling tropical deforestation: Implications for climate change. Climatic Change 44:311-329.
Petty, G., and W. F. Krajewski. 1996. Satellite estimation of precipitation. Hydrological Sciences Journal 41:433-451.
Petty, G. W. 1995. The status of satellite-based rainfall estimation over land. Remote Sens. Environ. 51:125-137.
Pielke, R. A., and X. Zeng. 1994. Long-term variability of climate. J. Atmos. Sci. 51:155-159.
Pielke, R. A. 1998. Climate prediction as an initial value problem. Bull. Amer. Meteor. Soc. 79:2743-2746.
Pielke, R. A. 2000. Influence of the spatial distribution of vegetation and soils on the prediction of cumulus convective rainfall. Rev. Geophys.
Pielke, R. A., G. E. Liston, J. L. Eastman, L. Lu, and M. Coughenour. 1999. Seasonal weather prediction as an initial value problem. J. Geophys. Res. 104:19463-19479.
Pielke, R., Sr., K. Reckhow, and F. Swanson. 2000. New Interdisciplinary Initiative Combines Water, Earth, and Biota, Trans. AGU (EOS).
PIP-1. 1994. The first WetNet precipitation intercomparison project. Remote Sensing Reviews 11:373.
Pitman, A., R. Pielke Sr., R. Avissar, M. Claussen, J. Gash, and H. Dolman, The role of the land surface in weather and climate: Does the land surface matter. IGBP Newsletter, 39, 4-11, 1999.
Reiners, W. A. 1988. Complementary models for ecosystems. American Naturalist 127:59-73.
Ross, R. J., and W. P. Elliot. 1996. Tropospheric water vapor climatology and trends over North America: 1973-1993. J. Clim. 9:3561-3574.
Schlosser, C. A., and P. C. D. Milly. 2000. The potential impact of soil moisture initialization on soil moisture predictability and associated climate predictability. Proceedings of the GEWEX/BAHC International Workshop on Soil Moisture Monitoring, Analysis, and Prediction for Hydrometeorological and Hydroclimatological Applications. Pg. 31.
Seo, D. J., J. P. Breidenbach, R. Fulton, D. Miller and T. O’Banon. 2000. Real time adjustment of range dependent biases in WSR-88D rainfall estimates due to nonuniform vertical profile of reflectivity. Journal of Hydrometeorology.
Shimizu, K., D. A. Short, and B. Kedem. 1993. Single- and double-threshold methods for estimating the variance of area rain rate. J. Meteor. Soc. Japan 71:673-683.
Short, D. A., K. Shimizu, and B. Kedem. 1993a. Optimal thresholds for the estimation of area rain rate moments by the threshold method. J. Appl. Meteor. 32:182-192.
Short, D. A., D. B. Wolff, D. Rosenfeld, and D. Atlas. 1993b. A study of the threshold method utilizing rain gauge data. J. Appl. Meteor. 32:1379-1387.
Shukla, J. 1998. Predictability in the midst of chaos: A scientific basis for climate forecasting. Science 728-731.
Simpson, J., C. Kummerow, W.-K. Tao, and R. F. Adler. 1996. On the tropical rainfall measuring mission (TRMM). Meteor. Atmos. Phys. 60:19-36.
Steiner, M., J. A. Smith, S. J. Burges, C.V. Alonso, and R. W. Darden. 1999. Effect of bias adjustment and rain gauge data quality control on radar rainfall estimation. Water Resour. Res. 35(8):2487-2503.
Sun, J.-Z., and Crook, N. A. 1997. Dynamical and microphysical retrieval from Doppler radar observations using a cloud model and its adjoint. 1. Model development and simulated data experiments. Journal of the Atmospheric Sciences 54:1642-1661.
Trenberth, K. E. 1998. Atmospheric moisture residence times and cycling: Implications for rainfall rates with climate change. Climatic Change 39:667-694.
Tustison, B., D. Harris, and E. Foufoula-Georgiou. 2000. Scale issues in verification of precipitation forecasts. J. Geophys. Res.
Vieux, B. E., V. F. Bralts, L. J. Segerlind, and R. B. Wallace. 1990. Finite element watershed modeling: One-dimensional elements. J. of Water Resources Management Planning 116:803-819.
Vieux, B. E. 1991. Geographic information systems and nonpoint source water quality modeling. J. of Hydrological Processes 5:110-123.
Vieux, B. E. 1993. DEM aggregation and smoothing effects on surface runoff modeling. J. of Computing in Civil Engineering 7:310-338.
Vieux, B. E., and N. Gaur. 1994. Finite element modeling of storm water runoff using GRASS GIS. Microcomputers in Civil Engineering 9:263-270.
Vieux, B. E., F. LeDimet, and D. Armand. 1998. Optimal control and adjoint methods applied to distributed hydrologic model calibration. Proceedings of Int. Assoc. for Computational Mechanics, IV World Congress on Computational Mechanics, 29 June-2 July, Buenos Aires, Argentina. Pg. II1050.
Vieux, B. E. 2000. Distributed Hydrologic Modeling Using GIS. Kluwer Academic Publishers, Spuilboulevard 50, Dordrecht, The Netherlands. Water Science and Technology Series.
Vinnikov, K. Y., A. Robock, N. A. Speranskaya, and A. Schlosser. 1996. Scales of temporal and spatial variability of midlatitude soil moisture. J. Geophys. Res. 7163-7174.
Webster, P. J. 1994. The role of hydrological processes in ocean-atmosphere interactions. Reviews of Geophysics 32:427-436.
Wilson, J. W., N. A. Crook, C. K. Mueller, J. Sun, and M. Dixon. 1998. Nowcasting thunderstorms: A status report. Bulletin of the American Meteorological Society 79:2079-2099.
Yang, D., B. E. Goodisson, and J. R. Metcalfe. 1998. Accuracy of NWS 8” standard nonrecording precipitation gauge: Results and application of WMO intercomparison. Journal of Atmospheric and Oceanic Technology 15:54-67.
Young, B., A. A. Bradley, W. F. Krajewski, and A. Kruger. 2000. An evaluation study of NEXRAD multisensor precipitation estimates for operational hydrologic forecasting. Journal of Hydrometeorology 1:241-254.
Zawadzki, I., J. Morneau, and R. Laprise. 1999. Predictability of precipitation patterns--An operational approach. Journal of Applied Meteorology 33:1562-1571.
Zeng, X., R. A. Pielke, and R. Eykholt. 1990. Chaos in Daisy-world. Tellus 42B:309-318.
Zepeda-Arce, J., E. Foufoula-Georgiou, and K. Droegemeier. 2000. Space-time rainfall organization and its role in vali