Making Sense of Complexity: Summary of the Workshop on Dynamical Modeling of Complex Biomedical Systems (2002)

This report documents a recent workshop¹ at which approximately 85 biomedical scientists, mathematicians, and statisticians shared their experiences in modeling aspects of cellular function, disease states, and neuroscience. The topics were chosen to provide a sampling of the rapidly emerging research at the interface of the mathematical and biomedical sciences, and this summary has been prepared as an introduction to those topics for mathematical scientists who are exploring the opportunities from biomedical science. While a range of challenges and approaches was discussed at the workshop, its overall theme was perhaps best summarized by discussant Jim Keener, of the University of Utah, who noted that what researchers in these areas are really trying to do is “make sense of complexity.” The mathematical topics that play important roles in the quest include numerical analysis, scientific computing, statistics, optimization, and dynamical systems theory.

Many biological systems are the result of interwoven interactions of simpler behaviors, with the result being a complex system that defies understanding through intuition or other simple means. In such a situation, it is critical to have a model that helps us understand the structure of the phenomenon, and we look to the mathematical sciences for the tools with which to construct and investigate such models. Although the experimental data from biological systems and the resulting models can be bewildering in their complexity, a minimal model can sometimes expose essential structure. An example is given in Figure 1-1, which shows the simple (and pleasing) linear relationship between the level of DNA synthesis in a cell and the integrated activity of the ERK2 enzyme.² After understanding such basic elements of cell signaling and control, one may then be able to construct a more complex model that better explains observed biomedical phenomena. This evolution from basic to more complex was illustrated by several workshop talks, such as that of Garrett Odell, of the University of Washington,

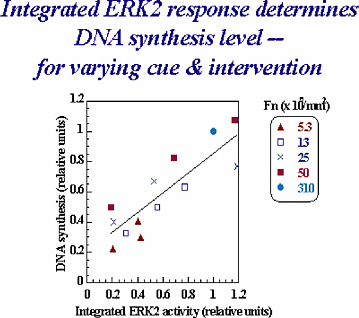
FIGURE 1-1 DNA synthesis dependence on ERK signal for varying cue and intervention. Fn is fibronectin. Figure courtesy of Douglas Lauffenburger.

which presented a model that grew from 48 to 88 parameters, and that of Douglas Lauffenburger, of the Massachusetts Institute of Technology, which described how a model grew in complexity as his group worked to capture the relationship between insulin response and ERK2. Because the phenomenology of most biomedical processes is so complex, a typical development path for biomedical modeling is to start with a model that is clearly too simple and then evolve it to capture more of nature’s complexity, always avoiding any detail whose effect on the phenomenology is below some threshold of concern.

The workshop opened with a welcome from Peter Bickel, the chair of the Board on Mathematical Sciences and Their Applications (BMSA). Bickel remarked that one mission of the BMSA is to showcase the role that the mathematical sciences play in other disciplines, and this workshop was planned to do that. The 16 talks, given by researchers at the interface between the mathematical and biomedical sciences, all illustrate how the mathematical and biological sciences can interact for the benefit of both. The presentations were videotaped and subsequently made available at <www.msri.org/publications/video/index6.html/>, with a link from <www.nas.edu/bms>.

Two important principles emerged from the workshop:

1. Successful modeling starts with simple models to gain understanding. If the simple model succeeds somewhat in capturing the known or anticipated behavior, then work to refine it.

2. When biomedical processes are modeled with mathematical and statistical concepts, the underlying structure of the biological processes can become clearer. Knowledge of that structure, and of the way its mathematical representation responds to change, allows one to formulate hypotheses that might not be apparent from the phenomenological descriptions.

While these principles are not new or unique to modeling in the biomedical sciences, they may not be obvious to mathematical scientists whose previous experience is with models that are based on well-established laws (e.g., mechanical or electromagnetic modeling) or who have not worked in data-intensive fields. In modeling very complex behaviors such as biomedical phenomena, these principles are the hallmark of good research.