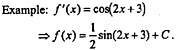Appendix D
Syllabus Details, IB Mathematics HL, Core Calculus Material
8 Core: Calculus Teaching time: 50 hours
The aim of this section is: to introduce the basic concepts and techniques of differential and integral calculus, and some of their applications.
|
CONTENT |
AMPLIFICATIONS/EXCLUSIONS |
TEACHING NOTES |
|
8.1 Informal ideas of a limit and convergence. |
Included: only a very informal treatment of limit and convergence, e.g. 0.3, 0.33, 0.333 ... |
Link with infinite geometric series in § 1.1. Link with the binomial theorem in § 1.3. Calculators can be used to investigate limits numerically. |
|
8.2 Differentiation from first principles as the limit of the difference quotient Differentiation of: x ↦ xn, n ∈Q; x ↦ sin x; x ↦ cos x; x ↦ tan x; x ↦ ex; x ↦ ln x. |
Included: a formal treatment for positive integer powers; informal extension to rational powers; a formal treatment for x ↦ sin x. Included: familiarity with the notation
|
Other derivatives can be predicted or verified by graphical considerations using graphic display calculator. Investigation of the derivative of xn from consideration of the function |
|
8.3 Differentiation of sums of function and real multiples of functions, The chain rule for composite functions. |
Included: derivatives of reciprocal trigonometric functions x ↦ sec x, x ↦ csc x, x ↦ cot x. Included: applications to rates of change. |
Link with composite functions in §2.1. Link with implicit differentiation in §8.7. Link with integration by parts in §8.10. |
|
8.4 Further differentiation: the product and quotient roles; the second derivative; differentiation of ax and logax. |
Included: understanding that 2x = exln2, etc. |
|
|
CONTENT |
AMPLIFICATIONS/EXCLUSIONS |
TEACHING NOTES |
|
8.5 Graphical behaviour of functions: tangents, normals and singularities, behaviour for large |x|; asymptotes. The significance of the second derivative; distinction between maximum and minimum points and points of inflexion. |
Included: both ‘global’ and ‘local’ behaviour; choice of appropriate window; (a, b) point of inflexion ⇒ ƒ″(a) = 0, but the converse is not necessarily true; points of inflexion with zero or non-zero gradient. |
Effective use of graphic display calculator envisaged here, combined with sketching by hand. Link with function graphing skills in §2.2. The terms ‘concave-up’ and ‘concave-down’ conveniently distinguish between ƒ″(x)> 0 and ƒ″(x) < 0 respectively. |
|
8.6 Applications of the first and second derivative to maximum and minimum problems. Kinematic problems involving displacement, s, velocity, |
Included: testing for maximum or minimum (e.g. volume, area and profit) using the sign of the first derivative or using the second derivative. |
Link with graphing functions in.§2.2. |
|
8.7 Implicit differentiation. Derivatives of the inverse trigonometric functions. |
Included: applications to related rates of change. Not required: second derivatives of parametric functions. |
Link with chain rule in §8.3. |
|
8.8 Indefinite integration as anti-differentiation. Indefinite integrals of: xn; n ∈Q, sin x; cos x; ex. Composites of these with x ↦ ax + b. Application to acceleration and velocity. |
|
Candidates could be made aware of the fundamental theorem of calculus,
|
|
CONTENT |
AMPLIFICATIONS/EXCLUSIONS |
TEACHING NOTES |
|
8.9 Anti-differentiation with a boundary condition to determine the constant term. Definite integrals. Areas under curves. |
Example of a boundary condition: if |
Area under velocity-time graph representing distance is a useful illustration. |
|
8.10 Further integration by substitution; integration by parts; definite integrals. |
Included: limit changes in definite integrals; questions requiring repeated integration by parts; integrals requiring further manipulation, |
Link with transformations of graphs in §2.3. Link with the chain rule in §8.3. |
|
8.11 Solution of first order differential equations by separation of variables. |
Included: transformation of a homogeneous equation by the substitution y = vx. |
Link with exponential and logarithmic functions in §2.10. |
SOURCE: (IBO, 1998)
Appendix E
Text of a Letter Endorsed by the Governing Boards of the Mathematical Association of America and the National Council of Teachers of Mathematics Concerning Calculus in the Secondary Schools34
TO: Secondary School Mathematics Teachers
FROM: The Mathematical Association of America
The National Council of Teachers of Math.
DATE: September, 1986
RE: Calculus in the Secondary School
Dear Colleague:
A single variable calculus course is now well established in the 12th grade at many secondary schools, and the number of students enrolling is increasing substantially each year. In this letter, we would like to discuss two problems that have emerged.
The first problem concerns the relationship between the calculus course offered in high school and the succeeding calculus courses in college. The Mathematical Association of America (MAA) and the National Council of Teachers of Mathematics (NCTM) recommend that the calculus course offered in the 12th grade should be treated as a college-level course. The expectation should be that a substantial majority of the students taking the course will master the material and will not then repeat the subject upon entrance to college. Too many students now view their 12th grade calculus course as an introduction to calculus with the expectation of repeating the material in college. This causes an undesirable attitude on the part of the student both in secondary school and in college. In secondary school all too often a student may feel "I don't have to study this subject too seriously, because I have already seen most of the ideas."