7
Uses of Polygraph Tests
The available evidence indicates that in the context of specific-incident investigation and with inexperienced examinees untrained in countermeasures, polygraph tests as currently used have value in distinguishing truthful from deceptive individuals. However, they are far from perfect in that context, and important unanswered questions remain about polygraph accuracy in other important contexts. No alternative techniques are available that perform better, though some show promise for the long term. The limited evidence on screening polygraphs suggests that their accuracy in field use is likely to be somewhat lower than that of specific-incident polygraphs.
This chapter discusses the policy issues involved in using an imperfect diagnostic test such as the polygraph in real-life decision making, particularly in national security screening, which presents very difficult tradeoffs between falsely judging innocent employees deceptive and leaving major security threats undetected. We synthesize what science can offer to inform the policy decisions, but emphasize that the choices ultimately must depend on a series of value judgments incorporating a weighting of potential benefits (chiefly, deterring and detecting potential spies, saboteurs, terrorists, or other major security threats) against potential costs (such as of falsely accusing innocent individuals and losing potentially valuable individuals from the security related workforce). Cost-benefit tradeoffs like this vary with the situation. For example, the benefits are greater when the security threat being investigated is more serious; the costs are greater when the innocent individuals who might be
accused are themselves vital to national security. For this reason, tradeoff decisions are best made by elected officials or their designees, aided by the principles and practices of behavioral decision making.
We first summarize what scientific analysis can contribute to understanding the tradeoffs involved in using polygraph tests in security screening. (These tests almost always use the comparison question or relevant-irrelevant formats because concealed information tests can only be used when there are specific pieces of information that can form the basis for relevant questions.) We then discuss possible strategies for making the tradeoffs more attractive by improving the accuracy of lie detection— either by making polygraph tests more accurate or by combining them with other sources of information. We also briefly consider the legal context of policy choices about the use of polygraph tests in security screening.
TRADEOFFS IN INTERPRETATION
The primary purpose of the polygraph test in security screening is to identify individuals who present serious threats to national security. To put this in the language of diagnostic testing, the goal is to reduce to a minimum the number of false negative cases (serious security risks who pass the diagnostic screen). False positive results are also a major concern: to innocent individuals who may lose the opportunity for gainful employment in their chosen professions and the chance to help their country and to the nation, in the loss of valuable employees who have much to contribute to improved national security, or in lowered productivity of national security organizations. The prospect of false positive results can also have this effect if employees resign or prospective employees do not seek employment because of polygraph screening.
As Chapter 2 shows, polygraph tests, like any imperfect diagnostic tests, yield both false positive and false negative results. The individuals judged positive (deceptive) always include both true positives and false positives, who are not distinguishable from each other by the test alone. Any test protocol that produces a large number of false positives for each true positive, an outcome that is highly likely for polygraph testing in employee security screening contexts, creates problems that must be addressed. Decision makers who use such a test protocol might have to decide to stall or sacrifice the careers of a large number of loyal and valuable employees (and their contributions to national security) in an effort to increase the chance of catching a potential security threat, or to apply expensive and time-consuming investigative resources to the task of identifying the few true threats from among a large pool of individuals who had positive results on the screening test.
Quantifying Tradeoffs
Scientific analysis can help policy makers in such choices by making the tradeoffs clearer. Three factors affect the frequency of false negatives and false positives with any diagnostic test procedure: its accuracy (criterion validity), the threshold used for declaring a test result positive, and the base rate of the condition being diagnosed (here, deception about serious security matters). If a diagnostic procedure can be made more accurate, the result is to reduce both false negatives and false positives. With a procedure of any given level of accuracy, however, the only way to reduce the frequency of one kind of error is by adjusting the decision threshold—but doing this always increases the frequency of the other kind of error. Thus, it is possible to increase the proportion of guilty individuals caught by a polygraph test (i.e., to reduce the frequency of false negatives), but only by increasing the proportion of innocent individuals whom the test cannot distinguish from guilty ones (i.e., frequency of false positives). Decisions about how, when, and whether to use the polygraph for screening should consider what is known about these tradeoffs so that the tradeoffs actually made reflect deliberate policy choices.
Tradeoffs between false positives and false negatives can be calculated mathematically, using Bayes’ theorem (Weinstein and Fineberg, 1980; Lindley, 1998). One useful way to characterize the tradeoff in security screening is with a single number that we call the false positive index: the number of false positive cases to be expected for each deceptive individual correctly identified by a test. The index depends on the accuracy of the test; the threshold set for declaring a test positive; and the proportion, or base rate, of individuals in the population with the condition being tested (deception, in this case). The specific mathematical relationship of the index to these factors, and hence the exact value for any combination of accuracy (A), threshold, and base rate, depends on the shape of the receiver operating characteristic (ROC) curve at a given level of accuracy, although the character of the relationship is similar across all plausible shapes (Swets, 1986a, 1996:Chapter 3). Hence, for illustrative purposes we assume that the ROC shapes are determined by the simplest common model, the equivariance binormal model.1 Because this model, while not implausible, was chosen for simplicity and convenience, the numerical results below should not be taken literally. However, their orders of magnitude are unlikely to change for any alternative class of ROC curves that would be credible for real-world polygraph test performance, and the basic trends conveyed are inherent to the mathematics of diagnosis and screening.
Although accuracy, detection threshold, and base rate all affect the
false positive index, these determinants are by no means equally important. Calculation of the index for diagnostic tests at various levels of accuracy, using various thresholds, and with a variety of base rates shows clearly that base rate is by far the most important of these factors. Figure 7-1 shows the index as a function of the base rate of positive (e.g., deceptive) cases for three thresholds for a diagnostic test with A = 0.80. It illustrates clearly that the base rate makes more difference than the threshold across the range of thresholds presented. Figure 7-2 shows the index as a function of accuracy with the threshold held constant so that the diagnostic test’s sensitivity (percent of deceptive individuals correctly identified) is 50 percent. It illustrates clearly that base rate makes more difference than the level of accuracy across the range of A values represented.
Figures 7-1 and 7-2 show that the tradeoffs involved in relying on a diagnostic test such as the polygraph, represented by the false positive index values on the vertical axis, are sharply different in situations with high base rates typical of event-specific investigations, when all examinees are identified as likely suspects, and the base rate is usually above 10 percent, than in security screening contexts, when the base rate is normally very low for the most serious infractions. The false positive index is
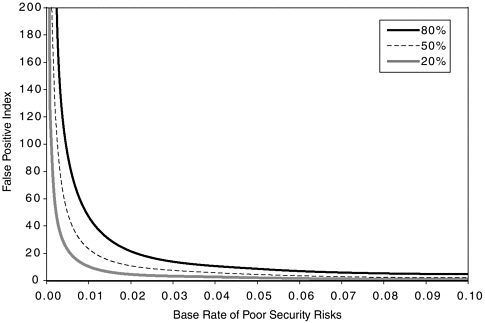
FIGURE 7-1 Comparison of the false positive index and base rate for three sensitivity values of a polygraph test protocol with an accuracy index (A) of 0.80.
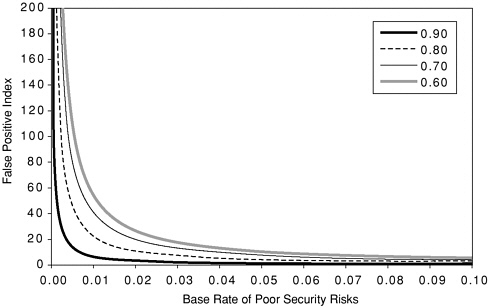
FIGURE 7-2 Comparison of the false positive index and base rate for four values of the accuracy index (A) for a polygraph test protocol with threshold set to correctly identify 50 percent of deceptive examinees.
about 1,000 times higher when the base rate is 1 serious security risk in 1,000 than it is when the base rate is 1 in 2, or 50 percent.
The index is also affected, though less dramatically, by the accuracy of the test procedure: see Figure 7-2. (Appendix I presents the results of calculations of false positive indexes for various levels of accuracy, base rates, and thresholds for making a judgment of a positive test result.) With very low base rates, such as 1 in 1,000, the false positive index is quite large even for tests with fairly high accuracy indexes. For example, a test with an accuracy index of 0.90, if used to detect 80 percent of major security risks, would be expected to falsely judge about 200 innocent people as deceptive for each security risk correctly identified. Unfortunately, polygraph performance in field screening situations is highly unlikely to achieve an accuracy index of 0.90; consequently, the ratio of false positives to true positives is likely to be even higher than 200 when this level of sensitivity is used. Even if the test is set to a somewhat lower level of sensitivity, it is reasonable to expect that each spy or terrorist that might be correctly identified as deceptive by a polygraph test of the accuracy actually achieved in the field would be accompanied by at least hundreds of nondeceptive examinees mislabeled as deceptive. The spy or terrorist would be indistinguishable from these false positives by poly-
graph test results. The possibility that deceptive examinees may use countermeasures makes this tradeoff even less attractive.
It is useful to consider again the tradeoff of false positives versus false negatives in a manner that sets an upper bound on the attractiveness of the tradeoff (see Table 2-1, p. 48). The table shows the expected outcomes of polygraph testing in two hypothetical populations of examinees, assuming that the tests achieve an accuracy index of 0.90, which represents a higher level of accuracy than can be expected of field polygraph testing. One hypothetical population consists of 10,000 criminal suspects, of whom 5,000 are expected to be guilty; the other consists of 10,000 employees in national security organizations, of whom 10 are expected to be spies.
The table illustrates the tremendous difference between these two populations in the tradeoff. In the hypothetical criminal population, the vast majority of those who “fail” the test (between 83 and 98 percent in these examples) are in fact guilty. In the hypothetical security screening population, however, because of the extremely low base rate of spies, the vast majority of those who “fail” the test (between 95 and 99.5 percent in these examples) are in fact innocent of spying. Because polygraph testing is unlikely to achieve the hypothetical accuracy represented here, even these tradeoffs are overly optimistic. Thus, in the screening examples, an even higher proportion than those shown in Table 2-1 would likely be false positives in actual practice. We reiterate that these conclusions apply to any diagnostic procedure that achieves a similar level of accuracy. None of the alternatives to the polygraph has yet been shown to have greater accuracy, so these upper bounds apply to those techniques as well.
Tradeoffs with “Suspicious” Thresholds
If the main objective is to screen out major security threats, it might make sense to set a “suspicious” threshold, that is, one that would detect a very large proportion of truly deceptive individuals. Suppose, for instance, the threshold were set to correctly identify 80 percent of truly deceptive individuals. In this example, the false positive index is higher than 100 for any base rate below about 1 in 500, even with A = 0.90. That is, if 20 of 10,000 employees were serious security violators, and polygraph tests of that accuracy were given to all 10,000 with a threshold set to correctly identify 16 of the 20 deceptive employees, the tests would also be expected to identify about 1,600 of the 9,980 good security risks as deceptive.2
Another way to think about the effects of setting a threshold that correctly detects a very large proportion of deceptive examinees is in terms of the likelihood that an examinee who is judged deceptive on the
test is actually deceptive. This probability is the positive predictive value of the test. If the base rate of deceptive individuals in a population of examinees is 1 in 1,000, an individual who is judged deceptive on the test will in fact be nondeceptive more than 199 times out of 200, even if the test has A = 0.90, which is highly unlikely for the polygraph (the actual numbers of true and false positives in our hypothetical population are shown in the right half of part a of Table 2-1). Thus, a result that is taken as indicating deception on such a test does so only with a very small probability.
These numbers contrast sharply with their analogs in a criminal investigation setting, in which people are normally given a polygraph test only if they are suspects. Suppose that in a criminal investigation the polygraph is used on suspects who, on other grounds, are estimated to have a 50 percent chance of being guilty. For a test with A = 0.80 and a sensitivity of 50 percent, the false positive index is 0.23 and the positive predictive value is 81 percent. That means that someone identified by this polygraph protocol as deceptive has an 81 percent chance of being so, instead of the 0.4 percent (1 in 250) chance of being so if the same test is used for screening a population with a base rate of 1 in 1,000.3
Thus, a test that may look attractive for identifying deceptive individuals in a population with a base rate above 10 percent looks very much less attractive for screening a population with a very low base rate of deception. It will create a very large pool of suspect individuals, within which the probability of any specific individual being deceptive is less than 1 percent—and even so, it may not catch all the target individuals in the net. To put this another way, if the polygraph identifies 100 people as indicating deception, but only 1 of them is actually deceptive, the odds that any of these identified examinees is attempting to deceive are quite low, and it would take strong and compelling evidence for a decision maker to conclude on the basis of the test that this particular examinee is that 1 in 100 (Murphy, 1987).
Although actual base rates are never known for any type of screening situation, base rates can be given rough bounds. In employee screening settings, the base rate depends on the security violation. It is probably far higher for disclosure of classified information to unauthorized individuals (including “pillow talk”) than it is for espionage, sabotage, or terrorism. For the most serious security threats, the base rate is undoubtedly quite low, even if the number of major threats is 10 times as large as the number of cases reported in the popular press, reflecting both individuals caught but not publicly identified and others not caught. The one major spy caught in the FBI is one among perhaps 100,000 agents who have been employed in the bureau’s history. The base rate of major security threats in the nation’s security agencies is almost certainly far less than 1 percent.
Appendix I presents a set of curves that allow readers to estimate the false positive index and consider the implied tradeoff for a very wide range of hypothesized base rates of deceptive examinees and various possible values of accuracy index for the polygraph testing, using a variety of decision thresholds. It is intended to help readers consider the tradeoffs using the assumptions they judge appropriate for any particular application.
Thus, using the polygraph with a “suspicious” threshold so as to catch most of the major security threats creates a serious false-positive problem in employee security screening applications, mainly because of the very low base rate of guilt among those likely to be screened. When the base rate is one in 1,000 or less, one can expect a polygraph test with a threshold that correctly identifies 80 percent of deceptive examinees to incorrectly classify at least 100 nondeceptive individuals as deceptive for each security threat correctly identified. Any diagnostic procedure that implicates large numbers of innocent employees for each major security violator correctly identified comes with a variety of costs. There is the need to investigate those implicated, the great majority of whom are innocent, as well as the issue of the civil liberties of innocent employees caught by the screen. There is the potential that the screening policy will create anxiety that decreases morale and productivity among the employees who face screening. Employees who are innocent of major security violations may be less productive when they know that they are being tested routinely with an instrument that produces a false positive reading with non-negligible probability and when such a reading can put them under suspicion of disloyalty. Such effects are most serious when the deception detection threshold is set to detect threats with a reasonably high probability (above 0.5), because such a threshold will also identify considerable numbers of false positive outcomes among innocent employees. And there is the possibility that people who might have become valued employees will be deterred from taking positions in security agencies by fear of false positive polygraph results.
To summarize, the performance of the polygraph is sharply different in screening and in event-specific investigation contexts. Anyone who believes the polygraph “works” adequately in a criminal investigation context should not presume without further careful analysis that this justifies its use for security screening. Each application requires separate evaluation on its own terms. To put this another way, if the polygraph or any other technique for detecting deception is more accurate than guess-work, it does not necessarily follow that using it for screening is better than not using it because a decision to use the polygraph or any other imperfect diagnostic technique must consider its costs as well as its benefits. In the case of polygraph screening, these costs include not only the
civil liberties issues that are often debated in the context of false positive test results, but also two types of potential threats to national security. One is the false sense of security that may arise from overreliance on an imperfect screen: this could lead to undue relaxation of other security efforts and thus increase the likelihood that serious security risks who pass the screen can damage national security. The other cost is associated with damage to the national security that may result from the loss of essential personnel falsely judged to be security risks or deterred from employment in U.S. government security agencies by the prospect of false-positive polygraph results.
Tradeoffs with “Friendly” Thresholds
The discussion to this point assumes that policy makers will use a threshold such that the probability of detecting a spy is fairly high. There is, however, another possibility: they may decide to set a “friendly” threshold, that is, one that makes the probability of detecting a spy quite low. To the extent that testing deters security violations, such a test might still have utility for national security purposes. This deterrent effect is likely to be stronger when there is at least a certain amount of ambiguity concerning the setting of threshold. (If it were widely known that no one “failed” the test, its deterrent effect would be considerably lessened.) It is possible, however, to set a threshold such that almost no one is eventually judged deceptive, even though a fair number undergo additional investigation or testing. There is a clear difference between employment in the absence of security screening tests, a situation lacking in deterrent value against spies, and employment policies that include screening tests, even if screening identifies few if any spies.
Our meetings with various federal agencies that use polygraph screening suggest that different agencies set thresholds differently, although the evidence we have is anecdotal. Several agencies’ polygraph screening programs, including that of the U.S. Department of Energy, appear to adopt fairly “friendly” effective thresholds, judged by the low proportion of polygraph tests that show significant response. The net result is that these screening programs identify a relatively modest number of cases to be investigated further, with few decisions eventually being made that the employee has been deceptive about a major security infraction.
There are reasons of utility, such as possible deterrent effects, that might be put forward to justify an agency’s use of a polygraph screening policy with a friendly threshold, but such a polygraph screening policy will not identify most of the major security violators. For example, the U.S. Department of Defense (2001:4) reported that of 8,784 counterintelli-
gence scope polygraph examinations given, 290 (3 percent) individuals gave “significant responses and/or provided substantive information.” The low rate of positive test results suggests that a friendly threshold is being used, such that the majority of the major security threats who took the test would “pass” the screen.4
On April 4, 2002, the director of the Federal Bureau of Investigation (FBI) was quoted in the New York Times as saying that “less than 1 percent of the 700” FBI personnel who were given polygraph tests in the wake of the Hanssen spy case had test results that could not be resolved and that remain under investigation (Johnston, 2002). Whatever value such a polygraph testing protocol may have for deterrence or eliciting admissions of wrongdoing, it is quite unlikely to uncover an espionage agent who is not deterred and does not confess. A substantial majority of the major security threats who take such a test would “pass” the screen.5 For example, if Robert Hanssen had taken such tests three times during 15 years of spying, the chances are that, even without attempting countermeasures, he would not have been detected before considerable damage had been done. (He most likely would never have been detected unless the polygraph protocol achieved a criterion validity that we regard as unduly optimistic, such as A = 0.90.) Furthermore, if Hanssen had been detected as polygraph positive (along with a large number of non-spies, that is, false positives), he would not necessarily have been identified as a spy.
There may be justifications for polygraph screening with a “friendly” threshold on the grounds that the technique may have a deterrent effect or may yield admissions of wrongdoing. However, such a screen will not identify most of the major security threats. In our judgment, the accuracy of polygraph testing in distinguishing actual or potential security violators from innocent test takers is insufficient to justify reliance on its use in employee screening in federal agencies.
Although we believe it likely that polygraph testing has utility in screening contexts because it might have a deterrent effect, we were struck by the lack of scientific evidence concerning the factors that might produce or inhibit deterrence. In order to properly evaluate the costs and benefits associated with polygraph screening, research is needed on deterrence in general and, in particular, on the effects of polygraph screening on deterrence.
Recent Policy Recommendations on Polygraph Screening
We have great concern about the dangers that may arise for national security if federal agencies use the polygraph for security screening with an unclear or incorrect understanding of the implications of threshold-setting choices for the meaning of test results. Consider, for instance,
decisions that might be made on the basis of the discussion of polygraph screening in the recent report of a select commission headed by former FBI director William H. Webster (the “Webster Commission”) (Commission for the Review of FBI Security Programs, 2002). This report advocates expanded use of polygraph screening in the FBI, but does not take any explicit position on whether polygraph testing has any scientific validity for detecting deception. This stance is consistent with a view that much of the value of the polygraph comes from its utility for deterrence and for eliciting admissions. The report’s reasoning, although not inconsistent with the scientific evidence, has some implications that are reasonable and others that are quite disturbing from the perspective of the scientific evidence on the polygraph.
The Webster Commission recognizes that the polygraph is an imperfect instrument. Its recommendations for dealing with the imperfections, however, address only some of the serious problems associated with these imperfections. First, it recommends increased efforts at quality control and assurance and increased use of “improved technology and computer driven systems.” These recommendations are sensible, but they do not address the inherent limitations of the polygraph, even when the best quality control and measurement and recording techniques are used. Second, it takes seriously the problem of false positive errors, noting that at one point, the U.S. Central Intelligence Agency (CIA) had “several hundred unresolved polygraph cases” that led to the “practical suspension” of the affected officers, sometimes for years, and “a devastating effect on morale” in the CIA. The Webster Commission clearly wants to avoid a repetition of this situation at the FBI. It recommends that “adverse personnel actions should not be taken solely on the basis of polygraph results,” a position that is absolutely consistent with the scientific evidence that false positives cannot be avoided and that in security screening applications, the great majority of positives will turn out to be false. It also recommends a polygraph test only for “personnel who may pose the greatest risk to national security.” This position is also strongly consistent with the science, though the commission’s claim that such a policy “minimizes the risk of false positives” is not strictly true. Reducing the number of employees who are tested will reduce the total number of false positives, and therefore the cost of investigating false positives, but will not reduce the risk that any individual truthful examinee will be a false positive or that any individual positive result will be false. That risk can only be reduced by finding a more accurate test protocol or by setting a more “friendly” threshold.
Because the Webster Commission report does not address the problem of false-negative errors in any explicit way, it leaves open the possibility that federal agency officials may draw the wrong conclusions from
negative polygraph test results. On the basis of discussions with polygraph program and counterintelligence officials in several federal agencies (including the FBI), we believe there is a widespread belief in this community that someone who “passes” the polygraph is “cleared” of suspicion. Acting on such a belief with security screening polygraph results could pose a danger to the national security because a negative polygraph result provides little additional information on deceptiveness, beyond the knowledge that very few examinees are major violators, especially when the test protocol produces a very small percentage of positive test results. As already noted, a spy like Robert Hanssen might easily have produced consistently negative results on a series of polygraph tests under a protocol like the one currently being used with FBI employees. Negative polygraph results on individuals or on populations of federal employees should not be taken as justification for relaxing other security precautions.
Another recent policy report raises some similar issues in the context of security in the U.S. Department of Energy (DOE) laboratories. The Commission on Science and Security (2002:62), headed by John H. Hamre (the “Hamre Commission”) issued a recommendation to reduce the use of polygraph testing in the laboratories and to use it “chiefly as an investigative tool” and “sparingly as a screening tool.” It recommended polygraph screening “for individuals with access only to the most highly sensitive classified information”—a much more restricted group than those subjected to polygraph screening under the applicable federal law.
Several justifications are given for reducing the use of polygraph screening, including the “severe morale problems” that polygraph screening has caused, the lack of acceptance of polygraph screening among the DOE laboratory employees, and the lack of “conclusive evidence for the effectiveness of polygraphs as a screening technique” (Commission on Science and Security, 2002:54). The report goes so far as to say that use of polygraphs “as a simplistic screening device . . . will undermine morale and eventually undermine the very goal of good security” (p. 55). Much of this rationale thus concerns the need to reduce the costs of false positives, although the report makes no reference to the extent to which false positives may occur.
The Hamre Commission did not address the false negative problem directly, but its recommendations for reducing security threats can be seen as addressing the problem indirectly. The commission recommended various management and technological changes at the DOE laboratories that would, if effective, make espionage more difficult to conduct and easier to detect in ways that do not rely on the polygraph or other methods of employee screening. Such changes, if effective, would reduce the costs inflicted by undetected spies, and therefore the costs of false
negatives from screening, regardless of the techniques used. Given the limitations of the polygraph and other available employee screening techniques, any policies that decrease reliance on employee screening for achieving security objectives should be welcomed.
Although the commission recommended continued polygraph security screening for some DOE employees, it did not offer any explicit rationale for continuing the program, particularly considering the likelihood that the great majority of positive test results will be false. It did not claim that screening polygraphs accurately identify major security threats, and it left open the question of how DOE should use the results of screening polygraphs. We remain concerned about the false negative problem that can be predicted to occur if people who “pass” a screening polygraph test that gives a very low rate of positive results are presumed therefore to be “cleared” of security concerns. Given this concern, the Hamre Commission’s emphasis on improving security by means other than screening makes very good sense.
Both the Webster and Hamre Commission reports make recommendations to reduce the costs associated with false positive test results, although neither takes explicit cognizance of the extent to which such results are likely to occur in security screening. More importantly, neither report explicitly addresses the problem that can arise if negative polygraph screening results are taken too seriously. Overconfidence in the polygraph—belief in its validity that goes beyond what is justified by the evidence—presents a danger to national security objectives because it may lead to overreliance on negative polygraph test results. The limited accuracy of all available techniques of employee security screening underlines the importance of pursuing security objectives in ways that reduce reliance on employee screening to detect security threats.
Making Tradeoffs
Because of the limitations of polygraph accuracy for field screening applications, policy makers face very unpleasant tradeoffs when screening for target transgressions with very low base rates. We have summarized what is known about the likely frequencies of false positive and false negative results under a range of conditions. In making choices about employee security policies, policy makers must combine this admittedly uncertain information about the performance of the polygraph in detecting deception with consideration of a variety of other uncertain factors, including: the magnitude of the security threats being faced, the potential effect of polygraph policies on staff performance, morale, recruitment, and retention; the costs of back-up policies to address the limi-
tations of screening procedures; and effects of different policies on public confidence in security organizations.
In many fields of public policy, such tradeoffs are informed by systematic methods of decision analysis. Appendix J describes what would be involved in applying such techniques to policy decisions about polygraph screening. We were not asked to do a formal policy analysis, and we have not done so. Considering the advantages and disadvantages of quantitative benefit-cost analysis, we do not advocate its use for making policy decisions about polygraph security screening. The scientific basis for estimating many of the important parameters required for such an analysis is quite weak for supporting quantitative estimation. Moreover, there is no scientific basis for comparing on a single numerical scale some of the kinds of costs and of benefits that must be considered. Reasonable and well-informed people may disagree greatly about many important matters critical for a quantitative benefit-cost analysis (e.g., the relative importance of maintaining morale at the national laboratories compared with a small increased probability of catching a spy or saboteur or the value to be placed on the still-uncertain possibility that polygraph tests may treat different ethnic groups differently). When social consensus appears to be lacking on important value issues, as is the case with polygraph screening, science can help by making explicit the possible outcomes that people may consider important and by estimating the likelihood that these outcomes will be realized under specified conditions. With that information, participants in the decision process can discuss the relevant values and the scientific evidence and debate the tradeoffs. Given the state of knowledge about the polygraph and the value issues at stake, it seems unwise to put much trust in attempts to quantify the relevant values for society and calculate the tradeoffs among them quantitatively (see National Research Council, 1996b). However, scientific research can play an important role in evaluating the likely effects of different policy options on dimensions of value that are important to policy makers and to the country.
Other Potential Uses of Polygraph Tests
The above discussion considered the tradeoffs associated with polygraph testing in employee security screening situations in which the base rate of the target transgressions is extremely low and there is no specific transgression that can be the focus of relevant questions on a polygraph test. The tradeoffs are different in other applications, and the value of polygraph testing should be judged on the basis of an assessment of the aspects of the particular situation that are relevant to polygraph testing
choices. Because of the specific considerations involved in making decisions for each application, we have not attempted to draw conclusions about other applications. Here, we note some of the important ways in which polygraph testing situations differ and some implications for deciding whether and how to use polygraph testing.
A critically important variable is the base rate of the target transgressions or, put another way, the expected likelihood that any individual potential examinee is guilty or has the target information. We have already discussed the effects of base rate on the tradeoffs involved in making decisions from polygraph tests and the way the use of polygraph testing as an aid to decision making becomes drastically less attractive as the base rate drops below a few percent.
The costs of false positive and false negative errors are also important to consider in making policy choices. Consider, for example, the difference between screening scientists employed in the DOE laboratories and preemployment screening of similar scientists. False positives are likely to cost both government and examinee less in preemployment screening because the people who test positive have not yet been trained in the laboratories and do not yet possess critical, specialized skills and national security information. The costs of false positives also vary across different preemployment screening applications. For example, these costs are likely to be greater, for both the government and the potential employee, if the job requires extensive education, training, or past experience, because it is harder for the employer to find another suitable candidate and for the applicant to find another job. Thus, denying employment to a nuclear physicist is probably more costly both to the government and the individual than denying employment to a prospective baggage screener. When false positive errors have relatively low cost, it makes sense to use a screening test with a fairly suspicious threshold.
The costs of false negative errors rise directly with the amount of damage a spy, saboteur, or terrorist could do. Thus, they are likely to be greater in preclearance screening in relation to the sensitivity of the information to which the examinee might gain access. This observation suggests that if polygraph testing is used for such screening, more suspicious thresholds make the most sense when a false negative result is a major concern. The incentive to use countermeasures is also greater when the cost of a false negative result is greater. Thus, the possibility of effective and undetectable polygraph countermeasures is a more important consideration in very high-stakes screening situations than in other applications.
Another important factor is whether or not the situation allows for asking questions about specific events, activities, places, and so forth. Theory and limited evidence suggest that polygraph testing can be more
accurate if such questions can be asked than if they cannot. In addition, if the target answers to these questions are known only to examiners and to the individuals who are the targets of the investigation or screening, it is possible to use concealed information polygraph test formats or to use other tests that rely on orienting responses, such as those based on brain electrical activity. Thus, polygraph testing in general and concealed information tests (either with the polygraph or other technologies) are more attractive under these conditions than otherwise.
Employee security screening in the DOE laboratory is a situation that is quite unfavorable for polygraph testing in terms of all of the factors just discussed. Other potential applications should be evaluated after taking these factors into account. Polygraph testing is likely to look more attractive for some of these applications, even though in all applications it can be expected to yield a sizable proportion of errors along with the correct classifications.
In this connection, it is worth revisiting the class of situations we describe as focused screening situations. Events occurring since the terrorist attacks of September 11, 2001, suggest that such situations may get increased attention in the future. Focused screening situations differ both from event-specific investigations and from the kinds of screening used with employees in national security organizations. An illustrative example is posed by the need to screen of hundreds of detainees captured in Afghanistan in late 2001 to identify those, perhaps a sizable proportion, who were in fact part of the Al Qaeda terrorist network. Such a focused screening situation is like typical security screening in that there is no specific event being investigated, but it is different in that it may be possible to ask specific relevant questions, including questions of the concealed information variety.6 It is thus possible to use concealed information polygraph tests or other tests that require the same format and that are not appropriate for screening situations in which specific questions cannot be constructed. For example, members of Al Qaeda might be identifiable by the fact that they have information about the locations and physical features of Al Qaeda training camps that is known to interrogators but not to very many other people. Another example might be the screening of individuals who had access to anthrax in U.S. biological weapons facilities to identify those who may be concealing the fact that they have the specific knowledge needed to produce the grade of anthrax that killed several U.S. citizens in the fall of 2001. Again, even though the examiners do not know the specific target action, they can ask some focused relevant questions.
The tradeoffs in focused screening are often very different from those in other screening situations because the base rate of the target activities may lie below the 10 percent or higher typical of criminal investigations
and above the small fractions of 1 percent typical with employee security screening in national security organizations. Tradeoffs may also be different in terms of the relative costs of false positive and false negative test results and in terms of incentives to use countermeasures. A polygraph or other screening procedure that is inappropriate or inadvisable for employee security screening may be more attractive in some focused screening situations. As with other applications, the tradeoffs should be assessed and the judgment made on how and whether to use polygraph screening on the basis of the specifics of the particular situation. We believe that it will be helpful in most situations to think about the tradeoffs in terms of which sensitivities might be used for the screening test, which false positive index values can be expected with those sensitivities, and whether these possibilities include acceptable outcomes for the purpose at hand.
USING THE POLYGRAPH MORE EFFECTIVELY
One way to make the tradeoffs associated with polygraph screening more attractive would be to develop more accurate screening protocols for the use of the polygraph. This section discusses the two basic strategies for doing this: improving polygraph scoring and interpretation and combining polygraph results with other information.
Improving Scoring and Interpretation
The 11 federal agencies that use polygraph testing for employee screening purposes differ in the test formats they use, the transgressions they ask about in the polygraph examination, the ways they combine information from the polygraph examination with other security-relevant information on an examinee, and the decision rules they use to take personnel actions on the basis of the screening information available. Despite these differences, many of the agencies have put in place quality control programs, following guidance from the U.S. Department of Defense Polygraph Institute (DoDPI), that are designed to ensure that all polygraph exams given in a particular agency follow approved testing procedures and practices, as do the reading and interpretation of polygraph charts.
Quality Control
Federal agencies have established procedures aimed at standardizing polygraph test administration and achieving a high level of reliability in the scoring of charts. The quality control procedures that we have ob-
served are impressive in their detail and in the extent to which they can remove various sources of variability from polygraph testing when they are fully implemented. We have heard allegations from polygraph opponents, from scientists at the DOE laboratories, and even from polygraph experts in other agencies that official procedures are not always followed—for example, that the atmosphere of the examination is not always as prescribed in examiners’ manuals and that charts are not always interpreted as required by procedure. A review of testing practice in agency polygraph programs is beyond this committee’s scope. We emphasize two things about reliable test administration and interpretation. First, reliable test administration and interpretation are both desirable in a testing program and essential if the program is to have scientific standing. Second, however, it is critical to remember that reliability, no matter how well ensured, does not confer validity on a polygraph screening program.
Attempts to increase reliability can in some cases reduce validity. For example, having N examiners judge a chart independently, and averaging their judgments, can produce a net validity that increases when N increases, because the idiosyncratic judgments of different examiners tend to disappear in the process of averaging. Having independent judgments produces what appear to be unreliable results, i.e., the examiners disagree. If examiners see the results of previous examiners before rendering a judgment, apparent reliability would increase because the judgments would probably not differ much among examiners, but such a procedure would likely reduce the accuracy of the eventual decision. Even worse, suppose instructions given to the examiners regarding scoring are made increasingly precise, in an effort to increase reliability, but the best way to score is not known, so that these instructions cause a systematic mis-scoring. The result would increase reliability, but would also produce a systematic error that would decrease accuracy. A group of examiners not so instructed might use a variety of idiosyncratic scoring methods: each would be in error, but the errors might be in random directions, so that averaging the results across the examiners would approach the true reading. Here again there is a tradeoff between reliability and validity. These are just illustrations. We can envision examples in which increases in reliability would also increase accuracy. The important point is that one should not conclude that a test is more valid simply because it incorporates quality control procedures that increase reliability.
Computerized Scoring
In addition to establishing examiner training and quality control practices at DoDPI and other agencies, the federal government has sponsored
a number of efforts to use computing technology and statistical techniques to improve both the reliability of polygraph test interpretation and its ability to discriminate between truthful and deceptive test records. This approach holds promise for making the most of the data collected by the polygraph. Human decision makers do not always focus on the most relevant evidence and do not always combine different sources of information in the most effective fashion. In other domains, such as medical decision making (Weinstein and Fineberg, 1980) computerized decision aids have been shown to produce considerable increases in accuracy. To the extent that polygraph charts contain information correlated with deception or truth-telling, computerized analysis has the potential for increasing accuracy beyond the level available with hand scoring.
The most recent computerized scoring systems, and perhaps the ones that use the most complex statistical analyses, are being developed at the Applied Physics Laboratory at Johns Hopkins University (JHU-APL). The investigators from JHU-APL, in their publications and in oral presentations to the committee, have made claims about their methodology and its successful testing on criminal case data through cross-validation. We made extensive efforts to be briefed on the technical details of the JHU-APL methodology, but although we were supplied with the executable program for the algorithms, the documentation provided to us offered insufficient details to allow for replication and verification of the claims made about their construction and performance. JHU-APL was unresponsive to repeated requests for detail on these matters, as well as on its process for building and validating its models. On multiple occasions we were told either that the material was proprietary or that reports and testing were not complete and thus could not be shared. Appendix F documents what we have learned about (a) the existing computerized algorithms for polygraph scoring, both at JHU-APL and elsewhere, (b) the one problematic effort at external independent validation carried out by DoDPI (Dollins, Kraphol, and Dutton, 2000), and (c) our reservations and concerns about the technical aspects of the JHU-APL work and our inability to get information from APL.
From the information available, we find that efforts to use technological advances in computerized recording to develop computer-based algorithms that can improve the interpretations of trained numerical evaluators have failed to build a strong theoretical rationale for their choice of measures. They have also failed to date to provide solid evidence of the performance of their algorithms on independent data with properly determined truth for a relevant population of interest. As a result, we believe that their claimed performance is highly likely to degrade markedly when applied to a new research population and is even vulnerable to the prospect of substantial disconfirmation. In conclusion, computerized scor-
ing theoretically has the potential to improve on the validity of hand scoring systems; we do not know how large an improvement might be made in practice; and available evidence is unconvincing that computer algorithms have yet achieved that potential.
We end with a cautionary note. A polygraph examination is a process involving the examiner in a complex interaction with the instrument and the examinee. Computerized scoring algorithms to date have not addressed this aspect of polygraph testing. For example, they have treated variations in comparison questions across tests as unimportant and have not coded for the content of these questions or analyzed their possible effect on the physiological responses being measured. Also, examiners may well be picking up a variety of cues during the testing situation other than those contained in the tracings (even without awareness) and letting those cues affect the judgments about the tracings. It is, therefore, possible that the examiner’s judgments are based on information unavailable for a computerized scoring algorithm and that examiners may be more accurate for this reason. Little evidence is available from the research literature on polygraph testing concerning this possibility, but until definitive evidence is available, it might be wise to include both computerized scoring and independent hand scoring as inputs to a decision process.
Combining Polygraph Results with Other Information
In most screening applications, information from polygraph examinations (chart and interview information) is not by itself determinative of personnel actions. For example, the DOE’s polygraph examination regulation reads in part, “DOE or its contractors may not take an adverse personnel action against an individual solely on the basis of a polygraph examination result of ‘deception indicated’ or ‘no opinion’; or use a polygraph examination that reflects ‘deception indicated’ or ‘no opinion’ as a substitute for any other required investigation” (10 CFR 709.25 [a]; see Appendix B). Thus, polygraph information is often combined in some way with other information.
We have been unable to determine whether DOE or any other federal agency has a standard protocol for combining such information or even any encoded standard practice, analogous to the ways the results of different diagnostic tests are combined in medicine to arrive at a diagnosis. We made repeated requests for the DOE adjudication manual, which is supposed to encode the procedures for considering polygraph results and other information in making personnel decisions. We were initially told that the manual existed as a privileged document for official use only; after further requests, we were told that the manual is still in preparation
and is not available even for restricted access. Thus it appears that various information sources are combined an in informal way on the basis of the judgment of adjudicators and other personnel. Quality control for this phase of decision making appears to take the form of review by supervisors and of policies allowing employees to contest unfavorable personnel decisions. There are no written standards for how polygraph information should be used in personnel decisions at DOE, or, as far as we were able to determine, at any other agency. We believe that any agency that uses polygraphs as part of a screening process should, in light of the inherent fallibility of the polygraph instrument, use the polygraph results only in conjunction with other information, and only as a trigger for further testing and investigation. Our understanding of the process at DOE is that the result of additional investigations following an initial positive reading from the polygraph test almost always “clears” the examinee, except in those cases where admissions or confessions have been obtained during the course of the examination.
Incremental Validity
Policy decisions about using the polygraph must consider not only its accuracy and the tradeoffs it presents involving true positives and false positives and negatives, but also whether including the polygraph with the sources of information otherwise available improves the accuracy of detection and makes the tradeoffs more attractive. This is the issue of incremental validity discussed in Chapter 2. It makes sense to use the polygraph in security screening if it adds information relevant to detecting security risks that is not otherwise available and with acceptable tradeoffs.
Federal agencies use or could use a variety of information sources in conjunction with polygraph tests for making personnel security decisions: background investigations, ongoing security checks by various investigative techniques, interviews, psychological tests, and so forth (see Chapter 6). We have not located any scientific studies that attempt directly to measure the incremental validity of the polygraph when added to any of these information sources. That is, the existing scientific research does not compare the accuracy of prediction of criminal behavior or any other behavioral criterion of interest from other indicators with accuracy when the polygraph is added to those indicators.
Security officials in several federal agencies have told us that the polygraph is far more useful to them than background checks or other investigative techniques in revealing activities that lead to the disqualification of applicants from employment or employees from access to classified information. It is impossible to determine whether the incremental
utility of the polygraph in these cases reflects validity or only the effect of the polygraph mystique on the elicitation of admissions. If the value of the polygraph stems from the examinees’ belief in it rather than actual validity, any true admissions it elicits are obviously valuable, but that is evidence only on the utility of having a test that examinees believe in and not on the incremental validity of the polygraph.
Ways of Combining Information Sources
There are several scientifically defensible approaches to combining different sources of information that could be used as part of polygraph policies. The problem has been given attention in the extensive literature on decision making for medical diagnosis, classification, and treatment, a field that faces the problem of combining information from clinical observations, interviews, and a variety of medical tests (see the more detailed discussion in Appendix K).
Statistical methods for combining data of different types (e.g., different tests) follow one of two basic approaches. In one, called independent parallel testing, a set of tests is used and a target result on any one is used to make a determination. For example, a positive result on any test may be taken to indicate the presence of a condition of interest. In the other approach, called independent serial testing, if a particular test in the sequence is negative, the individual is concluded to be free of the condition of interest, but if the test is positive, another test is ordered. Validating a combined test of either type requires independent tests or sources of information and a test evaluation sample that is representative of the target population.7
Polygraph security screening more closely approximates the second, serial, approach to combining information: people who “pass” a screening polygraph are not normally investigated further. Serial screening and its logic are familiar from many medical settings. A low-cost test of moderate accuracy is usually used as an initial screen, with the threshold usually set to include a high proportion of the true positive cases (people with the condition) among those who test positive. Most of those who test positive will be false positives, especially if the condition has a low base rate. In this approach, people who test positive are then subject to a more accurate but more expensive or invasive second-stage test, and so on through as many stages as warranted. For example, mammograms and prostate-specific antigen (PSA) tests are among the many first screens used for detecting cancers, with biopsies as possible second-stage tests.
The low cost of polygraph testing relative to detailed security investigation makes the polygraph attractive for use early in the screening series. Detailed investigation could act as the second-stage test. According
to the security screening policies of many federal agencies, including DOE, this is how the polygraph is supposed to be used: personnel decisions are not to be made on the basis of polygraph results that indicate possible security violations without definitive confirming information.
Such a policy presents a bit of a dilemma. If the purpose of using the polygraph is like that of cancer screening—to avoid false negatives—the threshold should be set so as to catch a high proportion of spies or terrorists. The result of this approach, in a population with a low base rate of spies or terrorists, is to greatly increase the number of false positives and the accompanying expense of investigating all the positives with traditional methods. The costs of detailed investigations can be reduced by setting the threshold so that few examinees are judged to show significant response. This approach appears to be the one followed at DOD, DOE, and the FBI, judging from the low rate of total positive polygraph results reported. However, setting such a friendly threshold runs the risk of an unacceptably high number of false negative results.
A way might be found to minimize this dilemma if there were other independent tests that could be added in the sequence, either before the polygraph or between the polygraph and detailed investigation. Such tests would decrease the number of people who would have to pass the subsequent screens. If such a screen could be applied before the polygraph, its effect would be to increase the base rate of target people (spies, terrorists, or whatever) among those given the polygraph by culling out large numbers of the others. The result would be that the problem of high false positive rates in a population with a low base rate would be significantly diminished (see Figures 7-1 and 7-2, above). If such an independent screen could be applied after the polygraph, the result would be to reduce the numbers and costs of detailed investigations by eliminating more of the people who would eventually be cleared. However, there is no test available that is known to be more accurate than the polygraph and that could fill the typical role of a second-stage test in serial screening.
We have not found any scientific treatments of the relative benefits of using the polygraph either earlier or later in a series of screening tests, nor even any explicit discussion of this issue. We have also not found any consideration or investigation of the idea of using other tests in sequence with the polygraph in the manner described above. The costs and benefits of using the polygraph at different positions in a sequence of screening tests needs careful attention in devising any policy that uses the polygraph systematically as a source of information in a serial testing model for security screening.
Some people have suggested that polygraph data could be analyzed and combined with other data by nonstatistical methods that rely on expert systems. There is disagreement on how successful such systems
have been in practice in other areas, but the most “successful” expert systems for medical diagnosis require a substantial body of theory or empirical knowledge that link clearly identified measurable features with the condition being diagnosed (see Appendix F). For screening uses of the polygraph, it seems clear that no such body of knowledge exists. Lacking such knowledge, the serious problems that exist in deriving and adequately validating procedures for computer scoring of polygraph tests (discussed above) also exist for the derivation and validation of expert systems for combining polygraph results with other diagnostic information.
Insufficient scientific information exists to support recommendations on whether or how to combine polygraph and other information in a sequential screening model. A number of psychophysiological techniques appear promising in the long run but have not yet demonstrated their validity. Some indicators based on demeanor and direct investigation appear to have a degree of accuracy, but whether they add information to what the polygraph can provide is unknown (see Chapter 6).
LEGAL CONTEXT
The practical use of polygraph testing is shaped in part by its legal status. Polygraph testing has long been the subject of judicial attention, much more so than most forensic technologies. In contrast, courts have only recently begun to look at the data, or lack thereof, for other forensic technologies, such as fingerprinting, handwriting identification and bite marks, which have long been admitted in court. The attention paid to polygraphs has generally led to a skeptical view of them by the judiciary, a view not generally shared by most executive branch agencies. Judicial skepticism results both from questions about the validity of the technology and doubt about its need in a constitutional process that makes juries or judges the finders of fact. Doubts about polygraph tests also arise from the fact that the test itself contains a substantial interrogation component. Courts recognize the usefulness of interrogation strategies, but hesitate when the results of an interrogation are presented as evidentiary proof. Although polygraphs clearly have utility in some settings, courts have been unwilling to conclude that utility denotes validity. The value of the test for law enforcement and employee screening is an amalgam of utility and validity, and the two are not easily separated.
An early form of the polygraph served as the subject of the wellknown standard used for evaluating scientific evidence—general acceptance—announced in Frye v. United States (1923) and still used in some courts (see below). It has been the subject of a U.S. Supreme Court decision, United States v. Scheffer (1998), and countless state and federal deci-
sions (see Appendix E for details on the Frye case). In Scheffer, the Court held that the military’s per se rule excluding polygraphs was not unreasonable—and thus not unconstitutional—because there was substantial dispute among scientists concerning the test’s validity.
Polygraphs fit the pattern of many forensic scientific fields, being of concern to the courts, government agencies and law enforcement, but largely ignored by the scientific community. A recent decision found the same to be true for fingerprinting (United States v. Plaza, 2002). In Plaza, the district court initially excluded expert opinion regarding whether a latent fingerprint matched the defendant’s print because the applied technology of the science had yet to be adequately tested and was almost exclusively reviewed and accepted by a narrow group of technicians who practiced the art professionally. Although the district court subsequently vacated this decision and admitted the evidence, the judge repeated his initial finding that fingerprinting had not been tested and was only generally accepted within a discrete and insular group of professionals. The court, in fact, likened fingerprint identification to accounting and believed it succeeded as a “specialty” even though it failed as a “science.”8 Courts have increasingly noticed that many forensic technologies have little or no substantial research behind them (see e.g., United States v. Hines [1999] on handwriting analysis and the more general discussion in Faigman et al. [2002]). The lack of data on regularly used scientific evidence appears to be a systemic problem and, at least partly, a product of the historical divide between law and science.
Federal courts only recently began inquiring directly into the validity or reliability of proffered scientific evidence. Until 1993, the prevailing standard of admissibility was the general acceptance test first articulated in Frye v. United States in 1923. Using that test, courts queried whether the basis for proffered expert opinion is generally accepted in the particular field from which it comes. In Daubert v. Merrell Dow Pharmaceuticals, Inc. (1993), however, the U.S. Supreme Court held that Frye does not apply in federal courts. Under the Daubert test, judges must determine whether the basis for proffered expertise is, more likely than not, valid. The basic difference between Frye and Daubert is one of perspective: courts using Frye are deferential to the particular fields generating the expertise, whereas Daubert places the burden on the courts to evaluate the scientific validity of the expert opinion. This difference of perspective has begun to significantly change the reception of the scientific approach in the court-room.9
Much of the expert opinion that has been presented as “scientific” in courts is not based on what scientists recognize as solid scientific evidence, or even, in some cases, rudimentary scientific methods and prin-
ciples. The polygraph is not unusual in this regard. In fact, topics such as bite mark and hair identification, fingerprinting, arson investigation, and tool mark analysis have a less extensive record of research on accuracy than does polygraph testing. Historically, the courts relied on experts in sundry fields in which the basis for the expert opinion is primarily assertion rather than scientific testing and in which the value of the expertise is measured by effectiveness in court rather than scientific demonstration of accuracy or validity.
These observations raise several issues worthy of consideration. First, if the polygraph compares well with other forensic sciences, should it not receive due recognition for its relative success? Second, most forensic sciences are used solely in judicial contexts, while the polygraph is also used in employment screening: Do the different contexts in which the technique is used affect the determination of its usefulness? And third, since mainstream scientists have largely ignored forensic science, how could this situation be changed? We consider these matters in turn.
Polygraph Testing as a Forensic Science
Without question, DNA profiling provides the model of cooperation between science and the law. The technology was founded on basic science, and much of the early debate engaged a number of leading figures in the scientific community. Rapidly improving technology and expanded laboratory attention led to improvements in the quality of the data and the strengths of the inferences that could be drawn. Even then, however, there were controversies regarding the statistical inferences (National Research Council, 1992, 1996a). Nonetheless, from the start, judges understood the need to learn the basic science behind the technology and, albeit with certain exceptions, largely mastered both the biology and the statistics underlying the evidence.
At the same time, DNA profiling might be somewhat misleading as a model for the admissibility of scientific evidence. Although some of the forensic sciences, such as fingerprinting (see Cole, 2001), started as science, most have existed for many decades outside mainstream science. In fact, many forensic sciences had their start well outside the scientific mainstream. Moreover, although essentially probabilistic, DNA profiling today produces almost certain conclusions—if a sufficient set of DNA characteristics is measured, the resulting DNA profiles can be expected to be unique, with a probability of error of one in billions or less (except for identical twins) (National Research Council, 1996a). This near certainty of DNA evidence may encourage some lawmakers’ naive view that science, if only it is good enough, will produce certain answers. (In fact, the one
area in which DNA profiling is least certain, laboratory error, is the area in which courts have had the most difficulty in deciding how to handle the uncertainty.)
The accuracy of polygraph testing does not come anywhere near what DNA analysis can achieve. Nevertheless, polygraph researchers have produced considerable data concerning polygraph validity (see Chapters 4 and 5). However, most of this research is laboratory research, so that the generalizability of the research to field settings remains uncertain. The field studies that have been carried out also have serious limitations (see Chapter 4). Moreover, there is virtually no standardization of protocols; the polygraph tests conducted in the field depend greatly on the presumed skill of individual examiners. Thus, even if laboratory-based estimates of criterion validity are accurate, the implications for any particular field polygraph test are uncertain. Without the further development of standardized polygraph testing techniques, the gulf between laboratory validity studies and inferences about field polygraph tests will remain wide.
The ambiguity surrounding the validity of field polygraphs is complicated still further by the structure of polygraph testing. Because in practice the polygraph is used as a combination of lie detector and interrogation prop, the examiner typically is privy to information regarding the examinee. While this knowledge is invaluable for questioning, it also might lead to examiner expectancies that could affect the dynamic of the polygraph testing situation or the interpretation of the test’s outcome. Thus, high validity for laboratory testing might again not be indicative of the validity of polygraphs given in the field.
Context of Polygraph Testing
The usefulness of polygraph test results depends on the context of the test and the consequences that follow its use. Validity is not something that courts can assess in a vacuum. The wisdom of applying any science depends on both the test itself and the application contemplated. A forensic tool’s usefulness depends on the specific nature of the test (i.e., in what situation might it apply?), the import or relevance of the test (i.e., what inferences follow from “failing” or “passing” the test?), the consequences that follow the test’s administration (e.g., denial of employment, discharge, criminal prosecution), and the objective of the test (lie detection or interrogation).
A principal consideration in the applied sciences concerns the content of a test: what it does, or can be designed to, test. Concealed information polygraph tests, for example, have limited usefulness as a screening device simply because examiners usually cannot create specific questions
about unknown transgressions. (There may be exceptions, as in some focused screening applications, as discussed above.) The application of any forensic test, therefore, is limited by the test’s design and function. Similarly, the import of the test itself must be considered. For instance, in the judicial context, the concealed information test format might present less concern than the comparison question format, even if they have comparable accuracy. The concealed information test inquires about knowledge that is presumed to be possessed by the perpetrator; however, a “failed” test might only indicate that the subject lied about having been at the scene of the crime, not necessarily that he or she committed the crime. Like a fingerprint found on the murder weapon, knowledge of the scene and, possibly, the circumstances of the crime, is at least one inferential step away from the conclusion that the subject committed the crime. There may be an innocent explanation for the subject’s knowledge, just as there might be for the unfortunately deposited fingerprint.
In contrast, the comparison question test requires no intervening inferences if the examiner’s opinion is accepted about whether the examinee was deceptive when asked about the pivotal issue. With this test, such an expert opinion would go directly to the credibility of the examinee and thus his or her culpability for the event in question. This possibility raises still another concern for courts, the possibility that the expert will invade the province of the fact finder. As a general rule, courts do not permit witnesses, expert or otherwise, to comment on the credibility of another person’s testimony (Mueller and Kirkpatrick, 1995). This is the jury’s (and sometimes the judge’s) job. As a practical matter, however, witnesses, and especially experts, regularly comment on the probable veracity of other witnesses, though almost never directly. The line between saying that a witness cannot be believed and that what the witness has said is not believable, is not a bright line. Courts, in practice, regularly permit experts to tread on credibility matters, especially psychological experts in such areas as repressed memories, post-traumatic stress disorder, and syndromes ranging from the battered woman syndrome to rape trauma syndrome.
The legal meaning of a comparison question test polygraph report might be different if the expert opinion is presented in terms of whether the examinee showed “significant response” to relevant questions, rather than in terms of whether the responses “indicated deception.” Significant response is an inferential step away from any conclusion about credibility, in the sense that it is possible to offer innocent explanations of “significant response,” based on various psychological and physiological phenomena that might lead to a false positive test result.
When courts assess the value of forensic tools, the consequences that follow a “positive” or “negative” outcome on the test are important. Al-
though scientific research can offer information regarding the error rates associated with the application of a test, it does not provide information on what amount of error is too much. This issue is a policy consideration that must be made on the basis of understanding the science well enough to appreciate the quantity of error, and judgment about the qualitative consequences of errors (the above discussion of errors and tradeoffs is thus relevant to considerations likely to face a court operating under the Daubert rule).
Finally, evaluating the usefulness of a forensic tool requires a clear statement of the purpose behind the test’s use. With most forensic science procedures, the criterion is clear. The value of fingerprinting, handwriting identification, firearms identification, and bite marks is closely associated with their ability to accomplish the task of identification. This is a relatively straightforward assessment. Polygraph tests, however, have been advocated variously as lie detectors and as aids for interrogation. They might indeed be effective for one or the other, or even both. However, these hypotheses have to be separated for purposes of study. For purposes of science policy, policy makers should be clear about for which use they are approving—or disapproving—polygraphs.
Courts have been decidedly more ambivalent toward polygraphs than the other branches of government. Courts do not need lie detectors, since juries already serve this function, a role that is constitutionally mandated. Policymakers in the executive and legislative branches, in contrast, do perceive a need for lie detection and may not care about whether the polygraph’s contribution is due to its scientific validity or to its value for interrogation.
Mainstream Science and Forensic Science
Many policy makers, lawyers, and judges have little training in science. Moreover, science is not a significant part of the law school curriculum and is not included on state bar exams. Criminal law classes, for the most part, do not cover forensic science or psychological syndromes, and torts classes do not discuss toxicology or epidemiology in analyzing toxic tort cases or product liability. Most law schools do not offer, much less require, basic classes on statistics or research methodology. In this respect, the law school curriculum has changed little in a century or more.
The general acceptance test of admissibility enunciated in the Frye decision expects little scientific sophistication of lawyers or judges. Courts, and presumably juries as well, have thus evaluated expertise based on consensus. The problem with this test has come in fields that purport to be rigorous but may not be. For instance, if the question is the validity of bite mark identification analysis, researchers who study the
various factors that challenge this expertise (e.g., uniqueness of the mark, the identification of the mark in different substances, proficiency testing, etc.) would probably give the courts a solid scientific evaluation of the value of this kind of evidence. However, if the courts only consider the expert opinions of forensic odontologists who do bite mark identifications for police laboratories, they are unlikely to get a full view of the value of this kind of evidence. Unfortunately, in many fields of forensic science there are no communities of scientists conducting basic research and the only people who are asked as expert witnesses are interested practitioners with little proficiency in scientific methods.
Good forensic science can have salutary results and, in some cases, profound consequences. DNA profiling is a particularly salient example of how good science can be used for both good law enforcement and in the interests of the falsely accused. Lawyers, under the influence of Daubert, are beginning to open their eyes and ears to empirical criticisms of fields long thought settled. In the area of lie detection, good forensic research could directly contribute to national security.
Forensic science has not kept up with the state of science more generally for two basic reasons: the legal community’s basic ignorance of science and statistics, and the lack of interest among research scientists in the practical (and especially forensic) applications of science. In lie detection, for instance, policy makers have not demanded better work, and few scientists have been interested in pursuing the subject. This powerful combination of ignorance and apathy has, in general, deprived policy makers of good scientific data. More particularly, it has led to convictions of the innocent (see Scheck, Neufeld, and Dwyer, 2000), acquittals for the guilty, and numerous costs to individuals, ranging from job loss to social ostracism.
Another institutional reality bears mentioning. The law very often asks empirical questions to which there are no scientific answers. Moreover, while science can take any amount of time to pursue a question and develop an answer, the law has to render a decision in a short time frame. A particularly good example of this is clinical prediction of violence. A large number of legal contexts call for predictions of future violence. These include capital sentencing, parole and pardon hearings, ordinary civil commitment, sexual predator commitments, and community notification laws. Courts and legislatures have been undeterred by the fact that psychologists and psychiatrists readily admit that science cannot provide such predictions—though the state of the art is improving. For policy makers, the inability to accomplish some task scientifically does not always mean that it cannot be done legally. In Schall v. Martin (1984), for instance, the Supreme Court upheld the pretrial detention of juveniles on a finding that there is a “serious risk” that if released the juvenile would
commit a crime before his next court appearance. Responding to the argument that such predictions could not be made reliably, the Court said that “our cases indicate, however, that from a legal point of view there is nothing inherently unattainable about a prediction of future criminal conduct” (at 278).
CONCLUSIONS
Decisions about whether or how to use polygraph tests in particular applications must consider these tests’ capabilities and limitations, as well as the tradeoffs posed by any imperfect diagnostic procedure.
Tradeoffs in Interpretation
The tradeoffs of false positives and false negatives are strikingly different in event-specific and screening applications, primarily because of the great difference in the base rate of guilt in the two settings. Even those who believe the polygraph “works” adequately in a criminal investigation should not presume without further careful analysis that this justifies its use for security screening.
Given the very low base rates of major security violations, such as espionage, that almost certainly exist in settings such as the national weapons laboratories, as well as the scientifically plausible accuracy level of polygraph testing, polygraph screening is likely to identify at least hundreds of innocent employees as guilty for each spy or other major security threat correctly identified. The innocent will be indistinguishable from the guilty by polygraph alone. Consequently, policy makers face this choice: either the decision threshold must be set at such a level that there will be a low probability of catching a spy (thereby reducing the number of innocent examinees falsely identified), or investigative resources will have to be expended to investigate hundreds of cases in order to find whether there is indeed one guilty individual (or more) in a pool of many individuals who have positive polygraph results. Although there are reasons of utility that might be put forward to justify an agency’s use of a polygraph screening policy that produces a very low rate of positive results, such a policy will not identify most of the major security violators. In our judgment, the accuracy of polygraph testing for distinguishing actual or potential security violators from innocent test takers is insufficient to justify reliance on its use in employee security screening in federal agencies.
Although formal benefit-cost analysis might in principle be used to help decision makers evaluate the difficult tradeoffs posed by the use of the polygraph for security screening, in actuality the scientific basis for
estimating many of the important parameters required for a benefit-cost analysis is too weak to support quantitative estimates. Moreover, no scientific basis exists for comparing on a single numerical scale many of the qualitatively different kinds of costs and of benefits that must be considered.
The tradeoffs presented by polygraph testing vary with the application. For example, some focused screening applications may present more favorable tradeoffs for polygraph use than those involved in employee security screening in the DOE laboratories.
Increasing Polygraph Effectiveness
The quality control program organized by DoDPI and implemented by DOE in its screening activities is impressive in its rigor and the extent to which it has removed various sources of examiner and other variability. Highly reliable polygraph scoring and interpretation, such as these programs aim to provide, are essential if polygraph screening is to have scientific standing. Reliability, however, is insufficient to establish the validity of the polygraph for screening purposes. The effects of DoDPI efforts to increase reliability on the validity of polygraph screening are untested and unknown.
The primary advances in polygraph technology since the 1983 Office of Technology Assessment report have come in the computerization of physiological responses and their display. Computerized polygraph scoring procedures have the potential in theory to increase the accuracy of polygraph testing because they improve the ability to extract and appropriately combine information from features of psychophysiological responses, both obvious and subtle, that may have differing diagnostic values. However, existing computerized polygraph scoring methods have a purely empirical base and are not backed by validated theory that would justify use of particular measures or features of the polygraph data. Such theory simply does not yet exist. Moreover, existing computerized polygraph scoring methods have not been tested on a sufficient number and variety of examinees after development to generate confidence that their validity is any greater than that of traditional scoring methods.
Although in theory, combining the results of polygraph tests with information from other sources is possible—for example, in serial screening protocols—such approaches have not been seriously investigated. Similarily, evidence on the incremental validity of the polygraph, that is, its ability to add predictive value to what can be achieved by other methods, has not been gathered. Moreover, the difficulties that exist with computerized scoring of polygraph tests also exist, and may be multi-
plied, with possible expert systems for combining polygraph results with other data.
Polygraphs in Legal Contexts
Courts following the Daubert rule on admissibility of scientific evidence are likely to look increasingly to scientific validation studies in judging the uses of polygraph data in court. The existing validation studies have serious limitations. Laboratory test findings on polygraph validity are not a good guide to accuracy in field settings. They are likely to overestimate accuracy in field practice, but by an unknown amount. The available field studies are also likely to overestimate the accuracy achieved in actual practice. Assessments of the polygraph for the purposes of forensic science should take into account the test’s design, function, and purpose because both the accuracy of the test and the practical meaning of particular accuracy levels are likely to depend on these factors.
NOTES
|
1. |
This is the model we used to extrapolate A from reports that provided single sensitivity-specificity combinations (see Appendix H). |
|
2. |
If A = 0.80, the false positive index is greater than 100 for any base rate below 1 in 250, and if A = 0.70, it is greater than 100 for any base rate below about 1 in 160. If the actual base rate is equal to or less than 1 in 1,000, the false positive index is at least 208 if the test has A = 0.90; at least 452 if A = 0.80; at least 634 if A = 0.70, and at least 741 if A = 0.60. Thus, if there are 10 serious security violators among 10,000 employees who are polygraphed and the criterion is set to correctly identify 8 of the 10, the test could be expected to erroneously classify as deceptive at least 1,664, 3,616, 5,072, or 5,928 of the 9,990 nonviolators, depending on which of the accuracy indexes applied to the test. |
|
3. |
Other assumptions about the accuracy and sensitivity of polygraph testing procedures yield similarly dramatic differences between the predictive values of positive test results in screening versus event-specific investigation contexts. |
|
4. |
A polygraph screening policy that produces 3 percent positive results, of which virtually all are false positives, will have a sensitivity of 48 percent (that is, it will correctly identify 48 percent of major violators) if the test procedure’s actual accuracy index (A) is 0.90; 25 percent if its accuracy index is 0.80; or 14 percent if its accuracy index is 0.70. |
|
5. |
A polygraph screening policy that produces 1 percent positive results, of which virtually all are false positives, will have a sensitivity of 30 percent (identify 30 percent of the major violators) if the test procedure’s actual accuracy index (A) is 0.90; 13 percent if its accuracy index is 0.80; and 7 percent if its accuracy index is 0.70. |
|
6. |
Polygraph testing of suspected Al Qaeda members is different from security screening of federal employees in other ways that should be recognized explicitly. Problems of language translation and of possible cultural differences in the meanings of deception and truthfulness are likely to create uncertainty in the meaning of polygraph charts and raise questions about whether these tests can be as accurate as similar tests conducted on English-speaking Americans. |
|
7. |
We note that this criterion was rarely met in the simulation studies that have been used to assess polygraph validity for screening to date. |
|
8. |
See United States v. Plaza, 188 F. Supp.2d 549, 2000 WL 389163 [E.D.Pa. March 13, 2002] vacating United States v. Plaza, 179 F. Supp.2d 492, 2002 WL 27305 [E.D.Pa Jan. 7, 2002]. |
|
9. |
The implications of Daubert for polygraph evidence are not straightforward. Some courts have interpreted Daubert to undermine the per se rule excluding polygraph evidence (e.g., United States v. Posado, 57 F.3d 428, 429 [5th Cir. 1995]), and some federal district courts have admitted polygraph evidence. It is reasonable to expect continued argument in the courts over whether or not the scientific evidence on polygraph testing justifies the use of test results as evidence. |


































