Appendix K
Combining Information Sources in Medical Diagnosis and Security Screening
In medical diagnosis, a physician uses a patient’s medical history, the clinical interview, reported symptoms, and physician-observed clinical signs to decide what tests to undertake. Subsequently, the physician combines test results with the other information sources in arriving at a diagnosis. In terms of the use of information, the problem is similar enough to that of security screening that much of the extensive literature on medical diagnosis may be consulted for insights relevant to security screening.
In making judgments about whether an examinee is a security risk or has committed security violations, government security officials might take into account polygraph charts and at least five other types of information:
-
Biographical data on the examinee, such as might be gathered by a background check, including any specific incriminating information when a particular crime (e.g., act of espionage) is in question.
-
Contextual information that might affect the dynamics between the examinee and examiner or otherwise affect the interpretation of the charts. This information might include the examinee’s race, sex, educational level, and native language and the social status of both examiner and examinee.
-
The examiner’s observations during the examination on the subject’s demeanor: affect, body language, voice patterns, facial expressions, etc.
-
Follow-up information, including additional polygraph examinations to elucidate problem areas in the initial examination.
-
Other objective measures that might supplement or replace the polygraph: examples include voice stress measurements, infrared measures of skin temperature, and various direct measures of brain activity (see Chapter 6).
This appendix provides an overview of approaches used for combining information with statistical or other formal objective numerical algorithms, largely with reference to the medical diagnosis literature. These approaches, increasingly though inconsistently applied in clinical medical practice, contrast greatly with what we have seen in government security screening programs, in which polygraph and other information are combined essentially by clinical judgment, which can be considered as an informal, practitioner-specific algorithm incorporating hunches and rules of thumb. There are two major classes of formal methods for combining information, statistical classification approaches and expert systems (computer-aided diagnosis); we discuss each in turn.
STATISTICAL CLASSIFICATION
Statistical classification systems assume, at least implicitly, an underlying probability model relating the diagnostic groups (class labels) and the classifying information. These methods start with a training set or design sample, consisting of cases with known diagnoses and a dataset containing values for a vector, x, of q potential classifier variables or features. For example, if one summarized the information in a polygraph test by overall scores for each of the four channels, there would be only four (q) classifiers. One expects the distributions of these variables to be different for deceptive and nondeceptive individuals. If f(x|i) is the joint probability function of the classifying variables for diagnostic group i, one can mentally visualize these q classifying variables as “inhabiting” a geometric space of q dimensions. The goal of statistical classification methods is to divide this space into regions, one for each diagnostic group, so that the rule which classifies all individuals whose vectors fall into region k as belonging to group k has good properties.
One widely used criterion is minimization of overall risk. This is defined as the expected total cost of all classification errors. Technically, this is the sum of costs cij associated with misclassifying a person of class i into class j, summed over j, then weighted by the class i prevalences (probability of occurrence), denoted by pi and summed over i. Thus, .
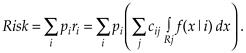
Forming the regions, Rj, to minimize the overall risk is the Bayes classification rule.
When misclassification costs, prevalences, and group-specific distributions are known, one can find this rule in a straightforward fashion. For two diagnostic groups, we chose the region R1 to consist of all those points
f(x|1)/f(x|2) > p2c12/p1c21,
with R2 making up the rest of the space. In Bayesian statistical terminology, region j consists of points with a relatively large posterior probability of membership in group j. This basic idea holds for any number of groups (for details, see Hand, 1998).
Unfortunately, the misclassification costs, prevalences, and group-specific probability distributions are rarely known. The distributions can be estimated from a training sample, consisting of representative (ideally, random and large) samples from each of the diagnostic groups with each individual measured on (ideally) all variables thought to be potentially useful classifiers. The group prevalences and misclassification costs are typically estimated from other sources of information.
It is tempting to simply plug these estimates into the Bayes classification formula, but this approach is fraught with pitfalls. First, it can at best be an approximation to a proper Bayesian solution, and the only way to assess its quality is to perform a full statistical assessment of the unknown, estimated components of the formula. For this reason, the Kircher and Raskin approach to computerized scoring (see Appendix F) is not really a Bayesian approach.
Second, estimating the components is not easy. Estimating the costs often requires an in-depth policy analysis. Estimating the joint distributions can be unreliable, especially when the number of classifiers is large.
One can get a sense of at least one of the pitfalls by addressing the specification of joint probability function f(x|i). Suppose each of the p variables can take any one of L possible values. Then each joint probability function f(x|i) will assign a probability to each of Lp cells. This requires a sample size much larger than Lp. This exponential growth in the problem size as the number of variables increases is often dramatically termed the “curse of dimensionality.” Thus, one really needs to use some type of statistical model to estimate the probability distribution. Methods differ in how they deal with this exponential growth problem, typically
by imposing restrictions on the numbers of variables, on the probability distributions assumed, or on the shapes and configurations of the regions. There are six main approaches: (1) linear or quadratic discrimination; (2) logistic regression; (3) nearest neighbor and kernel methods; (4) recursive partitioning (e.g., classification and regression trees, CART); (5) Bayes independence models; (6) artificial neural networks. The first two approaches are discussed in Appendix F. Hastie, Tibshirani, and Friedman (2001) and Hand (1992, 1998) give useful overviews. All these methods have proponents and critics and are supported by examples of excellent performance in which they equaled or surpassed that of experienced clinicians in a reasonably narrowly defined domain of disease or treatment. These methods have been applied in many areas, not just to problems of medical classification.
Two simple special cases of the logistic regression method reduce to simple calculations and do not require the technical details of logistic regression to describe. We describe these here because they exemplify some common aspects of methods for combining information and are often considered to provide useful guidance in medical diagnostic analyses. They also have relevance for polygraph screening.
Independent Parallel Testing
Independent parallel testing assumes that a fixed collection of diagnostically informative dichotomous variables is obtained for each subject. The disease or other feature that is the target of detection is inferred to be present if any of the individual tests is positive. Consequently, the parallel combination test is negative only when all of its component tests are negative. In personnel security screening, one might consider the polygraph test, the background investigation for clearance, and various psychological tests administered periodically as the components of a parallel test: security risk is judged to be absent only if all the screens are negative for indications of security risk.
Under the assumed independence among tests, the specificity (1 – false positive rate) of the parallel combination test is the product of the specificities of the individual component tests. Since the component specificities are below 1, the combined or joint specificity must be lower than that of any components. Similarly, the false negative rate of the parallel combination test is the product of the false negative rates of the individual component tests, hence, also lower than that of any component. Consequently, the sensitivity of the parallel combination test is higher than the sensitivity of any component test, and the parallel combination yields a test of higher sensitivity but lower specificity than any component.
As shown in Chapter 2, a similar tradeoff of specificity for sensitivity can be obtained with a single test based on a continuous measurement by changing the cutoff or threshold used for classification on the basis of the test result and thus moving to the right on the receiver operating characteristic (ROC) curve for that test. The virtue of the parallel combination is that it brings more information to bear on the problem. Hence, if one begins with component tests of fixed cutoff points and generates the parallel combination test from them, the result will have a greater sensitivity and lower specificity than any of the component tests using the same cutoff point. In general, sensitivity is the test characteristic that most strongly drives negative predictive value, which in turn governs the ability to rule out a diagnosis. Hence, negative parallel tests are often used in medical care for the explicit purpose of excluding a disease diagnosis.
If the component tests each have some discriminating power, the parallel test will often also have a greater sensitivity than any component test calibrated to the specificity achieved by the combination. The gain in accuracy, however, is limited by the degree to which each new test in the parallel combination is correlated with the feature one is trying to detect. Any dependence between tests would reduce the amount of new information available, and consequently, diminish the potential gain. With many tests, it is unlikely that the best discriminating function will be obtained by requiring that a person is classified negative only if all tests are negative—better decision rules will come from the various classification methods listed above.
The independent parallel testing argument suggests that polygraph testing might be useful in the security screening context even if it were not sufficiently valid by itself to be useful. A negative polygraph examination combined with other negative data might increase the certainty of a decision to grant or continue access to sensitive information. The degree to which the polygraph improved the decision-making process in such a context, however, would depend on whether polygraph test results can appropriately be treated as statistically independent of other screening modalities, as well as on the discriminating power of the polygraph. The false positive rate of the parallel combination will exceed that of any component, so the polygraph cutoff in a parallel investigation might have to be set accommodate this (that is, to increase the range of scores considered as indicating truthfulness) with a corresponding sacrifice in sensitivity.
Independent Serial Testing
In independent serial testing a sequence of tests is specified, with each test used only if its predecessors in the sequence have all been positive. Serial tests are the general rule in medical practice, especially if one
considers nonlaboratory components of medical diagnosis as informal tests within an information collection sequence. By comparison with parallel tests, serial tests are cost-effective because the most powerful and expensive tests are not performed on many examinees. A serial test usually begins with relatively inexpensive and noninvasive measures and proceeds to more expensive and more invasive procedures as the accumulation of information makes the presence of the feature of interest increasingly likely. One can imagine a polygraph test as the first step in a personal security screening sequence, with more expensive background checks, detailed interrogations, and possibly levels of surveillance as later stages in the process. Indeed, at least one agency uses serial polygraph testing, where positive results of one type of test lead to a second test of somewhat different nature, and so on.
The accuracy of serial combination testing is much like that for parallel combination testing but with the roles of sensitivity and specificity— and, hence, of false positive and false negative rates—reversed. The feature of interest is not diagnosed unless all tests are positive, so the sensitivity of the serial combination is the product of the sensitivities of the component tests, and the false positive rate of the serial combination is the product of the false positive rates of the individual component tests. Thus, serial testing yields a combination with lower sensitivity but higher specificity than its components. In general, specificity drives the false positive index, and so positive serial tests are often used in medical care to arrive at a firm basis for taking action. As with parallel testing, the potential gain in accuracy of serial testing is limited by the accuracy and extent of dependence of each additional test added to the sequence. In contrast with parallel testing, however, each rearrangement of the ordering of a given set of tests yields a new serial test with different properties from other orderings of the component tests.
For personnel security screening, the relative inexpensiveness of polygraph makes it attractive as an early step in a serial screening process. But this requires other suitable tests with known degrees of accuracy for follow-up. Moreover, if one wanted to avoid large numbers of false positives and the associated costs of following them up, polygraph testing would have to be used at a high specificity, incurring the risk of early termination of the screening sequence for some serious security risks.
EXPERT SYSTEMS
In contrast to the above approaches, nonstatistical expert systems typically codify and represent existing knowledge using collections of rules, for instance, of the form “if-then-else,” with deterministic or subjective probabilistic outcomes and heuristic “inference engines” for operat-
ing on these rules (see Buchanan and Shortliffe [1984] for an early example, and the overview in Laskey and Levitt [2001]). Examples can be found in psychiatric diagnosis from coded interview schedules, e.g., DMS III/DIS (Maurer et al., 1989) and PSE/CATEGO (Wing et al., 1974). There is evidence that combining rule-based systems and statistical classification in particular neural networks may help the dimensionality problem (Vlachonikolis et al., 2000). A general feature of rule-based systems, however, is that they require a substantial body of theory or empirical knowledge involving clearly identified features with reasonably straightforward logical or empirical relationships to the definition or determination of the outcome of interest. For screening uses of the polygraph, it seems clear that no such body of knowledge exists. This may severely limit the practical application of expert systems in this context.
Both statistical and expert system methods could in principle be implemented in the polygraph context. Indeed, some of these ideas are being explored in the context of computerized scoring of polygraph charts (Olsen et al., 1997). However, it is not clear that this can be fruitful. If the polygraph examination is low in accuracy, combining it with other information will not be helpful.
There are additional important caveats involving the manner of incorporating contextual variables and the adequacy of training samples in terms of size and representativeness. Regarding context, only recently are medical research and practice recognizing the importance of the social interaction between patient and physician in treatment. The contextual variables described above have thus far played little role in medical classification and computer-aided diagnosis. For any individual medical problem, it may be unclear how best to incorporate them into models. They may act as additional predictors or confounders as effect modifiers that change the relationships of selected other predictors to the target classification, or even as stratification variables that define separate groups in which potentially quite different prediction models may be necessary. Neither are such choices clear in the polygraph context. It is possible that having two distributions of variables, one for deceptive individuals and one for nondeceptive ones, is overly simple. A plausible example is the possibility that the distribution of blood pressure readings obtained during the polygraph examination may differ dramatically for African American and white examinees (evidence making this hypothesis plausible is reported by Blascovich et al., 2001).
We have noted above that the statistical pattern recognition approaches require the training sample to be representative of the target population. In many respects, one needs to question whether training samples based on samples of a community, college students, or basic trainees in the military are at all representative for target populations to
be screened for espionage, terrorism, or sabotage at government weapons laboratories and other high-security installations. Ideally, a representative sample would include subpopulations of spies, terrorists, and saboteurs that might be screened, as well as truthful scientists, engineers, and technicians. And in the latter group, one would also want individuals who have committed minor security violations and are deceptive in their responses in that regard. Furthermore, as a consequence of the “curse of dimensionality,” these techniques tend to require large samples. Medical classification studies typically involve at least several hundred in each diagnostic group. In contrast, in the standard polygraph field study the problem of objectively ascertaining truth means that it is difficult and unusual to obtain that many verified deception cases. In this circumstance, it is likely that uses of pattern recognition methods will have to be restricted to small numbers of variables.
Finally, realistic assessments of the performance of classification rules must be available. If the data used to develop the rule are also used to assess its performance, the result will typically suggest better—perhaps much better—performance than is likely to be found when the rule is applied to future data. This problem will exist whether misclassification rate, sensitivity and specificity, any other summary numbers or, when applicable, the entire ROC curve, are used. The expected discrepancy is inversely related to the number of individuals in the development dataset relative to the number of candidate variables and is negligible only when the sample size is at least an order of magnitude higher than the number of candidate variables. Thus, pattern recognition approaches that analyze dozens or hundreds of variables will significantly overestimate their true validity unless they are developed on training samples with hundreds or thousands.
Many methods for using the original data to give a more realistic assessment of future performance have been proposed. The most important are variants of cross-validation or what is sometimes referred to as the “leave-one-out” or “round-robin” approach. In the statistics literature, these methods go back to the 1940s and are now commonly linked to the jackknife and bootstrap techniques (Davison and Hinkley, 1997). In the simplest of the cross-validation approaches, each individual is omitted sequentially, classified using the rule developed on the basis of all the other individuals’ data, and then applying the classification rule to the omitted case. But individuals can also be omitted in groups, with the other groups used for cross-validation. For cross-validation to give an honest estimate of the predictive value of the classification rule, one needs to incorporate the entire rule-building process, including any variable selection procedures, but this caveat is unfortunately too often ignored in practice.
Of course, the gold standard is assessment of performance on a genuinely new and independent data set. A recent editorial in the journal Medical Decision Making (Griffith, 2000:244) makes this point:
The general problem is how to make probability-based clinical decision aids not only accurate on a specific dataset but also effective in general practice. Automated computational algorithms for estimation and decision making need to be held to the same standards that would be expected from a clinical research study. Thus, these prediction models must demonstrate high accuracy on independent datasets large enough to capture the inherent variability between patients at risk for a given medical outcome.
Appendix G addresses more explicitly the importance of this warning in the context of statistical approaches to computerized polygraph scoring.
REFERENCES
Blascovich, J., S.J. Spencer, D. Quinn, et al. 2001 African Americans and high blood pressure: The role of stereotype threat. Psychological Science 12(3):225-229.
Buchanan, B., and E. Shortliffe 1984 Rule-based Expert Programs: The MYCIN Experiments of the Stanford Heuristic Programming Project. Reading, MA: Addison Wesley.
Davison, A.C., and D.V. Hinkley 1997 Bootstrap Methods and Their Applications. Cambridge, UK: Cambridge University Press.
Griffith, J. 2000 Artificial neural networks: Are they ready for use as clinical decision aids? Editorial. Medical Decision Making 20(2):243-244.
Hand, D.J. 1992 Statistical methods in diagnosis. Statistics in Medical Research 1:49-67.
1998 Discriminant Analysis. Pp. 1168-1179 in Encyclopedia of Biostatistics, Volume 2, P. Armitage and P. Colton, eds. New York: John Wiley and Sons.
Hastie, T., R. Tibshirani, and J. Friedman 2001 The Elements of Statistical Learning: Data Mining, Inference and Prediction. New York: Springer-Verlag.
Laskey, K.B., and T.S. Levitt 2001 Artificial intelligence: Uncertainty. Pp. 799-805 in International Encyclopedia of the Social and Behavioral Sciences, Vol. 2, P. Baltes and N. Smelser, eds. Oxford: Elsevier.
Maurer, K., H. Biel, et al. 1989 On the way to expert systems. European Archives of Psychiatry and Neurological Sciences 239:127-132.
Olsen, D.E., J. Harris, et al. 1997 Computerized polygraph scoring system. Journal of Forensic Sciences 41(1):61-71.
Vlachonikolis, I.G., D.A. Karras, et al. 2000 Improved statistical classification methods in computerized psychiatric diagnosis. Medical Decision Making 20(1):95-103.
Wing, J.K., J.E. Cooper, and N. Sartorius 1974 Measurement and Classification of Psychiatric Symptoms. Cambridge, UK: Cambridge University Press.











