6
Using, Presenting, and Reviewing Health Benefits Analyses
Estimating the health benefits of a reduction in ambient air pollution concentrations involves the series of steps described in Chapter 1 of this report. To summarize, the regulatory options to be evaluated must be clearly defined with regard to scope, timing, and implementation. Boundaries of the analysis must be established, and the regulatory baselines must be defined. Once the analysis has been structured, changes in pollutant emissions can be estimated and translated into changes in pollutant concentrations or exposures. Changes in health outcomes can then be estimated from the changes in pollutant concentrations or exposures and concentration- or exposure-response functions. As discussed in Chapter 5, uncertainties at each stage of the analysis should be quantified and carried through the entire process.
The results of health benefits analyses are often used in cost-benefit or cost-effectiveness analyses of air pollution regulations. Although the philosophical foundations of cost-benefit analysis and especially the economic valuation of benefits remain controversial, it is important to discuss the implications of cost-benefit analysis for conducting a health benefits analysis. Accordingly, this chapter discusses how health benefits should be computed to be compatible with cost-benefit and cost-effectiveness analyses. Methods of presenting the results of health benefits analyses and issues regarding quality assurance and quality control are also addressed.
COMPATIBILITY OF HEALTH BENEFITS ANALYSES WITH COST-BENEFIT ANALYSES
The goal of a cost-benefit analysis is to compare the monetized benefits of a regulation with its costs. Regulations are often ranked according to the size of their net benefits (benefits minus costs). As a result, health benefits must be calculated and then converted to dollars using a value per avoided casetoallowcomparisontothecosts.
Monetization of Health Benefits
Economists estimate the value of avoided morbidity by determining the amount a person is willing to pay to avoid an illness. The estimate should include the value of avoided pain and suffering, the value of time lost due to illness (both leisure and work time), and the costs of medical treatment. If some of the costs are not borne by the individual and therefore not reflected in the person’s “willingness to pay” (WTP), these costs must be added to the estimate to measure the total benefits to society of reduced morbidity. For certain chronic illnesses, such as chronic bronchitis, economists try to measure what a person would be willing to pay to reduce his risk of contracting the illness. The amount is usually expressed in terms of the “value of a statistical case” of a given illness, such as chronic bronchitis, and represents the sum, across different individuals, of WTPs for risk reductions that together equal one statistical case.
Similarly, for premature mortality, economists try to measure what a person would be willing to pay to reduce his risk of dying. The amount is usually expressed in terms of the “value of a statistical life” (VSL) and represents the sum, across different individuals, of WTPs for risk reductions that together equal one statistical life. For example, if 10,000 people are willing to pay $100 each to reduce their risk of dying by 1 in 10,000, together they are willing to pay $1 million for risk reductions that equal one statistical life. The $1 million is the VSL. The VSL includes the lost income associated with dying prematurely but does not reflect the medical costs that might precede death. These costs are assumed to be included in the value of morbidity.
Empirical estimates of the value of avoided morbidity that include all three components (WTP to avoid pain or discomfort, lost earnings, and
medical costs) do not exist for many of the health outcomes associated with air pollution in epidemiological studies. For example, there are few studies of WTP to avoid the discomfort associated with a hospital admission or to reduce the risk of a heart attack or stroke. For these outcomes, the unit values typically used in EPA analyses reflect medical costs and lost earnings.
Implications of Monetization for Estimation of Health Benefits
Does the monetization of health benefits imply that health benefits estimates should be reported in a particular way, such as by income, age, or health status? According to economic theory, WTP to reduce risk of death and WTP to avoid illness should increase with income. For equity reasons, however, unit health values are currently not varied according to the income of the affected population. The relation between WTP and income is used only to adjust unit health values over time to reflect the impact of income growth on the value of avoided morbidity or death. Therefore, for purposes of monetization, health benefits do not need to be reported by income group.
For chronic illnesses and mortality, one might expect WTP to vary with age and possibly health status and conclude that health benefits (avoided cases) should be estimated and reported by these factors. There is no evidence that WTP to reduce risk of death varies with current health status (Alberini et al. 2002; Krupnick et al. 2002). However, statistical lives saved might need to be reported by age group with estimates of remaining life expectancy. The empirical literature suggests that WTP to reduce risk of death and hence the VSL eventually decline with age (Jones-Lee et al. 1985; Krupnick et al. 2002). To allow for the possibility that the VSL varies with age, estimates of statistical lives saved by air pollution control programs should be presented by the age of the beneficiaries.
The remaining life expectancy for each age group must also be reported if mortality reductions are monetized using the “value of a statistical life-year” (VSLY) approach. To illustrate this approach, suppose that the VSL is $5 million and that the average age of people receiving this benefit is 40. If remaining life expectancy at age 40 is 35 years and the interest rate is zero, then the VSLY is approximately $140,000. The value of preventing the death of an 80-year-old, with 8 years of remaining life expectancy, would be 8 times $140,000 or $1.2 million. Thus, applying the VSLY re-
quires an estimate of the remaining life expectancy. The committee notes that this procedure has been criticized because it implicitly assumes that each year of life is equally valuable and that the VSL is strictly proportional to remaining life expectancy. It has been used by EPA (1997, 1999), however, and is commonly used in the European Union (ExternE 1999).
COMPATIBILITY OF HEALTH BENEFITS ANALYSES WITH COST-EFFECTIVENESS ANALYSES
The goals of a cost-effectiveness analysis are to aggregate the health benefits of a program by using a measure that reflects the magnitude and the duration of improvements in health status and to express the cost of the program as a cost per unit of health benefit received. This practice should not be confused with the use of cost-effectiveness to screen pollution control options, which expresses the cost of the measure as cost per ton of emissions reduced. A commonly used measure of health benefits for this analysis is the “quality adjusted life-year” (QALY) (Gold et al. 1996), where a weight of one represents optimal health and a weight of zero represents death.1 The cost-effectiveness estimate of a program is expressed as the ratio of the program costs (numerator) to the QALYs achieved by a program (denominator).
In a cost-effectiveness analysis for a program, the value of avoided morbidity is the product of the duration of the avoided illness and the difference between the health status index, such as QALY, with and without the program. To illustrate, suppose that an air pollution regulation prevents a person from contracting chronic bronchitis at age 40 and living with the
disease for 30 years. The regulation would save 30 times the difference between the QALY weight assigned to the individual’s current health state and the QALY weight assigned to living with chronic bronchitis (30 × [QALYcurrent health • •QALYchronic bronchitis]). See Gold et al. (1996) for a discussion of the different methods used to assign QALY weights and for alternative health-related quality of life scales.
As the example above implies, avoided cases of chronic morbidity and mortality must be reported in terms of age at onset or age at which mortality is prevented and in terms of remaining life expectancy if the benefits estimates are to be used as inputs into a cost-effectiveness analysis. In the case of avoided mortality, it is also useful to have some knowledge of the health status of persons whose deaths are postponed. If reducing air pollution is more likely to prevent the deaths of persons with congestive heart failure or coronary artery disease than persons in the general population, the number of QALYs saved will be fewer than if the deaths were evenly distributed over the population. That is because the QALY weights assigned to coronary artery disease and congestive heart failure are smaller than the average QALY weight assigned to the current health of the general population.
For avoided cases of acute morbidity, the QALY approach also requires an indication of the period of avoided illness. For example, if 10 million fewer restricted-activity days (RADs) are experienced in a year in a population of 20 million then an average of 0.5 fewer RADs per person per year are experienced. The annual QALYs gained per person would be the difference between the QALY weight assigned to having 0.5 fewer RADs and the baseline QALY weight. To calculate the total QALYs gained, the number of QALYs gained per person would be multiplied by the size of the exposed population, which is 20 million in this example.
COMPATIBILITY OF HEALTH BENEFITS ANALYSES WITH COST ANALYSES
In estimating health benefits, assumptions must be made about the size of the population exposed to air pollution for each year of the analysis and about the baseline incidence of each health outcome evaluated. Assumptions must also be made about remaining life expectancy when a VSLY or a QALY approach is used. In monetizing benefits, assumptions are made
about the rate of income growth, and those assumptions are used to estimate how the unit values assigned to each health outcome change over time.
The assumptions made about disease incidence and mortality and especially income and population growth used in the health benefits analysis must be consistent with assumptions made in computing the costs of air pollution control. The choice of years for which to compute health benefits must also correspond in a sensible way to the period for which costs are computed.
COMMUNICATION OF METHODS AND RESULTS OF ANALYSIS
A common complaint about EPA benefits analyses is that the methods, the rationale behind the decision-making, and the results are not clearly presented or described. After review of the four EPA analyses, the committee agrees that the presentation could be improved and is concerned that factors that drive the analysis are buried in appendixes or technical support documents. Furthermore, the committee noted that the lengths of discussion devoted to certain components of the analysis are not based on their importance to the analysis. For example, for the heavy-duty engine and diesel-fuel rule, EPA uses four pages of text to describe Voronoi neighbor averaging to interpolate ambient air pollution concentrations at the mid-point of each spatial grid used in the atmospheric model (EPA 2000). The method of interpolation is a technical issue that is unlikely to be a key determinant of the ultimate prediction of air quality. The fact that simulations of ozone concentrations were done only for the eastern United States and were based on meteorological data for only 30 days in the summer of 1995 is of much greater importance. This limitation, however, is dealt with in one sentence. For further contrast, the entire topic of statistical uncertainty is covered in approximately one page.
Although the documents reviewed by the committee contained executive summaries, the committee believes that the summary should be more detailed, such as 20-30 pages in length, and present the key information summarized in Table 6-1. Subsequent chapters should describe the methods used in each step of the analysis, the validation of models used in the analysis, and the uncertainty associated with the estimates at each stage of the
TABLE 6-1 Items to Be Reported in the Summary of a Benefits Analysis of an Air Pollution Control Regulation
|
Framing the Analysis |
Emissions and Air Quality |
Health Benefits |
|
Describe each regulatory option Geographic scope Timing Parties affected Describe the boundaries of the analysis Time period of benefits analysis Intervals at which benefits are calculated Pollutants evaluated Degree of compliance with regulation Describe the regulatory baseline Conditions without regulation, including other regulations in place and assumptions about the economy and population. Highlight any assumptions that have a substantial impact on the results of the analysis |
Summarize emissions at the national level by sector with and without the regulation Compare baseline emissions to historical trends Present emissions changes associated with the regulation in absolute and in percentage terms Summarize ambient air quality by region and at the national level with and without the regulation Report as population-weighted annual averages Compare baseline air quality to historical trends Present pollution changes associated with the regulation in absolute and in percentage terms |
List health outcomes evaluated and describe each Indicate time path of avoided cases for each health outcome For quantified outcomes at each time period for which results are presented, the following information should be presented Size of exposed population Baseline number of cases (cases/100,000) Coefficient of concentration-response function Number of avoided cases For avoided mortality and chronic morbidity, information indicated above should be presented by age at onset and remaining life expectancy |
analysis. EPA should discuss more fully the components that are the important contributors to the benefits estimates and that may have substantial uncertainty associated with them.
The summary should begin with a description of the regulatory options considered, including their timing, scope, and assumptions made about the degree of compliance with each option. This description should be contrasted with the conditions that are assumed to exist without the regulation—that is, the regulations that are in place and the air quality without enactment of the proposed regulation.
It is critical that the implications of a regulation for emissions and ambient air quality be presented clearly. Summary information should be provided describing emissions of the air pollutants with and without enacting the regulation. An excellent example of how this information should be presented is contained in Appendix A of the prospective analysis of the Clean Air Act (EPA 1999). The charts show aggregate emissions of each criteria pollutant (one chart for each pollutant) with and without the 1990 Clean Air Act Amendments (CAAA) over the period of analysis. Historical emission trends for 1980-1997 are shown on each graph so that the reader can judge how reasonable the predictions without CAAA regulations are. The changes in emissions (in absolute and percentage terms) attributable to the regulation should also be presented. Similar statistics should be provided for ambient concentrations and changes in ambient concentrations. In the case of ambient concentrations, it would be useful to describe changes in population-weighted average concentrations both for regions of the country and for the nation as a whole.
The summary should include a description of health outcomes evaluated in the study. For quantified outcomes, the number of avoided cases should be listed for each year of the analysis, both in absolute terms and as a percentage of baseline cases of the outcome (see EPA 1999, Table 5-3). Avoided cases of mortality and chronic morbidity, such as chronic bronchitis, should be broken down by age group with estimates of average remaining life expectancy presented for each age group. The benefits may also need to be presented by various demographic or other subgroups when the expected changes in pollution and thus the health benefits are not uniformly distributed across the population. The presentation of this information would alert and aid decision-makers when issues of equity are concerned. Explanations for not quantifying certain health outcomes should also be provided.
In addition to presenting numbers of avoided cases, enough information should be provided for at least 1 year of the analysis to permit approximation of the estimates of health benefits provided at the national level. For example, the number of avoided cases of chronic bronchitis resulting from
a reduction in air pollution is the product of (1) the size of the exposed population, (2) the baseline incidence of chronic bronchitis (cases per 100,000), (3) the percentage change in incidence per unit of pollution, and (4) the population-weighted change in pollution. The committee acknowledges that this calculation would only approximate a similar calculation performed at the county level and then aggregated across counties; however, summarizing this information for each health outcome would allow the reader to at least approximate the calculations.
As discussed in Chapter 5, the analysis of the uncertainty is an important component of health benefits analysis. The summary chapter should discuss briefly the methods used to address and quantify uncertainty and should highlight sources of uncertainty that could not be adequately assessed. EPA should strive to present the results of the analyses in ways that avoid conveying an unwarranted degree of certainty. Such ways include rounding to few significant digits, increasing the use of graphs, and placing less emphasis on single numbers and greater emphasis on ranges.
To clarify further the methods used in the health benefits process, a detailed flow diagram should be added to the introduction of the summary (see Figure 6-1). This diagram would provide at a glance the regulatory options considered, the time frame of the analysis, and any assumptions that substantially affect the results of the analysis. Pollutants and modeling techniques should be indicated, and the health outcomes and basis for their quantification should be presented in this diagram. The diagram would serve as a reference point for the discussion that follows. Figure 6-1 could be considered an expansion of the diagrams that EPA provides in its analyses that simply indicate generic steps of a benefits analysis (see EPA 2000, Table 7-1).
If the benefits analysis is an integral part of a cost-benefit analysis, then enough information should be provided to allow approximation of the monetized estimates or to produce alternative results where there is disagreement with the assumptions used. The information shown below should be provided in the summary.
-
Unit values used to monetize health outcomes should be listed in a table with the year in which dollar estimates apply (see EPA 1999, Table 6-1).
-
Each unit value should indicate whether it includes WTP for pain and suffering, medical costs, and lost earnings.
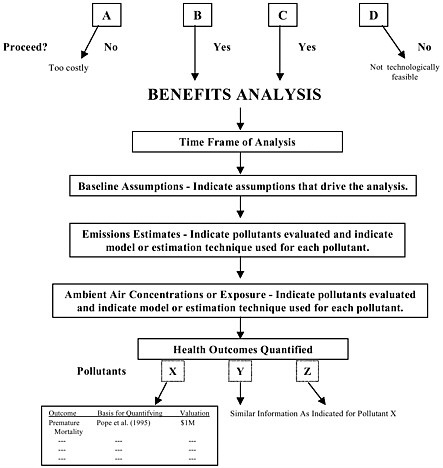
FIGURE 6-1 Flow diagram of a health benefits analysis.
-
Information should be provided on how unit values are assumed to change over time.
-
Total monetized value of health benefits by year and current discounted value of health benefits should be provided.
-
The discount rate used should be clearly stated, and alternative rates should be presented for sensitivity analysis.
If the benefits analysis is a part of a cost-effectiveness analysis, then
additional information should be provided. In this case, the weights used to aggregate the avoided cases of morbidity and mortality and the durations of avoided illnesses should be presented. The analysis should be explicit about how avoided lost earnings and medical costs were incorporated into the analysis.
Presentation of the information discussed in this section would allow a more complete and straightforward assessment of the methods and results of the analysis. With the presentation of the avoided cases of morbidity and mortality and the unit valuations, estimates of the annual dollar value of health benefits achieved or annual QALYs avoided could be checked. This would increase confidence in the estimates generated.
QUALITY ASSURANCE AND QUALITY CONTROL
Reporting the information in Table 6-1 in a summary at the beginning of each report will not guarantee that the study is scientifically sound and satisfies the following criteria:
-
The study considers the appropriate regulatory options.
-
The study chooses an appropriate time period for analysis.
-
The study uses state-of-the-art data and validated models.
-
The study uses models and data comparable to those in similar analyses.
The issues of quality control that are specific to a particular study include the regulatory options that are considered relevant, the appropriate time period for the analysis, and the assumptions regarding compliance and the regulatory baseline. Clearly, peer review of these aspects of the study would be most useful at the beginning of the study. Although an expert panel similar to a subcommittee of the EPA’s Science Advisory Board could be assigned such a task, few experts have the technical knowledge to evaluate these aspects of study design. Therefore, a standing, independent technical review panel with a professional staff should be established to evaluate analyses at the initial stages and throughout the process. This panel should include members with expertise in regulatory options analysis, emissions and exposure assessment, epidemiology, toxicology, risk analysis, biostatistics, and economics and should be appointed with strict attention to
avoiding conflict of interest, balancing bias, and ensuring broad representativeness. This panel could ensure that there is reasonable consistency among similar types of analyses produced within EPA and across other agencies.
CONCLUSIONS
-
The results of health benefits analyses are typically used as inputs to cost-benefit or cost-effectiveness analyses; therefore, the results need to be presented in ways compatible for these analyses.
-
The presentation of methods, rationale, and results from health benefits analyses is sometimes inadequate. For example, EPA’s analyses do not highlight key assumptions that drive the analysis, do not indicate the rationale behind study selection, and do not present results in ways that allow verification of estimates obtained.
-
Benefits analyses are typically not scrutinized at the initial stages of study design, during the process, or at the final stages of the process.
RECOMMENDATIONS
-
EPA should provide health benefits estimates in ways that will support multiple kinds of analysis, including various approaches to mortality valuation and aggregation of benefits using quality-adjusted life-years.
-
EPA should provide a summary of the analysis containing information as outlined in Table 6-1. This information would allow the reader to evaluate the study design and verify estimates obtained in the analysis.
-
Each analysis should provide results according to demographic or other subgroups when the expected changes in pollution and thus the health benefits are not distributed uniformly across the population. This information would aid decision-makers in situations in which equity issues might be involved.
-
To enhance the quality of future regulatory benefits analyses, a standing, independent, technical review panel should advise EPA in the initial stages of its benefits analysis. This panel should have expertise in regulatory options analysis, emissions and exposure assessment, toxicology, epidemiology, risk analysis, biostatistics, and economics and should be ap-
-
pointed with strict attention to avoiding conflict of interest, balancing biases, and ensuring broad representation. This panel should be supported by permanent technical staff to ensure consistency of reviews over time. EPA should follow the panel’s guidance on the need for peer review.
REFERENCES
Alberini, A., A. Krupnick, M. Cropper, and N. Simon. 2002. The Willingness to Pay for Mortality Risk Reductions: A Comparison of the United States and Canada. Nota di Lavoro 92.2001. Fondazione Eni Enrico Mattei, Milan, Italy. December 2001.
EPA (U.S. Environmental Protection Agency). 1997. Final Report to Congress on Benefits and Costs of the Clean Air Act, 1970 to 1990. EPA 410-R-97-002. Office of Air and Radiation, U.S. Environmental Protection Agency. Cincinnati, OH: National Service Center for Environmental Publications. October 1997.
EPA (U.S. Environmental Protection Agency). 1999. Final Report to Congress on Benefits and Costs of the Clean Air Act, 1990 to 2010. EPA 410-R-99-001. Office of Air and Radiation, U.S. Environmental Protection Agency. November 1999.
EPA (U.S. Environmental Protection Agency). 2000. Regulatory Impact Analysis: Heavy-Duty Engine and Vehicle Standards and Highway Diesel Fuel Sulfur Control Requirements. EPA 420-R-00-026. Office of Air and Radiation, U.S. Environmental Protection Agency, Washington, DC. December 2000.
ExternE. 1999. Externalities of Energy, Vol. 7. Methodology 1998 Update. EUR 19083. European Commission DGXII, Science Research and Development. Luxembourg: Office for Official Publications of the European Communities.
Gold, M.R., J.E. Siegel, L.B. Russell, and M.C. Weinstein. 1996. Cost-Effectiveness in Health and Medicine. New York: Oxford Press University.
Jones-Lee, M.W., M. Hammerton, and P.R. Philips. 1985. The value of safety: Results of a national sample survey. Econ. J. 95(337):49-72.
Krupnick, A., A. Alberini, M. Cropper, N. Simon, B. O’Brien, R. Goeree, and M. Heintzelman. 2002. Age, health, and the willingness to pay for mortality risk reductions: A contingent valuation survey of Ontario residents. J. Risk Uncertainty 24(2):161-186.
Murray, C.J.L., and A.D. Lopez. 1996. The Global Burden of Disease: A Comprehensive Assessment of Mortality and Disability from Disease, Injuries, and Risk Factors in 1990 and Projected to 2020; Summary. Cambridge: Harvard University Press.
WHO (World Health Organization). 2002. World Health Report 2002. Geneva: WHO. In press.
World Bank. 1993. Investing in Health. New York: Oxford University Press.













