2
State of the Art of PTTI Physics and Devices
This section outlines briefly the basics of (1) frequency standards and clocks, discussing the standards currently available and those under development, (2) clock synchronization and syntonization, and (3) environmental effects on the performance of PTTI devices. A more thorough discussion of the science behind PTTI and more detailed descriptions of current standards are provided in Appendix B.1
BASIC DESCRIPTION OF FREQUENCY STANDARDS
A greatly simplified block diagram of an atomic frequency standard (also called an atomic clock) is shown in Figure 2.1. This consists of an atomic resonator, a local oscillator, and additional components. An atomic frequency standard produces an output signal whose frequency is related to an intrinsic atomic transition energy through Planck’s constant. The atomic resonator frequency is generated from a local oscillator’s frequency by frequency multiplication or frequency synthesis. The local oscillator frequency is locked to the frequency of the atomic resonator through the synthesizer and frequency multiplier with a servoloop time constant that is selected to provide optimum performance for the intended application. The atomic resonator determines the long-term stability of the standard; the local oscillator (also called the flywheel oscillator) determines the short-term stability.
Figure 2.2 shows the basic elements of a quartz crystal oscillator. Unlike the frequency of an atomic resonator, the frequency of a crystal oscillator is dependent on the properties of the individual crystal and how it is fabricated. Quartz crystal oscillators are used as clocks in those applications of PTTI in which some aspects of clock performance can be sacrificed to achieve devices of small size, low power, and light weight. Quartz crystal oscillators are also used as local oscillators for lower-performance atomic standards. High-performance laboratory atomic standards require higher-performance local oscillators such as the rubidium standard or the hydrogen maser.
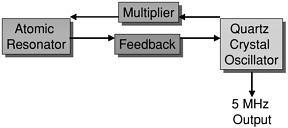
FIGURE 2.1 A simplified diagram of an atomic frequency standard.
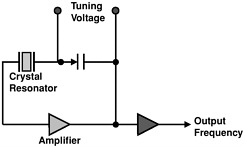
FIGURE 2.2 A simple circuit diagram showing the basic elements of a crystal oscillator.
PERFORMANCE OF FREQUENCY STANDARDS
The performance of any frequency standard, whether atomic or crystal, is described by three characteristics:
-
Accuracy is a measure of how closely the frequency generated by the standard corresponds to its assigned value (e.g., the atomic transition frequency for an atomic standard). Accuracy can also be applied to a frequency measuring instrument, where it tells how close the instrument’s reading is to the actual frequency being measured. A measurement of a 100-Hz frequency that is accurate to the sixth decimal place is said to be accurate to 1 part in 108, or to have 10−8 accuracy.
-
Precision is a measure of the repeatability of a frequency measurement. It is generally expressed in terms of a standard deviation of the measurement.
-
Stability is a measure of the maximum deviation of the standard’s frequency when operating over a specified parameter range. Frequency aging, or long-term stability, is the slow change of the standard’s frequency with time if all other parameters are fixed. Short-term stability is the deviation of the standard’s frequency with time as the result of noise or other internal effects if other parameters are fixed. It is often expressed in terms of the Allan deviation (see Appendix D, Glossary).
CURRENT FREQUENCY STANDARDS
Atomic Frequency Standards
Cesium Beam Standard
These standards are based on measurements of atomic transitions in a beam of cesium-133 atoms. The accuracy of a laboratory cesium beam standard is typically about 1 part in 1014 averaged over one day. These frequency standards have been adapted for use in space, where some accuracy and short-term stability of the signal have been sacrificed to achieve ruggedness, reliability, small size, and low power requirements. There are currently five commercial suppliers of cesium beam standards, three of which are U.S. suppliers. These commercial standards vary in their accuracy, short-term stability, environmental effect on performance, and price, the best having an accuracy of a few parts in 1013 and an Allan deviation of about 8 × 10−12τ−1/2. They are used as clocks in laboratories that contribute to the international atomic time scale, at the GPS ground control station that uploads time to the GPS satellites, and aboard Navy ships.
Cesium Fountain
These standards are also based on transitions in cesium-133 but differ from the cesium beam standards in that they probe collections of laser-cooled cesium atoms, which are launched upward like a fountain and probed during their free fall. This arrangement allows longer interrogation of the atomic transition. The longer interrogation time translates into a more accurate device, with fountain standards having an accuracy of about 1 part in 1015. Cesium fountain standards are currently in use only in laboratories. They are being used by some laboratories to contribute to the international atomic time scale. Similar fountainlike, slow atom-beam devices are under development in both Europe and the United States for operation on the International Space Station (ISS).
Trapped Mercury Ion
In microwave-frequency trapped-mercury-ion standards, mercury-199 ions are confined using a radio-frequency quadrupole trap before probing a microwave-frequency ionic resonance. The large number of trapped ions probed increases the signal-to-noise ratio, and the long interaction time with the microwave radiation enables very good short-term stability (about 4 × 10−14τ−1/2) if an extremely good local oscillator is used. This type of standard is currently installed in all three complexes of NASA’s Deep Space Network and provides the highest stability of any standard in support of NASA missions. The GPS Joint Program Office has supported the development of a prototype spaceborne standard based on this linear ion trap standard (LITS) for future advanced GPS satellites.
NIST is developing a mercury standard using optical frequency transitions. This optical frequency standard is based on probing a single mercury-199 ion in a quadrupole trap; its potential for application is greatly enhanced by recent breakthroughs in optical frequency combs that link optical and microwave frequency sources (see discussion in Appendix B, “Connection Between Microwave and Optical Regions”). Probing a single ion using a highly stabilized laser source promises much better accuracy than current standards; an accuracy considerably better than one part in 1016 is expected to be achieved.
Hydrogen Maser
In current hydrogen maser (H maser) standards, molecular hydrogen is dissociated into atoms, which are state separated in a magnetic field so that the higher-energy-state atoms are directed into a bulb inside a microwave cavity resonant at the transition frequency. The interior of the bulb is coated to minimize the effects of atomic collisions with its walls. Nonetheless, although the short-term frequency stability of the hydrogen maser is excellent, its accuracy is inferior to that of cesium devices owing to wall-induced effects.
Research is ongoing on a cryogenically cooled hydrogen maser, which may be able to achieve frequency stability as good as 1 × 10−18. There is also an ongoing effort to qualify a hydrogen maser for spaceflight. This unit has demonstrated Allan deviation stability of 5 × 10−15 at 100 seconds averaging time and weighs 100 kg. Ongoing programs in Switzerland and the United States seek to qualify H masers for extended operation in space.
There is presently one U.S. supplier of active hydrogen masers. Passive and active2 hydrogen masers can be purchased from Russia. Hydrogen masers are finding increased use in time-scale ensembles owing to their excellent short-term stability.
Rubidium Gas Cell
The rubidium gas cell standard is based on rubidium-87 atoms sealed in a gas cell with a buffer gas. The buffer gas confines the rubidium atoms, thus largely preventing collisions with the cell walls. However, rubidium atom collisions with buffer gas atoms cause a pressure- and temperature-dependent frequency shift; another effect, the so-called light shift, is dependent on both the light intensity and spectral distribution of the lamp used to state select the atoms. Thus the rubidium gas cell standard has much poorer accuracy than the cesium beam standard and has frequency aging. However, its short-term stability can be very good if the standard is properly designed. In the laboratory, an Allan deviation of 1 × 10−13τ−1/2 has been demonstrated, with perhaps an order of magnitude improvement possible.
Space-qualified rubidium gas cell standards are a modification of the laboratory device, with increased emphasis on small size, ruggedness, long life, and moderately good short-term stability. Rubidium cells flown on GPS block IIR satellites are providing better short-term stability than the cesium beam standards flown on earlier GPS satellites. Rubidium standards are also the principal timekeeping devices on MILSTAR military communications satellites.
Rubidium gas cells are by far the best selling commercial atomic standard. Commercial units are produced with an emphasis on low cost and moderately small size (~100 cm3). They find use primarily in base stations for cellular telephone service and in other telecommunications applications.
Atomic Standards Under Development
Optical Standards Other Than Mercury
NIST is working on an optical frequency standard using trapped calcium atoms. Because the linewidth of the calcium transition is much larger than that of the mercury ion standard, the achievable accuracy is much poorer. However, the large number of atoms being interrogated in the calcium system gives a very good signal-to-noise ratio and, consequently, good short-term stability.
|
2 |
See Appendix B for a discussion of the difference between active and passive frequency standards. |
A number of other ions and atoms are also under investigation as candidates for optical standards. Among these are single trapped ions of indium and ytterbium. Work is also being done on standards using trapped neutral atoms of strontium. Neutral atoms have the advantage that many can be held in the trap, giving a good signal-to-noise ratio and, consequently, good short-term stability. However, the transitions currently being investigated in neutral atoms have much larger linewidths than those of the ions, so the achievable accuracy is much poorer.
Coherent Population Trapping
Although discussed in the early 1970s, the coherent population trapping (CPT) approach has only recently received much attention, primarily because suitable lasers for pumping are only now available. Several groups are working in this field. The excitation of the atoms in this system is all optical, using two coherent optical signals to pump on two ground-state levels of the atoms. Unlike the other atomic standards discussed here, no microwave cavity is needed, so this device is potentially much easier to miniaturize.
Crystal Oscillators
The most common crystal oscillator is based on quartz. A quartz crystal acts as a stable mechanical resonator, which, by its piezoelectric behavior and high Q, determines the frequency generated in the oscillator circuit. The crystal resonator (also called the “crystal unit”) is also the primary frequency-stability-determining element in the oscillator.
In the manufacture of quartz resonators, wafers are cut from a quartz crystal along directions precisely controlled with respect to the crystallographic axes. The properties of the device depend strongly on the angles of cut. After shaping the quartz to the required dimensions, metal electrodes are applied to the quartz wafer, which is mounted in a holder structure. The assembly is hermetically sealed, usually in a metal or glass enclosure. To cover the wide range of frequencies, different cuts vibrating in a variety of modes can be used.
There are three categories of crystal oscillators, based on the method of dealing with the crystal unit’s frequency versus temperature (f versus T) characteristic. The uncompensated crystal oscillator, XO, does not contain means for reducing the crystal’s f versus T variation. The temperature-compensated crystal oscillator, TCXO, uses temperature-dependent reactance variations to produce frequency changes that are equal and opposite to the crystal’s temperature-dependent frequency changes—that is, the reactance variations compensate for the crystal’s f versus T variations. Analogue TCXOs can provide about a 20-fold improvement over the uncompensated crystal’s f versus T variation. Hysteresis, the nonrepeatability of the f versus T characteristic of the crystal, is the main TCXO stability limitation. The third category—the oven-controlled crystal oscillator (OCXO)—uses an oven to maintain the crystal unit and other temperature-sensitive components of the oscillator circuit at an approximately constant temperature. The crystal is manufactured to have an f versus T characteristic that has zero slope at or near the desired oven temperature. OCXOs can provide more than a 1,000-fold improvement over the crystal’s f versus T variation. A special case of a compensated oscillator is the microcomputer-compensated crystal oscillator, MCXO, currently in advanced development. The MCXO minimizes the two main factors that limit the stabilities achievable with TCXOs: thermometry and the stability of the crystal unit. Instead of a thermometer that is external to the crystal unit, such as a thermistor, the MCXO uses a more accurate “self-temperature-sensing” method. To reduce the f versus T variations, the MCXO uses digital compensation techniques.
There is a significant commercial market for quartz crystal oscillators, but only the most high-end devices with the greatest stability are relevant to PTTI. Most of the commercial market is for low-end devices such as quartz watches and other consumer goods.
Optoelectronic Oscillators
NASA, DARPA, the Army, the Air Force, and NIST have invested in the development of a new approach for the generation of highly spectrally pure references. The approach, based on an optoelectronic feedback loop, provides the highest spectral purity at frequencies above 10 GHz by utilizing high-efficiency optical and photonic components in place of less-efficient microwave elements. A performance of 145 decibels relative to the carrier (dBc) at 10 kHz from a 30-GHz carrier has been demonstrated. A major feature of the optoelectronic oscillator (OEO) is that its design lends itself to miniaturization. A chip-based OEO can significantly reduce the cost, size, and power requirements and would be an important benefit for a number of ground, mobile, and space systems. Originally developed at JPL, the OEO technology was transferred to the commercial sector and is being advanced with private and government funds.
SYNCHRONIZATION AND SYNTONIZATION OF CLOCKS
A clock’s time must be set initially to agree with some chosen time scale; this is synchronization. The clock’s frequency must also be set so that its rate matches that of the chosen time scale; this is syntonization. An error in synchronization gives a time offset to the clock. An error in syntonization gives the clock a time error whose magnitude increases linearly with passing time (assuming the clock rates are constant).
There are four methods for synchronization and syntonization of high-performance clocks: GPS common view, GPS one way, GPS carrier phase, and two-way satellite time transfer.
GPS Common View
In GPS common view, observers at different locations receive the same time signal from the same GPS satellite and record the difference between their local clocks and the GPS time. Then by communicating their results and subtracting them, the GPS time drops out, with the result being the time difference between the local clocks. This result can then be used to synchronize the clocks. By using all the satellites in common view and averaging, the results can be improved. With well-calibrated receiver and antenna cable delays, the accuracy can be better than 10 nanoseconds. The stability of the measurements can be about 1 nanosecond. One uncertainty is the difference in ionosphere delays over the two paths. The Sagnac effect, due to Earth’s rotation, and the relativistic effects of gravitational potential and of second-order Doppler must be taken into account in the measurement.
If measurements are made separated by some time, say 1 day, the change in time difference between the two measurements can be determined. This gives a measure of the rate, or frequency, difference between the clocks. The fractional frequency difference, Δf/f, is equal to the change in time, Δt, between the two clocks, divided by the time between measurements, t. This is the syntonization technique. With 1 nanosecond root mean square (rms) stability of the timing measurements, the accuracy of the Δf/f determination in 1 day is about 1 × 10−14 rms. With averaging for 10 days, about 1 × 10−15 rms is achieved, assuming the clock rates are constant.
GPS One Way
If the position of a GPS receiver antenna is known, either by well-averaged GPS measurements or by survey, the user can determine the difference between the time of a local clock and that transmitted by the GPS satellite clock. This is known as GPS one way. Since the difference between satellite clock time and GPS system time is transmitted, the user can relate the local clock time to GPS time. The same is true for UTC (USNO) since that difference is also transmitted. The time difference accuracy can be about 10 nanoseconds over a day’s averaging time if delays are well calibrated. The timing stability over 1 day can be 2 nanoseconds rms if UTC (USNO) is used with a good local clock and all satellites in view are observed. This gives a frequency accuracy of 2 × 10−14 rms averaged over 1 day.
GPS Carrier Phase
Monitoring the GPS carrier phase relative to the local clock can give frequency only since the actual cycle being tracked is unknown. The best results are obtained with post-processed ionosphere and orbit data. If the user keeps track of the signals as satellites come and go, averaging over 1 day the time stability can be better than 100 picoseconds rms, giving a frequency accuracy of 2 × 10−15 rms averaged over the day.
Two-Way Satellite Time Transfer
The two-way satellite time transfer (TWSTT) technique requires both sites to have two-way communications with the same geostationary communications satellite. Each site transmits a pulse from its own local clock and receives the pulse from the other site’s clock. The time difference between the local clock pulse and the received pulse is recorded at both sites, and from those data and calibration of all the delays, many of which tend to cancel, the time difference between the local clocks at the two sites can be determined. The equipment for this method is moderately expensive, and satellite time must be scheduled and paid for, so this method is not as easy to use as the others. Time average accuracy ranges from 1 to 5 nanoseconds rms and time stability ranges from about 0.1 to 2 nanoseconds rms, giving a frequency accuracy at 1 day between 0.1 and 2 × 10−14 rms. Again, the Sagnac effect must be taken into account.
Table 2.1 summarizes the stability and accuracy of the available synchronization and syntonization technologies.
TABLE 2.1 Summary of Stability and Accuracy Available from Current Synchronization and Syntonization Technologies
|
Technology |
RMS Time Accuracy (ns) |
RMS Time Stability (ns) |
RMS Frequency Accuracy 1 day |
Comments |
|
GPS one way |
10 to 40 |
2 to 7 |
2 × 10−14 |
Simple |
|
GPS common view |
1 to 10 |
1 to 2 |
1-2 × 10−14 |
Best GPS |
|
GPS carrier phase |
— |
0.1 |
0.1 × 10−14 |
Not in real time |
|
TWSTT |
1 to 5 |
0.1 to 2 |
0.1-2 × 10−14 |
Complex and expensive |
ENVIRONMENTAL EFFECTS ON THE PERFORMANCE OF PTTI DEVICES
The accuracy and stability of a clock depends on its environment. A clock may have orders of magnitude higher stability in a quiet laboratory environment than in a military environment. The accuracy available for a given application also depends on the power and size the system allows for the clock. For example, small handheld systems cannot use atomic clocks, or even high-end quartz clocks, owing to size and power constraints.
Shock
The effects of moderate shock levels on quartz LOs include transient frequency offsets or, if mechanical damage is done, permanent offsets. Higher levels may break the crystal or its mounts. However, crystals have been designed and built to withstand being shot from a howitzer (16,000 g). Atomic standards can lose lock and fail if the transient effects are large enough in either the LO or the atomic resonator. In a passive standard used as a clock, if the LO has a step change in frequency due to shock or some other cause, the time output of the clock can have zero offset after the transient dies out if the loop filter contains at least two digital integrators.
Vibration
Vibration affects quartz LOs mainly through its acceleration effects on the resonator. Typical sensitivities of good quartz resonators are in the range of 10−9 to 10−10 per g. The effect is frequency modulation of the oscillator output. Sinusoidal vibration can cause disappearance of the carrier to an extent that depends on the vibration level and frequency. This effect can cause an atomic standard to lose lock and fail. If the vibration frequency is low compared with the reciprocal of the loop time constant in the standard, the LO frequency modulation due to the vibration will be reduced in the standard’s output by the filtering action of the loop. Above the resonant frequency of the isolators, mounting the LO on vibration isolators reduces the effect.
Vibration can also modulate the output signal from atomic resonators. Vibration frequency at the interrogation modulation frequency can cause large frequency offsets or loss of lock. Fountain standards are particularly susceptible because the atoms in the fountain have low velocities.
Linear Acceleration
Good quartz resonators, as mentioned above, have sensitivities in the range of 10−9 to 10−10 per g. Using Mach’s principle, this sensitivity is easily measured by rotating the oscillator 180 degrees relative to Earth’s gravitational field for various initial orientations and measuring the frequency change due to the resulting 2 g change in acceleration. Acceleration can also affect the LO frequency indirectly owing to the resulting change in the temperature distribution or stress on the oscillator’s electronic components.
Acceleration affects microwave atomic resonators by deforming and detuning the cavity. The effect is particularly severe in masers. Atomic trajectories in beam and fountain standards are affected by acceleration. The slower the atoms, the more severe the effect, so fountain standards are very susceptible.
Temperature
Temperature effects on quartz LOs have been mentioned above. For the precision LO applications, temperature control is usually necessary. The other types of LOs also require temperature control and/ or compensation.
Temperature also affects atomic resonators. The frequency dependence on temperature due to buffer gas in rubidium standards is fairly large, but with moderate temperature control, the standard can perform at a few parts in 1010 over a fairly large temperature range.
The hydrogen maser has a frequency shift of −1.4 × 10−13 per degree C owing to the relativistic velocity effect. In addition, the cavity resonance for the maser is temperature sensitive, so that temperature control of the combined storage bulb and cavity is necessary. The magnetic field may also be temperature dependent.
In cesium beam standards, cavity detuning is important but much less so than in a maser. There can also be temperature effects due to changes in the gain of the beam tube and in the magnetic field. In the best performance standards, these effects are almost completely removed by digital monitoring and control of the microwave amplitude, magnetic field, and overall system gain.
Temperature effects in the advanced mercury-199 trapped-ion microwave standards are fairly small. Moderate temperature and magnetic field control are necessary.
Humidity
Humidity affects mainly the device’s electronics, since the resonators, both LO and atomic, are sealed. Proper electronics design, with digital monitoring and control of important parameters, and proper construction can minimize the effect.
Magnetic Field
Quartz is diamagnetic; however, magnetic fields can affect magnetic materials in the crystal unit’s mounting structure, electrodes, and enclosure. Time-varying electric fields will induce eddy currents in the metallic parts. Magnetic fields can also affect components in the oscillator circuitry, such as inductors. When a crystal LO is designed to minimize the effects of magnetic fields, the sensitivity can be ±10−10 per gauss.
Microwave atomic frequency standards are particularly sensitive to magnetic fields because the hyperfine transition frequency that is the basis of the standard is proportional to the energy of the magnetic interaction between the outer electron and the nucleus. All these standards use hyperfine transitions with small quadratic magnetic-field dependence at the operating magnetic field of the unit— typically a few thousandths of a gauss. The sensitivity to field changes is smaller for large hyperfine transition frequency. Several layers of magnetic shielding provide a stable magnetic environment. Typical sensitivity for a shielded miniature rubidium standard is ±2 × 10−11 per gauss change in the external field. The best commercial cesium standards have external magnetic-field sensitivity of ±10−14 per gauss, obtained by good shielding as well as digital monitoring and control of the magnetic field inside the atomic resonator.
The sensitivity of the hydrogen maser is about ±3 × 10−14 per gauss, obtained by good shielding.
Atmospheric Pressure
Ambient pressure changes can affect LO resonator frequency, causing changes in the deformation of the enclosure that affect the resonator through the mounting structure. They can also cause changes in the heat transfer, thus indirectly inducing frequency changes due to temperature variations. A well-designed quartz LO will change less than ±5 × 10−9 with a pressure change of 1 atmosphere.
Atomic resonators can also be affected by atmospheric pressure changes, either through direct
interaction or through indirectly inducing temperature changes. In rubidium gas cell standards, the gas cell deformation is pressure dependent, inducing buffer gas density changes. This produces frequency change of about ±1 × 10−13 per torr owing to increases in interatomic collisions. The hydrogen maser can be affected by “cavity pulling” if the cavity is not extremely well isolated from the pressure changes. The best commercial cesium beam standards change frequency less than ±1 × 10−16 per torr.
Aging
Aging is a slow change in frequency with time under constant ambient conditions. The best crystal LOs age less than ±1 × 10−10 per day. The effects of aging of the LO on an atomic standard can be virtually eliminated if the loop filter has at least two digital integrators.
Aging in rubidium gas cell devices can be due to changes in the buffer gas composition with time because of outgassing of the cell walls or helium diffusion. Another source of aging is change in the optical spectrum of the lamp and change in cell wall optical properties and the consequent change in pump spectrum with respect to the rubidium absorption spectrum, called the light shift. Typical aging in rubidium standards is ±3 × 10−13 per day.
Aging in the best commercial cesium standards is typically less than ±1 × 10−16 per day. Aging in hydrogen masers without cavity autotuning is on the order of ±1 × 10−15 per day, chiefly the result of slow changes in cavity dimensions. With cavity autotuning, ±1 × 10−16 can be achieved.
Retrace
Retrace is how well the standard or LO reproduces its frequency after a powerdown and cold restart. The best quartz LOs can retrace within a few parts in 1010. Retrace of the best commercial cesium standards is about ±1 × 10−13. Retrace of rubidium gas cell devices is about ±5 × 10−11. Retrace of hydrogen masers is about ±1 × 10−13.
Noise
Frequency noise in quartz LOs is due partially to thermal noise in the resonator and noise in the sustaining amplifier. In addition, there are low-frequency sources of noise. One such source is temperature fluctuations, which cause frequency changes dependent on the temperature coefficients of the resonator and other sensitive elements. Another is called flicker, or 1/f noise, since its power spectral density is proportional to 1/f, where f is the frequency of the noise spectrum being observed.
The atomic resonator in well-designed passive atomic standards determines frequency noise at times longer than the loop time constant. Atomic shot noise in beam standards and shot noise in the optical detector in gas cell standards are the primary source of frequency noise until flicker noise, with spectrum proportional to 1/f, takes over at low frequencies or long times. The Allan deviation due to shot noise is proportional to τ−1/2, where τ is the averaging time. The Allan deviation due to flicker noise is independent of τ. Aging as well as low frequency noise more severe than flicker noise cause the Allan deviation to increase with averaging time.
A plot of Allan deviation, σy(τ), versus averaging time, τ, for several standards is shown in Figure 2.3.
Power Supply
Power supply variations can induce frequency changes in at least two ways. Residual voltage changes after imperfect voltage regulation cause shifts by means of voltage coefficients. LOs with voltage-variable tuning capacitors are particularly susceptible. Input voltage variations will cause variations in the power dissipated in the voltage regulators, and the resulting temperature changes can induce frequency changes.
Good quartz LOs have typical voltage coefficients of ±5 × 10−11 per volt. Rubidium gas cell devices are perhaps five times better. The best cesium beam standards will change less than ±1 × 10−13 over the full voltage range.
Radiation
In space-based clocks, radiation effects are a significant determinant of clock performance and lifetime. Background radiation particularly affects the performance of the quartz crystals, whether they are used as clocks or as the LO, by inducing defects in the crystals over time.
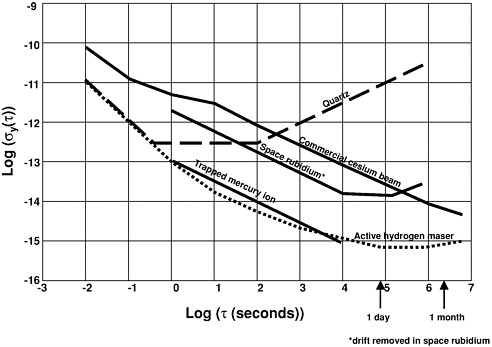
FIGURE 2.3 Short-term stability of some state-of-the-art standards.











