2
High Energy Density Astrophysics
INTRODUCTION
In ancient times, the heavens were thought of as perfect, static, and immutable. Today we see the universe as a place of titanic violence and continuous upheaval. The twin engines of gravitational collapse and nuclear fusion power phenomena on a nearly unimaginable scale. Giant black holes consume the fiery hearts of galaxies, sweeping entire star systems into their immense accretion disks; relativistic particle jets, powered by unknown acceleration mechanisms, focus their extreme energies with incredible precision across millions of light years; supernovae shocks sweep up turbulent plasma and dust, creating the seeds for stellar rebirth; neutron stars the size of Manhattan spin at kilohertz rates, weaving their huge magnetic fields through the surrounding plasma and creating brilliant x-ray lighthouses. Meanwhile, in our own relatively placid corner of the Galaxy, we are pelted by cosmic rays of such immense energy that their very existence is difficult to understand, and the formation, structure, and dynamics of the most massive of our solar companions, the giant planets, remain a mystery.
The immense energy densities associated with these phenomena could never be reproduced on Earth. Or could they? Certainly, these conditions can be recreated mathematically using computer models and analytical calculations (if only we had better understanding of the physics!). Perhaps, tiny portions of these extreme environments can be made to flash in and out of existence in accelerator collision chambers, in the focal spots of high-power lasers or particle beams, or at the core of
magnetic Z-pinch machines. With the aid of such experiments, and through new analytical, computational, and technical breakthroughs, it may soon be possible to gain improved understanding of the physics underlying some of the universe’s most extreme phenomena and to answer some of the fundamental questions outlined in the following sections. Indeed, over the past decade a new genre of laboratory astrophysics has emerged, made possible by the new high energy density (HED) experimental facilities, such as large lasers and Z-pinch generators. On these facilities, macroscopic collections of matter can be created in astrophysically relevant conditions, and their collective properties measured. Examples of processes and issues that can be experimentally addressed include compressible hydrodynamic mixing, strong-shock phenomena, radiative shocks, radiation flow, high-Mach-number jets, complex opacities, photoionized plasmas, equations of state of highly compressed matter, and relativistic plasmas. These processes are relevant to a wide range of astrophysical phenomena, such as supernovae and supernova remnants (see Figure 2.1), astrophysical jets (see Figure 2.2), radiatively driven molecular clouds, accreting black holes, planetary interiors, and gamma-ray bursts. In this chapter these phenomena are discussed in the context of laboratory astrophysics experiments possible on existing and future HED facilities. Key questions in each area will be raised, with the hope and expectation that future experiments on HED facilities will play some role in their resolution.
HIGH ENERGY DENSITY DEFINITIONS FOR ASTROPHYSICS
Stars are plasma. This state requires energy in excess of the binding energy of molecular or solid matter—which for the most abundant element, hydrogen, corresponds to 4.4 electronvolts or to a gas temperature of about 23,000 K.
More extreme conditions abound. They may be classified by equating a thermal kinetic energy (a temperature), or a quantum degeneracy energy (a Fermi energy) to the specified energy. For example, the temperature corresponding to the rest-mass energy of an electron is 6 billion K, and the density at which the electron Fermi energy equals its rest-mass energy is 1 million times that of water.
Another set of extremes can be constructed from velocities. Relativistic conditions are energetically extreme: as the velocity of light is approached, the energy of a particle exceeds the rest-mass energy. For typical conditions in the interstellar medium, the sound velocity is about 10 kilometers per second (km/s), while gas motions often exceed this by factors of 10 to 100. Under these conditions, strong shocks, with Mach numbers of 10 to 100, are generated.
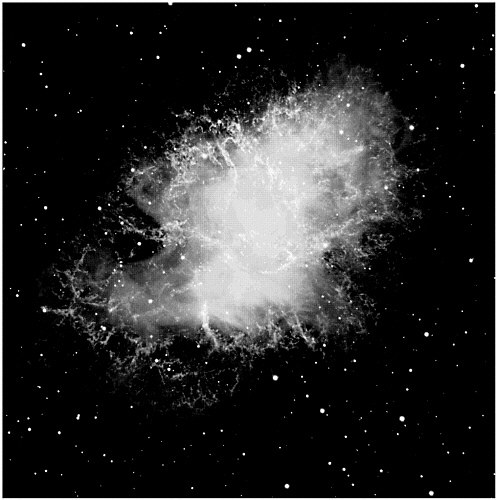
FIGURE 2.1 Crab Nebula in the optical. The Crab Nebula, a supernova remnant whose parent supernova was recorded by Chinese astronomers in the summer of A.D. 1054, is a beautiful example of a relatively young remnant, whose appearance is thought to be largely driven by particle acceleration processes tied to the Crab Pulsar; the observed radiation is due to synchrotron emission from highly relativistic electrons accelerated within the structure seen in this image. The precise nature of the connection between the pulsar and its magnetosphere, and the surroundings, remains uncertain. Courtesy of the European Southern Observatory.
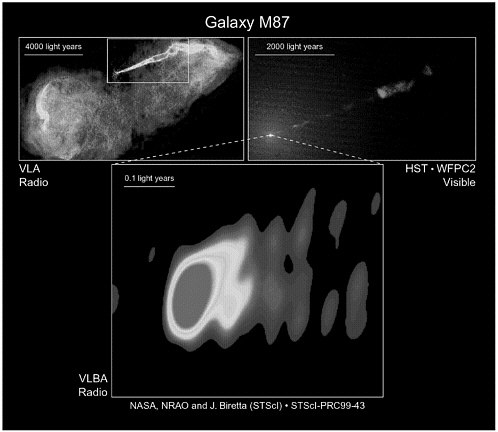
FIGURE 2.2 Jet formation. Images of the active galaxy M87. Using a variety of high angular resolution observations, astrophysicists have been able to disentangle the spatial structure of jets emanating from the core of active galaxies. Such jets present a wealth of unsolved physics problems, ranging from the precise composition of the material composing the jet itself, to its stability, and—most uncertain—its ultimate origin: acceleration to relativistic energies and remarkable collimation. The “engine” producing these jets is most likely one of the most extreme physical environments encountered in astrophysics, namely, the vicinity of a massive black hole lying near the core of active galaxies (see Figure 2.6 in this chapter). Courtesy of W.Junor, University of New Mexico/Los Alamos National Laboratory; and J.A.Biretta and M.Livio, Space Telescope Science Institute.
THE FUNDAMENTAL QUESTIONS FOR HIGH ENERGY DENSITY ASTROPHYSICS
How Does Matter Behave Under Conditions of Extreme Temperature, Pressure, and Density?
A fundamental quest of physics is to determine the properties of matter—its equation of state, its opacity, and its transport properties (thermal conductivity, viscosity, particle diffusivity, electrical conductivity, and so on). The universe offers a huge range of conditions for matter, far beyond what can be directly obtained in a terrestrial laboratory setting. Following are some examples of new opportunities for studies of matter under extraordinary conditions, spanning both laboratory and astrophysical settings.
The Origin and Evolution of the Giant Planets and Brown Dwarfs and of Planetary Interiors
The discovery of extrasolar planets and brown dwarfs represents one of the most exciting astronomical developments of the decade. The newly discovered planets tend to be giant gas planets with small, highly eccentric orbitals. These new “hot giants” raise many questions about existing models for planetary formation and planetary interiors. Models exist for the interiors of the extrasolar planets as well as for the solar planets, but these models rely upon a quantitative understanding of cold, dense matter at extreme pressures. At such high pressures, the matter is pressed so closely together that the outer electronic orbitals overlap, causing pressure ionization. This serves as an energy sink, which affects the compressibility. Such coupled quantum-mechanical-thermodynamic effects are notoriously difficult to calculate theoretically.
In order to solve the many fundamental questions of planetary formation, evolution, and structure, it is essential to improve our understanding of hydrogen in the ultrahigh-pressure environment found in the interior of brown dwarfs and giant planets. This environment is characterized by moderate temperatures of order 0.1 to 1 eV, and extreme pressures of order 1 to 10 Mbar. Under these conditions, hydrogen is expected to form a degenerate strongly coupled plasma/fluid. The basic thermodynamic properties of such plasmas are still incompletely characterized.
In the specific case of the interior of Jupiter (see Figure 2.3), model calculations predict that molecular hydrogen (H2) dissociates to atomic hydrogen and ionizes in the mantle, changing from a dielectric to a conductor. The relevant pressure and temperature for this transition is 0.5 to 5 Mbar at temperatures of a fraction of an electronvolt. Deeper in the interior of Jupiter, the pressure and temperature increase to above 40 Mbar and a few electronvolts near the center. For reference, the
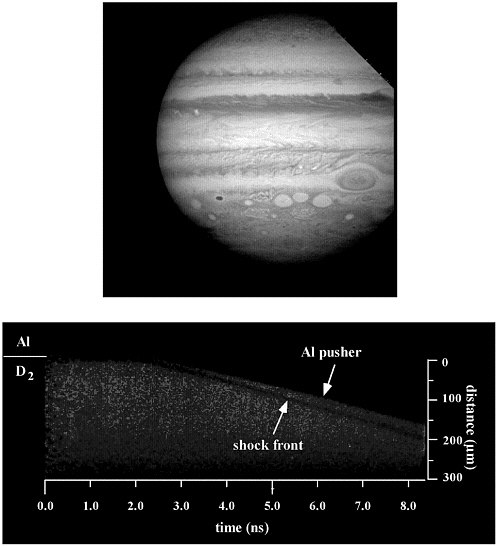
FIGURE 2.3 Planetary interiors and their equation of state. The internal structure of the giant gaseous planets, such as Jupiter shown in the top image, is an ongoing puzzle, primarily because of uncertainties regarding the properties of matter at extreme pressures. One of the few ways to explore such questions experimentally is to probe the relevant materials (primarily hydrogen) in lasers and magnetic pinch facilities, which give us access to the relevant physical regimes; an example of such an experiment is shown in the image on the bottom, drawn from an equation-of-state experiment carried out at a laser facility. The ultimate aim of such studies is to be able to discriminate between different planetary formation models. Courtesy (top) of NASA and Space Telescope Science Institute, and (bottom) R. Cauble and G. Collins, Lawrence Livermore National Laboratory.
corresponding conditions for the brown dwarf GL 229 are similar in the mantle, but 4 orders of magnitude higher in pressures at the core, Pcore ≈ 105 Mbar. The molecular dielectric to atomic metallic transition in hydrogen (H2→H++H+) is important because convection of pressure-ionized, metallic hydrogen is thought to create the 10 to 15 gauss magnetic field of Jupiter. Of particular concern is whether a first-order plasma phase transition exists, as this critically affects the internal structure in the important convection zone and the degree of gravitational energy release due to sedimentation of helium (He) and heavier elements. Jupiter and Saturn’s atmospheres are observed to be helium-poor, and the energy release from helium sedimentation is required to explain Saturn’s intrinsic heat flux.
Among the open questions are these:
-
What is the phase diagram of high-pressure hydrogen?
-
Is there a (first-order) plasma phase transition?
-
Does hydrogen form a metallic state at high pressure?
-
What is the solubility of other chemical elements (especially He) in a high-pressure hydrogen plasma? Can H and He become immiscible, with the formation of “He rain,” at high pressure and density?
In addition, transport properties in general (such as electrical and thermal conductivity) are poorly understood, but are essential if we are to understand dynamical processes such as magnetic field generation and thermal convection.
An improved understanding of hydrogen in the high-pressure regime would directly impact the following fundamental questions of planetary science:
-
What is the structure of a gas giant as a function of depth?
-
Where (and what) is the region within which the magnetic field is generated?
-
Are such planets fully convective?
-
Do these planets form by direct collapse of the solar nebula, or do they form around a preexisting rock-ice core? By inferring the core conditions of Jupiter, can the planetary formation mechanism for the solar system be inferred?
-
What high-pressure chemistry goes on within such planets?
While much of the hydrogen equation of state is well known, many of the important questions require accuracy at the 1 percent level in density for a given pressure and temperature. (For example, 1 percent of Jupiter’s mass is 3 Earth masses, comparable to the postulated core mass.) Transport properties are currently much less-well understood, and even a factor-of-2 knowledge of the electric and thermal conductivity would be useful. Miscibilities of various cosmically abundant elements in hydrogen within a factor of 2 would also be a great advance relative to current
knowledge. It is possible that new experiments involving high energy density plasmas may soon be able to answer these questions, while improved astronomical observations will allow us to explore more fully the mass range of extrasolar giant gaseous planets down to values characteristic of such planets in our solar system.
Another area of interest is the atmosphere and envelope of white dwarfs. Accreting white dwarfs are thought to be the starting point of Type Ia supernovae, which in turn are used as “standard candles” to map out the expansion of the deep universe. Cooling white dwarfs can be used as “clocks,” or cosmochronometers, to determine the age of regions of the Galaxy. An understanding of the equation of state, opacity, and heat conductivity in the atmospheres and envelopes of white dwarfs would be very beneficial, and may be experimentally accessible, especially with future facilities, as described in this subsection.
Experimental techniques are being developed on pulsed-power facilities, lasers, gas guns, and diamond anvil cells to probe the properties of matter under extreme conditions of pressure and compression. The conditions achieved to date cover pressure ranges of 0.1 to 40 Mbar in equation-of-state measurements, planar shock pressures of up to 750 Mbar in a proof-of-principle demonstration experiment, and ≈10 gigabars (Gbar) at the core of an imploding spherical capsule. Using modern pulse shaping techniques on lasers and on magnetic pinch facilities, pressures in the megabar regime under quasi-isentropic compressions have been achieved. In the coming decade, with the advent of the National Ignition Facility and Laser Megajoule (LMJ) lasers, this parameter space will be filled in and extended. On these future facilities, quasi-isentropic compressions of well over 10 Mbar should be possible. These laboratory conditions correspond to the interiors of terrestrial and giant gas planets, brown dwarfs, average mass stars, and the envelopes of white dwarfs. Even the simplest case studied experimentally so far, the equation of state of hydrogen, shows the humbling complexity of the behavior of matter under extreme conditions of compression. To develop and have confidence in theoretical and numerical models that pertain to the interiors of the astronomical objects referred to above will require experimental data to guide the way.
Strongly Coupled Plasmas
Most of our understanding of plasmas comes from study of tenuous, ionized gases, in which the electromagnetic behavior is a modest modification of the simpler gas behavior. This Debye (weak coupling) limit breaks down as density increases and/or temperature decreases. At the other extreme, we are familiar with the liquid and solid states. The intermediate condition, “strongly coupled” plasmas, is complex and challenging to understand theoretically. It corresponds to the conditions in giant planets, brown dwarf and white dwarf stars, and the progenitors of Type Ia
supernovae. It occurs naturally in HED plasma experiments, and a fertile interaction between astronomy and HED plasma physics has begun in this area. (See Figure 1.1 in Chapter 1 and Figure 3.3 in Chapter 3 for a summary of relevant regimes.) The line labeled E(coulomb)=kT in Figure 1.1 represents the boundary for strongly coupled plasmas: they lie to the right (at higher density).
The Opacities of Stellar Matter
Historically, one of the oldest areas of overlap between HED plasma physics and astronomy has been the radiative opacity of matter. The opacity of stellar plasma controls the rate at which energy leaks from stars, that is, their luminosity. If large enough, opacity causes the onset of mixing currents which, in turn, modifies the structure of stars and their evolution. For example, a well-mixed Betelgeuse would be blue, not red. The bumps in the opacity curves (the changes with temperature and density) can drive pulsations and probably mass loss. Cepheid pulsating stars are the other cosmological yardstick.
Type Ia supernovae provide a particularly fundamental and important challenge: the luminosity and effective temperature we observe is governed by leakage of light from the plasma, but the expansion is so great that the light is red-shifted between emission and absorption, making the probability of its escape too difficult to solve accurately. Observations of these supernovae seem to imply that the universe is expanding at an accelerated rate, contrary to prediction. This conclusion is based on empirical rules for behavior of relatively nearby supernovae, and involves a light curve shape-luminosity correction based on an opacity hypothesis. An understanding based on laboratory experiment would be much more compelling. For example, measurement of the radiation transport in a rapidly expanding, inhomogeneous, fully three-dimensional target would greatly contribute to our understanding of the behavior of Type Ia supernovae.
The error budget for the ages of stellar clusters is dominated by uncertainties in opacity. Continued refinement of our knowledge will allow us to better place a time scale on the formation and development of our Galaxy and nearby galaxies.
Degenerate Plasma Convection
Type Ia supernovae, novae, and the core helium flash are supposed to be initiated under conditions of strong degeneracy of electrons. Thermonuclear burning begins in a degenerate plasma and proceeds to thermal runaway; as the temperature rises in the flame region, a convective instability develops and eventually proceeds to explosion. Similar convective motions under degenerate plasma conditions—
albeit without the local nuclear burning and possible runaway—are thought to occur in the outer regions of brown dwarf stars. Unfortunately, there are no experimental data on convection in an (electron) degenerate plasma; thus, unlike the case of, for example, Boussinesq convection, very little is known about degenerate convection. For this reason, both experiments and fundamental theory and simulations directed at convection under degenerate conditions are very important.
Physics of Nuclear Burning
Historically, the study of nuclear reactions has been based on acceleration of particles and study of their scattering off a target. In a burning plasma, one must also account for the effects of the more complex environment. Instead of bare nuclei, the “projectile” and the “target” have an associated cloud of electrons, and there are other ions and their electrons around. A short term for these additional effects is “screening.” At present, a debate rages over the question of whether plasma screening of reacting nuclei is static or dynamic. As plasmas so often exhibit subtle behavior, even sophisticated physical models can be misleading.
In the Sun, the plasma screening only affects the reaction rate at the level of a few percent. However, in progenitors of supernovae, the screening factors are large (a few million), which makes a purely theoretical estimate dubious. A better theory would result from experimental tests, making the necessary extrapolation to more extreme conditions more reliable.
Detailed laboratory measurements could settle these important issues. HED experiments promise to allow the study of a nuclear-burning plasma, that is, the source of stellar energy. Accelerator experiments have provided means to study nuclear reactions in a piecemeal way; HED experiments will allow us to place the phenomena into the context of a burning plasma. In estimating the rate of stellar nuclear reactions, some assumptions about the plasma medium must be made; HED experiments will allow these to be tested directly. As Figure 1.1 shows, the experimentally accessible range already overlaps stellar conditions of temperature and density. Well over 99 percent of the stars in the sky are burning hydrogen and/or helium, and there conditions are mostly in the range that is now available to OMEGA and will be available to NIF.
Stellar burning is slow because the basic fusion reactions that the stars use are slow. Experiments with burning plasmas that are based on faster reactions are feasible—in fact, that is one way of expressing the goal of thermonuclear ignition for NIF. Burning plasma experiments will allow us to study the same process, if not the identical reactions, that powers the stars.
The Nature of Matter at the Extremes
The quark-gluon plasma is a new phase of matter—in the sense that it has not yet been detected in the laboratory—whose elementary constituents are the quarks, antiquarks, and gluons that make up the strongly interacting particles. It is also the oldest phase of matter, the form of matter that filled up the early universe, until the first few microseconds after the big bang. Appropriate for this report, quark-gluon plasmas are the densest plasmas in the universe. They may possibly be present deep in the cores of neutron stars, and may even be made in stellar collapse. To probe the densest states of nuclear matter, the nuclear physics community has embarked on a large-scale program of studying collisions of ultrarelativistic heavy ions, at Brookhaven National Laboratory and the European Organization for Nuclear Research (CERN). A major step in the program is the construction of a large colliding beam accelerator at Brookhaven—the Department of Energy’s Relativistic Heavy Ion Collider (RHIC)—which will provide the capability of colliding nuclei as heavy as gold on gold at 100 GeV per nucleon in the center of mass (equivalent to 20 teraelectronvolts [TeV] per nucleon in a fixed target experiment), and should, early in this century, enable one to produce and study quark-gluon plasmas in the laboratory.
The basis for expecting a quark-gluon plasma at high densities or temperatures is that quite generally as matter is heated or compressed, its degrees of freedom change from composite to more fundamental. For example, by heating or compressing a gas of atoms, one eventually forms a plasma in which the nuclei become stripped of the electrons, which go into continuum states forming an electron gas. Similarly, when nuclei are squeezed (as happens in the formation of neutron stars in supernovae where the matter is compressed by gravitational collapse), they merge into a continuous fluid of neutrons and protons. Nucleons and the other strongly interacting particles, or hadrons, are made of quarks that are confined to the individual hadrons. One can thus go a step farther and predict that a gas of nucleons, when squeezed or heated, turns into a gas of uniform quark matter, composed of freely roaming quarks, and at a finite temperature, antiquarks and gluons—the mediators of the strong interaction. The physics is basically the same as that leading to the formation of ordinary plasmas.
The regions in the phase diagram of matter in the temperature-baryon density plane where quark-gluon plasmas are expected to occur are outside the phase space included in Figure 1.1 in Chapter 1. In the low-temperature-low-baryon-density region, the basic degrees of freedom are hadronic, those of nucleons, mesons, and internally excited states of the nucleon, while in the high-temperature-high-baryon-density regions (temperatures above about 200 MeV, equivalent to a few times 1012 K, and densities of order 5 to 10 times the density of matter inside a large nucleus, approximately 0.16 particles per cubic femtometer [fm−3], equivalent to
2×1014 grams per cubic centimeter [g/cm3]), the basic degrees of freedom should become those of quarks and gluons. The transition between these regions may be first or second order, or not a sharp transition at all, but washed out. Under any circumstances, the physics between the two regimes changes strongly.
Where are quark-gluon plasmas expected to occur in nature? In the first microseconds of the early universe, the temperature falls as T≈1 MeV tsec−1/2, so that prior to around 5 to 10 microseconds (µs) after the big bang, when temperatures are above hundreds of MeV, matter is in the form of a quark-gluon plasma and follows the downward trajectory practically along the vertical axis of the phase diagram. The matter of the early universe has a relatively small net baryon density, of order 1 part in 109 (as inferred from the present photon/baryon ratio). As the universe expands, it cools, and matter hadronizes, undergoing the reverse of the deconfinement transition and emerging primarily in the form of pions, with a slight baryon excess. If the transition is first-order, one expects the formation of bubbles of hadrons—the ordinary neutrons, protons, and pions—in the middle of the plasma.
A second possible astrophysical situation in which quark-gluon plasmas might play a role is in neutron stars. Measured masses of neutron stars are ≈1.4 solar masses, with radii calculated to be about 10 km. Typical temperatures are relatively low, less than 1 MeV. The central density in a neutron star can reach 5 to 10 times the density inside an ordinary atomic nucleus and may be in the form of a quark plasma. Not only may neutron stars have quark cores, but one cannot rule out the possibility that there exists a distinct family of quark stars with higher central densities than that of neutron stars. The order of the quark-gluon phase transition may have important implications for gravitational-wave radiation from stellar collapse.
A third astrophysical situation in which these issues arise is the formation of neutron stars and black holes by the gravitational collapse of stars. Any discussion of the source of energy for gamma-ray bursts (GRBs) and core collapse supernova explosions, as well as of the nature of the formation of the dense remnants, requires assumptions regarding the equation of state of (warm) matter at and above nuclear densities. This regime lies between that of the big bang (hot) and neutron stars (cold), and involves similar questions of physics.
The only reliable approach at present to determine the properties of strongly interacting quark-gluon plasmas and the deconfinement transition is through Monte Carlo calculations of lattice gauge theory. These calculations require very large computing capabilities to achieve good statistics on large lattices. Lattice gauge theory is approaching the point at which it will be able to give quantitative information on the properties of quark matter over large ranges of temperature and also baryon density. Calculations to date have been successful only for the case of zero baryon density at finite temperature, and the results depend strongly on the masses assumed for the quarks. Lattice gauge calculations at nonzero baryon density are
beset by technical problems; we do not have a reliable estimate of the transition density at T=0 from nuclear to quark matter, or even compelling evidence that there is a sharp phase transition. In the absence of a good theory of the equation of state at very high densities, the question of whether neutron stars can have quark matter cores remains open, as is the issue of whether a distinct family of quark stars with higher central densities than those of neutron stars can exist.
The Most Energetic Particles in the Universe
It has long been known—since the early 20th century—that Earth is constantly subjected to showers of extraordinarily energetic particles, ranging in energy from kiloelectronvolts up to the remarkable value of over 1020 eV.
Collisionless Shocks and Cosmic-Ray Acceleration High-Mach-number collisionless shocks present an environment in which turbulence must have quite a different character from that of ordinary hydrodynamic turbulence. Here suprathermal particles and cosmic rays create a nonlinear wave spectrum through velocity space instabilities that scatter these particles which, in turn, are important in moderating the shock. These instabilities are referred to by the astrophysics community as magnetic hoop instabilities and by the laboratory HED community as hosing instabilities, Weibel instabilities, or filamentation instabilities. However, we do not understand the nature of this turbulence or even if it is stationary. Laser and beam instability experiments carried out in large chambers filled with magnetized plasma are quite capable of creating collisionless shocks, the properties of which can be studied.
A key question for many of these fluid issues is the character of the microphysical dissipation at the smallest scale of a turbulence spectrum, in an anomalously resistive reconnection site, and at a shock front. Theories abound, but confident understanding is rare. Turbulence has been proposed to terminate through reconnection, ion cyclotron resonance, or transit time damping. The partition of the dissipated energy between the ions and the electrons controls the dynamics and the radiative properties of the flow. Anomalous resistivity is rarely invoked astrophysically, although much is already understood experimentally. High-Mach-number shock dissipation is barely observed from spacecraft measurements and not understood at all. Relativistic shocks, which are central to the most energetic and interesting phenomena, must be quite different on purely kinematic grounds, as magnetized particles cannot outrun or catch the shock.
What Is the Origin of the Highest-Energy Particles in the Universe? Cosmic rays with energies above 1020 eV have been detected by a number of ultrahigh-energy cosmic
ray (UHECR) experiments. In 1991, the largest fluorescence detector, the High Resolution Fly’s Eye, recorded a surprising event with 3×1020 eV, or about 50 joules (J), which is comparable to the kinetic energy of macroscopic objects such as baseballs. Presently, the largest operating ground array, the Akeno Giant Air Shower Array (AGASA), has now measured 10 events above 1020 eV, while the Fly’s Eye fluorescence detector has observed about 2 events above 1020 eV. These events are detected either through the fluorescence light generated by the electromagnetic cascade produced as the UHECR interacts in Earth’s atmosphere or by direct detection of the cascade particles in ground arrays. The data were calibrated by numerical shower simulations, and typical energy errors are estimated to be 10 to 20 percent.
These UHECR events have an unexpectedly high flux and a surprisingly isotropic arrival directional distribution. If these particles are protons, the galactic magnetic field is not strong enough to contain them, and the sources are most certainly extragalactic. The flux observed on Earth from extragalactic high-energy proton sources are expected to have a large drop at energies around 1020 eV, due to the interaction of UHE protons with the cosmic microwave background radiation. This drop is due to the threshold for pion production by protons interacting with the background radiation; it is known as the Greisen-Zatsepin-Kuzmin (GZK) cutoff. The lack of a GZK cutoff challenges most astrophysical acceleration models and is often claimed as evidence for new physics at the highest energies.
HED plasmas play a key role in many aspects of this problem. First, the observations of such particles are made through the sampling of showers in the atmosphere. Large systematic errors arise from the lack of direct calibration of the shower development codes and from the different techniques used in ground arrays versus fluorescence detectors. Recent studies have shown that validation of shower simulations can be achieved by studying showers in a hybrid high-energy physics and plasma physics laboratory, such as the high-intensity particle and photon beam facility proposed as a Laboratory for Astrophysics at the Stanford Linear Accelerator Center (SLAC).
A second key role for HED plasmas is in explaining the nature of the astrophysical accelerators proposed as the origin of UHECRs. The most common extragalactic accelerator proposals involve shock acceleration in a number of astrophysical sources such as active galactic nuclei (AGN), radio lobes and jets around AGN, cluster shocks, and gamma-ray bursts. One possible resolution for the UHECR puzzle involves a new source of extragalactic UHE protons with a surprisingly hard (high-energy) injection spectrum. It is yet to be shown that shock acceleration can reach the spectral and maximum energy requirements on any known source. Fast reconnection is often invoked, but precise spectrum predictions in these alternative models are still lacking. The hardest predicted spectra are reached by relativistic
magnetohydrodynamic (MHD) winds created in unipolar inductors around fast-spinning, highly magnetized neutron stars. These powerful magnets can be sites where heavy nuclei are accelerated in the Galaxy or in the Local Group—a group of galaxies about 3 million light-years in diameter, which contains our Galaxy, the Milky Way. The propagation of heavy nuclei in the Galaxy can still be diffusive at these highest energies, depending on the structure of the galactic magnetic field. Unipolar inductors may also be active in accretion disks around massive black holes. The detailed understanding of these relativistic MHD processes requires both theoretical and numerical advances as well as experimentally validated studies of the numerical simulations.
The propagation of the UHECRs from source to Earth probes magnetized plasmas on the largest scales in the universe, the scales of clusters and superclusters of galaxies. The strength and structure of extragalactic magnetic fields are largely unknown. There is evidence for magnetized large-scale regions in clusters and between clusters, but the origin of magnetic fields on the large scales are still unknown. On the largest scales, the strength and structure of extragalactic fields are loosely constrained by indirect observations such as Faraday rotation of emission from high redshift quasars. The study of the origin and evolution of magnetic fields in galaxies and in clusters and superclusters of galaxies plays a key role in predicting the propagation of UHECR in the extragalactic medium, while observations of UHECR correlations can, in principle, give the strongest constraints on the largest-scale magnetic fields in the universe. AGASA data show a significant correlation of events on small angular scales (about 2°). If these small-scale correlations are confirmed to be extragalactic sources by future experiments such as the international Pierre Auger Observatory project, the extragalactic magnetic field will be most strongly constrained.
In the near future, detection of UHECRs with the Pierre Auger Observatory will greatly improve the data at the highest energies. The broad characteristics of the highest energy accelerators in nature will be unveiled. Detailed understanding of acceleration and propagation of the highest-energy particles ever observed demands a coordinated effort from the plasma physics, particle physics, and astrophysics communities.
Cosmic Magnetic Fields and Their Impact
Observations indicate that the universe is pervaded by magnetic fields, from Earth’s interior and immediate surroundings (its magnetosphere) to the interplanetary medium, the Sun itself, the interstellar medium, and even the space between galaxies. The origin of these magnetic fields remains a mystery, including especially the origins of magnetic fields in astronomical objects specifically relevant to HED astrophysics—the magnetic fields of neutron stars and giant gaseous planets.
Over the past few decades, however, substantial progress has been made in the fundamental understanding of the general magnetic-field generation (the “dynamo problem”); and in a specific case, namely Earth, a fairly complete understanding of why it has pervasive magnetic fields appears close. These results are due to a combination of observational, theoretical, and large-scale numerical computational studies. A similarly detailed understanding of the origin of Jupiter’s magnetic fields, or of the magnetic fields of neutron stars, is still absent. In these cases, models have been proposed, but the detailed calculations and measurements that would allow an understanding of how these magnetic fields came to be present have not been carried out.
If magnetic fields were simply passive constituents of the universe, then the question of origin would not be particularly pressing. However, magnetic fields are far from passive—indeed, it has been said that magnetic fields are what prevent stars from being simple self-gravitating gas spheres: the phenomenon known as stellar activity, which in the case of the Sun is manifested by its sunspot cycle, its corona, and the dramatic surface phenomenology (ranging from solar flares to coronal mass ejections, see Figures 2.4 and 2.5) all are thought to be a consequence of the interaction between magnetic fields and conducting astrophysical fluids. Indeed, magnetic fields play significant roles in a number of astrophysical phenomena. A few examples of those roles are illustrated below.
Solar and Stellar Activity There has been a revolution in solar physics. We are now able to watch magnetic instability and topological rearrangement of field lines on the surface of the Sun under conditions that are not dominated by solid boundaries, fixed magnets, and initial conditions. The slow winding and squeezing of flux tubes below the photosphere make it restless and explosive. Laboratory experiments interpreted with large numerical simulations are starting to bring out the principles, notably those involving magnetic helicity, that determine how the field rearranges itself.
Astrophysical plasmas are famous for their impressively large magnetic Reynolds numbers, with dissipation almost always and everywhere negligibly small. However, just as in aerodynamics, it is the exceptions that make all the difference. They control the heating of the solar corona and the launching of the solar wind. They determine the circulation of planetary magnetospheres and the emissivity of accretion disks. One key effect is magnetic reconnection, which remains a highly controversial topic. We do not know if and when it is “fast.” We do not agree if heating occurs mostly on small scales, in nanoflares, or on large scales. In addition, new modes of reconnection are mathematically possible, but we do not know how relevant they are in practice. It is likely that most of the current flow occurs in thin sheets and filaments, as opposed to uniformly, and this has a major impact on the

FIGURE 2.4 TRACE probe image of solar surface. This image of a portion of the multimillion-degree solar corona, taken through the 171-angstrom passband of the TRACE satellite, shows the characteristic emergence of a large-scale structure—the so-called coronal loops—whose appearance is apparently controlled by physical processes on far smaller spatial scales. Because we can resolve these structures, the Sun’s activity can serve as an astronomical Rosetta stone for decoding spatially unresolved observations of much more distant astrophysical objects in terms of physical processes that can be explored in terrestrial laboratories. Courtesy of NASA and Stanford-Lockheed Institute for Space Research.
stability properties. What experience we have from tokamak physics research has not permeated the astrophysical community.
As with regular fluids, turbulence is central to MHD. It can be studied using radio waves propagating through the interplanetary and interstellar media, and it appears to be anisotropic. In the incompressible limit, the governing principle appears to be that as energy cascades to smaller scales, the field gradient becomes more strongly directed perpendicular to the mean magnetic field, with implications for reconnection. Applying these ideas to understanding the nature of dissipation in
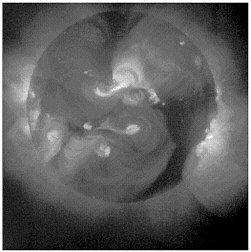
FIGURE 2.5 Yohkoh x-ray image of the Sun. This soft x-ray image of the full-disk Sun, taken by the U.S.-built Soft X-ray Telescope (SXT) onboard the Japanese Yohkoh satellite, illustrates the remarkable propensity of astrophysical objects to produce magnetic fields on spatial scales ranging from the smallest resolvable scales to the scale of the system taken as a whole. In the case of an object such as the Sun, this field generation—the stellar dynamo—leads directly to solar “activity,” accompanied by particle acceleration, vigorous (transient) plasma heating, and occasional huge mass ejections into the interplanetary medium. Courtesy of Lockheed-Martin Solar and Astrophysics Laboratory, the National Astronomical Observatory of Japan, the University of Tokyo, the Japanese Institute of Space and Astronautical Science, and NASA.
accretion disks is problematic. We are not sure if an inertial range turbulence develops or if the cascade is to large scales or takes the form of Alfvén waves that escape the disk altogether. Numerical simulations are playing a large role here, but there is an opportunity for beam-plasma experiments in which we generate turbulence at an interface as well.
Accretion Disk Magnetic-Field Dynamics: Magnetohydrodynamic Turbulence and Angular Momentum Transport Accretion is the main source of energy in many astrophysical objects, including binary stars, binary x-ray sources, and quasars and active galactic nuclei. While the first development of accretion theory began a long time ago, intensive development of this theory began after the discovery of the first x-ray sources. Accretion onto stars, including neutron stars, terminates at an inner
boundary. This may be the stellar surface or the outer boundary of a magnetosphere for a strongly magnetized star. In this case, all of the gravitational energy of the infalling matter is transformed into heat and radiated outward.
The situation is quite different for accretion to black holes (see Figure 2.6), which are deduced to be present in some binary x-ray sources in our Galaxy as well as in active galactic nuclei. Here, matter falls into the event horizon of the black hole, and no radiation escapes from within it. The radiative efficiency of accretion is not known a priori, in contrast with the case of accretion onto a star, and depends strongly on factors such as the angular momentum of the incoming matter and the magnetic field embedded in it. For spherical accretion of nonmagnetized gas, the efficiency of radiation may be as small as 10−8 for low mass accretion rates; the presence of a magnetic field in the accreting matter can increase the efficiency up to
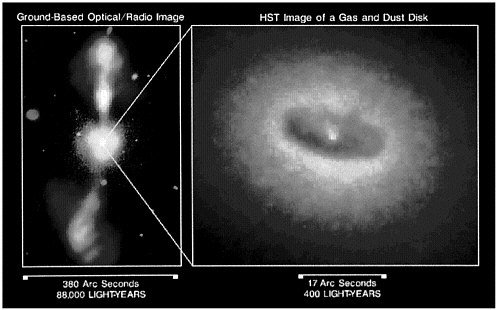
FIGURE 2.6 Spectroscopy of emission from accreting black-hole systems, together with modeling and laboratory experiments (such as on the Z-machine, where similar values of the photoionization parameter to those characterizing the astrophysical system can be achieved), allows us to understand the spectral signatures characterizing the dynamics and conditions of matter as it spirals into a black hole. Courtesy of W.Jaffe, Leiden Observatory, the Space Telescope Science Institute, and NASA.
about 10 percent. Recent attention has focused on advection-dominated accretion flows and convection-dominated accretion flows, where it is possible that the efficiencies are much less than 10 percent. Understanding the low efficiencies is crucial to understanding the very low luminosities of some black holes, such as that in the center of our Galaxy. The low luminosities may also result from jets and outflows.
The viscosity is the most speculative aspect of current accretion disk theory and modeling. The viscosity generally acts to transport angular momentum outward, away from the star or black hole, facilitating the accretion of matter. In the laminar case of microscopic (atomic or plasma) viscosity, which is very small, a stationary accretion disk must be very massive and very thick; in this limit, it is known that the accretion rate onto the central object must be very small. This contradicts observations of x-ray binaries, where a considerable accretion rate is required. This can be explained only when the viscosity coefficient is much larger than the microscopic one; for example, if matter in the disk is turbulent, one can parameterize the viscous stress tensor as trϕ=−αρvs2=−αp, where α is a dimensionless constant ≤1, vs is the sound speed, ρ is the density, and p is the pressure. This simple parameterization corresponds to a turbulent viscosity coefficient ηt≈ρvtl with an eddy velocity vt and a length scale of the turbulent element l. The expression for trϕ with l≈h, with h the half-thickness of the disk, becomes trϕ=ρvthr(dΩ/dr)≈ρvtvs=−αρvs2, where the relation between turbulent and sound speeds is vt=αvs.
The development of turbulence in an accretion disk cannot be explained simply. A Keplerian disk is stable in the linear approximation to the development of axially symmetric perturbations, conserving angular momentum. That is, the disks satisfy the Rayleigh criterion for stability. It has been proposed that in the presence of very large Reynolds numbers, Re=ρvl/η about or greater than 1010, the amplitude of perturbations at which nonlinear effects become important is very low, so that turbulence may develop due to nonlinear instability even when the disk is linearly stable. Whether this mechanism works can in principle be tested via simulations; but such studies must await advances in simulation capabilities to allow systematic direct numerical studies of fully turbulent flows.
A magnetohydrodynamic instability as a source of the turbulence in accretion disks has been studied extensively by linear stability studies and MHD simulations during the past several years. The linear instability—the magnetorotational instability—was originally discovered in the late 1950s, but rediscovered and applied for the first time to accretion disks by astrophysicists in the 1980s; it occurs for a weak magnetic field in a differentially rotating disk (Alfvén speed<sound speed). In this context, there has been a considerable development of MHD simulations of turbulence and the associated viscosity coefficient αMHD, and they now involve full three-dimensional parallelized Eulerian grid calculations running on large numbers
of processors. This problem represents an important test case for compressible MHD simulation codes and techniques in that the linear theory is well understood. This instability could be important in the absence of any other source of turbulence and if the magnetic fields are sufficiently weak. Stronger fields probably occur in actual disks, and unstable singular modes have been recently discovered in a strongly magnetized accretion disk. This represents a promising area of future study for both linear stability analysis and MHD simulations.
A fundamental limitation on the MHD simulations of accretion flow turbulence is that the flows are only weakly collisional: the smallest scale of the turbulence (about a gyroradius) is much smaller than the mean free path. This is very different from turbulence in, say, the atmosphere, where the Navier-Stokes equations provide in principle a complete description. In fact, the entire issue of the smallest-scale dissipation—heating of electrons versus heating of ions—in MHD accretion flow turbulence is open. This dissipation is a crucial issue for advection-dominated accretion flows, and it requires a particle-in-cell type of simulation.
Laboratory experiments to investigate the MHD instability of differentially rotating liquid metals are under way at the New Mexico Institute of Technology, Princeton Plasma Physics Laboratory, and the University of Wisconsin. The experimental setups are similar to those used to create laboratory dynamos, and they suffer from the same limitation that magnetic Reynolds numbers are only moderately large compared with unity. Other experimental approaches need to be explored. The production of transient megagauss (100 kilotesla [kT]) fields in laser-induced explosions is probably due to inertial forces but may still turn out to be relevant to accretion flows. Large magnetic Reynolds numbers are more difficult to achieve in HED experiments because of the large magnetic diffusivity of these plasmas, though values of ReM of about 102 to 103 seem feasible.
In addition to the magnetorotational instability, other processes may be important, such as the macroscale hydrodynamic, Rossby wave instability recently shown to occur in nonmagnetized disks that have nonmonotonic profiles of surface density, pressure, and/or specific entropy. The instability has been found in two-dimensional hydrodynamic simulations and has been shown to give rise to a small number (3 to 5) of long-lived vortices that give outward transport of angular momentum. These vortices may have a key role in planet formation in disks around young stars.
Cosmic Jets Powerful, greater than 1046 ergs per second (ergs/s)=1039 watts (W), highly collimated, oppositely directed, relativistic jets are observed in many active galaxies and quasars and in old compact stars in binaries (1038 ergs/s). These present us with some of the most visually captivating images encountered in astronomy and astrophysics. In some of the most active quasar sources, the electromagnetic emissions extend from the radio about 108 hertz (Hz) to extreme gamma-
ray energies of about 1027 Hz (~1013 eV). Further, well-collimated emission line jets with velocities of 100 to 300 km/s are seen in many young stellar objects.
Recent observations, such as the Hubble Space Telescope images of HH 30, and theoretical and simulation studies support models where the twisting of an ordered magnetic field threading an accretion disk acts to magnetically accelerate the jets. The power in the jets is thought to come from matter accretion in the disk, but it may include power extracted electromagnetically from a spinning black hole. There are two main regimes:
-
The hydromagnetic regime, where energy and angular momentum are carried by both the electromagnetic field and the kinetic flux of matter, is relevant to the jets from young stellar objects; and
-
The Poynting flux regime, where energy and angular momentum from the disk are carried dominantly by the electromagnetic field, is relevant to extragalactic and microquasar jets and possibly to gamma-ray burst sources.
The theory of the origin of hydromagnetic outflows from accretion disks has been developed by many authors, starting from seminal work carried out in the early 1980s. MHD simulations (axisymmetric)—first done using a Lax-Wendroff method— have greatly increased the physical understanding of these outflows. Stationary MHD outflows have been discovered using a Godunov-type method. These stationary solutions have the five constants of the motion predicted by ideal magnetohydrodynamics. Within the simulation region, the outflows are observed to accelerate from thermal speed in the disk to a much larger asymptotic poloidal flow velocity of the order of 0.5 (GM/ri)1/2, where M is the mass of the central object and ri is the inner radius of the disk. This asymptotic velocity is much larger than the local escape speed and is larger than the fast magnetosonic speed by a factor of about 1.75. The acceleration distance for the outflow, over which the flow accelerates from about 0 to, say, 90 percent of the asymptotic speed, occurs at a flow distance of about 80 ri. The flows are approximately spherical outflows, with only small collimation within the simulation region. The distance over which the flow becomes collimated (with divergence less than, say, 10°) is much larger than the size of the simulation region. This lack of collimation conflicts with the common notion that the jets collimate due to the pinching force associated with the axial current flow.
Laboratory experiments on supersonic hydromagnetic jets relevant to understanding astrophysical jets can be done using conical, linear, and radial wire arrays in a Z-pinch facility, and the interaction of these flows—both collisional and collisionless—with target plasmas and with counter-propagating flows can be studied. In collisional systems, one can study the region of kinetic energy deposition,
the production of radiation, and the generation of shocks. Reducing the target density allows the study of the collisionless penetration of jets into target plasmas. Indeed, experiments on high-Mach-number, hydrodynamic jets and radiatively collapsing jets have been demonstrated both on lasers and on pulsed-power facilities, with internal Mach numbers of 5 to 10 for purely hydrodynamic jets, and Mach numbers as high as 50 to 60 for strongly radiatively cooled jets. Finally, a new class of very energetic, electrically neutral proton jets has been observed on ultrahigh-intensity, short-pulse lasers. The mechanism behind their formation is still being debated, but their existence at energies of up to 100 MeV is well established.
Poynting jets have been discovered in axisymmetric MHD simulations of the opening of magnetic-field loops threading a Keplerian disk. A typical initial disk magnetic-field configuration is a dipolelike field threading the disk where the field lines are in meridian planes (BrBz in cylindrical coordinates). The situation is analogous to a “foil-less,” magnetically insulated diode, because the rotation of the disk gives rise to electric potential variation F across the face of the disk (that is, Er=−vϕ×Bz/c, owing to the high conductivity of the disk). The potential variations are much larger than mec2/e, and they give rise to an outflow of positive and negative charges from the disk plane.
Laboratory simulations of the formation of Poynting jets can be done using a Z-pinch facility by imposing a pulsed potential difference Φ>106 V between cathode and anode surfaces on the disk plane z=0. Further, an initial dipolelike poloidal magnetic field can be supplied by a coil in the z=0 plane. A collimated Poynting jet is predicted to occur under conditions where Bz(0)≈µu0lz/(2πrC), where Bz(0) is the dipole field at the system center, lz is the current outflow from the cathode, and rC is the radius of the cathode. Appropriate diagnostics would allow measurements of the collimation and energy outflow of such a diode.
Exciting challenges in future magnetohydrodynamic simulation studies are understanding highly relativistic jets or Poynting flows with Lorentz factors of about 10 that are observed to emanate from some active galaxies, and the jets in gamma-ray burst sources that may have Lorentz factors of about 100. Recent progress has been made in the development of robust relativistic magnetohydrodynamic codes, including the Kerr metric of a rotating black hole. Ultimately, we would like to know the following:
-
Is there a universal jet formation mechanism operative for stellar, microquasar, active galaxy, and gamma-ray burst jets?
-
How do the jets remain collimated for so long?
-
Can the central engine dynamics, energetics, and history be inferred from the jet morphology?
A further puzzle is the nature of the acceleration of the radiating particles (electrons, and possibly positrons) that give rise to the observed synchrotron radiation from jets. It has been long recognized that this acceleration must be in situ in at least some jets (such as those of the quasar 3C 273 and the giant elliptical galaxy M87): the very high energy (up to x-ray) of the synchrotron radiation implies radiative lifetimes much shorter than the travel time from the central source. Lepton acceleration may occur in collisionless shocks distributed along the length of the jet. Alternative ideas such as particle acceleration in sporadic reconnection events have also been discussed. Thus, a remaining puzzle for jets is—
-
How are electrons and possibly positrons accelerated in jets?
How Does Matter Interact with Photons and Neutrinos Under Extreme Conditions?
Physics seeks to determine how matter interacts with the nonbaryonic components of the universe—ranging from photons to neutrinos to yet more exotic forms of matter. Here again, recent results from astrophysics have led us into new and unusual domains in which these interactions can be studied.
Intense Photoionization: Accreting Black Holes
One of the most exciting areas of modern astrophysics is understanding the nature of accretion-powered compact objects. Many of these are binary systems in which one of the members is a collapsed object such as a neutron star or black hole, in the case of an x-ray binary, or a white dwarf in the case of a “cataclysmic variable.” At the extreme end lie the active galactic nuclei and quasars. Their enormous luminosities are thought to result from the energy conversion of matter falling into supermassive black holes at the center of galaxies. The intense x-ray emissions from these compact objects produce photoionized plasma conditions in the infalling accretion disk. One of the goals of high-energy astrophysics is to understand the dynamics of these black-hole accretion disk systems. The most promising observational tool is high-resolution spectroscopy of the emerging x-ray emissions. Two new space-based x-ray observatories currently in orbit, Chandra and XMM, are acquiring high-quality data of just such x-ray emissions. Turning these data into a better understanding of the dynamics of accreting black holes, however, will require a better understanding of photoionized plasmas, both in equilibrium and in nonequilibrium conditions.
Computer models for photoionized plasmas exist, but these complex codes differ in their predictions and have not been directly validated owing to a lack of
relevant laboratory data. Modern Z-pinches and large lasers are now capable of generating intense bursts of photoionizing x rays. Experiments on the Z-machine have shown that astrophysically relevant equilibrium photoionized plasmas can be created and diagnosed. It may also be possible to access photoionized plasma conditions on large laser facilities. These new HED laboratory capabilities will allow complex x-ray photoionization theories and models to be tested under relevant conditions, thereby serving as a critical component in the effort to understand the dynamics of accreting black holes.
Gamma-Ray Bursters
Gamma-ray bursts are among the greatest enigmas in contemporary astrophysics. Detected at a rate of more than one per day from random directions in the sky, GRBs have typical burst durations of a few seconds, but signal variability as short as about 1 ms, at photon energies of 0.1 to 100 MeV. At least some of the GRBs are at cosmological distances of several billion light-years, and their total source energies of 1051 to 1053 ergs per burst appear to be emitted from very compact sources. Their power law spectral shape is often interpreted as suggesting that the source plasma is optically thin to the radiation observed.
The fireball scenario is the most widely discussed model of GRBs. Here, an initial release of about 1052 ergs of energy into a volume of spatial extent about 107 cm creates a relativistically hot fireball of photons and leptons, with a small admixture of baryons. This initial fireball of leptons and photons at an initial temperature of 1 to 10 MeV expands relativistically; the gamma rays are produced by synchrotron or inverse Compton radiation from Fermi-accelerated electrons in optically thin shocks in the fireball. A small admixture of baryons is also accelerated to relativistic velocities, thereby transferring the fireball thermal energy to the kinetic energy of the radially expanding baryons. The baryons sweep into the interstellar medium (ISM), creating a system of a forward shock and several reverse shocks, with the observed GRB emission coming from the reverse shocks. The much-longer-lived x-ray afterglow then comes from the forward shock in the ISM, and the prompt optical emission from the corresponding reverse shock. In this scenario, the GRB can be thought of as a relativistic supernova remnant. All of the GRB localized so far with the BeppoSAX satellite belong to the class of long bursts with durations Δtγ≥2 s, and there is increasing evidence that these occur in star-forming galaxies.
For this class at least, comprising nearly two-thirds of all bursts, it is widely assumed that a massive, collapsing star (“collapsar”) is the progenitor. The shocks producing the gamma rays must occur after the fireball has emerged from the stellar envelope (and later, also an x-ray, optical, radio afterglow, as the fireball decelerates by sweeping up an increasing amount of matter encountered). The preferred escape
route for the fireball is along the centrifugally lightened stellar rotation axis, and the stellar pressure tends to collimate the fireball into a jet.
The second class of “short” bursts with durations Δtγ~2 s is less well understood—one hypothesis being that they may be caused by mergers of double neutron star or neutron-star-black-hole binaries. These binary mergers would also lead to a central black hole plus a shorter-lived accreting torus, and a (probably less collimated) MHD or pair-dominated jet along the rotation axis. These mergers are prime candidates for producing gravitational waves detectable with the second-generation Laser Interferometer Gravitational-wave Observatory (LIGO) or France’s VIRGO detectors (whereas collapsar-type long bursts may be weaker gravitational-wave sources due to a smaller quadrupole moment). The difference between the two classes of bursts will be further probed with spacecraft such as Swift and GLAST, now under construction.
The rest-mass densities that characterize the inner portions of the accretion disk and the jet are ρ≥1014 g cm−3, comparable to those inside nuclei and in neutron stars. As the fireball expands, inelastic nuclear collisions are expected when the n and p fluids decouple and their relative drift velocity becomes comparable to the speed of light. Inelastic n,p collisions lead to charged pions and gigaelectronvolt muon and electron neutrinos, as well as π0 decay gamma rays, which should be detectable with the GLAST spacecraft. The relativistic jets from the GRB outflows are inferred to lead to highly relativistic terminal bulk Lorentz factors (Γ≥100), with extremely high energy fluxes (1050 to 1052 erg s−1, or 1043 to 1045 W) on the beam, corresponding to an isotropic flux comparable to that of the entire universe over the 10- to 100-s duration of the burst. The energy density at the base of the jet is of order 1030 ergs cm−3 (1029 J/m3), enough for electron-positron and nuclear processes to be, initially at least, in near-equilibrium.
Farther out, at distances of ≥1011 cm, the photon-electron scattering mean free paths become longer than the characteristic dimensions of the flow, and collisionless internal and external shocks in the jet can accelerate electrons via the Fermi mechanism leading to a highly relativistic power law energy distribution. These, interacting with turbulently generated magnetic fields, lead to nonthermal gamma rays and, subsequently, in the jet deceleration phase, to an x-ray, optical, and radio afterglow, which has served to pinpoint the location of dozens of bursts and their distances. The interaction of waste heat bubbles or a decaying jet with the stellar envelope or with external debris can also lead to characteristic x-ray line spectra, in addition to a power law continuum.
Interesting issues of shock physics arise in connection with the GRB fireball radiation mechanism. The nonthermal spectrum in the fireball shock model results from assuming that Fermi acceleration accelerates electrons to highly relativistic energies following a power law N(γe)∝γe−p, with p≈2 to 2.5, in agreement with
observations. To get reasonable efficiencies, the accelerated-electron-to-total-energy ratio εe~1 must not be far below unity, while the magnetic-to-total-energy ratio εb~<1 depends on whether the synchrotron or the inverse Compton spectral peak represents the observed MeV spectral break. The radiative efficiency and the electron power law minimum Lorentz factor also depends on the fraction ζ<1 of swept-up electrons injected into the acceleration process.
While many afterglow-snapshot or multiepoch fits can be done with time-independent values of the shock parameters εb, εe, p, in some cases the fits indicate that the shock physics may be a function of the shock strength. For instance, p, εb, εe or the electron injection fraction ζ may change in time. While these are, in a sense, time-averaged shock properties, specifically time-dependent effects would be expected to affect the electron energy distribution and photon spectral slopes, leading to time-integrated observed spectra that could differ from those in the simple time-averaged picture. The back-reaction of protons accelerated in the same shocks and magnetic fields may also be important, as in supernova remnants. Turbulence may be important for the electron-proton energy exchange, while reactions leading to neutrons and vice versa can influence the escaping proton spectrum.
The same shocks responsible for accelerating the electrons can accelerate protons up to energies of order 1020 eV, comparable to the highest-energy cosmic rays measured with the Fly’s Eye and AGASA arrays. New experiments under construction, such as the Pierre Auger Observatory array, will provide much stronger constraints on whether GRBs are associated with such events. Relativistic protons can lead also to neutrinos with energies εv≥1014 eV via interactions with the ≈MeV gamma rays, and with energies εv≥1018 eV via interactions with ultraviolet photons. Protons accelerated in internal shocks in the buried jet while it advances through the star interact with thermal x rays to produce teraelectronvolt neutrinos, for which the detection probability is maximized in cubic kilometer Cherenkov detectors such as ICECUBE or ANTARES.
In the laboratory, the most promising means for accessing these relativistic plasma dynamics and flows are with experiments done on ultraintense, short-pulse lasers (see Figure 2.7). Experiments on such lasers have reached intensities of ≈1020 W cm−2 and have yielded many fascinating results. Jets of protons with energies of tens of MeV have been created in a very well collimated “beam.” Also, less-collimated directional outflows of electrons and positrons with energies of up to 100 MeV have been generated. In terms of an effective temperature, the high-energy electrons have a “slope parameter” of 1 to 10 MeV, making these plasmas thermally relativistic, with Te>mec2, corresponding to a “laboratory microfireball.” Similar temperatures are inferred from a fireball analysis of gamma-ray bursts. Another intriguing observation in these ultraintense laser experiments was the generation of ultrastrong magnetic fields. Strong magnetic-field generation (>100 MG=104 T) has
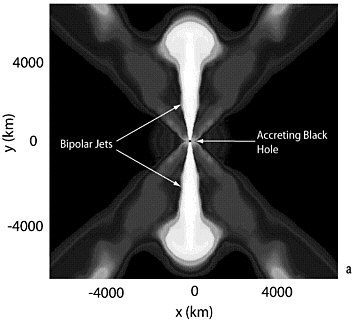
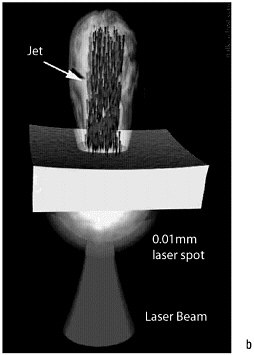
FIGURE 2.7 A combination of theory, simulation, and laboratory experiments is expected to yield new insights into the physics of gamma-ray bursts (GRB). (a) An example of a current model for gamma-ray bursts; (b) an example of a proposed laboratory experiment exploring aspects of the astrophysical model. SOURCES: Images (a) courtesy of S.Woosley, University of California Observatories/Lick Observatory; and (b) courtesy of S.C.Wilks, Lawrence Livermore National Laboratory.
been experimentally observed on such ultraintense laser experiments, with simulations predicting fields of up to 1 GG (105 T) or more. Such extreme conditions, albeit over small volumes and exceedingly short times, may overlap with aspects of the relativistic fireball dynamics thought to occur in gamma-ray bursts.
Pair Plasmas: Pair Creation in Magnetospheres and in the Laboratory
The development of petawatt-class lasers opens the door to the study of relativistic and e+e− plasmas in the laboratory. It is well known that lasers with intensities exceeding ≈2×1018 W cm−2 couple most of their energy to superthermal electrons with temperature kT>mc2, where m is the electron rest mass. Pairs can then be created when the relativistic electrons interact with high-Z target ions via the trident and Bethe-Heitler processes. Using particle-in-cell (PIC) simulations, the pair production rate for a thin (few micrometers) gold foil has been estimated, with the conclusion that petawatt lasers with sufficient duration can in principle achieve in situ pair densities as high as ~10−3 of the background electron density, or approximately 1022 cm−3 for solid gold. Detailed numerical simulations have confirmed this result and have further shown that for a thick gold foil (>20 µm), the positron yield may be even higher.
Subsequent experiments conducted at Lawrence Livermore National Laboratory using a single petawatt laser hitting 250-µm gold foils showed that the positron yield may be higher than even the theoretical estimates cited above. This demonstrates that petawatt lasers are indeed capable of producing copious pairs and has led to a proposal to use double-sided illumination to partially confine the pairs and to create multiple generations of pairs via reacceleration. PIC simulations show that, after the lasers are turned off, the pairs will expand much faster than the heavier gold ions. Hence a miniature fireball of relativistically expanding pure pairs can be created. This pair fireball can be made to collide with another pair fireball to mimic the internal shock model of gamma-ray bursts, allowing us to study how the expansion energy of pair fireballs can be converted into internal energy and gamma rays. Introduction of external equipartition magnetic fields (≈10 T) may be useful in creating collisionless shocks in such plasmas.
Another exotic future application is to study the static pair-balanced plasmas theorized to be the source of the episodic annihilation line flares from black-hole candidates. Two megajoule-class 0.1-petawatt lasers of 10-ns pulse duration, illuminating a gold target on both sides, could in principle create pair densities hundreds of times higher than the background electron density. Such steady-state pair plasmas can then be used to test the BKZS (Bisnovatyi-Kogan, Zel’dovich, Sunyaev) limit of kT≈20 mc2.
Radiative Blast Waves
When a blast wave sweeps up a high-density medium, the optically thin radiative cooling time at the shock front may become shorter than the dynamical time. Such radiative blast waves are expected to occur in the late phase of supernova remnants, gamma-ray burst afterglows, and even young supernova remnants in dense molecular clouds. Such radiative blast waves exhibit over stable radial oscillations when the cooling rate increases sufficiently slowly with temperature. Also the cooled dense shells eventually become unstable against the nonradial thin-shell instability. Numerical simulations in the past two decades consistently found that such thin-shell radiative blast waves in a solar-abundance interstellar medium expand as a power law in time, with an expansion index n (=d ln R/d ln t)≈1/3, significantly below the adiabatic Sedov-Taylor limit of 2/5, but higher than the pressure-driven snowplow limit of 2/7. Hence, radiative blast waves remain a major challenge in astrophysics because they couple the complex plasma radiation processes with hydrodynamics.
To simulate radiative blast waves in the laboratory, we need to generate highly radiative yet optically thin shocked gas. Laser experiments with xenon gas first demonstrated that radiative blast waves can indeed be created in the laboratory. Recent experiments using the short-pulse Falcon laser at Lawrence Livermore National Laboratory heating Xe gas jets have allowed probing the detailed physics of radiative blast waves, albeit in a cylindrical, rather than spherical, geometry. The key to such experiments lies in the fact that Xe gas with temperatures around tens to hundreds of electronvolts is highly radiative, yet optically thin for typical laboratory dimensions. The Falcon experiments confirm that Xe radiative blast waves expand as a power law in time, with an index intermediate between the Sedov-Taylor and pressure-driven snowplow limits.
It has been proposed that the n≈1/3 numerical simulation results and the Xe data are consistent with the theory that the radiative blast waves with temperatures below the cooling peak only radiate away the thermal component of the postshock energy. This hypothesis remains to be confirmed by further experiments and by numerical simulations with gases of different adiabatic indices. Radiative blast waves with radiatively preheated upstream gas and radiative blast waves with magnetic fields are also being investigated analytically and numerically. They will be priorities for future experiments.
Radiatively Driven Molecular Clouds
Cold dense molecular clouds illuminated by bright, young, nearby massive stars serve as the stellar incubators of the universe. The intense stellar radiation incident on the cloud creates a high-pressure source at the surface by photoevaporation
(ablation), augmented by the ram pressure from the stellar wind. The result is that the cloud is shock compressed, and subsequently accelerated, as the star clears away the cloud out of which it was born. Well-known examples of such systems are the Eagle Nebula, the Horsehead Nebula, the Rosette Nebula, and NGC 3603. Interest in dense molecular clouds in the vicinity of bright young stars is due in part to the hypothesis that these clouds serve as “cosmic nurseries,” harboring and nurturing regions of active star formation.
The Eagle Nebula is intriguing because of its famous columns, the so-called pillars of creation. These “elephant trunk” structures may arise as a result of hydrodynamic instabilities such as the Rayleigh-Taylor instability acting at the photoevaporation front, as first suggested 50 years ago. An alternative explanation, the so-called cometary tail model, attributes the columns to the flow of photoevaporated plasma from and around preexisting dense clumps of matter embedded in the molecular cloud, much like the dynamics that lead to the plasma tail of a comet.
Detailed information about the physical conditions in the hot ionized flow and in the cold gaseous cloud interior of the Eagle Nebula has recently been obtained, using both the Hubble Space Telescope and the ground-based millimeter-wavelength BIMA (Berkeley Illinois Maryland Association Array) interferometer array. In particular, hydrodynamic velocities as a function of position inside the cold gas have been determined by recent observations, allowing models of the dynamics of the columns to be tested. The key questions to be answered include these:
-
Are the column shapes seen in the Eagle Nebula and other driven molecular clouds due to hydrodynamic instabilities?
-
Do the radiative shocks launched into the molecular clouds trigger star formation?
-
Do the shapes of these driven molecular clouds record the history of the star turn-on phase?
Experimentally, aspects of the dynamics of radiatively driven molecular clouds, and therefore aspects of these questions, can be tested in the laboratory. Using the radiation emitted from tiny radiation cavity “point sources” on large lasers and pulsed-power facilities, it appears possible to reproduce the dominant photoevaporation-front hydrodynamics of radiatively driven molecular clouds. Off-setting and collimating the source of Planckian radiation from the simulant cloud (foam foil) mean that the incoming “drive” photons would be sufficiently directional (quasi-parallel) to reproduce the dominant features of radiatively driven molecular clouds. In particular, new modes of radiative-hydrodynamic instability may arise owing to the directionality of the incident photons, an effect that could in principle
be reproduced and observed on HED experiments. Also, the strong shock launched into the dense molecular cloud is likely to encounter density inhomogeneities, triggering localized regions of shock-induced turbulent hydrodynamics. Such hydrodynamics can also be reproduced in scaled strong-shock experiments on lasers and Z-pinch facilities. The shock launched into the dense molecular cloud is thought to be radiative. Progress on producing radiative shocks in the laboratory has also been demonstrated on several facilities. A magnetic field embedded in the cloud may be a key component to the dynamics, adding “stiffness” to the compressibility of the cloud. Strong-shock MHD experiments may also be possible on lasers and pulsed-power facilities. The possibility of forming an integrated program of theory, modeling, testbed laboratory experiments, and astronomical observations would be very beneficial, and several groups are moving in that direction.
High-Density Plasma in Strong Magnetic Fields and the Study of Surface Emission from Isolated Neutron Stars
Background The study of thermal radiation from isolated neutron stars can provide important information on the interior physics, magnetic fields, surface composition, and other properties of neutron stars. Such study has been a long-term goal of neutron star physics/astrophysics since early theoretical works indicated that neutron stars should remain detectable as soft x-ray sources for approximately 105 to 106 years after their birth. The past 35 years have seen significant progress in our understanding of various physical processes responsible for the thermal evolution of neutron stars. The advent of imaging x-ray telescopes in recent years has made it possible to observe isolated neutron stars directly by their surface emission. For example, the ROSAT X-ray Observatory has detected pulsed x-ray emission from about 30 rotation-powered radio pulsars, and some of these clearly show a thermal component in their spectra, indicating emission from the neutron star surface. Several radio-quiet, isolated neutron stars have also been detected in the x-ray and optical bands, and have thermal spectra arising from the neutron star atmosphere. Finally, in the past few years, soft gamma-ray repeaters and anomalous x-ray pulsars have emerged as a possibly new class of neutron stars (“magnetars”) endowed with superstrong magnetic fields, B>1014 G (>109 T). According to the magnetar model, the x-ray luminosity from anomalous x-ray pulsars and the quiescent x-ray emission from soft gamma-ray repeaters are powered by the decay of a superstrong magnetic field. Thermal radiation has already been detected (e.g., by ASCA and Chandra) in several anomalous x-ray pulsars and soft gamma-ray repeaters; fits to the spectra with blackbody or with crude atmosphere models indicate that the thermal x rays can be attributed to magnetar surface emission. Clearly, detailed observational and
theoretical studies of thermal emission can potentially reveal much about the physical conditions and the true nature of magnetars.
The new generation of x-ray telescopes (e.g., Chandra and XMM-Newton currently in orbit, and Constellation-X in the future) are bringing great promise to the study of isolated neutron stars (including radio pulsars, radio-quiet neutron stars, and magnetars). The greatly improved sensitivity and spectral/angular resolution in the x-ray band will lead to detailed spectroscopy (and continuum observation) of neutron star surfaces. In order to interpret the future observations properly, it is crucial to have a detailed understanding of the physical properties of the dense (partially ionized) plasma in the outer layers of neutron stars in the presence of intense magnetic fields (B≈1011 to 1016 G), and to calculate the emergent thermal radiation spectra from the neutron star surfaces. This radiation is determined by the physical properties of the surface layers, but the surface composition of the neutron star is unknown. The atmosphere could consist of iron-peak elements formed at the neutron star birth, or it could be composed of light elements such as H and He due to accretion and fallback. The immense gravity of the neutron star makes the atmosphere very thin (0.1 to 10 cm) and dense (0.1 to 100 g cm−3), so that the atmospheric matter is highly nonideal, with interactions between particles nonnegligible. If the surface temperature is not too high, light atoms, molecules, and metal grains or droplets may form in the envelope; if the magnetic field is sufficiently strong, the envelope may transform into a condensed phase with very little gas above it. A superstrong magnetic field will also make quantum electrodynamic effects (e.g., vacuum polarization) important in calculating the surface radiation spectrum. All of these problems present significant challenges to the theoretical astrophysics and dense plasma physics communities. The following subsections provide a few more detailed examples of the kinds of new physics problems that one confronts when studying these extreme objects.
Microscopic Calculations of Atoms, Molecules, and Dense Matter in Strong Magnetic Fields It is well known that a strong magnetic field can dramatically change the properties of atoms, molecules, and condensed matter. For B≫B0=me2e3c/ℏ3=2.351×109 G, the cyclotron energy of the electron, ℏ ωc=ℏ (eB/mec)=11.58 B12 keV [where B12=B/1012 G], is much larger than the coulomb energy. Thus, the coulomb forces act as a perturbation to the magnetic forces on the electrons, and at typical temperatures of isolated neutron stars, the electrons settle into the ground Landau level. Because of the extreme confinement of electrons in the transverse direction, the atom attains a cylindrical shape and a large binding energy. Moreover, it is possible for these elongated atoms to form molecular chains by covalent bonding along the field direction. Interactions between the linear chains can then lead to the formation of three-dimensional condensate. Much work remains to be done to understand the
electronic structure of various forms of matter in strong magnetic fields. In particular, the atomic structure of heavy atoms has only been studied for a limited range of field strengths, the excitation energies of molecules (and chains) have only been considered qualitatively, and the cohesive properties of three-dimensional condensed matter are only understood in certain limiting field regimes.
Equation of State and Opacities of Dense Plasma in Strong Magnetic Fields A crucial ingredient in modeling neutron star atmospheres and surfaces is the equation of state (including the ionization-recombination equilibrium) of dense plasma in strong magnetic fields. Besides the usual difficulties associated with strong coulomb interactions in dense, zero-field plasmas, there are additional subtleties related to the nontrivial coupling between the center-of-mass motion and the internal structure of atoms and molecules. So far, only very crude models for the equation of state of dense plasma in strong magnetic fields have been constructed. To apply to neutron star atmospheres, various atomic and molecular opacities must be estimated or calculated. For sufficiently high magnetic fields and low temperatures (but still realistic for neutron stars), the condensed phase is more stable than the atoms and molecules, and there is a first-order phase transition from the nondegenerate gas to the macroscopic condensed state. With increasing field strength and decreasing temperature, the saturation vapor density and pressure of the condensate are expected to decrease, and eventually the optical depth of the vapor becomes less than unity. Therefore, thermal radiation can directly emerge from the nearly degenerate condensed metallic liquid. So far these issues have only been studied using very crude approximations.
Radiative Transfer in Strong Magnetic Fields Recent study of radiative transfer in strong magnetic fields has focused on transport of photon modes in ionized plasma. Incorporating neutral species self-consistently in the atmosphere models is an important challenge for the future. Even for ionized models (valid for sufficiently high temperatures, T>a few×106 K), several important issues related to the superstrong field regime (B>1014 G) remain to be studied. One of these concerns the effect of ion cyclotron resonance at photon energy 0.63(Z/A)B14 keV, where B14≡B/1014 G, and Z and A are the charge and mass numbers of the ion, respectively. Another concerns the effect of vacuum polarization. Polarization of the vacuum due to virtual e+e− pairs becomes important when B>BQ=me2c3/eℏ=4.414×1013 G. Vacuum polarization modifies the dielectric property of the medium and the polarization of photon modes, thereby altering the radiative opacities. Of particular interest is the “vacuum resonance” phenomenon, which occurs when the effects of vacuum and plasma on the linear polarization of the modes cancel each other, giving rise to a “resonant” feature in the absorption and scattering opacities. The
vacuum resonance is located at photon energy EV(ρ)≈1.0(Yeρ)1/2B14−1f(B) keV, where ρ is the density (in g cm−3), Ye=Z/A is the electron fraction, and f(B) is a slowly varying function of B [f(B)≈1 for B<BQ, and ranges from 1 to a few for B≈1014 to 1016 G]. Because EV depends on density (which spans a wide range in the atmosphere), proper treatment of this vacuum resonance feature presents a significant challenge for the atmosphere modeling. Another related effect is the resonant mode conversion: a photon propagating down the density gradient in the atmosphere can change its mode characteristics (e.g., an extraordinary mode photon gets converted to ordinary mode) at the density where vacuum resonance occurs; such mode conversion is particularly effective for photons with energies greater than a few kiloelectronvolts. Since the two modes have very different opacities in strong magnetic fields, mode conversion can have a significant effect on the radiative transport and the emergent spectra from the magnetar atmosphere.
Plasma physics with ultrahigh magnetic-field strengths becomes particularly interesting at B>B0=me2e3c/ℏ3~109 G. At these field strengths, the orbitals of bound electrons become strongly perturbed by the applied magnetic field, that is, (ℏωc)/Eb≥1, where ℏωc is the energy of the electron at the cyclotron frequency due to the magnetic field, and Eb is the electron coulomb binding energy. The details of plasma emission and absorption spectra will be significantly affected, which could be relevant to emission spectra from neutron star atmospheres. With the new genre of ultraintense, short-pulse lasers, magnetic-field strengths in plasmas of order ~109 G have already been demonstrated, with the promise of higher field strengths on future facilities. If such fields could be sufficiently well understood and controlled, it might become feasible to measure emission spectral modifications due to such strong fields.
THE ROLE OF COMPUTING IN HIGH ENERGY DENSITY ASTROPHYSICS
An essential aspect of numerical modeling in the context of HED astrophysics is that the range of spatial and temporal scale that typically needs to be spanned far exceeds what can be plausibly computed. Another way of looking at this difficulty is that the dimensionless control parameters characterizing astrophysical systems (e.g., Reynolds number, Rayleigh number, and so on) are typically much larger than what can be simulated on existing (or even imagined) computing platforms.
In this sense, computing plays a very different role in HED astrophysics than in HED laboratory physics. HED astrophysics computing is used for the following purposes:
-
To develop models for spatially or temporally unresolved physics. Astrophysics-focused simulations invariably use subgrid models in order to describe
-
processes not captured by the simulations themselves; common examples of such modeling include the insertion of turbulent viscosity and (in the case of collisionless plasmas) magnetic diffusivity. An important role for joint laboratory and simulation studies is the validation of such (astrophysical) subgrid models.
-
To validate ideas about physical processes thought to take place in an astrophysical context, but which can be explored under less restrictive conditions. In many instances, physical processes arising under astrophysical conditions have counterparts under laboratory conditions—mixing instabilities such as Rayleigh-Taylor exemplify such processes. In such cases, laboratory experiments can be used to validate astrophysics simulation codes; this is a necessary condition for ensuring that such simulations properly describe the astrophysical situation (albeit not a sufficient condition).
-
To explore and develop intuition for highly nonlinear physical processes. The challenging problems in astrophysics are largely related to processes that operate in a fully nonlinear regime. In this regime, reasoning based on the behavior of systems in the linear regime usually proves to be very inadequate, but our physical intuitions are generally based on linear theory. For this reason, there is a broad need to inform practitioners about the complexity of possible behaviors in the nonlinear limit; the numerical exploration of the fully nonlinear development of magnetic dynamos is an excellent example of this type of study.
The preceding discussion makes clear that the size (both in memory requirements and computation time) and complexity (in the level of detail of the physics description) of HED astrophysics-oriented simulations are typically set primarily by what is possible: computational HED astrophysicists are rarely heard to say, “We do not need more memory size or computation time.” Thus, computational HED astrophysics drives some of the largest simulations that are typically attempted on leading-edge computing platforms. By the same token, computational HED astrophysics has a profound need for access to state-of-the-art computational resources— thus, it is widely believed that major advances in problems such as Type Ia and Type II (core collapse) supernovae will relate to advances in high-end computational capabilities. For example, it is now possible to do two-dimensional hydrodynamic simulations of Type II supernovae, with nuclear reactions and neutrino transport, on a modern personal computer; it will take days to weeks. But full three-dimensional simulations with good resolution are necessary in order to see the development of low-order modes of instability and at the same time to resolve the boundary between the collapsed core and the ejecta. An obvious estimate of the additional computational resources needed is scaling according to the number of zones needed for the
new third dimension: roughly 500 to 1,000 personal computers. This translates to at least days or weeks of dedicated time on an ASCI-level parallel system. The Type Ia supernova problem seems to be worse. In addition to demands such as those just mentioned, at least two other issues arise: subgrid models for burning, and grid distortion in the strongly differentially rotating system of a binary merger. These crucial roles played by computations in HED astrophysics have been recognized by the Department of Energy (DOE) and strongly supported within the DOE National Nuclear Security Administration’s ASCI Alliances program and the DOE Office of Science’s Science Discovery through Advanced Computing (SciDAC) program.
CONCLUSIONS
In summary, there is a wide variety of areas in which theory, numerical simulations, and experiments on HED facilities can address aspects of astrophysical phenomena. Areas of promising overlap include the physics of supernova explosions and supernova remnant evolution, high-Mach-number astrophysical jets, planetary interiors, photoevaporation-front hydrodynamics of molecular clouds, photoionized plasmas around accreting black holes, and relativistic plasmas in gamma-ray burster fireballs. This selection of topics may well be just the “tip of the iceberg” as more experience is obtained in carrying out both large-scale numerical simulations and scaled HED experiments in support of astrophysics.





































