3
Current Research in Reliability Modeling and Inference
Four of the seven sessions at the workshop addressed reliability-related areas (other than reliability growth) in which recent advances and ongoing research could especially benefit the DoD test and evaluation community in its current activities and applications. This chapter presents the issues, methods, and approaches that were raised in these sessions. The topics to be discussed here include: (1) approaches to combining information from disparate sources that are aimed at achieving improvements in the accuracy and precision of the estimation of a system’s reliability; (2) model-based approaches to selecting inputs for software testing; (3) current models for estimating the fatigue of materials; and (4) reliability management to support estimates of system life-cycle costs. Before proceeding to fairly detailed coverage of the sessions on each of these topics, we briefly describe the motivation for the selection of these as topics worthy of special attention at the workshop and give a brief overview of each.
The combination of information from disparate sources (the value of which is discussed in Chapter 2) is a problem that has interested statisticians for many years. Indeed, the fields of Bayesian statistics, empirical Bayes methods, and meta-analysis all emerged to address this problem. The idea of exploiting “related information” in the process of interpreting the outcome of a given experiment arises in many different forms. In the DoD acquisition process, data are collected during the various stages of developmental testing, and these data may well be of use in the process of analyzing
the outcomes of the subsequent operational test. In the workshop session on combining information, Duane Steffey described use of a parametric hierarchical Bayes framework for combining data from related experiments, and Francisco Samaniego followed with a description of nonparametric methods for handling the same problem. These presenters argued that existing methods and others under current investigation constitute promising ways of modeling the data-combination challenges that arise in developmental and operational testing.
Some of the earliest work on fatigue modeling occurred in the context of addressing problems that were common in the aircraft industry during and following World War II. While some of the early attempts at modeling fatigue in the materials used in aircraft construction were primarily mathematical in nature, the field has evolved and seen some notable advances and achievements through the collaboration of mathematical/statistical workers, materials engineers, and other scientists. Sam Saunders described some of the early work in this area at Boeing, including the development of the widely used Birnbaum-Saunders model, and underscored the importance of understanding the science involved in a particular application before attempting to model the problem statistically. Joe Padgett’s presentation was focused on a class of models for fatigue of materials or systems due to cumulative damage and the modeling of crack growth due to fatigue. This work, which combines current thinking in materials science and sophisticated statistical modeling, provides a broad collection of models on which to base estimation and prediction in this area.
Modern military systems have become increasingly dependent on computer software for their successful and reliable operation. Given that the area of software reliability is broad enough to merit a workshop of its own, the goal of the session was scaled down to providing the flavor of two particular lines of research in the area. Siddhartha Dalal’s presentation focused on efficient methods of selecting factorial experiments with attractive coverage possibilities. He described approaches to experimental design that allow the experimenter to sample a reasonably broad array of combinations of factors while controlling the scale of the overall experiment. Jesse Poore’s presentation focused on methods of testing software that take special account of anticipated usage patterns, thereby enhancing the likelihood of good performance in the software’s intended domains of application.
APPROACHES TO COMBINING INFORMATION FROM DISPARATE SOURCES
A variety of sources of information on the reliability of a defense system under development are available at the different stages of system development. Data from developmental and operational tests and from field performance for systems with similar or identical components are typically available at the beginning of system development. There are also data from the developmental tests (contractor and government) of the system in question. Finally, there are often field use and training exercise data, as well as “data” from modeling and simulation.
Attempts to combine data from tests or field experience for a related system with those for a given system must be made with caution since large changes in reliability can result from what would ordinarily be considered relatively minor changes to a system, and even identical components can have importantly different impacts on system reliability when used in different systems. Data from field and training exercises must be carefully considered since field use and training exercises are not well-controlled experiments. Further, the utility of modeling and simulation results depends heavily on the validity of the models in question.
Even identical systems can have dramatically different reliabilities in developmental and operational testing as a result of the different conditions involved. In developmental testing, the system operators are typically fully acquainted with the system, the test conditions are carefully controlled, and the test is often at the component level (e.g., hardware-in-the-loop testing). On the other hand, operational testing involves using the full system in operational conditions as realistic as possible, with the actions of the participants relatively unscripted and the system being operated by personnel more typical of real use (with the anticipated amount of training). Clearly, these are distinctly different conditions of use.
On the other hand, the cost of operational testing (and the need for expeditious decision making) necessarily limits the number of operational test replications. Given the importance of assessing the reliability of defense systems in development, including how this assessment factors into the ultimate decision on whether to proceed to full-rate production, it is extremely important to base reliability assessments of defense systems in development on as much relevant information as possible. As a result, it has been suggested, especially of late, that the various sources of information be combined, if possible, to provide the best possible estimates of sys-
tem reliability in an operational setting (see also Chapter 2). Given the differences in conditions of use, however, the combination of developmental and operational test data for identical systems (and data from test and field use for similar systems) must be considered carefully. It was stressed repeatedly at the workshop that any attempt to combine information from disparate sources should be preceded by close scrutiny of the degree of “relatedness” of the systems under consideration and the conditions of use, and the appropriateness of modeling these relationships. It is clear that without this care, use of these additional sources of information could result in assessments that are less accurate or precise than those relying exclusively on operational test data. Combining of information is therefore an important opportunity, but one that must be explored with caution.
One session of the workshop focused specifically on the use of models for combining information from developmental and operational tests when the failure modes in these separate environments of use are well understood (or otherwise approximately satisfy the necessary assumptions). It was argued that in those instances, use of the proposed models can provide improved estimates and thereby support better decision making. Two specific approaches to combining information were proposed at the workshop, as described below.
The Steffey Paper
Duane Steffey reported on recent research on the estimation of mean time to failure under specified conditions of use, given information about the performance of the same system under different test conditions. (For details, see Samaniego et al., 2001). Of course, a key application for which such extrapolation would be needed is one in which the former conditions of use were developmental test conditions and the latter operational test conditions, with the hope of combining developmental and operational test information to support an operational evaluation. There are two questions of interest: (1) How can a meaningful notion of relatedness be characterized in a statistical model? (2) What method or methods of estimation are most appropriate for this problem? The approach relies on the following assumption: that the complexity of and difference between the two sets of experimental conditions make it impossible to link the information derived under those sets of conditions using parameters that define the test conditions. In other words, a trustworthy parametric model of reliability as a function of the test conditions (that is, covariates such as amount of
TABLE 1 Fictitious Developmental and Operational Test Data
|
Developmental Test Data |
Operational Test Data |
|
|
28.73 |
18.01 |
13.48 |
|
21.76 |
1.55 |
18.63 |
|
6.01 |
35.54 |
4.54 |
|
46.68 |
22.06 |
23.51 |
|
7.58 |
2.58 |
5.34 |
|
11.27 |
20.89 |
8.39 |
|
16.08 |
7.15 |
39.97 |
|
8.06 |
10.19 |
7.79 |
|
9.97 |
67.03 |
33.14 |
|
41.66 |
7.79 |
6.14 |
training) cannot be developed. The estimation approach described by Steffey is (Bayesian) hierarchical modeling using a relatively simple characterization of relatedness of conditions of use.
A dataset motivated the discussion. Consider the following (fictitious) lifetimes of experimental units (hours to failure) from developmental and operational testing (DT and OT) as displayed in Table 1. For developmental testing, the mean time to failure is 19.53, whereas for operational testing, it is 16.09.
The statistical model used assumes that there exists a probability distribution with mean μD that generates DT mean times to failure. Likewise, there also exists a probability distribution that generates OT mean times to failure. These means of the distributions that generate mean times to failure (μD, μO) are referred to as grand means. Then, to obtain the observed time to failure for a given system for either developmental or operational test, one draws a random waiting time from a distribution with the appropriate mean. This can be considered a staged process in which the second and final stage represents the variability of an individual system’s waiting times to failure about each individual system’s mean, and the initial stage represents the variability between the mean times to failure for individual systems (from the same manufacturing process) about a grand mean time to failure. It makes sense to assume that the DT grand mean is some factor larger than the OT grand mean, since operational test exposes a system to more opportunities for failure. This multiplicative factor is designated λ. (There are non-Bayesian approaches in which a λ factor is used to convert
operational test hours into “developmental test hours” for purposes of weighting as combined estimates.)
The goal for combining information in this framework is estimation of μO. To this end, three alternative estimators were considered: (1) the unpooled estimator, here the average time to failure relying solely on data collected during operational test; (2) a specific weighted average of the observed OT individual mean time to failure and the observed DT individual mean time to failure, referred to as the linear Bayes estimator; and (3) an estimator that makes full use of the hierarchical Bayes approach. To compare the performance of these (and other potential) estimators, the natural metric is Bayes risk relative to a true prior representing the true state of nature, which is the average squared error (averaged over the process described above that first draws a mean reliability for a specific system, in either developmental or operational test, and then draws a time to failure from the assumed probability distribution centered at those means). The reduction in average squared error that results from switching from an unpooled to a pooled estimator measures the gain from the use of developmental test data.
The linear Bayes estimator is considered since (1) it can be computed explicitly and can serve as an approximation of the full hierarchical approach (one simply chooses the weights to minimize Bayes risk), (2) it makes explicit the use of developmental test data, and (3) it is possible to characterize the circumstances under which this estimator is preferred to the unpooled estimator. For discussion of linear Bayes methods, see: Hartigan (1969), Ericson (1969, 1970), Samaniego and Reneau (1994), and Samaniego and Vestrup (1999).
Returning to the above dataset, the unpooled estimator is the mean operational test waiting time to failure, or 16.09. Assuming that λ = 0.75— which of course would not be known in practice—and some additional but reasonable assumptions about the developmental and operational test experiments, the optimal coefficients for the linear Bayes estimator are c1* = .4 and c2* = .43 (see Samaniego et al. [2001] for details), producing the linear Bayes estimate of .4 (19.53) + .43 (16.09) = 14.73, which is considerably lower than the unpooled estimator of 16.09.
Steffey demonstrated analytically that the Bayes risk for the linear Bayes estimator, when λ is known, is necessarily smaller than that for the unpooled estimator. This begs the question of what happens in the case when λ is not known.
To proceed it is necessary to place a prior distribution around λ, de-
noted π(λ). Two possible approaches can now be used. First, one can construct a different linear Bayes estimator that makes use of the mean and variance of the probability distribution. Second, one can make use of a hierarchical Bayes estimator that assumes a joint prior distribution for the means of the distributions of the operational test and developmental test mean waiting times to failure.
In the earlier linear Bayes approach, the optimal coefficients for the developmental and operational test (observed) mean times to failure were selected to minimize the Bayes risk. Now, the optimal coefficients of the developmental and operational test mean times to failure are selected to minimize the expected Bayes risk, given that one must average over the uncertainty in λ. This makes the resulting optimal coefficients slightly more complicated than when λ was assumed to be a known constant. Analytic results show that the expected Bayes risk for the unpooled estimator is greater than that for the optimal linear estimator, as in the case for fixed λ, when the assumed π(λ) has nearly the same center as the true prior distribution. When the assumed prior distribution is substantially incorrect, the unpooled estimator can be preferable to the optimal linear Bayes estimator. Therefore, the benefits of pooling depend on the information available about the relationship between the two testing environments.
Steffey also examined the less analytically tractable hierarchical Bayes estimator, providing some information on the differences between its performance and that of the linear Bayes estimator in simulation studies. Generally speaking, use of the more complicated hierarchical estimator results in additional benefits relative to use of the optimal linear Bayes estimator, although much of the improvement over the unpooled estimator is realized at the linear Bayes stage.
The Samaniego Paper
Nonparametric estimation and testing avoids the use of parametric assumptions and instead uses quantities such as empirical distributions or the relative ranks of observations to support estimation and inference.1
Because parametric models describing a probability distribution that is assumed to generate the data are avoided, nonparametric approaches are much more likely to be valid. This greater validity comes with the disadvantage that nonparametric methods are typically outperformed by parametric alternatives when the assumptions used by the parametric approach are approximately correct. It is generally understood, however, that the loss in efficiency sustained by nonparametric methods when parametric assumptions hold exactly is often quite modest, and is thus a small price to pay for the broad protection these methods offer against model misspecification. Francisco Samaniego offered a brief review of nonparametric methods in reliability, and then suggested some nonparametric approaches to combining information from “related” experiments.
Parametric models that are often used to describe the distribution of times to failure include the exponential, Weibull, gamma, and lognormal distributions. Selection of parameters (e.g., the mean and variance) identifies specific members from these distributional families. In shifting from one family of distributions to another, say, from the lognormal to the gamma, different shapes for failure time distributions are obtained, though they are all typically skewed distributions with long right-hand tails. Samaniego demonstrated a phenomenon often encountered in applied work—the futility of performing goodness-of-fit tests based on small samples. He displayed a simulated dataset that appeared to be reasonably well fit by all four of the aforementioned parametric models on the basis of sample sizes of 20, but were clearly poorly fit by these models when sample sizes of 100 were available. Generally speaking, the use of goodness-of-fit tests to test for a specific parametric form should be preceded by use of graphical and other exploratory tools, and consideration of applicable physical principles, to help identify reasonable parametric distributional models. However, for small sample sizes, these techniques typically will not provide sufficient information to identify good parametric models. This inability to distinguish among various parametric families for the smaller datasets that are typical of defense operational testing motivates the use of nonparametric estimation for which no parametric form is assumed.
Nonparametric reliability models are typically based on certain distributional assumptions, such as notions of aging or wear-out, that are motivated by experience with the application of interest. One notion of aging is “increasing failure rate” (IFR). Systems having time-to-failure distributions with this property are increasingly less likely to function for t additional units of time as they grow older. (A related characteristic is “increas-
ing failure rate average” [IFRA].) Another model of aging is “new is better than used” (NBU). For systems with time-to-failure distributions having this characteristic, the probability of lasting t units of time when the system is new is greater than the probability of lasting an additional t units of time given that one such system has already lasted ∆ units. (This notion is slightly distinct from IFR since it links the performance of older systems to that of a new system and not to the performance of intermediate aged systems.) Another widely used modeling assumption is that of decreasing mean residual life (DMRL). This assumption characterizes a time-to-failure distribution in which the expected additional or residual lifetime of a system of age t is a decreasing function of t. This concept is distinguished from IFR since it relates mean lifetimes rather than lifetime probabilities.
Samaniego argued that instead of assuming a specific distributional form for the time-to-failure distribution and estimating parameters to identify a particular member of these distributional families, one could estimate the lifetime distribution under one of the above nonparametric assumptions. For example, under the assumption that the time-to-failure distribution is IFR, the nonparametric maximum-likelihood estimate of the hazard rate (the instantaneous failure rate conditional on the event that the system has lasted until time t, which is essentially equivalent to estimation of the time-to-failure distribution) at time t is a nondecreasing step function whose computation involves the well-understood framework of isotonic regression. Similar constraints from assumptions such as NBU produce alternative nonparametric estimators.
These are one-sample techniques for the problem of estimating the properties of a single time-to-failure distribution. With respect to the problem of combining information, the natural situation is that of comparing samples from two related experiments. Rather than make the linked-parameter assumption of Samaniego et al. (2001) (i.e., the λ factor), Samaniego instead used nonparametric assumptions about the relationship between the time-to-failure distributions for developmental and operational testing of a system. Three well-known formulations of the notion that a sampled quantity (failure time) from one distribution tends to be smaller than a sampled quantity from another distribution are as follows (see Shaked and Shanthikumar [1994] for further details): (1) stochastic ordering, when the probability that the next failure will be t time units or greater for a system in developmental test is greater than the probability that the next failure will be t time units or greater for the same system in operational test, for all t; (2) hazard-rate ordering, when the instantaneous failure rate,
given that a system has lasted until time t, for the system in developmental test is smaller than that for the system in operational test, for all t; (3) likelihood ratio ordering, when the ratio of the time-to-failure density for developmental test to that for the time-to-failure density for operational test is a decreasing function of time.
Samaniego then discussed a new type of ordering of distributions, referred to as “stochastic precedence.” Distribution A stochastically precedes distribution B if the probability is greater than .5 that a random variable from distribution A is less than a random variable from distribution B. The assumption that operational test failure times stochastically precede developmental test failure times has repeatedly been verified empirically in a wide array of applications. When the assumption is warranted, relying on it and using the associated inference substantially improves estimation of the cumulative time-to-failure distribution function for operational test data.
Attention was then turned to the process of estimating the lifetime distributions from two experiments under the assumption that one experiment (for example, OT) stochastically precedes the other (for example, DT). The estimation process is accomplished as follows. Should the standard estimates of the empirical cumulative distribution functions (ecdf) for failure times from operational and developmental testing satisfy the property of stochastic precedence, those ecdf’s are used, unchanged, to estimate the operational and developmental test time-to-failure distributions. However, if the ecdf’s fail to satisfy stochastic precedence, the ecdf’s can be “adjusted” in one of several ways to arrive at a pair of estimators that do satisfy stochastic precedence. Samaniego discussed two specific approaches to such adjustment—the first involving a rescaling of the data from both samples to minimally achieve stochastic precedence, and the second involving data translation (that is, a change of location). Under the assumption that stochastic precedence holds, both methods were shown to offer improvement over estimators that rely exclusively on data from just one of the experiments. Asymptotic results show improvement in the integrated mean squared error of the competing estimators, and simulations demonstrate their efficacy in small-sample problems as well (see Arcones et al. [2002] for details).
In summary, this research demonstrates that developmental test data can be used to improve an estimator of the time-to-failure distribution of operational test data under quite minimal assumptions. Such an approach might also be used in gauging the robustness of parametric approaches to estimation. As research advances, more nonparametric models and infer-
ential methods will be available and will constitute an increasingly comprehensive collection of tools for the analysis of life-testing data.
Discussion of Steffey and Samaniego Papers
The discussion focused on the ability to capture the degree to which the reliabilities of different systems tested in different environments are related. The argument was made that developmental testing conditions are by nature quite different from those for operational testing, in part because they have somewhat different objectives. The goal of developmental test is to identify key areas of risk and then determine how to mitigate that risk. For this reason, much of the effort in developmental test focuses on the working of individual components. On the other hand, the goal of operational testing and evaluation is to examine whether the entire system is consistently effective and suitable in an operationally realistic environment with its intended users. Clearly many operational problems that may not arise in a laboratory setting cause system redesigns late in the development process, when they are more costly. As a result, there are now increasing efforts to make greater use of conditions in developmental testing that approximate more closely the most realistic operational test conditions. Such efforts will increase the opportunities for combining information since they will lessen the differences between developmental and operational testing.
One of the discussants, Fred Myers, argued further that if combining data is to be part of the operational test evaluation, it must be factored into the entire testing strategy and planning. It should be described in the test and evaluation master plan so that the developmental and operational test environments can be linked in some manner. This is a natural assignment for an integrated test team. Further, if contractor (as opposed to governmental) developmental test data are to be used, a better understanding is needed of the specific test conditions used and what the results represent, and there must be full access to all of the test data.
Myers added that some caution is needed because of the requirement of Title 10 U.S.C. 2399 for the independence of the operational tester. To effect this combination, operational evaluation data must be validated by the operational tester independently of the developmental tester. Another caution is that for combining information models to have a good chance of success, it must be determined that the prototypes used in developmental testing are production-representative of the system. If not, this complicates
the relationship between the reliability of the system in developmental and operational test events.
The second discussant, Ernest Seglie, expressed his belief that experts in operational test agencies would be able to guess the ratio of the mean waiting time to failure for operational test to that for developmental test (λ in Steffey’s notation). Presumably, program managers would not allow a system for which they were responsible to enter operational test unless they were relatively sure it could meet the reliability requirement. In data just presented to the Defense Science Board (2000), one finds that 80 percent of operationally tested Army systems failed to achieve even half of their requirement for mean time between failures. This finding reveals that operational test is demonstrably different from developmental test, and that perhaps as a result, priors for λ should not be too narrow since it appears that the information on system performance is not that easy to interpret.
Seglie stated that there are two possible approaches for improving the process of system development. First, one can combine information from the two types of testing. Seglie admitted that he had trouble with this approach. The environments of developmental and operational testing are very different with very different failure modes. In addition, combining information focuses too much attention on the estimate one obtains instead of on the overall information about the system that one would like to give to the user from the separate test situations. It is extremely important to know about the system’s failure modes and how to fix them. Therefore, one might instead focus on the size of λ and use this information to help diagnose the potential for unique failure modes to occur in operational test and not in developmental test. Doing so might demonstrate the benefits of broadening the exposure of the system during developmental test to include operational failure modes. Until a better understanding is developed of why developmental and operational tests are so different, it appears dangerous to combine data. A better understanding of why λ differs from 1 should allow one to incorporate (operational test-specific) stresses into developmental testing to direct design improvements in advance of operational test.
Samaniego commented on Seglie’s concerns as follows. First, it should be recognized that Bayesian modeling has been shown to be remarkably robust to the variability in prior specifications. The Achilles heel of the Bayesian approach tends to be overstatement of the confidence one has in one’s prior mean (that is, in one’s best guess, a priori, of the value of the parameters of interest). With prior modeling that is sufficiently diffuse,
accompanied by a sensitivity analysis comparing a collection of plausible priors in a given problem, what some think of as the “arbitrariness” of Bayesian analysis can be minimized (see, e.g., Samaniego and Reneau [1994], for results and discussion on this issue). Second, the use of methods for data combination by no means precludes the investigation of failure sources and the various steps that are associated with reliability growth management. Samaniego suggested that it is critical for theoretical and applied research to proceed simultaneously and interactively on both of these fronts.
In the floor discussion, Larry Crow asked whether anyone had compared failure modes in developmental versus operational test. Specifically, he wanted to know how much of the increased failure rate in operational test is due to new failure modes and how much is due to higher failure rates of known failure modes. Jim Streilein responded that his agency has an idea of what λ is for some systems. He added that efforts are being made to carry out failure modes and effects analyses, but the problem is that these estimates are never fully cognizant of the environment of use. Further, for most components, there is no physical model that can be used to provide reliability estimates for a given material or manufacturing process. Streilein is therefore not sanguine about combining information models until more information is available.
TWO MODEL-BASED APPROACHES TO SELECTING INPUTS FOR SOFTWARE TESTING
It is well known that software is essentially a ubiquitous component of today’s complex defense systems and that software deficiencies are a primary cause of problems in defense system development (see Mosemann, 1994). Software reliability, while sharing some aspects of hardware reliability, is clearly distinct in critical ways. For example, the smallest change to a software system can have a dramatic impact on the reliability of a software system. Further, there are no analogous notions to burn-in or fatigue for software components. Given the distinct nature of problems involving software and the broad aspects of the subject area, the hope during the planning stages of this workshop was that an entire subsequent workshop would be devoted to this issue, for which two presentations on software engineering at this workshop would serve as a preview. (This workshop was held July 19–20, 2001.)
This preview session outlined two approaches to the selection of in-
puts to software systems for testing purposes. The first selects a very small set of inputs with the property that all pairwise (more generally k-wise) choices for fields (which comprise the inputs) are represented in the test set. It has been demonstrated empirically that a large majority of the errors can be discovered in such a test set. The second approach uses a graphical model of software usage, along with a Markov chain representation of the probability of selection of inputs, to choose test inputs so that the high-probability inputs are selected for the testing set. The session’s goal was to demonstrate that a number of recently developed statistical methods in software engineering are proving useful in industrial applications.
The Dalal Paper
The number of potential inputs to a software system is often astronomically high. In testing a software system, therefore, there is much to be gained by carefully selecting inputs for testing. Consider the interoperability problem in which a number of component systems must interact smoothly, and each of the components has a separate schedule for release of updated versions. To test the combined system, one must consider the (potentially) large number of possible configurations, with each configuration representing the joint use of specific releases. Given the time required to put together a specific configuration, the value of techniques that can reduce the number of tests needed to examine the reliability of all k-wise (for some integer k) combinations is clear. More generally, for any software system, input fields play the same role as system components in the interoperability problem, except that the combinatorial complexity is typically much greater. An empirically supported assumption is that the large majority of software faults are typically due to the interaction of a small number of components or fields, often just two or three. Thus one approach to software testing in this situation is to test all two-way (and possibly three-way) combinations of configurations or fields. That is, for two-way combinations, each version of the first software component is used with each version of the second software component, and so on.
Siddhartha Dalal discussed new test designs that include inputs, for a very modest number of test runs, covering all possible two-way (or generally k-way) combinations of fields. For even moderate-sized problems, these designs include dramatically fewer test cases than standard designs having the given coverage property. Consider, for example, a user interface with 13 entry fields and 3 possible values per field. In this case, the number of
possible test cases is extremely large—1,594,323. (In more realistic applications, it is common to have 75 or 80 different fields; in that case, even with dichotomous field inputs, one would have billions of potential inputs that might require testing.)
One possible approach for efficiently choosing inputs that cover all two- or three-way interactions involves the use of orthogonal arrays. An example of an orthogonal array with seven fields, each with two possible input values, is shown below in Table 2. In this example, eight test cases can be identified that provide coverage of all pairwise field values for each of the seven fields. For instance, the possible input pairs of field 1 and field 2 are (1,1), (1,2), (2,1), and (2,2). All of these possible pairs are represented in the Field 1 and Field 2 columns of Table 2; the same is true for any combination of two fields. Unfortunately, there are substantial problems with the use of orthogonal arrays. First, they do not exist for all combinations of fields and numbers of values per field. For an orthogonal array to exist, each field must have the identical number of values per field. More constraining, orthogonal arrays exist only for the case of pairwise changes, leaving open which approach to use for examining simultaneous changes to three, four, or more fields.
Dalal and others have shown that there are designs offering the same advantages as orthogonal designs but having substantially fewer test cases to examine. The reason for the inefficiency in orthogonal designs is that they are constrained to cover all pairs (or triplets, and so on) of field values an equal number of times. The new approach to this problem is referred to
TABLE 2 Example of an Orthogonal Array for Seven Fields, Each with Two Possible Values
|
Test |
Field 1 |
Field 2 |
Field 3 |
Field 4 |
Field 5 |
Field 6 |
Field 7 |
|
# 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
# 2 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
|
# 3 |
1 |
2 |
2 |
1 |
1 |
2 |
2 |
|
# 4 |
1 |
2 |
2 |
2 |
2 |
1 |
1 |
|
# 5 |
2 |
1 |
2 |
1 |
2 |
1 |
2 |
|
# 6 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
|
# 7 |
2 |
2 |
1 |
1 |
2 |
2 |
1 |
|
# 8 |
2 |
2 |
1 |
2 |
1 |
1 |
2 |
as Automatic Efficient Test Generator (AETG) (see, e.g., Cohen et al., 1996; Dalal et al., 1999). With AETG, one ignores the requirement of balance, and as a result one can identify designs that select fewer test cases that maintain coverage of the same pairwise (or k-wise) combinations of field values. In the test outlined above with seven fields, eight test cases are required. AETG, in contrast, generates the matrix of test inputs shown in Table 3 for the problem of 10 dichotomous fields. Here, even with an additional two fields, one is able to test all pairwise field values for all combinations of two fields with only six test inputs. In the case of 126 dichotomous fields, one needs only 10 test cases. There is a great deal of interesting mathematics associated with this new area of combinatorial design, with much more work remaining to be carried out.
For the problem mentioned at the outset of the presentation—13 fields, each with 3 possible values—AETG produces the array of test inputs shown in Table 4, with the given input values for the 13 fields. It was necessary to have 1.5 million inputs to cover all of the possible combinations of field values. With AETG, however, if one requires only test cases that cover all pairwise input values, one needs only the 15 test cases shown in Table 4. (It is, of course, important to consider the consequences of using a model of such modest size for problems in which the natural parameter space is of very high dimension. Therefore, sensitivity analysis is recommended to validate such an approach.)
It should be stressed that in real applications, the problems are typically more challenging since various complicating constraints operate when one is linking fields of inputs. Such complexity also can be accommodated with this methodology.
More broadly, AETG represents a game plan for efficiently generating test cases, running these cases to identify failures, analyzing the results, and making improvements to the software system, and then iterating this entire process to attain productivity and quality gains.
Jerry Huller at Raytheon has used this procedure and obtained a 67 percent cost savings and a 68 percent savings in development time. The effort required to carry out AETG is typically longer than is generally allocated to testing because the approach requires careful attention to the constraints, the various fields, and so on. Therefore, a cost-benefit argument must be made to support its use.
TABLE 3 AETG Test Design for Ten Dichotomous Fields Covering All Pairwise Input Choices
|
Test |
Field 1 |
Field 2 |
Field 3 |
Field 4 |
Field 5 |
Field 6 |
Field 7 |
Field 8 |
Field 9 |
Field 10 |
|
# 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
# 2 |
1 |
1 |
1 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
|
# 3 |
1 |
2 |
2 |
2 |
1 |
1 |
1 |
2 |
2 |
2 |
|
# 4 |
2 |
1 |
2 |
2 |
1 |
2 |
2 |
1 |
1 |
2 |
|
# 5 |
2 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
2 |
1 |
|
# 6 |
2 |
2 |
2 |
1 |
2 |
2 |
1 |
2 |
1 |
1 |
TABLE 4 AETG Test Design for 13 Trichotomous Fields Covering All Pairwise Input Choices
|
Test |
Field 1 |
Field 2 |
Field 3 |
Field 4 |
Field 5 |
Field 6 |
Field 7 |
Field 8 |
Field 9 |
Field 10 |
Field 11 |
Field 12 |
Field 13 |
|
# 1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
# 2 |
1 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
2 |
1 |
1 |
1 |
|
# 3 |
1 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
|
# 4 |
2 |
1 |
1 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
2 |
2 |
1 |
|
# 5 |
2 |
2 |
2 |
3 |
3 |
3 |
1 |
1 |
1 |
2 |
2 |
2 |
1 |
|
# 6 |
2 |
3 |
3 |
1 |
1 |
1 |
2 |
2 |
2 |
3 |
2 |
2 |
1 |
|
# 7 |
3 |
1 |
1 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
3 |
3 |
1 |
|
# 8 |
3 |
2 |
2 |
1 |
1 |
1 |
3 |
3 |
3 |
2 |
3 |
3 |
1 |
|
# 9 |
3 |
3 |
3 |
2 |
2 |
2 |
1 |
1 |
1 |
3 |
3 |
3 |
1 |
|
# 10 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
2 |
|
# 11 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
|
# 12 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
2 |
|
# 13 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
3 |
|
# 14 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
3 |
|
# 15 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
2 |
1 |
3 |
The Poore Paper
Jesse Poore described a model for software testing that has as its basis a Markov chain representation of the transition from one state of use to another as a software system executes, where the transitions are generated by the user taking various actions. (See, e.g., Whittaker and Thomason, 1994; Walton et al., 1995). As mentioned above, there is a potentially astronomical number of scenarios of use of a software system. It is therefore natural to consider using statistical principles as a basis for the selection of the inputs to use in testing.
The particular approach taken makes use of an operational usage model, which is a formal statistical representation of all possible states of use of a system. The specific structure of the model is a directed graph, where the nodes are the states of use and the arcs are possible transitions from one state of use to another. (The states of use should not be confused with the state of the software system operating in a computer, that is, which line of code is being executed.) The states of use can be defined at any desired level of the software’s natural hierarchical structure. Thus, for example, if a specific module is well known to be error free, one might model only the entering and exiting of that module. The stimuli that cause the current state to change are represented on these arcs connecting the states of use. For example, a human being hitting a key on a keyboard or pointing and clicking a mouse is a stimulus that can result in a state change. On the directed graph are a starting state and a terminal state, and use of the system is a path from the starting to the terminal state across the arcs. If one is interested in generating random test cases, one can use information on how the software is used to provide probabilities for these paths.
Given this structure, it is natural to model the working of the software system as a Markov chain, which assumes that the probabilities of moving from one state to another (the transition probabilities) are independent of the history of prior movement, conditioned on knowledge of the current state of the system. These transition probabilities can be set to values based on knowledge of specific environments of use, or in the absence of this knowledge, can be set uniformly across all states with which the given state “communicates.” (That is, some movements from one state to another may be forbidden given the assumed functioning of the system, and these are the states with which a given state does not communicate.)
While a system has only one structure of states and arcs, it may be applied in many different environments. For example, a word processor
may be used by a novice writing a letter or by a technical writer, and the two will use the system differently. The usage environment, which provides the probability of a transition from each state to any other state in the system, is a modeling structure that can and should be implemented separately in each intended environment of use, therefore requiring different transition probabilities. The selection of test inputs based on a model of user behavior permits the software test to focus on those inputs that are most likely to appear in operational use
“Testing scripts” are also attached to each arc. By this is meant not only that the stimuli or the inputs that would cause movement along each arc are attached, but also that, when the input is applied and this arc is followed, there is an anticipated change in some output that accompanies the state change. Failure to observe this change will indicate an error in the code. For manual testing, the expected result given a stimulus can be checked against the actual result given written instructions. Using automated testing, one can add commands to the automated test equipment on each arc so that software commands are communicated to the test equipment when a test case is generated; these commands can be used to automatically measure the degree of agreement with the software requirements.
Development of these models is a top-down activity. There is generally a model initially at some high level of aggregation, with more detail being added incrementally as more of the detail of submodules is required. As submodules are incorporated into other software products, the associated models can be transplanted as well.
This Markov chain representation of the functioning of a software system supports the following standard analyses (and others) that derive from a test: (1) the probability that at a random time the system is in a given state; (2) the expected number of transitions in a test (and the variance in the number of transitions); (3) the expected number of transitions until a state first appears (and the associated variance); and (4) importantly and in a rigorous sense, how much testing is enough. These outputs can be compared with external understanding of the system to judge the validity of the model. (Small changes in transition probabilities can have unanticipated large impacts on the probabilities of paths through the system.) Various measures can also be developed to estimate test resources required to provide a given level of understanding of system performance. Some of this analysis can be carried out before coding. Therefore, one could use this analysis to argue against development of an untestable system.
In addition to these more standard analyses, one can obtain, through simulation, estimates of answers to any additional well-framed questions concerning states, arcs, paths, and so on. Also, one can specify transition probabilities by developing a system of constraints, that is, linear equalities and inequalities involving the transition probabilities, and then optimizing an objective function using linear programming.
Discussion of Dalal and Poore Papers
In the discussion of these papers, Margaret Myers asked software experts to examine four questions: (1) How does one estimate the reliability of a software system that is structured as a series of component software systems? (2) How does one address the integration of commercial off-the-shelf software systems, and how does one estimate the reliability of the resulting system? (3) How does one estimate reliability for a system that is being acquired in a spiral environment? (4) What sort of regression testing is useful in evolutionary acquisition?
Jack Ferguson pointed out that software methods are extremely important to DoD. DoD spends approximately $38 billion a year on research, development, testing, and evaluation of new defense systems, and it is estimated that approximately 40 percent of that cost is for software. Any method that can help DoD to make even a small improvement in software development can represent a large amount of savings. However, it should be kept in mind that the software is not always the problem. DoD is using software to do more and more, mainly to provide the flexibility required to meet new environments of use. Therefore, the problem is often fundamentally a domain-analysis problem.
Ferguson added that given the widespread use of commercial off-the-shelf systems, it is important to consider the use of black-box testing, as discussed in Poore’s (and Dalal’s) presentation. The workshop devoted to software reliability should devote a good deal of time to these methods.
Ferguson remarked that the traditional way of determining software reliability required a great deal of inspection, which is no longer workable. It was stressed that models such as those used by Dalal and Poore need to be developed as early as possible in system development, since, as with hardware systems, it is generally much less costly to fix a problem discovered early in the design phase.
CURRENT MODELS FOR ESTIMATING THE FATIGUE OF MATERIALS
Fatigue is likely the leading cause of failure of military hardware in the field. Thus it is extremely important for DoD to develop a better understanding of the sources of fatigue, to control the rate of fatigue, and to measure and predict fatigue in deployed hardware. Therefore, a high priority at the workshop was a session on the evolution and current status of statistical work in fatigue modeling.
The field of fatigue modeling lies at the interface of the disciplines of statistics and materials science, and success stories in this field invariably involve close collaboration between both disciplines. Materials scientists understand the structure and properties of the relevant materials while statisticians can model the behavior of these materials and analyze experimental or observational data that help refine these models. The products of this collaboration form the basis for replacement and repair policies for fatigue-prone systems and for the general management of hardware subject to fatigue. It is important to pursue efforts to enhance the statistics/materials science collaboration.
The Saunders Paper
Sam Saunders provided a historical perspective on fatigue modeling. Attention to this problem stems from analysis of the Comet, a post–World War II commercial jet aircraft. In the mid-1960s, around two dozen separate deterministic fatigue decision rules had been published, but none of them was very successful. The most accurate on average was found to be Miner’s rule: that the damage after n service cycles at a stress level that produces an expected lifetime of N cycles is proportional to n/N. Subsequently, it was proven that Miner’s rule made use of (apparently unknowingly) the expected value for fatigue life assuming that damage increments were generated from a specific class of distribution functions. However, the distribution of fatigue life about its expectation was either not considered or ignored.
A useful stochastic approach to the problem of fatigue modeling was provided by the development and application of the inverse Gaussian distribution (see, e.g., Folks and Chhikara, 1989). (The Birnbaum-Saunders distribution was developed first, but it is a close approximation to the inverse Gaussian distribution, which is easier to work with analytically.) Some
mathematical details are as follows. Let X(t) denote cumulative damage until time t, and assume that X(t) ≥ 0. Assuming that as t grows, X(t) becomes approximately normal, and assuming that μ E(X(t)) = μt and Var(X((t)) = o2t, the distribution of the first t at which X(t) exceeds ∆ can be shown to be:
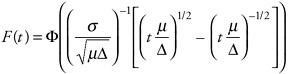
There are many generalizations of this argument, including those (1) for means and variances that are other functions of t, (2) for means and variances that are functions of other factors, and (3) where the distribution of X(t)is substantially non-normal.
Saunders described a current application derived from the generalized inverse Gaussian distribution applied to waiting times to failure for polymer coatings. These coatings often have requirements that they last for 30– 40 years. Modeling this requires some understanding of the chemical process of degradation, which in turn entails understanding how sun, rain, ultraviolet exposure, temperature, and humidity combine to affect coatings. Further, the chemistry must be linked to observable degradation, such as loss of gloss, fading, and discoloration. (For more details, see Saunders [2001].)
The Padgett Paper
Joe Padgett outlined several currently used approaches he has been researching that can be applied to either the modeling of the failure of material or systems due to cumulative damage or the modeling of crack growth due to fatigue. A good motivating example is the modeling of the tensile strength of carbon fibers and composite materials. In fibrous composite materials, it is essentially the brittle fibers that determine the material’s properties. To design better composites, it is important to obtain good estimates of fibers’ tensile strength. Numerous experiments have been conducted to provide information on the tensile strength of various single-filament and composite fibers. Failure of the fibers due to cumulative damage can be related to times to “first passage,” that is, times at which a sto-
chastic process exceeds a threshold, which naturally suggests use of the inverse Gaussian distribution. (There is also empirical evidence to support this model.)
In his research, Padgett has used fatigue modeling in conjunction with accelerated testing. The overall strategy is to use fatigue modeling to draw inferences about system failure during normal use based on observations from accelerated use. A key example is the case in which the length (L) of a carbon fiber serves as the accelerating variable, since the longer a carbon fiber is, the weaker it is. A key assumption of accelerated testing is that there is a functional relationship between the acceleration variable, L here, and the parameters (mean and variance) of the failure distribution.
To carry out such a program, the system is first observed for various values of the accelerating variable. Then a model of system reliability as a function of the accelerating variable is developed. Finally, the model is used to translate back to estimate the reliability at levels of typical use. Of course, one is extrapolating a model to a region in which little or no data are collected, making the inference somewhat risky. For this reason, efforts to validate models and to derive models using relevant physical principles (physics-of-failure models) are of critical importance.
The above represents the general approach that is currently being explored. A specific model that can be applied to the situation of discrete damage is as follows (for details, see Durham and Padgett, 1997, 1991; a related method is discussed in Castillo and Hadi, 1995). Consider a load being placed on a system as increasing in discrete increments. The system is assumed to have an unknown, fixed strength Ψ. The initial damage to the system is caused by its manufacture and is assumed to be due to the most severe flaw in the system. This flaw is quantified by a random variable X0, which can be the associated initial crack size or “flaw size.” The system is then placed under increasing loads, with each additional increment of stress causing some further damage D ~ FD. The amount of damage at each step i, Di, is a random variable, which can be viewed as crack extension due to the added load. The initial strength of the system is denoted by W, which is the result of a reduction of Ψ by X0. The approach assumes that additional increments of stress are loaded on the system until failure, and the model provides estimates of the mean number of increments of load to system failure, the mean critical crack size, and the full distribution of the number of increments until failure. The model is completed by the specification of the distribution of W, which should be based on knowledge of the physics of failure of the system of interest. Durham and Padgett (1991)
apply this methodology to the modeling of crack formation in gun barrels, using linear programming to estimate the various parameters.
In some situations, it may be more appropriate to model the damage process (e.g., crack size) as a continuous rather than a discrete process. Here, the “system” of size L is placed under continuously increasing loads (e.g., tensile stress) until failure. (Or analogously, a stress is increased until a crack extends, resulting in failure.) Various estimated acceleration functions are used to provide estimated parameters for the inverse Gaussian distribution. Examples include the power law model, the Gauss-Weibull additive model, or the Bhattacharyya-Fries inverse linear acceleration law. One can use various goodness-of-fit tests to determine which model fits the data best. Finally, approximate confidence intervals from maximum-likelihood considerations can be constructed.
Discussion of Saunders and Padgett Papers
In the discussion of these papers, Ted Nicholas outlined two methods for modeling fatigue currently used by the Air Force. First is a typical functional form that models expected lifetime (before a crack initiates) as a function of stress, which in the Air Force’s case is the number of cycles an engine is operational. There is natural variability among individual systems about this mean; thus systems are designed so that the lower bound of, say, a 99.5 percent tolerance interval lies above a required level given a certain rate of cycles of use. This is referred to as the “design-allowable curve.” An unsolved problem is that the functional form often must be fit on the basis of limited data, especially at the tail end with respect to amount of use.
Another approach to fatigue modeling used by the Air Force is the damage tolerance methodology. With the above approach, all of the items subject to fatigue are thrown out as soon as they have been operated the number of cycles determined by the design-allowable curve. Of course, a number of the items thus discarded have residual lifetimes many times longer than the number of cycles for which they were operated. This process can therefore be extremely expensive. The damage tolerance methodology assumes that one is sophisticated at predicting how cracks grow. If there is an inspection interval at a given number of cycles, and one can be sure by examination that there are no cracks larger than the inspection limit, one can institute a process whereby any crack will be discovered during the next inspection period before it can grow to a critical size. To accomplish this, the intervals between inspections are set at
one-half or one-third of the minimum time it takes a crack to grow from the inspection limit to the critical size. This approach can play a role in engine design.
Nicholas then discussed a substantial remaining problem—high-cycle fatigue—which is due to low-amplitude, high-frequency vibrations. With low-cycle fatigue, a crack typically develops early in an item’s life, and gradually propagates until it can be discovered when it grows to be larger than the inspection limit. With high-cycle fatigue, one typically has no indication of any fatigue damage until it is almost too late. As a result, there is as yet no reliable method for detecting high-cycle fatigue damage in the field. The current idea is to stay below a statistically significant stress level so the item will never fail. (This is not a notion of accumulated stress, but a notion of current stress levels.) However, there is no guidance on what to do when there are transient events during which the stress level exceeds the limit. If the perspective of accumulated stress is taken, should cycles during these transient events count more than cycles within the stress limit? The model that underlies this approach is that there are distributions of stresses and of material strength, and one does not want to have a pairing in which the individual stress received from the stress distribution exceeds the individual strength received from the strength distribution. The important complication is that the strength distribution for an aging system is moving toward lower values during service, and it can decrease substantially as a result, for example, of damage from a foreign object.
Fighting the accumulation of stress is highly complicated. Both vibratory and steady stresses must be considered, along with the statistics of material behavior. In addition, computational fluid dynamics plays a role. One must also take into account the effects of friction, damping, and mistuning. Finally, one can have certain types of fatigue failures, only say, when an aircraft is flown under particular operational conditions. Linking a vibrational problem with flight conditions is important, but can be extremely difficult. Nicholas agreed that enhanced communication between materials scientists and statisticians is needed to continue work on these issues.
RELIABILITY MANAGEMENT TO SUPPORT ESTIMATES OF SYSTEM LIFE-CYCLE COSTS
The workshop sponsors were extremely interested in exploring the issue of how early reliability assessments of defense systems in development
might be used to address issues involving the life-cycle costs of proposed systems and systems under development. Defense systems incur costs during the development process (including testing costs), costs in production, costs through use and repair, and sometimes redesign costs. Maintenance, repair, and redesign costs increase with the decreased reliability of a system and its components. Today there is a widespread perception within DoD that the percentage of the costs of defense systems that is incurred after production is too large, and thus that greater resources should perhaps be expended during the design and development stages to reduce postproduction costs, thereby reducing life-cycle costs. Estimating life-cycle costs and their contributing components can help in evaluating whether this perception is true and what specific actions might be taken to reduce lifecycle costs to the extent possible.
An introduction to the session was provided by Michael Tortorella of Bell Laboratories, who discussed some general issues concerning warranties and life-cycle costs. Systems with different reliabilities can have substantially different production costs. In industry, given a cost model that is sufficiently precise, it is possible to offer maintenance contracts or warranties that can be profitable to the producer.
Two primary areas of focus in the field of reliability economics are risk analysis and spares management. Risk analysis involves a supplier who needs to assess the probability that a product and a warranty will be profitable, which requires estimation of system life-cycle costs. A way to think about risk analysis is that every time a supplier produces a product or warranty for sale to a customer, the supplier is placing a bet with the company’s money that the product or warranty will be profitable. Reliability engineering represents an attempt to improve the odds on that bet. Spares management involves inventory investments, storage costs, transportation costs, and the consequences of outages during delays. Two approaches used are (1) stocking the spares inventory to a service continuity objective, which means stocking an inventory to ensure that, with some designated probability, a spare will be available; and (2) the preferred approach of taking into consideration the various costs associated with different stocking strategies and minimizing those costs while meeting the availability objective of the system. (For more information, see Chan and Tortorella [2001], Blischke and Murthy [1998], Murthy and Blischke [2000], and a variety of papers in Tortorella et al. [1998].)
The Blischke Paper
Wallace Blischke provided an overview of the analysis of warranties and life-cycle costs. Analysis of life-cycle costs typically is carried out from the point of view of the producer, examining the costs of a system from conception to withdrawal from the marketplace. The earlier life-cycle and associated costs can be estimated, the better it is for the decision maker, though the earlier in development these estimates are attempted, the more difficult they are to produce. Blischke stated his preference for a Bayesian approach in this effort, since that paradigm provides a basis for the use of engineering judgment and information derived from similar systems, as well as a natural method for updating predictions.
It is important not only that reliable estimates of life-cycle costs be produced, but also that reliable estimates of their uncertainty also be developed and communicated to assist in decision making. Further, an understanding of the origin of the uncertainties can help in assessing how best to improve the quality of future predictions. This is especially true for defense systems, which of course can be much more complex than consumer goods. (For example, costs for defense systems sometimes include disposal costs, which can be nontrivial.)
The Bayesian approach is initiated before initial testing with the use of all available information to form a prior distribution describing system reliability. Prototypes are then produced and tested. The data from these tests are employed using Bayes’ theorem to update the prior distribution to form a posterior distribution, and the posterior distribution is used in turn to produce estimates and prediction intervals concerning parameters that govern life-cycle costs, the profitability of warranties, and related constructs.
As an example, Blischke discussed the analysis of life-cycle costs for a propulsion system in development. To achieve a required level of reliability, preliminary reliability levels are specified for the basic subsystems and components. Some of the standard tools used for this purpose are fault trees; reliability block diagrams; and failure modes, effects, and criticality analysis. One important issue is whether reliability problems are due to the design, the process, or the operations. Often, operational errors are more important than design errors. Engineering judgment based, for example, on information on components used in previous propulsion systems, can support a preliminary Bayesian assessment of system reliability (although such information will be very limited when the system involves a new tech-
nology). This analysis is followed by a detailed design analysis and then full-scale testing, leading to an operational system.
Blischke then focused on warranty concepts and costs. A warranty is a contractual agreement between the buyer and the seller that establishes buyer responsibilities and seller liability, and provides protection to both buyer and seller. Cost models are used to examine the properties of a given warranty; as the reliability of a system increases, the cost of a given warranty decreases. On the other hand, producing a highly reliable system is likely to require large up-front costs, which suggests a trade-off between the costs of fielding and those of development and production that needs to be understood and analyzed. Optimization approaches can be used in performing this analysis.
Warranty costs can be predicted empirically if enough systems are produced early. The advantage of doing so is that no modeling assumptions are needed. In the defense area, this possibility is less likely. Alternatively, one can carry out testing on prototypes or components of prototypes to obtain information on the distribution of waiting times to failure so they can be modeled.
For a simple, real example, Blischke analyzed a free-replacement, nonrenewing warranty (i.e., the replacement item is warrantied to work for the time left in the original warranty period). In this example, the supplier agreed to provide a free replacement for any failed component up to a maximum usage time. If at the end of the warranty period the purchased item was still working, the next replacement would be paid for by the buyer.
Blischke presented some mathematical details, using the following notation: w is the warranty period, m(w) is expected number of replacements per item during the warranty period (the renewal function), cs is average cost per item to seller, and cb is average cost to buyer. The cost of offering a free-replacement warranty is analyzed as follows. First, the cost to the buyer of each new item is cb. The expected cost to the seller, factoring in the cost of prewarranty failures, is cs (1 + m(w)). For the exponential time-to-failure distribution with mean time to failure of 1/λ, m(w) = λw. In this case, it is easy to determine when cs (1 + m(w)) is less than cb. Unfortunately, for distributions other than the exponential, the renewal function can be difficult to work with analytically. However, software exists for calculating renewal functions for the gamma, Weibull, lognormal, and inverse Gaussian distributions and various combinations of these.
From the buyer’s perspective (ignoring the profit of the seller), the
expected life-cycle costs in a life cycle of length L with warranty period w can also be computed. This computation involves a different renewal function that is the solution to an integral equation. This perspective may be more appropriate for DoD.
Blischke indicated that reliability-improvement warranties are popular in the defense community. These are warranties in which the seller will provide spares and field support, analyze all failures, and then make engineering changes to improve reliability for a given period of time for an extra fee. As above, to develop a model of life-cycle costs, one must model all of the various cost elements and the probabilities associated with each. One of the first models for the expected cost of an item sold under a reliability-improvement warranty is described in Balaban and Reterer (1974). This and other similar approaches are based on a comparison of expected costs. To have a model that can answer more complicated questions, however, one must have a representation of all probabilistic elements and distributional assumptions, rather than simply an analysis of expected values.
In general, there are various models of life-cycle costs from either the buyer’s or the seller’s point of view for various kinds of warranties (e.g., pro rata, combination warranty, just rebates). To decide which defense systems should be developed to carry out a task from the perspective of minimizing life-cycle costs, one must derive estimates of life-cycle costs relatively early in the system development process, which, as mentioned above, is very difficult to do well. With respect to just the warranty component of lifecycle costs, a Bayesian approach has some real advantages. First, one collects all relevant information, including data on similar systems, similar parts, materials data, and engineering judgment, and aggregates this information into prior distributions for system reliability. All the information collected must be accompanied by an estimate of its uncertainty to elicit the spread of the prior distributions. (For details, see Blischke and Murthy, 2000; Martz and Waller, 1982.) Such reliability assessments require the use of logic models that relate the reliability of various components for which one may have some real information to the reliability of the entire system. (For specifics, see Martz and Waller, 1990; Martz et al., 1988.) These priors are then used to predict parameters of the distribution of total time to failure, which can be used to predict warranty costs. Bayesian methods are then used to update these priors based on new information on component or system reliability.
Blischke believes a comprehensive Bayesian cost prediction model can be based on an analog to a Bayesian reliability prediction model. Roughly
speaking, costs are another element besides reliability for which one acquires and updates information. This computation is very similar to those used in PREDICT. One complication is that reliability and costs are related, so a bivariate model may be needed (see, e.g., Press and Rolph, 1986). Given today’s computing capabilities and the recent development of powerful new ways to carry out Bayesian computations, this approach is likely feasible. Thomas and Rao (1999) can serve as an excellent introduction to many of these ideas. Finally, to support this approach to life-cycle costs and warranties, information on systems, tests, costs, and reliabilities all must be maintained in an accessible form.
The Camm Paper
Frank Camm outlined some management hurdles that complicate the application of life-cycle cost arguments in DoD acquisition. Camm made four major points. First, the policy environment provides an important context for examining system life-cycle costs. Second, improved tools for assessment of life-cycle costs can aid DoD decision makers in their pursuit of priorities relevant to reliability as a goal in system development. However, those tools cannot change the priorities themselves. Third, as systems age the demands for reliability seem to increase, probably because of changes in the way systems are deployed. Fourth, initiating a formal maturation program provides a setting in which to conduct reliability analysis, as well as an element of acquisition planning important to the projection of future system reliability.
Most expenditures per unit time of a defense system in development are paid out during production, and the fewest are made during the initial design phase. However, the majority of expenditures for a system are postproduction, including operations and related support as well as modifications. Because these costs are viewed as being far in the future, they are to some extent ignored during acquisition.
In producing estimates of life-cycle costs for a system in development, it is usually necessary to base the analysis on several assumptions, some of which are tenuous. For example, the years for which a system will be in operation are difficult to predict. The Air Force currently has weapon systems that are expected to be in use well past their intended length of service. Further, various complicating factors that are difficult to incorporate into an analysis should be taken into account when estimating life-cycle costs. Some examples are use of the system for purposes not originally
envisioned (e.g., flying a plane faster than planned), operating an engine for more cycles than planned, flying a plane with a different profile, or using a different support plan. These factors can lead to substantial changes in the reliability of a system and hence in life-cycle costs. Also, for nonmodular systems, postproduction modifications can be very difficult to predict a priori and are often relatively costly. One needs to be aware of the sensitivity of estimates of life-cycle costs to these kind of changes and their impacts on system reliability.
Camm added that the source of failure in many systems turns out to be a single essential component that was poorly designed or improperly installed or integrated into the overall system. These are the “bad actors” (see Chapter 4 for further discussion), and if they could be identified and fixed early, performance could be substantially improved.
From the perspective of defense system development, it will often be important to choose between reducing system costs and increasing system capabilities. Alternatively, one could decide to add greater flexibility into the system so that it will be easier to make modifications when necessary. This latter approach makes it possible to learn more about the system and facilitates improvement of the system over time. The underlying question of how much reliability is enough requires a highly complex set of analyses examining a variety of difficult trade-offs between increasing design and production costs and reducing operating costs.
Some external changes will have predictable impacts on the importance of system reliability. For example, decreases in the discount rate make future money more valuable, and therefore result in a decision to build more-reliable systems. Also, as the size of a fleet grows, the payoff from system development becomes greater, and this, too, argues for greater reliability.
This perspective has other implications as well. For example, it might be useful to have much smaller fleets but still allow for the use of many components across all fleets. Doing so would increase the total number of components being built, which in turn would make it possible to learn something about the components in one weapon system that might be useful in another. This is a key aspect of system maturation. Also, if one increases the expected life of a fleet or the amount it is used, one is forced to place greater priority on system reliability. Considerations of system reliability are also dependent on deployment. When projecting the costs of a force deployed from the United States, one must consider the costs of the entire support base associated with the deployment, which is again a function of system reliability.
Questions about system reliability must be addressed within a context, and a component of that context is the incentives that exist within DoD concerning reliability. An interesting question is why DoD continues to make optimistic estimates of system reliability and costs early in development. The reason for this is that a constituency needs to be formed for systems in development, and to this end a system must be promoted. Once various groups have become committed to a system, they are more likely to support increases in costs or reductions in reliability. Developers become accustomed to viewing early estimates of final system reliability as somewhat unrealistic goals. Also, there is an incentive to wait to deliver bad news about system costs and reliability so a program is not threatened while its constituency is being developed. As a result, fixing problems becomes more costly. Early overoptimism, then, is likely not a problem of analysis, but instead one of incentives surrounding the system development process within DoD.
Another context issue lies behind the evident difficulty of making the argument that reliability improvement would be cost-effective. This difficulty is explained by at least three factors. First, there is a historical lack of emphasis of system reliability relative to system effectiveness. Second, there are very separate environments within DoD for those involved in initial design (acquisition) and in system operations (logistics), in part because of the differing time horizons of these activities. Third, Congress tends to view funding decisions within a short time frame. That is, it is difficult to argue that an extra $5 million spent this year will save $30 million over the next 10 years when those charged with distributing funds are concerned primarily with the next year or two. This problem resulted in formulation of a concept referred to as “cost as an independent variable,” which asserts that cost is a relevant factor in evaluating a proposed answer to a defense need.
One approach to increasing defense system reliability through a change in context is the introduction of warranties for defense systems. Two possibilities have been suggested. The first is compliance with specifications on delivery. This is basically an acceptance inspection to ensure that specifications are met. Once the specifications are met, the warranty is over. The second possibility is performance warranties, which promise a certain level of performance from a system over a period of time. This approach is being promoted by many as an answer to the reliability shortcomings of defense systems, but it raises some difficult questions.
First, this increase in reliability would come at a price since warranties
are not free. Paying for these warranties raises some of the contextual problems identified above. Assuming funding can be arranged, there are real analytic and implementation problems. One key problem is identifying a reasonable set of incentives or penalties for keeping or not keeping the promises made. Also, it is difficult to enforce these warranties because of the many factors that are not under the control of the developer and producer of the weapon system. These factors include the behavior of the user, the environment of use, the operational support system, and the specific counterforces used against the system. It is difficult to prove that a system has not met performance requirements.
Discussion of the Blischke and Camm Papers
Allen Beckett agreed that reliability estimation is extremely challenging. How does one estimate the reliability of an engine that has been overhauled? What are its failure modes? How does one develop a spares budget for a system in development? Beckett acknowledged that collecting relevant data is necessary and that there are promising modeling approaches. But the key is to understand the operational issues so the models will represent all of the complexities.
The related issue of surveillance testing was raised by Rob Easterling. The objectives of such testing are to find and fix reliability problems, and then update the estimate of system reliability. For defense systems, surveillance testing poses some difficult problems. First, in the case of complicated defense systems, it is unlikely that a large number of replications for surveillance testing will be available. Second, there are a multitude of environments and missions with potentially different reliabilities and failure modes for a given system. The fundamental complication, however, is that it is difficult to quantify the goals of surveillance testing. For example, what is the tolerable probability of failing to detect a fault leading to a reduction in reliability of more than 10 percent in 2 years of testing? It may be that surveillance test plans cannot be driven solely by statistical arguments.
However, statistical constructs should be part of the decision process regarding surveillance testing. Like a warranty, surveillance testing should be considered a type of insurance policy, whereby some amount of protection is being purchased for the price of additional testing. The general point is that, regardless of how a surveillance test plan and the associated decision rule based on the test results are derived—whether through eco-
nomic analysis, classical hypothesis testing, Bayes methods, or the like—a test has (statistical) operating characteristics. These operating characteristics are the probabilities of making various decisions based on underlying properties of the system under test. (The operating characteristics of a simple hypothesis test are the probability of rejecting the null hypothesis when it is true and the probability of failure to reject the null hypothesis when it is false.) Generalizing the notion of operating characteristics would provide the correct basis for decision rules; for example, a decision rule based on a specific test design would ideally have a high probability of passing a system that met the requirement and a high probability of failing a system that did not meet the requirement. Estimates of the operating characteristics of a test should be communicated to decision makers and recognized in the decision process. Finally, a decision rule could be enriched through use of information from such sources as simulations and developmental test results (a relevant paper is Fries and Easterling, 2002).



































