5
Approaches for Estimating Emissions
INTRODUCTION
In the absence of effective and efficient means to measure air emissions from each animal feeding operation (AFO) directly, regulatory or management agencies seeking to mitigate emissions need reasonably accurate means to estimate them and attribute them to particular operations or activities. The committee has considered three possible approaches: (1) emission factors from representative AFOs; (2) regression analysis equations that relate air emissions to specific aspects of individual AFOs; and (3) process-based models that estimate the flows of emission-generating substances through the sequential processes of the farm enterprise. The committee favors the third approach which is discussed in greater detail in this chapter.
The “emission factors” approach is based on measurement of air emissions from a defined set of “average” AFOs that presumably represent a substantial proportion of the national population. Emission factors, expressed as the mass of each substance emitted per animal or other base unit per unit of time, are then used to estimate air emissions from other AFOs, which are assumed to fall into one of the categories in the defined set of average AFOs used to estimate the emission factors. Weaknesses in this approach noted in the committee’s interim report (NRC, 2002a) include the difficulty of defining a small set of average AFOs that can represent the broad range of AFOs for varied livestock industries in various geographic regions. As with the other approaches, obtaining the data upon which to base useful estimates of air emissions requires many direct measurements, which do not exist today in sufficient numbers to provide reasonable confidence in the results.
The “regression analysis” approach uses standard least-squares multivariate regression equations to relate measures of air emissions to various factors that are hypothesized to affect them (e.g., number of animals, animal type and production system, productivity, housing, manure management, weather, climate). Once the equations are verified, they are used to gauge the importance of various factors that determine emissions and to estimate air emissions from other AFOs based on their individual characteristics. The weakness of this approach is the assumption that the within-factor variation of emissions is small relative to the among-factors variation for any category of operation. In addition, the current database for estimating regression equations is very limited and a major effort would be required to obtain them.
The “process-based” approach follows the fate of relevant elements (e.g., nitrogen, carbon and sulfur) step by step through the animal feeding process and identifies the chemical transformations that take place. It provides estimates of the characteristics and amount of air emissions that occur at each step as controlled by a mass balance approach (i.e., the emission of an element from the system, or from a part of the system, is equal to the input of that substance minus any accumulation that might occur). The advantages and limitations of this approach are described in some detail later in this chapter.
EMISSION FACTOR ESTIMATES
The goal of the U.S. Environmental Protection Agency (EPA, 2001a) is “to develop a method for estimating [air] emissions at the individual farm level that reflects the different animal production methods that are commonly used at commercial scale operations.” The approach was intended to provide estimates of total annual air emissions from AFOs for defined geographic areas by kind of animal and manure handling practices for each of eight kinds of emissions. It did this with a model farm construct that provides estimates of average annual emissions per EPA animal unit (AU) for twenty-three model farms (two for beef, eight for dairy, two for poultry-broilers, two for poultry-layers, two for poultry-turkeys, five for swine, and two for veal; EPA, 2001a). Each model is defined by three variable elements that describe manure management practices for typical large AFOs: (1) confinement and manure collection system, (2) manure management system, and (3) land application. The manure management system is further subdivided into solids separation and manure storage activities. Insofar as combinations of these elements are regionally distinctive, the model farms also reflect regional variations in air emissions.
Model farms, as described by EPA (2001a), are useful for aggregating emission rates across diverse sets of AFOs. A model farm can be used to represent the average emissions across some geographic area over some period of time per unit capacity of a class of farms (e.g., all pig farms in the United States that use an
enclosed house with pit recharge and irrigation of supernatant onto forage land; model farm S2).
The utility of this kind of model farm construct depends on the following:
-
defining models in which the dependent variable—the amount of each air emission per unit of time—is closely related to independent variables that accurately depict real feeding operations and that explain a substantial share of the variation in the dependent variable;
-
providing accurate estimates of the relationship between the dependent and independent variables; and
-
having estimates of the relationships between dependent and independent variables that clearly distinguish among the kinds of AFOs being modeled.
A critical requirement for estimating the appropriate emission factors is a statistically representative survey of emissions from a class of AFOs over several iterations of the time period to be represented. The size of the sample required to estimate the mean emission rate with a given degree of accuracy increases with the variability in the dependent variable to be measured (e.g., the average emission rate) across the set of independent variables that affect it. Independent variables that have been discussed include animal type and age, diet, local climate, building type, land application method, and management practices. To the extent that some of these variables change over time (e.g., trends in farm organization, location, practices, and technology), updating of estimates and estimates of trends may be required.
The model farm construct is represented by Equation 5-1:
E = Σi (wi • ei)
(Eq. 5-1)
in which the total emission (E) of a particular pollutant from an AFO during a period of time is the product of the emission (ei) from each unit (i) on the model farm and the number of units (wi) of that type, summed over the farm.
One use of model farms might be to predict emission rates and local effects of a single AFO or a cluster of AFOs in a small area. This use differs from that described by EPA (2001a), and it would require a detailed model or models describing the effects of selected variables on the rates of emissions and their downwind concentrations. An example is an odor dispersion model that predicts odor intensity as a function of time at various locations, given information on odor sources and local meteorological conditions. More data (perhaps hourly) and statistical analyses of the relationships between various explanatory variables and pollutant concentrations or impacts are required.
The committee believes that EPA’s proposal (2001a) is inadequate to meet these standards. It does not provide a method to adequately determine air emis-
sions from individual AFOs because both the model farm construct and the data are inadequate. The model farm construct used by EPA (2001a) cannot be supported for estimating air emissions from an individual AFO because it cannot account for a great deal of variability among AFOs. In particular, important factors not included in the EPA model include animal feeding and management practices; animal productivity; housing, including ventilation rate and confinement area; use of abatement strategies such as sprinklers to decrease dust; and physical characteristics of the site such as soil type and whether the facility is roofed. In addition, emissions are likely to differ for different climatic (long-term) and weather (short-term) conditions including temperature, wind, and humidity. Accurately predicting emissions on individual AFOs would require determination of emission factors that reflect these characteristics.
More specifically, improvements in the model farm construct would be needed for both discrete variables (e.g., management, confinement conditions, location) and continuous variables (e.g., nutrient input, productivity, meteorology). Concerns about the quality of data (much of it not reviewed), great gaps in the data, inappropriate use of data, and representativeness of the data were discussed in the committee’s interim report (NRC, 2002a; see Appendix L).
FINDING 8. Estimating air emissions from AFOs by multiplying the number of animal units by existing emission factors is not appropriate for most substances.
RECOMMENDATION: The science for estimating air emissions from individual AFOs should be strengthened to provide a broadly recognized and acceptable basis for regulations and management programs aimed at mitigating the effects of air emissions.
While the committee favors a process-based modeling approach, there are some substances, such as particulate matter (PM) and odor for which an emission factor approach may still be the best approach. An example of an emission factor approach utilizing mass balance constraints for the emission of PM from a feed mill is given in Appendix I. A critical need exists to determine emission factors or fluxes for AFO emissions of PM and odor-causing constituents emanating from either area or point sources. Specific short-term research needs include the following:
-
development of protocols to determine emission fluxes from downwind concentration measurements,
-
evaluation of dispersion models to determine the best method to calculate fluxes,
-
determination of the best method to establish volumetric flow rates for mechanically and naturally ventilated AFOs,
-
comparison of emission factors for naturally ventilated and mechanically ventilated AFOs, and
-
determination of the applicability of utilizing PM samplers designed and calibrated for the urban environment in a rural setting.
MULTIPLE REGRESSION APPROACH TO DEVELOP EMISSION FACTORS
Given the inadequacy of the model farm construct described above, the committee discussed developing a different construct by systematically identifying factors that contribute to changes in emission rates. The approach would still be empirically based on measured total emissions from individual representative farms. A comprehensive and representative data set would be developed largely from new investigations. The various emission measurements (e.g., for ammonia [NH3] and methane [CH4]) would be regressed against several independent variables hypothesized to affect emission rates (e.g., animal type, management system, abatement strategy). Significant terms could be included in an empirical model to predict emissions from farms. Principal component analysis might be used to determine which factors contribute the most to emission rates and to evaluate whether certain practices give significantly different results than others. Compared to the existing emission factor approach, this alternative would result in more accurate estimates of emissions from individual farms and the identification of strategies to decrease emissions.
A comprehensive data set would have to be developed from existing literature and new investigations. Given the paucity of research in which total emissions from individual farms have been measured accurately, most of these data would have to come from new studies. The measurements would have to be accurate and representative of the emissions that occur for the time period of interest (e.g., an hour, or a full year). The data set would also have to include farms representing all factors that are hypothesized to affect emissions. In particular, it should include enough distinctive measurements to differentiate the types of classifications made in the EPA model farm construct (e.g., animal type and manure management systems), as well as additional factors not included in the EPA model that are likely to affect emissions. For example, farms would have to be included that represent different types of animal management; levels of animal productivity; housing including ventilation and confinement area; use of abatement strategies such as sprinklers to decrease dust; and physical characteristics of the site, such as soil type and whether the facility is roofed. The data set would also have to be replicated under different climatic and weather conditions and would require adequate replication on farms of similar type so that the variance not accounted for in measurements could be determined. Developing a robust set of equations would require sampling hundreds of AFOs representing different management and meteorological conditions. The cost of accurately measuring emissions on the number of AFOs (i.e., thousands) that would be needed to replicate
all common situations would be very high, and the time required would probably be too long in the face of the demands for regulation.
PROCESS-BASED MODELING APPROACH
The committee recommends using a process-based modeling approach to predict emissions from both individual AFOs and regions. A process-based approach would involve analysis of the farm system through study of its component parts. It would integrate mathematical modeling and experimental data to simulate conversion and transfer of reactants and products through the farm enterprise (Denmead, 1997; Jarvis, 1997). In many cases, this approach makes use of mass balance equations to represent mass flows and emissions of major elements (e.g., nitrogen, carbon, sulfur) through the system. In other cases (e.g., particulate matter and odors), alternative approaches such as emission factors may be the best way to predict emissions. In either case, models are needed to estimate emissions from individual AFOs to identify farms that should be targeted for control strategies and to predict the impact of management techniques to decrease emissions. Models are also needed to estimate emissions across specific regions and globally. Currently, emission factors are multiplied by the animal inventories to make these estimates. Process-based models may be used with data on animal and crop inventories and specific information on management strategies. Additional data may have to be collected by the agricultural census to use new process-based models.
FINDING 9. Use of process-based modeling will help provide scientifically sound estimates of air emissions from AFOs for use in regulatory and management programs.
RECOMMENDATIONS:
-
EPA and the U.S. Department of Agriculture (USDA) should use process-based mathematical models with mass balance constraints for nitrogen-containing compounds, methane, and hydrogen sulfide to identify, estimate, and guide management changes that decrease emissions for regulatory and management programs.
-
EPA and USDA should investigate the potential use of a process-based model to estimate mass emissions of odorous compounds and potential management strategies to decrease their impacts.
-
EPA and USDA should commit resources and adapt current or adopt new programs to fill identified gaps in research to improve mathematical process-based models to increase the accuracy and simplicity of measuring and predicting emissions from AFOs (see Chapter 7).
Components of the AFO system
The system for animal production includes several components shown in Figure 5-1. Of course, all AFOs by definition contain animals on a lot or in housing. Emissions can occur directly from living animals or from animal mortality that is discarded. The animals also produce manure that is either handled on the farm or exported to other farms. In either case, manure is applied to soil on which crops are grown. Crops that produce feed for animals may or may not have been fertilized with manure, but invariably they will have been fertilized in some way. Emissions can occur from many components of the AFO. For example, ammonia may be volatilized from the animal housing, manure storage, or field. The amount lost from one component of the farm affects the amount that can be emitted from subsequent components. For example, if nitrogen is volatilized from an animal house, it is not available to be volatilized again from manure storage or field.
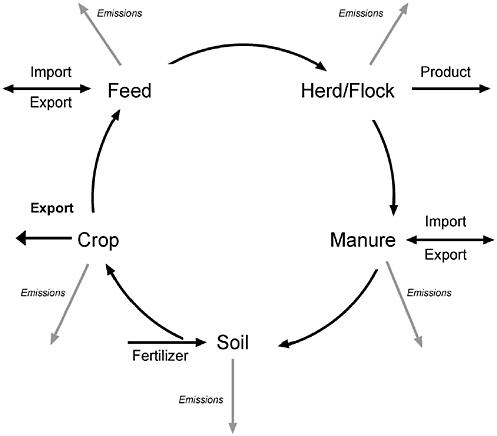
FIGURE 5-1 A schematic representation of a process-based model of emissions from an animal production system. Emissions can be to air or water.
Moreover, transformations that occur in one of the farm components might affect emissions and further transformations in other components. The committee recommends modeling the major farm processes in such a way as to include the effects of transformations in each farm component on the others.
An animal feeding operation may not include all of the components shown in Figure 5-1 on one farm. However, a complete system for animal production must include crop production and manure utilization or disposal even if these activities are carried out on separate farms. When emissions from AFOs are considered, the environmental impact depends on management of the complete production system. For example, an AFO may decrease emissions from its property by importing feeds or exporting manure to a separate farm. Unless the handling of crops or manure is superior on the other farms, the overall emissions to the environment would not be decreased; they would simply be moved off farm and possibly increased. This raises an important issue related to regulation of emissions from individual farms. If crop production and manure handling are not regulated in a similar way on AFO and non-AFO farms, there will be an incentive to outsource crop production and manure use to decrease AFO emissions, but with no benefit to the environment. Emissions from the operations that produce feeds for animals, including crop farms and feed processors, must be considered as part of the animal production system. In addition, the way in which different foods are processed and used once they leave the farm affects total air and water emissions.
Comparison of the Committee’s Approach to the EPA Model Farm Approach
The EPA model farm approach (EPA, 2001a) uses emissions from housing, manure storage, and field application and adds them together. Using this approach, one would predict that a technology to decrease emissions from manure storage (e.g., covering manure lagoons) would decrease total farm ammonia emissions by the amount that was prevented from leaving the lagoons. In reality, this ammonia would be concentrated in the lagoon liquid—increasing the emissions in the barn when flushing with lagoon liquid and in the field during land application. In a process-based approach, rather than simply adding the emissions from each farm element, a mathematical model is used to represent the interactions between the system components. This alternative to EPA’s model farm approach would resolve many problems such as the one cited above and prevent predicting more manure nitrogen volatilized than excreted. Manure nitrogen production is used to predict the nitrogen available for conversion to ammonia for possible subsequent volatilization.
Development of a process-based model does not obviate the need for data collection, but it enables the use of data representing only part of the farm system, and will help identify gaps in the existing literature. In fact, data will be needed to represent transformations that occur on farms other than air emissions (e.g., or-
ganic N degradation in lagoons). Some of the necessary data may be available in the existing literature; however, additional studies will be necessary as outlined for specific emissions in the sections that follow. The accuracy of process-based models will still need to be determined with collected research data. The accuracy to which model inputs can be determined and their impacts on the model estimates will also have to be determined using sensitivity analysis.
Predicting Differences Among Farms
The process-based model has to account for differences among farms that may affect substances emitted, emission rates, pollutant concentrations, or flow of mass between farm components. These differences among farms include animal type and species; farm size (animal number and area) and density; animal or crop production system and productivity; housing type; manure collection, storage, and application; soil type and capacity; cropping systems (including tillage method, crop rotation, and irrigation practices); and weather (short term) and climate (long term). The way in which each of these differences among farms should be represented in the model is discussed in a general way below, and more specifically for individual emissions in the sections that follow.
The size of a farm, as represented by the number of animals or area of cropland, is likely to affect the amount of emissions from it. For any animal type (e.g., swine, dairy cattle, chickens), the rate of animal production (e.g., growth, production of milk or eggs) will also affect intake of feed nutrients and subsequent excretion of elements found in manure (e.g., N, C, S, P). In general, higher rates of production result in greater rates of nutrient excretion per animal and lower rates of excretion per unit of animal product. How animals are managed may also affect rates of nutrient excretion. In particular, improved feeding practices increase the efficiency of nutrient utilization and decrease excretion rates. Some feeds are more digestible or metabolizable than others. The proper combination of certain feeds to provide the optimal balance of energy and protein, or complementation of different amino acids, results in more efficient metabolism and lower feeding requirements. Some feed additives improve digestion or metabolism or decrease protein requirements, and thereby decrease emissions of ammonia and methane. Other management factors that affect productivity include the use of hormones to change partitioning of nutrients within the animal, or grouping animals to decrease feed variations among individuals getting the same diet. The efficiency of animal production has increased continuously and is improving still, resulting in lower methane emissions from the animals and lower nutrient transfers to manure (Havenstein et al., 1994).
Unless a process-based modeling approach is used, it is unlikely that any group will be able to develop a model to represent all of the techniques used to improve the efficiency of nutrient use by animals and to incorporate all of the possible current technologies, or to keep up with the development of new tech-
nologies. Animal management has a profound impact on the total nutrients transferred to manure and then lost from the farm to pollute air and water. Thus, it is essential that a means be developed to predict these flows to manure. Using the mass balance approach, the quantity of each element (e.g., N, S, C) excreted in manure or volatilized must equal the amount consumed by animals minus the amount transferred productively to meat, milk, or eggs (minus any carbon volatilized directly to the air from the animals) if there is no net accumulation. Since little nitrogen or sulfur is volatilized directly from animals to the air, that which is fed and not accounted for in animal products must leave the animal in manure.
The approaches to models for each pollutant depend on whether the pollutant is important because of long-term global consequences (e.g., methane), short-term local consequences (e.g., hydrogen sulfide), or both (e.g., ammonia), as described previously. In the case of long-term and global predictions, the annual rates of emissions are likely to be adequate, but for local consequences, concentrations (for short-term or chronic exposures) at the farm boundary or nearby homes may be of greater importance.
Predicting Emissions Important on a Global Scale
A system-level approach is recommended for predicting emissions that are important on a global scale (i.e., ammonia, methane, nitrous oxide, nitric oxide). In this case, system level refers to the overall animal production system, which may be contained on several farms (i.e., crops may be produced on a farm different from the one where the animals are housed). The goal is to decrease emissions from the system per kilogram of food (or other product) produced. Individual AFOs may still be regulated in terms of their contribution to system-level emissions, but it would not help to decrease emissions from an AFO only to have them transferred to a different farm, or many smaller farms.
The process-based, mass balance approach begins by predicting nitrogen, carbon, and sulfur in manure by subtracting the quantities of these elements in animal products from the quantities consumed. For every major type of farm animal and every production group within these types, such predictions of intake are already available. Current publications from the National Research Council (NRC, 1994, 1998a, 2000, 2001a) detail nutrient requirements for various animal types and production systems and with varying amounts of production. Moreover, these publications have been updated periodically. Tables D-1 to D−3 in Appendix D are based on the assumption that animals are fed to meet National Research Council recommendations. These tables show that different types of animals convert feed nutrients to human-consumable products at differing efficiencies. The whole-system analysis also requires understanding that cattle, which appear to use feed nutrients least efficiently, in fact consume whole plant feeds (forages) that can be produced with lower environmental impact or by-products that might otherwise be wasted.
To illustrate, nitrogen composition can be determined from the protein content of feed consumed. Thus, for any given AFO, manure nutrient output can be estimated from the number of animals of each type and their average feed consumption and production. Since some farms feed more or less of certain nutrients than the National Research Council recommends, a more accurate estimate of manure output can be made by quantifying the actual feed inputs and the export of animal farm products. Farm feed and export receipts can be used to document this balance, or diets formulated and feed composition can be used. Many producers already maintain good records of the quantities of animal products purchased.
Once the quantity and characteristics of excreted manure have been defined for an AFO, the fate of the elements in that manure has to be predicted. Animal housing, manure collection system, and manure storage facilities affect the transformation of components to volatile forms and the volatilization of manure components. Thus, distribution factors (fractions of manure elements converted to volatile forms) must be determined for different systems, with different types of manure and different climates. Factors would also be needed to predict the fraction of potentially volatile elements of manure that are actually volatilized in different housing or manure systems. These factors might be expressed as functions of exposed surface area in housing and manure storage.
Once the flows of elements to manure storage and the transformations and emissions there have been predicted, the remaining opportunities for emissions from the AFO occur during the removal of manure from storage and its application on crops. These estimates are expressed as a fraction of precursors available for emission from the farm and may be affected by animal type, soil type, cropping system, cropping area, weather and climatic conditions, and concentrations and amounts of the elements in manure.
Ammonia
The committee recommends making estimates and directing control strategies toward decreasing total reactive nitrogen emissions to the environment rather than specifically toward decreasing ammonia volatilization (see section “Reactive Nitrogen Emissions”). However, the prediction of ammonia emissions is necessary for other planning and research purposes. Ammonia emissions on a global scale and extended time frame (e.g., one year) can be predicted from a process-based model that uses mass balances. These long-term emission estimates are adequate for addressing global concerns with ammonia emissions such as nitrogen loading to the environment. However, daily ammonia emissions are also needed to address regional air quality issues such as particle and smog formation and ammonia deposition. Therefore, the committee addresses models for predictions at both annual and daily time frames. Three major steps are needed for a mass balance approach: (1) excretion of manure nitrogen, (2) conversion of ma-
nure nitrogen to ammonia, and (3) volatilization of ammonia in housing, from manure storage, and field application.
Total nitrogen excretion from animals, in the absence of changing herd or flock size, is equal to total nitrogen intake (mostly as protein) minus nitrogen in animal products. Most of excreted nitrogen occurs in one of two forms: urea (mammals) or uric acid (birds) in urine and complex organic compounds in feces. When proteins are fed that are not readily digestible, fecal nitrogen increases. When excess amounts of digestible nitrogen are consumed, urine nitrogen amounts increase. Once excreted, enzymes in feces hydrolyze urea and uric acid to ammonia, which can be volatilized from housing (especially at high pH), storage (especially if uncovered), and during land application (especially when not incorporated into soil). Although fecal nitrogen is converted to ammonia more slowly, over long periods of storage (especially in warm climates) considerable fecal nitrogen can be volatilized as NH3.
Total nitrogen intake can be quantified and documented for an individual AFO by one of three different methods. The easiest approach is to assume that the herd or flock consumes the amount of nitrogen recommended by the National Research Council (1994, 1998a, 2000, 2001a) for its production level. Whereas many producers feed larger or smaller quantities of nitrogen than recommended by the NRC, one of two alternative approaches can be used to quantify nitrogen intake on a particular AFO. Total nitrogen in crops produced on the farm and in the feeds imported can be quantified over a year using farm records. Most producers can estimate quantities of feed produced and keep records of feed purchases. Feed tables can be used to estimate nitrogen content for grains, and chemical analyses are routinely performed on feeds that vary in nitrogen content. An alternative to this approach is to add the nitrogen consumed by each production group on the farm over a specific period of time. In this case, the amount of each diet consumed is multiplied by its nitrogen content. Since diets are carefully formulated for specific crude protein amounts, the nitrogen percentage of each diet is generally available. The quantity of diet consumed is also estimated or measured directly on most farms.
Total net nitrogen in animal products sold can be determined by multiplying the quantity of each product sold by its nitrogen content and subtracting the nitrogen in animals purchased. Total urine and fecal nitrogen can be determined as total nitrogen intake minus net nitrogen in animal products. Fecal nitrogen can be calculated as the indigestible feed nitrogen and endogenous losses as described by current diet formulation models for different species (NRC, 1994, 1998a, 2000, 2001a). Urinary nitrogen is the remainder of the excreted nitrogen. These estimates of nitrogen excretion could be made for longer or shorter time intervals for use in estimating annual or daily ammonia emissions.
Once the total amount of nitrogen excreted has been determined, the rapid ammonia emissions from housing can be calculated as a fraction of the urine nitrogen. For each major type of housing system, coefficients would be needed to
predict the percentage of urine nitrogen likely to be converted to ammonia and volatilized for the type of housing and geographic area (for annual emissions) and short-term weather conditions (daily emissions). Limited data are available currently to make such estimates (Muck and Steenhuis, 1982; Monteny and Erisman, 1998).
Nitrogen in manure storage would be estimated from the flows of inorganic and organic nitrogen into storage, measured or assumed removal for field application, and predicted emissions during storage. A typical predictive model for daily or annual ammonia emissions from manure storage would include two modules: ammonia generation in the manure, and ammonia emission from the manure surface. Ammonia in manure is generated partly from urea via enzymatic conversion, which is a rapid process; and partly from the mineralization of organic nitrogen in manure, which is a relatively slow process. Normally, for typical manure collection systems where urine and feces are mixed, urea is assumed to already have been converted to ammonia when the manure reaches storage. Additional ammonia may be generated by mineralization of organic (e.g., fecal, bedding) nitrogen over time and is controlled by the following factors:
-
storage time;
-
environmental conditions such as temperature; and
-
characteristics of the wastes such as biodegradability, moisture content, oxygen content, and pH.
Thus, the amount of ammonical nitrogen in stored manure is a function of the amount and form (urine versus fecal) of nitrogen and other compounds coming into storage; the length of the storage period, and other factors that affect oxygen content, pH, and temperature of the stored manure. The ammonical nitrogen in manure storage at each time could be estimated as the amount at a previous time plus additions from animal housing and mineralization of organic nitrogen in storage, minus removal and nitrogen emissions. The amount of organic nitrogen in manure storage must be estimated because it affects the rate of ammonical nitrogen formation. It would be equal to the previous organic nitrogen plus additions from animal housing, minus losses to inorganic nitrogen and removal for fertilizer application.
Quantitative information on the production of ammonia in animal manures is scarce in the literature. Zhang et al. (1994) developed equations for predicting the production rate of ammonia during storage of swine manure as a function of time and depth in the manure. However, their study did not account for the influence of different temperatures, manure solid content, and oxygen content. More research is needed to develop accurate prediction models for quantifying the production rate of ammonia due to organic nitrogen mineralization in different types of manure management systems.
Once ammonia is generated in animal housing or manure storage, emission of ammonia from the manure to the atmosphere is controlled by the aqueous chemistry of ammonia in the manure and convective mass transfer at the manure surface. The factors that affect emission rates from manure storage include the following:
-
water temperature,
-
air temperature,
-
relative humidity,
-
wind velocity, and
-
manure characteristics such as pH and solids content.
The rate of emission of ammonia from manure can be calculated as the product of the convective mass-transfer coefficient (KLN) and the concentration of ammonia at the surface layer.
The mass-transfer coefficient KLN is a function of manure temperature, air temperature, wind velocity, and relative humidity. Various equations are available in the literature for KLN. However, most of those equations were developed from controlled experiments with convective mass-transfer chambers and have not been validated well using field-scale experiments. More research is needed to calibrate and validate them. An example is given in Appendix J, which is based on the two-film theory.
The concentration of gaseous NH3 in air at the manure surface depends on the total concentration of dissolved ammonical nitrogen (NH3 + ammonium ion [NH4+]) at the surface of the liquid manure. Thus, the greater proportions of ammonical nitrogen in the form of NH3, the greater are the emissions from the solution. The ratio of NH3 to NH4+ depends on the pH of the solution and the equilibrium constant (Ka) of the reaction interconverting NH3 and NH4+. As the pH of the solution increases, more of the ionic form is converted to NH3 and the emissions of ammonia increase. It has been found by researchers that the Ka in wastewater has a different value from that of pure water (Zhang et al., 1994; Liang et al., 2002). The Ka in animal manure (Ka,m) is 25-50 percent of the Ka in water, depending on the characteristics of manure, such as solids content. If the stratification of NH3 in manure is negligible, total ammonical nitrogen can be assumed to be the concentration in the bulk liquid. On any given day, the ammonical nitrogen concentration can be calculated from the concentration at the end of previous day, the change in concentration due to influx from animal housing and the degradation of organic nitrogen in stored manure.
The amount of nitrogen applied to cropland can be predicted as the input to manure storage minus the losses from storage. The amount volatilized depends on the form of nitrogen applied and an additional set of coefficients for different climatic regions, soil types, crops, and management systems (Denmead, 1997).
As with estimates of nitrogen excretion, using on-farm measurements may improve the accuracy of predictions and provide an incentive to decrease emissions by means not considered by regulators. Nitrogen lost from housing and storage can be calculated as nitrogen excreted (as determined previously) minus nitrogen applied to fields from storage (as measured). The nitrogen applied may be determined as manure volume applied times nitrogen concentration (mass per volume) of applied manure. Ammonia emissions from storage can then be estimated as a fraction of nitrogen lost from storage depending on housing and storage type.
Whereas a large amount of the nitrogen excreted by animals is lost from the production system as ammonia, it is vitally important to accurately predict nitrogen excretion from animals. These estimates can be made quite readily for typical farms with typical feeding levels for specific production rates. However, some AFOs use different practices that increase (e.g., overfeeding of protein) or decrease (e.g., feeding specific amino acids) the nitrogen excreted per unit of animal product compared to typical farms. Therefore, calculation of manure production rates from feed nitrogen and product nitrogen may improve the estimate of nitrogen emissions. On the other hand, although sampling and analysis can be used to estimate the manure nitrogen applied, many manure systems are difficult to sample and such measurements may not be useful in some cases. Most of the nitrogen lost from animal production systems is volatilized ammonia, and it can be quantified as nitrogen emissions. Therefore, mass balance-based prediction models can be used to identify farms according to their management practices and to quantify the impact of management techniques on ammonia emissions. These predictions could be improved by determining the percentage of nitrogen emissions as ammonia, as opposed to molecular nitrogen (N2) or other forms of nitrogen, for different management systems.
Prediction of ammonia emissions in animal housing, manure storage, and field application is feasible in the near term (i.e., five years) using a process-based model. However, as discussed in the section “Reactive Nitrogen Emissions,” this may not be the best option for predicting emissions on individual farms for regulatory or incentive programs.
Molecular Nitrogen, Nitrous Oxide, and Nitric Oxide
As with ammonia, the committee recommends predicting and directing control strategies toward decreasing total reactive nitrogen emissions to the environment rather than specifically toward nitrous oxide and nitric oxide (see discussion of reactive nitrogen emissions). However, prediction of global nitrous oxide (N2O) and nitric oxide (NO) emissions is needed for other planning and research purposes. As with NH3, emissions of other nitrogen-containing compounds can best be estimated as a fraction of nitrogen excreted to emittant (Müller et al., 1997). Many other factors, including soil moisture, compaction, and pH, also
contribute substantially to these emission rates. As a general rule, N2O is 3 to 5 percent of available nitrogen emitted from manure or other nitrogen fertilizer applied to soil (Hansen et al., 1993; Flessa et al., 1996; Flessa and Beese, 2000). These emissions derive from fields used to produce feed for animals using inorganic forms of nitrogen fertilizer as well as animal manures. In addition, 1 to 2.5 percent of the nitrogen that leaves the farm as volatilized ammonia or nitrogen oxides, or leaches or runs off as nitrate, volatilizes as nitrous oxide elsewhere in the environment (IPCC, 2000).
Although N2 gas is not harmful, estimation of its emissions from manure handling and cropping systems would improve our ability to predict total nitrogen emissions and to develop better management strategies. Nitrogen gas is formed from nitrate in an anaerobic process called denitrification after nitrate has been produced from ammonia in an aerobic process called nitrification (Thompson et al., 1987). Thus, N2 may evolve from manure storage structures or soils where both anaerobic and aerobic compartments exist. Research is needed to determine the ratio of N2O to N2 and the factors that affect it because generation rates of both gases are linked to rates of nitrification and denitrification (Abbasi et al., 1997), and management may be able to shift reactions to favor the benign product N2 (Dendooven et al., 1996).
Reactive Nitrogen Emissions
The committee has recommended in several places in this report that EPA and USDA take a systems approach to develop control strategies aimed at decreasing undesirable emissions from AFOs. With regard to ammonia, N2O, and NO, a systems approach would help optimize the animal production systems to decrease the overall environmental impact of all of these emissions. An example of the opposite would be to promote strategies to decrease ammonia emissions that simultaneously increased N2O emissions. A systems approach is also needed to decrease total reactive nitrogen emissions to air and water simultaneously. Water quality regulations for AFOs might require nitrogen-based nutrient management plans. In many situations, the most cost-effective plans would be those that result in the greatest volatilization of ammonia to the atmosphere in order to decrease the need to “dispose” of excess nitrogen from the AFO in the form of water-soluble nitrate. A systems approach is also needed to decrease total emissions of reactive nitrogen per unit of animal product, rather than simply decreasing reactive nitrogen emissions from individual AFOs. Control strategies to decrease nitrogen emissions from AFOs might inadvertently provide incentives for producers to ship their problems to other farms, rather than improving the efficiency of the whole animal production system. For example, nitrogen emissions from an AFO can be decreased by purchasing more feed and by shipping manure off-farm. In this way, nitrogen emissions will occur from the farms that grow the crops or apply the manure, rather than from the AFO, but the emissions of nitro-
gen to the environment may not be affected. Because of the importance of the systems approach, the committee recommends using a farm nitrogen balance as described below.
FINDING 10. A systems approach, which integrates animal and crop production systems both on and off (imported feeds and exported manure) the AFO, is necessary to evaluate air emissions from the total animal production system.
RECOMMENDATION: Regulatory and management programs to decrease air emissions should be integrated with other environmental (e.g., water quality) and economic considerations to optimize public benefits.
Reactive nitrogen in the form of NH3, N2O, or NO may be lost to the atmosphere; as soluble nitrogen running off into surface water, or as nitrate leaching into groundwater. Some nitrogen may be converted back to harmless N2 gas. The total emission of nitrogen from the farm (Nloss) is therefore composed of those environmentally destructive emissions to air (Nair) and water (Nwater) and the harmless conversions to N2:
Nloss = Nair + Nwater + N2.
(Eq. 5-2)
Measurements of individual emissions (e.g., ammonia volatilization, N runoff, and nitrate leaching) are difficult and expensive, leading to the predicament that few data are available on which to base mathematical models for predicting individual emissions. In contrast, the aggregate of all nitrogen emissions to the environment can be predicted from reliable measurements that can be documented on individual farms based on nitrogen inputs (Ninput) in imported feed, legumes produced on-farm, and imported fertilizers and on nitrogen exports (Noutput) in animal products and exported feeds:
Nloss = Ninput − Noutput.
(Eq. 5-3)
Not all of these nitrogen emissions from the production system are destructive to the environment because some N2 gas is also formed. The reactive nitrogen emissions can be calculated by subtracting estimates of N2 gas formed for different types of management from the total nitrogen emissions. For most animal production systems, only a small percentage of the nitrogen that is not accounted for is thought to be lost as N2. In soils, N2 emissions are associated with N2O emissions (Abbasi et al., 1997). Emissions of N2 can occur from anaerobic or aerobic lagoons (most are a combination of both), biogas generation and combustion, constructed or natural wetlands, and cropping systems. Little is known about how much of the nitrogen lost from these systems is converted to N2 gas
and how the systems can be optimized to increase N2 as they decrease other nitrogen emissions. Nonetheless, in the near term, predicting total reactive nitrogen emissions from individual AFOs, using a mass balance approach, is likely to be less costly and more accurate than attempting to estimate the individual types of nitrogen emissions from measurements of concentrations and flow rates (Box 5-1).
Control strategies for nitrogen emissions should consider using estimates of total reactive nitrogen emissions. These strategies can include both performance standards based on predicted reactive nitrogen emissions for production systems and technology standards that can be documented to be effective using the models of reactive nitrogen emissions. For individual AFOs, reactive nitrogen emissions can be predicted and documented (Dou et al., 1996). Total nitrogen inputs can be quantified and documented using nitrogen compositions, feed and bedding purchases, fertilizer imports, estimated legume nitrogen fixation (legume production divided by an efficiency factor), and imported animals. (Another input includes atmospheric nitrogen deposition, but this cannot be controlled by AFO operators.) Known farm nitrogen outputs can be quantified as feeds sold, and animals and animal products shipped, each times its nitrogen content. The emissions of N2 currently cannot be predicted accurately because of a lack of research in this area, but with new research on different types of manure and cropping systems such predictions may become feasible in the near term.
Control strategies to decrease reactive nitrogen emissions to the environment are likely to be applied to individual AFOs. However, the objective is to decrease emissions from the entire animal production system, which includes off-farm crop production and manure handling. If an AFO exports manure or imports crops, its predicted reactive nitrogen emissions will decrease, and those of the farms handling the manure or producing the crops will increase. The goal of control strategies should be to provide incentives for improving the efficiency of nitrogen utilization among all contributors to the production system. Incentives can be created to encourage AFOs to decrease these predicted reactive nitrogen emissions to the environment as a fraction of animal products produced. For an individual AFO, the reactive nitrogen emission to the environment can be predicted. In order to calculate the reactive nitrogen losses from the entire production system, after calculating the reactive nitrogen emission from the AFO, typical emissions for production of imported feeds or exported manure can be added. This process would put all AFOs on a similar footing.
FINDING 11. Nitrogen emissions from AFOs and total animal production systems are substantial and can be quantified and documented on an annual basis. Measurements and estimates of individual nitrogen species components (i.e., NH3, N2, N2O, NO) should be made in the context of total nitrogen losses.
|
BOX 5-1 Nitrogen may leave an AFO when ammonia volatilizes, inorganic or organic nitrogen runs off from fields or holding areas, nitrate leaches into groundwater, or nitrous oxide volatilizes. In addition, some molecular nitrogen may be released from manure storage or treatment facilities, wetlands, or fields. Although it is very difficult to estimate any of these potential emissions of nitrogen from individual AFOs, the aggregate of all emissions can be estimated reliably as the nitrogen balance. To identify weak points on the farm, the efficiency of farm components must be determined and compared to alternative practices. Dou et al. (1996) describe software to estimate nitrogen balances on farms retrospectively and to predict future nitrogen balances based on different management decisions. Using this software, the nitrogen balance results for recommended management practices can be compared to results from observed practices. Sample nitrogen balances were calculated for two Pennsylvania dairy farms (Dou et al., 1998). One farm had 109 lactating Holstein cows, 29 dry cows and bred heifers, and 84 unbred replacement heifers or calves. Manure was scraped every other day and stored in a concrete pit for up to a year. Soils ranged from low to medium productivity, and the crop area and total crop dry matter (DM) yield per year were 69 ha (hectares) of corn silage (320 Mg DM/yr), 33 ha winter rye haylage (93 Mg DM/yr), and 23 ha alfalfa hay or haylage (86 Mg DM/yr). The farm purchased hay (89 Mg DM/yr) soybean meal (55 Mg DM/yr), corn grain (102 Mg DM/yr), corn distiller’s grain (34 Mg DM/yr), and whole cottonseed (42 Mg DM/yr). Nitrogen contents of milk, live animals, crops, and feeds were determined by using laboratory analyses that were already employed for diet formulation and milk pricing or by using book values provided by the software (Dou et al., 1996). The quantities of all imports and exports were obtained from receipts for purchased feeds or fertilizers and milk and animal sales. Legume nitrogen fixation was estimated as a fraction (0.6) of the legume nitrogen harvested on the farm, with the remainder (0.4) coming from crop or manure residues. The quantity of nitrogen in imports and exports is shown in |
RECOMMENDATION: Control strategies aimed at decreasing emissions of reactive nitrogen compounds (Nr) from total animal production systems should be designed and implemented now. These strategies can include both performance standards based on individual farm calculations of nitrogen balance and technology standards to decrease total system emissions of reactive nitrogen compounds by quantifiable amounts.
|
the table below. The difference between imports and exports (N balance) was 12.5 Mg N/yr which represents the emissions of nitrogen to the environment or accumulated in soil.
It may be useful to calculate the nitrogen utilization efficiencies of the different farm components (e.g., herd, manure storage and application, crops). The efficiency of herd production is calculated as nitrogen in milk and live animals produced (3.9 + 0.6) divided by nitrogen intake (11.4, data not shown). In this case, it was 0.22. This estimate was compared to an alternative diet formulation that would have provided an efficiency of 0.27. The improved diet formulation was expected to increase imported feed nitrogen as well as milk production, so the total nitrogen emissions to the environment would not be changed. However, with the higher milk production, total emissions from the farm per unit of milk produced were lower, and the environmental impact would be favorable. Manure storage efficiency is calculated as nitrogen applied to crops divided by nitrogen excreted, where nitrogen excreted equals nitrogen intake minus that exported in milk, live animals, and crops. In this case, nitrogen excreted plus bedding nitrogen was 17.5 Mg/yr and the amount measured as applied on crops was 8.5 Mg/yr for a storage efficiency of 0.66. Using the Dou software (Dou et al., 1996), the quantity of manure nitrogen application was estimated as 10.0 Mg/yr, or 0.63 times manure nitrogen excreted. In this case, emissions of nitrogen from manure storage could be estimated for different types of storage systems, and the impact on the whole farm could be calculated. |
||||||||||||||||||||||||||||
Enteric Methane Production
For all of the compounds considered in this report, only methane is known to be emitted directly from animals, and methane is produced in significant quantities only in cattle or other ruminant animals. The EPA (2001a) emission factor approach did not consider enteric methane emissions, although these account for
the majority of methane emissions from agriculture. In the United States, enteric emissions account for 19 percent and anaerobic manure lagoons account for 13 percent of all anthropogenic methane emissions (EPA, 2000a). Globally, about six times more methane is estimated to come from enteric emissions than from decomposition of animal manure, but if anaerobic manure storage became more common, the latter source would increase (Johnson and Ward, 1996).
Methane emissions from ruminant livestock in the United States currently are estimated by EPA by (1) dividing animals into homogeneous groups; (2) developing emission factors for each group; (3) collecting population data; (4) multiplying the population of each group by its emission factor; and (5) summing emissions across animal groups and geographic regions (EPA, 1993a). Among livestock, cattle are examined more closely than other animals because they are responsible for the majority of U.S. livestock emissions.
Johnson and Johnson (1995) used a more accurate and robust approach based on energy consumption by cattle. Methane production was estimated to be 6.0 percent of dietary gross energy consumption for cow-calf, stocker, or dairy systems and 3.5 percent for feedlots. This approach was based on research demonstrating the similarity for different breeds and stages of cattle production but accounts for methane inhibition with the high-concentrate diets fed to feedlot cattle.
Other approaches considering feed characteristics may improve the accuracy of these estimates but also increase the complexity. Blaxter and Clapperton (1965) developed an equation based on a series of methane production measurements from sheep fed different diets. Methane was predicted from the digestible energy (rather than the gross energy) and the energy intake relative to maintenance requirements. Moe and Tyrrell (1979) derived an equation that predicted enteric methane from diet composition, based on measurements made on cattle fed high-quality dairy diets:
Methane (megajoules per day) = 3.406 + 0.510 (cell solubles) + 1.736 (hemicellulose) + 2.648 (cellulose).
(Eq. 5-4)
The number of megajoules refers to the amount of heat that could be released if all of the enteric methane produced were burned to carbon dioxide and water. Wilkerson et al. (1994) concluded that this methane prediction equation resulted in the lowest prediction error of six equations that were compared.
Methane Emissions from Manure Storage
Methane is produced from microbial decomposition of animal manure under anaerobic conditions. The major factors that determine methane production are
-
types and populations of microorganisms present;
-
storage or retention time;
-
environmental conditions such as temperature; and
-
characteristics of the wastes such as biodegradability, nutrient availability, moisture content, oxygen content, and pH.
Many microorganisms are involved in the decomposition of animal manure, including fungi, bacteria, and protozoa. Anaerobic decomposition that leads to methane production involves hydrolytic, acid-forming, and methanogenic organisms. The presence and population of methanogenic bacteria are important for methane production. Manure from ruminants contains more methanogenic bacteria than manure from nonruminant animals. Temperature affects the rate of biochemical reactions, the types of functioning microorganisms, and therefore, the rate of methane production. Methanogenesis in animal manure has been observed in a large temperature range of 4-75°C. Methane production generally increases with increasing temperature. The characteristics of animal manure are governed by animal diet and by manure handling, collection, and storage methods. The greater the energy content and biodegradability of the feed, the greater is the methane production potential of the manure. For example, manure from animals fed with grain-based, high-energy diets is more degradable and has higher methane production potential than manure from animals fed with a roughage diet. All manure has a maximum (or ultimate) methane production potential, which is determined by its chemical composition. The maximum methane production potential is defined as the quantity of methane that can be produced per unit mass of volatile solids (VS) in the manure and is commonly expressed as B0 with a units of cubic meters of CH4 per kilogram of VS. Volatile solids, also called organic matter, are approximately 55 percent carbon on a mass basis for manure.
In theory, the maximum (ultimate) methane production capacity of a quantity of manure can be predicted from the gross elemental composition. In practice, however, insufficient information exists to implement this approach, and direct laboratory measurement is recommended for determining methane production capacity (EPA, 1992). The effects of animal diet on the maximum methane production potential are illustrated in Table 5-1.
Microbial growth requires nutrients such as nitrogen, phosphorus, and sulfur. Animal manure typically contains sufficient nutrients to support microbial growth so that nutrient availability is not a limiting factor in methane production under most circumstances. Moisture content relates to the availability of water to the microorganisms and the ability to maintain an oxygen-free environment in the manure. More than 80 percent moisture content is conducive to methane production. Animal manure as excreted contains 70-91 percent moisture or 9-30 percent total solids (MWPS, 1985). Its moisture content may change to higher or lower amounts depending on the methods of manure collection, handling, and storage in the animal waste management systems. Based on the total solids (TS) content of manure and the requirements for different handling methods, animal waste management systems can be classified into three types: (1) solid system (TS > 20
TABLE 5-1 Maximum Methane Production Potential of Animal Manure as Affected by Different Diets
|
Animal Type |
Diet |
Methane Yield B0 (m3/kg VS)a |
|
Swine |
Corn-based, high-energy diet |
0.44-0.52 |
|
|
Barley-based diet |
0.36 |
|
Dairy cattle |
58-68% silage |
0.24 |
|
|
72% roughage |
0.17 |
|
Beef cattle |
Corn-based, high-energy diet, manure collected from concrete |
0.33 |
|
|
7% corn silage, 87% corn, manure collected from dirt lot |
0.29 |
|
|
91.5% corn silage, 0% corn, manure collected from dirt lot |
0.17 |
|
Poultry, caged layer |
Grain-based diet |
0.39 |
|
aVolume of methane under standard conditions of 1 atmosphere of pressure and 25° C. SOURCE: Safley and Westerman (1990). |
||
percent); (2) slurry system (TS = 10-20 percent); and (3) liquid system (TS < 10 percent) (MWPS, 1985). Examples of different systems are solid manure storage, dry lot, deep-pit stacking, and litter for solid manure management; under-floor deep-pit storage and slurry storage for slurry systems; and anaerobic lagoons for liquid systems. Methane production potential increases in sequence from solid manure to slurry manure to liquid manure systems. Methanogenic bacteria are obligate anaerobes (i.e., they require an absolutely oxygen-free environment to survive). They are also sensitive to low pH of the manure. The optimum pH is near 7.0, but methane can be produced in a pH range from 6.2 to 8.5, and a pH outside the range 6.8-7.6 will decrease methane production. The retention time of manure in waste storage systems is also an important factor. If all the other conditions are the same, longer times will lead to more methane production.
The maximum methane production potential (B0) can be determined in the laboratory using anaerobic digestion assay. For the purposes of municipal wastewater treatment, an assay called Biochemical Methane Potential is commonly used by researchers and wastewater plant operators (Speece, 1996). The assay uses 100-mL serum bottles, which are incubated at 35°C, as the testing reactors. Because of the presence of relatively large particles and the nonhomogeneous nature of animal manure, larger reactors are recommended to ensure the accuracy of measurements. A standard anaerobic digestion assay for determining B0 for animal manure still has to be developed. Laboratory protocols used by animal manure researchers typically use batch digestion of 5 to 15 g VS of manure in an
anaerobic reactor of 1- to 3-L volume at 35°C and the measurement of hourly or daily methane production. When the manure stops producing methane, which means that it has been exhausted of biodegradable organic matter, the total volume in liters of methane produced during the whole testing period is divided by the initial VS in grams in the manure to give the maximum methane production potential (B0, liters of CH4 per gram of VS or cubic meters of CH4 per kilogram of VS). The anaerobic reactor must contain sufficient bacterial culture that has been well adapted to the manure to be tested. The actual methane production in manure storage is lower than the maximum methane production potential.
Actual methane production from manure may be estimated from the maximum methane production potential with considerations of animal waste characteristics, manure storage type and time, and climatic conditions. The following methane emission estimation procedures are adapted from EPA (1992), which is used to estimate emissions from livestock and poultry manure. A similar approach has also been adopted by the Intergovernmental Panel on Climate Change (IPCC) for estimating methane emissions from animal manure (IPCC, 2000). The methane emission production on a livestock farm may be calculated using the following equation:
TMCH4 = ΣVSi • B0i • MCFj • WSij • CAF,
(Eq. 5-5)
where
|
|
total annual methane emission from manure storage on the farm in cubic meters of CH4 per year; |
|
VSi = |
volatile solids produced annually by animal i in kilograms; |
|
B0i = |
maximum methane production potential of the manure from animal i in cubic meters of CH4 per kilogram of VS; |
|
MCFj = |
methane conversion factor for manure storage j, which represents the extent to which B0 is realized (note: 0 ≤ MCF ≤ 1); |
|
WSij = |
fraction of animal i’s waste handled in the manure storage j; and |
|
CAF = |
climate adjustment factor for the farm, which represents the extent to which B0 is realized under climatic conditions (e.g., temperature, rainfall) on the farm (note: 0 ≤ CAF ≤ 1). |
The MCF varies for different types of manure storage and may assume a value from 0.1 for solid manure storage to 0.9 for anaerobic lagoons (Chen et al., 1988; EPA, 1992). The moisture content and retention time of manure in storage affect the MCF. A relationship between the MCF and manure storage conditions, such as moisture content or total solids concentration and retention time may be developed. Research is needed to determine MCF for different types of manure management systems. The CAF mainly varies with ambient temperature. The effect of temperature on methane production from animal manure has been exten-
sively studied (Hobson, 1990), and mathematical relationships have been developed for predicting the effect of temperature on methane production in certain types of anaerobic processes, including anaerobic lagoons. Most research has focused on mesophilic (25-40°C) and thermophilic (40-65°C) temperature ranges (Hobson, 1990) for the purpose of producing methane from animal manure. The temperature of manure storage systems is mostly in the psychrophilic temperature range (less than 25°C). Safley and Westerman (1988) and Safely (1992) published the relationships between the temperature and methane yield of dairy and swine manure using laboratory digesters operated at different degrees ranging from 10 to 23°C. The information was used to predict methane production from anaerobic lagoons. More research is needed to correlate the CAF to the ambient temperatures for different types of manure management systems.
Predicting Emissions Important on a Local Scale
Odor
The odor of animal manure is complex both because of the large number of compounds that contribute to it and because it involves a subjective human response. Much research has been conducted to identify odorous compounds in animal manure. More than 75 compounds were initially identified (Miner, 1975; Barth et al., 1984). Recently, Schiffman et al. (2001) identified 331 odor-causing compounds in swine manure. Odorous compounds include ammonia, amines, sulfides, mercaptans, organic acids, alcohols, aldehydes, esters, and carbonyls. The volatile fatty acids (VFAs), phenols (phenol and p-cresol), and indoles have been considered to be the major odorous compounds (Schaefer, 1977; Spoelstra, 1980; Williams, 1984).
The odor intensity and characteristics of animal manure change over time and are affected by manure handling and storage conditions. For example, in fully aerated manure, biochemical oxidation of various organic compounds occurs. Chen et al. (1994) reported that aeration of swine manure degrades VFAs, phenol, p-cresol, and skatol within 24 hours. Aerobic treatment is known for its effectiveness in decreasing manure odors. In partially aerated manure where low dissolved oxygen limits aerobic organisms, the production of odorous compounds is highly related to redox potential (ORP) in the manure. Beard and Guenzi (1983) studied the evolution of sulfur gases, including hydrogen sulfide, dimethyl sulfide (DMS), methanethiol (MeSH), carbonyl sulfide (COS), and carbon disulfide (CS2), in cattle manure at different ORP levels ranging from −200 to +300 mV (millivolts) and found that the gases produced varied with the ORP. For example, DMS and dimethyl disulfide (DMDS) were highest at the ORP of 0 mV, while hydrogen sulfide (H2S) and MeSH were greatest at an ORP of −100 mV or less. Under anaerobic conditions, if the environment is conducive to acetogens and methanogens, the degradation of manure is more complete, and gases such as
methane, carbon dioxide, ammonia, and hydrogen sulfide are the main gaseous products. However, if the environment is not suitable for bacteria to carry out complete degradation, other bacterial metabolic processes can produce many odorous compounds. Generally speaking, more completely degraded manure, (e.g., in anaerobic digesters or lagoons), will give off fewer odors than less completely degraded manure (e.g., in manure storage pits or tanks) (Pain et al., 1990). The major factors that can affect the anaerobic degradation process include pH, temperature, solids content, and presence of inhibitory substances such as high concentrations of ammonia and VFAs. Odor-causing compounds must be water soluble to reach the olfactory nerve; so using impermeable covers on manure storage will retard the release of these compounds and aid in controlling odors.
Understanding the production rates of odorous gases in manure with different characteristics and storage conditions is critical for predicting odor emission rates. More research is needed in this area. Correlating types and concentrations of odorous gases and their mixtures to the odor strength measured by human olfactory responses (e.g., using the olfactometry method) is another critical step. Some effort has been made to correlate individual gases to odor concentration. Schaefer (1977) correlated 13 compounds with odor intensity measured by a mobile olfactometer and found that odor intensity had the highest correlation with p-cresol. Spoelstra (1980) and Williams (1984) reported that VFAs could be used as a significant indicator of manure odor. More recently, Hobbs et al. (2001) developed a correlation between human olfactory response and an odor mixture of four gases, including hydrogen sulfide, 4-methylphenol, ammonia, and acetic acid, and indicated that determining the odor intensity of pig manure using these main odorants would be a suitable approach.
Until a better understanding of odor generation related to the manure characteristics and environmental conditions in various types of manure storage is achieved and quantitative relationships between various odorous gases as well as their mixtures, and odor intensity have been established, prediction of odor emission rates from manure storage is not possible. At present, conducting on-site measurement of odors is the only available approach for quantifying odor emission rate from a particular farm or manure facility.
Particulate Matter
As discussed in Chapter 3, primary particulate matter emissions in animal feeding operations result from mechanical generation and entrainment. In cattle feedlots, the activity level of the cattle, along with the moisture content of the ground, affect the amount of particulate emissions. Particulate emissions from enclosed animal houses also depend on building ventilation rates and whether the ventilation is natural or mechanical. On-farm sources of particulate emissions may also include unpaved roads, grain mills or storage facilities, crop production equipment, and feeding equipment.
Unlike nitrogen emissions, particulate emissions do not lend themselves to a process modeling approach based on conservation principles. Moreover, there is little information published on particulate emission rates from various components of AFOs. For example, particulate emissions from cattle feed yards are affected by the animals’ level of activity, which varies during the day, and may be a function of other parameters such as ambient temperature or density of animals per paddock. For other farm components, models are already available for predicting particulate emissions. For example, models to predict emissions given the silt content of the road surface, mean vehicle speed, mean vehicle weight, mean number of wheels per vehicle, and precipitation are available for particulate emissions from unpaved roads (e.g., Fitzpatrick, 1987). Regression analysis might be used to develop models to similarly calculate emission factors from various AFO components once the key variables have been identified. Given the paucity of research on particulate emissions from AFOs, this effort will require new data on emission rates from AFO components.
Hydrogen Sulfide
Hydrogen sulfide (H2S) is produced by sulfur-reducing bacteria during anaerobic decomposition of animal manure. The major factors that influence its production rate are
-
population of sulfur reducing bacteria;
-
amount of sulfur in the manure;
-
characteristics of the manure such as moisture content, oxygen content, and pH;
-
environmental conditions such as temperature; and
-
manure storage time.
The sulfur content of animal manure is directly related to the animals’ diet. The major sources of sulfur in animal diets include sulfur-containing amino acids (methionine, cystine, and cysteine) and water-soluble vitamins (biotin and thiamine), as well as some inorganic sulfate. Sulfur is excreted as sulfate, sulfide, and organic compounds in both feces and urine. Reduction of inorganic sulfate to sulfide occurs to a limited extent in nonruminants (Kline et al., 1971) but is prevalent in the anaerobic conditions of the rumen and hind gut of other herbivores. Therefore, for swine and poultry it appears that most of the production of hydrogen sulfide and other volatile sulfur-containing gases occurs as a result of manure decomposition during storage. Emissions may directly occur from a ruminant, but no data are available to date. The characteristics of and environmental conditions in the manure affect the production rate of H2S. Beard and Guenzi (1983) found that in cattle manure slurry, the level of redox potential affects the production of hydrogen sulfide and other sulfur gases. Their experimental results indi-
cated that production of H2S was high at the ORP level below −100 mV. Production of hydrogen sulfide at other ORP levels has also been also reported (Farwell et al., 1979).
Hydrogen sulfide likely originates mainly from microbial reduction of sulfate, although it can also be produced by microbial degradation of cysteine and cystine (Freney, 1967; Riviere et al., 1974). Sulfate-reducing bacteria are present in animal manure, but their populations in different manures are not well understood. Riviere et al. (1974) found that the sulfate-reducing bacteria were present in swine manure in amounts up to 104/mL.
Sulfate in the water supply is another source of sulfur in manure. It is reported that the sulfate concentration in the U.S. water supply varies greatly from 0 to 770 mg/L (AWWA, 1990). The relationship between high sulfate concentration in manure and the production of hydrogen sulfide is well demonstrated by Arogo et al. (2000), who studied initial sulfate concentrations (5.89-275 mg/L) in swine manure during a 30-day storage period. Based on biochemistry, sulfide production from sulfate is faster than from organic sulfur. In waste management systems where a large quantity of water is added to animal manure, sulfate in the water supply can be an important source of sulfur.
In aqueous solution such as liquid manure, hydrogen sulfide maintains equilibrium with bisulfide (HS−) and sulfide (S2−) ions. The presence of hydrogen sulfide as a fraction of total sulfide is affected mainly by pH and temperature. Studies have found that ionization in animal manure differs from ionization in water. Solids content of animal wastewater may also be a factor. The pH of animal waste has a large influence on the hydrogen sulfide fraction. Below pH 5, the H2S fraction in total sulfide is 100 percent; at pH 7, the fraction is about 50 percent; and above pH 10, the fraction is 0.1 percent.
Emissions of hydrogen sulfide rise with the concentration. For a given amount of total sulfide, lower pH will result in a higher emission rate. Any effort to lower the pH of animal manure that contains hydrogen sulfide and/or has conditions conducive to its production will raise emissions of H2S. Emission of hydrogen sulfide, like other soluble gases such as ammonia, involves diffusion in wastewater to the water surface and release into the atmosphere. The major factors controlling the emission rate of hydrogen sulfide include air temperature, wind speed, water temperature, and surface area of wastewater. For the same volume of wastewater, a larger surface area will result in higher emissions. Therefore, a waste storage structure with a larger depth and smaller surface area will have a lower emission rate than a structure with a smaller depth and larger surface area. This also explains why agitation of manure in storage tends to increase emissions of hydrogen sulfide. Avery et al. (1975) studied H2S production in swine confinement finishing buildings and found that it was highly correlated with air temperature, ratio of pit surface area to pit volume, air exchange rate of the building, and daily dietary sulfur intake. Banwart and Bremner (1975) studied the production of H2S and other sulfur gases from swine manure and found that
the volatile sulfur gases produced were predominantly hydrogen sulfide and methyl mercaptan (80 percent) under simulated anaerobic storage conditions. However, during a one-month incubator period, only 0.03 percent of the total sulfur present in swine manure was volatilized. Beard and Guenzi (1983) studied the production of hydrogen sulfide and other sulfur gases in cattle manure slurry and found that sulfur gases volatilized during a three-week period removed 1.7 percent of the total sulfur in the manure. This points out the difficulties in using mass balance approaches for predicting emission of hydrogen sulfide.
Production and emission of gases, including hydrogen sulfide, from manure storage are dynamic processes. Prediction of the emission rate of hydrogen sulfide involves prediction of the production rate of H2S in the manure and of mass transfer of H2S from the manure into the atmosphere. Based on the aqueous chemistry of hydrogen sulfide, the mass-transfer processes and governing parameters for H2S are the same as for ammonia. However, Ni et al. (2000, s2000d) observed that H2S could be released from manure in bursts, which were characterized by a sudden increases of hydrogen sulfide concentrations in the swine building monitored. It appears that hydrogen sulfide emission shares the characteristics of both ammonia (continuous) and methane (bubbles or bursts) emission. The emission of H2S from manure storage is a complicated and poorly understood phenomenon.
Production of Hydrogen Sulfide in Animal Manure
Because of the potential health effects of hydrogen sulfide, prediction models for H2S should have a time scale of hours or days. An approach similar to that for methane production can be used to predict hydrogen sulfide production, except that total sulfur content is used as the manure characteristic instead of volatile solids, a time factor is added to account for the effect of storage time, and the time scale should be on daily basis. The production rate of hydrogen sulfide may be predicted using the following equation:
TMS−,k = ΣSi • S0i • SCFj • WSij • CAF,
(Eq. 5-6)
where:
|
|
total sulfide production from manure storage on the farm in grams of sulfide, for day k; |
|
Si = |
sulfur excreted by animal i, plus sulfur per animal added from the water supply, in grams per day; |
|
S0i = |
maximum sulfide production potential of the manure from animal i in grams of sulfide per gram of sulfur; |
|
SCFj = |
sulfur conversion factor for manure storage j, which represents the extent to which S0 is realized (note: 0 ≤ SCF ≤ 1); |
|
WSij = |
fraction of animal i’s waste handled in the manure storage j; |
|
CAF = |
climate adjustment factor for the farm, which represents the extent to which B0 is realized under climatic conditions (e.g., temperature, rainfall) on the farm (note: 0 ≤ CAF ≤ 1); and |
Quantitative information in the literature on production of hydrogen sulfide in animal manures is limited. Arogo et al. (2000) developed equations for predicting the production rate of hydrogen sulfide in swine manure storage as a function of time and depth in the manure. However, their study did not account for the influence of different temperatures, manure solid content, and oxygen content. More research is needed to develop accurate prediction models for quantifying the production rate of hydrogen sulfide from different types of manure management systems.
Emission of Hydrogen Sulfide from Animal Manure
Continuous emission of hydrogen sulfide from manure to the atmosphere is controlled by the aqueous chemistry of hydrogen sulfide in the manure and convective mass-transfer mechanisms at the manure surface. The pH, manure temperature, air temperature, wind velocity, and relative humidity are major factors that affect the emission process. The pH controls the partitioning of sulfide among three species, H2S, HS−, and S2−. The emission rate ![]() of hydrogen sulfide from manure on the kth day can be calculated using the following mass-transfer equation:
of hydrogen sulfide from manure on the kth day can be calculated using the following mass-transfer equation:
(Eq. 5-7)
where KLS is the convective mass transfer coefficient and [S−]total is the total sulfide concentration at the manure surface. If the stratification of total sulfide is negligible, [S−]total can be assumed to be the total sulfide concentration in the bulk liquid. On any given day, the [S−]total,k can be calculated by the concentration at the end of the previous day [S−]total,k−1, and the new concentration generated, which can be calculated from generation rate ![]() divided by the volume of the liquid in storage (V), as shown below,
divided by the volume of the liquid in storage (V), as shown below,
(Eq. 5-8)
In Equation 5-7, α is a fraction and can be calculated from the pH and ionization constants Ks,1 and Ks,2 (Arogo et al., 1999):
α = (10−pH)2/[(10−pH)2 + Ks,1 (10−pH) + Ks,1Ks,2],
(Eq. 5-9)
where Ks,1 is the ionization constant for the equilibrium reaction H2S = H+ + HS−, and Ks,2 is the constant for HS− = H+ + S2−. Their relationships to the temperature in aqueous solutions are well defined. However, the influence of manure charac-
teristics, such as solids content and the presence of metals, is not well understood. In contrast to ammonia, little research has been conducted to quantify the differences between the ionization constants of sulfide in animal manure versus water. The mass-transfer coefficient KLS is a function of manure temperature, air temperature, wind velocity, and relative humidity. Arogo et al. (1999) developed a correlation for KLS for under-floor pit manure storage. More research is needed to define KLS for outside manure storage.
SUMMARY
Whereas it is difficult and expensive to measure most emissions from AFOs directly, and the measurements may be of questionable accuracy, regulatory and management agencies seeking to mitigate emissions need reasonably accurate methods to estimate and attribute them to particular enterprises or activities. One approach is to develop emission factors for different animal production sectors, and estimate emissions as the product of the specific factor for that sector and the number of animals associated with the enterprise or geographic region. The committee found and reported in its Interim Report (NRC, 2002a) that existing data were not adequate at this time to determine accurate emission factors, and that a greater number of emission factors than originally proposed would be needed to explain the variation in emissions from different enterprises. The committee debated the cost and time requirements to conduct necessary studies and develop appropriate emission factors. The approach would require a considerable number of new measurements to represent all conditions (e.g., farm sectors, animal productivity levels, management choices, climates) that could affect emissions. Regression analysis would be used to determine empirically which factors were of greatest importance. After having considered the emission factor approach, the committee recommended an alternative: to estimate emissions using process-based models rather than strictly empirical models.
Process-based models would involve analysis of the farm enterprise through study of its component parts. The analysis would use mathematical modeling and experimental data to simulate conversion and transfer of reactants and products through the farm enterprise. In many cases, this approach would make use of mass balance equations to represent mass flows and losses of major elements through the system. Development of process-based models would still require research studies to obtain measurements of transformations (changes in form of relevant compounds) and transfers (changes in location of compounds), as well as emissions in animal enterprises. Nonetheless, the estimates would be based on the understanding of processes inherent to animal production. System-level models would be needed to predict the effect of management changes simultaneously on different compounds emitted and to estimate the effects of management changes on multiple farms associated with animal production either directly or indirectly (e.g., crop production).































