F
Ammonia Emissions from Manure Storage
The production of ammonia from animal manure via mineralization of organic nitrogen on the kth day of storage can be predicted using the following equation:
TMTAN,k = ΓNi · N0i · NCFjk · WSij · CAF,
where
|
TMTAN,k = |
production of total ammoniacal nitrogen (TAN) from manure storage on the farm in grams per day on the kth day of storage; |
|
Ni = |
total nitrogen excreted by animal i in grams per day; |
|
N0i = |
maximum TAN production potential of the manure from animal i in grams per grams of total nitrogen; |
|
NCFjk = |
nitrogen conversion factor for manure storage j, for k days of storage time, which represents the extent to which the N0 is realized (note: 0 ≤ NCF ≤ 1); |
|
WSij = |
fraction of waste of animal i handled in manure storage j; |
|
CAF = |
climate adjustment factor for the farm, which represents the extent to which N0 is realized under climatic conditions (e.g., temperature and rainfall) on the farm (note: 0 ≤ CAF ≤ 1). |
Quantitative information on the production of ammonia in animal manure is scarce in the literature. Zhang et al. (1994) developed equations for predicting the production rate of ammonia in swine manure storage as a function of time and depth in the manure. However, their study did not account for the influence of
different temperatures, manure solid content, and oxygen content. More research is needed to develop accurate prediction models for quantifying the production rate of ammonia due to mineralization of organic nitrogen in different types of manure management systems.
Once ammonia (NH3) is generated in animal housing or manure storage, its emission from the manure to the atmosphere is controlled by the aqueous chemistry of NH3 in the manure and the convective mass-transfer mechanism at the manure surface. The pH, manure temperature, air temperature, wind velocity, and relative humidity are major factors affecting the emission process. The pH controls the partitioning of ammonia between NH3 and NH4+ (ammonium ion) in the water. The emission rate of ammonia from manure on the kth day can be calculated using the following mass-transfer equation,
where M is g/m2, 86,400 is the number of seconds in a day, KL is the mass transfer coefficient in meters per second, F is the fraction factor for free ammonia in total ammonia and has a value of 0-1, and [TAN]k is the concentration of total ammoniacal nitrogen in milligrams per liter after k days. F can be determined as a function of pH and ionization constant (Ka) of ammonia in water, using the following equation:
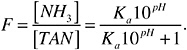
Ka is a function of water temperature (Taq, kelvin) as shown in the following equation:
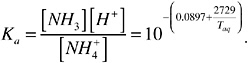
It has been found by researchers that the Ka in wastewater has a different value from that in water (Zhang et al., 1994; Liang et al., 2002). The Ka in animal manure (Ka,m) is 25-50 percent of the Ka in water, depending on the characteristics of manure, such as its solids content.
KL is the convective mass-transfer coefficient and [TAN] is the concentration of total ammoniacal nitrogen at the manure surface. If the stratification of NH3 in the manure is negligible, [TAN] can be assumed to be the concentration in the bulk liquid. For any given day k, [TAN]k can be calculated by the concentra-
tion at the end of previous day, [TAN]k−1, and the ammonia generated on the kth day (TMTAN,k, grams) divided by the volume (V, cubic meters) of the liquid manure in storage, as shown below:
[TAN] k = [TAN]k−1 + TMTAN,k /V.
The mass-transfer coefficient KL is a function of manure temperature, air temperature, wind velocity, and relative humidity. Various equations for KL are available in the literature. However, most of them were developed using controlled experiments by means of convective mass-transfer chambers, and have not been well validated using field-scale experiments. More research is needed to calibrate and validate them. An example is given below is based on the two-film theory.
AMMONIA MASS-TRANSFER COEFFICIENT
The mass-transfer coefficient for ammonia as derived from the two-film theory (Whitman, 1923) is given as follows:
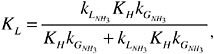
where KL is the overall mass-transfer coefficient in meters per second, KH is Henry’s law constant (dimensionless) calculated as a function of water temperature (Taq, kelvin),
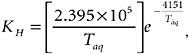
and ![]() and
and ![]() are mass-transfer coefficients (meters per second) through gaseous and liquid films, respectively, at the interface of water and air, and are related to the diffusivities (square meters per second) of ammonia and water in air (
are mass-transfer coefficients (meters per second) through gaseous and liquid films, respectively, at the interface of water and air, and are related to the diffusivities (square meters per second) of ammonia and water in air (![]() and
and ![]() ), and of ammonia and oxygen in water (
), and of ammonia and oxygen in water (![]() and
and ![]() ):
):
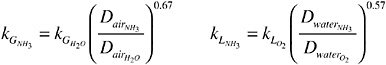
where u8 is the wind velocity (meters per second) at 8 m above the water surface. The diffusivities are calculated using the following equations:
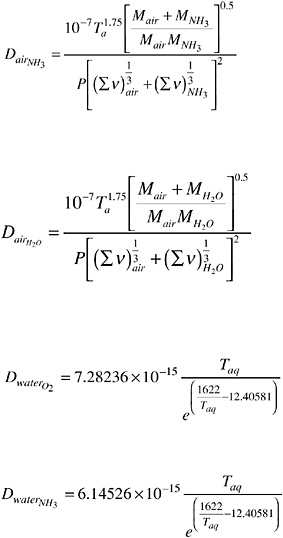
where M is the molecular weight (grams per mole), Ta and Taq are the air and water temperatures (kelvin), and v is the molecular diffusion volume (cubic centimeters per mole).
SYMBOL DEFINITIONS, UNITS
|
KL |
Overall mass-transfer coefficient of ammonia, cm/h |
|
KH |
Henry’s coefficient, dimensionless |
|
|
Mass-transfer coefficient of ammonia in liquid phase, cm/h |
|
|
Mass-transfer coefficient of ammonia in gas phase, cm/h |
|
|
Mass-transfer coefficient of oxygen in liquid phase, cm/h |
|
|
Mass-transfer coefficient of water in gas phase, cm/h |
|
u8 |
Wind speed at 8-m height, m/s |
|
uz |
Wind speed at an anemometer height z, m/s |
|
z0 |
Roughness height, m |
|
P |
Atmospheric pressure, atm |
|
|
NH3 diffusion coefficient in air, m2/s |
|
|
H2O diffusion coefficient in air, m2/s |
|
|
O2 diffusion coefficient in water, m2/s |
|
|
NH3 diffusion coefficient in water, m2/s |
|
Mair |
Molecular weight of air (average), g/mol (29) |
|
|
Molecular weight of NH3, g/mol (17) |
|
|
Molecular weight of H2O, g/mol (18) |
|
(Σv)air |
Air molecular diffusion volume, 20.1 cm3/mol |
|
|
NH3 molecular diffusion volume, 14.9 cm3/mol |
|
Ta |
Air temperature, K, mg/l |
|
[TAN] k |
Total ammoniacal concentration at the manure surface on the kth day of storage |
|
Taq |
Water (manure) temperature, K |





