Quantum Cryptography
STEVEN J. VAN ENK
Bell Laboratories, Lucent Technologies
Murray Hill, New Jersey
Cryptography has a very long history (Singh, 2000). The ancient civilizations of the Chinese, Egyptians, Greeks, Romans, and Arabs all developed methods of keeping messages secret. Early on, often all that was necessary was hiding the existence of a message (steganography). A method developed in China, for instance, involved shaving the head of a messenger, writing the message there, and waiting for the hair to grow back. This method was obviously both inconvenient and time consuming. But the main drawback of steganography is that once the hiding place of a message has been discovered, all of the information in the message is revealed at once.
Thus, cryptography, the art of hiding the meaning of a message, was born. There are two basic methods of encrypting a message—transposition and substitution. In transposition, the order of the letters is changed; in substitution, each character (or sometimes a whole word) is replaced by another character (or word), according to certain procedures known to both sender and receiver. Over the course of thousands of years, increasingly complicated versions of encryption protocols have been designed, but in the end, almost every one has been broken. Every language contains structure—particularly certain letters or letter combinations that appear more often than others—and, if one is not careful, encrypted texts reveal the same structure. Nowadays we know that the only secure way of encrypting a text is by shifting each letter by a random amount. In modern terminology, each bit must be XOR-ed with a random bit. Only then does the encrypted text itself contain no information.
The remaining problem is key distribution, how to get the sender and receiver to agree on the random sequence of bits to be used. Modern methods, the ones used for encryption of Internet communications for instance, all rely on so-called
one-way functions—functions that are easy to calculate (roughly speaking, with resources that scale polynomially with the number of bits of the numbers involved) but very hard (scaling exponentially) to invert. For example, public key cryptography (particularly, the well known RSA encryption scheme) is based on the difficulties of factoring large numbers and of taking the discrete logarithm. This type of protocol has two weaknesses. First, neither of these two tasks has been proven to be exponentially hard. Indeed, a quantum computer can solve both problems in polynomial time (Ekert and Jozsa, 1996; Shor, 1997). Second, with increasingly powerful classical computers and algorithms, or with a powerful quantum computer, a code that cannot be cracked now may be cracked in the future. Therefore, if the encrypted message is stored, it could eventually be deciphered. For most messages this may not be important, but for certain military messages, it may be essential, especially if the time span turns out to be short. Perhaps surprisingly, both problems can be solved with quantum mechanics, which provides an unconditionally secure protocol that relies only on the laws of physics and not on unproven mathematical assumptions (Bennett and Brassard, 1984; Bennett et al., 1992).
Here is how quantum key distribution (QKD) works. Alice (the sender) and Bob (the receiver) wish to create a shared random key. Alice sends Bob a series of polarized photons. First she tosses her coin many times to produce two random sequences of 0’s and 1’s. One sequence determines which bit she is going to send, the other which polarization basis she will use, either horizontal/ vertical polarization, or left-hand/right-hand circular polarization. An eavesdropper cannot find out with certainty which bit was sent. For example, a polarization filter set to block vertical polarization will make no distinction at all between the two circular polarizations because both will be blocked 50 percent of the time. Moreover, if Alice uses such a filter, even a circularly polarized photon that passes through will have vertical polarization. The disturbance of the quantum state caused by measurements is what Alice and Bob will notice. Let’s say Bob chooses a basis too randomly for his polarization measurement. In the absence of errors and eavesdroppers, Bob would find the correct polarization if he happened to choose the same basis as Alice (which occurs with 50 percent probability). To detect the presence of an eavesdropper, they can check a small subset of the bits that should be the same. The fraction of errors they find is the upper bound on how much information an eavesdropper may have gathered. It is only an upper bound, however, because errors may also be caused by other, innocent effects. Once they have an upper bound, Alice and Bob can distill, by purely classical privacy amplification techniques, a shorter random key that is secure to an arbitrary degree. In a simplified example, let’s suppose Alice and Bob share two random bits, but they know an eavesdropper knows at most one. If they simply take the sum (XOR) of their two bits, they will have a perfectly secure new random bit.
I have just sketched the ideal protocol. In practice, single photons are very
hard to generate. Instead, faint laser pulses are used (the number of photons in a pulse is not fixed but distributed according to a Poisson distribution). The laser light is attenuated so strongly that the average number of photons is only about 0.1 to 0.01. Despite these differences, and despite all kinds of other inevitable imperfections (e.g., losses in fibers, misalignments of optical elements, etc.), such protocols have been proven secure (Inamori, 2002). Because the total number of errors is limited (otherwise the upper bound on the information the eavesdropper has would indicate she knows everything!), and because the main errors are caused by losses inside optical fibers, QKD is possible only over a limited distance.
The state of the art in QKD (Gisin et al., 2002; Townsend, 1998) is as follows: the world record in distance for free-space QKD is 23 km (Kurtsiefer et al., 2002). To avoid turbulence, the communication line was between two mountaintops in Germany. The secure bit rate was about 300 to 400 bits/sec. For QKD over standard optical telecom fibers, the record is 67 km with a secure bit rate of about 60 bits/sec (Stucki et al., 2002). It is important to note that these numbers refer to a protocol with conditional, rather than unconditional, security. The security is based on relaxed, but realistic, assumptions—the eavesdropper cannot store photons, cannot measure the number of photons in a pulse without destroying them, and cannot replace the channel by a channel with no losses. Secure distances for the unconditional security promised by the original protocols are limited to about 15 to 20 km for fibers, less for free-space QKD. Nevertheless, because no one knows at this moment how to store quantum data for a substantial amount of time, QKD does provide a new type of protection against eavesdropping. In effect, today’s QKD messages are safe against tomorrow’s technology, which cannot be said of RSA-encrypted data.
As the state-of-the-art experiments have shown, QKD has been advanced beyond proof-of-principle demonstrations in physics laboratories. In fact, the devices developed for QKD are available as commercial products (Stucki et al., 2002), and a whole QKD setup, including the software to perform the classical calculations for privacy amplification, may soon be available. Does this mean a quantum computer is around the corner? Unfortunately, the answer is no, because two requirements for quantum computing are very hard to achieve, although they are not necessary for quantum communication. First, in a quantum computer the quantum states of many qubits, the quantum counterpart of the classical bit, must be stored for roughly as long as the computation runs; for QKD, qubits may be measured and destroyed as soon as they have reached the receiver. Second, the many qubits of a quantum computer must interact with each other in a carefully controlled way; in QKD, the qubits can be sent separately and never have to interact with each other.
Future research will focus on two aspects of QKD—miniaturization of the devices and improved secure bit rates and longer distances for secure key distribution. The latter will require the development of better single-photon detectors
and true single-photon generators. In addition, until “lossless” fibers are developed, the only technique for overcoming fiber losses is quantum error correction, which is a challenging task, comparable in difficulty to building a small quantum computer (van Enk et al., 1998). Despite the challenges that lie ahead, quantum mechanics will someday make communications more secure.
REFERENCES
Bennett, C.H., and G. Brassard. 1984. Quantum Cryptography: Public Key Distribution and Coin Tossing. Pp. 175-179 in Proceedings of the IEEE International Conference on Computers, Systems, and Signal Processing. New York: IEEE.
Bennett, C.H., G. Brassard, and A. Ekert. 1992. Quantum cryptography. Scientific American 269(4): 26-33.
Ekert, A., and R. Jozsa. 1996. Quantum computation and Shor’s factoring algorithm. Review of Modern Physics 68(3): 733-753.
Gisin, N., G. Ribordy, W. Tittel, and H. Zbinden. 2002. Quantum cryptography. Review of Modern Physics 74(1): 145-195.
Inamori, H., N. Lutkenhaus, and D. Meyers. 2002. Unconditional Security of Practical Quantum Key Distribution. Available online at: <http://xxx.lanl.gov/abs/quant-ph/0107017>.
Kurtsiefer, C., P. Zarda, M. Halder, H. Weinfurter, P.M. Gordon, P.R. Tapster, and J.G. Rarity. 2002. A step towards global key distribution. Nature 419(6906): 450.
Shor, P.W. 1997. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Journal on Computing 26(5): 1484-1509.
Singh, S. 2000. The Code Book. New York: Anchor Books.
Stucki, D., N. Gisin, O. Guinnard, G. Ribordy, and H. Zbinden. 2002. Quantum key distribution over 67km with a plug&play system . New Journal of Physics 4(41): 1-8. Available online at: <http://www.idquantique.com/qkd.html>.
Townsend, P.D. 1998. Quantum cryptography on optical fiber networks. Optical Fiber Technology 4(4): 345-370.
van Enk, S.J., J.I. Cirac, and P. Zoller. 1998. Photonic channels for quantum communication. Science 279(5348): 205-208.
Ion-Trap Quantum Computation
DIETRICH LEIBFRIED
National Institute of Standards and Technology
University of Colorado
Boulder, Colorado
In the early 1980s, Feynman, Benioff, Bennett, and Deutsch pointed out that a quantum computer could have advantages in speed and overhead for solving certain problems; and because of their reversibility, quantum computers might dissipate much less heat than irreversible classical computers. In 1994, Shor presented a quantum algorithm for efficiently finding the prime factors of large numbers that gave the field practical meaning. For example, because most modern encryption schemes work on the assumption that it is inefficient to find prime factors of large numbers, a quantum computer would put the safety of all of these schemes in jeopardy. Shor’s algorithm also raised hopes that other quantum algorithms could outperform their classical counterparts. Moreover, if one takes Moore’s law seriously, in a few years (around 2020) the size of a memory unit in a classical computer should be as small as a single atom. At atomic dimensions, the unit’s function will be determined by quantum mechanics, no matter whether it is part of a classical or quantum computer.
Why is quantum computing more powerful than its classical counterpart? A classical bit can have the logical values 0 or 1. The qubit, its quantum counterpart, can have the values 0 and 1 at the same time. This is directly related to other seemingly paradoxical statements often heard in connection with quantum mechanics, such as, “Schrödinger’s cat is both dead and alive.” This example can be easily associated with a qubit by assigning “dead” to 0 and “alive” to 1.
In the trapped-ion system, the qubit levels are two electronic states of the trapped charged atom. Using superpositions, states in which the qubit is in 0 and 1, one can process all possible input states at once with a given algorithm (quantum parallelism). The only catch is that once the algorithm terminates, the answer must be read out. Similar to Schrödinger’s cat, which, upon looking, is
found either dead or alive, reading the output register collapses the superposition of all possible answers to one particular answer. Knowing this, one can infer the structure of problems for which a quantum computer could be useful. The input should contain a great number of possibilities, for example, for factoring large numbers, all integer numbers up to the given large number. The output should contain a much smaller number of meaningful answers, in our example all of the prime factors of that number. Even if the output collapses to only one of the factors upon readout, we can divide our large number by that factor and thus simplify the original problem.
ION TRAPS, A SUCCESS STORY
In 1989, Wolfgang Paul and Hans Dehmelt won the Nobel Prize for their work on ion traps. The most precise atomic clock built so far (at the National Institute of Science and Technology [NIST]) has a single mercury ion in a Paul trap (Diddams et al., 2001). The clock will lose about one second in the estimated age of the universe (14 billion years). Atomic clocks have a lot in common with qubits. Both rely on a two-level system that is extremely well isolated from its environment but can still be manipulated in a precisely controlled way, with lasers, for example.
ARCHITECTURE OF AN ION-TRAP-BASED QUANTUM COMPUTER
Ignacio Cirac and Peter Zoller first proposed using a string of ions confined in an ion trap for a quantum computer in 1995 when they realized that ions could be exceptionally good qubits and that their motion in the trap could provide a means of performing logic gates between them. Ions are charged, so they experience a strong repelling interaction. When lined up like a string of pearls, a kick to the ion on one end of the string propagates to the other end and back, similar to the way a collection of balls connected by springs responds. Because of this coupling, the motion of these ions must be considered a collective motion that can be described with normal modes. Ions in a trap can be laser cooled to the quantum mechanical state with the lowest energy (ground state), very close to absolute zero temperature.
Cirac and Zoller realized that the collectively shared motion could transfer information between different ion-qubits. A gate between qubit-ion A and qubit-ion B amounts to the following steps: (1) the state of the ion-qubit A is “written” onto the state of the collective motion with a laser pulse; ( 2) depending on the state of the motion, the state of qubit-ion B is either flipped or not; (3) the state of the motion is then transferred back onto qubit-ion A.
The NIST group was able to demonstrate step 2 that same year (Monroe et al., 1995). Since then, several extensions and refinements have been added to the original proposal. In 2000, the NIST group was able to demonstrate quantum
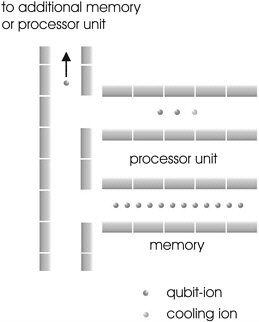
FIGURE 1 Architecture of a multitrap quantum computer.
gates on two and four ions (Sackett et al., 2000). In the same year, David DiVincenco published five criteria for quantum computation that have been widely adopted as a test for determining if a physical system is a serious candidate for quantum computing (DiVincenco, 2001). Four-and-one-half of the criteria have been experimentally demonstrated in the ion-trap system; the only undemonstrated point is the scalability to a large qubit number in DiVincenco’s first criterion, “a scalable physical system with well characterized qubits.”
To fulfill this last criterion, it seemed appropriate to modify the original proposal slightly. Instead of one long string of ions in one trap, the computer could consist of several interconnected traps (see Figure 1) (Kielpinski et al., 2002; Wineland et al., 1998). The ion-qubits could be moved in and out of these traps by an appropriate sequence of voltages applied to their electrodes. Similar to a classical computer, some of the trap units would serve as “memory” (the qubit-ions would be just stored there, but no gates performed). Other units would be the “processors” in which the qubit-ions would be brought together; a third ion of a different species could be added as a cooling agent. The collective motion in the trap would couple the three ions so they could be cooled by applying laser pulses to the third ion without ever touching the internal states of the two qubit-ions. After cooling, one could perform quantum gates on the two qubit-ions. They would then be transferred back into the memory unit, and the algorithm could proceed by applying gates to different qubits. Once the algorithm had terminated, the final state of the qubits could be read out with high efficiency (>99 percent) by laser-induced fluorescence.
FROM QUANTUM MECHANICS TO QUANTUM ENGINEERS
In 2001, we built a two-trap setup to demonstrate the basic features of our envisioned architecture. To implement our ideas, we had to resort to manufacturing techniques developed for microengineering and integrated circuits. The double trap (Figures 2a and 2b) consists of two alumina wafers into which the basic electrode structure is cut with lasers. A thin film of gold (ca. 0.5 µm) is then deposited through a shadow mask onto the wafers where conducting surfaces are desired. Subsequently, an additional layer of gold 3 µm thick is electroplated onto these surfaces to ensure uniform, low-resistance electrodes. The trap areas 2 and 4 have a distance of 1.1 mm. In this trap array, we moved an ion from area 2 to area 4 within 28 µs, while preserving the qubit information, and we separated two ions trapped in area 3 into areas 2 and 4, thereby proving the feasibility of two main ingredients of the multitrap scheme (Rowe et al., 2002). We have just verified the final ingredient, cooling of the qubit-ion species with a different species without disturbing the qubit information. Simultaneously we are working on two traps, based on different technologies (Figures 3 and 4).
In the boldest approach so far, we are trying to build an all-silicon trap (Figure 4). The conductive electrodes are made of silicon doped with boron;
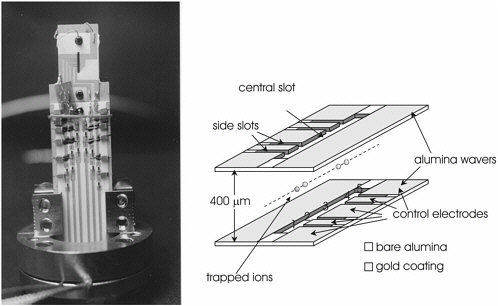
FIGURE 2(a) Photograph of the complete trap structure, including SMD filter electronics. (b) Schematic drawing of the trap. The numbers over the lower wafer indicate the trap units.

FIGURE 3 Gold-leaf trap. The electrodes are made of a thin gold foil (200 µm) clamped by two alumina wafers.
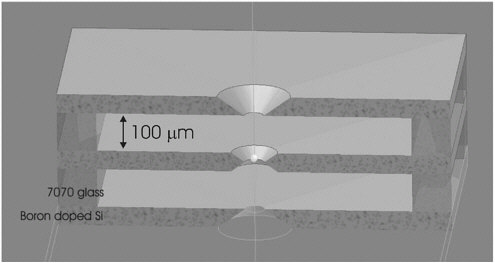
FIGURE 4 Schematic drawing of the prototype silicon trap for one ion (shown as a dot in the center hole). The silicon is doped with boron to make it conductive, and all substructures are fabricated by etching. The three boards are fixed to 7070 glass spacers by anodic bonding.
isolating spacers are made of Corning 7070 glass. The monocrystalline silicon electrodes should provide an atomically smooth, grain-boundary-free surface that might allow us to scale the trap size down from the 400 µm range currently used to about 40 µm with a greatly improved packing density and tight confinement of the trapped ions.
As we close in on our goal, we will have to tackle problems familiar to engineers. We will have to route smaller and more complex electrode structures and switch their voltages quickly with minimum cross talk. We will have to further miniaturize and integrate our approach using cutting-edge technologies. We would also like to integrate the laser optics on the chip using optical fibers and microoptics components. The ultimate ion-trap computer would only have to be hooked up to power supplies and laser light sources. Even those might someday be integrated using on-chip laser diodes.
REFERENCES
Diddams, S.A., Th. Udem, J.C. Bergquist, E.A. Curtis, R.E. Drullinger, L. Hollberg, W.M. Itano, W.D. Lee, C.W. Oates, K.R. Vogel, and D.J. Wineland. 2001. An optical clock based on a single trapped 199Hg+ ion. Science 293: 825-828.
DiVincenco, D.P. 2001. The Physical Implementation of Quantum Computation. Pp. 7-13 in Scalable Quantum Computers: Paving the Way to Realization, S.L. Braunstein and H.K. Lo, eds. Berlin: Wiley-VCH.
Kielpinski, D., C.R. Monroe, and D.J. Wineland. 2002. Architecture for a large-scale ion-trap quantum computer. Nature 417: 709-711.
Monroe, C., D.M. Meekhof, B. E. King, W.M. Itano, and D.J. Wineland. 1995. Demonstration of a fundamental quantum logic gate. Physics Review Letters 75(25): 4714-4717.
Rowe, M.A., A. Ben-Kish, B. DeMarco, D. Leibfried, V. Meyer, J. Beall, J. Britton, J. Hughes, W.M. Itano, B. Jelenkovic, C. Langer, T. Rosenband, and D.J. Wineland. 2002. Transport of quantum states and separation of ions in a dual RF ion trap. Quantum Information and Computation 2(4): 257-271.
Sackett, C.A., D. Kielpinski, B.E. King, C. Langer, V. Meyer, C.J. Myatt, M. Rowe, Q.A. Turchette, W.M. Itano, D.J. Wineland, and C. Monroe. 2000. Experimental entanglement of four particles. Nature 404: 256-258.
Wineland, D.J., C. Monroe, W.M. Itano, D. Leibfried, B.E. King, and D.M. Meekhof. 1998. Experimental issues in coherent quantum-state manipulation of trapped atomic ions. Journal of Research at the National Institute of Standards and Technology 103(3): 259-328.
ADDITIONAL READING
Nielsen, M.A., and I.L. Chuang. 2000. Quantum Computation and Quantum Information. Cambridge, U.K.: Cambridge University Press.
Scalable Quantum Computing Using Solid-State Devices
BRUCE KANE
Laboratory for Physical Sciences
University of Maryland
College Park, Maryland
The field of solid-state quantum computing is in its infancy. Coherent operations on single qubits (the simplest type of quantum logical operation) have only recently been demonstrated (Nakamura et al., 1999; Vion et al., 2002). Nevertheless, there is a great deal of optimism that solid-state implementations of quantum computers will ultimately lead to scalable architectures in the same way that the invention of the transistor and integrated circuit presaged the development of large-scale and networked conventional computers. The optimism is based on the tremendous amount of research being done over a broad front that is heading steadily toward the development of devices for conventional computation built on nearly the atomic scale. This limit is the end of Moore’s Law scaling, but only the threshold of the quantum realm. Thus, the nascent field of solid-state quantum computing can capitalize on research intended for the development of smaller and faster conventional logical devices.
Many difficulties will have to be overcome before qubits can be integrated into solid-state systems. Because there are on the order of 1023 atoms in a solid-state device, it is very difficult to attain the decoupling from extraneous degrees of freedom that is necessary for large-scale quantum computing. Hence, much of the early research on solid-state quantum computing has been focused on identifying potential qubits inherently isolated from their surroundings. Most current research is focused either on superconducting qubits (quantum information is stored on flux states in a SQUID or on charge states of a small “Cooper pair box”) or on electron-spin or nuclear-spin qubits in semiconductors. To have the necessary long decoherence times, these devices must invariably operate at
low temperatures (< 1 K). Even if research is successful, it is still not obvious that these technologies will be scalable (it is noteworthy that many conventional solid-state devices, such as bipolar transistors and tunnel diodes, proved to be unsuitable for very large-scale integrated circuits for reasons that only became apparent years after they were developed). Figure 1 shows the range of research being done on quantum computers.
A major surprise in the early days of quantum computing theory was that quantum error correction was possible at all; it has been shown that if a qubit of quantum information is redundantly coded into several qubits, errors in quantum computation can be reduced just as they can be corrected in classical communications channels (Nielsen and Chuang, 2000). One certainty is that the operation of scalable quantum computers will rely heavily on error correction. There is a “threshold for error corrected continuous quantum computation.” When errors at the single-qubit-level quantum operations are reduced below this threshold, quantum computation becomes possible.
The error threshold is still very stringent. At most, one error can occur in
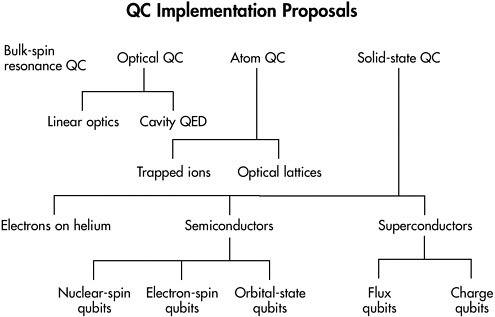
FIGURE 1 Diagram of the many possible realizations of quantum computers currently being explored experimentally. Bulk-spin resonance, optical, and atom-based qubits have all demonstrated elementary quantum logical operations, but solid-state implementations will particularly benefit from fabrication technologies being developed for conventional computer manufacturing. This synergy means that solid-state technologies are likely to be scalable and to benefit from continued advances in solid-state technology.
every ~104 operations. This level of accuracy is beyond the level of device variability of most, if not all, solid-state devices currently manufactured. Meeting the accuracy threshold will undoubtedly be one of the major challenges advocates for solid-state quantum computation will have to overcome. Even if the accuracy threshold can be reached, error correction will place a substantial overhead on the resources of a quantum computer because many physical qubits encode the same logical qubit. Also, most logical operations in the computer will simply be implementing error correction protocols (Steane, 2002).
KEY ISSUES
Scaling of quantum computing will undoubtedly be a formidable task that justifies the skepticism expressed by many people (Keyes, 2001). Nevertheless, an outline of the leading issues can be helpful for a preliminary assessment of current approaches to large-scale quantum computing. Many of these issues relate to information flow rather than to individual quantum operations on which most current research is focused.
Efficient on-chip quantum communication will be essential for the development of large-scale solid-state quantum computing. Communication between devices is also important in conventional computers, but the need for quantum error correction necessitates the continuous transfer of redundant qubits throughout the computer. Rapid flow of quantum information will thus be essential for scalable quantum computing.
Cross talk must be minimized. As the number of qubits increases, the potential for errors due to unwanted coupling between qubits also increases. Spatially localized qubits could minimize this type of error.
Parallel logical and measurement operations must be possible. We usually distinguish between the coherent logical operations of a quantum computer and the measurements of 0’s and 1’s that must ultimately produce the results of an algorithm. Error correction, however, requires that both types of operations go on together; in large-scale quantum computers they should occur simultaneously.
Logic, measurement, and communication must be able to be performed at high speed. Because of the exponential acceleration of quantum algorithms, a quantum computer operating at any clock speed will outperform its classical counterpart. However, given a choice between two otherwise equivalent quantum computer architectures, the faster architecture will be the most desirable.
Individual quantum devices must be precisely engineered. The accuracy threshold for quantum computing suggests that the variability between quantum logical devices must differ by no more than 1 part in 104.
MAJOR LIMITATIONS
As yet, no proposed implementation for large-scale quantum computers has addressed all of these criteria. However, it is possible to outline the major limitations of the approaches currently receiving the most attention.
Trapped-ion quantum computers. Although ion traps are not traditionally thought of as solid-state devices, recent proposals include complex metallizations on substrates to control and move ions between sites and are similar in many important ways to solid-state implementations. Kielpinski et al. (2002) have addressed many scaling issues, but moving ions to move quantum information is an intrinsically slow process because ion masses are typically 105 that of electrons. Therefore, it would be desirable if quantum information could be carried on lighter particles (like electrons).
Superconducting-qubit quantum computers. The primary advantage of superconducting qubits is that they are macroscopic. Consequently, devices are being fabricated with relatively simple micron-scale lithography. A drawback is that quantum information must be moved in the computer by electromagnetic excitations on metal traces. Large-scale implementations of superconducting quantum computers may thus be vulnerable to cross talk, a problem also encountered in conventional computers that have complex metal interconnects.
Electron-spin and nuclear-spin quantum computers. Quantum computer architectures that use electron spins or nuclear spins as qubits in a solid-state quantum computer are perhaps the most technologically challenging (Kane, 2000). These architectures also have some compelling advantages: spin qubits are known to be extremely well isolated from their environments in some materials and have longer quantum lifetimes (measured using electron-spin and nuclear-spin resonance techniques) than any other qubit under investigation in solids. Interestingly, silicon—the material in which almost all conventional computers are implemented—is also characterized by extremely long-lived spin states that can potentially be used for quantum computing. Spin coupling is extremely local, so cross talk is minimal if spins can be well isolated. Spin can be conveniently transported rapidly on electrons driven by electric fields (Skinner et al., 2002). Finally, parallel, rapid quantum logic and measurement appear to be possible using spin qubits (Figure 2).
The major difficulty with spin-based implementations of quantum computers is that they require measurement and control of single electron spins or nuclear spins, a task that is only now on the threshold of realization. Scalable spin-based quantum computing will probably require the development of a new technology in which single atoms can be accurately positioned to create devices with the precision necessary for quantum computation. Fortunately, several promising approaches (Figure 3) for fabricating these single-atom devices are currently being explored (O’Brien et al., 2001).
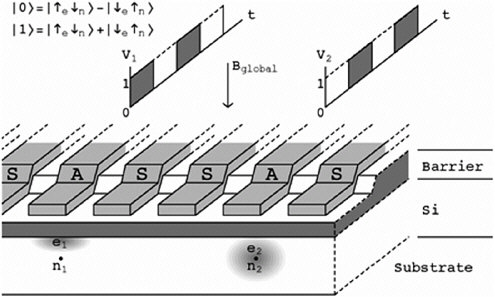
FIGURE 2 Diagram of a silicon-based quantum computer architecture. Single nuclear spins are the qubits; mobile electrons are used to manipulate the nuclear-spin states and move quantum information within the computer. Voltage pulses applied to metal gates on the top of the structure control the positions of electrons inside the silicon.

FIGURE 3 One possible route to the realization of single-spin quantum logical devices in silicon (Si) is via scanning tunneling microscope (STM) lithography. A single monolayer of hydrogen is formed on a pure Si surface (left). Using an STM, holes are punctured in the hydrogen; phosphorus is then introduced through the holes onto arrays in the Si crystal (right). Source: O’Brien et al., 2001. Reprinted with permission.
CONCLUSION
The development of large-scale quantum computers will require an unprecedented combination of precision and complexity. Extremely complex conventional information processors are only possible because digital logic is tolerant to device variation. Quantum logic is much less forgiving. Thus, realizing the dream of a large-scale quantum computer will require that engineers overcome the daunting challenge of combining the precision of an atomic clock with the complexity of a modern microprocessor.
REFERENCES
Kane, B.E. 2000. Silicon-based quantum computation. Fortschritte der Physik 48(9/11): 1023-1042.
Keyes, R.W. 2001. The cloudy crystal ball: electronic devices for logic. Philosophical Magazine B 81(9): 1315-1330.
Kielpinski, D., C. Monroe, and D.J. Wineland. 2002. Architecture for a large-scale ion-trap quantum computer. Nature 417(6890): 709-711.
Nakamura, Y., Y.A. Pashkin, and J.S. Tsai. 1999. Coherent control of macroscopic quantum states in a single-Cooper-pair box. Nature 398(6730): 786.
Nielsen, M.A., and I.L. Chuang. 2000. Quantum Computation and Quantum Information. Cambridge, U.K.: Cambridge University Press.
O’Brien, J.L., S.R. Schofield, M.Y. Simmons, R.G. Clark, A.S. Dzurak, N.J. Curson, B.E. Kane, N.S. McAlpine, M.E. Hawley, and G.W. Brown. 2001. Towards the fabrication of phosphorus qubits for a silicon quantum computer. Physical Review 64(16): 161401(R).
Skinner, A.J., M.E. Davenport, and B.E. Kane. 2002. Hydrogenic spin quantum computing in silicon: a digital approach. Available online at: <http://arxiv.org/abs/quant-ph/0206159>.
Steane, A.M. 2002. Quantum computer architecture for fast entropy extraction. Quantum Information and Computation 2: 297-306.
Vion, D., A. Aassime, A. Cottet, P. Joyez, H. Pothier, C. Urbina, D. Esteve, and M.H. Devoret. 2002. Manipulating the quantum state of an electrical circuit. Science 296(5569): 886-888.


















