4
Improving Environmental Information by Reducing Uncertainty
|
This chapter points out that:
|
As discussed in the previous chapters, the meteorological and oceanographic (METOC) enterprise can be viewed as an organized effort to provide information useful to naval operations about the current and future state of the environment. This process is not perfect, but instead introduces errors that can be characterized by associated uncertainties. Thus, environmental information either explicitly or implicitly contains uncertainty that is inherit in the stochastic nature of environ-
mental processes or that is introduced by imperfect sampling or numerical calculations using data from imperfect sampling. Understanding and living with these uncertainties, especially understanding when it is important to reduce them and how, are a primary focus of this report.
Webster’s defines uncertainty as (1) the quality or state of being uncertain and (2) something that is uncertain. Thus, to the layperson, such predictions might be viewed as efforts to reduce the uncertainty associated with the nature of the terrain just over the horizon or forthcoming weather conditions. In statistics, the physical sciences, and other technical fields, however, the term uncertainty holds several specific definitions that can be expressed mathematically.
According to Ferson and Ginzburg (1996), there are two basic kinds of uncertainty. The first kind, objective uncertainty, arises from variability in the underlying stochastic system. The second kind, subjective (epistemic) uncertainty, results from incomplete knowledge of a system. Objective uncertainty cannot be eliminated from a prediction regardless of the number of previous observations of the state of a particular environmental condition (e.g., no matter how many thousand previous waves are observed, the height of the next incoming wave cannot be predicted without some uncertainty). Data collection and research into the environmental processes shaping future states can be used to understand and, to some degree, reduce uncertainty, but not without some additional cost (not just in terms of resource expenditure but also in tactical advantage as some efforts may alert opponents to a pending military operation). Probability theory, and other approaches, may provide methods appropriate for projecting random variability through the calculations that result in quantitative predictions of future states.
TACTICAL IMPLICATIONS OF UNCERTAINTY
Military decisionmakers rarely deal with uncertainty in a formal, statistical manner. Nevertheless, many decisions can be examined in such terms. In situations where uncertainty about environmental conditions is straightforward—that is, when uncertainty about current conditions will not impact predictions of future states—commonsense approaches are very effective and are typical of sound decisionmaking. Such examples are common in military situations. By examining such tactical decisions involving environmental information one can gain insight into how more complex situations may be dealt with.
In the following example from mine warfare (modified from an example presented at the Symposium on Oceanography and Mine Warfare organized by the National Academies’ Ocean Studies Board, in Corpus Christi, Texas, in September 1998; see National Research Council, 2000), coalition forces have been tasked with securing a seaport to expedite pacification of a hostile coastal nation (see Figure 4-1). The geology of two offshore islands lends itself to the natural development of many small boulders, which occur on the adjacent sea-
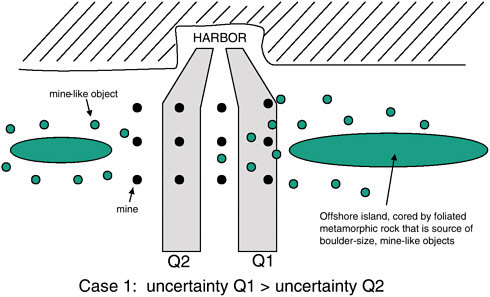
FIGURE 4-1 Cartoon of the distribution of mine-like objects and mines offshore of a foreign harbor. Since resources must be expended to determine whether each object is or is not a mine, the cost of uncertainty associated with Q-route 1 is much greater than that for Q-route 2. Thus, Q2 is the preferred route.
floor in large numbers. Typical seafloor mapping techniques can resolve objects of this size, referred to as mine-like objects, but distinguishing mines from other mine-like objects requires the use of unmanned underwater vehicles (UUVs), EOD (explosive ordinance disposal) divers, or other means. Because this is time-consuming and often dangerous work, practical decisionmaking simply identifies a shipping lane (referred to by the U.S. Navy as a Q-route) with the fewest number of mine-like objects. Thus, in Figure 4-1 the uncertainty associated with the nature of mine-like objects (are they mines or not?) is greater along Q1 than along Q2. Q2 becomes the obvious choice, and appropriate mine countermeasures would be applied as needed. No sophisticated or rigorous effort to quantify uncertainty is needed. It is interesting to note, however, that if the opposing forces understood the nature of the seafloor and incorporated consideration of uncertainty even in an informal manner into their mine-laying plans, a more efficient use of the limited number of mines available could have been achieved.
As shown in Figure 4-2, by concentrating mine laying in areas with a lower density of naturally occurring mine-like objects, opposing forces would eliminate the most obvious Q-route, forcing coalition forces to expand additional resources to identify and eliminate mines. This practical tactical application may seem implausible, as Q1 is not actually protected by mines. However, if the com-
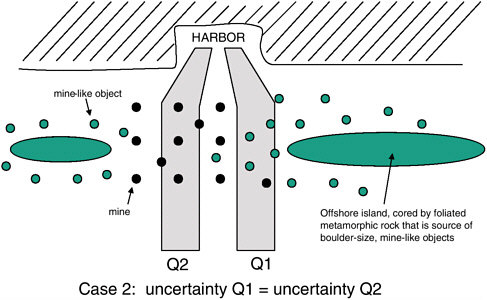
FIGURE 4-2 Cartoon of the distribution of mine-like objects and mines offshore of a foreign harbor. Since resources must be expended to determine whether each object is or is not a mine, the cost of uncertainty associated with either possible route is roughly equal.
mander of the opposing force is convinced that coalition forces will delay efforts to secure the harbor until risk to transport ships can be held to a minimum, mine laying becomes more of a delaying tactic and the distribution of mines in Figure 4-2 is a better tactical decision. This example points out several aspects of dealing with uncertainty that can be explored in more rigorous ways in more complex examples. Foremost among these is the decision to balance the benefit of reducing uncertainty against the cost. In more complex decisionmaking scenarios involving environmental uncertainty, cost versus benefit will become a more important factor.
Propagation of Uncertainty in Complex Systems
In the previous example, uncertain knowledge of the true nature of mine-like objects is easily quantifiable, and given some assumption about the resources needed to determine the true nature of those mine-like objects, the cost of that uncertainty can be approximated. In more complex situations, where uncertainty in one or more parameters is compounded when values are used as input to mathematical models of future states or far-field conditions, understanding the impacts (i.e., the cost of uncertainty) becomes more complicated. Understanding how

A side-scan sonar unit is lowered from the high-speed vessel Joint Venture (HSV-X1) into the waters off the coast of California during Fleet Battle Experiment Juliet. Sonar was used to locate underwater mines, to enable safe navigation of amphibious forces to reach the shoreline, during exercises in support of “Millennium Challenge 2002” (Photo courtesy of the U.S. Navy).
uncertainty propagates through the various steps involved in converting data into information is an important component of the production process and of conveying the value of that information to the decisionmaker (i.e., the commanding officer).
Environmental uncertainty propagates through a chain to the commanding officer to influence his decision; moreover, there is feedback to the several links that can be used to optimize his decision process. Figure 4-3 illustrates several aspects of this. For sonar systems the useful environmental databases are typically bathymetric charts, GDEMs, DDB (Digital Data Base) at various scales, ETOPO5 by location and time of year, sound speed profiles (e.g., as generated by MODAS [Modular Ocean Data Assimilation System]), and bottom loss (BLUG [bottom loss upgrade]), plus other terms that enter the sonar equation. The coverage and resolution of these databases drive various acoustical prediction models often incorporated as tactical decision aids (SFMPL and PCIMAT) for describing how the environment modulates the acoustic propagation. Since the ocean is a very reverberant and refractive medium, the propagation can be quite complicated. One of the current perceptions is that these tools are solely limited by the fidelity and resolution of the environment.
There are, however, some realms where the propagation physics are not well modeled. If there is environmental uncertainty, there is also acoustic uncertainty, and it is not yet clear how to robustly describe how this uncertainty propagates. Certainly, there needs to be feedback from the acousticians to the environmental characterization of what is needed. Next, the acoustical output enters the signal
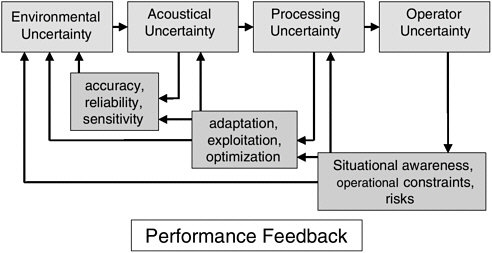
FIGURE 4-3 Propagation of uncertainty in a sonar system and the advantages that appropriate performance feedback can play in reducing its impact.

The Remote Minehunting System is an organic, off-board mine reconnaissance system that will offer carrier battle group ships an effective defense against mines by using an unmanned remote vehicle. Current plans call for the system to be first installed aboard the destroyer USS Pinckney (DDG 91) in 2004 (Photo courtesy of the U.S. Navy).
processor. While there is a good understanding of the processor, acoustical output is often so highly nonlinear with respect to errors in the acoustic models, statistical fluctuations, and system calibration errors that it is often difficult to provide a statistical prediction of its output. The so-called sonar equation is a useful guide, and receiver operating characteristics can be predicted, but they are only descriptive. There is also feedback to the rest of the components, as changing certain parameters of the signal processing can adapt and optimize the performance. Finally, the commanding officer must integrate all this uncertainty. He observes what is happening with the incoming data and must reconcile this to the prediction models. He wants to maintain his tactical advantage of position, situational awareness, and risks. If he is confident in his environmental predictions, he can exploit them to fulfill his mission objectives.
Cost of Uncertainty
In this section the goal of the METOC enterprise is assumed to be to reduce uncertainty (i.e., lack of knowledge about the nature of environmental conditions at some future time or different location) due to environmental processes, with the operational cost of that uncertainty providing guidance to optimum strategies. During tours of the committee to the various centers, members continually tried to explore the issue of expressing uncertainty in METOC. One of the most interesting insights came from a METOC officer who described his working relationship with a previous operational commander1 in terms of a betting metaphor. With each forecast, particularly those with tactical importance, he was asked to rate his confidence in the forecast for the mission in terms of one of three categories: no bet, minimal bet, and high bet. This case of an individual (and successful) relationship between a METOC officer and his operational commander illustrates several important points. First, it recognizes the fact of uncertainty and the fact that it should affect command decisions. Second, it institutionalizes uncertainty for operational purposes in a simple set of levels (a useful example of a concept of operation or CONOPS). Third, it includes an implicit assessment of the impact of the prediction on the operation in placing the bet. That is, uncertainty in certain situations or for certain variables has no operational impact, while in other situations it is critical.
This creative solution to dealing with prediction uncertainties parallels the concepts of traditional risk analysis practiced in the business world, as discussed in Chapter 2. In risk analysis, potential adverse conditions are identified, and then estimates are made of the probability and consequences of their occurrence.

Rigid Hull Inflatable Boats stand ready for launch in the ship’s well deck, in preparation for an upcoming Mine Countermeasures Exercise. Following the decommissioning of the mine countermeasure support ship USS Inchon (MCS 12), amphibious assault ships have provided transportation and support to the mine countermeasures units operating out of Naval Station Ingleside and Naval Air Station Corpus Christi (Photo courtesy of the U.S. Navy).
Consequences of Uncertainty—Relative Operating Characteristics
In the meteorology literature the consequences of prediction uncertainty have been studied using the concept of Relative Operating Characteristics (ROCs; see Mason and Graham, 1999, for a good introduction). ROCs form a basis for understanding decisions made from predictions for which confidence intervals are available (in this case through ensemble forecasts). In their discussion, Mason and Graham study the problem of issuing warnings for either drought or heavy rainfall seasons over eastern Africa, but the approach is equally applicable to decisions on whether to send the fleet to sea prior to an impending hurricane or a go/no go decision for a SEAL infiltration.
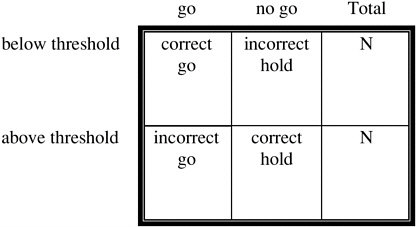
ROC analysis is based on contingency tables, matrices that compare the joint probability of the prediction and occurrence of events (see Table 4-1). For example, if wave heights were correctly predicted to be too large for a SEAL operation, the forecast would be counted as a “hit,” while correct prediction of low-wave energy (no warning) is a “correct rejection.” Similarly, incorrect prediction of high waves (issuing a “no go warning”) is an “incorrect warning,” while incorrect prediction of safe conditions is called a “miss.” Each of these outcomes has a cost that can be assessed by the Navy. For example, a miss might be viewed as more expensive than an incorrect warning since the lives of SEALS could be threatened. The cost of uncertainty, then, is the cost of each prediction failure mode times the probability of its occurrence. The extension of this calculation to a range of variables, missions, and conditions is straightforward but is best illustrated by way of an example.
TABLE 4-1 Contingency Table for Risk Analysisa
Example Use of ROC to Find the Cost of Uncertainty
Consider a SEAL infiltration mission onto a sandy beach. The mission depends on a number of environmental variables. This discussion will start with an examination of one variable, wave height, first introducing uncertainty and then moving on to quantify the cost of that uncertainty. The concept will then expand to the composite cost of all variables and then the merging of costs from more than one mission.
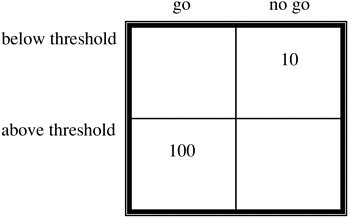
For illustration, threshold criterion for wave height for this mission is assumed to be 1.5 m. Further assume that the predicted wave height for the time of the operation is 1.1 m. In addition, assume there is a known uncertainty to this estimate, represented by a standard deviation of 0.3 m (in the interest of brevity, discussion of possible methods for estimating confidence intervals is omitted here but is an important consideration). Thus, the actual wave height at the time of operation can be represented by a probability distribution function (see Figure 4-4). From this figure it can be seen that waves will most likely not be an impediment, and we would give a “weather go” to the operation. However, there is a 9 percent chance (marked on the graph) that the actual wave height will be greater than the threshold. Thus, if these same circumstances occurred many times, in 9 percent of these cases our prediction would be in error, and we would count these cases in a contingency table as cases of “incorrect go” (Table 4-1). Similarly, if the prediction had been for waves of 1.6 m in height, the METOC prediction would be “no go” or “hold.” Most of the time this would be the correct call. However, there would again be a number of cases (37 percent) where the actual waves at the time of operation were less than the threshold. These would constitute an “incorrect hold” and would contribute to the incorrect hold quadrant of the contingency table. A full contingency table is found by computing an ensemble of example cases (see Table 4-2).
Each type of prediction error from the contingency table would have an associated cost. The cost of an incorrect go is probably judged to be high, since such a situation can lead not only to mission failure but also threat to life. On the other hand, the cost of an incorrect hold may be much lower, merely representing a missed mission. However, if the mission is critical or is a critical component of a complex interdependent mission package, the cost of an incorrect hold will rise. For example, a missed evacuation of key civilian personnel prior to a conflict may necessitate very expensive and dangerous rescue operations later on and so would be associated with a higher cost for an incorrect hold. This would not mean that the SEAL operation would be attempted in impossible conditions, but it does mean that the cost of an incorrect hold could be very high depending on the duration.2 The impacts of missed predictions can be represented in a cost
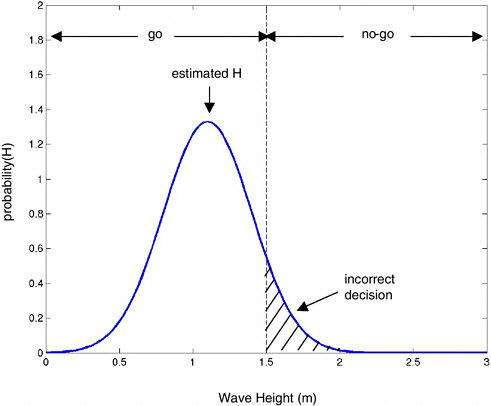
FIGURE 4-4 Example wave height prediction. The predicted value is 1.1 m for this example, with a standard deviation of 0.3 m. For this operation, the threshold for operational safety is 1.5m, so the METOC decision would be a “go”. However, it can be seen that 9 percent of the time, wave heights above threshold limits would be encountered. In those conditions, the METOC decision would have been incorrect.
table (see Table 4-3) that parallels the contingency table. Values are placed in the “incorrect go” and “incorrect hold” quadrants.3 The cost of uncertainty, then, is the sum of the likelihood of each type of failure times the cost of that failure. Correct predictions are viewed as having no cost beyond normal operations.
A question can now be asked whether the quality of wave height forecasts is sufficient or whether additional research investment is needed. Answering this question requires an assessment of the likely range of conditions that would be
TABLE 4-2 Hypothetical Contingency Table Showing Accuracy of Wave Height Predictions for a Suite of Test Cases
|
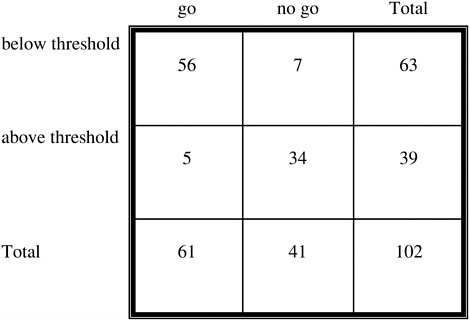 |
TABLE 4-3 Contingency Cost Tablea
faced by the U.S. Naval Forces for this type of mission. Thus, the entries in the contingency table will be the average overall expected conditions for some future planning life. If it is anticipated that most missions will be in enclosed seas with wave heights of less of than 0.5 m, the total likelihood of an incorrect go will be small, and the cost of the current level of uncertainty is small. Similarly, if the anticipated tactical interests lie in areas with extreme wave environments, decisionmakers will nearly always be correct in their “hold” predictions and, again, further R&D is not needed. On the other hand, if a fair portion of anticipated missions will occur in conditions that are “near” thresholds, it becomes important to be able to reduce the uncertainty of those predictions and hence reduce the rate and cost of prediction errors.
In fact, the question is not whether to invest in one variable such as wave height, but instead how to prioritize investment across the many variables and processes that affect naval forces. Continuing the case of the SEAL infiltration, it needs to be recognized that the mission is dependent on the environment in many ways. For illustration, consider the effects of water temperature and nearshore currents on the mission. One can proceed in the same way as outlined above for wave height. Uncertainty in the estimate of each variable (confidence interval) must be estimated (e.g., 3° C for water temperature). A contingency table is then created by considering the likely range of conditions to be faced in the future and thereby the likelihood of incorrect predictions (either “incorrect go” or “incorrect hold”). It is possible that the “thresholds” for different environmental variables may represent different levels of danger to the mission. Thus, there may be relative weightings of the impact of the variables, with water temperature perhaps having much less severe impact than wave height (for example). This would be represented in the cost tables, with a lower cost for a temperature “incorrect go” than for a wave height “incorrect go.”
Finally, the impact of different variables on different missions can be considered. Contingency tables can be built for each mission type and environmental variable. The total cost of uncertainty, then, is the sum over the entire anticipated mission portfolio of the costs of uncertainty for each mission. For example, it may be anticipated that over the next 10 years missions will be allocated as 35 percent carrier air operations and strike warfare, 30 Naval Special Warfare, 15 percent Undersea Warfare and Anti-submarine Warfare, 15 percent Amphibious Warfare and expeditionary warfare, etc. (This distribution of activities among the various warfare missions is purely hypothetical.)0
Implementation of this concept would obviously require a moderate amount of bookkeeping and an in-depth introspection on the current capabilities of prediction systems (confidence intervals for different environmental variables) as well as the likely future mission portfolio. In addition, consideration of enemy actions, both in terms of impairing data collection or communications will need
to be accounted for.4 Much of this information does not exist. Thus, it is not necessary, or even desirable, that the operational naval METOC enterprise itself become bogged down in providing a value basis for METOC investment strategy. However, a focused effort by a qualified study group organized by the Office of Naval Research (ONR) and working closely with the Office of the Oceanographer of the Navy and the Naval Meteorology and Oceanography Command (CNMOC) could further explore this concept, laying out uncertainties and their costs for a number of the main mission problem areas.
The application of such analysis to complex systems often results in unexpected insights. The human ability to make practical and appropriate decisions in relatively simple cases involving uncertainty often results in unwarranted confidence in making decisions in more complex situations. Thus, it would be surprising if unexpected details did not emerge from a more rigorous examination of the cost of environmental uncertainty across the breadth of naval activities. For instance, it may be possible that the naval METOC enterprise now predicts environmental conditions at large spatial and temporal scales sufficiently well for most purposes that further investment would have small impact on the cost of uncertainty, compared to other uses of R&D funds. Even the process of estimation of confidence intervals will raise questions that have been ignored for too long.
Reduction of Uncertainty by Further Investment
The sections above attempt to provide a methodology for placing value on METOC knowledge and predictions by introducing the cost of uncertainty. However, the charge to the committee calls for developing a rational basis for investment in METOC R&D. Improvements in the process for providing METOC information (whether through more efficient data acquisition, incorporation of improved understanding of natural processes in forecasting tools, or other means not yet identified) will yield reduced uncertainty in predictions and hence reduced cost of uncertainty. The best investment strategy is that which provides the largest reduction in the cost of uncertainty for the smallest research investment cost. The general field of risk reduction through incorporation of improved knowledge is related to the topic of Bayesian statistics.
There are a number of methods of reducing uncertainty in a METOC prediction. The most straightforward method is to take additional measurements of the domain to be used as initial values in a model run. Such measurements can
include in situ sampling or remote sensing. Increased sampling may come with a cost, owing to both the cost of expendables and the associated cost of operations. It may also be either risky or impossible for denied areas of interest.
Over longer periods of time, uncertainty in predictions can be reduced through research. In general, the research can be directed toward improvement in the models (through either improved understanding of the physics or improved hardware and modeling strategies), increases in remote sensing or in situ measurement capability, or improved understanding of the optimum choice of initial value samples for model performance (model sensitivities). There are many choices on how R&D money can be invested, each with a different return value.
The cost of data acquisition varies depending on the nature of the source. The cost of collecting new data may be low in some conditions; thus, users may not pursue acquiring data previously collected by other sources. This tendency can become a liability if easy access to new data discourages the development of

An F-14 “Tomcat” fighter assigned to the “Jolly Rogers” of Fighter Squadron One Zero Three (VF-103) leads a formation comprised of F/A-18 “Hornet” strike fighters from the “Blue Blasters” of VFA-34, the “Sunliners” of VFA-81, and the “Rampagers” of VFA-83. Two Croat MiG-21 “Fishbed” fighter-interceptors flank each side of the formation. U.S. Navy aviation squadrons assigned to Carrier Air Wing Seventeen (CVW-17) have sent a detachment to Croatia in order to participate in Joint Wings 2002. Joint Wings is a multi-national exercise between the U.S. and the Croat Air Force designed to practice intelligence gathering. Supporting multinational forces is an ever-increasing demand for the U.S Navy METOC enterprise (Photo courtesy of the U.S. Navy).
effective mechanisms to find and acquire data from other sources, because constantly evolving geopolitical realities can make what had previously been seen as routine data collection impractical. Thus, an evaluation of various sources of data would seem to be helpful. Furthermore, a formal analysis of the payoff for such investment can be handled through a Bayesian statistics analysis. In particular, formal decision theory can be used to examine the value of new information or improved predictions to decisionmaking.
Database Issues
As evidenced in previous chapters, METOC data needs span a broad range of data types, sources, and formats (see Box 4-1). The user community within U.S. Naval Forces spans an equally broad range of sophistication and experience in the production and use of METOC data products. To achieve the vision of a network-centric naval force as it relates to METOC issues, the supportive data systems must be fully interoperable at the machine level. This means that computers in the data system must be able to exchange data in a semantically meaningful fashion without human intervention. Furthermore, increased use by naval METOC personnel of non-Navy data sources suggests that the Navy’s METOC systems would benefit if they were interoperable with non-Navy data systems (see Box 4-2).
At present, naval METOC systems are not interoperable, although elements of them may be. It is not unusual that a METOC officer requires access to several different computer displays, each addressing one data type, and the data visible on one display (system) may not be overlaid on or with data from another display (system). This is especially true for those who would like to view oceanographic data products with meteorological data products and for those interested in integrating data products generated by the Naval METOC enterprise with those generated by other DOD services or by non-DOD. The Department of the Navy (DON) does recognize the need for interoperability among its systems and is working toward this goal with the Navy Integrated Tactical Environmental Sub-system5 (NITES, 2000) installed on 70 of the U.S. Navy’s major surface ships (as well as at shore activities) is used by forecasters to process weather and ocean data from anywhere in the system. A critical element of NITES 2000 is the
|
5 |
The current version of the Navy Integrated Tactical Environmental Sub-system is a modular open-architecture software subsystem that is integrated as a segment of the Navy C4I system onboard all ships and at all major Navy/Marine Corps commands and staffs, both onshore and afloat. NITES 2000 integrates derived products into command and control tactical decision aids for use with strategic and tactical computer systems on smaller ships and sites. The open-system design of NITES will provide complete interoperability with other DOD, federal, and allied command and control systems connected to the new Global Command and Control System (http://www.matthewhenson.com/usnshenson4.htm). |
|
BOX 4-1 Accessing METOC Data in Naval War Games At present, METOC data and product requirements vary dramatically from user group to user group. In particular, the fleet generally requires access to near real-time data or to predicted fields, whereas war gaming requires realistic but simulated conditions. Simulated weather (both atmosphere and ocean) conditions, when used for a hypothetical conflict, are presently obtained by selecting a period in the past for which good weather observations are available for the region of interest and for which the suite of weather conditions desired for the war games occur. The observations and predictions obtained from this period are then used to simulate weather conditions for the games. The two sides in the simulated conflict have access to different-quality predictions and observations. Surprisingly, one side is provided with “perfect” predictions (i.e., if Team Blue is provided at the outset with the actual weather for the duration of the games, Team Red will be given less accurate “predictions”). In addition, regarding the need for simulated fields for actual war games, developing war game scenarios often requires access to statistical summaries or climatologies of various meteorological and oceanographic parameters (e.g., what is the probability that sea state exceeds 15 feet in the eastern North Atlantic in winter and for how long can such conditions be expected to persist?). Not surprisingly, data systems being developed by the U.S. Navy for the METOC community are focused on the needs of the fleet; the fleet is by far the largest user of such systems among U.S. Naval Forces. The result is that these data systems do not meet the broader range of war-gaming needs; specifically the systems currently under development do not provide access to a wide range of historical data, nor do they provide the capability to readily work with these data and/or with climatologies when obtained from a “non-DOD” source. As a result, generating realistic simulations for war games is tedious at best. Furthermore, the METOC community is denied an opportunity to fully evaluate the METOC data systems of the future. |
Tactical Environmental Data Server (TEDS). TEDS is a “Defense Information Infrastructure (DII) Common Operating Environment (COE) compliant set (see http://www.sei.cmu.edu/str/descriptions/diicoe.html for a description of DII/ COE) of database, data, and software segments that serve as the primary repository and source of Meteorology and Oceanography (METOC) data and products for NITES 2000. TEDS is composed of a METOC database and a set of Application Program Interfaces (APIs) that provide storage for and access to dynamic
|
BOX 4-2 Opportunities and Challenges to Deriving Environmental Observations from Imagery Collected for Intelligence Purposes All METOC personnel are trained in the basics of weather observation. These first-hand human observations have historically formed the nucleus of the synoptic observation system that is key to forecasting. Today, satellite imagery and automated in situ weather stations provide the preponderance of observational data used by the METOC community. The electrooptical imagery collected by satellite or other means, therefore, can be considered as dislocated weather observations. Deriving a useful observation from such an image is a teachable skill that, when employed properly, reduces the electrooptical signal to a numerical parameter that can be handled just like any other measurement. Thus, the fact that these observations are derived from imagery rather than human observation or some other source cannot be determined from the derived values. In many military situations, however, the only available imagery for a given area is that which is collected for intelligence purposes. Often, the resulting images in and of themselves are not particularly sensitive so much as the time and location or other ephemeral and associated information. The limit to deriving useful observational data from such imagery is finding adequate numbers of technical staff trained in the relevant techniques who also hold adequate clearance to work with the imagery. The utility of such capability has been explored and validated on a small scale at the Naval Pacific METOC Command-Joint Typhoon Warning Center (NPMOC-JTWC) at Pearl Harbor, Hawaii. NPMOC-JTWC personnel with adequate clearance process imagery on a limited basis and derive valuable environmental data that are then distributed throughout the METOC community. Because all sensitive attributes have been removed, these data (which are indistinguishable from data from other sources) can be used as model input to improve forecasts over tactically important regions where other sources of information are limited. Currently, production-scale extraction of information from highly classified imagery is limited not by connectivity, technical understanding, or facility space but by the lack of resources needed to carry out security checks and other steps needed to grant existing center personnel with appropriate clearances. In other words, if adequate numbers of technically competent personnel exist, the only additional investments needed are the resources to grant them adequate clearance. Expanding the capability to other METOC centers of sea assets would involve some expanded connectivity but would largely require the commitment of resources proportional to the number of staff needed to fully integrate the approach into all relevant METOC production efforts. |
METOC data (e.g., analysis/forecast grid field data, observations, textual observations and bulletins, image data, and remotely sensed data) in a heterogeneous networked environment.”6
Despite the significant steps being taken for interoperability among naval forces and to a lesser degree between DON and other DOD services, the lack of an effort to interface these systems with non-naval, non-DOD systems is seen as limiting at present and as a potential serious omission in the not too distant future (order of 10 years; see Box 4-1).
TARGETING DATABASE DEVELOPMENT
The uncertainty model developed earlier in this chapter should be applied to the determination of what data are needed, so that a plan for what data should be collected and saved in the future can be developed. There are four potential sources of data that need to be considered in developing METOC databases: (1) environmental data currently collected but discarded after primary use; (2) data that can be collected by sensors devoted to other uses, such as intelligence gathering, surveillance, or reconnaissance; (3) data that would result from the addition of additional dedicated METOC sensors on current naval platforms; and (4) increased exploitation of nontraditional sources.
A Policy for Saving Data Currently Collected and Discarded
The DON collects a vast quantity of data with existing sensors. A subset of these data is saved for future use. The procedures for saving data do not, however, appear to be well established. In particular, data that are discarded today may prove to be important in the future.
Dual Use of Intelligence Sensors for METOC in the Littorals
Dual use refers to approaches that provide benefit for some purpose from data that were collected for a different purpose. Since the data are already in hand, there are no further costs of acquisition. Thus, dual-use techniques are generally very cost effective.
One of the best examples of the dual use of a non-METOC sensor for METOC purposes involves the Aegis radar system mounted on major combatants. The propagation and performance characteristics of this system depend on aspects of the environment, particularly atmospheric and ocean conditions that affect ducting, attenuation, and scatter of radar signals. In-dual use application this sensitivity to the environment is inverted such that radar performance can be exploited to yield estimates of characteristics of the environment of radar propagation.
Dual use may be particularly important in the littoral environment, a zone whose short time- and space scales of variability force frequent, high-resolution sampling for proper battlespace characterization. Since access will be denied to most areas of tactical interest, in situ sampling is dangerous and generally limited in scope. For example, Navy SEALs hold mission responsibility for bathymetry measurements in depths of less than 20 feet. Their work involves either personal observation or installation and retrieval of instruments. Both missions are clandestine and are of a type that the SEAL would rather not have to do. Thus, it is evident that the preferred METOC sampling strategy in nearshore regions should be based on remote sensing, preferably at stand-off distances.
The applicability of spaceborne data collection for describing littoral environments has been the subject of considerable recent discussion (e.g., Poulquen et al., 1997). The view that success can only be had at larger scales and that the fine-grain resolution needs for nearshore sampling make course-grained data, such as are available from most satellites, of limited use may be changing. Spatial resolutions of 1 m for hyperspectral and 8 m for SAR are now available, with daily to three-day time intervals. Some spaceborne sensors may, therefore, supply data of sufficient spatial resolution (SPOT, for example), but timely access to satellite orbit limitations, tasking conflicts, or problems with rapid dissemination is still a concern.
By contrast, these are just the scales that are needed for intelligence sensors. The U.S. Navy already owns a wide range of intelligence assets that could contribute to the METOC mission through either direct tasking or enroute supplements to normal intelligence missions. Many of these sensors are forward deployed and so are under the control of theater operational commanders. Examples of intelligence packages are TARPS or sensors on Global Hawk.
The very shallow water and surf zone regions of the littorals provide a wide range of surface signatures that can be exploited to allow estimation of variables of METOC interest (Holman et al., 1997). Methods have been developed and tested for the estimation of wave period and direction (e.g., Lippmann and Holman, 1991), the strength of nearshore currents (Chickadel et al., in review), nearshore swash (e.g., Holland et al., 1995), sand bar morphology (Lippmann and Holman, 1989), and subaerial and subaqueous beach profiles (Holman et al., 1991; Stockdon and Holman, 2000). Key to these techniques is sampling of time domain variability over a short period of dwell, usually less than two minutes (although useful but degraded results can be found for significantly shorter record lengths). This requires a sensor that can keep a region of interest in view either “in passage” or by staring.
While the above references refer to the use of optical data, similar signatures are also available from active sensors (principally radar) and from other passive bands. Each band can be, and has been, exploited for similar purposes.
Imagery and other information collected as part of intelligence-gathering efforts are generally classified as high level, introducing potential complications
in transfer to and handling by METOC units. However, on aircraft carriers these activities are located adjacent to each other, and wider use of such information at the various METOC centers is limited largely by the number of technicians with adequate clearance to allow work on a production scale (Box 4-2). It seems likely that an appropriate CONOPS could be developed, as done at the War-fighting Support Center, to handle these issues. The advantages of having forward-deployed sensor capability coupled to onboard exploitation could greatly improve fleet METOC capability, particularly in a political flashpoint area, where contention for tasking of national assets can be high.
Adding Data Collection Capabilities to Navy and Marine Platforms
A simple mechanism for the improvement of naval METOC data collection capability could be the addition of small automated sensors on a range of naval platforms. Naval surface ships, submarines, and aircraft log millions of miles per year in all of the world’s oceans. Naval aircraft fly up and down the atmospheric air column thousands of time per day. Ships sail routinely in areas where surveys are either very old or nonexistent and bottom obstruction mapping has not been attempted for decades. Submarines are diving through the water column through

Although modern technology has greatly enhanced efforts to provide timely and accurate forecasts, lookouts on surface vessels still provide valuable in situ information on sea state and current weather conditions (Photo courtesy of the U.S. Navy).
out the world and in most cases are not recording or saving valuable environmental data.
Few U.S. Navy or Marine Corps operational units have any automated environmental sensors or the equipment required for processing and storing data. There are several barriers to deployment of these types of systems. Initially, sensing systems tended to be big, expensive, power hungry, and fragile. Accurate positioning and precise time were not readily available to automatically register data in time and space. Finally, there was the question of who would pay for development and deployment of such equipment. Generally speaking, the various warfare communities—surface, submarine, and aviation—were not interested in budgeting for items that would not directly contribute to warfighting capabilities.
Today, lightweight, rugged, low-cost, low-power environmental sensors are available off the shelf. The Global Positioning System (GPS) now provides accurate locating data and precise time that can easily be integrated into computer-based systems. Personal computers are not expensive and can quickly register new data and store them on internal hard drives that can handle up to 100 gigabytes. Attached storage units are now in the terabyte range. In practical terms, a year’s worth of METOC observations and bathymetric images could be stored on one hard drive and easily be backed up on CD-R or DVD-R drives. This information can serve as a valuable resource for intelligence, navigation, climatology, and scientific research.
The most useful data for surface ships would be air and sea surface temperature, humidity, water column bathymetry, and bottom swath bathymetry. Aircraft should be extracting temperature, humidity, lapse rates, and altitude. Submarines could easily extract conductivity, temperature, and depth, the basic building blocks of oceanographic research. This information could be displayed locally in graphic format for tactical use and passed by datalink for strategic modeling and research onshore.
Other Nonstandard Data Sources
One of the most important assets to U.S. Naval Forces is personnel. METOC officers gain a great deal of knowledge related to the meteorology and oceanography of the regions they visit, as do the enlisted personnel who support them. Some of this experience is captured and saved in cruise reports generated by METOC officers. There is also potentially useful information exchanged by METOC officers in online chat sessions7 across SIPRNET (referred to as IRC
Chat, these interactions have become an extremely popular and effective mechanism for forward-deployed METOC officers to interact with colleagues stateside or on other naval platforms. Since these sessions are electronic, the information all exists in a form that is easily saved. At present, though, this information is either not being saved or is not organized for easy access. This is because systems do not exist today that can effectively mine such databases. There is, however, a great deal of research being undertaken in the mining of textual databases with significant progress being made, and it is not unreasonable to think that in the not too distant future (less than 10 years) sufficient progress will have been made for the naval METOC community to make more effective use of these data.
Non-DOD Data Repositories
As discussed in Chapter 3, data systems under development for the METOC community are focused on access to relevant data and products generated by DON efforts and/or passed through naval (and in some cases other DOD) data centers. There is little to no consideration in the development of these systems for direct access to data that are generated and held outside of DOD despite the use of such data sources via standard Web browsers by METOC personnel in recent naval operations. The trend toward increased development of and open access to real-time data and data products in the commercial and non-DOD research sectors can be attributed to two factors: (1) substantial improvement in computational power available at costs that are affordable to the academic researcher or the commercial data provider, and (2) the development of instrumentation that provides real-time access to data obtained at remote sites. Virtually every oceanographic and meteorological research institution is involved in one way or another with the development of smart sensors that relay their data back to the home institution in near real time. At the same time there is increasing interest in incorporating these data into data assimilation experiments and regional predictions. There is also increased use by the research community in real-time feeds from major satellite (and other) data systems in data product generation using sophisticated retrieval algorithms and/or advanced assimilation techniques. These state-of-the-art products are often the best available at the time for the region of interest. Good examples of this are the TRMM (Tropical Rainfall Mapping Mission), sea surface temperature, and QuikScat and SSM/I (Special Sensor Microwave/Imager) wind data products available in near real time from Remote Sensing Systems, a private research company (http://www.ssmi.com).
At the same time that non-DOD near real-time data sources are coming online, there is growing interest in providing seamless access to such sites. For example, the National Virtual Ocean Data System (http://nvods.org) currently provides access in a consistent form to more than 300 datasets stored in a variety of formats from approximately 30 sites in the United States, ranging from government facilities to private companies to academic research institutions. Recently
several sites have also been established abroad (France, Great Britain, Australia, and Korea). As more clients are developed for this system (there are currently eight application packages from which data served via the system can be accessed), there is more interest in adding sites. At present (May 2002), new sites are being added in the United States and abroad every two to three weeks.
Given current trends in data availability and data product generation, together with the development of data systems designed to provide seamless access to data in a distributed heterogeneous environment taking place outside of the DON, it seems clear that in the not too distant future the non-DOD research and commercial sectors both in the United States and abroad could become a significant source of useful METOC data for naval forces. Surprisingly, however, there does not appear to be any effort in the development of DON systems to provide for interoperability with systems in the non-DOD sector.
RAPID ENVIRONMENTAL ASSESSMENT
As the pace of warfare increases during the 21st century, there is an emerging need for Rapid Environmental Assessment as an aid to warfighters. Whereas in the past the decision cycle for warfare operations might have been weeks to days, in the 21st century the decision cycle for many naval operations is compressed into hours and sometimes minutes (see Figure 4-5).
Rapid Environmental Assessment Versus Optimized Environmental Characterization
Discussions throughout this study often return to the fundamental utility of environmental data and use of such data by warfighters as an exploitable component of modern warfighting doctrine. In this regard, two modes of environmental information acquisition and use were identified: Rapid Environmental Assessment (REA) and Optimized Environmental Characterization (OEC). Both are explored briefly below with the objective of providing readers with a working definition of each.
Assessing the environment within the 4-D battlespace is a major task facing the naval METOC community. In particular, as the pace and scale of warfare operations increase and become more spatially fragmented, providing accurate environmental information in a timely manner so that warfighters can meaningfully exploit their environment becomes a daunting task. REA refers to environmental information gathered through networked battlespace sensor arrays and timely processing of environmental information into meaningful data products that can be disseminated to fleet assets. As such, REA is fundamentally a method for providing warfighters with synoptic views of the battlespace. Such views are useful in directing fleet or other warfighting assets during the prosecution of specific warfare operations. Ideally, these views of the battlespace are updated
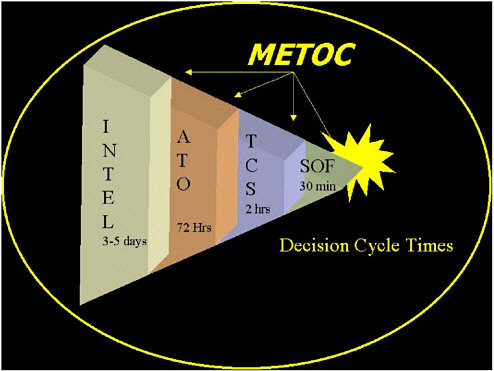
FIGURE 4-5 Decision cycle times for typical naval operations requiring environmental information.
frequently (i.e., every few minutes) to provide military commanders with sequential synoptic views of the evolving battlespace environment. The Naval Fires Network (NFN) is an example of a weapons system developed to utilize REA concepts.
OEC differs somewhat from REA in that a goal of OEC is to utilize REA information to parameterize various models and develop predictions that forecast the evolution of the battlespace. As such, OEC is fundamentally a method for providing warfighters with a predictive view of the battlespace. A critical component of a successful OEC system is the ability to ingest high-priority REA data (in other words, optimize the process) in order to compute predictions about the future environmental state of the battlespace and receive continuous updates of battlespace conditions from REA sensors in order to dynamically update battle-space forecasts. Such forecasts not only are useful for planning scenarios but may also ultimately find use during naval combat operations to dynamically modify warfighting strategy in order to gain continuous tactical advantages or minimize threats to fleet assets. For example, an array of REA sensors in a battlespace may transmit information regarding wind speed, direction, and vertical wind structure in the atmosphere. These data might be merged with high-
resolution terrain models in an OEC system designed to predict and forecast dispersion of biological, chemical, or radiological agents at a pace set by the operational tempo. Whereas the synoptic view of a dispersing plume provided by REA may aid naval commanders in understanding conditions occurring within the battlespace, OEC model output would help commanders make decisions regarding where to move assets in order to minimize the effects of a plume from weapons of mass destruction on warfighters. Furthermore, OEC output could be used to predict the rate of dispersion of such a plume, providing commanders with information about when it might be safe to move assets back into the affected area.
It is clear from the brief discussion above that REA and OEC, though somewhat distinct concepts, are also closely related and that successful application of one depends on the relative state of development of the other. As such, REA and OEC should be viewed as separate but complementary elements of a more thorough naval environmental information system.
REA represents the need for theater-wide environmental information gathering through sensor arrays and timely processing of environmental information

A Seabee assigned to Beach Master Unit Two based at Little Creek, Va., directs a Landing Craft Air Cushion onto Onslow Beach at Camp LeJeune, N.C. Understanding the environmental thresholds for a variety of naval platforms will be key to how to enhance current efforts to provide timely and valuable information to U.S. Naval Forces (Photo courtesy of the U.S. Navy).
TABLE 4-4 Naval Mission Areas Where REA May Be a Critical Component
|
Mission Area |
Acronym |
|
Anti-Air Warfare |
AAW |
|
Amphibious Warfare |
AMW |
|
Anti-Surface Warfare/Over-the-Horizon Targeting |
ASU/OTHT |
|
Command/Control/Communications/Computers, Intelligence, Surveillance and Reconnaissance |
C4ISR |
|
Operations Other Than War |
OOTW |
|
Naval Special Warfare |
NSW |
|
Strategic Deterrence and Weapons of Mass Destruction |
STRAT/WMD |
|
Strike Warfare |
STRIKE |
|
Wargames and Training Issues |
WGT |
into meaningful data products that can be disseminated to fleet assets. Some naval warfare operations (e.g., time-critical strike and special warfare) have evolved a need for environmental information that is both comprehensive and rapidly updated to ensure success.
Development of all-weather precision munitions (e.g., GPS-guided weapons) minimizes the need for rapidly updated environmental data since weapon delivery depends on accurate target locations rather than specific environmental conditions (such as an ability to see the target).8 However, some warfare operations have become more dependent on timely environmental information (e.g., time-critical strike, special warfare operations, ship self-defense, weapons of mass destruction, etc.).
Further, reducing the exposure time of naval forces during combat operations is among the most effective strategies to minimize combat losses. As such, reliable and up-to-date environmental information is critical to attaining mission objectives. Examples of naval warfare operations where REA is an increasingly critical component are listed in Table 4-4.
In many of the operations listed in Table 4-4, REA capabilities to provide near real-time assessment of environmental conditions throughout the 4-D battle-space would greatly enhance probabilities for successful execution of mission tasks. For example, emerging capabilities to engage in time-critical strike warfare (TCS) against mobile or elusive targets would greatly benefit from the ability to rapidly and accurately assess and evaluate environmental conditions such as atmospheric radio frequency propagation characteristics, visibility over target
areas, atmospheric refractive properties, surface to high-altitude winds (both direction and velocity), relative humidity, and so forth. Rapid assessment and ingestion/processing of near real-time environmental data would have similar benefits to dispersion models used to determine “red zones” of weapons of mass destruction.
To make REA a reality across multiple mission areas, there is a broad spectrum of R&D issues that need to be addressed by the METOC community and these issues need to be integrated into the overall mission of naval METOC. The principal issues related to developing REA capabilities by naval METOC are related to (1) environment assessment, (2) sensor optimization, and (3) determining customer needs. Each of these topics will be addressed briefly below to provide a sense of the present state of development and areas where significant advances in R&D might be achieved in the future.

Marines with Company D, Light Armored Reconnaissance, Battalion Landing Team 3/1, 11th Marine Expeditionary Unit (MEU) (Special Operations Capable), focus down range during recent live-fire training. With the aid of their Light Armored Vehicle Two Five (LAV-25), the Marines can undertake a number of missions, to include facilitating reconnaissance, artillery direction, and hit-and-run missions. Each LAV-25 is equipped with a 25-mm chain gun and two M-240E1 machine guns, enabling the Marine gunners to accurately fire on targets while moving at speeds of up to 10 mph due to the vehicle’s stabilization system. Providing timely and valuable environmental information to such forward-deployed and highly mobile units presents a challenge to the U.S. Navy and Marine METOC communities (Photo courtesy of the U.S. Marine Corps).
ENVIRONMENTAL ASSESSMENT
Assessing the environment of the 4-D battlespace remains among the most vexing tasks facing the naval METOC community. In particular, as the pace and scale of warfare operations increase and become more spatially fragmented, providing accurate environmental information in a timely manner so that warfighters can meaningfully exploit their environment becomes a daunting task. Relevant issues in the development of REA capabilities are questions regarding:
-
determination of appropriate environmental parameters for different mission areas,
-
the granularity (resolution and sampling frequency) of gathered environmental data,
-
sensor optimization (types of sensors and optimized sensor arrays) for obtaining environmental information at the appropriate granularity,
-
quality control and quality assurance of rapidly acquired environmental data,
-
processing/analysis of data,
-
development and dissemination of relevant derived products, and
-
personnel training in the use and significance of environmental data products.
REA Parameters
Defining appropriate REA parameters requires close integration among the naval METOC community and it customers, the warfighters, as well as sensor developers. For each mission area, a decision system identifying those required parameters, desired parameters, and relatively unimportant parameters could be available (the General Requirements Data Base is a start toward a more robust parameter identification system).
REA Granularity and Sampling Frequency
REA data acquisition and assimilation needs for improved modeling scales and refresh rates need to be identified (see Tables 4-5 and 4-6). These needs are applicable to aerosol modeling efforts, high-resolution tide/surf/wave models, atmospheric dispersion models, etc. In addition, data needs for data-sparse regions of the earth will need to be identified and strategies to populate these regions with sensor arrays developed.
Additional data are necessary in order to enhance initialization of models at all scales and are particularly important as the forecast frequency becomes shorter (from 12 hours to 6 hours or less). Denser sensor arrays will also yield improved tropical storm intensity forecasts and improved storm track prediction.
TABLE 4-5 Present REA Granularity and Production Cycle
|
Atmosphere/ocean modeling scales Global: 81 km (FNMOC) Regional: 27, 9, 3 km (FNMOC) “On scene”: 27, 9, 3 km (FNMOC, regional centers) Nowcast: 3 km and less |
|
Atmosphere/ocean timescales Global: 24 to 144 hours Regional: 12 to 48 hours (72 hours possible) “On scene”: 12 to 48 hours (72 hours possible) Nowcast (6.2 R&D): 0 to 6 hours |
TABLE 4-6 Future REA Granularity and Production Cycle
|
Atmosphere/ocean modeling scales Global: 27 km (FNMOC)—coupled Regional: 3, 1, 0.3 km (FNMOC)—coupled “On scene”: 3, 1, 0.3 km (FNMOC, regional centers) Nowcast: 3 km and less |
|
Atmosphere/ocean timescales Global: 24 to 240 hours (ensembles) Regional: 72 to 96 hours “On scene”: 72 to 96 hours (72 hours possible) Nowcast (6.2 R&D): 0 to 6 hours |
SENSOR AND SENSOR ARRAY OPTIMIZATION
The need for environmental data on short timescales throughout the 4-D battlespace may drive the development of new sensors or multisensor packages or new ways to deploy sensors (e.g., unmanned airborne vehicles [UAVs] and UUVs). Obviously, the necessity for acquiring environmental data will be weighed against other options (such as deployment of weapons systems on UAVs and UUVs), and a decision system for selecting appropriate sensors will need to be developed. Optimization of sensors and sensor arrays will again require close coordination between METOC personnel and warfighters to ensure that appropriate data are collected and transformed into meaningful METOC products.
Quality Control and Quality Assurance of REA Data
Acquiring large quantities of environmental data will require development of new algorithms to assess and assure data quality. While this process might be

Timely weather forecasts play a critical role in the safe operation of aircraft at sea (Photo courtesy of the U.S. Navy).
most efficiently developed utilizing an automated system of some kind, it should be recognized that in some instances data outliers may represent significant perturbations in the environment that might be of interest to warfighters because those perturbations could significantly impact a mission. Thus, mechanisms for recognizing these perturbations and including or excluding them from model runs should be developed. At the very least, some system for determining whether anomalous environmental readings represent real environmental anomalies or sensor malfunctions should be developed. Quality control and quality assurance schemes will also aid in verification and validation of high-frequency forecast models.
Processing and Analysis of Data
Present capabilities in the naval METOC community to provide REA are evolving, and several successful trial programs are being evaluated (e.g., Distributed Atmospheric Mesoscale Prediction System, or DAMPS, and NFN). Each of
these REA test systems relies on through-the-sensor data gathering, assimilation, processing, and dissemination. In each case, sophisticated METOC computer models are forward deployed such that on-scene modeling capabilities provide warfighters with enhanced environmental information related to the immediate area of operations. Each of these systems has reach-back capabilities or can serve as the primary data-gathering/processing node and is capable of providing a common operation picture through network dissemination.
Development of Relevant Data Products
The METOC community needs to receive frequent evaluations of its products from the end-user community at sea to determine the relevance of data products forwarded to the fleet. During wartime, METOC products should have a high degree of customizability such that different actors in the fleet might be able to extract environmental information most relevant to their immediate warfighting needs. For instance, naval aviators involved in close air support and amphibious assault groups have a need for access to near-surface wind data, but each actor needs to be able to interpret wind data differently. Aviators need to know how wind speed and direction might affect weapons performance, whereas amphibious assault personnel need to know the effect of wind velocity and direction on sea state. In each instance the available data need to be presented as relevant products.
Personnel Training
As the sophistication and complexity of forward-deployed REA sensors, sensor arrays, processing/analytical capabilities, and forecast products increase, there will be an increasing need for highly trained analysts to accompany the fleet in order to provide interpretive expertise. The naval METOC community should attempt to identify or develop personnel for these roles and implement career reward systems for those individuals who may serve in these billets. A recurring theme among a number of the sites visited by the committee was the lack of a career path for navy aerographers and METOC specialists. In view of the evolving importance of METOC (especially forward-deployed REA capabilities), the Office of the Oceanographer of the Navy in particular should initiate a plan to enable motivated personnel to pursue this career path.
Statistical and Other Approaches to Decisionmaking in the Face of Uncertainty
Many fields of endeavor face the consequences of decisionmaking in the presence of uncertainty (for a good introduction, see Berger, 1985). One means of providing quantitative support to decisionmaking in the presence of uncertainty is through the use of Bayesian statistical analysis (Bayesian statistical analy-

Traditional means of atmospheric sampling are both costly and manpower intensive. New capabilities in remote sensing provide for more timely and efficient synoptic measurements (Photo courtesy of the U.S. Navy).
sis is a distinct field from Bayesian decision theory). This section discusses the problem of building models of complex systems having many parameters that are unknown or only partially known and the use of Bayesian methodology. There are numerous papers and books related to the application of Bayesian analyses that have some implications for using Bayesian statistical approaches to uncertainty analysis (e.g., Berger, 1985; Gelman et al., 1995; Punt and Hilborn, 1997). This discussion is intended simply to suggest that such techniques may have value
in helping set priorities for data collection under a variety of conditions. Thus, while aspects of these approaches are discussed here, the reader is encouraged to more fully explore these through the rich literature that exists.
There are three major elements in the Bayesian approach to statistics that should be indicated clearly: (1) likelihood of describing the observed data, (2) quantification of prior beliefs about a parameter in the form of a probability distribution and incorporation of these beliefs into the analysis, and (3) inferences about parameters and other unobserved quantities of interest based exclusively on the probability of those quantities given the observed data and prior probability distributions.
In a fully Bayesian model, unknown parameters for a system are replaced by known distributions for those parameters observed previously, usually called priors. If there is more than one parameter, each individual distribution, as well as the joint probability distributions, must be described.
A distinction must be made between Bayesian models, which assign distributions to the parameters, and Bayesian methods, which provide point estimates and intervals based on the Bayesian model. The properties of the methods can be assessed from the perspective of the Bayesian model or from the frequentist9 perspective. Historically, the “true” Bayesian analyst relied heavily on the use of priors. However, the modern Bayesian has evolved a much more pragmatic view. If parameters can be assigned reasonable priors based on scientific knowledge, these are used (Kass and Wasserman, 1996). Otherwise, “noninformative” or “reference” priors are used.10 These priors are, in effect, designed to give resulting methods properties that are nearly identical to those of the standard frequentist methods. Thus, the Bayesian model and methodology can simply be routes that lead to good statistical procedures, generally ones with nearly optimal frequentist properties. In fact, Bayesian methods can work well from a frequentist perspective as long as the priors are reasonably vague about the true state of nature. In addition to providing point estimates with frequentist optimality properties, the posterior intervals for those parameter estimates are, in large datasets, very close to confidence intervals. Part of the modern Bayesian tool kit involves assessing the sensitivity of the conclusions to the priors chosen, to ensure that the exact form of the priors did not have a significant effect in the analysis.
There are two general classes of Bayesian methods. Both are based on the posterior density, which describes the conditional probabilities of the parameters
given the observed data. This is, in effect, a modified version of the models’ prior distribution, where the modification updates the prior based on new information provided by the data. In one form of methodology, this posterior distribution is maximized over all parameters to obtain “maximum a posteriori” estimators. It has the same potential problem as maximum likelihood in that it may require maximization of a high-dimension function that has multiple local maxima. The second class of methods generates point estimators for the parameters by finding their expectations under the posterior density. In this class the problem of high-dimension maximization is replaced with the problem of high-dimension integration.
Over the past 10 years, Bayesian approaches have incorporated improved computational methods. Formerly, the process of averaging over the posterior distribution was carried out by traditional methods of numerical integration, which became dramatically more difficult as the number of different parameters in the model increased. In the modern approach the necessary mean values are calculated by simulation using a variety of computational devices related more to statistics than traditional numerical methods. Although this can greatly increase the efficiency of multiparameter calculations, the model priors must be specified with structures that make the simulation approach feasible.
Although they are not dealt with extensively here, a number of classes of models and methods have an intermediate character. For example, there are “empirical Bayes” methods in which some parameters are viewed as arising from a distribution that is not completely known but rather known up to several parameters. There are also “penalized likelihood methods” in which the likelihood is maximized after addition of a term that avoids undesirable solutions by assigning large penalty values to unfeasible parameter values. The net effect is much like having a prior that assigns greater weight to more reasonable solutions and then maximizes the resulting posterior. Another methodology used to handle many nuisance parameters is the “integrated” likelihood in which priors are assigned to some of the parameters to integrate them out while the others are treated as unknown. This provides a natural hybrid modeling method that could have fishery applications.
Limitations of Applying Formal Decision Theory
The case for Bayesian methods presented above must be tempered with some limitations of any formal approach to decision theory. Bayesian decision and risk-benefit analysis needs an assignment of the a priori and transition probabilities as development of a cost matrix. This has led to many historical and philosphical discussions about the foundations of this approach. How does one assign a cost matrix? How does one assign a cost to casualties? Often political risks defy a cost assignment that is needed when calculating the posterior probability of mission success or failure.
Similarly, the probabilities must be assigned. Does one estimate prioris from a database? If so, how much variability is there in the estimate? What is an appropriate assignment in a changing environment? Extremals (i.e., low-probability events) are especially vexsome because they happen so rarely. Transition probabilities are also problematic. The outcome of an observation can often depend on the system used or a tactical decision aid whose performance is questionable given an environmental database. Again, how does one quantify these probabilities and incorporate the variability into the analysis?
The important point here is that the inputs needed by a Bayesian-like approach are often not readily available or precisely defined without error. Estimating and/or assigning these are difficult problems in their own right. There needs to be an investment and infrastructure to quantify the needed probabilities and costs for this approach. This cannot be done on intuition or subjectively for this renders the results equally subjective. Certainly, one can give conditional outputs and one of the important aspects of the Bayesian approach is quantitative consideration of the inputs.
Whether setting priorities based on some cost-benefit analysis or simply determining which actions are the most pressing involves placing some value on the outcome. Such formalized efforts require considerable effort to establish a cost function associated with any given action (or even lack of action). In addition, understanding the transfer function (how costs or benefits are accrued) requires detailed understanding of how various processes interact. In a complex system, such as the battlespace, simplifying assumptions can reduce the numerical complexity but also introduce the possibility of reducing the problem to unrealistic levels. At some point, the resulting numerical model simply becomes invalid. Overcoming these barriers will require a consistent and committed effort, one that is likely best undertaken by ONR, working closely with the METOC community and warfighters. Such an effort, however, would likely bring greater focus and awareness of exactly how important specific environmental information is or can be.
In addition, Bayesian approaches present several important issues of which the user should be aware, including the following:
-
Specification of priors in a Bayesian model is an emerging art. To do a fully Bayesian analysis in a complex setting, with no reasonable prior distributions available from scientific information, requires a careful construction whose effect on the final analysis is not clear without sensitivity analysis. If some priors are available but not for all parameters, a hybrid methodology, which does not yet fully exist, is preferred.
-
In a complex model it is known by direct calculation that the Bayesian posterior mean may not be consistent in repeated sampling. However, little information is available to identify circumstances that could lead to bad estimators.
-
Although modern computer methods have revolutionized the use of Bayesian methods, they have created some new problems. One important practical issue for Monte Carlo-Markov Chain methods is construction of the stopping rule for the simulation. This problem has yet to receive a fully satisfactory solution for multimodal distributions. Additionally, if one constructs a Bayesian model with noninformative priors, it is possible that even though there is no Bayesian solution in the sense that a posterior density distribution does not exist, the computer will still generate what appears to be a valid posterior distribution (Hobert and Casella, 1996).
-
There is a relative paucity of techniques and methods both for diagnostics of model fit, which is usually done with residual diagnostics or goodness-of-fit tests, and for making methods more robust to deviations from the model. Formally speaking, a Bayesian model is a closed system of undeniable truth, lacking an exterior viewpoint to make a rational model assessment or to construct estimators that are robust to the model-building process. To do so and retain the Bayesian structure requires constructing an even more complex Bayesian model that includes all reasonable alternatives to the model in question and then assessing the posterior probability of the original model in this setting.
Despite progress in the numerical integration of posterior densities, models with large numbers of parameters can be difficult to integrate. Two of the most commonly used methods—ampling importance resampling and Monte Carlo-Markov Chain—have difficulty with multimodalor, highly nonelliptical, density surfaces.
Other Approaches
There is an ongoing effort to address uncertainty by a variety of means. One approach that may deserve additional investigation in its application to environmental uncertainty is “fuzzy arithmetic.” Fuzzy numbers have been described by Ferson and Kuhn (1994) as a generalization of intervals that can serve as representations of values whose magnitudes are known with uncertainty. Fuzzy numbers can be thought of as a stack of intervals, each at a different level of presumption (alpha), which ranges from 0 to 1. The range of values is narrowest at alpha level I, which corresponds to the optimistic assumption about the breadth of uncertainty.
Using fuzzy arithmetic software minimizes the possibility of computational mistakes in complex calculations. In summary, fuzzy arithmetic is possibly an even more effective method than interval analysis for accommodating subjective uncertainty; its utility should be examined more carefully for use in addressing uncertainty in environmental information for naval use.
SUMMARY
ROC is discussed above as a possible method for placing value on METOC information, and decision theory is examined for its potential value for quantifying optimum investment strategies. The committee was not familiar with examples of these approaches having been applied to the type of environmental problems faced by the U.S. Navy and Marine Corps—with one notable exception. ONR, which supported much pioneering work on decision theory, recently made capturing uncertainty in acoustic propagation the focus of a department research initiative (DRI). This DRI, entitled “Capturing Uncertainty in the Common Tactical/Environmental Picture,” is scheduled to continue through 2004 and is intended to “to characterize, quantify, and transfer uncertainty in the ocean environment to calculations of acoustic fields and to the subsequent use of acoustic fields in performance prediction, in estimating and displaying the state of targets, and in other Navy relevant applications.” This initiative, though early in its history, appears to offer some opportunity to address a significant tactical problem in undersea warfare (see Chapter 2 for more discussion). ONR should expand this initiative to cover other environmental problems and processes in order to more directly support operational challenges facing the fleet and Marine Corps and the METOC community supporting them.
In the absence of more specific knowledge of the ultimate payoff from such focused ONR activities, this introductory discussion should serve to raise a number of important points concerning METOC within the U.S. Navy and Marine Corps. Foremost is the need to recognize uncertainty in METOC prediction as fundamental to the value system for METOC investment. In the absence of some method to quantify the cost of METOC uncertainty—that is, the risk due to METOC prediction failure and the likelihood and cost of that failure—no objective basis can be found for R&D investment strategies or data acquisition.
As discussed previously, uncertainty can be reduced in many instances by the acquisition of additional data. However, the cost of such acquisition may exceed the benefit derived from its use. In some instances the stochastic nature of some processes means that some uncertainty will remain regardless of the number of observations made (objective uncertainty). In other cases increased understanding of the system, whether through acquisition of additional data or better understanding of the process involved, may be impractical due to lack of assets or time. In other cases, it may be practical to collect additional data, but the need for more accurate predictions of future states is low (i.e., naval operations are not sensitive to the process involved), making additional data collection unnecessary. Understanding the nature of the uncertainty, and its potential cost, associated with any environmental parameter of interest is a key step in improving the quality of environmental information provided to the fleet and Marine Corps. War gaming, SeaTesting, and other approaches to developing naval doctrine are important opportunities to more fully evaluate the importance of reliable and
accurate environmental information and the impact of uncertainty or efforts to reduce the cost of that uncertainty. The Oceanographer of the Navy and the Chief of Naval Research should make every effort to ensure that environmental conditions and predictions of those conditions are realistically depicted in simulations and that their effects are faithfully and accurately captured so that the fleet and Marine Corps, as well as the METOC community, can more fully evaluate the importance of METOC information in naval operations.
Once a decision for additional information has been made, it seems sensible to assume that the cost of acquiring those data is a function of their availability. It appears that too often data collected previously, whether for other purposes or not, are not made use of by the METOC community. Thus, the benefit of collecting those data is not fully utilized. Several opportunities for less expensive data acquisition bear fuller evaluation. Because data for denied areas are often the most valuable, especially for REA, particular emphasis should be placed on making fuller use of data collected in these areas. Typically, the best source of such data is the electronic intelligence community, as it possesses the most capable assets. Many data collected in these areas are classified simply because their recovery involves acknowledgement of sensitive ground assets (e.g., it appears that information from UAVs collected for the Defense Threat Reduction Agency [DTRA] may be held for an extended period of time before it is released to METOC archives, so as not to release information about the existence of information-gathering assets).
Current sensors provide data not only in optical bands but also from active sensors (radar) and in other passive bands. Each provides a new window into the environment. Exploitation techniques are already available in the literature and could easily be forward deployed. It is strongly recommended that existing intelligence-gathering sensors be examined for potential exploitation as dual-use METOC sensors. Particular emphasis should be placed on airborne sensor packages, since these are forward-deployed theater assets that are already under the control of operational commanders. Data collection could be either specifically tasked or en route to other missions, while analysis could be easily handled onboard.