Appendix C Risk Assessment in the Testing, Evaluation, and Use of Standoff Detectors
OVERVIEW OF RISK
A risk is an uncertainty about future gains or losses. That is, there are events in the future that may or may not occur, and different outcomes lead to different sets of benefits and decrements. The way to describe a risk is as a set of distinct potential future courses of events that together describe the classes of possible outcomes of interest. Each course of events can be characterized as a triplet, the elements of which are (1) an outcome, (2) the likelihood (i.e., the probability according to current judgment) that the outcome will occur, and (3) the consequences that follow if the outcome does indeed occur, expressed as the degree of gain or loss that will be suffered as a result.22
At least some risks can be reduced by taking appropriate actions to avoid or protect against potential adverse events. It may be possible to alter any of the three triplet elements; that is, (1) to block the threat (so that its appearance is no longer a possible course of events), (2) to alter the probabilities that different outcomes will occur (favoring outcomes with less expected loss), or (3) to mitigate the consequences of bad outcomes should they actually occur (so that losses will be less than they otherwise would be).
In many circumstances, however, it is not possible to avoid adverse possibilities completely. One is faced with an uncertainty about future losses because one does not know ahead of time what among the alternative courses of events will actually occur. Faced with an array of possible futures (each a triplet of event, likelihood, and consequences), one has an expectation of future loss that is the statistical expected value of this distribution of possibilities. The expected value is the average loss over all the possible events, each consequence weighted by its probability of actually occurring. Of course, only one set of events will actually happen, so the actual realized loss (or gain) after the fact will usually be less or more (perhaps enormously less or more) than the expected value before the fact, depending on whether the actual outcome was one with a big or a small consequence.
In a threat environment where chemical warfare agents (CWAs) might plausibly be used in an attack, a commander must decide whether to implement certain protective measures for the troops. One such decision, for example, might be to have troops don protective clothing.23 This decision must be made before the attack occurs. This is a classical problem of decision making under uncertainty. One must decide on an action (suiting up or not) before one finds out which course of events transpires (there is a CWA attack or there is not), and there are consequences to guessing wrongly. In making a risk management decision, the commander faced with an uncertain threat considers the possible futures, assesses their relative likelihood and the losses that will accrue under each eventuality, and makes a decision that is in some way optimal for the protection of forces and accomplishment of the mission.
If the commander decides to order the troops to don their protective gear (and if the protection afforded by the gear against the CWA is perfect), the losses consist of the reduced fighting efficiency of the unit and the decay of their physical well-being for future actions that wearing protective gear entails. This could be characterized as a moderate loss but one that is certain to follow from the decision to don protective gear. The impact on the troops exists whether or not there is a chemical attack. If the commander orders the troops to remain unprotected, however, the loss is zero if there is no CWA attack (since the troops are unencumbered by the suits), but the loss is very great if the attack does occur (consisting of the casualties caused by the agent and the threat to the mission’s success).
The commander’s decision is thus one of balancing the certain but moderate loss of suiting up against the expected loss from not suiting up. The loss from not suiting up is uncertain because it is contingent on an event that may or may not occur (the CWA attack).
Risk Decision Diagrams
The decision can be diagrammed as shown in Figure 4. The decision (shown by a square node) must be made before the uncertain event (shown by the circular node). In the threat situation the probability that a CWA attack will occur is estimated to be Pr(CW), and hence the probability that there will be no CWA attack is 1–Pr(CW). If the decision is to don protective gear, there is the loss of “performance decrement of suits” that is suffered whether or not a CWA attack ensues, but if no gear is donned, the losses depend on the outcome—no losses (“0”) if it turns out there is no attack and “casualties and mission risk” if there is indeed an attack.
Clearly, the decision rests heavily on the perceived likelihood of a CWA attack, Pr(CW). If this likelihood is judged to be very small, a commander may decide not to don protective gear, risking the small chance of a big loss (if one guesses wrong) to avoid the certain chance of a moderate loss from suiting up. On the other hand, if a CWA attack is likely, there is a large chance of a large loss by not donning the gear, and it is almost certainly worth the performance decrement to avoid jeopardizing the troops and mission. This “decision analysis” formalizes the intuitive conclusion that, owing to the asymmetry of the consequences of guessing wrong about whether a CWA attack is coming, donning protective gear makes sense even when an attack is fairly unlikely, as long as it is credible, but that it does not make sense when the likelihood of an attack is remote. The question is one of how likely need the attack be and how different must the losses be under different scenarios.
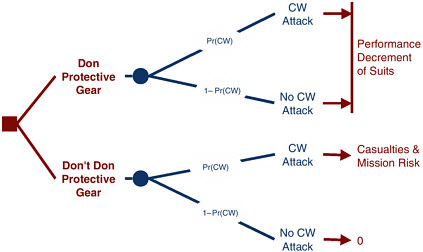
FIGURE 4 Command basic decision in the event of an alarm
In a business setting, when the same decision is made repeatedly and the gains and losses (in easily measured dollars) are accumulated over many similar episodes (e.g., underwriting insurance policies, speculating on stocks), the best decision is to take the choice that has the highest statistical expected value of gain (or the lowest expected value of loss). In the long run, this leads to the most success. In a military setting, however, it may be hard to express the different kinds of gains and losses in comparable units. Depending on the situation, the commander may wish to act in a way that is “risk averse” (i.e., accepting moderately increased losses in order to achieve a more certain albeit less favorable outcome) or in a way that is “risk taking” (accepting more chance of a significant loss in order to make possible a big gain if one guesses correctly). Nonetheless, the same sort of decision analysis framework applies.
Decision making under uncertainty can be improved if one can add information about the uncertain future event. For instance, a standoff detector can provide the commander with information about whether or not exposure of the troops to a CWA is imminent. If CWA exposure is imminent, a decision to don protective gear is clearly favored to avoid a highly likely large loss. If no CWA is detected (and if the commander can count on a useful warning of any attack), then going without protective gear is optimal. The essence of “perfect information” in a decision-analytic context is that it allows the decision maker to know which outcome of an uncertain process is going to occur before he or she has to make the decision. (This reverses the order with no such information, where the decision must be made before the outcome is learned.) Perfect information does not entirely obviate losses—if there is a CWA attack, the performance decrement to the suited-up troops from their gear cannot be avoided—but one can assure that the losses are the smallest possible for the outcome that actually happens.
The decision with perfect information is diagrammed in Figure 5. The standoff alarm either goes off or it does not. Since it provides perfect information, if it goes off, there is an imminent exposure to CWA coming, and so the decision to don protective gear is clearly favored. If there is no alarm, there is no imminent exposure, and the decision to go without protective gear is best.
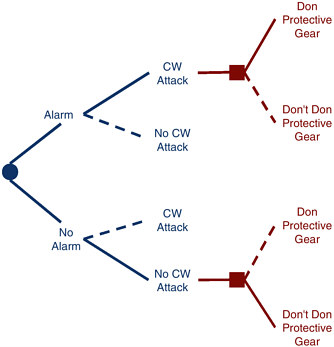
FIGURE 5 Decision tree with perfect information.
In practice, however, information is never perfect. First, it usually costs something to get. For standoff detectors this includes the costs of developing and testing the equipment, procuring the detectors, and transporting them, and devoting personnel to their maintenance and operation in the field. It also includes the “opportunity costs” of the other equipment that a unit must forgo in order to have the detectors, given limits on what can be transported and supported in the field. Whether these costs are worthwhile depends in part on the likelihood that the detectors will ever have anything to detect. Second, information is never perfect because it is rarely entirely predictive of future events. Typically, the information only reduces uncertainty about future events, but some uncertainty remains.
False Positives and False Negatives
For standoff detectors a detector in a threat environment will not always provide sufficient warning for every attack. There is some probability, for example, that a CWA shell will burst too close to the troops’ position to provide time to don protective gear. There is also the possibility that the detector fails to detect the presence of CWA at concentrations that are nonetheless sufficient to inflict casualties. These are false negatives in that the detector’s information that no CWA exposure is imminent proves to be wrong. Any decisions to remain unsuited made on the presumption that the detector’s information is perfect will be in error if a false negative occurs.
A standoff detector may also have false positives, in which the detector warns of a CW attack that is not in fact occurring. This may be because of the “tuning” of the detector, but it could also occur if unanticipated environmental signals not investigated during testing cause alarms or if deliberate “spoofing” of the detector is carried out by the adversary, say by releasing chemicals that mimic CWAs, causing troops to suffer the performance decrement of operating in protective gear. Again, a decision made on the presumption that the detector is perfect will be in error, although the losses will be less than for false negatives. The losses will include the performance decrement attributable to protective gear and the gradual loss of confidence in the detector if false positives prove common (i.e., the “crying wolf” effect).
Weighing the Costs
When faced with a decision in the face of uncertainty, and when provided imperfect information, the decision maker still needs to trade off the costs of the various possibly wrong guesses. The information reduces but does not eliminate the possibility of guessing wrong. In the context of standoff detectors, a commander in a CWA threat situation must still decide whether to order troops to don protective gear. If the detector says there is no CWA present, the commander must decide whether this is a true negative or a false one.
In decision analysis this is approached as a problem in Bayesian probabilities.24 There is a prior probability that the threat situation will entail a CW attack—this may be low for some settings and high for others, but it is the same assessment of the likelihood of attack that a commander would have to rely on if there were no detector. This probability is modified by the (imperfect) information of the detector, which either raises an alarm or does not. If the perceived probability of an attack is low and the detector fails to go off, the confidence that there is no CWA present is increased, and decisions to act accordingly are more likely to be correct than if the detector were not available. On the other hand, if the likelihood of an attack is perceived to be very low and the detector does go off, the likelihood that there is no real CWA attack drops precipitously, but it does not go to zero. There is still the possibility that this is a false positive alarm. If the plausibility of an attack is very low and the detector is known to produce false positives with some frequency, it may still be possible for the commander to decide that there is no attack and that the troops should not don protective gear. Similarly, if the perception that one is under CWA attack is very high and the detector does not go off, a commander might conclude that the failure to raise an alarm is a false negative and order the troops to suit up nonetheless.
Making the Decision
Risk analysts have an established methodology known as value-of-information analysis to analyze this kind of decision problem. The elements that enter this analysis are the description of risk in terms of the uncertain events, their alternative possible outcomes, the likelihood and loss consequences of each outcome, and the false positive and false negative rates of the source of information. Understanding the risk consequences of an imperfect detector (or one for which the degree of reliability is uncertain) is not simply a matter of looking at the consequences of a false positive or false negative alarm. The optimal decision is not simply to follow the detector’s advice blindly, suiting up or not depending on whether it
has raised an alarm or not. Instead, the optimal decision is the one that correctly balances the low likelihood of major losses from failing to don protective gear during an actual CWA attack against the highly likely but moderate losses from suiting up when no attack in fact occurs. How to make the decision to don protective gear depends not just on the detector’s behavior but also on the prior likelihood of an attack, the detector’s perceived false positive and negative rates, and the stakes for protection of the troops and the success of their mission.
The decision tree applicable to a value-of-information analysis is shown in Figure 6. In essence, the gear-donning decision diagrammed in Figure 4 can occur in two settings: (1) an alarm sounds or (2) no alarm sounds. What is different is that the probabilities that there will or will not be a CWA attack are changed—instead of the prior probabilities (based solely on the assessment of the threat situation) these are now the posterior probabilities of that assessment updated by the (imperfect) information provided by the detector. That is, if the alarm sounds, the likelihood that an attack is coming is Pr(CW|Alarm), the probability of an attack given that the alarm has sounded, and if the alarm does not sound, the likelihood that an attack comes nonetheless is Pr(CW|No Alarm).
Calculating these posterior or conditional probabilities can be done using Bayes’s rule.25 The calculation depends on the prior probabilities of attack as well as the false positive and false negative rates of the detector. For instance, if the false negative rate is designated a (and is equal to the probability of no alarm given that there truly is a CWA attack, i.e., Pr[No Alarm|CW]), and if the false positive rate is designated ß (i.e., Pr[Alarm|No CW]), and if the prior probability of attack Pr(CW) is called q, then
Pr(CW|Alarm) = q(1–a)/[q(1–a)+(1–q)ß], and
Pr(CW|No Alarm) = (1–q)ß/[q(1–a)+(1–q)ß].
Because of the added information provided by the detector, the commander’s basis for guessing whether there will be a CWA attack is improved—without the detector this guess must be based on the assessment of the threat situation (expressed as Pr[CW]), but with the detector this likelihood either goes up considerably if there is an alarm (since Pr [CW|Alarm] is much bigger than Pr[CW]) or goes down considerably if there is no alarm (since Pr[CW|No Alarm] is smaller than Pr[CW]). As a result, the expected losses are reduced because it is much more likely that the commander can guess right about whether to order the use of protective gear. If there is an alarm, the decision to suit up has less chance of leading to the unproductive and unnecessary decrement of troops’ effectiveness due to the cumbersome suits in the absence of a CWA to protect against; if there is no alarm, the decision not to suit up has less chance of leading to casualties and mission risk.
The difference between the commander’s expected value of the loss in Figure 6 (with the detector) compared to Figure 4 (without the detector) is a measure of how much the commander can expect to gain by having the standoff detector. In the terminology of value-of-information analysis, it is the “expected value of testing information.” (If it can be monetized, it gives the amount that the decision maker should be willing to pay to obtain the information.) That is, it is a measure of the degree to which use of the detector would be expected to lead to better outcomes (lower expected losses).
Whether the detector has a large or a small value of information depends on its false positive and false negative rates as well as on the probability that it will have something to detect; that is, the likelihood of a CWA attack in the threat situation of interest.
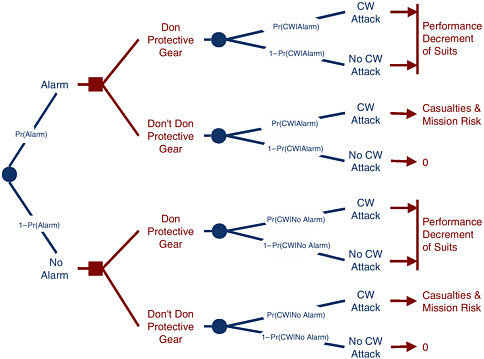
FIGURE 6 Decision tree in a value-of-information analysis.
Working through these questions was beyond the scope of the committee’s charge, but we would urge that such an analysis be undertaken in the process of developing a risk management analysis of the use of any standoff detectors in the field and in the development of doctrine and training for detector-equipped units. It is an important part of understanding the risk management consequences of a standoff detector’s reliability, and hence the risks of field testing the detector with live CWA or relying only on stimulant testing. Such a value-of-information analysis is the appropriate approach to answering the committee’s Task 4—to assess the risks associated with operationally employing standoff CWA detectors that have been tested at different levels (see Appendix A—Statement of Work). The risk consequences of the detector’s performance will be realized in its use in the field, and those consequences will depend on how a commander makes decisions based on the detector’s outputs.
The Value of Information
It is clear from the above discussion that the key element about detector design and testing is the characterization of false positive and false negative rates. These rates are the quantitative characterization of the reliability of a detector, and alternative testing protocols will differ in the degree to which the uncertainty about a detector’s field performance can be reduced. The way to approach Task 4 is to
evaluate the differences in value of information provided by the detector, which in turn depends on the false positive and false negative rates that emerge from the testing. Indeed, the purpose of the testing protocol should be to characterize the false positive and false negative rates of the detector because they would affect battlefield decisions. This point bears some elaboration.
First, one must distinguish between the points of view of detector developers and field commanders. For the developers, false positive and false negative rates have to do with measuring the ability of a detector to meet technical specifications about detecting concentrations of a fixed set of CWAs in a defined set of testing conditions. From the point of view of a field commander, however, false positive and false negative refer to the correspondence of the detector’s status to the actual threats to the troops. If an adversary uses a novel CWA that the detector was not designed to see or if a shell lands amid a concentration of troops and exposes them all just as the detector goes off (i.e., with no prior warning), these are “false negatives”—failure of the detector to provide sufficient warning—from the point of view of the field commander’s decision analysis regarding use of protective gear.
Second, a testing program cannot test every possible environment and setting. If the wider variety of settings in the field lead to more frequent failures to perform accurately, this is a case where the actual operational false positive and false negative rates may be higher than those measured during testing. A good testing program will try to minimize this problem by testing over a wide variety of environments.
Third, the risk consequences of false negatives and false positives depend on the field commander’s decisions and how they are influenced by the detector, and those decisions will be based on the per ceived false positive and false negative rates, which may differ from the actual rates. Less than optimal decisions arise both when the decision maker overrates the detector’s reliability and when he or she underrates it.
Fourth, there is typically a design trade-off between false positive and false negative reports. Although one strives to minimize both, in practice there is a limit to the degree that this can be accomplished. Since failing to warn of an actual CWA attack is a much more serious error than falsely warning of an attack, the detector should be “tuned” so as to minimize false negatives even at the expense of increasing the false positive rate. The optimal ratio of false negatives to false positives depends on the relative consequences of the two types of errors or, more precisely, the relative consequences of the erroneous decisions that are made in view of the detector errors (and as noted above, the rate of decision errors depends on more than just the detector’s performance). The projected risk management consequences of the detector’s field performance thus become an important part of the design process, influencing the optimal tuning between false positives and false negatives.
Comments on False Positive Rates
It is important to appreciate that, when true positives are rare, even for a very small false positive rate, most of the positives are false ones. In the present context, if actual CWA attacks are rare (as they have been historically), then most detector alarms in the field will be false positive. Specifications for detector design that call for a certain small proportion of alarms to be false are not useful, since the proportion of false alarms is mostly controlled by the frequency of true CWA attacks, something that is beyond the control of detector designers. In any case, a favorable proportion of true positives is only achievable by increasing the rate of true CWA attacks, which is not a good policy goal. The only other way to make a small fraction of alarms be false alarms is to design the detector to have an extraordinarily small false positive rate, but this must be achieved at the cost of increasing the false negative rate. Since the consequences of a false negative are much greater than those of a false positive, this is a bad policy as well. To illustrate, if the true frequency of CWA attacks on units with detectors is 0.1% (i.e., 1 in
TABLE 1 Calculations of Alarm Incidents Under Two Different Scenarios
|
True Frequency |
True Incidents |
False Positive Rate |
False Negative Rate |
No. of Alarms |
True Positive Alarms |
False Positive Alarms |
False Negatives |
True Positive |
|
1/1,000 |
100 |
1% |
1% |
1,099 |
99 |
1,000 |
1 |
9.0% |
|
1/1,000 |
100 |
0.1% |
10% |
190 |
90 |
100 |
10 |
47% |
|
True frequency = frequency of CWA release in threat situations True incidents = number of threat situations times true frequency False positive rate = percentage of analysis resulting in alarm False negative rate = percentage of actual incidents not detected No. of Alarms = number if signals given by the instrument that a CWA is present True positive alarms = number of true incidents alarmed by instrument False positive alarms = number of alarms that do not coincide with incidents False negatives = number of incidents that did not trigger alarm |
||||||||
1,000 threat situations lead to an actual attack) and the false positive and false negative rates are both 1%, then 1.1% of threat situations will have a positive alarm, and only 9.0% of these alarms will be true positives, while 90.9% will be false positives. If in response to this result the detector were retuned to achieve a 10-fold lower false positive rate (0.1%) at the cost of a proportional rise in the false negative rate (to 10%), the fraction of alarms that are false will be only 53%, but 10% of actual CWA attacks will not set off the alarm. Table 1 gives an illustration of how these changes in the false positive/false negative rate would give different decision criteria for the commander in the field. For illustrative purposes assume that there are 100,000 threat situations.
The above discussion concerns the risks stemming from the performance of the detector, and it emphasizes the role of testing in determining false positive and false negative rates. One can also speak of the risks associated with different modes of testing the detector. Here the risks arise from poorly estimating the false positive and false negative rates for CWA detection.
Value of Field Testing with CWAs
The testing protocol can also be looked at as a value-of-information question. We considered above the value of the information provided by the detector to the field commander, who has to make a choice in the face of imperfect information about the presence of CWAs. Now we can consider the value of information provided by field testing the detector with live agent and not just simulants. We have the choice to make whether to deploy the detector after simulant testing and chamber studies or to pay the higher cost, as outlined in the body of the report, if field testing with live agent is also carried out. The uncertain future event is how well the detector will perform in battlefield use. In particular, the uncertainty is how well the testing program has established the actual false positive and false negative rates. The value-of-information question is how much the additional field testing with live agent improves our confidence in the false positive and false negative rate characterization of the testing program.
A decision tree diagram could be made in which each branch represents an alternative testing protocol (e.g., with and without final open-air, live-agent testing). From each such branch tip would extend a sub-tree corresponding to the whole tree of Figure 6; that is, each subtree showing the decision-analytic problem that follows after a detector is deployed with a different set of testing procedures. The
subtrees will differ only in their false positive and false negative rates, but these differences will affect the calculation of the expected losses a commander would have if he or she had to depend on a detector with the given values of a and ß.
It should be noted that, once a detector is deployed, actual field experience would supplant the testing as the best basis for judging the detector’s value. Information on the false positive rate in the field will accrue more quickly since most settings do not have CWAs present. Given the rarity of actual CWA attacks, the false negative rate will be difficult to determine through experience, and no additional information on this rate (beyond that provided by testing) will accrue until actual attacks occur. The losses from a false negative (casualties owing to failure of the detector to warn of an actual attack in the field) may be high, but they will not be suffered repeatedly. If it ever becomes clear through experience that the detector has a substantial false negative rate, commanders will cease to rely on it. On the other hand, the losses from false positives (suiting up when it is unnecessary) will likely be suffered repeatedly since the fraction of alarms that are true is necessarily small (as shown above) and since the costs of failing to heed a true alarm are large.
Identifying the Risks
The risks associated with testing or not testing with live agent are triplets of something that could go wrong, the likelihood that it will go wrong, and the magnitude of the consequences. The value of information provided by live-agent testing is judged by the degree to which the probabilities of the bad outcomes are reduced by the additional testing, and the resulting decrease in the expected value of losses. Briefly, the risks are:
-
The detector will not work at all with real CWAs on the battlefield. This seems very unlikely if the testing program with simulants is well done, but if it were so it would have very large consequences since the detector would be falsely assumed to be showing the lack of CWAs when there may indeed be some. The actual risk depends on the likelihood that there is a CWA attack. If detectors that cannot actually detect the agent are deployed and their negative readings believed, this is only a problem if there is a true CWA attack. If there is no attack, there is no consequence. Thus, the ultimate risks of poor detector performance are all contingent on their ever being put to the test in a real battlefield situation, and the estimation of consequences of detector failure need to include the likelihood of a real challenge.
-
The detector has a higher actual false negative rate than the testing has led us to believe. This will cause commanders to place too much trust in the lack of alarms. This seems to be a fairly likely outcome—the challenge of detecting agents in the variety of field conditions that may be encountered may not be adequately probed by the testing.
-
The detector has a lower actual false negative rate than the testing has led us to believe. This seems unlikely. The consequences are likely to be good—better than expected detection and (if the alarms are believed even though they are thought to be less reliable than they indeed are) more likelihood of a decision that avoids CWA casualties. There may be more tendency to suit up in the absence of an alarm, however, since the lack of alarm is being given insufficient credence.
-
The detector has a higher false positive rate than the testing has led us to believe. This seems fairly likely. The immediate consequences would be that units often unnecessarily don protective gear and suffer the performance decrements that accompany this. In the longer run, as it becomes clear from experience that most of the alarms are false, there may be a tendency to undervalue and ignore the alarm information (the “crying wolf” effect), leading to vulnerability to a real attack.
-
The detector has a lower false positive rate than testing has led us to believe. As with a lower false
negative rate, this seems unlikely. It would lead to less than optimal readiness to don gear since the alarms would be given insufficient credence, and true attacks may find troops having ignored an alarm because it was perceived as likely to be a false alarm.
Beyond the question of the operational risks, one can examine the risks associated with the testing procedures themselves. These are adverse events that could happen during the testing. They can be broadly divided into risks not associated with detector performance and those that are associated with performance.
Risks of testing not associated with detector performance include the following:
-
Environmental risks. These include human and ecological health risks associated with releasing chemicals into the environment. The human health risks would probably be assessed as the consequence of accidents or unintended and unexpected turns of events during a chemical release. The analysis would have to include identifying the potential failures and their likelihood, as well as the transport of chemical away from safe areas and the likelihood of human exposures of various degrees. The ecological risks may also be a result of unintended turns of events, but there may also be some fairly certain impact in the test area itself. There will be environmental risks for testing live CWAs in the open air, but there will also be risks from the additional testing of simulants that would be necessary if live-agent testing were not carried out. Although the simulants are markedly less toxic, they are not all entirely benign, and their potential environmental toxicity should not be overlooked.
-
Political and public relations risks. These are risks of unfavorable public or political reaction to the testing program, with consequences to the image of the program and possibly to its funding and mode of operation. Again, there are risks associated with both live-agent testing and lack of such testing. Some constituencies will be more concerned about releases of live CWAs during tests, while others may be more concerned about the military preparedness consequences of failing to do live-agent tests.
-
Psychological and risk management risks. If live CWA testing is not conducted, there may be lack of confidence in the detector’s reliability among users, and this will affect the decisions they make in the field when detectors are deployed. Live-agent testing would probably increase confidence in the detectors on the part of troops. It may even result in overconfidence in the detectors, if the false positive and (especially) false negative rates are overly optimistic. The operational risks of the detectors (and hence their military effectiveness) will depend on the perceived reliability and the soundness of decisions made in view of the detector’s performance. Suboptimal decisions are made if users are either overconfident or underconfident in the detector’s abilities, and live-agent testing will affect this degree of confidence.
There are also risks associated with the technical performance of the detector. If live-agent testing is not conducted, these include the specific possibilities for failure of the logic by which simulant-only testing is presumed to provide sufficient understanding of the detector’s performance. For instance, if actual CWAs have chemical interactions with ambient substances when released into the air, if this property is not suspected, and if simulants lack this property, the validity of the simulant testing may fail—a failure that would only be uncovered when detectors do not perform as expected in the field, with consequent impact on troops. It is worthwhile to attempt to list the factors that could compromise the validity of simulant testing, but that would be revealed by live-agent testing and to estimate the likelihood that each problem might actually arise together with the consequences of failing to appreciate it. This list should include not just likely problems but also problems deemed unlikely yet possible. Some such factors include:
-
unexpected chemical interactions of CWAs with ambient substances,
-
unexpected properties of CWAs when released from exploding shells,
-
interferents whose spectral properties match those of a CWA in the spectral region being monitored, and
-
the role of aerosols in detectability of agents and differences in vapor pressure of simulants and live agents.
It is also worthwhile to consider risks that arise when live-agent, open-air testing is done, but the validity of such testing for the needed purposes is compromised. The point of a live test would be to test both the validity of the simulation and the performance of the instrument. This is why a few tests cannot make a statistically significant contribution. An alarm from a clear and unambiguous live agent release (a “successful test,” in that the detector “worked”) is not very informative about the actual performance to be anticipated in real use. Such a test can only uncover gross flaws in the detector—if it fails an easy test it is bound to fail in harder situations. Here the problem is with overinterpretation or overgeneralization of the testing to conclude that the properties of the detector are well characterized when in fact they are not. If the detector is not challenged during testing with sufficiently difficult detection tasks, or if conditions that would apply in the field (and that make the detector tend to fail) are not appreciated and therefore not tested during the live-agent tests, false confidence is engendered from the program of live-agent testing.
The comparability of the simulants and the live agent in the testing situation is likely to be contingent on the setting, background, climate, delivery mode, and so on. If correspondence of the detector’s performance with simulants and with live agents is to be considered telling about the detector’s abilities, then the correspondence ought to be tested over a range of settings.
SUMMARY
In sum, the purpose of testing is to establish the false positive and false negative rates of the detector in a way that applies to the performance of the apparatus in actual deployed situations. The value of the detector depends on these false positive and false negative rates, and the soundness of decisions based on the detector’s readings depends on accurate appraisal of the false positive and false negative rates. The risks associated with testing per se are the possibilities of unrecognized or uncharacterized factors that could compromise the validity of the measurement of false positive and false negative rates. The test protocols rigorously followed are intended to provide good estimates of the false positive/false negative rates for CWA detection in the field based on the protocol-specific signal-processing models.












