3
Education, Fertility, and Heritability: Explaining a Paradox
Hans-Peter Kohler and Joseph L. Rodgers
Wilson (1998:8) promoted the importance of “consilience” in science. Consilience is the “‘jumping together’ of knowledge by the linking of facts and fact-based theories across disciplines to create a common groundwork of explanation.” Such a process—in which disciplinary boundaries break down and then disappear (and then, perhaps, are reconstituted)—is occurring in research on human fertility. Our particular interest is in the interplay between demography and biology, as these two very different disciplines begin to blend in the long-standing effort to develop models and theories to explain human fertility. In fact, in this chapter our focus will be even sharper: We treat the interplay between genetics and fertility.
The signals that such a consilience between geneticists and demographers has been developing can be seen in the work of Adams et al. (1990) and Wood (1994). Udry (1995, 1996) added important impetus. There are two directions in which this disciplinary boundary can be crossed. The early work cited above represented (mostly) research in which demographers crossed the boundary from demography into biology and back again. Udry’s (1995) article, “Sociology and biology: What biology do sociologists need to know?,” is illustrative. A number of more recent publications show that the boundary is also being crossed in the other direction, as those trained in molecular and behavioral genetics present research using genetic methods but applied to topics in the traditional purview of demographers (e.g., Kohler et al., 1999; MacMurray et al., 2000; Miller et al., 1999, 2000; Rodgers et al., 2001a). Two recent papers in the journal Demography apply behavioral genetics
methods to human fertility (Rodgers et al., 2001b) and race differences in birth weight (van den Oord and Rowe, 2000).
The controversy that can occur when disciplinary boundaries are crossed in the consilience process is illustrated by the responses to the van den Oord and Rowe paper in a later issue of Demography (Frank, 2001; Zuberi, 2001).1 Similarly, a paper by Morgan and King (2001) that reviews the biological predispositions, social coercion, and individual incentives for having children in contemporary below-replacement fertility contexts resulted in diverging opinions about the usefulness of biodemographic or behavioral genetics approaches in understanding contemporary fertility behavior (Kohler, 2001; Capron and Vetta, 2001).
The idea that the disciplinary boundary can be crossed in either direction suggests two very different questions: What does genetics have to contribute to demographic research on fertility? What can demography contribute to a geneticist’s thinking about fertility? These questions cannot easily or naturally be addressed together because the specificity of the models and theories in the two disciplines are at such completely different levels. Further, Wilson (1998:198) implied that an asymmetry exists in how the goals of consilience will be received by the two disciplines. In comparing medical science to social science, he stated, “The crucial difference between the two domains is consilience: The medical sciences have it and the social sciences do not.” If he is correct, we can infer that genetics, as emergent from medical science, would be more naturally disposed to such an integrative and cross-disciplinary effort than demography, a social science.
We take the position that consilience is a positive development, that cross-disciplinary research has the potential to generate methods and models that are far beyond the sum of the separate contributions. Those more strongly wedded to a focal disciplinary perspective will undoubtedly be uncomfortable with our specific and also with broader efforts toward consilience. In this paper we are concerned primarily with the issue of how designs and methods that emerge from genetics research (more specifically from behavioral genetics) can contribute to demographic thinking about fertility. In particular, in this specific study we apply behavioral genetics methods to study the relationship of education, fertility, and heritability of fertility.
Before embarking on these specific analyses, we briefly consider the second question: Can demographic methods inform genetics research? In a sense the answer to that question is embedded in population genetics, and that interplay has been occurring for quite some time. Population geneticists are, fundamentally, demographers at heart. Accounting for the distri-
bution of genes in the population, and studying how gene frequencies change over time through adaptive processes, is similar to the study of various demographic phenomena. The ways that demographers deal with selection (their own type of selection, as opposed to the meaning of the term in genetic/evolutionary contexts) might be one example of a domain in which demography could inform genetics. That consideration, however, is for a different paper at a different time.
How can genetic thinking inform demographic research on fertility? We list several potential answers to this question:
-
Behaviors are always constrained by the limits of biological/genetic potential. Humans cannot run at 70 mph, though cheetahs can; each organism’s genotype helps define the “reaction norm” involved in performance. In the domain of fertility, humans are limited in the number of offspring they can produce in a given time period (e.g., limited by the menstrual cycle and the gestational period as well as social norms). Those constraints are defined by genetic influences on physiology (which, e.g., limit the human reproductive process to few children at a time) and by genetic influences on behavior (more on that later). Individuals always need to take these restrictions as given in their own decision making and behavior, and even on the population level these biological and genetic limits are fixed within time horizons that may not allow evolutionary adaptation.
-
Genes/biology limit not only the theoretical potential at the extremes but also the practical and achievable outcomes. Social behavior has genetic origins. In a distal sense, fertility motivation is influenced genetically (e.g., Miller et al., 2000). Social theories of fertility, which have long ignored the potential for genetic influence, may in fact be much closer to explaining the available variance than is commonly believed (see Rodgers, et al., 2001b). In other words, there may be less social variance available to be modeled than is widely appreciated.
-
Genetic influences interact with environmental influences in fascinating and subtle ways. For example, Neiss et al. (2002) showed that, while “education partially mediated the negative association between IQ and age of first birth” in a purely social model, this mediating effect virtually disappeared when genetic influences were entered into the model.
-
The assumed existence of preferences that guide behavior is a clear limitation in rational choice or the economic theories often invoked to explain fertility behavior and its change over time. Besides a set of regularity and consistency conditions, however, remarkably little can be said about the preferences for children themselves. Morgan and King (2001), for instance, realized the opportunity that evolutionary theories and behavioral genetics provide for improving our understanding of human preferences for children, and their arguments are closely related to other work that has
-
tried to interpret the preferences for children and related behaviors, like sexual intercourse, pair bonding, and changing fertility rates in an evolutionary perspective (e.g., Carey and Lopreato, 1995; Foster, 2000; Kaplan et al., 1995; Kohler et al., 1999; Miller and Rodgers, 2001; Potts, 1997; Udry, 1996). Hence, starting from genetic dispositions on the desire to have sex and the “joy” of nurturing, evolutionary reasoning suggests that important aspects of human reproductive behavior are shaped by genetic dispositions (which clearly must be distinguished from genetically “hard-wired” behavior). With proper designs, behavioral genetics models can therefore help to understand human preferences for children and motivations for fertility-related demographic behaviors, such as union formation or parental investments in children, and precursors of fertility such as menarche and sexual initiation.
-
Multivariate behavioral genetics modeling has the potential to identify overlapping sources of variance in both genetic and environmental domains. Topics of potential interest to demographers include the following: Are the genetic sources of influence on human fertility of the same nature for early fertility, general fertility, and later fertility? Are genetic influences on fertility similar when considered across generations as those occurring within generations? How do the precursors to fertility—puberty, sexual initiation, marriage, fertility planning—overlap with one another? Further, how do these processes overlap genetically, and environmentally, and how do genetic/environmental processes interact with one another? Rodgers et al. (2001b) and Kirk et al. (2001) illustrate how multivariate analysis can inform our understanding of the overlap between different fertility-related behaviors.
Many of the above issues are of considerable relevance for researchers interested in contemporary patterns of fertility. In the next section we provide an outline of a conceptual framework that facilitates the integration of behavioral genetics modeling and thinking into more standard socioeconomic approaches to fertility and related behaviors. Subsequently, we provide a brief review of the methodology on which behavioral genetics is based. In our empirical analyses, we then apply behavioral genetics design and models to study a question of interest to demographers concerning the role of education in fertility.
INTERPRETING BEHAVIORAL GENETICS IN RESEARCH ON FERTILITY AND RELATED BEHAVIORS
Behavioral genetics is both a way of thinking about causal influence and a set of methods developed to support that thinking. As a way of thinking about causality, it is motivated by the idea that genetic and envi-
ronmental influences both compete and interact with one another to influence behavior. Gottlieb (2000) criticized the “central dogma” of molecular biology that causality flows in one direction from the genes that activate DNA through proteins that they produce and ultimately to behavior. Rather, he reviewed evidence in support of probabilistic epigenesis, in which the environment also has causal influences on genes and the activation of DNA. Behavioral genetics, however, does not have a particular focus on genetic determinism. As Plomin and Rende (1991:162) noted, “The power of behavioral genetics lies in its ability to consider nurture as well as nature—that is, environmental as well as genetic sources of individual differences in behavior.” In fact, one of the coauthors of this paper came into the behavioral genetics arena because it provided mechanisms to control for genetic variations in the study of environmental (i.e., social and cultural) influences (e.g., Rodgers, Rowe, and Li, 1994a). For example, Rodgers, Rowe, and May (1994b) showed the influence of taking trips to museums on the mathematical ability in children and the influence of owning books on reading ability in children; each of these influences was a social/environmental influence observed after controlling for genetic processes that make children naturally similar to and dissimilar from one another.
In the application to fertility and related behaviors such as marriage, these interactions of genetic disposition with environmental contexts and individual characteristics can be naturally explored. Traditionally, demographers and related social scientists have emphasized the demand for children as a key factor in explaining contemporary fertility changes. The explanations of a shifting demand for children often focus on changes in education, income, labor market opportunities, female wages, child care arrangements, and so forth, that have been associated with the socioeconomic transformations in developed countries in recent years. These shifts in socioeconomic conditions have also led to changes in many fertility-related behaviors, such as marriage/union formation and female labor force participation, which are also closely related to changing demands for children.
It should be noted that such socioeconomic considerations of fertility change are rarely inconsistent with biological theories. To the contrary, recent evolutionary approaches to demographic change frequently incorporate transformations in the context of fertility decisions through socioeconomic changes or technical innovations. In particular, socioeconomic changes and technological innovations lead to adjustments in the optimal fertility strategies because they alter incentives for allocating scarce resources, such as time and energy, to reproductive efforts, child quality versus quantity, somatic investments, and several other competing uses (e.g., see Hill and Kaplan, 1999; Kaplan et al., 2000; Lam, this volume).
While evolutionary and socioeconomic theories are therefore quite compatible in their general approaches toward explaining levels of fertility, the
challenge for incorporating biological dispositions with sociological theories is in the explanation of within-population variations in behavior. In particular, differential biological dispositions of individuals—resulting, for instance, from genetic variations or hormonal influences—can be important determinants of individual behavioral differences in addition to socioeconomic incentives or structural influences. In order to see these potential interactions, we sketch a simplistic, but for our purposes sufficient, framework for fertility decisions in contemporary developed societies (see also Lam, this volume). In particular, the number of children of an individual in these contexts is strongly influenced by the age at marriage/union-formation and the number of reproductive years spent in stable unions, the level of education of the individual and his/her spouse, the abilities for and extent of labor force participation, and similar factors (Becker, 1981; Marini, 1981; Morgan and Rindfuss, 1999; Willis, 1973).
While there is some divergent assessment between economically and sociologically oriented scholars about the extent to which individuals rationally account for the potentially complex interactions between the above behaviors in their life course planning about fertility, it is probably not controversial to assert that individuals conduct conscious life course planning, including plans for marriage and fertility. These life course plans take into account an individual’s (potentially incomplete) knowledge about his/ her educational opportunities and returns to education, attractiveness in the marriage market (both in terms of physical and socioeconomic characteristics), assessments about opportunities in the labor market, preferences for children, and several other “goods” and/or goals. In addition, these plans are subject to important random elements, for instance, with respect to finding a partner in the marriage market, receiving positive or negative income ”shocks” upon entering the labor market, or shocks in the conception and gestation processes leading to the birth of a child.
Individuals are likely to update their life course plans as they learn more about their own relevant characteristics and as they experience different random shocks that affect fertility-related aspects of their life courses. Variations in individuals’ life courses—including variations with respect to important fertility outcomes—therefore arise for two reasons: First, individuals’ desired life courses differ because of different socioeconomic opportunities or constraints and because individuals have different abilities, preferences, physical characteristics, and so forth, that they take into account in making life cycle decisions and plans. Second, the realized life courses of individuals differ from their initial plans, as well as among individuals, due to shocks in fertility and fertility-related behaviors/processes, such as an unexpectedly long waiting time to conception or the death of a spouse.
This complex embeddedness of fertility outcome into life course deci-
sions and processes points to a broad framework of genetically mediated influences. In particular, differential genetic dispositions can exert influences on fertility and related behaviors through at least three distinct pathways. On the one hand, biological dispositions affect fertility relatively directly through genetically mediated variations in physiological characteristics affecting fertility outcomes. Genetic influences on fecundity are an obvious example (e.g., see Christensen et al., 2003), but there are also other possibilities, including, for instance, the fact that physical characteristics might render a person especially attractive in the marriage market, which increases the probability of an early marriage because of an unexpected high frequency of attractive marriage offers in early adulthood.
On the other hand, and potentially more interesting in the context of this paper, biological dispositions affect fertility through deliberate fertility decisions and a broad range of fertility-related behaviors that are subject to substantial volitional control. Within this category of influences, we can further distinguish between two different pathways. First, some biological dispositions exert their effect on behavior through conscious decision making and life course planning. Second, biological dispositions may also operate subconsciously on decision processes if individuals are not aware of their background influences on aspects such as emotions, preferences, or cognitive abilities. Examples for the former are individuals’ knowledge about their fecundity (e.g., see Rosenzweig and Schultz, 1985) or knowledge about their returns to schooling and delaying fertility (see, for instance, Behrman et al., 1994, 1996). In addition, Halpern et al. (2000) found that “smart teens don’t have sex or kiss much either,” which is consistent with higher cognitive abilities and an awareness about the high costs of early pregnancies due to foregone opportunities. Further examples of subconscious influences are variations in evolved preferences for nurturing (Foster, 2000; Miller and Rodgers, 2001). Moreover, early sexual activity, which is a predictor of early fertility, has also been related to nonvolitional factors such as hormone levels and body fat (e.g., Halpern et al., 1997, 1999), both of which are subject to strong genetic variations.
In summary, the above interpretations view genetic dispositions as part of individuals’ endowments that affect their life course patterns, including those pertaining to fertility and related behaviors, through their effect on (1) conscious decision making and deliberate life cycle planning, (2) nonvolitional processes affecting life course outcomes, and (3) physical characteristics or cognitive abilities that partially determine opportunities in the labor market and marriage market. Instead of focusing on these specific pathways of how genetic dispositions affect fertility outcomes, most current behavioral genetics designs try to identify and estimate the net contribution of a broad range of genetically mediated biological factors on the variations in fertility behavior within a population or within cohorts.
The advantage of this approach is that it provides an estimate of the overall relevance of genetically mediated biological effects on variations in fertility behavior. This information about the overall relevance of genetically mediated variations is interesting in itself. Moreover, this information will guide future research with respect to the scope of investigating specific mechanisms and pathways of biological influences: If the net overall variation attributed to genetic factors is high, the search for specific pathways (or possibly even specific gene factors) is likely to be more promising compared to a situation in which the overall influence is found to be low. In addition, studies of overall genetic variations in fertility outcomes can suggest specific socioeconomic contexts of cohorts that seem to facilitate genetically-mediated variation in fertility behavior, and these genetic-socioeconomic interactions will provide considerable scope for integrating sociological and biological theories about reproductive behavior.
Although most behavioral genetics work, including that applied to fertility, still focuses on partitioning variances into genetic and environmental components, broader applications are emerging (see Rutter, this volume). On the one hand, more sophisticated modeling and theorizing are supported by an increased availability of data, including large-scale twin and family data that are rich in socioeconomic life course information pertaining to education, marriage/union or labor market history, and genetic relatedness. Such data can be used to estimate multivariate behavioral genetics models that disentangle the pathways of genetic influences, such as the processes affecting marriage/union formation, age at first birth, educational attainment, and so forth. For an example of such an application, see the study by Rodgers et al. (2003), which uses age at first pregnancy attempt as an indicator of (volitional) fertility motivation and lag to pregnancy as a measure of (nonvolitional) fecundity. The study implements a methodology that allows competition between these two domains—the psychological and the biological—in accounting for the genetic variance underlying fertility outcomes.
In addition to suggesting the joint investigation of genetic dispositions and life course processes/decisions, the framework outlined above implies that the relevance of genetic factors for variations in fertility outcomes within cohorts is likely to be strongly conditioned by the socioeconomic context of the cohorts. A possibly surprising—but robust—finding in some of our earlier analyses (Kohler et al., 1999, 2002b), for instance, is a systematic relationship between fertility transitions and patterns in both heritabilities and shared environmental variance in data on female Danish twins: Increased opportunities for education and labor market participation and the emergence of relaxed and flexible reproductive norms in recent decades seem to have strengthened the genetic component in fertility outcomes. Finding these varying influences is consistent with, even predicted by, our
understanding of how genetic factors affect fertility decisions that are embedded in broader-context life cycle decision making. For instance, changes in patterns of female labor force participation may heighten the extent to which genetically mediated influences on ability and hence wages affect fertility, or higher mobility may increase the size of the marriage market and therefore strengthen the implications of variation in endowments on the timing and probability of marriage. We have argued (Kohler et al., 1999) that reduced social constraints on fertility and related behaviors, increased opportunities, and more egalitarian societies have increased the relevance of genetically mediated variation in preferences for children on fertility outcomes.
Few of these pathways have been explored in detail, but future studies with twin (or kinship) data that contain extensive socioeconomic information and life course histories can potentially overcome this limitation. Future analyses therefore not only need to estimate sophisticated behavioral genetics models for fertility and related behaviors but also need to allow for interactions between the socioeconomic context, individual characteristics and life histories, and patterns of heritability. In the empirical part of this chapter we apply behavioral genetics designs and models to study one such interaction between genetic dispositions and socioeconomic environments, specifically education, and show how the effect of genetic dispositions on fertility differs between individuals with different education levels. Before we embark on these empirical analyses, we provide a more general introduction to behavioral genetics designs and methods.
BEHAVIORAL GENETICS DESIGNS AND METHODS
The methodology of behavioral genetics begins with research design and then moves to a set of analytic models that can be used to estimate the parameters of the biometrical model. The classic behavioral genetics design is the twin design in which the similarity between identical and fraternal twins is compared on some trait of interest (e.g., completed fertility). Other designs include the family design, the adoption design, and the identical-twins-raised-apart design. As in any research arena, each design has logical weaknesses that leave threats to the validity of conclusions based on those designs. Also, each design rests on a set of assumptions. For example, assumptions of the twin design include no influence of assortative mating and equal environments (e.g., Plomin, 1990).
A complete statement of the behavioral genetics design logic and the basic quantitative genetics model is beyond the scope of this chapter, although we can summarize some of the basic theory and original references. Much of the original design work was done by Fisher (1930). The original and most complete statement of the quantitative genetics model on which
behavioral genetics research comes from Falconer (1981). A cogent and comprehensive textbook that reviews the field is that by Plomin et al. (1990), and a more accessible review is contained in Plomin (1990). A common feature of the analytic models used in behavioral genetics work is that the analyses estimate parameters related to genetic variability (usually referred to as heritability, or h2), shared environmental variability (or c2), and nonshared environmental variability (or e2). These parameters represent, respectively, the fraction of variance in a trait or outcome that is due to genetic factors, shared environmental influences like common family backgrounds, and finally individual-specific environmental factors. This interpretation of behavioral genetics results in terms of c2, h2 and e2, however, is correct only in a particular model that specifies how the different factors interact to jointly influence the outcome, quite similar to the fact that the structural interpretation of regression parameters in socioeconomic studies of fertility depends critically on the correctness of the underlying behavioral model and the appropriateness of the estimation strategy. Common—but not necessarily required—assumptions of behavioral genetics models include the additivity of the elements in the model (e.g., additive genetic and environmental influences). In principle, both the design and analytic assumptions are often violated. Extensive study has been given to the nature and effect of violating these assumptions, and these effects are well documented (e.g., Plomin, 1990).
In addition, there have been substantial developments in methods and data innovations that increase the value of twin and family designs. On the one hand, studies of twins are increasingly based on large-scale twin data, sometimes representing the complete population of twins of a country and including longitudinal follow-up (Kyvik et al., 1996, 1995; Pedersen et al., 1991), with low measurement error on key biological and socioeconomic variables and potentially extensive information about nonshared environments in childhood and adulthood. On the other hand, the limitations of the textbook behavioral genetics model are increasingly being overcome, including also in the application of behavioral genetics models to demography. For instance, Kohler and Rodgers (1999) have developed models for binary and ordered models, which are especially suited to the dependent variables such as “having at least one child” or “number of children,” and Yashin and Iachine (1997) describe behavioral genetics models suitable for the analysis of mortality or other duration data such as the timing of children. Major advances in disentangling gene-environment interactions are possible with large twin datasets that encompass cohorts that experience substantially different socioeconomic and demographic contexts. For instance, using local regression techniques and cohort interactions, we have shown that genetic influences on fertility have been subject to variations over time (Kohler et al., 1999, 2002b). These local regression techniques
therefore account for major gene-environment interactions that occur across cohorts. An alternative possibility is to test gene-environment interactions by incorporating additional socioeconomic conditions and information about the parental household and spouses of the twins. Moreover, these twin models sometimes allow for explicit tests of alternative genetic models, such as dominance effects. An additional development of particular value to demographers is the identification of kinship structure in large national datasets like the National Longitudinal Survey of Youth (NLSY). Using information from the survey, Rodgers et al. (1994) developed an algorithm that specified kinship structure in the children of the NLSY youth data and in another study Rodgers et al. (1999) reported a similar linking algorithm that specified kinship links for the NLSY youth respondents. These links open up the potential to do behavioral genetics analyses on national probability samples (a common criticism of the twins study is its low external validity) using the rich longitudinal and multivariate structure of such data sources.
Behavioral genetics methods have long been criticized by those outside the field (e.g., Lewontin et al., 1984, have defined a popular set of criticisms of the basic behavioral genetics design, including in particular the confounded nature of the genotype of monozygotic twins genotype and similar treatment by their families and peers).2 Interestingly, the behavioral genetic community itself is filled with internal critics who have carefully scrutinized and criticized these methods, and (arguably) the strongest and most cogent criticisms arise from behavioral geneticists themselves. For example,
Turkheimer (1998:782) suggested that “heritability and psychobiological association cannot be the basis for establishing whether behavior is genetic or biological, because to do so leads only to the banal tautology that all behavior is ultimately based in the genotype and brain.” Lest one interpret this as dismissive of past behavioral genetics research, Turkheimer (2000) published his “three laws of behavior genetics”: (1) All human behavior is heritable; (2) shared environmental influences are typically smaller than genetic influences on behavior; and (3) a great deal of behavioral variability is not based in either genetics or families. In addition, a recent review by Rose (1995:648-649) identified several emerging ideas and enduring issues in behavioral genetics, including a new design based on dividing pairs of MZ twins into those who shared a placenta in utero versus those who did not, and treatment of the question of whether (and how) family environment is relevant to development. Rose concluded: “Few areas of psychology are changing as rapidly as behavior genetics. Few are as filled with excitement and promise. Few are as surrounded by controversy.” Wahlsten (1999:599), in his review, described the blending of behavioral genetics and neurogenetics into the field of “neorobehavioral genetics, focusing on single-gene effects,” the type of consilience described in the opening sentences of this chapter. Finally, Rutter and Silberg’s (2002:465) review of behavioral genetics focused on gene-environment correlations and interactions. They emphasize that “the genes that influence sensitivity to the environment may be quite different from those that bring about main effects.”
In summary, therefore, while researchers need to be aware of the specific assumptions underlying behavioral genetics models (see Rutter, this volume), just as they must be aware of the assumptions underlying other domains of empirical work, recent methodological progress provides a powerful set of methods to investigate the relevance of genetic factors also in demography. The broad range of empirical and theoretical possibilities of how these methods can be used and integrated with demography is illustrated in two recent books on genetic influences on fertility and sexuality and the biodemography of fertility (Rodgers et al., 2000; Rodgers and Kohler, 2003).
EDUCATION, FERTILITY TRANSITION, AND FERTILITY OUTCOMES
Our goal in this section is to (begin to) explain a paradox. On the one hand, our previous analyses have shown that genetic factors contribute to variations in fertility outcomes, including the number of children, timing of the first child, and the age at first attempt to become pregnant (e.g., Rodgers et al., 2001a, 2001b). On the other hand, genetic influence related to natural selection changes very slowly; an exception is genetic influence related
to mutation that can change abruptly but also idiosyncratically and only in the individual (at least in the short term). But we have also shown that there can be rapid change in both heritabilities (h2) and coefficients of genetic variation (CVa) across very short periods of time (Kohler et al., 1999). The paradox is that a process, like genetic contributions to variations in fertility, which some would presume to be fixed and virtually immutable, can change rapidly in a short period of time.
Part of the answer to the paradox is that both heritabilities and coefficients of genetic variation are in no sense immutable. On the contrary, the understanding of genetic influences on fertility and related behavior outlined in the previous section suggests transformation in the pattern of how genetic shared environmental and individual-specific environmental factors contribute to variations in fertility outcomes in a population. Nevertheless, our previous research was not able to identify specific socioeconomic changes or characteristics that are the driving forces behind these transformations, and our earlier analyses relied on indirect explanation on the basis of overall socioeconomic and demographic changes across cohorts.
In this study we can overcome this limitation and investigate one particular aspect that is central to socioeconomic and demographic change over time and that is also likely to be an important factor behind the transformation of heritability patterns across cohorts: education.
In the Danish data used by Kohler et al. (1999), the very short periods of time during which heritabilities changed from essentially 0 to .40 and back again corresponded to a demographically important interval: the fertility transition resulting in lower fertility due to the adoption of conscious fertility limitation within marriage. Further, similar to many other European countries, Denmark experienced a second demographic transition staring in the late 1960 and early 1970s (Lesthaeghe and van de Kaa, 1986; van de Kaa, 1987) that was associated with further declines in fertility rates, a rise in cohabiting unions, and ideational changes toward more individualistic values and norms. Despite the somewhat different determinants of fertility change in the first and second demographic transitions the phenomenon of changing heritabilities is replicated, almost exactly, in each fertility transition.
It is worth considering the conceptual role of education in fertility transition in general. Virtually all accounts of fertility transition include education as either the cause or effect (or even both). For example, Cleland (2001:51) noted, “life expectancy and the level of adult education, or literacy, are the strongest predictors of fertility decline.” Declining fertility clearly provides opportunity for both women and men to spend the time they previously spent in childbearing and child rearing in other activities. Thus, fertility transition frees up time to support increased educational attainment, especially for women. At the same time, improvements in health care and reductions in mortality (especially maternal and infant mortality)
are driven in part by increased technical sophistication—that is, by the education level supporting technological development—inherent in society.
Thus, educational improvements can themselves drive fertility transitions. This causal direction is the one to which Bongaarts and Watkins (1996:639) refer: “As a society develops (modernizes), economic and social changes such as industrialization, urbanization, and increased education first lead to a decline in mortality, and subsequently also to a decline in fertility.” Our treatment does not require formal separation of these complex causal interrelationships; in fact, we view both causal directions to be critical features of any complete explanatory system of fertility transition. The variance partitioning methodology that underlies behavioral genetics methods is consistent with the sense derived from the literature on fertility transition that education is embedded in the transitional processes, as both cause and effect.
In this treatment we therefore investigate the relationship between education, heritability, and fertility, with special attention to our earlier finding that heritabilities can change rapidly during periods of rapid fertility change. Education is of particular importance in this context because, as noted above, many accounts and explanations of fertility change refer in some way or another to education. We describe next specific examples of how education can influence family size and vice versa.
Education is considered by some to be the prime cause of fertility transition, acting as the proximal stimulus that improves health care, drives down infant and maternal mortality, contributes to reversals of wealth, increases the ability to “produce” high-quality children in the household, and increases women’s opportunities in the labor market. The influence of education continues to be prominent also in posttransitional contexts with low fertility because it is an important determinant of female wages, which determine the opportunity costs of childbearing and shift the relative bargaining of males and females in households with potentially important effects on fertility decisions.
In addition, pursuing education, particularly higher education, is associated with specific social environments that can affect fertility preferences and desires if social interactions affect fertility decisions through social learning or social influence (e.g., Montgomery and Casterline, 1996; Kohler et al., 2002c). Evidence for this important role of education, among many other supportive findings, is the often-cited negative correlation between family size and various indicators related to maternal education (e.g., Higgins et al., 1962; Retherford and Sewell, 1988; Roberts, 1938). Rodgers et al. (2000) additionally asked the question, “Do large families make low-IQ children, or do low-IQ parents make large families?” Based on an analysis of recent national data from the United States, they concluded that the answers are “no” and “yes,” respectively.
Both the reasoning and the empirical data reviewed above point to the critical role that maternal education plays in models of fertility transition and posttransitional fertility behavior, and, more specifically, in the role that genetic processes play as influences of fertility during fertility transition. To investigate this role of education from a behavioral genetics perspective, we pursue two different set of analyses. First, we estimate multivariate behavioral genetics models to decompose the variance in fertility into genetic and shared environmental components and to assess the extent to which there are overlapping sources of genetic and shared environmental influences that affect both education and fertility. Second, we extend the results from Kohler et al. (1999) to further consider maternal education as a mediator of the process of how heritabilities change over cohorts and across socioeconomic contexts. In particular, we investigate whether patterns of heritability change across educational categories within cohorts in a similar fashion as across cohorts in our earlier study (Kohler et al., 1999).
DATA
The data for our analyses were obtained from Danish twins born between 1953 and 1970 who participated in the 1994 twin omnibus survey (see Christensen et al., 1998). Included in this survey was information about the level of completed education. The survey data were augmented by a register link (described in more detail below) to include the timing and level of fertility. The analyses are based on same-sex twin pairs with verified zygosity; the sample and cohort sizes are given in Table 3-1. Table 3-2
TABLE 3-1 Number of Twins by Birth Cohort
|
|
Complete Twin Pairs |
Complete Twin Pairs (with nonmissing data for fertility and education) |
||
|
Cohort |
Female |
Male |
Female |
Male |
|
1953-1954 |
342 |
418 |
302 |
388 |
|
1955-1956 |
400 |
506 |
364 |
488 |
|
1957-1958 |
546 |
474 |
508 |
452 |
|
1959-1960 |
570 |
594 |
524 |
562 |
|
1961-1962 |
648 |
496 |
600 |
442 |
|
1963-1964 |
748 |
496 |
678 |
456 |
|
1965-1966 |
742 |
586 |
680 |
532 |
|
1967-1968 |
712 |
492 |
630 |
422 |
|
1969-1970 |
542 |
460 |
504 |
404 |
|
Total |
5,250 |
4,522 |
4,790 |
4,146 |
TABLE 3-2 Completed Education for Females and Males by Birth Cohort
|
|
Cohort |
|||
|
Completed Education (% within cohorts) |
1953-1958 |
1959-1964 |
1965-1970 |
Total |
|
Females |
|
|||
|
No education beyond elementary school |
12.6 |
12.7 |
9.8 |
11.6 |
|
Semiskilled worker |
1.5 |
1.3 |
1.1 |
1.3 |
|
Standard basic training at apprentice school |
2.8 |
13.2 |
18.1 |
12.5 |
|
Less than 1 year of higher education |
3.3 |
2.8 |
1.9 |
2.6 |
|
1 to 3 years of higher education, possibly practical |
31.3 |
28.8 |
28.1 |
29.1 |
|
3 years of higher education (e.g., technician, pedagogue) |
24.2 |
18.4 |
10.4 |
16.8 |
|
More than 3 years of academic higher education |
15.4 |
12.4 |
7.7 |
11.4 |
|
Still in the process of training |
5.7 |
7.8 |
20.8 |
12.2 |
|
Males |
|
|||
|
No education beyond elementary school |
9.7 |
9.8 |
8.8 |
9.5 |
|
Semiskilled worker |
7.1 |
7.4 |
4.2 |
6.3 |
|
Standard basic training at apprentice school |
3.9 |
9.0 |
13.0 |
8.7 |
|
Less than 1 year of higher education |
1.7 |
2.3 |
0.6 |
1.6 |
|
1 to 3 years of higher education, possibly practical |
24.4 |
24.8 |
27.9 |
25.7 |
|
3 years of higher education (e.g., technician, pedagogue) |
20.8 |
18.4 |
13.0 |
17.4 |
|
More than 3 years of academic higher education |
21.9 |
19.0 |
9.3 |
16.8 |
|
Still in the process of training |
4.4 |
5.6 |
20.0 |
9.9 |
summarizes the completed education for males and females in the different cohorts in our study.
Education levels in Denmark are relatively high for all cohorts, with more than 60 percent of individuals pursuing some kind of tertiary education. The most important change in female education has been the decline of women with no education beyond elementary education and an increase in women with training at apprentice school. A surprising finding in Table 3-2, however, is the absence of an increase in higher education across cohorts, while in younger cohorts the proportion of individuals with more
than 3 years of education has diminished due to an increasing number of individuals still in the process of training.3
The most important aspect for our analysis has been the changes in the number with primary and secondary education, while changes in the level of higher education, or tertiary education, seem to have little potential to be related to heritability patterns. Table 3-3 therefore reports the mean and standard deviation of years in primary and secondary education, which are the most important education measures in our subsequent analyses (the questionnaire asked “How many years did you go to school? (Elementary school, high school, higher preparatory school)”).
In contrast to the proportion of each cohort obtaining various forms of tertiary education, there is a clear cohort trend for both males and females toward prolonged education. The number of years in primary and secondary education increased almost monotonically for females from about 10.5 years (cohort 1953-1954) to 11.9 years (cohort 1969-1970) and for males from about 10.1 years (cohort 1953-1954) to 11.2 years (cohort 1969-1970).
The 1994 twin omnibus survey also contains information about fertility of twins. In addition, we have obtained the fertility histories of participating twins from a link with the civil registration system (see Kohler et al., 2002a, for a description). This link has the advantage that it covers the period up to the end of 1998 (instead of up to 1994 as reported in the survey), and it also contains information about the timing of births and sex of the children. Moreover, these register data are free of potential recall errors.
Our analyses are thus based on the fertility information obtained from the register link that covers all births until the end of 1998. The average numbers of children born by birth cohort are given in Table 3-4. Female cohort fertility has been relatively constant across the cohorts born in the early 1960s (see also Knudsen, 1993) and then declines. This decline is partly due to the fact that women in these younger cohorts had not completed their childbearing by the end of 1998, which is the last year for which births to twins were obtained from the register. Male fertility follows a similar trend, with the primary difference that the decline of fertility
|
3 |
The youngest cohorts in Table 3-2 were only 24 years old at the time of the survey in 1994 and therefore had not completed tertiary education. In the 1965-1970 cohorts 20 percent of the male [and 20.8 percent of the female] respondents were still in training. Since this training primarily pertains to the highest education categories in the table, it can be expected that the 1965-1970 cohort attained the highest education levels in the table. Updated information about this completed education will be available soon from new survey data collected in 2002. |
TABLE 3-3 Years of Primary and Secondary Schooling
|
|
Females |
Males |
||
|
Cohort |
Mean |
Standard Deviation |
Mean |
Standard Deviation |
|
1953-1954 |
10.52 |
1.87 |
10.05 |
2.10 |
|
1955-1956 |
11.07 |
1.92 |
10.47 |
1.84 |
|
1957-1958 |
11.12 |
1.69 |
10.53 |
1.74 |
|
1959-1960 |
11.10 |
1.48 |
10.77 |
1.99 |
|
1961-1962 |
11.24 |
1.68 |
10.70 |
1.97 |
|
1963-1964 |
11.45 |
1.64 |
10.73 |
1.87 |
|
1965-1966 |
11.52 |
1.79 |
10.95 |
1.95 |
|
1967-1968 |
11.71 |
1.81 |
11.23 |
2.05 |
|
1969-1970 |
11.86 |
1.74 |
11.16 |
2.02 |
TABLE 3-4 Number of Children Born Until End of 1998
|
|
Females |
Males |
||
|
Cohort |
Mean |
Standard Deviation |
Mean |
Standard Deviation |
|
1955-1956 |
1.68 |
1.01 |
1.71 |
1.18 |
|
1957-1958 |
1.65 |
1.15 |
1.74 |
1.14 |
|
1959-1960 |
1.80 |
1.05 |
1.59 |
1.22 |
|
1961-1962 |
1.76 |
1.06 |
1.44 |
1.07 |
|
1963-1964 |
1.64 |
1.10 |
1.39 |
1.12 |
|
1965-1966 |
1.43 |
1.03 |
1.05 |
1.05 |
|
1967-1968 |
1.11 |
0.98 |
0.75 |
0.90 |
|
1969-1970 |
0.78 |
0.89 |
0.47 |
0.72 |
across cohorts began earlier—starting for cohorts born in the late 1950s— and is more pronounced. This difference is likely to be caused by the somewhat later age pattern of childbearing and the age difference between mothers and fathers.
A potential criticism of a study of the fertility of twins is that twins are not a random draw of all children. Twins are more likely to be born prematurely and to have lower birth weights than nontwins. In this survey DZ twins were born more frequently to older mothers for the birth years covered. A close congruence between the fertility patterns of twins and those of the general population is therefore an essential precondition in order to generalize the results of twin-based investigations into biosocial determinants of fertility to the general population. In Kohler et al. (2002a)
we estimated the fertility of the general Danish population at ages 34, 35, and 40 and combined different fertility indices (number of children, parity progression measures, age at first birth) with corresponding measures for the twins population (combined and separately by zygosity). The comparison was restricted to 14,600 twins in complete same-sex pairs born in 1945-1965, including the twins pairs from the present study. The comparison in Kohler et al. (2002c) found a very close correspondence between the fertility level and its change across cohorts in both the twins and the general population. There exist only a few statistically significant differences; the primary difference pertained to the fact that female twins seem to have a slightly later onset of childbearing, which may be due to sibling influences because twins always have at least one sibling (e.g., see Murphy and Knudsen, 2002). There are virtually no relevant differences between the fertility patterns of MZ and DZ twins.
MULTIVARIATE BEHAVIORAL GENETICS MODELS FOR EDUCATION AND FERTILITY
Our first set of analyses considers jointly the genetic and shared environmental variance components in completed education and fertility. We restrict these analyses to cohorts born prior to 1963—that is, the subset of cohorts at least 35 years old in 1998 when our fertility data were censored. For these cohorts we can therefore investigate completed or almost-completed fertility. We then analyze the number of children born to twins, together with a measure of completed education that was obtained by converting the education categories in Table 3-2 into years of tertiary education.4
The data include 539 female MZ, 844 female DZ, 524 male MZ, and 822 male DZ twin pairs with nonmissing information on education and fertility. The correlations for within-twin pairs obtained for our measure of completed education (years of tertiary schooling) are 0.37 for DZ males, 0.49 for MZ males, 0.34 for DZ females, and 0.50 for MZ females and for fertility 0.17 for DZ males, 0.30 for MZ males, 0.16 for DZ females, and 0.38 for MZ females. These within-variable patterns clearly suggest the presence of genetic components because the MZ twin correlations are nota-
bly higher than the DZ twin correlations. Also, for females the within-MZ twin-pair correlation for fertility is more than twice as large as the corresponding correlation for DZ twins. This pattern is suggestive of the possibility of nonlinear genetic influences such as dominance or epistasis. Detailed analysis of these effects, however, is beyond the scope of this chapter.
The starting point for most biometrical analyses using behavioral genetics designs is the ACE model, in which A refers to a latent genetic influence, C to a latent common (or shared) environmental influence, and E to a combination of measurement error and nonshared environmental influence. The relative importance of these influences is usually expressed in terms of heritability, h2, which is equal to the proportion of total phenotypic variance attributable to (additive) genetic variance, and the coefficient of shared environmental influences, c2, which is equal to the proportion of the total variance related to differences in shared-environmental conditions, such as parental background, and socialization. Estimates for heritability and shared environmental influence are conditional on a specific behavioral genetics model and are typically obtained by either structural equations modeling (SEM) or a regression method called DeFries-Fulker (or DF) analysis (DeFries and Fulker, 1985). SEM approaches use maximum likelihood as the fitting criterion and require both a structural model explaining the relationship between the constructs of the model and a measurement model explaining the relationship between the constructs and the variables used to measure the constructs. Mx (Neale et al., 1999) is a statistical software package that implements SEM methodology specifically to estimate behavioral genetics models.
Once the basic ACE model is fit to a particular dependent variable (often called the “phenotype” in the literature), additional adjustments can be made in the models to help understand the processes that generated the data. For example, fitting dominance models instead of additive models is possible (e.g., an ADE model). Dropping parts of the model with statistically meaningless parameter values results in fitting AE or CE models.
In the context of this chapter, the most interesting and valuable extension of the basic ACE model is the bivariate or multivariate model, in which overlapping sources of variance are evaluated. We estimate this model in Mx using the Cholesky decomposition model shown in Figure 3-1 for females and Figure 3-2 for males.5,6 Because completed education is
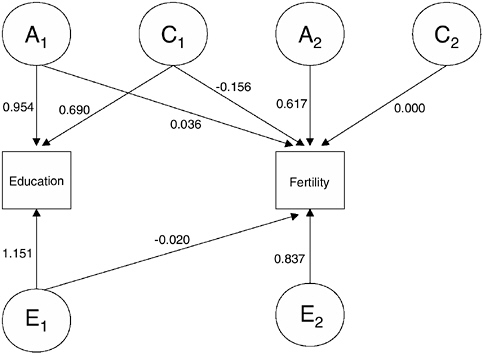
FIGURE 3-1 Bivariate behavioral genetics model for education and fertility, females.
entered first, this bivariate behavioral genetics model provides information regarding the degree to which the same set of genetic and environmental factors influence variations in education and fertility. In addition, the model provides estimates of residual amounts of genetic and environmental variance that affect fertility independent of variations associated with education.
For females the results of the bivariate behavioral genetics model shown in Figure 3-1 imply a heritability of our education measure (years of tertiary education) of h2 = 0.33 (95 percent CI: 0.17 to 0.48) and a coefficient of shared environmental influences of c2 = 0.18 (95 percent CI: 0.06 to 0.30). For fertility the coefficients of heritability and shared environmental influences are equal to h2 = 0.35 (95 percent CI: 0.23 to 0.42) and c2 = 0.02 (95 percent CI: 0.0 to 0.1). The model therefore suggests that about 33 percent of the variance in our education measure and 35 percent of the variance in fertility are related to genetic factors, while 18 percent and 2 percent, respectively, are related to shared environmental influences.7 The model
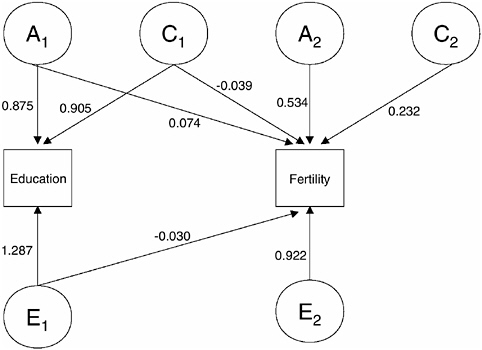
FIGURE 3-2 Bivariate behavioral genetics model for education and fertility, males.
also reveals that there are overlapping sources of genetic and shared environmental factors that affect both education and fertility. For genetic influences, however, this overlap is almost negligible, and only about 0.3 percent [= 0.0362 / (0.0362 + 0.6172)] of the genetic variance in fertility is shared with education. Genetic variance in fertility is therefore almost exclusively due to residual genetic influences that affect fertility but not education. The situation is strikingly different for shared environmental influences, where the results in Figure 3-1 reveal no residual shared environmental influences for fertility; all shared environmental influences on fertility result from factors that also affect education, and shared environmental influences that increase education tend to decrease fertility. The overall effect of the contribution of these shared environmental influences to variance in fertility remains low (c2 = 0.02 for fertility).
|
|
sum of all squared coefficients on the paths leading to education (or fertility). For instance, heritability of education in Figure 3-1 is obtained as 0.9452 / (0.9452 + 0.6902 + 1.152) = 0.332 and that of fertility is obtained as (0.0362 + 0.6172) / (0.0362 + 0.6172 + (–0.156)2 + 0 + (–0.020)2 + 0.8372) = 0.345. We note some violations of the additive genetics model among these path coefficients. |
The corresponding results for males are shown in Figure 3-2 and imply a heritability of our education measure (years of tertiary education) of h2 = 0.24 (95 percent CI: 0.07 to 0.40) and a coefficient of shared environmental influences of c2 = 0.25 (95 percent CI: 0.12 to 0.38). For male fertility the results imply a coefficient of heritability and shared environmental influences equal to h2 = 0.25 (95 percent CI: 0.04 to 0.36) and c2 = 0.05 (95 percent CI: 0.0 to 0.20). Similar to females, there is only a very small amount of overlapping genetic influence between education and fertility. In contrast to females, however, there is a substantial amount of residual shared environmental influence that affects fertility but not education, and only small amounts of shared environmental influences are common to both education and fertility.
In summary, the bivariate behavioral genetics model in Figures 3-1 and 3-2 confirms our earlier findings that fertility in low-fertility settings, such as contemporary Denmark, is subject to important genetic influences. A new and somewhat unexpected result of the above analyses is that genetic variance in fertility is not necessarily shared with genetic variance in completed education (measured in years of tertiary education). Instead, our results show that for both males and females most genetic variance in fertility is residual variance that affects the number of children but not educational attainment.8 Overlapping influences mainly exist for shared environmental factors in female analyses, where all shared environmental factors affecting fertility also affect education.
EDUCATION AND CHANGES IN HERITABILITIES ACROSS COHORTS
The scope for analyzing education and fertility from a behavioral genetics perspective is not restricted to the above bivariate models that decompose the variance in education and fertility into genetic and environmental factors. In addition, our analysis in this section addresses whether changes in education levels across cohorts have contributed to the changing pattern of heritabilities found in our earlier studies. In particular, the hypothesis for our analyses in this section is that the increase in heritabilities for female fertility observed in younger cohorts (Kohler et al., 1999, 2002b) is partly due to increased education for females. That is, we predict that females with higher education in the older cohorts were already subject to the higher heritabilities that became characteristic later for the overall fe-
male population, and females with lower education were subject to lower heritabilities during the early part of this transition. We also hypothetize that the time trend toward increased heritabilities in younger cohorts is reduced once an interaction between education and heritability is incorporated into the analyses.
To investigate these hypotheses about changing cohort patterns in heritabilities, we extend the data to include all twins born during 1953-1970 for whom we observed fertility until the end of 1998 (see description of the data above). We also choose a slightly different methodology and estimate the polychoric correlation in the latent “propensity” to have children for MZ and DZ twins using bivariate ordered probit models (see Kohler and Rodgers 1999).9 The advantages of these models are that (1) they are better suited to ordered outcomes, such as fertility, than standard behavioral genetics models and (2) the models can include various twin-pair-specific or individual-specific covariates known to influence the level of fertility. In our application, controlling for cohort trends in fertility is particularly important since there is a marked cohort trend in the average number of children born to respondents (see Table 3-4), due to the fact that younger cohorts had not completed their childbearing as of 1998. We include in the bivariate probit models 2-year cohort dummies that capture cohort trends in fertility and especially the decline in the level of fertility in younger cohorts. In addition, in some analyses we include education as another observed characteristic that affects the level of fertility of individuals. Finally, the
focus of our analyses on polychoric MZ and DZ twin-pair correlations, instead of heritabilities, is advantageous because these analyses do not assume a specific behavioral genetics model that is based on assumptions such as additive genetic influences or the absence of assortative mating. Within-pair correlations therefore provide a more direct assessment of changes in the similarity of fertility patterns of MZ and DZ twins across cohorts, and these correlations do not require assumptions about a specific genetic model that is required in order to translate these correlations into coefficients of h2 and c2.10 In other words, we report statistics more closely related to the raw data and less influenced by assumptions of the additive genetics model.
In contrast to our bivariate behavioral genetics model in the previous section, which focused on completed education and (almost) complete fertility, we characterize education in our subsequent analyses by the number of years of primary and secondary education. This different specification is motivated by two considerations. First, in young cohorts many respondents had not completed their education at the time of the twin omnibus survey in 1994, and there is substantial uncertainty about the level of completed education in young cohorts in our data. Second, primary and secondary education is usually completed prior to fertility, and years of primary and secondary education therefore provide an indicator of educational and professional opportunities in early adulthood that are an important determinant of life course decisions regarding fertility and related decisions. If these opportunities are an important factor affecting the relevance of genetic influences on fertility, as we argued in our earlier studies, our reasoning suggests that primary and secondary education should interact with the genetic etiology of fertility.
In our subsequent bivariate probit analyses of the within-MZ and within-DZ pair correlations in the propensity to have children, we include the above education measure (years of primary and secondary education) in a twofold manner: First, we include individual education as a determinant of the level of fertility. Second, we calculate the average number of years of schooling for each twin pair and estimate interactions between the level of education in a twin pair and the MZ/DZ twin-pair correlation in the propensity to have children. These latter interaction models will be of primary interest since the interaction terms with education reveal whether the pattern of heritability in fertility changes systematically with different levels of educational attainment.
Table 3-5 reports the results of the following analyses:
TABLE 3-5 Females—Bivariate Ordered Probit Estimation for Number of Children
|
|
Number of Children |
||||
|
Females |
Model 1 |
Model 2 |
Model 3 |
Model 4 |
Model 5 |
|
Variables influencing mean level |
|
||||
|
Cohort (reference category: cohort 1953-54) |
|
||||
|
1955-1956 |
–0.085 (0.092) |
–0.056 (0.091) |
–0.057 (0.090) |
–0.058 (0.091) |
–0.058 (0.090) |
|
1957-1958 |
–0.109 (0.086) |
–0.075 (0.086) |
–0.077 (0.084) |
–0.075 (0.085) |
–0.076 (0.084) |
|
1959-1960 |
0.050 (0.085) |
0.084 (0.085) |
0.082 (0.084) |
0.081 (0.085) |
0.080 (0.084) |
|
1961-1962 |
–0.002 (0.083) |
0.040 (0.083) |
0.038 (0.082) |
0.039 (0.083) |
0.038 (0.082) |
|
1963-1964 |
–0.104 (0.082) |
–0.051 (0.082) |
–0.053 (0.081) |
–0.051 (0.082) |
–0.052 (0.081) |
|
1965-1966 |
–0.327 (0.082)** |
–0.272 (0.082)** |
–0.273 (0.081)** |
–0.273 (0.082)** |
–0.274 (0.081)** |
|
1967-1968 |
–0.667 (0.084)** |
–0.601 (0.084)** |
–0.603 (0.083)** |
–0.599 (0.084)** |
–0.600 (0.083)** |
|
1969-1970 |
–1.041 (0.089)** |
–0.968 (0.089)** |
–0.968 (0.089)** |
–0.968 (0.089)** |
–0.968 (0.089)** |
|
Years of elementary and secondary education |
–0.063 |
–0.063 (0.010)** |
–0.064 (0.010)** |
–0.064 (0.010)** |
(0.010)** |
|
Constant |
1.019 (0.070)** |
1.694 (0.128)** |
1.695 (0.127)** |
1.700 (0.127)** |
1.699 (0.126)** |
-
Model 1: bivariate probit estimation with only birth-year dummies.
-
Model 2: bivariate probit estimation with birth-year dummies and education (years of elementary and secondary schooling).
-
Model 3: bivariate probit estimation with birth-year dummies, education, and interaction of correlation with birth year (centered around mean birth year).
-
Model 4: bivariate probit estimation with birth-year dummies, education, and interaction of correlation with twin-pair average years of schooling (centered around overall mean of schooling).
-
Model 5: bivariate probit estimation with birth-year dummies, education, and interaction of correlation with birth year and education.
Our first set of analyses in Model 1 reflects the trend in the level of fertility through the increasingly negative size of the cohort dummies that measure the decrease in the latent propensity to have children in the ordered probit models in younger cohorts as compared to the reference category. Moreover, the analyses also reveal a DZ correlation in the propensity to have children of about 0.164 and a MZ correlation of about 0.486. As we have already mentioned above, it is interesting that the MZ correlation is more than twice as large as the DZ correlation, which is suggestive of either genetic dominance (i.e., the presence of gene interactions at the same loci) or epistasis (i.e., genetic interactions across different loci). Focusing on the DZ and MZ twin correlations in our present analyses, instead of heritabilities and shared environmental influences, avoids the need to specify these interactions in more detail at this stage of the analysis.
In further analyses we additionally include education in order to investigate two questions of how human capital formation affects fertility behavior and how these education effects influence the cohort trends in heritability found in our earlier analyses (Kohler et al., 1999). First, in Model 2 we allow for the possibility that education (measured separately for each twin) affects the level of fertility. This is achieved by including years of primary and secondary education of each twin in a pair in the xijβ term of the bivariate probit model (see footnote 9), and the respective coefficient is reported under variables influencing the mean level in the tables representing our bivariate probit analyses. The results for Model 2 show first that, as expected, higher levels of education are associated with lower fertility levels, with a coefficient suggesting that one additional year of schooling decreases the latent propensity to have children by about 0.06. It is also worth noting these effects of education in Denmark are relatively modest due to institutional arrangements, such as day care provision, that facilitate very high female labor force participation (e.g., see Knudsen, 1993). In addition, the results for Model 2 show that the DZ and MZ correlations are slightly reduced after the direct effect of education on the level of fertility is controlled for, as expected,
because part of the similarity in twin pairs is due to correlated education outcomes; however, the effect is relatively modest.
In the third set of analyses (Model 3), we include an interaction of the DZ and MZ correlations with the birth year. Because the interaction is centered around the mean birth year, the coefficients for DZ and MZ twins reflect those correlations for twin pairs born around the mean birth year (1961.5), while the interaction term reveals the change in the DZ or MZ within-pair correlation from one birth cohort to the next (i.e., for a 1-year difference in birth year). The analyses reveal that there is no clear cohort trend in the DZ correlation, although there is a trend for the MZ correlation. This correlation tends to increase by about 0.013 per year from younger to older cohorts. Because the DZ correlation is approximately constant (or only very slightly increasing), this result is consistent with an increasing relevance of genetic factors for variation in fertility outcomes.
In the fourth set of analyses (Model 4), we allow for the possibility that education affects not only the level of fertility but also the relevance of genetic and shared environmental influences on fertility. In particular, we interact the within-twin-pair correlation in the propensity to have children with the average education level in a pair (measured as the mean years of primary and secondary education in a twin pair, centered around the overall mean education) (see footnote 9 for detailed specification). This specification therefore tests whether twin pairs with higher levels of education share higher within-pair correlations and also reveals whether this effect differs by zygosity. The coefficients of these interaction terms are reported under correlation within twin pairs in the tables that report our bivariate probit results.11 Because the interaction is centered around the mean education, the coefficients for DZ twins and MZ twins reflect the correlations for twin pairs with average education (11.04 years). The interaction term indicates the change in the MZ/
DZ within-twin-pair correlations for each additional year of education. Most importantly, the analyses show that one additional year of education increases the MZ correlation in the latent propensity to have children by about 0.05, while it has virtually no effect on the DZ correlation. In terms of a heritability model with shared environmental and genetic influences, this suggests that higher education tends to increase the proportion of variance attributed to genetic factors and to decrease the fraction attributed to shared environmental factors. In the final set of analyses (Model 5), we combine both interaction effects to see whether the interaction with birth year or with years of education dominates. Our analyses show that only the interaction of the MZ correlation with years of education remains statistically significant, with an only modestly reduced size at 0.044, while the effect of birth year is reduced and no longer significant.
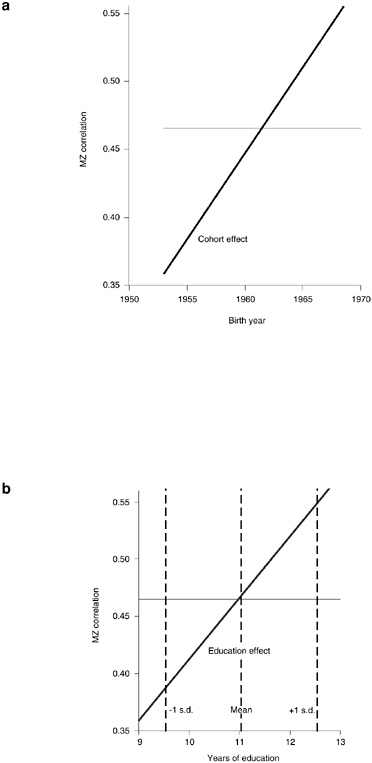
The results implied for monozygotic twins by Models 3, 4, and 5 in Table 3-5 are visualized in Figure 3-3. Figure 3-3a reports the results of Model 3, which includes only an interaction with birth year in the specification of the within-twin-pair correlation. The horizontal line gives the within-MZ-twin-pair correlation for the birth year 1961.5 (“mean birth year”) of 0.47, while the diagonal line gives the cohort trend resulting from the interaction with birth year: cohorts born in the mid-1950s have a within-MZ correlation of below 0.4, while cohorts born in the late 1960s exhibit a within-MZ correlation of above 0.55. The linear relationship in Figure 3-3a is, of course, a consequence of our model specification in Table 3-5, and this linear cohort trend should be interpreted as a first-order approximation to a potentially more complicated cohort pattern that levels off for the youngest and oldest cohorts included in our data. Nevertheless, the figure clearly reveals the changing MZ correlation across cohorts. Whereas the DZ correlation remains approximately constant, there is a marked increase in the within-MZ-twin-pair correlation as we progress from the oldest to the youngest cohorts. This pattern suggests that genetic influences gain in relevance for variations in completed fertility in young cohorts.
Figure 3-3b depicts the results of Model 2, which includes an interaction with education in the specification of the within-twin-pair correlation, and the figure visualizes our earlier discussion. Within-MZ correlations are below 0.4 for twin pairs with relatively low education, while the MZ correlation increases to above 0.5 for twin pairs with relatively high education (years of elementary and secondary schooling). The coefficients in Table 3-5 also reveal that this interaction of the MZ correlation with education is statistically significant. The vertical lines in Figure 3-3b also indicate the mean and mean plus or minus one standard deviation of our education measure. The corresponding values of the MZ correlation reveal that this education effect is sizable and quite relevant: the within-pair corre-
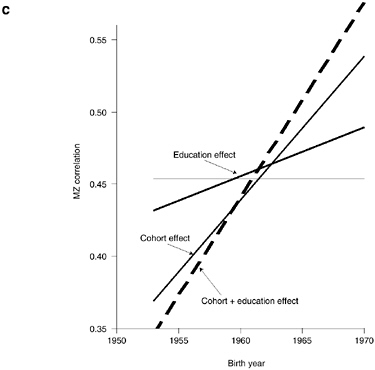
FIGURE 3-3 Cohort and education effects on within-MZ correlation.
lations of MZ twin pairs one standard deviation above and below the mean education differ by almost 0.15.
Figure 3-3c presents the results of Model 5, which includes interaction with birth year as well as education levels and shows the extent to which the within-MZ correlation across the 1953-1970 cohorts increases due to the interaction with birth cohort (holding education constant at 11.04 years) and the interaction with education (holding birth year constant at 1961.5). The former effect is shown by the dashed line. Once education is included in the specification of the MZ correlation, this cohort effect is weakened compared to Model 3 and looses its statistical significance. Nevertheless, the point estimate of the coefficient continues to suggest a relevant increase in heritabilities that occurs due to the interaction of the MZ twin-pair correlation with birth year. The broken line in Figure 3-3c, on the other hand, reveals the increase in the average MZ correlation across cohorts owing to the fact that the mean years of schooling increased from 10.5 to 11.9 years for the 1953-1970 cohorts. While statistically significant at the 5 percent level and quite sizable for a marginal increase in years of education, the change in MZ correlation due to this education effect is
modest for the overall cohort trend because mean education increased by only 1.4 years across the cohorts included in our data. The full line in Figure 3-3c represents the combined effect of the increase in the within-MZ-twin-pair correlation due to the joint effect of education and birth-year interactions. The increase in education across cohorts therefore explains a significant part of the increase in within-MZ correlations across the 1953-1970 cohorts. At the same time, the individual-specific effect of education, which changes the within-MZ correlation according to the average education in a pair, seems to be more relevant than the education effect operating through the increased educational attainment of cohorts. The strong education effect in Figure 3-3b is only slightly diminished in Model 5, which includes both interactions, compared to Model 4, which includes only the interaction with education.
The analyses in Table 3-5 and Figure 3-3 therefore suggest that education, as measured by years of primary and secondary schooling, is an important factor mediating the role of genetic variance in fertility outcomes. Within birth cohorts, patterns of heritability tend to vary with education in a manner that seems counterintuitive at first sight: A higher education level in a twin pair tends to imply a higher MZ correlation in the propensity to have children and does not seem to affect the DZ correlation. Within cohorts, higher education therefore is associated with higher heritabilities in fertility outcomes. In addition, the trend toward increased female education across cohorts seems to be an important factor that helps explain the increased relevance of genetic variance in fertility outcomes in younger cohorts found by Kohler et al. (1999).
In robustness tests for the above results, we investigated whether our findings about the interactions between education and patterns of within-twin-pair correlations are sensitive to our specific education measure. In additional analyses, not reported here in detail, we replaced years of schooling with a simple dummy variable indicating whether a respondent has 12 or more years of education. The education level of twin pairs can then be represented by a variable that equals 0 if both twins have less than 12 years of education, 0.5 if one twin has more than 12 years of education, and 1 if both twins have more than 12 years of education. If the analyses in Table 3-5 are replicated using this alternative education measure, the results remain unchanged: Twin pairs with higher education levels are subject to significantly higher MZ (but not DZ) correlations in the propensity to have children, and the increase in educational attainment across cohorts partially explains the cohort trend toward increased heritabilities for fertility in younger cohorts. In addition, it is worth noting that “years of primary and secondary education” (or the derived indicator variable “more than 12 years of schooling”) is the only measure of education that yields robust,
consistent, and significant interaction effects in the above analyses. Similar estimations with years of tertiary education did not yield systematic interactions (the signs are consistent with the above analyses, but the effects were not sufficiently strong to be significant). Hence, education measures that are determined relatively early in life seem to be the most important for these interactions with MZ and DZ correlations and subsequently also heritabilities.
In additional analyses we also investigated the patterns of DZ and MZ correlations for male twins (see Table 3-6). In earlier studies we found a significant relevance of genetic factors also for male fertility outcomes, but within these male patterns of heritabilites the social conditioning was substantially less relevant than for females. In the long-term cross-cohort comparisons, male heritabilities neither declined nor increased markedly and especially did not increase as strongly in the most recent cohorts as did the female heritabilities.
This pattern is confirmed in the present analyses. In Models 1 through 5 in Table 3-6 we report the bivariate probit estimates of the male DZ and MZ correlations that are analogous to the female models discussed above. Our first set of analyses (Model 1) reveal a DZ correlation of 0.21 and a MZ correlation of 0.32. The difference between MZ and DZ twins is substantially lower than in our analyses for females, and this implies somewhat lower estimates for heritabilities (consistent with our earlier findings). As expected, including education as a covariate that influences the level of fertility reduces these correlations (Model 2), but the effect is relatively small. Most importantly for the present context are again the interactions of the DZ and MZ correlations in the propensity to have children with birth year and education. Our analyses show that both interactions are relevant also for MZ males (Model 3 and 4), and the MZ correlations tend to increase the more recent the birth cohort is and the higher the education level is within a twin pair. These interactions are not statistically significant nor substantively relevant for the within-DZ-pair correlation. In the combined analyses that include both interactions (Model 5), the interaction of birth year with the MZ correlation is the only effect that remains relevant and (weakly) significant. The education effect is in the same direction as in our results for females, but the magnitude and the level of statistical significance are less than for females. In summary, these findings for males are consistent with our earlier findings in Kohler et al. (1999): There seem to be relevant genetic influences on fertility outcomes also for males, but the social conditioning of these heritability patterns is weaker. In particular, education does not seem to have the same strong effect on the MZ and DZ correlations for males as it does for females.
TABLE 3-6 Males—Bivariate Ordered Probit Estimation for Number of Children
|
|
Number of Children |
||||
|
Males |
Model 1 |
Model 2 |
Model 3 |
Model 4 |
Model 5 |
|
Variables influencing mean level |
|
||||
|
Cohort (reference category: cohort, 1953-1954) |
|
||||
|
1955-1956 |
0.013 (0.079) |
0.032 (0.079) |
0.034 (0.078) |
0.028 (0.079) |
0.030 (0.078) |
|
1957-1958 |
0.053 0.081) |
0.077 (0.081) |
0.077 (0.079) |
0.073 (0.081) |
0.073 (0.079) |
|
1959-1960 |
–0.083 (0.077) |
–0.049 (0.077) |
–0.050 (0.076) |
–0.054 (0.077) |
–0.055 (0.076) |
|
1961-1962 |
–0.228 (0.082)** |
–0.197 (0.082)* |
–0.198 (0.081)* |
–0.201 (0.082)* |
–0.201 (0.081)* |
|
1963-1964 |
–0.269 (0.081)** |
–0.236 (0.081)** |
–0.235 (0.080)** |
–0.244 (0.081)** |
–0.243 (0.080)** |
|
1965-1966 |
–0.626 (0.079)** |
–0.584 (0.080)** |
–0.584 (0.079)** |
–0.592 (0.080)** |
–0.592 (0.079)** |
|
1967-1968 |
–0.947 (0.085)** |
–0.892 (0.086)** |
–0.893 (0.086)** |
–0.897 (0.086)** |
–0.899 (0.086)** |
|
1969-1970 |
–1.327 (0.090)** |
–1.279 (0.090)** |
–1.276 (0.090)** |
–1.281 (0.090)** |
–1.280 (0.090)** |
DISCUSSION
Changes in the levels of and returns to education, especially female education, are central to many theories of demographic and related social changes. For instance, education features prominently in theories about fertility decline, changing female labor force participation, and household allocation modes. Here we investigate whether education, and changes in education, are also an important aspect in biodemographic approaches to fertility. The analyses presented in this chapter investigate these questions from a twofold perspective and provide a clear indication that education constitutes an important aspect related to the biodemography of fertility.
In our first analyses, we applied a multivariate behavioral genetics model to investigate genetic and shared environmental contributions to the variance and covariance in completed education and (almost) completed fertility. These analyses showed that both education and fertility are subject to genetic and shared environmental influences, but the overlapping sources of genetic influences are relatively small. Variation in fertility for both males and females is therefore primarily related to residual genetic variance that is independent of genetic influences on completed education.
Our second analyses focused on the question of whether changes in educational attainment across cohorts provide an explanation for the increased heritabilities in fertility observed in our earlier studies. In particular, our analyses estimated the correlations in the latent propensity to have children in MZ and DZ twins and included tests for interactions of those correlations with birth year and levels of education.
For females these analyses revealed that education and cohorts are two key factors that interact with MZ twin correlations, while DZ twin correlations are almost not affected by including these interactions. This implies that it is primarily the genetic factors consistent with variation in fertility outcomes that are affected by education and cohorts. In particular, our analyses suggested that genetic influences tend to become stronger in twin pairs with a higher level of education and that genetic influences tend to become stronger in more recent cohorts. However, this secular trend across cohorts was substantially reduced once the interaction with education was included, suggesting that increased levels of education constitute an important factor contributing to the increased heritabilities in younger cohorts found in our earlier studies. For males the interaction with education was present but seemed to be weaker in terms of both statistical significance and the magnitude of the effect. Again, this is consistent with our earlier findings that cohort trends in heritabilities are much weaker for males than for females.
An interesting aspect of the above analyses is the fact that years of primary and secondary education, not years of tertiary education, resulted in important interactions with the within-twin-pair correlations in the pro-
pensity to have children. This may be due to the fact that years of primary and secondary education are an important determinant of the overall “options” available to young adults in Denmark. Hence, in many ways the primary and secondary years of education are a key determinant of the “life course options” available to young adults, and this finding is consistent with our arguments in Kohler et al. (1999) and Rodgers et al. (2001b): Genetic variation in fertility outcome may become most relevant in societies and contexts where there is a large set of life course options that affect fertility and related demographic outcomes.
Udry (1996) developed this argument on purely theoretical grounds, anticipating these empirical findings. These options increase the set of potential pathways through which genetic influences affect fertility outcome, and increased opportunities—for instance in the labor market—are likely to heighten the implications of endowments for labor market outcomes and therefore indirectly also on fertility. The theoretical framework of fertility behavior that is embedded in a broad context of life cycle decisions and processes provides a basis for analyzing and understanding these changing contributions of genetic factors to variations in fertility outcomes, and future analyses that combine detailed socioeconomic information and multivariate behavioral genetics models can investigate these different pathways in greater detail.
Another interesting aspect of our analyses is that for females the standard additive genetic model does not seem to hold. In particular, the MZ correlations are more than twice as high as the DZ correlations, which indicates that more complicated gene interactions—for instance, due to dominance effects or epistasis—are present. There are several potential interpretations for those types of nonadditive patterns. Genetic interactions are implied by dominance (interaction within alleles) and epistasis (interaction across alleles). Or complex polygenic patterns can be caused by a particular configuration of genes (Lykken et al., 1992), a process called emergenesis. These effects are implied by sizable MZ twin correlations and very small—approximately zero—correlations for all other relatives (because only MZ twins will share a genetic configuration). The presence of such gene interactions is consistent with the evolutionary theory of life history traits, where Fisher’s (1930) fundamental theorem of natural selection suggests that additive variance tends to be diminished over time and is reintroduced again only through “perturbing forces,” such as mutations, changes in socioeconomic or normative contexts, or contraceptive (or proceptive) technologies (see Rodgers et al., 2001a).
In our analyses we avoided the specification of a specific genetic model by reporting within-pair correlations instead of heritabilities and shared environmental influences. Nevertheless, the presence of such gene interactions is an important question for future research, and we have argued in
related research (Christensen et al., 2003) that genetic factors contributing to fecundity, as measured by the waiting time to pregnancy, occur primarily through relatively complicated gene interactions across different loci.
The main conclusion of our analyses that the patterns of genetic variance, whether measured as heritabilities or by comparing MZ and DZ twin correlations, are strongly socially conditioned and that contemporary societies might lead to a strengthening instead of a weakening role of genetic favors for variation of fertility outcomes is supported by recent investigations of the intergenerational transmission of fertility. Studies in a number of countries and time periods (e.g., Anderton et al., 1987; Berent, 1953; Johnson and Stokes, 1976; Pullum and Wolf, 1991) have shown that there is usually a positive correlation between the number of children of parents and their offspring, while there is also the possibility of a negative relation due to cohort size effects (e.g., see Easterlin, 1980). Studies of intergenerational correlation without indicators of genetic relatedness can obviously not identify the contribution of genetic and social factors to this intergenerational transmission of fertility. Nevertheless, because (additive) genetic influences on fertility tend to cause a positive intergenerational correlation (though not necessarily if genetic factors operate through epistatis), findings that intergenerational correlations are also not weakened in posttransitional societies and more recent cohorts is supportive of our behavioral genetics analyses.
Murphy and Wang (2001), for instance, estimated the correlations between number of siblings and children for different contemporary developed countries, including Italy, Great Britain, Australia, Norway, and Germany, and found that the positive intergenerational relationship in fertility is not only substantial and present in all countries investigated but also that this relationship has been increasing in younger cohorts and persists even after controlling for socioeconomic characteristics. Similarly, in a study using Danish register data, Murphy and Knudsen (2002) did not find that the intergenerational fertility transmission weakened in younger cohorts, despite the fact that the socioeconomic and ideational changes experienced by these cohorts during the second demographic transmission would tend to attenuate parental influences and intergenerational transmission.
In summary, our empirical work falls into the category of research encouraged by Rutter and Silberg (2002) of gene-environment interplay. The specification of models in which behavioral genetics design/analysis is complemented by environmental measures is a natural way to formalize the goals of developing consilience between biodemographic and demographic approaches to studying fertility. Further, our empirical finding that the genetic variance implied by analysis of the twin design is strongly conditioned on educational level is an example of how the ultimate result of such efforts toward consilience can be greater than the sum of the parts.
ACKNOWLEDGMENTS
The authors contributed equally to this paper. Much appreciation is extended to Kaare Christiansen, Kirstin Kyvik, and others involved in collecting and managing the Danish Twin Registry in Odense, Denmark.
REFERENCES
Adams, J., A. Hermalin, D. Lam, and P. Smouse 1990 Convergent Issues in Genetics and Demography. New York: Oxford University Press.
Anderton, D.L., N.O. Tsuya, L.L. Bean, and G.P. Mineau 1987 Intergenerational transmission of relative fertility and life course patterns. Demography 24:467-480.
Becker, G.S. 1981 A Treatise on the Family. Cambridge, MA: Harvard University Press.
Behrman, J.R., M.R. Rosenzweig, and P. Taubman 1994 Endowments and the allocation of schooling in the family and in the marriage market: The twins experiment. Journal of Political Economy 102(6):1131-1173.
1996 College choice and wages: Estimates using data on female twins. Review of Economics and Statistics 73(4):672-685.
Berent, J. 1953 Relationship between family sizes of the successive generations. Milbank Memorial Fund Quarterly Bulletin 31:39-50.
Bongaarts, J., and S.C. Watkins 1996 Social interactions and contemporary fertility transition. Population and Development Review 22:639-682.
Capron, C., and A. Vetta 2001 Comments on “Why have children in the 21st century?” European Journal of Population 17(1):23-30.
Carey, A.D., and J. Lopreato 1995 The evolutionary demography of the fertility-mortality quasi-equilibrium. Population and Development Review 21(3):613-630.
Christensen, K., O. Basso, K.O. Kyvik, S. Juul, J. Boldsen, J.W. Vaupel, and J. Olsen 1998 Fecundability of female twins. Epidemiology 9(2):189-192.
Christensen, K., H.-P. Kohler, O. Basso, J. Olsen, J.W. Vaupel, and J.L. Rodgers 2003 The correlation of fecundability among twins: Evidence of a genetic effect on fertility? Epidemiology 14(1):60-64.
Cleland, J. 2001 Potatoes and pills: An overview of innovation-diffusion contributions to explanations of fertility decline. Pp. 39-65 in Diffusion Processes and Fertility Transition. Committee on Population, J. Casterline, ed. Division of Behaviorial and Social Sciences and Education. Washington, DC: National Academy Press.
DeFries, J.C., and D.W. Fulker 1985 Multiple regression analysis of twin data. Behavior Genetics 15(5):467-473.
Easterlin, R.A. 1980 Birth and Fortune: The Impact of Numbers on Personal Welfare. Chicago: University of Chicago Press.
Falconer, D. S. 1981 Introduction to Quantitative Genetics. New York: Longman.
Fisher, R.A. 1930 The Genetical Theory of Natural Selection. Oxford: Clarendon Press.
Foster, C. 2000 The limits to low fertility: A biosocial approach. Population and Development Review 26(2):209-234.
Frank, R. 2001 The misuse of biology in demographic research on racial/ethnic differences: A reply to van den Oord and Rowe. Demography 38:563-568.
Gottleib, G. 2000 Environmental and behavioral influences on gene activity. Current Directions in Psychological Science 9:93-97.
Halpern, C.T., J.R. Udry, and C. Suchindran 1997 Testosterone predicts initiation of coitus in adolescent females. Psychosomatic Medicine 59(2):161-171.
Halpern, C.T., J.R. Udry, B. Campbell, and C. Suchindran 1999 Effects of body fat on weight concerns, dating, and sexual activity: A longitudinal analysis of black and white adolescent girls. Developmental Psychology 35(3): 721-736.
Halpern, C.T., K. Joyner, J.R. Udry, and C. Suchindran 2000 Smart teens don’t have sex (or kiss much either). Journal of Adolescent Health 26(3):213-225.
Higgins, J.V., E. Reed, and S.C. Reed 1962 Intelligence and family size: A paradox resolved. Eugenics Quarterly 9:84-90.
Hill, K., and H. Kaplan 1999 Life history traits in humans: Theory and empirical studies. Annual Review of Anthropology 28:397-430.
Johnson, N.E., and C.S. Stokes 1976 Family size in successive generations: The effects of birth order, intergenerational change in lifestyle, and familial satisfaction. Demography 13(2):175-187.
Kaplan, H., K. Hill, J. Lancaster, and A.M. Hurtado 2000 A theory of human life history evolution: Diet, intelligence, and longevity. Evolutionary Anthropology 9(4):156-185.
Kaplan, H., J. Lancaster, and S. Johnson 1995 Does observed fertility maximize fitness among New Mexican men? Human Nature 6(4):325-360.
Kirk, K.M., S.P. Blomberg, D.L. Duffy, A.C. Heath, I.P.F. Owens, and N.G. Martin 2001 Natural selection and quantitative genetics of life history traits in Western women: A twin study. Evolution 55:423-435.
Knudsen, L.B. 1993 Fertility Trends in Denmark in the 1980s: A Register Based Socio-demographic Analysis of Fertility Trends. Copenhagen: Denmark Statistics.
Kohler, H.-P. 2001 Comments on Morgan and King (2001): Three reasons why demographers should pay attention to evolutionary theories and behavior genetics in the analysis of contemporary fertility. European Journal of Population 17(1):31-35.
Kohler, H.-P., L. Knudsen, A. Skytthe, and K. Christensen 2002a The fertility pattern of twins and the general population compared: Evidence from Danish cohorts 1945-64. Demographic Research 6(14):383-408.
Kohler, H.-P., J.L. Rodgers, and K. Christensen 2002b Between Nurture and Nature: The Shifting Determinants of Female Fertility in Danish Twin Cohorts 1870-1968. Unpublished document, Max Planck Institute for Demographic Research, Rostock, Germany.
Kohler, H.-P., F.C. Billari, and J.A. Ortega 2002c The Emergence of Lowest-Low Fertility in Europe During the 1990s. Population and Development Review 28(4).
Kohler, H.-P., J.L. Rodgers, and K. Christensen 1999 Is fertility behavior in our genes? Findings from a Danish twin study. Population and Development Review 25(2):253-288.
Kohler, H.-P., and J.L. Rodgers 1999 DF-like analyses of binary, ordered and censored variables using probit and tobit approaches. Behavior Genetics 29(4):221-232.
Kyvik, K.O., K. Christensen, A. Skytthe, B. Harvald, and N.V. Holm 1996 The Danish twin register. Danish Medical Bulletin 43(5):465-470.
Kyvik, K.O., A. Green, and H. Beck-Nielsen 1995 The new Danish twin register: Establishment and analysis of twinning rates. International Journal of Epidemiology 24:589-596.
Lewontin, R.C., S. Rose, and L.J. Kamin 1984 Not in Our Genes: Biology, Ideology, and Human Nature. New York: Pantheon.
Lesthaeghe, R., and D. van de Kaa 1986 Twee demografische transities? Pp. 9-24 in Bevolking: Groei en Krimp, R. Lesthaeghe and D. van de Kaa, eds. Deventer: Van Loghum Slaterus.
Loehlin, J.C., and R.C. Nichols 1976 Heredity, Environment, and Personality. Austin: University of Texas Press.
Lykken, D.T., M. McGue, A. Tellegen, and T.J. Bouchard 1992 Emergenesis: Genetic traits that may not run in families. American Psychologist 12:1565-1577.
MacMurray, J., B. Kovacs, M. McGue, J.P. Johnson, H. Blake, and D.E. Comings 2000 Associations between the endothelial nitric oxide synthase gene (NOS3), reproductive behaviors, and twinning. In Genetic Influences on Human Fertility and Sexuality. J.L. Rodgers, D.C. Rowe, and W.B. Miller, eds. Boston: Kluwer Academic Press.
Marini, M.M. 1981 Effects of the timing of marriage and first birth on fertility. Journal of Marriage and the Family 43(1):27-46.
Miller, W.B., D.J. Pasta, J. MacMurray, C. Chiu, H. Wu, and D.E. Comings 1999 Dopamine receptors are associated with age at first sexual intercourse. Journal of Biosocial Science 31:43-54.
Miller, W.B., D.J. Pasta, J. MacMurray, D. Muhleman, and D.E. Comings 2000 Genetic influences on childbearing motivation: Further testing a theoretical frame work. In Genetic Influences on Human Fertility and Sexuality. J.L. Rodgers, D.C. Rowe, and W.B. Miller, eds. Boston: Kluwer Academic Press.
Miller, W.B., and J.L. Rodgers 2001 The Ontogeny of Human Bonding Systems: Evolutionary Origins, Neural Bases, and Psychological Manifestations. Boston: Kluwer Academic Press.
Montgomery, M.R., and J.B. Casterline 1996 Social learning, social influence, and new models of fertility. Population and Development Review 22(Suppl.):151-175.
Morgan, S.P., and R.B. King 2001 Why have children in the 21st century? Biological predispositions, social coercion, rational choice. European Journal of Population 17(1):3-20.
Morgan, P.S., and R.R. Rindfuss 1999 Reexamining the link of early childbearing to marriage and to subsequent fertility. Demography 36(1):59-75.
Murphy, M., and L.B. Knudsen 2002 The relationship of full and half sibs, birth order and gender with fertility in contemporary Denmark. Population Studies.
Murphy, M., and D. Wang 2001 Continuities in childbearing in low fertility societies. European Journal of Population 17(1):75-96.
Neale, M.C., S.M., Boker, G. Xie, and H.H. Maes 1999 Mx: Statistical Modeling, 5th ed. Richmond, VA: Department of Psychiatry.
Neiss, M., D.C. Rowe, and J.L. Rodgers 2002 Does education mediate the relationship between IQ and age of first birth? A behavioral genetic analysis. Journal of Biosocial Science 34:259-275.
Pedersen, N.L., G.E. McClearn, R.Plomin, J.R. Nesselroade, S. Berg, and U. de Faire 1991 The Swedish adoption/twin study of aging. Acta Geneticae Medicae et Gemmellologiae 40:7-20.
Plomin, R. 1990 Nature and Nurture. Pacific Grove, CA: Brooks/Cole.
Plomin, R., J.C. DeFries, and G.E. McClearn 1990 Behavioral Genetics: A Primer. New York: Freeman.
Plomin, R., and R. Rende 1991 Human behavioral genetics. Pp. 161-190 in Annual Review of Psychology. M.R. Rosenzweig and L.W. Porter, eds. Palo Alto, CA: Annual Reviews Inc.
Potts, M. 1997 Sex and the birth rate: Human biology, demographic change and access to fertility-regulation methods. Population and Development Review 23(1):1-39.
Pullum, T.W., and D.A. Wolf 1991 Correlations between frequencies of kin. Demography 28:391-409.
Retherford, R.D., and W.H. Sewell 1988 Intelligence and family size reconsidered. Social Biology 35:1-40.
Roberts, J.A.F. 1938 Intelligence and family size. Eugenics Review 30:237-247.
Rodgers, J.L., H.H. Cleveland, E. van den Oord, and D.C. Rowe 2000 Resolving the debate over birth order, family size, and intelligence. American Psychologist 55:599-612.
Rodgers, J.L., K. Hughes, H.-P. Kohler, K. Christensen, D. Doughty, D.C. Rowe, and W.B. Miller 2001a Genetic influences help explain variation in human fertility outcomes: Evidence from recent behavioral and molecular genetic studies. Current Directions in Psychological Science 10:184-188.
Rodgers, J.L., and H.-P. Kohler, eds. 2003 The Biodemography of Human Reproduction and Fertility. Boston: Kluwer Academic Press.
Rodgers, J.L., H.-P. Kohler, and K. Christensen 2003 Genetic variance in human fertility: Biology, psychology, or both? Pp. 229-250 in The Biodemography of Human Reproduction and Fertility. J.L. Rodgers and H.-P. Kohler, eds. Boston: Kluwer Academic Press.
Rodgers, J.L., H.-P. Kohler, K. Kyvik, and K. Christensen 2001b Behavior genetic modeling of human fertility: Findings from a contemporary Danish twin study. Demography 38(1):29-42.
Rodgers, J.L., D.C. Rowe and M. Buster 1999 Nature, nurture, and first sexual intercourse: Fitting behavioral genetic models to NLSY kinship data. Journal of Biosocial Science 31:29-41.
Rodgers, J.L., D.C. Rowe, and C. Li 1994a Beyond nature versus nurture: DF analysis of nonshared influences on problem behaviors. Developmental Psychology 30:374-384.
Rodgers, J.L., D.C. Rowe, and K. May 1994b DF analysis of NLSY IQ/achievement data: Nonshared environmental influences. Intelligence 19:157-177.
Rodgers, J.L., D.C. Rowe, and W.B. Miller 2000 Genetic Influences on Human Fertility and Sexuality: Theoretical and Empirical Contributions from the Biological and Behavioral Sciences. Boston: Kluwer Academic Press.
Rose, R.J. 1995 Genes and human behavior. In Annual Review of Psychology. J. Spence, J. Darley, and D. Foss, eds. Palo Alto, CA: Annual Reviews.
Rosenzweig, M.R., and T.P. Schultz 1985 The demand for and supply of births: Fertility and its life cycle consequences. American Economic Review 75(5):992-1015.
Rutter, M., and J. Silberg 2002 Gene-environment interplay in relation to emotional and behavioral disturbance. In Annual Review of Psychology. S. Fiske, D. Schacter, and C. Zahn-Waxler, eds. Palo Alto, CA: Annual Review.
Scarr, J.C., and L. Carter-Salzman 1979 Twin method: Defense of a critical assumption. Behavior Genetics 9:527-542.
Turkheimer, E. 1998 Heritability and biological explanation. Psychological Review 105:782-791.
2000 Three laws of behavior genetics and what they mean. Current Directions in Psychological Science 9:160-164.
Udry, J.R. 1995 Sociology and biology: What biology do sociologists need to know? Social Forces 73:999-1010.
1996 Biosocial models of low-fertility societies. In Fertility in the United States: New Patterns, New Theories. J.B. Casterline, R.D. Lee, and K.A. Foote, eds. New York: The Population Council.
van de Kaa, D.J. 1987 Europe’s second demographic transition. Population Bulletin 42:1-57.
van den Oord, E.J., and D.C. Rowe 2000 Racial differences in birth health risk: A quantitative genetic approach. Demography 37:285-298.
Wahlsten, C. 1999 Single-gene influences on brain and behavior. In Annual Review of Psychology. J. Spence, J. Darley and D. Foss, eds. Palo Alto, CA: Annual Reviews.
Willis, R.J. 1973 A new approach to the economic theory of fertility behavior. Journal of Political Economy 81(2, pt. 2):14-64.
Wilson, E.O. 1998 Consilience: The Unity of Knowledge. New York: Vintage.
Wood, J. 1994 Dynamics of Human Reproduction: Biology, Biometry, Demography. Hawthorne, NY: Aldine.
Yashin, A.I., and I.A. Iachine 1997 How frailty models can be used for evaluating longevity limits: Taking advantage of an interdisciplinary approach. Demography 34(1):31-48.
Zuberi, T. 2001 One step back in understanding racial differences in birth weight. Demography 38:569-572.