Enforcement of Patent Rights in the United States1
Jean O. Lanjouw
Department of Agricultural and Natural Resource Economics
University of California, Berkeley and the Brookings Institution
Mark Schankerman
Department of Economics
London School of Economics and Political Science
ABSTRACT
We study the determinants of patent suits and their outcomes over the period 1978-1999 by linking detailed information from the U.S. Patent and Trademark Office, the federal court system, and industry sources. The probability of being involved in a suit is very heterogeneous, being much higher for valuable patents and for patents owned by individuals or by firms with small patent portfolios. Thus the patent system generates incentives, net of expected enforcement costs, which differ across inventors. Patentees with a large portfolio of patents to trade, or having other characteristics that encourage “cooperative” interaction with disputants, more successfully avoid court actions. At the same time, key post-suit outcomes do not depend on observed characteristics. This is good news: Advantages in settlement are exercised quickly, before
extensive legal proceedings consume both court and firm resources. But it is bad news in that the more frequent involvement of smaller patentees in court actions is not offset by a more rapid resolution of their suits. However, our estimates of the heterogeneity in litigation risk can facilitate development of private patent litigation insurance to mitigate this adverse affect of high enforcement costs.
INTRODUCTION
Although the central purpose of the patent system is to encourage R&D investment, there is increasing concern among scholars and the business community that “patent thickets” are beginning to impede the ability of firms to conduct R&D activity effectively (Eisenberg, 1999; Shapiro, 2001). The perception is that patenting strategies have increasingly made disputes over rights unavoidable and that, as a result, research firms are burdened by growing enforcement costs. The fact that patent litigation grew rapidly during the period 1978-1999 encourages this view. The number of patent suits rose by almost tenfold, with much of this increase occurring during the 1990s. We show here, however, that a focus on the level of litigation gives a misleading picture. The growth in patenting has been comparable to the growth in litigation, with the consequence that the rate of suit filings has been roughly constant over these two decades. Nonetheless, although our data indicate that the likelihood of litigation has not increased, survey evidence suggests that involvement in a patent suit has become substantially more costly over the past decade (American Intellectual Property Law Association, 2001). Thus the overall burden of enforcement may well be on the rise.
Perhaps of greater importance, we show that the exposure to litigation varies widely across technology fields and patent profiles. Although the average rate is relatively low, 19.0 suits per thousand patents, rates vary from a low of 11.8 per thousand chemical patents to 25-35 per thousand computer, biotechnology, and nondrug health patents. Moreover, within any given technology field, probabilities of litigation differ very substantially and are systematically related to patent characteristics associated with their economic value and to characteristics of their owners.
This variation in litigation risk across patents and their owners is a central issue for the enforcement of intellectual property rights and its economic consequences. Lerner (1995), for example, provides evidence that small firms avoid R&D areas where the threat of litigation from larger firms is high. Lanjouw and Lerner (2001) argue that the use of preliminary injunctions by large firms can discourage R&D by small firms, and this may apply to other legal mechanisms. Even if parties can settle their patent disputes without resorting to suits, the threat of litigation will influence settlement terms and thus, ultimately, the incentives to undertake R&D. Using a comprehensive new data set covering all recorded patent
litigation in the United States over the period 1978-1999, we determine the characteristics that affect the decision to begin a suit and the decision of whether to end with a settlement or to proceed to adjudication at trial.2
One of our key empirical findings is that the observed characteristics of both patents and their owners only affect the decision to file suits. The key post-suit outcomes—the probability of settlement and the plaintiff win rates at trial—are almost completely independent of these characteristics. This implies that advantages in resolving disputes come into play quickly, before a suit is filed. This helps to mitigate legal costs and reduce the private (and social) costs of enforcement. Two additional findings are encouraging: First, post-suit settlement rates are high (about 95 percent), and second, most settlement occurs soon after the suit is filed, often before the pretrial hearing is held.
Patentees have a number of mechanisms for settling disputes without resorting to litigation. They may “trade” intellectual property. Trading takes various forms, including cross-licensing agreements and patent exchanges, sometimes with balancing cash payments (Grindley and Teece, 1997). One motivation for accumulating patents may be to facilitate such trading (Hall and Ziedonis, 2001). From this perspective, extensive patenting may be beneficial by lowering costs once a dispute arises. Settlement may also be promoted if patentees interact with each other often and expect to continue doing so in the future. Theoretical models suggest that repeated interaction increases both the ability and the incentive to settle disputes “cooperatively”—that is, without filing suits (Tirole, 1994, Chapter 6). However, there is very little econometric evidence to support this prediction.3
The role of patent trading and the role of repeated interaction over time both imply that there may be economies of scale in resolving patent disputes. Greater research and patenting experience may speed settlement as parties become better able to anticipate the result should a dispute go to court. Experienced firms may also make higher-quality patent applications that give rise to fewer disputes in the first place (Graham et al., 2003). Three key findings in this chapter support the importance of scale. First, we find strong evidence of a patent portfolio effect: Having a larger portfolio of patents reduces the probability of filing a suit on any individual patent, conditional on its observed characteristics. The quantitative effect is large. For a (small) domestic unlisted company with a small portfolio of 100 patents, the average probability of litigating a given patent is 2 percent. For a similar company but with a moderate portfolio of 500 patents, the figure drops to only 0.5 percent. Second, we find that the (marginal) effect of patent portfolio size is stronger for smaller companies, as measured by employment. This is con-
sistent with the idea that having a portfolio of patents to “trade” is the key mechanism for avoiding litigation for small firms, whereas larger firms can also rely on repeated interaction in intellectual property and product markets to discipline behavior. Third, firms operating in technology areas that are more concentrated (in which patenting is dominated by fewer companies) are much less likely to be involved in patent infringement suits. Such firms are likely to have more interaction with one another. Together these results are consistent with the view that having either a portfolio of intellectual property to trade or other dimensions of interaction that promote “cooperative” behavior confers important advantages in avoiding litigation. We also find that asymmetry of firm size affects litigation risk. Patent owners who are large relative to the disputants they are likely to encounter less frequently resort to the courts to settle disputes.
The characteristics of a given patent also strongly affect litigation risk in ways that are consistent with existing hypotheses in the economics literature (as in Lanjouw and Schankerman, 2001). We illustrate this with two examples. First, more valuable patents, as measured by the number of claims and citations per claim, are much more likely to be involved in suits. Second, patents that are related to subsequent technological activity by the firm (cumulative innovation), as measured by the extent of self-citation in patents, are more likely to be litigated. This supports the idea that when there are interlinkages between inventions owners are more willing to protect each of them, especially the key (early) innovations (Scotchmer, 1991). We show here that differences in these, and other, patent characteristics lead to wide variations in the probability of litigation within any given technology field.
The chapter is organized as follows. The second section summarizes the analytical framework, including the litigation stages and outcomes that we study. The third section describes the construction of the data set and the main characteristics of the patents and their owners on which we focus and discusses how they relate to economic hypotheses about the causes of litigation. The fourth section presents and discusses evidence on the relationship between these characteristics and the filing of suits and their outcomes. The fifth section presents econometric analyses of the determinants of litigation for infringement suits and declaratory judgment suits and the determinants of post-suit settlement. Concluding remarks summarize directions for future research.
ANALYTICAL FRAMEWORK
For analytical purposes, we break down the litigation process into four stages:
-
suit filing,
-
the pretrial hearing,
-
commencement of the trial, and
-
adjudication at the conclusion of trial.
According to our discussions with patent lawyers, legal costs are more closely related to how many stages the case reaches than to the actual length of the case, which is strongly affected by the availability of court resources and other external factors.
There are three possible outcomes to a suit:
-
settlement,
-
win for the plaintiff, or
-
win for the defendant (the identity of the patentee depends on whether it is an infringement or invalidity suit).4
If a patent dispute is settled before a suit is filed, we do not observe the dispute in the data. Thus low filing rates can either reflect low rates of infringement (disputes) or high probability of pre-suit settlement. After a suit is filed, settlement can occur before the pretrial hearing, after the hearing but before the trial begins, or during the trial. Otherwise, the trial concludes with a court judgment in favor of one of the parties.5
Lanjouw and Schankerman (2001) analyzed the determinants of the probability of litigation (case filings). For this chapter, we have constructed a larger data set that allows us to study both case filings and post-suit outcomes. In particular, we analyze:
-
The probability of a suit being filed
-
The probability of settlement, conditional on a suit being filed
-
The timing of settlement, i.e., the conditional probability that the suit is resolved before the pretrial hearing or after
-
The plaintiff win rates, conditional on adjudication at trial
Information on win rates is relevant for assessing overall litigation risk (e.g., in pricing patent insurance). Such information is also useful in testing competing economic models of litigation because the models generate different predictions about plaintiff win rates at trial (Waldfogel, 1998; Siegelman and Waldfogel, 1999). There are two main models, divergent expectations (Priest and Klein, 1984) and asymmetric information (Bebchuk, 1984). In the divergent expectations model, each party estimates the quality of his or her case (equivalently, the rel-
evant legal standard) with error and cases go to trial when the plaintiff is sufficiently more optimistic than the defendant. This is most likely to occur when true case quality is near the court’s decision standard. This selection mechanism drives the plaintiff win rate at trial toward 50 percent.6 In the asymmetric information model, one party knows the probability that the plaintiff will win at trial, whereas the other party knows only the distribution of plaintiff win rates. The uninformed party makes a settlement offer (or a sequence of offers, in dynamic versions of the model; Spier, 1992), which will be accepted only by informed defendants who face a relatively low probability of winning at trial. Trials can arise in equilibrium because settlement offers have some probability of failing when one of the parties has private information. Because of this one-sided selection mechanism, the asymmetric information model predicts that the win rate for the party with private information should tend toward 100 percent. As we discuss in the fourth section of this chapter, the empirical evidence for patent litigation strongly favors the divergent expectations model.
Litigation models explain why cases reaching trial are a selected sample of filed cases. Similar selection will be at work on filed cases, to the extent that potential plaintiffs may not file suits on certain types of patents (or defendants may settle before suit). Lanjouw and Schankerman (2001) show that the observed characteristics of patents and their owners strongly affect the probability of filing a suit. We confirm, and extend, those findings in this chapter. At the same time, we find that post-suit outcomes—for example, whether parties settle or who wins if the case reaches trial—are unrelated to these same characteristics.
DESCRIPTION OF DATA
The data source used to identify litigated patents is the LitAlert database produced by Derwent, a private vendor. This database is primarily constructed from information collected by the U.S. Patent and Trademark Office (USPTO). The data used include 13,625 patent cases filed during the period 1978-1999. Each case filing identifies the main patent in dispute, although other patents may also be listed. We use only the main listed patent in our analysis, for reasons explained below. There are 9,345 patents involved in our sample of suits.
We also obtained information on all U.S. patent-related cases (those coded 830) from the court database organized by the Federal Judicial Center (FJC). This information runs through the end of 1997 and includes the progress or resolution of suits—for example, whether the case is settled and at which stage of the proceedings this occurs, whether the case proceeds to trial, and the outcome of the
trial.7 The form of docket numbering was made (by hand) consistent across the two data sets, so they could be merged.
To create a control group, we generated a “matched” set of patents from the population of all U.S. patents (both litigated and unlitigated) from the USPTO. For each litigated patent, a patent was chosen at random from the set of all U.S. patents with the same application year and primary three-digit U.S. Patent Classification (USPC) class assignment. With a population sample constructed in this way, the comparisons we present between litigated patents and matched patents largely control for technology and cohort effects. The control is not perfect, however, because we have 12,771 matched patents. This is more than the number of litigated patents for two reasons. First, the more recent part of our sample includes matches for both main and other patents in each suit, whereas we only use the main litigated patents in the analysis. Second, in combining our old (1978-1991) and new (1990-1999) data, we dropped duplicate cases in the overlapping years when counting litigated patents. We do not have identifiers in either round of subsetting the litigated data that would allow us to easily delete the corresponding matched patents. We do not expect this to create any systematic bias.
Although the U.S. federal courts are required to report to the USPTO every case filing that involves a U.S. patent, underreporting occurs in practice. Thus the USPTO (and Derwent) data comprise a subset of all patent cases. To estimate the reporting rates, we take the number of cases filed according to Derwent divided by the number in the same year that are coded as a patent case by the FJC. We can compute the reporting rates through 1998 (we use the last value for 1999). They stabilize in the 1990s at about 55 percent (see Appendix 1). We found no evidence of selection bias in the underreporting by the courts to the USPTO: There are no significant differences between reported and unreported cases for a range of variables in the federal database.
A truncation issue arises because we observe suit filings only through 1999, so later cohorts of patents look like they are less litigated by construction. We use the lag structure for case filings for cohorts 1982-1986 to adjust for this truncation. The estimates are based on the pooled sample and are applied to each technology field. The truncation rate is about 50 percent for the 1992 cohort (i.e., lag of 7 years), and it jumps sharply to 75 percent for the 1995 cohort. Appendix 1 presents the estimated truncation rates.
From the main USPTO database we obtained information on the following characteristics for each litigated and matched patent:
Number of Claims: A patent is composed of a set of claims that delineates the boundaries of the property rights provided by the patent. The principal claims define the essential novel features of the invention in their broadest form, and the subordinate claims are more restricted and may describe detailed features of the innovation claimed. The patentee has an incentive to claim as much as possible in the application, but the patent examiner may require that the claims be narrowed before granting.
Technology Field: Each patent is assigned by the patent examiner to three-digit classes of the USPC system, of which there are 421 in total. The USPC is a hierarchical, technology-based classification system, and patents may be assigned to more than one class. In the empirical analysis, we use the set of all three-digit classes to which a patent was assigned. We use the categorization developed by Adam Jaffe to aggregate these classes to a two-digit level (used for some purposes explained later) and then to the eight broad technology groups used in most of this paper: Drugs, Other Health, Chemical, Electronics (excluding computers), Mechanical, Computers, Biotechnology, and Miscellaneous. Assignments to the biotechnology group are based on the categorization used by the USPTO when determining who examines a patent. The technology field composition of cases is given in Table 1.
Citations: An inventor must cite all related prior U.S. patents in the patent application. A patent examiner who is an expert in the field is responsible for ensuring that all appropriate patents have been cited. Like claims, the citations in the patent document help to define the property rights of the patentee. For each patent in the litigated and matched data, we obtained the number of prior patents cited in the application (backward citations) and their USPC subclass assignments. We obtained the same information on all of the subsequent patents that had cited a given patent in their own applications, as of 1998 (forward citations).
TABLE 1 Composition of Sample: All Filed Cases, Cohorts 1978-1995
|
Technology |
Number |
Percent |
|
Drugs |
573 |
5.6 |
|
Other Health |
825 |
8.0 |
|
Chemical |
1,378 |
13.4 |
|
Electronics |
1,924 |
18.7 |
|
Mechanical |
2,848 |
27.7 |
|
Computers |
183 |
1.8 |
|
Biotechnology |
92 |
0.9 |
|
Miscellaneous |
2,456 |
23.9 |
|
TOTAL |
10,279 |
100.0 |
For recent patents there is substantial truncation in the number of forward citations, because citation lags can be long (Jaffe and Trajtenberg, 1999). To minimize truncation bias, we limit parts of the analysis to cohorts before 1993. For older patents there is considerable missing information on the USPC subclass assignments of backward citations, because comprehensive data are only available from about 1970, but the number of backward citations is complete for all patents.
Ownership: We identify each patent owner as an individual, an unlisted company, or a listed company.8 Individual and firm owners are indicated as such in the USPTO data. Bronwyn Hall and Adam Jaffe were generous in providing us with their link between USPTO company codes and Standard and Poor’s CUSIP identification code, based on the 1989 industry structure. We call a patent-owning company “listed” if we are able to identify it as having a Standard and Poor’s CUSIP code at that time.9 Unlisted companies are typically smaller than listed ones, but there is wide variation in both categories. Individuals and listed companies are more predominantly domestic (81.0 and 95.6 percent, respectively) than unlisted companies (60.4 percent). We also break down listed firms into “large” firms (those with employment above the median of 5,425) and “small” firms with employment below the median. Unless otherwise noted, we classify the nearly 40 percent of firms without employment data as large firms because they have similar litigation and settlement patterns.
Nationality: We use the USPTO designation of companies as domestic or foreign if there is an assignee and the address of the first listed inventor if there is no assignee. Domestic patents account for 73.4 percent of the total.
Case Type: We manually matched the owner of each litigated patent to the appropriate party in the suit (plaintiff, defendant, neither). We identify a filed case as an infringement suit if the patent owner is a plaintiff and as a suit for a declaratory judgment if the patent owner is a defendant. This could be done for about 65 percent of the suits. For those cases, infringement suits account for about 85 percent of the total. In most of the analysis we treat those suits in which the patentee is not one of the litigants as infringement suits, because they are likely to be suits brought either by an exclusive licensee or by a subsidiary or head office of the patent-owning entity.
Patent Portfolio Size: The USPTO gives a company code to each company that is assigned a patent by the inventor. This allows us to construct a measure of the size of an owner’s patent portfolio, as it looks around the application date of
each of our sample patents. The relevant portfolio variable (Portsize) is defined as the number of patents owned by a company that have an application date within 10 years in either direction of the patent in question. It should be noted that this portfolio size variable may differ across patents for a given company. As expected, domestic listed companies tend to have larger portfolios—roughly one-third of patents owned by domestic listed companies are in portfolios in each of size groups 1-100, 100-900, and >900 patents. By contrast, about 90 percent of patents owned by domestic unlisted companies, and two-thirds of patents owned by foreign companies, are in portfolios with fewer than 100 patents.
Relative Size: We construct a measure of the asymmetry in portfolio size between a patentee and the “representative” disputant he/she can expect to face on each patent. Disputes will often occur between firms engaged in similar research. Firms pursuing similar research programs will also be in the position of citing each other’s patents as prior art. Thus we identify firms patenting in the same technology areas as a given patent’s forward citations as the likely potential disputants for the patent. This identification is supported by an analysis of the three-digit classifications of patents owned by actual defendants. We compare these to the technology classes of the forward citations to the patent in a suit. The share of classes that overlap ranges from 0.16 to 0.47 depending on the type of innovation. By contrast, the overlap for a random set of patents from the same cohorts is about one-tenth the size, ranging from 0.016 to 0.059. On the basis of this result, relative portfolio size is defined as the firm’s total portfolio size (including all patents since 1978) divided by a weighted average of the portfolio size of firms in classes from which its forward citations come.10
For a patentee who is the plaintiff (infringement suits) being relatively large confers greater threat power (e.g., holding cross-licensing of other patents hostage to this dispute), and this should facilitate settlement with the infringer. This is less clear-cut when the patentee is the defendant. A stronger defendant may be less willing to settle (or be able to extract more favorable settlement terms from the plaintiff). Thus we expect the probability of litigation to decline with relative size in infringement suits, but the prediction for declaratory judgment suits is ambiguous.
Technology Concentration: We construct a measure of firm concentration in the technology area of each patent. To do this, we first construct, for each two-digit USPC class, a four-firm concentration index, measured as the patenting share of the top four firms. A firm’s share is the size of its patent portfolio in that class divided by the sum of all firms’ patents in that class. For each patent we then
construct a weighted average of the concentration indices for the different classes, where the weights are the shares of the forward citations to the patent that fall in that technology class.11 If a company operates in more concentrated technological areas, it faces a greater chance of encountering other firms in patent disputes more than once. This expectation of repeated interaction should lower the litigation rate (i.e., promote pre-suit settlement).
Other Information: From Standard and Poor’s information on listed companies, we downloaded financial and other company information for the listed firms either owning patents involved in litigation or in our matched sample.
The preceding variables are designed to capture the main determinants of patent suits:12
-
the number of potential disputes—measured by the number of claims, the diversity of technology classes into which the patent falls, and the technological similarity of future patents that cite the original patents;
-
the size of the stakes—measured by the number of future citations the patent receives and the extent of self-citation (as an indicator of the firm’s cumulative investment in that technology);
-
the degree of certainty about outcomes—measured by patent portfolio size and ownership type (as indicators of experience); and
-
relative costs of settlement and prosecuting a suit—again measured by patent portfolio size and ownership type and, in addition, technology concentration, relative size, and nationality of the patentee.
NONPARAMETRIC EVIDENCE
Although the number of patent infringement suits has risen by almost tenfold since 1978, the increase has not been uniform across technology fields—it was particularly high in Drugs, Biotechnology, Computers, and Other Electronics. Closer examination of the data shows that the increase in the aggregate number of suits has been driven both by the sharp increases in the number of patent applications in each technology field and by the shift of patenting toward technology fields with higher litigation rates. The total number of patent applications grew by 71 percent over the period, but in Drugs, Biotechnology, and Medical Instruments patenting nearly tripled, and in Computers it grew by fourfold. Once the
growth in patenting is taken into account, we find that there has been no trend increase in the filing rates of suits in any technology field over this period. (Note again, however, that with increasing expenditures per suit, legal enforcement costs may well have grown over the period.)
Table 2 presents estimates of average filing rates for three subperiods: 1978-1984, 1985-1990, and 1991-1995. We measure filing rates as the number of suits filed per thousand patents from a given cohort.13 These include all of the suits filed in connection with these patents through 1999 (that is, we count multiple cases for the same patent), and they are adjusted both for underreporting in the Derwent data and truncation associated with time lags in case filings.14
TABLE 2 Filing Rates by Technology Fields and Cohort Groups
The table also shows that mean filing rates vary substantially across technology fields. A formal test that the filing rates are the same across fields is strongly rejected [χ2(7) = 1,103; P-value < 0.001]. For the aggregate (pooled technology field) data, there are 19.0 case filings per thousand patents. The lowest rates are found in Chemicals (11.8), Electronics (15.4), and Mechanical (16.9). Interestingly, filing rates for pharmaceutical patents are only modestly higher than the average. The filing rates are much higher for patents in Other Health, Computers, Biotechnology, and Miscellaneous. Computers and Biotechnology are both newer areas in which one might expect there to be greater uncertainty about legal outcomes.
Although we observe little evidence of trends in filing rates, the level of filing rates may be understated by Table 2. These are calculated by using only the main patents in each suit, whereas there may in fact be several patents per suit. We present these calculations because, for filing years before 1990, we only have information about the main patents (mixing the subsidiary patents for later years would distort litigation trends). The filing rates we compute are underestimates of the “true” rates if one views being a subsidiary patent in a case as equivalent to being the main litigated patent. To estimate the difference, one could scale up the filing rate by dividing by the ratio of subsidiary to main patents. This ratio is 0.24 percent overall, but it varies across technology fields.15
It is important to look beyond average filing rates for given technology fields, because they conceal huge heterogeneity. Lanjouw and Schankerman (2001) showed that litigated patents have more claims and more forward citations per claim. Table 3 confirms this finding on the larger data set. The table presents the mean number of claims, and citations per claim, for litigated and matched patents, broken down by ownership type. Litigated patents have far more claims than matched patents, and this holds for each ownership type. They also have more forward citations per claim and fewer backward cites per claim (i.e., more backward citations are an indication that the technology area is well-developed and the innovation is more likely to be derivative and less valuable). Both of these findings indicate that valuable patents are more likely to be involved in litigation.
There are also large differences across different types of patent owners. Table 4 summarizes the mean filing and settlement rates for four ownership categories: individuals, domestic unlisted and listed companies, and foreign companies. Domestic listed companies are far less likely to file suits on their patents than unlisted companies and individuals: Their mean filing rate is 10.4 suits per thousand patents, compared to 35-45 suits for the smaller owners. Moreover, filing rates
TABLE 3 Mean Citations and Claims per Patent, by Ownership Type
for foreign patentees (mostly unlisted firms) are much lower than for their domestic counterparts. These differences in mean filing rates are statistically significant, and the joint null hypothesis that they are the same is decisively rejected [χ2 (3) = 11,853; P-value < 0.001].
Although filing rates differ sharply across ownership types, we find that ownership does not affect the probability that a suit is settled before it reaches the end
TABLE 4 Filing and Settlement Rates, by Ownership Type
|
|
Individuals |
Domestic Unlisted |
Domestic Listed |
Foreign Firms |
|
Filing Rate |
35.2 |
46.0 |
10.4 |
4.2 |
|
(cases/thousand) |
(0.65) |
(0.78) |
(0.27) |
(0.16) |
|
Settlement Rate |
94.7 |
94.0 |
94.1 |
94.5 |
|
(percent) |
(1.4) |
(0.4) |
(0.7) |
(0.9) |
|
NOTE: Foreign firms include both listed and unlisted companies. The filing rate is the number of suits filed per thousand patents, including multiple suits on the same patent, from cohorts 1978-1995 (as in Table 2). The settlement rate is the fraction of filed cases reported to have been settled at some time before court judgment, according to the FJC. Settlement rates are computed for suits filed during the period 1978-1992 to minimize truncation bias and include only infringement suits. Estimated standard errors are in parentheses. Numbers in bold are statistically significant at the 0.01 level. |
||||
of trial—which we call post-suit settlement. The formal χ2(3) test statistic is 4.55 (P-value ≈ 0.2). Overall, about 95 percent of all patent suits filed are settled by the parties before the conclusion of trial (and most of those before the trial begins). However, which suits these are is not related to observed characteristics.
One explanation for why listed and unlisted firms have such different filing rates may be that the listed firms are typically larger and there may be advantages to size. As discussed above, there are several distinct aspects to such advantages. First, firms with larger patent portfolios may be more experienced or better able to settle disputes through trading intellectual property, without resorting to suits (the portfolio size effect). Second, if imperfect capital markets constrain the ability of smaller firms to finance litigation, relatively large firms may be better able to settle because they pose greater litigation threats when confronting smaller firms. And when large firms have disputes with each other, they are likely to have many points of interaction other than trading intellectual property, especially through competition in product markets. This expectation of repeated interaction in other dimensions should promote settlement. Large firms are also likely to be relatively experienced. We call these latter aspects firm size effects. The detailed patent data enable us to discriminate between the portfolio size and firm size effects on litigation.
We begin by examining how the probability of litigation (i.e., of being involved in at least one suit over the life of the patent) and the probability of post-suit settlement vary with different portfolio sizes. To compute these probabilities, we adjust for the fact that patents from large portfolios are disproportionately represented in the matched data (because the matching was not stratified by portfolio size—see Appendix 2 for details). Table 5 shows that the probability of litigation sharply declines with portfolio size. A formal test confirms this finding [χ2(6) = 2,610; P-value < 0.001]. The probability of filing a suit involving a patent in a portfolio with a small number of other patents (0-10) is 1.7 percent, compared to about 0.5 percent for a patent in a portfolio with 100-300 other
TABLE 5 Probability of Litigation and Settlement, by Patent Portfolio Size
|
Portfolio Size |
Probability of Litigation (percent) |
Settlement Rate (percent) |
||
|
0-10 |
1.71 |
(0.05) |
95.0 |
(0.5) |
|
11-100 |
1.20 |
(0.05) |
93.3 |
(0.7) |
|
101-200 |
0.52 |
(0.05) |
93.0 |
(1.7) |
|
201-300 |
0.43 |
(0.06) |
97.0 |
(1.3) |
|
301-600 |
0.39 |
(0.04) |
90.9 |
(1.9) |
|
601-900 |
0.34 |
(0.04) |
93.3 |
(2.5) |
|
>900 |
0.26 |
(0.01) |
93.2 |
(1.1) |
|
NOTE: The probability of litigation is adjusted for underreporting and truncation and for the overrepresentation of patents from large portfolios (Appendix 2). Estimated standard errors are in parentheses. See also notes to Table 4. |
||||
patents and only 0.25 percent for those in large portfolios (>900 patents). These are large differences, and they show that having bigger portfolios confers substantial advantages in settling patent disputes without filing suits, but again, we observe only small differences in the post-suit settlement rates across portfolio size. The differences in point estimates are marginally statistically significant [χ2(6) = 14.2; P-value ≈ 0.05].
To distinguish between the advantages of portfolio size and firm size, we divide domestic listed firms into two groups—those with employment around 1989 above the median level of 5,463 (“large”) and those below the median (“small”).16 Panel A in Table 6 presents the litigation probability broken down by
TABLE 6 Probability of Litigation and Settlement, by Patent Portfolio Size and Ownership Type
|
Panel A. Probability of Litigation (percent) |
||||||||
|
Portfolio |
Large Domestic Listed |
Small Domestic Listed |
Domestic Unlisted |
Foreign Firms |
||||
|
0-10 |
0.55 |
(0.26) |
1.09 |
(0.49) |
2.63 |
(0.09) |
0.48 |
(0.03) |
|
11-100 |
1.16 |
(0.25) |
1.78 |
(0.32) |
2.00 |
(0.09) |
0.37 |
(0.03) |
|
101-200 |
0.70 |
(0.14) |
0.77 |
(0.28) |
0.67 |
(0.12) |
0.23 |
(0.03) |
|
201-300 |
0.49 |
(0.17) |
0.82 |
(0.32) |
0.84 |
(0.27) |
0.18 |
(0.04) |
|
301-600 |
0.54 |
(0.10) |
0.70 |
(0.31) |
0.56 |
(0.10) |
0.19 |
(0.03) |
|
601-900 |
0.62 |
(0.10) |
0.44 |
(0.25) |
0.34 |
(0.12) |
0.18 |
(0.04) |
|
>900 |
0.39 |
(0.02) |
nc |
0.37 |
(0.06) |
0.12 |
(0.01) |
|
|
Panel B. Settlement Rates (percent) |
||||||||
|
Portfolio |
|
|
Domestic Listed |
Domestic Unlisted |
Foreign Firms |
|||
|
0-10 |
|
|
90.0 |
(3.1) |
95.0 |
(0.5) |
95.9 |
(1.3) |
|
11-100 |
|
|
95.0 |
(1.3) |
93.0 |
(0.9) |
91.2 |
(2.3) |
|
101-200 |
|
|
92.9 |
(2.4) |
92.1 |
(3.4) |
95.0 |
(3.4) |
|
201-300 |
|
|
98.8 |
(1.2) |
97.9 |
(2.1) |
90.3 |
(5.3) |
|
301-600 |
|
|
92.0 |
(2.4) |
85.2 |
(3.9) |
100.0 |
(0.0) |
|
601-900 |
|
|
96.3 |
(2.6) |
87.5 |
(5.8) |
94.4 |
(5.4) |
|
>900 |
|
|
94.1 |
(1.3) |
88.8 |
(3.0) |
95.3 |
(2.6) |
|
NOTE: The probability of litigation is the number of patents involved in suits (multiple suits not counted) per hundred patents, adjusted for underreporting and truncation and for the overrepresentation of patents from large portfolios (Appendix 2). “nc” denotes an empty cell. Estimated standard errors are in parentheses. See also notes to Table 4. |
||||||||
both portfolio size and this measure of company size. First, we see a fall in litigation probability with portfolio size within each ownership type, at least in terms of the point estimates. However, the fall is by far more precipitous for domestic unlisted companies. For a patent owned by such a company and in a portfolio of 0-10 other patents, the average probability of being involved in litigation is 2.6 percent, whereas for patents in the same-sized portfolio but owned by listed domestic companies it is closer to 1 percent. At the same time, there is little evidence that size—either in terms of public listing or employment—matters once more than about 100 patents are held. For any given portfolio size, foreign companies are much less likely to file suits than other types of firms. The relationship between probability of litigation and portfolio size holds in each of the technology fields (not reported).
Consistent with the results in Table 2, we find that the probability of litigation differs substantially across technology areas for any given ownership type (see Table 7). However, here we also see that the pattern of differences across technology fields depends on the type of owner.
One explanation for these differences in litigation probabilities is that firms with larger portfolios may have a higher propensity to patent their innovations (harvesting) and thus more often have patents that are not worth fighting over. However, the evidence contradicts this hypothesis. Portfolio size is positively, and significantly, correlated with forward citations and forward citations per claim. The correlation coefficients are 0.10 and 0.06, respectively (these are computed with the matched sample and cohorts 1978-1988 to avoid spurious correlation due to both portfolio size and citations being truncated). Even within electronics, where firms have often been described as following a patent harvesting strategy, there is no evidence that the average quality of patents falls in larger
TABLE 7 Probability of Litigation, by Technology and Firm Ownership (in percent)
|
Technology |
Domestic Unlisted |
Small Domestic Listed |
Large Domestic Listed |
Foreign Firms |
||||
|
Drugs |
9.1 |
(0.2) |
2.9 |
(0.2) |
4.2 |
(0.2) |
3.3 |
(0.1) |
|
Other Health |
10.5 |
(0.2) |
9.1 |
(0.4) |
4.1 |
(0.3) |
2.2 |
(0.1) |
|
Chemicals |
3.8 |
(0.1) |
3.9 |
(0.1) |
1.2 |
(0.05) |
0.5 |
(0.02) |
|
Electronics |
6.6 |
(0.1) |
12.3 |
(0.1) |
11.2 |
(0.1) |
0.8 |
(0.02) |
|
Mechanical |
6.8 |
(0.1) |
3.9 |
(0.1) |
11.2 |
(0.1) |
0.7 |
(0.02) |
|
Computers |
14.9 |
(0.6) |
nc |
1.3 |
(0.2) |
0.3 |
(0.06) |
|
|
Biotechnology |
20.1 |
(0.7) |
3.9 |
(0.6) |
3.4 |
(0.6) |
7.2 |
(0.5) |
|
Miscellaneous |
11.2 |
(0.2) |
4.2 |
(0.1) |
2.6 |
(0.1) |
1.3 |
(0.04) |
|
NOTE: Estimated standard errors are in parentheses. See notes to Table 5. |
||||||||
portfolios (Hall and Ziedonis, 2001). The same positive and significant relationships are found, and the same is true for all other technology areas. Thus it appears that the link between litigation probability and portfolio size does actually reflect the advantages that large portfolios give to firms in settling disputes. However, this is only half the story. Panel B in Table 6 presents the average probability of settlement for different portfolio sizes and ownership categories, conditional on a suit being filed. Here we see that post-suit settlement rates do not vary significantly with portfolio size or with ownership type controlling for portfolio size.
In short, the likelihood of filing a suit (i.e., of not settling beforehand) is much higher for patents owned by individuals and unlisted companies and for patentees with smaller patent portfolios to trade. However, these differences do not appear in post-suit settlement rates. Thus almost all of the settlement of disputes, as determined by observed characteristics of patents and patentees, occurs before suits are filed, not afterwards in the courts.
To this point we have focused on the probability of litigation and of post-suit settlement. We now turn to the timing of such settlements and the win rates for cases that reach the trial adjudication stage. Table 8 summarizes this information broken down by ownership type—domestic listed, domestic unlisted, and foreign firms and all individuals. About 80 percent of all suits that are ever settled (without third-party adjudication) are settled before a pretrial hearing is held. This suggests that the filing of a suit sends a strong signal about the seriousness of the plaintiff to use legal means and quickly triggers resolution before substantial le
TABLE 8 Timing of Settlement and Trial Win Rates, by Ownership Type
gal costs are incurred.17 Nearly all of the remaining settlement occurs before the trial commences. However, the table shows that the timing of settlements differs little by ownership type.
The table also shows the trial win rates (for infringement suits). For domestic listed and unlisted firms, the win rates are very close to 50 percent, as predicted by the divergent expectations model of litigation. They are sharply inconsistent with the win rates of either zero or 100 percent predicted by the asymmetric information models. The point estimate of the win rate for foreign corporate patentees is only 42.7 percent, but the standard error is relatively large.
ECONOMETRIC ANALYSIS
In this section we present estimates of probit regressions on the determinants of the probabilities of infringement suits and post-suit settlement for the pooled data. These endogenous variables are related to the following regressors: the number of claims, forward citations per claim, backward citations per claim, and the percentage of backward and forward citations that are self-citations (as measures of cumulative technology), the number of three-digit USPCs as a measure of patent breadth, the size of the patent portfolio, the relative size of the patent portfolio (as a measure of asymmetry between a patent owner and likely disputants), the technology concentration index, and ownership dummy variables that distinguish between patentees who are foreign or domestic individuals and unlisted or listed firms. The effects of technology and cohort on litigation probabilities are largely controlled by the matching, but because the litigated and matched data contain somewhat different numbers of patents, we also include technology group dummies.
We use the Derwent data as the basis for the sample, because it contains the link to patent numbers, and then include only those cases that can also be linked into the FJC database, which contains the outcomes information. This procedure yields 6,538 litigated main patents. In analyzing the determinants of the litigation probability (filing of suits), we do not count multiple cases involving the same patent. We do this to avoid undue influence by a few patentees suing many infringers in separate but related cases. We include multiple cases in the econometric analysis of the suit outcomes for two main reasons: first, it is unclear how one would choose the “representative” suit when there are multiple cases and, second, the sample size for outcomes (especially trials) is relatively small even when we include multiple cases.18
Panel A in Table 9 summarizes the parameter estimates and the sample marginal effect of each variable on the probability of litigation for a randomly drawn patent in the matched sample (i.e., at matched sample means). This is done separately for patent infringement and declaratory judgment suits. Because the sample litigation rate is close to 40 percent by construction, we must multiply the reported marginal effects by a conversion factor to obtain the marginal effects for a randomly drawn patent in the population (the conversion factors are given at the bottom of Table 9; see Appendix 3 for computational details). The statistical significance of variables and the relative size of their effects are preserved through this conversion, although magnitudes will depend on the specific population of interest. We focus the discussion on the results for patent infringement cases. Because the pattern of results is similar for declaratory judgment suits (Panel B of Table 9), we do not discuss them in detail. Variable definitions are listed in Table 10.
The probability of litigation increases with the number of claims and forward citations per claim at a declining rate, and the effects are substantial. Evaluated at population means (litigation probability of 1.35 percent), a 10 percent increase in the number of claims (1.2 claims at the mean) implies an increase of 3.1 percent in the population probability of litigation. We also find that a 10 percent increase in the number of forward citations per claim raises the probability of an infringement suit by 1.8 percent. These findings confirm the importance of the value of a patent in determining infringement suits. In related work on the determinants of re-examinations at the USPTO and opposition proceedings at the European Patent Office—both events suggesting that the use of a patent is subject to dispute— Graham et al. (2003) and Harhoff and Reitzig (2000) find similar positive relationships.
The likelihood of an infringement suit falls with the number of backward citations per claim (at a declining rate). At mean values, a 10 percent increase in the number of backward citations per claim reduces the litigation probability by 0.7 percent. Although the effect is small, this finding is consistent with the view that backward citations are an indication that the patent is in a relatively well-developed technology area, in which many related patents have been taken out and where uncertainty about property rights is less likely to cause frequent patent disputes (Lanjouw and Schankerman, 2001).
We have also argued that forward self-citation to a patent (given its total number of forward citations) indicates the presence of “cumulative innovation” by the patentee. That is, the patent owner is engaged in subsequent inventions that build on this earlier patent and, as a result, he has a greater incentive to protect his property rights in this area. This hypothesis is supported by the positive and significant coefficient on the variable FWDSELF, the percentage of citations that is self-citation. At the mean (FWDSELF = 0.065), increasing the percentage of forward self-citations by 10 percent would raise the probability of an infringement suit by 0.4 percent (the estimate is proportionately higher for larger
TABLE 9 Probit Estimation of Litigation Probability: Case Filings
|
|
Panel A Infringements |
Panel B Declaratory Judgments |
||
|
Variable |
Parameter |
Marginal |
Parameter |
Marginal |
|
Claims |
0.023 |
0.007 |
0.029 |
0.002 |
|
|
(0.001) |
|
(0.003) |
|
|
Claims2 (× 103) |
−0.024 |
|
−0.15 |
|
|
|
(0.002) |
|
(0.038) |
|
|
FWD cites/claim |
0.19 |
0.059 |
0.20 |
0.0008 |
|
|
(0.008) |
|
(0.017) |
|
|
[FWD cites/claim]2 (× 103) |
−4.38 |
|
−5.65 |
|
|
|
(.32) |
|
(.83) |
|
|
BWD cites/claim |
−0.056 |
−0.017 |
−0.072 |
−0.005 |
|
|
(0.010) |
|
(.019) |
|
|
[BWD cites/claim]2 (× 103) |
0.89 |
|
1.47 |
|
|
|
(0.43) |
|
(.62) |
|
|
FWDSELF |
0.51 |
0.17 |
0.63 |
0.05 |
|
|
(0.058) |
|
(.10) |
|
|
BWDSELF |
−0.31 |
−0.10 |
−0.16 |
−0.01 |
|
|
(0.08) |
|
(.15) |
|
|
NO3USPC |
−0.068 |
−0.022 |
−0.014 |
−0.003 |
|
|
(.008) |
|
(.015) |
|
|
Portsize (× 103) |
−0.104 |
−0.025 |
–0.21 |
–0.015 |
|
|
(.037) |
|
(.13) |
|
|
Portsize2 (× 106) |
0.009 |
|
0.005 |
|
|
|
(0.001) |
|
(.0003) |
|
|
PortNondrug (× 103) |
−0.061 |
−0.021 |
0.056 |
0.004 |
|
|
(0.033) |
|
(.12) |
|
|
PortUNLIST (× 103) |
−0.027 |
−0.009 |
–0.07 |
–0.005 |
|
|
(0.013) |
|
(.04) |
|
|
PortFLIST (× 103) |
0.001 |
0.0003 |
0.05 |
0.004 |
|
|
(0.020) |
|
(.05) |
|
|
PortDLIST-S (× 103) |
−0.6 |
−0.20 |
–0.36 |
0.028 |
|
|
(.27) |
|
(.41) |
|
|
Tech. Concentration (C4) |
−4.17 |
−1.36 |
−6.15 |
−0.48 |
|
|
(.23) |
|
(.46) |
|
|
Relsize (× 103) |
−3.1 |
−1.01 |
–0.91 |
–0.07 |
|
|
(1.12) |
|
(2.67) |
|
|
FIND |
−0.54 |
−0.12 |
−1.84 |
−0.036 |
|
|
(0.09) |
|
(.17) |
|
|
DIND |
0.13 |
0.14 |
−1.30 |
0.012 |
|
|
(0.08) |
|
(.15) |
|
|
FUNLIST |
−0.69 |
−0.22 |
−1.81 |
−0.045 |
|
|
(.08) |
|
(.15) |
|
|
DUNLIST |
0.21 |
0.19 |
−1.06 |
0.058 |
|
|
(.08) |
|
(.15) |
|
|
FLIST |
–0.15 |
0.007 |
−1.77 |
−0.030 |
|
|
(.19) |
|
(.42) |
|
|
|
Panel A Infringements |
Panel B Declaratory Judgments |
||
|
Variable |
Parameter |
Marginal |
Parameter |
Marginal |
|
DLIST-S |
0.27 |
0.17 |
0.46 |
0.060 |
|
|
(.11) |
|
(.15) |
|
|
D-LIST-B |
−0.23 |
−0.03 |
−0.98 |
−0.006 |
|
|
(.08) |
|
(.20) |
|
|
No. Observations |
17,443 |
|
11,061 |
|
|
Pseudo-R2 |
0.162 |
|
0.164 |
|
|
χ2 |
3858.3 |
|
1098.9 |
|
|
Conversion Factors to Estimate Population Marginal Effects |
||
|
Technology Field |
Infringements |
Declaratory Judgments |
|
Aggregate |
.048 |
.021 |
|
Drugs |
.050 |
.018 |
|
Other Health |
.089 |
.039 |
|
Chemicals |
.031 |
.014 |
|
Electronics |
.038 |
.020 |
|
Mechanical |
.045 |
.021 |
|
Computers |
.063 |
.034 |
|
Biotechnology |
.076 |
.030 |
|
Miscellaneous |
.084 |
.031 |
|
NOTE: Estimated standard errors are in parentheses. Numbers in bold are significant at the 0.01 level. The conversion factors are computed as described in Appendix 3. |
||
values of self-citing). At the same time, we find that greater backward self-citation (BWDSELF) significantly reduces the likelihood of litigation, but the effect is again small at the mean: Raising the percentage of backward self-citations by 10 percent lowers the litigation probability by about 0.25 percent. Greater backward self-citation in a patent indicates that an invention builds more extensively on one’s own past research and is thus more likely to be a “derivative” invention. This evidence supports the idea that there is complementarity among technologically related inventions in a firm’s R&D portfolio and that this raises the willingness to protect the property rights of the key, early inventions in the chain.
In our earlier work (Lanjouw and Schankerman, 2001), we found that greater technological similarity of forward citations increased the probability of litigation.19 The similarity measure was used as an index of whether the technology
TABLE 10 Variable Definitions
|
Claims |
Number of claims in the patent specification |
|
FWD cites/claim |
Number of citations to the patent by subsequent patents, divided by claims. |
|
BWD cites/claim |
Number of citations to prior patents in the patent specification, divided by claims. |
|
FWDSELF |
Percentage of forward citations that are from patents owned by the same company code. For individuals it is set to zero. |
|
BWDSELF |
Percentage of backward citations that are to patents owned by the same company. For individuals it is set to zero. |
|
NO3USPC |
Number of unique three-digit technology classes to which the patent is assigned by the patent office examiner. |
|
Portsize |
Number of other patents owned by the same assignee that have an application year within a ten-year window of the application year of the patent in question. For individuals it is set to one. |
|
PortNondrug |
Portsize times an indicator variable that is one if the patent is not a drug innovation, zero if it is a drug innovation. |
|
PortUNLIST |
Portsize times UNLIST (see below) |
|
PortFLIST |
Portsize times FLIST (see below) |
|
PortDLIST-S |
Portsize times DLIST-S (see below) |
|
Tech. Concentration (C4) |
Firm C4 concentration measures – weighted average over the technology areas of the patent’s forward citations. |
|
Relsize |
Total portfolio size of the patent owner divided by a weighted average of portfolio sizes of firms in the technology areas of the patent’s forward citations. |
|
FIND |
Foreign (non-U.S.) individual |
|
DIND |
Domestic (U.S.) individual |
|
FUNLIST |
Foreign company assignee without a Standard & Poor’s (S&P) CUSIP code |
|
DUNLIST |
Domestic company assignee without an S&P CUSIP code |
|
FLIST |
Foreign publicly listed company with an S&P CUSIP code |
|
DLIST-S |
Domestic publicly listed company with fewer than the median number of employees for such firms (5,425) |
|
DLIST-B |
Domestic publicly listed company with more than the median number of employees. |
area was “crowded” and thus more likely to generate potential disputes. However, we do not find any evidence of that link in the current expanded data set.
Lerner (1994) suggests that patents with uses in many technological areas— “broad” patents—are more likely to be litigated because they face more potential infringers. Using the number of technology class assignments as a measure of patent breadth, he confirmed the hypothesis on a sample of biotechnology patents. Using more comprehensive data for various technology fields, Lanjouw and Schankerman (2001) found that broader patents are less likely to be involved in suits, but the evidence was weak. We test this hypothesis on our expanded and more recent data set, using the number of three-digit USPC classes as the mea-
sure of breadth (NO3USPC). The estimated coefficient is similar to the earlier estimate by Lanjouw and Schankerman and highly significant. A 10 percent increase in NO3USPC (the mean number of technology field assignments is 2.2) reduces the litigation probability by about 1.7 percent.20 This finding suggests that it is harder to detect infringements when the patented innovation is used in more technology areas and that this effect dominates any increase in the number of potential infringers associated with greater patent breadth.
An important finding is that the probability of litigation is negatively related to the size of the patent portfolio, with an elasticity (at the mean) of – 0.13. The marginal effect of portfolio size declines with larger portfolios (positive quadratic term), but the point estimate of the portfolio effect is negative over most of the sample range. This means that having a larger portfolio of patents reduces the probability of being involved in a suit on any individual patent owned by the firm, e.g., there are beneficial “enforcement spillovers” across patents within a given firm. We can compute by how much increasing portfolio size reduces the litigation probability of any constituent patent. For example, raising the portfolio from 100 to 500 patents lowers the litigation probability on an “average” patent (with characteristics at their mean values) by 0.13 percentage points, or about 10 percent of the mean probability. Going from a portfolio of 500 to 2,500 reduces the probability by 0.21 percentage points, or by about 15 percent. Harhoff and Reitzig (2000) find that larger portfolios also tend to keep owners out of European opposition proceedings.
The impact of portfolio size on the probability of litigation is smaller for drug patents than for patents in other technology fields. Estimation at the technology field level (not reported) suggested this hypothesis (the other differences in the estimated portfolio coefficients across technology fields were not statistically significant). To test the hypothesis, we include a portfolio dummy variable for nondrug technology fields (PortNondrug). The estimated coefficient is negative and large relative to the baseline portfolio effect. Using the estimated coefficients on Portsize and PortNondrug, we find that the marginal effect of portfolio size on the litigation probability is nearly twice as large for nondrug patents as compared to drug patents. This finding is consistent with the idea that trading intellectual property is especially important in areas in which innovation is “complex” in the sense that it may rely on multiple components or research tools that may be patented by other firms (see Cohen et al., 2000). This feature has been less important in drugs. Somaya (2003) finds a similar difference, using somewhat overlapping technology definitions and a related variable for portfolio size. He finds that the size of a patentee’s portfolio has an insignificant effect on the litigation of patents for research medicine, whereas it has a negative effect for computer patents.
The portfolio effect captures the ability of firms to trade patents as a means of settling disputes. Smaller companies may have few alternative mechanisms to facilitate settlement, so we expect portfolio size to be more important for smaller firms. To test this hypothesis, we include interaction effects between portfolio size and ownership type (unlisted and small domestic and foreign listed, with large domestic listed firms being the reference category). The point estimates strongly support the hypothesis that company size affects the importance of having larger patent portfolios. For a small domestic listed company with the mean portfolio size (1,420 patents), the marginal effect of portfolio size on the probability of litigation is about eight times larger than for a large listed company with the same portfolio (compare marginal effects for Portsize and PortDLIST-S). The marginal effect of portfolio size for small listed firms is even greater than that for unlisted firms.
Additional evidence that the expectation of repeated interaction promotes settlement is provided by the technology concentration variable (C4), defined in the third section of this chapter. If a company operates in concentrated technology areas (i.e., where the top four firms account for a larger share of patenting), there is a greater chance that the company will be involved in repeated patent disputes with the same firms. This should increase the likelihood of settlement and thus reduce the probability of litigation. As predicted, the estimated coefficient on the technology concentration index is negative and highly significant and the quantitative effect on the litigation probability is large. A 10 percent increase in the four-firm technology concentration index reduces the probability of a suit by 4.6 percent.
The portfolio size, company size, and technology concentration variables capture the ability to trade and the role of repeated interaction. We also find that the litigation probability is influenced by the asymmetry in portfolio size between the patent owner and likely disputants, which we interpret as reflecting relative threat power of the parties. The coefficient on the relative size variable (RelSize) is significantly negative for infringement suits, as expected.21 If a patent owner is large relative to typical disputants, the probability of litigation is lower (settlement is more likely). However, the effect is not very large—a 10 percent increase in relative size lowers the litigation probability by 0.5 percent. Interestingly, relative size does not matter in declaratory judgment suits, those in which the patent owner is the defendant (Panel B of Table 9). The prediction was that larger relative size (of the patentee) would make settlement more difficult or have no effect for declaratory judgment suits, and we find the latter.
We easily reject the hypothesis that there are no ownership differences when we control for other factors [χ2(6) = 978.8; P-value < 0.001]. The pattern of marginal effects on the ownership dummies points to five main findings about the conditional effects of ownership type on the propensity to litigate. First, foreign individuals and unlisted (smaller) companies are much less likely to engage in infringement suits than their domestic counterparts. Comparing the marginal effects of FIND and DIND, we see that the probability of litigation is much lower— by about 1.2 percentage points—for foreign individual owners than for their domestic counterparts. Comparing foreign and domestic unlisted companies (FUNLIST and DUNLIST), the difference is even larger, about 2.0 percentage points. Second, larger domestic and foreign listed companies are equally likely to file suits. Third, domestic individuals and unlisted and small listed companies are equally likely to litigate (the differences in point estimates are not statistically significant). Fourth, domestic individuals and unlisted companies are more likely to litigate than large domestic listed firms, by about 0.9 percentage points. And finally, small listed companies are far more likely to file suits than larger ones, the difference being about 1.0 percentage points on average.
To summarize, we find the following ranking of the propensity to litigate, in descending order: Small domestic listed companies, domestic unlisted companies and domestic individuals have the highest propensity to sue (given the characteristics of a patent), and there are no significant differences among them. Large domestic listed companies and foreign listed companies have the next highest propensity to litigate. Foreign individuals and foreign unlisted companies are least likely to be involved in patent infringement suits.22 Because these effects are conditional on portfolio and company size (both of which relate to the cost of settling), this ranking should reflect two main factors, the cost of litigation and access to information about potential infringements. We expect that the cost of litigating for domestic patentees is less than (or equal to) that for foreign patentees and that it is harder for foreign owners to detect infringements in the United States. Given the cost of settling disputes, these hypotheses predict that domestic owners should litigate more often than their foreign counterparts. That is what we find, except for listed companies. This exception is not surprising, because foreign firms that are listed, and have a presence, in the United States are less likely to be at much disadvantage in terms of litigation costs and access to information.
Table 11 highlights the enormous variation in litigation risk implied by these estimation results. We calculate the population probability of involvement in an infringement suit for each patent in the matched sample, given the patent’s full set of characteristics. The 50th-99th percentile cutoffs for the distribution of these
TABLE 11 Predicted Probabilities of Infringement Suits
|
Percentile of Distribution |
99th |
95th |
90th |
50th |
|
Aggregate |
7.9% |
3.8% |
2.8% |
0.8% |
|
Technology Field |
||||
|
Drugs |
9.4% |
3.9% |
2.8% |
0.9% |
|
Other Health |
19.5 |
6.1 |
4.5 |
1.7 |
|
Chemicals |
4.2 |
2.1 |
1.6 |
0.5 |
|
Electronics |
7.1 |
2.8 |
2.1 |
0.5 |
|
Mechanical |
6.5 |
2.8 |
2.2 |
0.7 |
|
Computers |
14.8 |
4.5 |
3.4 |
0.6 |
|
Biotechnology |
12.9 |
6.3 |
5.3 |
1.3 |
|
Miscellaneous |
8.3 |
4.6 |
3.7 |
1.9 |
|
Ownership Type |
||||
|
Domestic Individual |
9.4% |
4.4% |
3.5% |
1.9% |
|
Domestic Unlisted |
13.7 |
5.9 |
4.2 |
1.9 |
|
Small Domestic Listed |
6.3 |
5.4 |
4.1 |
1.8 |
|
Large Domestic Listed |
4.8 |
2.0 |
1.5 |
0.5 |
|
Foreign Listed |
2.5 |
1.4 |
1.0 |
0.3 |
|
Foreign Individual |
4.2 |
1.4 |
1.1 |
0.6 |
|
Foreign Unlisted |
1.4 |
0.8 |
0.7 |
0.3 |
|
NOTE: The distribution of population probabilities for patents with different characteristics is calculated by first computing the sample probabilities with the parameter estimates for infringement suits in Table 9. These are then adjusted to reflect population probabilities with Appendix equation (A.3.1). |
||||
probabilities are given in the first row of the table. The probability of litigation for the median patent is just under 1 percent. However, among the top 1 percent of patents (99th percentile), the probability of involvement in a suit is over 8 percent. The table shows that the rates can be far higher when the patents are segregated into different technology and ownership groups. The top percentile of patents in areas that are most at risk have probabilities of litigation over 15 percent (see Other Health, Computers, and Biotechnology). Similarly, the top 1 percent of all patents held by domestic unlisted firms or individuals have a litigation risk over 10 percent. Because most evidence, from patent renewal data and firm surveys, indicates that private value of innovations is highly skewed—with most value attributable to the top patents—it is precisely the litigation risk in these top percentiles that is relevant for determining R&D incentives.
We now turn to the econometric analysis of post-suit outcomes. In estimating these regressions, we do not control for selection, i.e., we do not use a (filing) selection equation together with the outcomes equation. Selection bias arises if there is significant covariance between the disturbances in the filing and outcome
equations. We ask: Given the selection that occurs at filing, is there any remaining association between patent and patentee characteristics and the outcomes? For purposes of assessing ex ante litigation risk (e.g., for patenting decisions or insurance pricing), this is the relevant question. Controlling for selection in the analysis of outcomes (see, e.g., Somaya, 2003) is appropriate if one wanted to infer the effects of characteristics in a random sample at the outcomes stage. In any event, the evidence that there is any sample selection bias is mixed (Somaya, 2003).
The evidence presented in the previous section indicated that the main characteristics of patents and their owners do not affect the probability of settlement after a suit is filed or the plaintiff win rates for cases that reach trial. The probit regressions for settlement and win rates confirm this conclusion. For brevity, we summarize the findings but do not present the parameter estimates. The settlement regression has a meager pseudo-R2 of 0.01. The null hypothesis that the regression as a whole is insignificant is not rejected [χ2(29) = 39.7; P-value = 0.089]. The only positive finding is that the coefficients on three technology field dummies are significant and indicate that the settlement probability is about eight percentage points higher for patents in Electronics, Mechanical, and Miscellaneous.23 The probit regression for win rates has a pseudo-R2 of 0.02. The whole regression is statistically insignificant [χ2(28) = 19.7; P-value = 0.90], as is each individual coefficient. On the basis of our discussions with staff at the FJC, there is no reason to believe that the data on settlements and plaintiff win rates are systematically bad (these outcome data are recorded at different times and in many different courts). We are confident that the “insignificance” of these regressions is meaningful, i.e., settlement and win rate outcomes are almost completely independent of observed characteristics of patents and their owners.
The probability that the settlement of infringement suits occurs early (before the pretrial hearing) is also unrelated to most characteristics of the patent and its owner, with three noteworthy exceptions [the probit regression is significant: χ2(29) = 50.5; P-value = 0.008]. First, early settlement is more likely if the patent in dispute is part of a larger portfolio (Portsize). A one standard deviation increase in portfolio size (1,300 patents) raises the probability of early settlement by about 12.9 percent. This is consistent with our earlier result that portfolio size makes filing a suit less likely in the first place, because of a greater ability to “trade” intellectual property. Second, a higher technology concentration index (C4) makes early settlement somewhat less likely. A one standard deviation in-
crease (doubling) in the concentration index lowers the probability by about 2 percent. Finally, patent owners that are large relative to a representative disputant (Relsize) are also less likely to settle early. A one standard deviation rise in relative size reduces the probability of early settlement by about 5 percent.24 Recall that the probability that a suit is filed is lower when the relative size of the patentee is larger, which we interpret as reflecting greater threat power. But if the (implicit) threats do not succeed in preventing the need to file suit, it is important for the patentee to carry out those threats to maintain credibility (post-suit “toughness”). Similarly, if the discipline of repeated interaction has failed to keep firms in a concentrated area out of court in the first place, the dispute is probably very intractable. Both could delay any post-suit settlement, and this is what we find.
CONCLUDING REMARKS
We studied the determinants of patent infringement and declaratory judgment suits, and their outcomes, by linking detailed information from the USPTO to data from the U.S. federal court system, the Derwent database, and industry sources. This allows us to construct a suitable controlled random sample of the population of potential disputants. The data set we construct is the most comprehensive yet available, covering all patent suits in the United States reported by the federal courts during the period 1978-1999.
A major finding of the chapter is that almost all of the effect of observable characteristics on patent disputes that we examined occurs in the decision to initiate a suit. Among others, these characteristics included the technology field, the number of patent claims, the numbers of forward and backward citations, patent portfolio size, type of patentee, and technology concentration index. Major post-suit outcomes—the probability of settlement and plaintiff win rates at trial—do not depend on these characteristics. From a policy perspective, this is good news because it means that enforcement of patent rights relies on the effective threat of court action (suits) more than on extensive post-suit legal proceedings that consume court resources. This feature is reinforced by high post-suit settlement rates and the fact that most settlement occurs soon after the suit is filed, often before the pretrial hearing is held. These findings mean that the enforcement of patent rights minimizes the use of judicial resources for sorting out patent disputes. The bad news is that individuals and small companies are much more likely to be involved in suits, conditional on the characteristics of their patent, but they are no more likely to resolve disputes quickly in post-suit settlements.
We also provide evidence that there are considerable advantages to scale in patent enforcement. Being able to trade a portfolio of intellectual property and having other dimensions of interaction that promote “cooperative” behavior are
likely sources of this advantage. Thus there are two sides to aggressive patenting strategies. On one hand, the buildup of large patent portfolios and the creation of patent thickets can make disputes over intellectual property more likely. But those same patents can also make the suits easier to resolve at lower cost.
An important direction for future research is to explore the dynamic aspects of conflict between firms over intellectual property assets. This would include studying the determinants of the filing and outcomes of multiple (sequential) suits on the same patent with different parties and multiple suits on different patents involving the same parties. Initial work along these lines for a sample of cases has been done by Somaya (2003). Proceeding further requires matching the names of litigants across all cases, a project that is under way. When completed, these data will provide information about the role of reputation building in the area of patent enforcement and allow a more detailed assessment of litigation risk and its associated costs.
REFERENCES
American Intellectual Property Law Association. (2001). Report of the Economic Survey. Arlington, VA: American Intellectual Property Lawyers Association.
Bebchuk, L. (1984). “Litigation and Settlement Under Imperfect Information.” RAND Journal of Economics 15: 404-415.
Cohen, W., R. Nelson, and J. Walsh. (2000). “Protecting Their Intellectual Assets: Appropriability Conditions and Why U.S. Manufacturing Firms Patent (or Not),” NBER Working Paper, No. 7552.
Cooter, R., and D. Rubinfeld. (1989). “Economic Analysis of Legal Disputes and Their Resolution.” Journal of Economic Literature 27: 1067-1097.
Danish Ministry of Trade and Industry. (2001). “Economic Consequences of Legal Expense Insurance for Patents,” report prepared for the Danish Patent Office by the Economic Analysis Group. Copenhagen .
Eisenberg, R. (1999). “Patents and the Progress of Science: Exclusive Rights and Experimental Use.” University of Chicago Law Review 56: 1017-1055.
Federal Judicial Center, Federal Court Cases: Integrated Data Base, 1970-89. Ann Arbor, MI: Interuniversity Consortium for Political and Social Research. Tapes updated to 1999.
Graham, S., B. Hall, D. Harhoff, and D. Mowery. (2003). “Patent Quality Control: A Comparison of U.S. Patent Re-examinations and European Patent Oppositions.” In W. Cohen and S. Merrill, eds., Patents in the Knowledge-Based Economy. Washington, D.C.: National Academy Press.
Grindley, P., and D. Teece. (1997). “Managing Intellectual Capital: Licensing and Cross-Licensing in Semiconductors and Electronics.” California Management Review 39(2): 8-41.
Hall, B., and R. Ziedonis. (2001). “The Patent Paradox Revisited: An Empirical Study of Patenting in the Semiconductor Industry, 1979-1999.” RAND Journal of Economics 32(1): 101-128.
Harhoff, D., and M. Reitzig. (2000). “Determinants of Opposition against EPO Patent Grants—The Case of Biotechnology and Pharmaceuticals.” CEPR Discussion Paper No. 3645, Centre for Economic Policy Research, London.
Jaffe, A., and M. Trajtenberg. (1999). “International Knowledge Flows: Evidence from Patent Citations.” Economics of Innovation and New Technology 8: 105-136.
Lanjouw, J. O., A. Pakes, and J. Putnam. (1998). “How to Count Patents and Value Intellectual Property: Uses of Patent Renewal and Application Data.” Journal of Industrial Economics 46(4) (December): 405-432.
Lanjouw, J. O., and J. Lerner. (2001). “Tilting the Table? The Predatory Use of Preliminary Injunctions.” Journal of Law and Economics 44(2): 573-603.
Lanjouw, J. O., and M. Schankerman. (2001). “Characteristics of Patent Litigation: A Window on Competition.” RAND Journal of Economics 32(1): 129-151.
Lerner, J. (1994). “The Importance of Patent Scope: An Empirical Analysis.” RAND Journal of Economics 25: 319-333.
Lerner, J. (1995). “Patenting in the Shadow of Competitors.” Journal of Law and Economics. 38: 463-96.
P’ng, I. P. L. (1983). “Strategic Behavior in Suit, Settlement and Trial.” Bell Journal of Economics 14: 539-550.
Priest, G., and B. Klein. (1984). “The Selection of Disputes for Litigation.” Journal of Legal Studies 13: 1-55.
Schankerman, M. (1998). “How Valuable Is Patent Protection: Estimates by Technology Field.” RAND Journal of Economics 29(1): 77-107.
Scotchmer, S. (1991). “Standing on the Shoulders of Giants: Cumulative Research and the Patent Law.” Journal of Economic Perspectives 5: 29-41.
Shapiro, C. (2001). “Navigating the Patent Thicket: Cross Licenses, Patent Pools and Standard-Setting.” In A. Jaffe, J. Lerner, and S. Stern, eds., Innovation Policy and the Economy. Cambridge: MIT Press for the NBER, vol. 1, pp. 119-150.
Siegelman, P., and J. Waldfogel. (1999). “Toward a Taxonomy of Disputes: New Evidence Through the Prism of the Priest/Klein Model.” Journal of Legal Studies 18(1): 101-130.
Somaya, D. (2003). Strategic Decisions not to Settle Patent Litigation,” Strategic Management Journal 24(1): 17-38.
Spier, K. (1992). “The Dynamics of Pretrial Negotiation.” Review of Economic Studies 59(1): 93-108.
Tirole, J. (1994). The Theory of Industrial Organisation.Cambridge, MA: MIT Press.
Waldfogel, J. (1998). “Reconciling Asymmetric Information and Divergent Expectations Theories of Litigation” Journal of Law and Economics XLI (October): 451-476.
APPENDIX 1 Reporting and Truncation Rates for Case Filings (percent)
APPENDIX 2 Computing Population Filing Probabilities and Their Variance
Let Lgz, Mgz, and Ngz denote, respectively, the number of patents in the litigated and matched samples and in the population that are in portfolios of size z and from group g, where the latter is defined by technology field, cohort, and ownership type. The observed filing probabilities in the sample are Lgz /(Lgz + Mgz). The filing probabilities in the population are qgz = [Lgz /Ngz]. We cannot calculate these directly because Ngz is unobserved. However, because the matched sample is random with respect to portfolio size, we can use the sample share of the patents in group g that are in portfolios of size z, Ŝgz= [Mgz/Mg], as an unbiased estimator of the population share [Ngz/Ng]. Using this, our estimator is:
Now, treating the population itself as a random sample from an underlying distribution, Lgz /Ng will also be an estimate of an underlying probability, say p, with an associated sampling variance. Taking a Talyor expansion, we can capture both sources of error in the following approximation:
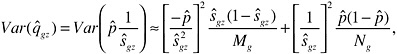
where the covariance terms are zero because the two sources of sampling error are independent. This simplifies to:
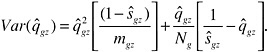
Filing probabilities at a more aggregated level are calculated as a weighted average of these rates, with weights based on Mg.
APPENDIX 3 Deriving Population Litigation Probabilities and Marginal Effects
Population Litigation Probabilities
We define classes by using characteristics with respect to which the sampling was nonrandom: USPC groups, cohort, infringement suits, and declaratory judgment suits. Let P(Xc) denote the population probability of litigation for a patent in class c with a vector of other characteristics Xc, and let Q(Xc) be the corresponding probability in the pooled (litigated and matched) sample. P(Xc) and Q(Xc) differ because the matched sample was constructed so that the overall litigation probability is 50 percent, controlling for technology and cohort. We want to infer P(Xc) from the estimated value of Q(Xc).
First we determine the extent to which we must inflate the matched sample for a given class to have it reflect the number of unlitigated patents in that class in the population. Let Q and P represent the aggregate sample and population litigation probabilities for a given class:
Q = L/(L + M)
Where L and M denote the number of litigated and matched patents in the sample. The population probability is
P = L/N
The number of litigated patents is the same in both cases because the sample contains all (reported) litigated patents, and N is the number of unlitigated patents in the class in the population. Using these equations, we get
N = {Q/(1 – Q)P}M = KM
Within a class, the matched patents are random draws so the distribution of characteristics in the matched sample is the same as the population. Thus the expected number of matched patents with characteristics Xc in the population, N(Xc), is greater than in the sample by the inflation factor, K, and so equals KM(Xc). Letting L(Xc) be the number of litigated patents with characteristics Xc, the expected population probability of litigation for such patents is
P(Xc) = L(Xc)/[KM(Xc)].
Similarly, Q(Xc) = L(Xc)/[L(Xc) + M(Xc)]. Solving for M and substituting, we get the result:
P(Xc) = Q(Xc)/[K(1 – Q(Xc))] (A.3.1)
Population Marginal Effects
For each characteristic Xk, the population marginal effect is
∂P(Xc)/∂Xkc = [dP(Xc)/dQ(Xc)] ∂Q(Xc)/∂Xkc
The last term is the sample marginal effect computed from the probit regression. From the expression for P(Xc) we get
dP(Xc)/dQ(Xc) = 1/K[1 – Q(Xc)]2
Measuring Q(Xc) by the sample probability of litigation in the class, Q, we get the result:
dP(Xc)/dQ(Xc) ≈ P/Q(1 – Q)
We measure P for each class as follows. For the denominator, we take the total number of patents in the class during 1978-1995. In the numerator we use the number of infringement or declaratory judgment suits that can be directly identified as such and include all others as infringement suits. These are inflated for underreporting and for truncation as described in Appendix 1. We then calculate marginal adjustment factors by USPC groups, infringement and declaratory judgment suits. Separate classes defined by cohort are not needed because of the maintained hypothesis that the litigation model applies to all cohorts, making nonsystematic sampling in this dimension unimportant. Results are at the bottom of Table 9. Because dP(Xc)/dQ(Xc) is the same for all Xk for a given class c, all sample marginal effects are adjusted by the same factor to convert them to population marginals.





































