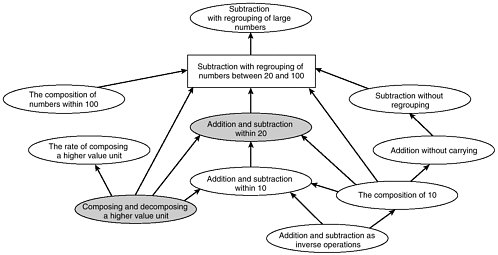
3
Mathematics
Debates about mathematics instruction have long focused on the relative importance of developing fluency with mathematical procedures and developing the ability to reason mathematically. Few on either side of the debate would disagree that both are necessary for competence in mathematics. There is disagreement, however, on the relative weight and share of instructional time to be given to each and on the approach to instruction that best supports mathematical competence.
Investment in recent decades by federal agencies and private foundations has produced a wealth of knowledge on the development of mathematical understanding and numerous curricula that incorporate that knowledge. As a result, elementary mathematics is ripe for investment in rigorous, independent evaluation to compare the outcomes of alternative approaches to teaching mathematics across a range of students, teachers, and contexts and making that knowledge usable and used widely by schools.
ELEMENTARY MATHEMATICS
STUDENT LEARNING
The Destination: What Do We Want Children to Know or Be Able to Do?
U.S. students fare poorly in international comparisons of mathematics achievement. They show weak understanding of basic mathematical concepts, and although they can perform straightforward computational procedures, they are notably
weak in applying mathematical skills to solve even simple problems (National Research Council, 2001c). These results have generally been attributed to the shallow and diffuse treatment of topics in elementary mathematics relative to other countries (National Research Council, 2001c).
The panel had the benefit of drawing on a recent synthesis of research on elementary mathematics (National Research Council, 2001c) and on the work of a RAND study group that produced a mathematics research agenda (RAND, 2002b). The National Research Council report presents a view of what elementary schoolchildren should know and be able to do in mathematics that draws on a solid research base in cognitive psychology and mathematics education. It includes mastery of procedures as a critical element of mathematics competence, but it places far more emphasis on conditional knowledge: understanding when and how to apply those procedures than is common in mathematics classrooms today. Conditional knowledge is rooted in a deeper understanding of mathematical concepts and a facility with mathematical reasoning. The NRC committee summarized its view in five intertwining strands that constitute mathematical proficiency (National Research Council, 2001c:5):
-
Conceptual understanding: comprehension of mathematical concepts, operations, and relations;
-
Procedural fluency: skill in carrying out procedures flexibly, accurately, efficiently, and appropriately;
-
Strategic competence: ability to formulate, represent, and solve mathematical problems;
-
Adaptive reasoning: capacity for logical thought, reflection, explanation, and justification;
-
Productive disposition: habitual inclination to see mathematics as sensible, useful, and worthwhile, coupled with a belief in diligence and one’s own efficacy.
A well-articulated portrait of mathematical proficiency is an important first step; it provides a well-defined goal for mathematics instruction. But important questions remain regarding the allocation of time and attention to the separate strands, as well as the approach to instruction that best supports the proficiency goal.
The Route: Progression of Understanding
Research has uncovered an awareness of number in infants shortly after birth. The ability to represent number and the development of informal strategies to solve number problems develop in children over time. Many studies have explored how preschoolers and children in the early elementary grades understand basic number concepts and begin operating with number informally well before formal instruction begins (Carey, 2001; Gelman, 1990; Gelman and Gallistel, 1978).
Children’s understanding progresses from a global notion of a little or a lot to the ability to perform mental calculations with specific quantities (Griffin and Case, 1997; Gelman, 1967). Initially the quantities children can work with are small, and their methods are intuitive and concrete. In the early elementary grades, they proceed to methods that are more general (less problem dependent) and more abstract. Children display this progression from concrete to abstract in operations first with single-digit numbers, then with multidigit numbers. Importantly, the extent and the pace of development depend on experiences that support and extend the emerging abilities.
Researchers have identified two issues in early mathematics learning that pose considerable challenges for instruction:
-
Differences in children’s experiences result in some children—primarily those from disadvantaged backgrounds—entering kindergarten as much as two years behind their peers in the development of number concepts (Griffin and Case, 1997).
-
Children’s informal mathematical reasoning and emergent strategy development can serve as a powerful foundation for mathematics instruction. However, instruction that does not explore, build on, or connect with children’s informal reasoning processes and approaches can have undesirable consequences. Children can learn to use more formal algorithms, but may apply them rigidly and sometimes inappropriately (see Boxes 3.1 and 3.2). Mathematical proficiency is lost because procedural fluency is divorced from the mastery of concepts and mathematical reasoning that give the procedures power.
|
BOX 3.1 When students attempt to apply conventional algorithms without conceptually grasping why and how the algorithm works, “bugs” are sometimes introduced. For example, teachers have long wrestled with the frequent difficulties that second and third graders have with multidigit subtraction in problems such as: A common error is: The subtraction procedure above is a classic case: Children subtract “up” when subtracting “down”—tried first—is not possible. Here, students would try to subtract 4 from 1 and, seeing that they could not do this, would subtract 1 from 4 instead. These “buggy algorithms” are often both resilient and persistent. Consider how reasonable the above procedure is: in addition problems that look similar, children can add up or down and get a correct result either way: Bugs often remain undetected when teachers do not see the highly regular pattern in students’ errors, responding to them more as though they were random miscalculations. |
|
BOX 3.2 Many examples can be cited in which students attempt to plug numbers into algorithms without thinking about their meaning, a phenomenon that stretches through all grades of schooling and all mathematical subjects. Even when students are capable of solving a problem correctly informally, they are found to produce incorrect answers when they use formal algorithms. In studies by Lochhead and Mestre (1988), for example, college students who were told that there are 6 times as many students as professors, and there are 10 professors, could correctly give the number of students. But when students are asked to write the formula to represent that situation, the majority write 6S = P. The formula seems correct to students even though the solution would yield 6 times as many professors as students. The occurrence of the word 6 near the word students is sufficient to lead to a formal representation of the problem that is at odds with their informal knowledge. |
The Vehicle: Curriculum Development
Past investments in R&D have produced curricular interventions to address each of the two problems raised above. With respect to the first, several curricula have been developed that introduce children to whole-number mathematics, with particular attention to the needs of young children who have had little preparation outside school. The most extensively researched of these is the Number Worlds curriculum, which has been tested in more than 20 matched, controlled trials. The results suggest that well-planned activities designed to put each step required in mastering the concept of quantity securely in place can allow disadvantaged students to catch up to their more advantaged peers right at the start of formal schooling (see Box 3.3). The curriculum has a companion assessment tool (the Number Knowledge Test) to help the teacher monitor and guide instruction. If results in controlled trials could be attained in schools across the country that serve disadvantaged populations, this would represent a major success with respect to narrowing the achievement gap, a long-standing national goal that has proven difficult to realize. Number Worlds is not the only curriculum designed to achieve this end. Others include Big Math for Little Kids (Ginsburg and Greenes, 2003) and Children’s Math Worlds (Fuson, 2003). While research to compare these curricula on a variety of dimensions is in order, it is clear that the tools to better prepare disadvantaged children for mathematics are now available.
With respect to the second concern—building children’s mathematical reasoning ability—controversy persists. While there is evidence that procedural knowledge without conceptual understanding leads to poor mathematical reasoning, it is also well documented that procedural knowledge is a critical element of mathematical competence (National Reasearch Council, 2001a; Haverty, 1999). Without adequate procedural knowledge, not only are children unable to engage in more challenging problem solving, but also, they are unable to engage in basic everyday transactions, like making change. The goal, then, must be one of strengthening mathematical reasoning without sacrificing procedural knowledge.
Research done in the 1990s investigated the effects on student achievement of instruction that builds on informal understandings and emphasizes mathematical concepts and reasoning. Cobb et al.’s problem-centered mathematics project (Wood
and Sellers, 1997), and cognitively guided instruction in problem solving and conceptual understanding (Carpenter et al., 1996) both reported positive effects. With support from the National Science Foundation (NSF), several full-scale elementary mathematics curricula with embedded assessments have been developed, directed at supporting deeper conceptual understanding of mathematics concepts and building on children’s informal knowledge of mathematics to provide a more flexible foundation for supporting problem solving. Three curricula developed separately take somewhat different approaches to achieving those goals: the Everyday Mathematics curriculum, the Investigations in Number, Data and Space curriculum, and the Math Trailblazers curriculum (Education Development Center, 2001).
All three curricula show positive gains in student achievement in implementation studies, in which the developers collect data on program effects. While such findings are encouraging, they must be viewed with a critical eye, both because those providing the assessment have a vested interest in the outcome and because the methodologies employed generally do not allow for direct attribution of the results to the program.1 Third party evaluations using comparison groups have been done in some cases, but none of these has involved random assignment, the condition that maximizes confidence in attributing results to the intervention. Nor do these studies measure either fidelity of implementation of the reform curriculum for the experimental group or the specific program features of the alternative used with the control group (see, for example, Fuson et al., 2000).
How students taught with these curricula compare with each other in mathematical proficiency and, perhaps more importantly, how they compare with students taught with curricula that devote more instructional time to strengthening formal procedural knowledge have not been carefully studied. From the perspective of practice, these are important omissions. To make informed curriculum decisions, teachers and school
|
BOX 3.3 From an early age, children begin to develop an informal understanding of quantity and number. Careful research conducted by developmental and cognitive psychologists has mapped the progression of children’s conceptual understanding of number through the preschool years. Just as healthy children who live in language-rich environments will develop the ability to speak according to a fairly typical trajectory (from single sound utterances to grammatically correct explanations of why a parent should not turn out the light and leave at bedtime), children follow a fairly typical trajectory from differentiating more from less, to possessing the facility to add and subtract accurately with small numbers. But just as a child’s environment influences language development, it influences the rate of acquisition of number concepts. For many children whose early years are characterized by disadvantage, there is a substantial lag in the development of the number concepts that are prerequisite to first grade mathematics. Between the ages of 4 and 6, most children develop what Case and Sandieson (1987) refer to as the “central conceptual structure” for whole number mathematics. The concepts are central in the sense that they are vital to successful performance on a broad array of tasks, and their absence constitutes the major barrier to learning. That structure involves four steps (pictured in Figure 3.1) that are developed in sequence: 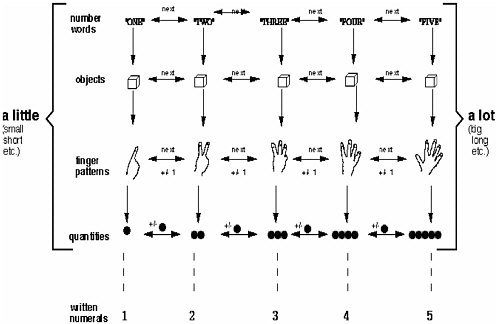 FIGURE 3.1 “Mental counting line” central conceptual structure. The bottom row of Figure 3.1 indicates that children recognize the written numerals. This information is “grafted on” to the conceptual structure above. |
While children with middle and higher socioeconomic status generally come to school with the central conceptual structure in place, many children from disadvantaged backgrounds do not. When first grade math instruction assumes that knowledge, these children are less likely to succeed. Sharon Griffin and Robbie Case designed a curriculum called Number Worlds that deliberately puts the central conceptual structure for whole number in place in kindergarten (Griffin and Case, 1997). Additional activities extend the knowledge base through second grade. Developed and tested with classroom teachers and children, the program consists primarily of 78 games that provide children with ample opportunity for hands-on, inquiry-based learning. Number is represented in a variety of forms—on dice, with chips, as spaces on a board, as written numerals. An important component of the program is the Number Knowledge Test, which allows teachers to quickly assess each individual student’s current level of understanding, and to choose individual or class activities that will solidify fragile knowledge and take students the next step. The Number Worlds program has been tested with disadvantaged populations in numerous controlled trials in both the United States and Canada with positive results. One longitudinal study charted the progress of three groups of children attending school in an urban community in Massachusetts for three years: from the beginning of kindergarten to the end of second grade. Children in both the Number Worlds treatment group and in the control group were from schools in low-income, high-risk communities where about 79 percent of children were eligible for free or reduced-price lunch. A third normative group was drawn from a magnet school in the urban center that had attracted a large number of majority students. The student body was predominantly middle income, with 37 percent eligible for free or reduced-price lunch. |
|
As Figure 3.2 shows, the normative group began kindergarten with substantially higher scores on the Number Knowledge Test than children in the treatment and the control groups. The gap indicated a developmental lag that exceeded one year, and for many children in the treatment group was closer to two years. By the end of the kindergarten year, however, the Number Worlds children narrowed the gap with the normative group to a small fraction of its initial size. By the end of the second grade, the treatment children actually outperformed the magnet school group. In contrast, the initial gap between the control group children and the normative group did not narrow over time. The control group children did make steady progress over the three years; however, they were never able to catch up. 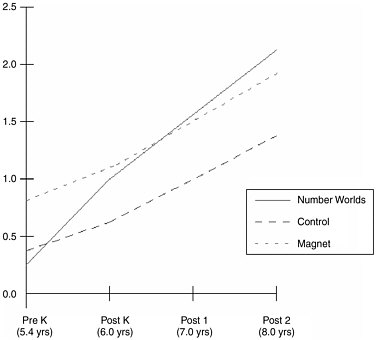 FIGURE 3.2 Mean developmental scores on number knowledge test at four time periods. |
administrators need to know what type of implementation of a specific curriculum produces what results, compared with the alternatives before them. Yet to provide the information that is most useful to practice is a major undertaking. These questions are answerable, but research carefully designed to provide those answers will take a substantial investment.
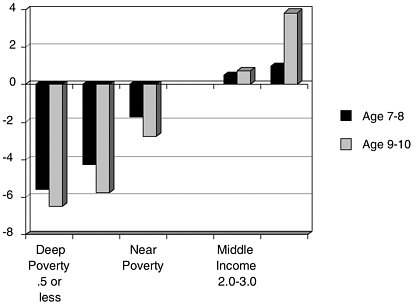 FIGURE 3.3 Income-to-needs and child cognitive ability: Deep poverty and math ability (PIAT-Math), NLSY-CS data set. SOURCE: Brooks-Gunn et al. (1999). The significance of these findings is suggested by the data in Figure 3.3 that plots Peabody Individual Achievement Test (PIAT) math scores against poverty level. Clearly the correlation is powerful; the deeper the level of poverty, the poorer the math scores. Importantly, as students move through school, the gap becomes more pronounced. Children ages 9-10 showed even larger score disparities than those ages 7-8. NAEP data indicate that in 1999 black 4- and 8-year-olds ranked in the 15th and 14th percentiles in math, respectively (Thernstrom and Thernstrom, in press). If the Number Worlds program can put poor children on a path to success in math, the contribution would be substantial. |
Checkpoints: Assessment
The curricula described above have embedded assessments that allow teachers to track student learning. A key feature of the Number Worlds curriculum is the Number Knowledge Test, which allows teachers to closely link instructional activities for children to the assessment results. How well other curricula link assessment and instruction is an issue worth investigation.
A separate issue is the assessment over time of the five strands that constitute mathematical proficiency. The past decade has seen the emergence of a spate of new tests and measures. No consensus has emerged, however, on critical measures. While there are some standard and widely used assessment tools to appraise young children’s emergent reading and language skills and competence, no such tools are used on any comparable basis in primary mathematics.
This type of assessment is required to evaluate the effectiveness of a particular curriculum and to make comparisons across curricula. For the most part, we lack sophisticated methods for tracking student learning over time or for examining the contribution of any particular instructional interventions, whether large or small, on students’ learning.
TEACHER KNOWLEDGE
Little is known about what it takes for teachers to use particular instructional approaches effectively, a necessary element of taking any approach to scale. The challenges can be substantial. The curricula mentioned above introduce major changes in approach to teaching mathematics, and effective implementation will require that teachers change their view of mathematics teaching and learning dramatically. In Everyday Mathematics, for example, teachers are expected to introduce topics that will be revisited later in the curriculum. Complete mastery is not expected with the first introduction. This has created some confusion for teachers, who are often unclear about when mastery is sufficient to move on to the next topic (Fuson et al., 2000).
All of the curricula encourage building on students’ own strategies for problem solving and supporting engagement through dialogue about the benefits of alternative strategies. The change required on the part of the teacher to relinquish control of the answer in favor of a dialogue among students has proven difficult when it has been studied (Palincsar et al., 1989). Adequate opportunities to learn and the ongoing supports for an entirely different approach to teaching will be critical to the effectiveness of efforts to scale up the implementation of the curricula. This is clearly an area in need of further study.
One clue regarding teacher knowledge requirements can be found in research pursued for the most part separately from the work on student learning and the design of curriculum ap-
proaches, tools, and materials discussed above. Investigations of teachers’ knowledge reveals that although teachers can, for the most part, “do” the mathematics themselves, they often are unable to explain why procedures work, distinguish different interpretations of particular operations, or use a model to closely map the meaning of a concept or a procedure. For example, teachers may be able to use concrete materials to verify that the answer to the subtraction problem in Box 3.1 is 37 and not 43. They can operate in the world of base ten blocks to solve 51–14 but may not be able to use base ten blocks to demonstrate the meaning of each step of the conventional (or other) algorithm.2
Similarly, teachers may be able to compute using familiar standard algorithms but not be able to recognize, interpret, or evaluate the mathematical quality of an alternative algorithm. They may not be able to ascertain whether a nonconventional method generalizes or to compare the relative merits and disadvantages of different algorithms (for example, their transparency, efficiency, compactness, or the extent to which they are either error-prone or likely to avert calculational error). These are clearly critical skills if teachers are to work with students’ informal understandings and strategies. Over and over, evidence reveals that knowing mathematics for oneself (i.e., to function as a mathematically competent adult) is insufficient knowledge for teaching the subject. In the domain of early number, studies suggest that most teachers’ own procedural knowledge is solid, but that their understanding of conceptual foundations is uneven. In a comparative study of elementary mathematics teachers in China and the United States, Liping Ma (1999) found a much larger proportion of U.S. teachers unable to explain whole-number problems—like subtraction with regrouping—using core mathematical concepts (see Box 3.4).
Following this work, some materials for use in teachers’ professional instruction have been developed.3 Modules and other curriculum materials contain focused work aimed at helping teachers learn the sort of mathematical knowledge of whole
|
BOX 3.4 A study by Liping Ma (1999) compares the knowledge of elementary mathematics of teachers in the United States and in China. She gives the teachers the following scenario: Look at these questions (52–25; 91–79, etc.). How would you approach these problems if you were teaching second grade? What would you say pupils would need to understand or be able to do before they could start learning subtraction with regrouping?(p.1). The responses of teachers were wide-ranging, reflecting very different levels of understanding of the core mathematical concepts. Some teachers focused on the need for students to learn the procedure for subtraction with regrouping: Whereas there is a number like 21–9, they would need to know that you cannot subtract 9 from 1, then in turn you have to borrow a 10 from the tens space, and when you borrow that 1, it equals 10, you cross out the 2 that you had, you turn it into a 10, you now have 11–9, you do that subtraction problem then you have the 1 left and you bring it down. (p.2). Some teachers in both the United States and China saw the knowledge to be mastered as procedural, although the proportion was considerably higher in the United States. Many teachers in both countries believed students needed a conceptual understanding, but within this group there were considerable differences. Some teachers wanted children to think through what they were doing, while others wanted them to understand core mathematical concepts. The difference can be seen in the two explanations below. They have to understand what the number 64 means … I would show that the number 64, and the number 5 tens and 14 ones, equal the 64. I would try to draw the comparison between that because when you are doing regrouping it is not so much knowing the facts, it is the regrouping part that has to be understood. The regrouping right from the beginning. This explanation is more conceptual than the first, and it helps students think more deeply about the subtraction problem. But it does not make clear to students the more fundamental concept of the place value system that allows the subtraction problems to be connected to other areas of mathematics. In the place value system, numbers are “composed” of 10s. Students already have been taught to compose 10s as 10 ones and 100s as 10 tens. A Chinese teachers explains as follows: What is the rate for composing a higher value unit? The answer is simple: 10. Ask students how many ones there are in a 10, or ask them what the rate for composing a higher value unit is, their answers will be the same: 10. However, the effect of the two questions on their learning is not the |
numbers and operations that is needed for teaching. As with the curricula developed for students’ learning discussed above, developers of teacher learning materials do provide some evidence of teachers’ learning of mathematics for teaching, but the role of this learning in their instructional practice and effectiveness has not been sufficiently explored. And still less is known about what teacher developers themselves need to know to support teachers’ learning and how their professional learning might be supported. The demand for skilled leaders who can teach teachers is growing, and yet the people who play these roles are more varied than any other category of educators and often have no professional preparation for working with teachers. Scaling up materials that can support teachers’ learning of mathematics for teaching will require attention to the knowledge requirements of those who will guide and support teachers.
RESEARCH AGENDA
Given the current state of practice and knowledge about learning and teaching of early number, then, what might a SERP program of research and development seek to do? How might it build on what currently exists and begin to extend and fill gaps in what is known and done, with the ultimate goal of more reliably and productively building evidence-based instructional practice? In other words, how could work be planned and carried out that would extend what is known and take that to scale in U.S. schools?
The proposed agenda is comprised of three major initiatives:
-
focus on developing assessments to measure student knowledge;
-
evaluation of promising curricula and the effects of their particular design features on student outcomes;
-
focus on the teacher knowledge requirements to comfortably and effectively use curricula that are built on research-based findings regarding student learning.
Initiative 1: Developing Early Mathematics Assessments
As described in Appendix A, quality assessments depend on three things: (1) clarity about the competencies that the assessment should measure, (2) tasks and observations that effectively capture those competencies, and (3) appropriate qualitative and quantitative techniques to give interpretive power to the test results. Clarity about the competencies to be measured requires a theoretical understanding (that is empirically supported) of mathematics learning. Unlike many other areas of the curriculum, early mathematics has the theoretical and conceptual models, as well as supporting empirical data, on which to build quality assessments. Substantial work has already been done to specify critical concepts and skills in this domain, providing assessment developers with substantial resources on which to draw in drafting the elements of a measurement strategy.
Even with a strong foundation on which to build in early mathematics, much work remains in designing and testing assessment items to ensure that inferences can accurately be drawn about student knowledge and competencies. And this work must be carefully crafted for the specific purpose and use of the assessment. This includes formative assessment for use in the classroom to assist learning. These assessments can, for example, provide feedback to the teacher on whether a particular skill or concept is mastered adequately, or whether some individual students need more time and practice before moving on. Summative assessments are also used in the classroom, but they come at the end of a unit, giving a teacher feedback on how well the students have mastered and brought together the set of concepts and skills taught in the unit. These may be helpful to the teacher in redesigning instruction for the next year, providing valuable data on students’ strengths and weakness that can inform instruction at the next level. School- or district-level assessments have a separate purpose. Rather than provide information on individual students, their purpose is to determine attainment levels for students as a group in order to evaluate the effectiveness of the school’s or the district’s instructional program and, in some cases, to hold schools accountable for the performance of their students.
Currently the different types of assessment are loosely con-
nected at best. Tensions are introduced when strong instructional programs and accountability assessments are at odds. Better aligning assessments, tying all assessments firmly to the theoretical and empirical knowledge base, are widely regarded as important to improving learning outcomes. In the area of mathematics, SERP affords a unique opportunity to pursue the development of an integrated assessment system with the three critical characteristics of comprehensiveness, coherence, and continuity described in Chapter 1 (National Research Council, 2001c). The construction of such a system is a major research, development, and implementation agenda that would require the stability, longevity, and support that SERP intends as its hallmark.
The work should be pursued as a collaborative effort involving teachers, content area specialists, cognitive scientists, and psychometricians. The effort could use as a departure point well-established standards in mathematics (e.g., National Council of Teachers of Mathematics), standards-based curricular resources, and rigorous research on content learning to identify and define what students should know in early mathematics, how they might be expected to show what they know, and how to appropriately interpret student performance. In the case of formative assessment, this extends to an understanding of the implications of what the evidence suggests for subsequent instruction. In the case of summative assessment, this means understanding the implications of student performance for mastery of core concepts and principles and its growth over time.
While there are several possible approaches to developing such a system of student assessments in early mathematics, one obvious place to begin is with a review of the assessment materials in existing widely used and exemplary curricular programs for formative and summative assessments, as well as state and national tests for policy making and accountability. These can be reviewed in light of cognitive theories of mathematical understanding, including empirical data regarding the validity of specific assessments. Research needs to focus on evidence of the effectiveness of specific assessments for capturing the range of student knowledge and proficiency for particular mathematical constructs and operations. A related line of inquiry should focus on issues of assessment scoring and reliability, particularly ease of scoring, consistency of scoring within
and across individuals, and consistency of interpretation of the results relative to the underlying cognitive constructs.
The power offered by assessments to enhance learning depends on changes in the relationship between teacher and student, the types of lessons teachers use, the pace and structure of instruction, and many other factors. To take advantage of the new tools, many teachers will have to change their conception of their role in the classroom. They will have to shift toward placing much greater emphasis on exploring students’ understanding with the new tools and then applying a well-informed understanding of what has been revealed by use of the tools. This means teachers must be prepared to use feedback from classroom and external assessments to guide their students’ learning more effectively by modifying the classroom and its activities. In the process, teachers must guide their students to be more actively engaged in monitoring and managing their own learning—to assume the role of student as self-directed learner. Clearly research of this type focuses on issues of teacher learning and knowledge that are poorly understood at present.
The development of assessments in early mathematics should therefore be closely tied to complementary initiatives in the areas of teacher knowledge and curriculum effectiveness. A strand of research focused on implementation issues should address the set of questions critical to successful use of quality assessments:
-
What teacher knowledge is necessary to support effective use of assessments in their instructional practice? These include teacher understanding of the assessments and their purpose, as well as practical considerations of the time to administer, score, and interpret results;
-
What forms of technology support are needed to assist teachers in the administration, scoring, and interpretation of a range of standards-based and theory-based assessments; and
-
How, and to what extent, does the process of implementing curriculum-based and standards-based assessments lead to changes in teachers’ instructional practices, and how do these changes affect student learning outcomes? This investigation should focus both on
-
changes in the near term and the stability of changes in the long term.
The power of new assessments to support learning also depends on substantial changes in the broader educational context in which assessments are conducted. For assessment to serve the goals of learning, there must be alignment among curriculum, instruction, and assessment. Furthermore, the existing structure and organization of schools may not easily accommodate the type of instruction users of the new assessments will need to employ. For instance, if teachers are to gather more assessment information during the course of instruction, they will need time to assimilate that information, thus requiring more time for reflection and planning. As new assessments are implemented, researchers will need to examine the effects of such factors as class size and the length of the school day on the power of assessments to inform teachers and administrators about student learning. It will be important for the work on learning and instruction to be closely tied to the work on schools as organizations.
Initiative 2: Teacher Knowledge
To take advantage of existing investments in research and development in elementary mathematics will require further work regarding teacher learning and knowledge requirements. There are two approaches to this teacher learning that could strategically build on work that has already been done. The first emphasizes teachers’ understanding of mathematical concepts and the connections among them, and the second focuses on the knowledge required for teachers to use promising curricula comfortably and effectively.
The work of Liping Ma described earlier (see Box 3.4) suggests that Chinese teachers who have a strong conceptual understanding of elementary mathematics organize their knowledge into “knowledge packages” in which core concepts are central and other required understandings and skills are organized around these concepts. Ma’s study is qualitative and so does not offer empirical support for the notion that the conceptual understanding of Chinese teachers is what produces higher student achievement. The power of the study is supported, however, by its theoretical underpinnings. Research on human
learning suggests that the organization of knowledge around core concepts is a key component to the effective acquisition, use, and transferability of that knowledge (National Research Council, 2000).
Ma’s work provides a point of departure for research that further explores the notion of knowledge packages and incorporates them into the preparation of elementary mathematics teachers. That research should be designed to measure the effects of that instruction at its conclusion, as well as at several periods of time after a teacher has engaged in practice. The research should be done in carefully controlled trials to allow for attribution of the outcomes to the program.
The second exploration of teacher knowledge should build on research that suggests that professional development is more productive when it is tied to specific curricula or instructional programs that teachers will then incorporate into their practice (Cohen and Hill, 2000). This research should begin with a clear articulation of the principles and assumptions about student learning that the curriculum incorporates, and comparing these to carefully solicited understandings of teachers. Learning experiences should be designed to address the points of divergence and tested for their power to change teacher conceptions.
In order to support taking curricula to scale, the support for teachers must be adequate when a researcher is not involved. This work on teacher knowledge should experiment with levels of support for teachers and involve cycles of design, testing, and redesign to create the materials and other supports that can allow teachers to use the curricula effectively independently.
The research on teacher learning should test effectiveness with regard to both teacher learning and the learning of their students. The relative benefits of teacher guides, videotaped cases, and opportunities to pose questions and receive support should be tested, as well as the timing effect (before instruction begins, during instruction, etc.) for different teacher learning opportunities.
Initiative 3: Curriculum Evaluation
The identification (and further development) of a set of approaches to the teaching of number and operations that vary on distinct and theoretically important dimensions would permit careful comparisons of how particular instructional regimes
impact students’ learning. Programs and approaches designed to build on students’ informal mathematical reasoning abilities, such as Number Worlds, Cognitively Guided Instruction, and the three NSF-supported curricula mentioned above, should be compared with more traditional curricula, like those produced by Saxon Publishers, Harcourt Brace, and McDougal Littell. This initial core would be expanded over time to include other theoretically and practically important alternatives.
Many of the evaluations of the curricula set out to answer the question “Does the curriculum improve student achievement?” While this is an important question for schools choosing a curriculum—and of particular interest to those who market a curriculum—the questions of importance for long-term improvements in practice are why, for whom, and compared with what? Exploring why an approach works can provide teachers and curriculum developers with critical information for improving their work. This kind of research will require going beyond evaluation of a curriculum as a whole into experimentation with particular features.
For example, Aleven and Koedinger (2002) compared groups of students who engaged in mathematics problem solving for the same amount of time, but one group was instructed to do self-explanation for each problem, and the other was not. Because self-explanation takes time, the latter group practiced almost twice as many problems, but their learning was more shallow and did not transfer as well as the self-explainers. Understanding the individual contributors (like self-explanation) to outcomes will require this level of probing.
School decision makers also need a knowledge base that will allow them to make more informed choices for their particular school(s). Number Worlds shows very promising results for disadvantaged children; Everyday Mathematics does as well. How, and for whom, do those outcomes differ? Are there trade-offs in the competencies children gain from each? Does the context in which they work best differ? Each of the three NSF elementary mathematics curricula takes a somewhat different approach to instruction. How are those differences reflected in outcomes for students? Does one better address the needs of low- or high-achieving students?
An analysis of existing candidate materials could illuminate important differences. The implementation, adaptation, and use of these different approaches could be followed over time, at-
tending to instructional practice, students’ opportunities to learn, and implementation issues. In addition, based on what is known about teachers’ knowledge of whole numbers and operations for teaching, as well as about their learning, systematic variations could be designed to support the implementation of these different instructional approaches. For example, in one set of schools, a teacher specialist model might be deployed and, in others, teachers might engage in closely focused study of practice (instruction, student learning, mathematical tasks), coplanning and analyzing lessons across the year. In still others, teachers might be given time and be provided incentives to spend time planning with the ample teacher guides.
The work could be conducted in carefully controlled, longitudinal studies carried out in SERP field sites. Because SERP would have relationships established with a number of field sites and data collection efforts in those sites already under way, taking on a controlled experimental study of alternative curricula would be far less daunting a task than it would be for researchers working independently. Moreover, the concern for undertaking research that is maximally useful to educational practice and the ability to design and conduct—or oversee the conduct of—that research will be combined in a single organization. Such a situation does not now exist.
ALGEBRA
STUDENT KNOWLEDGE
Algebra, foundational to so much other mathematics, and so poorly learned in general, is an area in critical need of concentrated research and development. Algebra is crucial to the development of mathematical proficiency because it functions as the language system for ideas about quantity and space. Algebra moves attention from particular numerical relations and computational operations to a more general mathematical environment with notation and representation useful across all areas of mathematics. These represent vital, but precarious, passages; students’ transitions into the domain of algebra are often plagued with problems.
Although it has long been considered important, attention
to the role of algebra has never been more intense. Traditionally, high school mathematics tended to have two tracks. The academic track included a Euclidean proof-oriented geometry course and a series of algebra courses focused on preparing students for calculus. The other was a nonacademic series of practical courses—sometimes called business math—which often were just a review of middle school mathematics, particularly rational number arithmetic. A series of studies found a strong positive correlation between participation in the academic mathematics stream and future earnings (Pelavin and Kane, 1990). Some studies have shown that this correlation may be causal (Bednarz et al., 1996). Children who would have been directed to the practical stream were successful in the academic stream (Porter, 1998).
All current curricular recommendations and frameworks place a high premium on algebra. The recent National Research Council report, Adding It Up, recommends that the basic ideas of algebra as generalized arithmetic be introduced in the early elementary grades and learned by the end of middle school. This is consistent with curricular opportunities in other countries (National Research Council, 2001a).
The Destination: What Do We Want Students to Know and Be Able to Do?
Algebra provides powerful abstract concepts and notation to express mathematical ideas and relationships and a set of rules for manipulating them. These tools are invaluable for solving a wide range of problems. Learning to make sense of and operate meaningfully and effectively with these tools is a central goal of instruction. This power involves both moving from contexts to abstract models and, conversely, interpreting abstract ideas skillfully in concrete situations. Moving beyond this core goal, however, one moves into contested terrain.
What should be the subject matter of algebra? Many new curricula take a view of algebra that is at variance with how it is conceived within the discipline and with how it has been treated historically in the school curriculum. In recent years, a number of individuals, groups, committees, and task forces have worked to provide definitions or characterizations to describe the continually evolving school algebra. These characterizations typically include such ideas as: algebra as a consolidation of, or generalization of, ideas in arithmetic; algebra as the study of
structures, patterns, and symbolic representations; algebra as the study of functions, covariation, and modeling.
Overlaid on the content debates are two different visions of how algebra should be taught. The first is motivated by the observation that students do not seem to really understand or value what they are doing in algebra. It therefore emphasizes algebra as a tool for solving real-world problems. In a somewhat caricatured form it might be seen as teaching students to be intelligent spreadsheet users who can create effective formulas and graphs. The second, more traditional view stresses algebra as a preparation for traditional college mathematics (which itself is in a state of reform and counterreform). In its extreme it emphasizes formal proofs and skills that are undoubtedly challenging for most high school students.
Algebra, of course, legitimately includes all of the content areas described above. Both the ability to solve real-world problems and to solve formal proofs are valuable outcomes for different purposes. Trade-offs become necessary only when the limits on instructional time force them. Currently there is little understanding of the affordances of different instructional emphases. It is therefore of little surprise that there is no consensus on how choices should be made or whether different options should be available for pursuing academic algebra.
The Route: Progression of Student Understanding in Algebra
Traditionally, students take a prealgebra course in the eighth grade and go on to a full algebra 1 course in the ninth grade, geometry in the tenth grade, Algebra 2 in the eleventh grade, and elementary functions in the twelfth. However, there are many variations on this pattern, including a substantial minority of students who begin this sequence a year early and many school systems that teach an integrated curriculum from grades 9 to 11 and do not have a year just for geometry. Traditionally, a large fraction of students never even begin this academic stream, and many who do fail to complete it.
Mastery of algebra builds on mastery of the mathematics taught in earlier years. One might wish that students coming into this curriculum would have mastered rational numbers, but this is often not the case and it causes difficulties for mastery of algebra. For instance, it is common to see students perform
flawlessly when solving simple linear equations involving integers but fail when the same equations involve fractions. Poor fluency with rational number arithmetic and arithmetic more generally adds to the cognitive demands on a student and interferes with learning of higher level ideas (Haverty, 1999). And poor understanding of rational numbers spells disaster when students come to later topics like rational expressions.
Students also often come with an understanding of their earlier curriculum that creates difficulty for algebra. For instance, the equal sign has typically had the meaning of an operation (e.g., 3 + 4 = is a request to perform addition) rather than of a relationship between two expressions. Still, students have informal ways of reasoning about problems that can be quite powerful. For instance, consider the following two problems:
As a waiter, Ted gets $6 per hour. One night he made $66 in tips and earned a total of $81.90. How many hours did Ted work?
Versus
x * 6 + 66 = 81.90
While only 42 percent of algebra 1 students can solve the second equation, a full 70 percent can solve the word problem (Koedinger and Nathan, in press). Students bring informal ways of reasoning about their mathematical knowledge that enables them to solve these problems. Often students have difficulties understanding why they are being taught algebraic symbol manipulation to solve such problems when initially this just makes solving them harder and more error-prone. Rather than replacing the informal with the formal, Koedinger and Anderson (1998) and Gluck (1999) have shown that by building on these informal processes, one can more effectively teach students to use the formalisms of algebra.
How do students develop the capacities to move from contexts to abstract models and, conversely, to interpreting abstract ideas skillfully in concrete situations? Beliefs abound about the directionality of these connections in learning: Some argue that all meaningful learning must move from the concrete to the abstract; others insist that the power of the generalized, abstract
forms affords learners greater insight. Notions of what counts as concrete or abstract remain vaguely and variously defined.
The Vehicle: Curriculum and Pedagogy
New curricular materials introduce algebra in various segments of the K-12 mathematics sequence using a variety of conceptions of algebra. Some take an equation-solving orientation; others take a function approach; still others take a mathematical modeling approach. Yet we do not know how these various curricular approaches affect students’ understanding and continued use of algebra.
The hypothesis that algebra instruction moves to abstraction without first connecting the abstractions with the concrete instances that justify them has led to the development of new curricula that emphasize richly contextualized problems. Some research evidence suggests that student engagement is higher and that students work meaningfully with important mathematical ideas, outperforming students whose curricular experiences do not include such rich investigative problems (e.g., Boaler, 1997; Brenner et. al., 1997; Nathan et. al., 2002). But some caution that such problems, if taken seriously, demand close attention to the contexts; whereupon students may become preoccupied with the contextual particularities in ways that distract from the mathematical ideas entailed (Lubinski et al., 1998). Consequently, they may not develop abstract knowledge central to mathematical proficiency. Some instructional approaches look for a middle ground in which algebra knowledge is contextualized, but the context is kept simple, and a single context is used extensively to help students see through to the underlying mathematical functions (Kalchman et al., 2001; Kalchman and Koedinger, forthcoming). Much remains to be investigated about how students develop the ability to work effectively with abstract ideas and notation, as well as about the relationships between abstraction and concrete experiences in learning.
A focus on algebra would afford opportunities to probe how different instructional uses of technology interact with the development of symbol manipulation skills. With the increased availability of technology, what is meant by “symbolic fluency” raises new questions. What is the role that graphing calculators
and computational algebraic systems might play? What is the role of paper and pencil computation in developing understanding as well as skill? These are questions that appear at every level of school mathematics.
Checkpoints: Assessment
Algebra represents a major challenge for many students. If more students are to succeed in meeting that challenge, it will be important to identify the points of difficulty for individual students and provide effective instructional responses before they are lost. The difficulty factors assessments of algebra reading (Koedinger and Nathan, In Press) and algebra writing (Heffernan and Koedinger, 1997, 1998) are examples of efforts to provide assessment tools for this purpose.
Two features of the subject make assessing individual progress very important. Algebra requires facility with much of the mathematics that has come before. If the mathematical foundation is weak in any of its components, algebra mastery will be undermined. Determining where students need to shore up the preparatory mathematics, as well as opportunities for doing so, are critical to success.
Second, algebra instruction moves toward high-level abstraction. The readiness of individual students to move from one level of difficulty to the next will differ. If the movement comes before a bridge is effectively built to a student’s prior knowledge or before new knowledge is consolidated, the student will be lost. If movement toward greater difficulty does not come soon enough, a student will make less progress in higher level algebra than is possible. Indeed, precisely this is at the heart of opposing views of algebra pedagogy. If formative assessment were sophisticated enough to determine individual student readiness to move on, then trade-offs between attending to the needs and preparedness of different students would not be necessary.
A research and development effort at Carnegie Melon University that generated the Algebra Cognitive Tutor has focused very productively on the second element of this problem (see Box 3.5). It began as a project to see whether a computational theory of thought, called ACT (Anderson, 1983), could be used as a basis for delivering computer-based instruction. The cognitive theory applies to problem solving more broadly. For pur-
poses of algebra teaching, it was the foundation for modeling the variety of different approaches—both correct and incorrect—that students typically take to solving algebra problems. A number of different approaches can lead to a correct solution, and the program does not favor one over another. However, some approaches lead the student astray. If the student is working effectively on a problem, there is no computer feedback. But when a student begins down an unproductive or erroneous path, the computer program recognizes this by a process called model tracing and provides hints and instruction to guide the student’s thinking.
The Algebra Cognitive Tutor also assesses mastery of elements of the curriculum by a process called knowledge tracing. When a student’s problem-solving efforts suggest that the relevant knowledge or skill is not yet consolidated, the computer selects instruction and problems appropriate to where that student is in the learning trajectory.
In studies of cognitive tutors more generally, it was found that under controlled conditions, students could complete the curriculum in about a third of the time generally required to master the same material, with about a standard deviation (approximately a letter grade) improvement in achievement (Anderson et al., 1995). In real classrooms, the impact has generally not been as large. A third-party evaluation of the tutors suggested that the scaffolding of learning that allowed students to experience success with challenging problems produced large motivational gains (Schofield et al., 1990).
TEACHER KNOWLEDGE
In the past, only teachers of high school students were thought to need knowledge of algebra. Although their preparation to teach does not include study of the objects and processes of high school algebra, little attention has been paid to whether or not secondary school teachers do in fact have adequate algebraic knowledge for teaching (Ferrini-Mundy and Burrill, 2002). Students preparing to be secondary school teachers typically take courses in abstract algebra and analysis, under the assumption that such mathematical background will serve them well as secondary school teachers. Yet the actual knowledge developed in such courses and its application by teachers in classrooms has not been thoroughly studied. Some research suggests that the
|
BOX 3.5 The Algebra Cognitive Tutor is one of a set of cognitive tutors developed at Carnegie Mellon. Of great relevance to the SERP vision, the tutors are a good illustration of how to make the transition from the laboratory to the classroom. The work at Carnegie Mellon began as a project to see whether a computational theory of thought, called ACT (Anderson, 1983), could be used as a basis for delivering computer-based instruction in algebra. The ACT theory of problem-solving cognition is the basis for modeling students’ algebra knowledge. These models can be captured in a computer program that can generate or identify a range of characteristic approaches to solving an algebra problem. These cognitive models enable two sorts of instructional responses that are individualized to students:
Developing cognitive models that accurately reflect competence and developing appropriate instructional responses is an iterative process. The success of the tutors depends on a design-test-redesign effort in which models are assessed for how well they capture competence and instructional responses are assessed for how effective they are. In studies of cognitive tutors more generally, it was found that in controlled laboratory condition students using a cognitive tutor could go through a curriculum in a third of the time, and in carefully managed classrooms students would show about a standard deviation (approximately a letter grade) improvement in achievement compared with students receiving standard instruction (Anderson et al., 1995). In real classroom situations, the impact of the tutors tends not to be as large, varying from 0 to 1 standard deviation across more than 13 evaluations. Another third-party evaluation, focusing on the social consequences of the tutors, documented large motivational gains resulting from the active engagement of students and the successful experiences on challenging problems (Schofield et al., 1990). However, unlike many such small-scale success stories in cognitive science, this project was able to grow to the point at which the cognitive tutors now are used in over 1,200 schools, 46 of 100 largest school districts, and interacting with about 170,000 students yearly. A number of features were critical to making this successful transition: |
While the cognitive tutor enterprise illustrates what needs to be done to transition research ideas into the American classroom, it does not represent a complete solution to even high school algebra. Early in the development of the Algebra Cognitive Tutor, a decision was made to place a heavy emphasis on contextualizing algebra to help students make the transition to the formalism. The course has been demonstrated to raise student achievement in urban schools and to reduce the number of students dropping out. However, high-achieving students may not be fully achieving the desired fluency in symbol manipulation and abstract analysis. There is no reason why the cognitive tutors could not more fully address these topics and, in fact, many tutor units do, particularly in the algebra 2 course. However, a more accelerated course may yield better results for high-achieving students. |
assumption that secondary school teachers have strong and flexible knowledge of algebra is unfounded (Ball, 1988). In fact, evidence suggests that secondary school teachers may often have rule-bound knowledge of procedures but lack conceptual, connected understanding of the domain. That some signals existed that high school teachers’ knowledge may not be as robust as had been suspected is not so surprising, since they are educated in the very mathematics classrooms that many seek to improve.
Still, this result signals a more significant problem. First, the changes in and expansion of what is meant by algebra mean that secondary school teachers are increasingly being called on to teach algebraic ideas and connections that they have not themselves studied or have not studied in such ways. Analyses of what the new curricula demand of teachers could make visible the mathematical demands of those curricula and permit investigation of teachers’ current knowledge to teach those materials. Second, the movement of algebraic ideas into the middle school and especially the elementary school curriculum means that teachers who have not in the past taught algebra are now being called on to teach ideas and processes for which they have not in the past been responsible. Prospective elementary school teachers’ knowledge of algebra may be based largely on their own experiences as high school students. The new requirements of elementary school teaching raise important and pressing needs for research on teacher knowledge, teaching, and teacher learning specifically in algebra.
Not only do teachers need knowledge of the mathematical content, however. Equally important (and related) is knowledge of how students think about and develop algebraic ideas and processes. What ideas or procedures are particularly difficult, both in reading and writing mathematical relationships, for many students? As algebra shifts to being a K-12 subject, rather than a pair of high school courses, new questions emerge that warrant investigation: If students learn about variables and equations sooner and engage earlier in algebraic reasoning (Carpenter and Franke, 2001), how will these earlier experiences shape the development of students’ algebraic proficiency over time? How do students of different ages manage and use symbolic notation, both in reading and writing mathematical relationships? What supports the development of meaningful and skilled fluency with mathematical symbols and syntax? In fac-
ing diverse classes of students, teachers also need to understand better the mathematical resources and difficulties that their students bring from their own environments, as well as how to make productive use of and mediate those (see Moses and Cobb, 2001, for a robust example of designing strong connections between the domain of algebra and students’ out-of-school activities and knowledge use).
RESEARCH AGENDA
There is little agreement at this point on what algebra should be taught or how it should be taught. As in other areas of the curriculum, the questions are in part a matter of valued outcomes for algebra instruction and the instructional time allocation across algebra and other subjects. But a study of the outcomes of different instructional choices can make the decisions far more rational than they can be in the absence of high-quality data.
We propose research and development on four major initiatives in this area:
-
Alternatives in the teaching and learning of algebra;
-
Teacher knowledge;
-
Developing algebra assessments and instruments;
-
Students’ development over time and the effects of different curricular choices.
Initiative 1: Research and Development on Alternatives in the Teaching and Learning of Algebra
Work supported by the National Science Foundation as well as by private foundations has generated a variety of curriculum materials for schools that constitute different perspectives on algebra, different ideas about what is important for students to learn, and different ideas about how students can most effectively be taught that can be contrasted with the best traditional approaches to teaching algebra. Since these curricula are already developed and in use, they provide an opportunity for understanding the consequences of the choices made.
For example, in some materials a functions approach to algebra is central, while in others, algebra is treated more as generalized arithmetic, and the solving of equations is more
prominent. In some approaches, students are engaged in using the tools of algebra to model situations and problems, while, in others, algebra as an abstract language is stressed. While much controversy surrounds the worth and merit of these different perspectives on the subject, additional debates center on the contribution of calculators and other technology, the structure of lessons, and the role of the teacher. Because curricula have already been developed that represent these different perspectives on the subject and on how it might best be taught, one important initiative of SERP might be to design comparative studies of how these curricula are taught in classrooms and what and how diverse students learn algebra over time.
In this initiative, cohorts of students could be followed longitudinally. Studies could gather information about the instruction they receive, exposure to curriculum, information on the teachers, and their use of the curriculum and other tools. This initiative will depend on the development of effective assessments (see Initiative 3).
As with elementary mathematics, however, knowing why particular curricular interventions produce particular outcomes will require companion controlled experiments at the level of particular program features to test for causality. This kind of research is necessary not only to advance scientific understanding, but also because it provides critical knowledge for teachers who adapt curricula and allows developers to improve curricula or design alternatives that are responsive to research findings.
Simultaneous with this effort, SERP can support curriculum development that extends existing curricula in promising directions. The Algebra Cognitive Tutor, for example, emphasizes highly contextualized problem solving. While many fewer students drop out and students master the material covered more quickly and effectively, the curriculum may not achieve the fluency in symbol manipulation and abstract analysis expected for high-achieving students. The developers suggest that the curriculum could quite easily be strengthened in this respect, and a separate accelerated algebra course is likely to yield even better results for high-achieving students. In studying the set of curricula as they are being implemented, SERP as a third-party entity would be well positioned to identify and support promising areas like this for further development.
Initiative 2: Research and Development on Teacher Knowledge
Important questions remain unanswered about the knowledge of mathematics needed to teach algebra effectively. As with elementary mathematics, the existence of different curricular approaches and efforts to study them, as outlined above in Initiative 1, provide the opportunity to investigate the demands for teachers in teaching different curricular approaches to algebra. For example, specifically what mathematical demands arise for teachers in teaching approaches to algebra that emphasize symbolic fluency compared with approaches that emphasize modeling and connections to situations? What sort of representational and notational fluency do teachers need? How do teachers need to understand the connections between algebra and other domains of mathematics, and what is demanded of teachers with respect to mathematical reasoning under different approaches to algebra?
The movement of algebra into the elementary school curriculum, as recommended both by the National Council of Teachers of Mathematics’ Principles and Standards for School Mathematics (2000) and Adding It Up (National Research Council, 2001a), creates the opportunity to examine what elementary teachers need to know with respect to algebra. Typically regarded as a secondary school subject, algebra has not played a central role in the preparation of elementary school teachers. Studies of teachers engaged with the new curricula that include elementary school skills and ideas of algebra could provide insight into the kinds of algebra knowledge useful to the teaching of young children. Where and how do ideas and skills of algebra surface in younger children’s learning, and what sorts of knowledge would help teachers address and develop those? As in other areas of the curriculum, it will be particularly important to identify the issues with which teachers struggle most, the conceptions that make effective teaching more difficult.
As in Initiative 1, the study of teacher knowledge requirements would provide the basis for research and development on effective teacher education interventions. The development efforts would be expected to target a variety of teacher learning opportunities, including pre-service education in teaching mathematics, teacher support materials, and in-service education associated with the use of particular curricula.
Initiative 3: Developing Algebra Assessments and Instruments
Efforts to improve algebra instruction, as well as to evaluate the effectiveness of alternative approaches to the teaching of algebra, will depend on the development of new assessments of students’ and teachers’ learning.
The development of formative assessments for instructional purposes will need to test hypotheses about what is difficult for students to learn, as well as hypotheses about the kinds of scaffolds that provide support for learning when students are struggling. For classroom effectiveness, these assessments must be closely tied to instructional materials. An investment in the development of algebra assessments that capture all aspects of algebra proficiency, including the robustness and flexibility of conceptual and procedural knowledge and the ability to transfer learning to novel problems, will need to be developed if outcomes of alternative approaches to instruction are to be meaningfully compared.
Assessments will also be needed that can discriminate different kinds and levels of knowledge for the teaching of algebra. These should include both the knowledge of subject matter and pedagogical content knowledge.
Moreover, in order to compare differences in students’ opportunities to learn in circumstances in which the teacher or the curriculum changes, instruments to gather information about instruction itself will be important. For example, the representations and tools that are used and the type, frequency, and duration of their use needs to be captured. Measures of fidelity of implementation and of teacher support will be required as well. These investments in instrumentation and assessment tools at the start will allow for subsequent work to be far more powerful for guiding instructional practice.
Initiative 4: Students’ Development Over Time and the Effect of Different Curricular Choices
Because algebra is increasingly seen as a K-12 strand of a mathematics curriculum, not merely as a high school course or pair of courses, the timing is right to design studies that track students across their school careers, investigating the develop-
ment of proficiency in algebra. Such longitudinal studies of algebra learning could be designed to examine how particular configurations of curricular and pedagogical choices affect what students learn. For example, do students whose experiences with number and operations are designed to develop deep conceptual understanding and procedural fluency fare differently in algebra than those whose opportunities to learn emphasize applications and modeling? How do differences in the development of arithmetic fluency affect the development of students’ algebraic proficiency?
Initially, the work involved will be to design careful procedures for longitudinal data collection. Doing so will hinge on Initiative 3, in which input and outcomes measures are tested and developed. While the fruits of this research would not be expected in the early years of the program, designing the data collection effort early and carefully will be critical to high-quality analysis further down the road.