E
Basic Principles of Statistics1
All measurements are subject to error. Analytical chemical measurements often have the property that the error is proportional to the value. Denote the ith measurement on bullet k as Xik (we will consider only one element in this discussion and hence drop the subscript j utilized in Chapter 3). Let ![]() denote the mean of all measurements that could ever be taken on this bullet, and let
denote the mean of all measurements that could ever be taken on this bullet, and let ![]() denote the error associated with this measurement. A typical model for analytical measurement error might be
denote the error associated with this measurement. A typical model for analytical measurement error might be
Likewise, for a given PS bullet measurement, Yik, with mean ![]() and error in measurement ηik,
and error in measurement ηik,
Notice that if we take logarithms of each equation, these equations become additive rather than multiplicative in the error term:
Models with additive rather than multiplicative error are the basis for most statistical procedures. In addition, as discussed below, the logarithmic transformation yields more normally distributed data as well as transformed measure-
ments with constant variance. That is, an estimate of log(µxk) is the logarithm of the sample average of the three measurements on bullet k, and a plot of these log(averages) shows more normally distributed values than a plot of the averages alone. We denote the variances of ![]() and
and ![]() as
as ![]() and
and ![]() and the variances of the error terms
and the variances of the error terms ![]() and
and ![]() as
as ![]() and
and ![]() respectively. It is likely that the between-bullet variation is the same for the populations of both the CS and the PS bullets; therefore, since
respectively. It is likely that the between-bullet variation is the same for the populations of both the CS and the PS bullets; therefore, since ![]() should be the same as
should be the same as ![]() we will denote the between-bullet variances as
we will denote the between-bullet variances as ![]() Similarly, if the measurements on both the CS and PS bullets were taken at the same time, their errors should also have the same variances; we will denote this within-bullet variance as
Similarly, if the measurements on both the CS and PS bullets were taken at the same time, their errors should also have the same variances; we will denote this within-bullet variance as ![]() or σ2 when we are concentrating on just the within-bullet (measurement) variability.
or σ2 when we are concentrating on just the within-bullet (measurement) variability.
Thus, for three reasons—the nature of the error in chemical measurements, the approximate normality of the distributions, and the more constant variance (that is, the variance is not a function of the magnitude of the measurement itself)—logarithmic transformation of the measurements is advisable. In what follows, we will assume that xi denotes the logarithm of the ith measurement on a given CS bullet and one particular element, µx denotes the mean of these log(measurement) values, and εi denotes the error in this ith measurement. Similarly, let yi denote the logarithm of the ith measurement on a given PS bullet and the same element, µy denote the mean of these log(measurement) values, and ηi denote the error in this ith measurement.
NORMAL (GAUSSIAN) MODEL FOR MEASUREMENT ERROR
All measurements are subject to measurement error:
Ideally, εi and πi are small, but in all instances they are unknown from measured replicate to replicate. If the measurement technique is unbiased, we expect the mean of the measurement errors to be zero. Let ![]() and
and ![]() denote the measurement errors’ variances. Because µx and µy are assumed to be constant, and hence have variance 0,
denote the measurement errors’ variances. Because µx and µy are assumed to be constant, and hence have variance 0, ![]() and
and ![]() The distribution of measurement errors is often (not always) assumed to be normal (Gaussian). That assumption is often the basis of a convenient model for the measurements and implies that
The distribution of measurement errors is often (not always) assumed to be normal (Gaussian). That assumption is often the basis of a convenient model for the measurements and implies that
(E.1)
if µx and σx are known (and likewise for yi, using µy and σy). (The value 1.96 is often conveniently rounded to 2.) Moreover, ![]() will also be normally
will also be normally
distributed, also with mean µx but with a smaller variance, ![]() therefore
therefore
Referring to Part (b) of the Federal Bureau of Investigation (FBI) protocol for forming “compositional groups” (see Chapter 3), its calculation of the standard deviation of the group is actually a standard deviation of averages of three measurements, or an estimate of ![]() in our notation, not of σx. In practice, however, µx and σx are unknown, and interest centers not on an individual xi but rather on µx, the mean of the distribution of the measured replicates. If we estimate µx and σx using
in our notation, not of σx. In practice, however, µx and σx are unknown, and interest centers not on an individual xi but rather on µx, the mean of the distribution of the measured replicates. If we estimate µx and σx using ![]() and sx from only three replicates as in the current FBI procedure but still assume that the measurement error is normally distributed, then a 95 percent confidence interval for the true{µx} can be derived from Equation E.1 by rearranging the inequalities using the correct multiplier, not from the Gaussian distribution (that is, not 1.96 in Equation E.1) but rather from Student’s t distribution, and the correct standard deviation
and sx from only three replicates as in the current FBI procedure but still assume that the measurement error is normally distributed, then a 95 percent confidence interval for the true{µx} can be derived from Equation E.1 by rearranging the inequalities using the correct multiplier, not from the Gaussian distribution (that is, not 1.96 in Equation E.1) but rather from Student’s t distribution, and the correct standard deviation ![]() instead of sx:
instead of sx:
Use of the multiplier 2 instead of 2.484 yields a confidence coefficient of 0.926, not 0.95.
CLASSICAL HYPOTHESIS-TESTING: TWO-SAMPLE t STATISTIC
The present situation involves the comparison between the sample means ![]() and
and ![]() from two bullets. Classical hypothesis-testing states the null and alternative hypotheses as
from two bullets. Classical hypothesis-testing states the null and alternative hypotheses as ![]() (reversed from our situation), and states that the two samples of observations (here, x1, x2, x3 and y1, y2, y3) are normally distributed as
(reversed from our situation), and states that the two samples of observations (here, x1, x2, x3 and y1, y2, y3) are normally distributed as ![]() and
and ![]() Under those conditions,
Under those conditions, ![]() and sp are highly efficient estimates of µx, µy, and σ, respectively, where sp is a pooled estimate of the standard deviation that is based on both samples:
and sp are highly efficient estimates of µx, µy, and σ, respectively, where sp is a pooled estimate of the standard deviation that is based on both samples:
(E.2)
Evidence in favor of H1:µx ≠ µy occurs when ![]() and
and ![]() are “far apart.” Formally, “far apart” is determined when the so-called two-sample t statistic (which, under H0, has a central Student’s t distribution on nx + ny − 2 = 3 + 3 − 2 = 4 degrees of freedom) exceeds a critical point from this Student’s t4 distribution. To ensure a false null hypothesis rejection probability of no more than 100α% where α is the
are “far apart.” Formally, “far apart” is determined when the so-called two-sample t statistic (which, under H0, has a central Student’s t distribution on nx + ny − 2 = 3 + 3 − 2 = 4 degrees of freedom) exceeds a critical point from this Student’s t4 distribution. To ensure a false null hypothesis rejection probability of no more than 100α% where α is the
probability of rejecting H0 when it is correct (that is, claiming “different” when the means are equal), we reject H0 in favor of H1 if
(E.3)
where tnx +ny − 2,α/2 is the value beyond which only 100 · α/2% of the Student’s t distribution (on nx + ny − 2 degrees of freedom) lies.
When ![]() Equation E.3 reduces to:
Equation E.3 reduces to:
(E.4)
This procedure for testing H0 versus H1 has the following property: among all possible tests of H0 whose false rejection probability does not exceed α, this two-sample Student’s t test has the maximum probability of rejecting H0 when H1 is true (that is, has the highest power to detect when µx and µy are unequal). If the two-sample t statistic is less than this critical value (2.776 for α = 0.05), the interpretation is that the data do not support the hypothesis of different means. A larger critical value would reject the null hypothesis (“same means”) less often.
The FBI protocol effectively uses sx + sy in the denominator instead of ![]() and uses a “critical value” of 2 instead of 2.776. Simulation suggests that the distribution of the ratio (sx + sy)/sp has a mean of 1.334 (10%, 25%, 75%, and 90% quantiles are 1.198, 1.288, 1.403, and 1.413, respectively). Substituting
and uses a “critical value” of 2 instead of 2.776. Simulation suggests that the distribution of the ratio (sx + sy)/sp has a mean of 1.334 (10%, 25%, 75%, and 90% quantiles are 1.198, 1.288, 1.403, and 1.413, respectively). Substituting ![]() suggests that the approximate error in rejecting H0 when it is true for the FBI statistic,
suggests that the approximate error in rejecting H0 when it is true for the FBI statistic, ![]() would also be 0.05 if it used a “critical point” of
would also be 0.05 if it used a “critical point” of ![]() Replacing 1.334 with the quantiles 1.198, 1.288, 1.403, and 1.413 yields values of 1.892, 1.760, 1.616, and 1.604, respectively—all smaller than the FBI value of 2. The FBI value of 2 would correspond to an approximate error of 0.03. A larger critical value (smaller error) leads to fewer rejections of the null hypothesis, that is, more likely to claim “equality” and less likely to claim “different” when the means are the same.
Replacing 1.334 with the quantiles 1.198, 1.288, 1.403, and 1.413 yields values of 1.892, 1.760, 1.616, and 1.604, respectively—all smaller than the FBI value of 2. The FBI value of 2 would correspond to an approximate error of 0.03. A larger critical value (smaller error) leads to fewer rejections of the null hypothesis, that is, more likely to claim “equality” and less likely to claim “different” when the means are the same.
If the null hypothesis is H0:µx − µy = δ(δ ≠ 0), the two-sample t statistic in Equation E.4 has a noncentral t distribution with noncentrality parameter (δ/σ)(nxny)/(nx + ny), which reduces to (δ/σ)(n/2) when nx = ny = n. When the null hypothesis is ![]() the distribution of the pooled two-sided two-sample t statistic (Equation E.4) has a noncentral F distribution with 1 and nx + ny − 2 = 2(n − 1) degrees of freedom and noncentrality parameter
the distribution of the pooled two-sided two-sample t statistic (Equation E.4) has a noncentral F distribution with 1 and nx + ny − 2 = 2(n − 1) degrees of freedom and noncentrality parameter ![]()
The use of Student’s t statistic is valid (that is, the probability of falsely rejecting H0 when the means µx and µy are truly equal is α) only when the x’s and y’s are normally distributed. The appropriate critical value (here, 2.776 for α = 0.05 and δ = 0) is different if the distributions are not normal, or if σx ≠ σy, or if H0: | µx − µy | ≥ δ ≠ 0, or if (sx + sy)/2 is used instead of sp (Equation E.2), as is used currently in the FBI’s statistical method. It also has the highest power (highest probability of claiming H1 when in fact µx ≠ µy, subject to the condition that the probability of erroneously rejecting H0 is no more than α.
The assumption “σx = σy” is probably reasonably valid if the measurement process is consistent from bullet sample to bullet sample: one would expect the error in measuring the concentration of a particular element for the crime scene (CS) bullet (σx) to be the same as that in measuring the concentration of the same element in the potential suspect (PS) bullet (σy). However, the normality assumption may be questionable here; as noted by (Ref. 1), average concentrations for different bullets tend to be lognormally distributed. That means that log(As average) is approximately normal as it is for all six other elements. When the measurement uncertainty is very small (say, σx < 0.2), the lognormal distribution differs little from the normal distribution (Ref. 2), so these assumptions will be reasonably well satisfied for precise measurement processes. Only a few of the standard deviations in the datasets were greater than 0.2 (see the section titled “Description of Data Sets” in Chapter 3).
The case of CABL differs from the classical situation primarily in the reversal of the null and alternative hypotheses of interest. That is, the null hypothesis here is H0:µx ≠ µy vs H1:µx = µy. We accommodate the difference by stating a specific relative difference between µx and µy, |µx − µy|, and rely on the noncentral F distribution as mentioned above.
EQUIVALENCE t TESTS2
An equivalence t test is designed to handle our situation:
H0: means are different.
H1: means are similar.
Those hypotheses are quantified more precisely as
We must choose a value of δ that adequately reflects the condition that “two bullets came from the same compositionally indistinguishable volume of mate-
|
2 |
Note that the form of this test is referred to as successive t-test statistics in Chapter 3. In that description, the setting of error rates is not prescribed. |
rial (CIVL), subject to specification limits on the element given by the manufacturer.” For example, if the manufacturer claims that the Sb concentrations in a given lot of material are 5% ± 0.20%, a value of δ = 0.20 might be deemed reasonable. The test statistic is still the two-sample t as before, but now we reject H0 if ![]() and
and ![]() are too close. As before, we ensure that the false match probability cannot exceed a particular value by choosing a critical value so that the probability of falsely rejecting H0 (falsely claiming a “match”) is no greater than α (here, we will choose α = 1/2,500 = 0.0004 for example. The equivalence test has the property that, subject to false match probability ≤ α = 0.0004, the probability of correctly rejecting H0 (that is, claiming that two bullets match when the means of the batches from which the bullets came are less than δ), is maximized. The left panel of Figure E.1 shows a graph of the distribution of the difference
are too close. As before, we ensure that the false match probability cannot exceed a particular value by choosing a critical value so that the probability of falsely rejecting H0 (falsely claiming a “match”) is no greater than α (here, we will choose α = 1/2,500 = 0.0004 for example. The equivalence test has the property that, subject to false match probability ≤ α = 0.0004, the probability of correctly rejecting H0 (that is, claiming that two bullets match when the means of the batches from which the bullets came are less than δ), is maximized. The left panel of Figure E.1 shows a graph of the distribution of the difference ![]() under the null hypothesis that δ/σ = 0.25 (that is, either µx − µy = −0.25σ, or µx − µy = +0.25σ) and n = 100 fragment averages in each sample, subject to false match probability ≤ 0.05: the equivalence test in this case rejects H0 when
under the null hypothesis that δ/σ = 0.25 (that is, either µx − µy = −0.25σ, or µx − µy = +0.25σ) and n = 100 fragment averages in each sample, subject to false match probability ≤ 0.05: the equivalence test in this case rejects H0 when ![]() The right panel of Figure E.1 shows the power of this test: when δ equals zero, the probability of correctly rejecting the null hypothesis (“means differ by more than 0.25”) is about 0.60, whereas the probability of rejecting the null hypothesis when δ = 0.25 is only 0.05 (as it should be, given the specifications of the test). Figure E.1 is based on the information given in Wellek (Ref. 3); similar figures apply for the case when α = 0.0004, n = 3 measurements in each sample, and δ/σ = 1 or 2.
The right panel of Figure E.1 shows the power of this test: when δ equals zero, the probability of correctly rejecting the null hypothesis (“means differ by more than 0.25”) is about 0.60, whereas the probability of rejecting the null hypothesis when δ = 0.25 is only 0.05 (as it should be, given the specifications of the test). Figure E.1 is based on the information given in Wellek (Ref. 3); similar figures apply for the case when α = 0.0004, n = 3 measurements in each sample, and δ/σ = 1 or 2.
DIGRESSION: LOGNORMAL DISTRIBUTIONS
This section explains two benefits of transforming measurements via logarithms for the statistical analysis.
The standard deviations of measurements made with inductively coupled plasma-optical emission spectroscopy are generally proportional to their means; hence, one typically refers to relative error, or coefficient of variation, sometimes expressed as a percentage, ![]() When the measurements are transformed first via logarithms, the standard deviation of the log(measurements) is approximately, and conveniently, equal to the coefficient of variation (COV), sometimes called relative error (RE), in the original scale. This can be seen easily through standard propagation-of-error formulas (Ref. 4, 5), which rely on a first-order Taylor series expansion for the transformation (here, the natural logarithm) about the mean in the original scale—
When the measurements are transformed first via logarithms, the standard deviation of the log(measurements) is approximately, and conveniently, equal to the coefficient of variation (COV), sometimes called relative error (RE), in the original scale. This can be seen easily through standard propagation-of-error formulas (Ref. 4, 5), which rely on a first-order Taylor series expansion for the transformation (here, the natural logarithm) about the mean in the original scale—
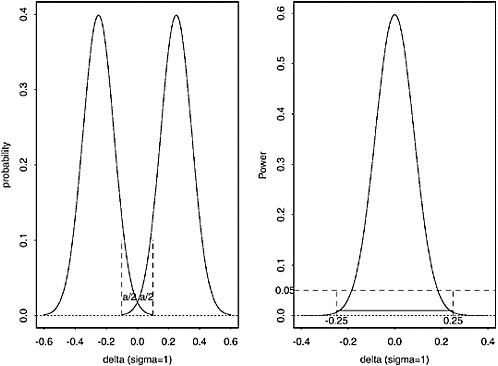
FIGURE E.1 The left panel shows a picture of the distribution of the difference ![]() under the null hypothesis that δ/σ = 0.25 and n = 100 fragment averages in each sample, subject to false match probability ≤ 0.05 : the equivalence test in this case rejects H0 when
under the null hypothesis that δ/σ = 0.25 and n = 100 fragment averages in each sample, subject to false match probability ≤ 0.05 : the equivalence test in this case rejects H0 when ![]() The right panel shows the power of this test: when δ equals zero, the probability of correctly rejecting the null hypothesis is about 0.60, whereas the probability of rejecting the null hypothesis when δ = 0.25 is only 0.05. Figure is based on information given in Wellek (Ref. 3).
The right panel shows the power of this test: when δ equals zero, the probability of correctly rejecting the null hypothesis is about 0.60, whereas the probability of rejecting the null hypothesis when δ = 0.25 is only 0.05. Figure is based on information given in Wellek (Ref. 3).
—because the variance of a constant (such as µx) is zero. Letting f(X) = log(X), and f′(µx) = 1/µx, it follows that
Moreover, the distribution of the logarithms for each element tends to be more normal than that of the raw data. Thus, to obtain more-normally distributed data and as a by-product a simple calculation of the COV, the data should first be transformed via logarithms. Approximate confidence intervals are calculated in the log scale and then can be transformed back to the original scale via the antilogarithm, ![]()
DIGRESSION: ESTIMATING σ2 WITH POOLED VARIANCES
The FBI protocol for statistical analysis estimates the variances of the triplicate measurements in each bullet with only three observations, which leads to highly variable estimates—a range of a factor of 10, 20, or even more ![]()
![]() Assuming that the measurement variation is the same for both the PS and CS bullets, the classical two-sample t statistic pools the variances into
Assuming that the measurement variation is the same for both the PS and CS bullets, the classical two-sample t statistic pools the variances into ![]() (Equation E.2), which has four degrees of freedom and is thus more stable than either individual sx or sy alone (each based on only two degrees of freedom). The pooled variance
(Equation E.2), which has four degrees of freedom and is thus more stable than either individual sx or sy alone (each based on only two degrees of freedom). The pooled variance ![]() need not rely on only the six observations from the two samples if the within-replicate variance is the same for several bullets. Certainly, that condition is likely to hold if bullets are analyzed with a consistent measurement process. If three measurements are used to calculate each within-replicate standard deviation from each of, say, B bullets, a better, more stable estimate of σ2 is
need not rely on only the six observations from the two samples if the within-replicate variance is the same for several bullets. Certainly, that condition is likely to hold if bullets are analyzed with a consistent measurement process. If three measurements are used to calculate each within-replicate standard deviation from each of, say, B bullets, a better, more stable estimate of σ2 is
Such an estimate of σ2 is now based on not just 2(2) = 4 degrees of freedom, but rather 2B degrees of freedom. A stable and repeatable measurement process offers many estimates of σ2 from many bullets analyzed by the laboratory over several years. The within-replicate variances may be used in the above equation. To verify the stability of the measurement process, standard deviations should be plotted in a control-chart format (s-chart) (Ref. 7) with limits that, if exceeded, indicate a change in precision. Standard deviations that fall within the limits should be pooled as in Equation E.3. Using pooled standard deviations guards against the possibility of claiming a match simply because the measurement variability on a particular day happened to be large by chance, creating wider intervals and hence greater chances of overlap.
To determine whether a given standard deviation, say, sg, might be larger than the sp determined from measurements on B previous bullets, one can com-
pare the ratio ![]() with an F distribution on 2 and 2B degrees of freedom. Assuming that the FBI has as many as 500 estimates, the 5% critical point from an F distribution on two and 1,000 degrees of freedom is 3.005. Thus, if a given standard deviation is
with an F distribution on 2 and 2B degrees of freedom. Assuming that the FBI has as many as 500 estimates, the 5% critical point from an F distribution on two and 1,000 degrees of freedom is 3.005. Thus, if a given standard deviation is ![]() times larger than the pooled standard deviation for that element, one should consider remeasuring that element, in that the precision may be larger than expected by chance alone (5% of the time).
times larger than the pooled standard deviation for that element, one should consider remeasuring that element, in that the precision may be larger than expected by chance alone (5% of the time).
REFERENCES
1. Carriquiry, A.; Daniels, M.; and Stern, H. “Statistical Treatment of Case Evidence: Analysis of Bullet Lead”, Unpublished report, 2002.
2. Antle, C.E. “Lognormal distribution” in Encyclopedia of Statistical Sciences, Vol 5, Kotz, S.; Johnson, N. L.; and Read, C. B., Eds.; Wiley: New York, NY, 1985, pp. 134–136.
3. Wellek, S. Testing Statistical Hypotheses of Equivalence Chapman and Hall: New York, NY 2003.
4. Ku, H.H. Notes on the use of propagation of error formulas, Journal of Research of the National Bureau of Standards-C. Engineering and Instrumentation, 70C(4), 263–273. Reprinted in Precision Measurement and Calibration: Selected NBS Papers on Statistical Concepts and Procedures, NBS Special Publication 300, Vol. 1, H.H. Ku, Ed., 1969, 331–341.
5. Cameron, J.E. “Error analysis” in Encyclopedia of Statistical Sciences, Vol 2, Kotz, S.; Johnson, N. L.; and Read, C. B., Eds., Wiley: New York, NY, 1982, pp. 545–541.
6. Mood, A.; Graybill, F.; and Boes, D. Introduction to the Theory of Statistics, Third Edition McGraw-Hill: New York, NY, 1974.
7. Vardeman, S. B. and Jobe, J. M. Statistical Quality Assurance Methods for Engineers, Wiley: New York, NY, 1999.









