|
||||||||||||||||
|
||||||||||||||||
The following HTML text is provided to enhance online readability. Many aspects of typography translate only awkwardly to HTML. Please use the page image as the authoritative form to ensure accuracy. F
|
||||||||||||||||
and 
are independent. Based on this specification (or “these assumptions”), statistical theory asserts that
and 
denotes the chi-squared distribution on four degrees of freedom. If σ2 is estimated from a pooled variance on B (more than 2) samples, then 
Let v equal the number of degrees of freedom used to estimate σ, for example, v = 4 if 
 |
 |
Page 142 |
 |
 |
 |
|
| ||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 142
Forensic Analysis Weighing Bullet Lead Evidence
F
Simulating False Match Probabilities Based on Normal Theory1
WHY THE FALSE MATCH PROBABILITY DEPENDS ON ONLY RATIO δ / σ
As a function of δ, we are interesed in P{match on one element is declared | |µx − µy| > δ}, where µx and µy are the true means of one of the seven elements in the melts of the CS and PS bullets, respectively. The within-replicate variance is generally small, so we assume that the sample means of the three replicates are normally distributed; that is,
where “~” stands for “is distributed as.” Thus, the difference in the means is δ. We further assume that the errors in the measurements leading to and are independent. Based on this specification (or “these assumptions”), statistical theory asserts that
where and denotes the chi-squared distribution on four degrees of freedom. If σ2 is estimated from a pooled variance on B (more than 2) samples, then Let v equal the number of degrees of freedom used to estimate σ, for example, v = 4 if
1
Note that the notation used in this appendix differs from that used in the body of the report.
OCR for page 143
Forensic Analysis Weighing Bullet Lead Evidence
…+ s2B)/B. The ratio of to is the same as the distribution of namely a Student’s tv (v degrees of freedom), so the two-sample t statistic is distributed as a (central) Student’s t on v degrees of freedom:
The FBI criterion for a match on this one element can be written
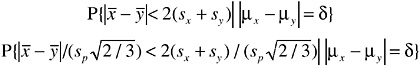
Because E(sx) = E(sy) = 0.8812σ, and E(sp) ≈ σ if v > 60, this reduces very roughly to
The approximation is very rough because E(P{t < S}) ≠ P{t < E(S)}, where t stands for the two-sample t statistic and S stands for But it does show that if δ is very large, this probability is virtually zero (very small false match probability because the probability that the sample means would, by chance, end up very close together is very small). However, if δ is small, the probability is quite close to 1.
The equivalence t test proceeds as follows. Assume
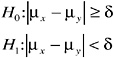
where H0 is the null hypothesis that the true population means differ by at least δ, and the alternative hypothesis is that they are within δ of each other. The two-sample t test would reject H0 in favor of H1 if the sample means are too close, that is, if where Kα(n,δ) is chosen so that does not exceed a preset per-element risk level of α (in Chapter 3, we used α = 0.30). Rewriting that equation, and writing Kα for Kα(n,δ),
When v is large sp ≈ 0, and therefore the quantity
OCR for page 144
Forensic Analysis Weighing Bullet Lead Evidence
That shows that the false match probability depends on δ and σ only through the ratio. (The argument is a little more complicated when v is small, because the ratio is a random quantity, but the conclusion will be the same.) Also, when v is large, the quantity which is distributed as a standard normal distribution. So the probability can be written
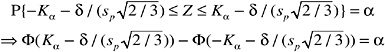
where Φ(·) denotes the standard cumulative normal distribution function (for example, Φ(1.645) = 0.95). So, for large values of v, the nonlinear equation can be solved for Kα, so that the probability of interest does not exceed α. For small values of v, Kα is the 100(1 − α)% point of the non-central t distribution with v degrees of freedom and noncentrality parameter (Ref. 14).
Values of Kα are given in Table F.1 below, for various values of α (0.30, 0.25, 0.20, 0.10, 0.05, 0.01, and 0.0004), degrees of freedom (4, 40, 100, and 200), and δ / σ (0.25, 0.33, 0.50, 1, 1.5, 2, and 3). The theory for Hotelling’s T2
TABLE F.1 Values of Kα(n,v) Used in Equivalence t Test (Need to Multiply by
α = 0.30, n = 3
(δ / σ)
0.25
0.33
0.50
1
1.5
2
3
v = 4
0.43397
0.44918
0.49809
0.81095
1.35161
1.94726
3.12279
40
0.40683
0.42113
0.46725
0.77043
1.31802
1.92530
3.13875
100
0.40495
0.41919
0.46511
0.76783
1.31622
1.92511
3.14500
200
0.40435
0.41857
0.46443
0.76697
1.31563
1.92510
3.14734
α = 0.30, n = 5
(δ / σ)
0.25
0.33
0.50
1
2
3
v = 4
0.44761
0.47385
0.56076
1.11014
2.63496
4.12933
40
0.41965
0.44436
0.52681
1.07231
2.63226
4.19067
100
0.41771
0.44232
0.52445
1.06984
2.63546
4.20685
200
0.41710
0.44167
0.52370
1.06906
2.63664
4.21278
OCR for page 145
Forensic Analysis Weighing Bullet Lead Evidence
α = 0.25, n = 3
(δ / σ)
0.25
0.33
0.50
1
1.5
2
3
v = 4
0.35772
0.37030
0.41092
0.68143
1.19242
1.77413
2.91548
40
0.33633
0.34818
0.38655
0.64811
1.16900
1.77305
2.98156
100
0.33484
0.34664
0.38484
0.64578
1.16765
1.77420
2.99223
200
0.33437
0.34615
0.38430
0.64503
1.16722
1.77461
2.99595
α = 0.25, n = 5
(δ / σ)
0.25
0.33
0.50
1
1.5
2
3
v = 4
0.36900
0.39075
0.46350
0.95953
1.70024
2.44328
3.88533
40
0.34696
0.36748
0.43648
0.92903
1.69596
2.47772
4.02810
100
0.34542
0.36586
0.43459
0.92698
1.69672
2.48365
4.05178
200
0.34493
0.36534
0.43399
0.92633
1.69700
2.48570
4.06021
α = 0.222, n = 3
(δ / σ)
0.25
0.33
0.50
1
1.5
2
3
4
0.31603
0.32716
0.36318
0.60827
1.09914
1.67316
2.79619
40
0.29754
0.30804
0.34207
0.57848
1.07949
1.68119
2.88735
100
0.29625
0.30670
0.34060
0.57638
1.07834
1.68290
2.90000
200
0.29584
0.30627
0.34013
0.57571
1.07798
1.68350
2.90436
α = 0.222, n = 5
(δ / σ)
0.25
0.33
0.50
1
1.5
2
3
3
0.32601
0.34528
0.41003
0.87198
1.60019
2.33249
3.74571
40
0.30695
0.32514
0.38655
0.84440
1.60422
2.38467
3.93060
100
0.30562
0.32374
0.38490
0.84252
1.60548
2.39187
3.95822
200
0.30520
0.32329
0.38438
0.84192
1.60592
2.39434
3.96795
(δ / σ)
0.25
0.33
0.50
1
2
3
v = 4
0.28370
0.29370
0.32612
0.55032
1.59066
2.69968
40
0.26736
0.27680
0.30744
0.52321
1.60451
2.80887
100
0.26622
0.27561
0.30613
0.52129
1.60656
2.82294
200
0.26585
0.27523
0.30571
0.52068
1.60725
2.82774
α = 0.20, n = 5
(δ / σ)
0.25
0.33
0.50
1
2
3
v = 4
0.29266
0.30999
0.36844
0.80094
2.24256
3.63322
40
0.27582
0.29219
0.34759
0.77521
2.30710
3.84954
100
0.27464
0.29094
0.34612
0.77341
2.31517
3.88010
200
0.27426
0.29054
0.34566
0.77285
2.31790
3.89081
α = 0.10, n = 3
OCR for page 146
Forensic Analysis Weighing Bullet Lead Evidence
(δ / σ)
0.25
0.33
0.50
1
2
3
v = 4
0.14025
0.14521
0.16138
0.28009
1.14311
2.19312
40
0.13257
0.13726
0.15256
0.26552
1.16523
2.36203
100
0.13203
0.13670
0.15193
0.26449
1.16738
2.38036
200
0.13186
0.13653
0.15174
0.26416
1.16808
2.38652
α = 0.10, n = 5
(δ / σ)
0.25
0.33
0.50
1
2
3
v = 4
0.14470
0.15332
0.18272
0.44037
1.76516
3.05121
40
0.13678
0.14493
0.17277
0.42178
1.86406
3.39055
100
0.13622
0.14434
0.17207
0.42044
1.87408
3.43264
200
0.13604
0.14416
0.17184
0.42001
1.87741
3.44712
α = 0.05, n = 3
(δ / σ)
0.25
0.33
0.50
1
2
3
4
0.07000
0.07241
0.08048
0.14085
0.80000
1.82564
40
0.06614
0.06847
0.07612
0.13329
0.80877
2.00110
100
0.06580
0.06812
0.07584
0.13280
0.80951
2.01774
200
0.06588
0.06822
0.07573
0.13263
0.80976
2.02351
α = 0.05, n = 5
(δ / σ)
0.25
0.33
0.50
1
2
3
4
0.07215
0.07645
0.09118
0.22900
1.41106
2.64066
40
0.06825
0.07232
0.08626
0.21748
1.50372
3.02532
100
0.06798
0.07203
0.08591
0.21672
1.51184
3.06786
200
0.06789
0.07194
0.08580
0.21647
1.51462
3.08296
α = 0.01, n = 3
(δ / σ)
0.25
0.33
0.50
1
2
3
4
0.01397
0.01447
0.01608
0.02823
0.25124
1.21164
40
0.01322
0.01369
0.01522
0.02671
0.24129
1.33049
100
0.01317
0.01364
0.01516
0.02660
0.24062
1.34080
200
0.01315
0.01352
0.01514
0.02656
0.24040
1.34432
α = 0.01, n = 5
(δ / σ)
0.25
0.33
0.50
1
2
3
4
0.01442
0.01528
0.01823
0.04651
0.79664
1.98837
40
0.01364
0.01446
0.01724
0.04400
0.83240
2.35173
100
0.01359
0.01440
0.01717
0.04383
0.83521
2.38989
200
0.01357
0.01438
0.01715
0.04378
0.83616
2.40330
OCR for page 147
Forensic Analysis Weighing Bullet Lead Evidence
α = 0.0004, n = 3
(δ / σ)
0.25
0.33
0.50
1
2
3
4.4
4
0.00056
0.00058
0.00064
0.00113
0.01071
0.34213
1.5877
40
0.00053
0.00055
0.00061
0.00107
0.01013
0.34139
1.9668
100
0.00053
0.00055
0.00061
0.00107
0.01009
0.34133
2.0072
200
0.00053
0.00055
0.00060
0.00106
0.01008
0.34131
2.0215
α = 0.0004, n = 5
(δ / σ)
0.25
0.33
0.50
1
2
3
4
0.00057
0.00061
0.00073
0.00186
0.07825
1.16693
40
0.00055
0.00058
0.00069
0.00176
0.07424
1.36013
100
0.00054
0.00057
0.00069
0.00175
0.07397
1.37811
200
0.00054
0.00057
0.00068
0.00175
0.07389
1.38431
Note: In each subtable, the row corresponds to different values of v = number of degrees of freedom used in sp to estimate σ (number of bullets = v / 2 + 1 with two measurements per bullet).
is similar (it uses vectors and matrices instead of scalars), and the resulting critical value comes from a noncentral F distribution (Ref. 15).2
ESTIMATING MEASUREMENT UNCERTAINTY WITH POOLED STANDARD DEVIATIONS
Chapter 3 states that a pooled estimate of the measurement uncertainty σ, sp, is more accurate and precise than an estimate based on only sx, the sample SD based on only three normally distributed measurements. That statement follows from the fact that a squared sample SD has a chi-squared distribution; specifically, (n − 1)s2 / σ2 has a chi-squared distribution on (n − 1) degrees of freedom, where s is based on n observations. The mean of the square root of a chi-squared random variable based on v = (n − 1) degrees of freedom is where Γ(·) is the gamma function. For v = (n − 1) = 2, E(s) = 0.8812σ; for v = 4 (i.e., estimating σ by E(s) = 0.9400σ; for v = 200 (that is, estimating σ by the square root of the mean of the squared SDs from 100 bullets), E(s) ≈ σ. In addition, the probability that s exceeds 1.25σ when n = 2 (that is, using only one bullet) is 0.21 but falls to 0.00028 when v = 200. For those
2
These values were determined by using a simple binary search algorithm for the value α and the R function pf(x, 1, dof, 0.5*n*E), where n = 3 or 5 and E = (δ / σ)2. R is a statistical-analysis software program that is downloadable from http://www.r-project.org.
OCR for page 148
Forensic Analysis Weighing Bullet Lead Evidence
reasons, sp based on many bullets is preferable to estimating σ by using only three measurements on a single bullet.
WITHIN-BULLET VARIANCES, COVARIANCES, AND CORRELATIONS FOR FEDERAL BULLET DATA SET
The data on the Federal bullets contained measurements on six of the seven elements (all but Cd) with ICP-OES. They allowed estimation of within-bullet variances, covariances, and correlations among the six elements. According to the formula in Appendix K, now applied to the six elements, the estimated within-bullet variance matrix is given below. The correlation matrix is found in the usual way (for example, Cor (Ag, Sb) = Covariance(Ag,Sb)/[SD(Ag) SD(Sb)]. Covariances and correlations between Cd and all other elements are assumed to be zero. The correlation matrix was used to demonstrate the use of the equivalence Hotelling’s T2 test. Because it is based on 200 bullets measured in 1991, it is presented here for illustrative purposes only.
Within-Bullet Variances and Covariances ×105, log(Federal Data)
ICP-As
ICP-Sb
ICP-Sn
ICP-Bi
ICP-Cu
ICP-Ag
ICP-As
187
27
31
31
37
77
ICP-Sb
20
37
25
18
25
39
ICP-Sn
31
25
106
16
29
41
ICP-Bi
31
18
16
90
14
44
ICP-Cu
37
25
29
14
40
42
ICP-Ag
77
39
41
44
42
681
Within-Bullet Correlations, Federal Data
ICP-As
ICP-Sb
ICP-Sn
ICP-Bi
ICP-Cu
ICP-Ag
(Cd)
ICP-As
1.000
0.320
0.222
0.236
0.420
0.215
0.000
ICP-Sb
0.320
1.000
0.390
0.304
0.635
0.242
0.000
ICP-Sn
0.222
0.390
1.000
0.163
0.440
0.154
0.000
ICP-Bi
0.236
0.304
0.163
1.000
0.240
0.179
0.000
ICP-Cu
0.420
0.635
0.440
0.240
1.000
0.251
0.000
ICP-Ag
0.215
0.242
0.154
0.179
0.251
1.000
0.000
(Cd)
0.000
0.000
0.000
0.000
0.000
0.000
1.000
BETWEEN-ELEMENT CORRELATIONS
In Chapter 3, correlations between mean concentrations of bullets were estimated by using the Pearson correlation coefficient (see equation 2). One reviewer suggested that Spearman’s rank correlation may be more appropriate, as it provides a nonparametric estimate of the monotonic association between two variables. Spearman’s rank correlation coefficient takes the same form as Equation 2, but with the ranks of the values (numbers 1, 2, 3, …, n = number of data
OCR for page 149
Forensic Analysis Weighing Bullet Lead Evidence
pairs) rather than values themselves. The table below consists of 49 entries, corresponding to all possible pairs of the seven elements. The value 1.000 on the diagonal confirms a correlation of 1.000 for an element with itself. The values in the cells on either side of the diagonal are the same because the correlation between, say, As and Sb is the same as that between Sb and As. For these off-diagonal cells, the first line reflects the conventional Pearson correlation coefficient based on the 1,373-bullet subset from the 1,837-bullet subset (bullets with all seven measured elements or with six measured and one imputed for Cd). The second line is Spearman’s rank correlation coefficient on rank(data), again for
Line 1:
conventional correlations on log(data),
1,373-bullet subset
Line 2:
Spearman correlations on rank(data),
1,373-bullet subset
Line 3:
Spearman correlations on rank(data),
1,837-bullet subset
Line 4:
Number of pairs in Spearman correlation,
1,837-bullet subset
(Note: 1.000 on the diagonal is indicated on line 1 only)
As
Sb
Sn
Bi
Cu
Ag
Cd
As
1.000
0.556
0.624
0.148
0.388
0.186
0.242
0.697
0.666
0.165
0.386
0.211
0.166
0.678
0.667
0.178
0.392
0.216
0.279
1750
1,381
1742
1,743
1,750
856
Sb
0.556
1.000
0.455
0.157
0.358
0.180
0.132
0.697
0.556
0.058
0.241
0.194
0.081
0.678
0.560
0.054
0.233
0.190
0.173
1,750
1,387
1829
1,826
1,837
857
Sn
0.624
0.455
1.000
0.176
0.200
0.258
0.178
0.666
0.556
0.153
0.207
0.168
0.218
0.667
0.560
0.152
0.208
0.165
0.385
1,381
1,387
1385
1380
1387
857
Bi
0.148
0.157
0.176
1.000
0.116
0.560
0.030
0.165
0.058
0.153
0.081
0.499
0.103
0.178
0.054
0.152
0.099
0.522
0.165
1,742
1,829
1,385
1,818
1,829
857
Cu
0.388
0.358
0.200
0.116
1.000
0.258
0.111
0.386
0.241
0.207
0.081
0.206
0.151
0.392
0.233
0.208
0.099
0.260
0.115
1,743
1,826
1,380
1818
1826
855
Ag
0.186
0.180
0.258
0.560
0.258
1.000
0.077
0.211
0.194
0.168
0.499
0.206
0.063
0.216
0.190
0.165
0.522
0.260
0.115
1,750
1,837
1,387
1829
1,826
857
Cd
0.242
0.132
0.178
0.030
0.111
0.077
1.000
0.166
0.081
0.218
0.103
0.151
0.063
0.279
0.173
0.385
0.165
0.251
0.115
857
857
857
857
855
857
OCR for page 150
Forensic Analysis Weighing Bullet Lead Evidence
the 1,373-bullet subset. The third line is Spearman’s rank correlation coefficient on the entire 1,837-bullet subset (some bullets had only three, four, five, or six elements measured). The fourth line gives the number of pairs in Spearman’s rank correlation coefficient calculation. All three sets of correlation coefficients are highly consistent with each other. Regardless of the method used to estimate the linear association between elements, associations between As and Sb, between As and Sn, between Sb and Sn, and between Ag and Bi are rather high. Because the 1,837-bullet subset is not a random sample from any population, we refrain from stating a level of “significance” for these values, noting only that regardless of the method used to estimate the linear association between elements, associations between As and Sb, between As and Sn, between Sb and Sn, and between Ag and Bi are higher than those for the other 17 pairs of elements.
Representative terms from entire chapter:
rank correlation