K
Statistical Analysis of Bullet Lead Data
By Karen Kafadar and Clifford Spiegelman
1. INTRODUCTION
The current procedure for assessing a “match” (analytically indistinguishable chemical compositions) between a crime-scene (CS) bullet and a potential suspect’s (PS) bullet starts with three pieces from each bullet or bullet fragment. Nominally each piece is measured in triplicate with inductively coupled plasma–optical emission spectrophotometry (ICP-OES) on seven elements: As, Sb, Sn, Cu, Bi, Ag, Cd, against three standards. Analyses in previous years measured three to six elements; in some cases, fewer than three pieces can be abstracted from a bullet or bullet fragment. Parts of the analysis below will consider fewer than seven elements, but we will always assume measurements on three pieces in triplicate even though occasionally very small bullet fragments may not have yielded three measurements. The three replicates on each piece are averaged, and then means, standard deviations (SDs), and ranges (minimum to maximum) for the three pieces and for each element are calculated for all CS and PS bullets. Throughout this appendix, the three averages (from the triplicate readings) on the three pieces are denoted the three “measurements” (even though occasionally very small bullet fragments may not have yielded three measurements).
Once the chemical analysis has been completed, a decision must be based on the measurements. Are the data consistent with the hypothesis that the mean chemical concentrations of the two bullets are the same or different? If the data suggest that the mean chemical concentrations are the same, the bullets or fragments are assessed as “analytically indistinguishable.” Intuitively, it makes sense that if the seven average concentrations (over the three measurements) of the CS bullet are “far” from those of the PS bullet, the data would be deemed more
consistent with the hypothesis of “no match.” But if the seven averages are “close,” the data would be more consistent with the hypothesis that the two bullets “match.” The role of statistics is to determine how close, that is, to determine limits beyond which the bullets are deemed to have come from sources that have different mean concentrations and within which they are deemed to have come from sources that have the same mean concentrations.
1.1. Statistical Hypothesis Tests
The classical approach to deciding between the two hypotheses was developed in the 1930s. The standard hypothesis-testing procedure consists of these steps:
-
Set up the two hypotheses. The “assumed” state of affairs is generally the null hypothesis, for example, “drug is no better than placebo.” In the compositional analysis of bullet lead (CABL) context, the null hypothesis is “bullets do not match” or “mean concentrations of materials from which these two bullets were produced are not the same” (assume “not guilty”). The converse is called the alternative hypothesis, for example, “drug is effective” or in the CABL context, “bullets match” or “mean concentrations are the same.”
-
Determine an acceptable level of risk posed by rejecting the null hypothesis when it is actually true. The level is set according to the circumstances. Conventional values in many fields are 0.05 and 0.01; that is, in one of 20 or in one of 100 cases when this test is conducted, the test will erroneously decide on the alternative hypothesis (“bullets match”) when the null hypothesis actually was correct (“bullets do not match”). The preset level is considered inviolate; a procedure will not be considered if its “risk” exceeds it. We consider below tests with desired risk levels of 0.30 to 0.0004. (The value of 0.0004 is equivalent to 1 in 2,500, thought by the FBI to be the current level.)
-
Calculate a quantity based on the data (for example, involving the sample mean concentrations of the seven elements in the two bullets), known as a test statistic. The value of the test statistic will be used to test the null hypothesis versus the alternative hypothesis.
-
The preset level of risk and the test statistic together define two regions, corresponding to the two hypotheses. If the test statistic falls in one region, the decision is to fail to reject the null hypothesis; if it falls in the other region (called the critical region), the decision is to reject the null hypothesis and conclude the alternative hypothesis.
The critical region has the following property: Over the many times that this protocol is followed, the probability of falsely rejecting the null hypothesis does not exceed the preset level of risk. The recommended test procedure in Section 4
has a further property: if the alternative hypothesis holds, the procedure will have the greatest chance of correctly rejecting the null hypothesis.
The FBI protocol worked in reverse. Three test procedures were proposed, described below as “2-SD overlap,” “range overlap,” and “chaining.” Thus, the first task of the authors was to calculate the level of risk that would result from the use of these three procedures. More precisely, we developed a simulation, guided by information about the bullet concentrations from various sources and from datasets that were published or provided to the committee (described in Section 3.2), to calculate the probability that the 2-SD-overlap and range-overlap procedures would claim a match between two bullets whose mean concentrations differed by a specified amount. The details of that simulation and the resulting calculations are described in Section 3.3 with a discussion of chaining.
An alternative approach, based on the theory of equivalence t tests, is presented in Section 4. A level of risk is set for each equivalence t test to compare two bullets on each of the seven elemental concentrations; if the mean concentrations of all seven elements are sufficiently close, the overall false-positive probability (FPP) of a match between two bullets that actually differ is less than 0.0004 (one in 2,500). The method is described in detail so that the reader can apply it with another value of the FPP such as one in 500, or one in 10,000. A multivariate version of the seven separate tests (Hotelling’s T2) is also described. Details of the statistical theory are provided in the other appendixes. Appendix E contains basic principles of statistics; Appendix F provides a theoretical derivation that characterizes the FBI procedures and equivalence tests and some extra analyses not shown in this appendix; Appendix H describes the principal-component analysis for assessing the added contributions of each element for purposes of discrimination; and Appendix G provides further analyses conducted on the data sets.
1.2 Current Match Procedure
The FBI presented three procedures for assessing a match between two bullets:
-
“2-SD overlap.” Measurements of each element can be combined to form an interval with lower limit mean −2SD and upper limit mean+2SD. The means and SDs are based on the average of three measurements in each of the specimens. If the seven intervals for a given CS bullet overlap with all seven intervals for a given PS bullet, the CS and PS bullets are deemed a match.
-
“Range overlap.” Intervals for each element are calculated as minimum to maximum from the three measurements in each of the specimens. If the seven intervals for a given CS bullet overlap with all seven intervals for a given PS bullet, the CS and PS bullets are deemed a match.
-
Chaining. As described in FBI Laboratory document Comparative Elemental Analysis of Firearms Projectile lead by ICP-OES (Ref. 1, pp. 10–11):
a. CHARACTERIZATION OF THE CHEMICAL ELEMENT DISTRIBUTION IN THE KNOWN PROJECTILE LEAD POPULATION
The mean element concentrations of the first and second specimens in the known material population are compared based upon twice the measurement uncertainties from their replicate analysis. If the uncertainties overlap in all elements, they are placed into a composition group; otherwise they are placed into separate groups. The next specimen is then compared to the first two specimens, and so on, in the same manner until all of the specimens in the known population are placed into compositional groups. Each specimen within a group is analytically indistinguishable for all significant elements measured from at least one other specimen in the group and is distinguishable in one or more elements from all the specimens in any other compositional group. (It should be noted that occasionally in groups containing more than two specimens, chaining occurs. That is, two specimens may be slightly separated from each other, but analytically indistinguishable from a third specimen, resulting in all three being included in the same compositional group.)
b. COMPARISON OF UNKNOWN SPECIMEN COMPOSITION(S) WITH THE COMPOSITION(S) OF THE KNOWN POPULATION(S)
The mean element concentrations of each individual questioned specimen are compared with the element concentration distribution of each known population composition group. The concentration distribution is based on the mean element concentrations and twice the standard deviation of the results for the known population composition group. If all mean element concentrations of a questioned specimen overlap within the element concentration distribution of one of the known material population groups, that questioned specimen is described as being “analytically indistinguishable” from that particular known group population.
The SD of the “concentration distribution” is calculated as the SD of the averages (over three measurements for each bullet) from all bullets in the “known population composition group.” In Ref. 2, the authors (Peele et al. 1991) apply this “chaining algorithm” on intervals formed by the ranges (minimum and maximum of three measurements) rather than (mean ± 2SD) intervals.
The “2-SD overlap” and “range-overlap” procedures are illustrated with data from an FBI-designed study of elemental concentrations of bullets from different boxes (Ref. 2). The three measurements in each of three pieces of each of seven elements (in units of parts per million, ppm) are shown in Table K.1 below for bullets F001 and F002 from one of the boxes of bullets provided by Federal Cartridge Company (described in more detail in Section 3.2). Each piece was mea-
TABLE K.1 Illustration of Calculations for 2-SD-Overlap and Range-Overlap Methods on Federal Bullets F001 and F002 (Concentrations in ppm)
|
|
|
Federal Bullet F001 |
|
|
|
|
|
|
icpSb |
icpCu |
icpAg |
icpBi |
icpAs |
icpSn |
|
a |
29276 |
285 |
64 |
16 |
1415 |
1842 |
|
b |
29506 |
275 |
74 |
16 |
1480 |
1838 |
|
c |
29000 |
283 |
66 |
16 |
1404 |
1790 |
|
mean |
29260.67 |
281.00 |
68.00 |
16 |
1433.00 |
1823.33 |
|
SD |
253.35 |
5.29 |
5.29 |
0 |
41.07 |
28.94 |
|
Mean − 2SD |
28753.97 |
270.42 |
57.42 |
16 |
1350.85 |
1765.46 |
|
Mean + 2SD |
29767.36 |
291.58 |
78.58 |
16 |
1515.15 |
1881.21 |
|
minimum |
29000 |
275 |
64 |
16 |
1404 |
1790 |
|
maximum |
29506 |
285 |
74 |
16 |
1480 |
1842 |
|
|
|
Federal Bullet F002 |
|
|
|
|
|
|
icpSb |
icpCu |
icpAg |
icpBi |
icpAs |
icpSn |
|
a |
28996 |
278 |
76 |
16 |
1473 |
1863 |
|
b |
28833 |
279 |
67 |
16 |
1439 |
1797 |
|
c |
28893 |
282 |
77 |
15 |
1451 |
1768 |
|
mean |
28907.33 |
279.67 |
73.33 |
15.67 |
1454.33 |
1809.33 |
|
SD |
82.44 |
2.08 |
5.51 |
0.58 |
17.24 |
48.69 |
|
mean − 2SD |
28742.45 |
275.50 |
62.32 |
14.51 |
1419.84 |
1711.96 |
|
mean + 2SD |
29072.21 |
283.83 |
84.35 |
16.82 |
1488.82 |
1906.71 |
|
minimum |
28833 |
278 |
67 |
15 |
1439 |
1768 |
|
maximum |
28996 |
282 |
77 |
16 |
1473 |
1863 |
sured three times against three different standards; only the average is provided, and in this report it is called the “measurement.” Table K.1 shows the three measurements, their means, their SDs (equal to the square root of the sum of the three squared deviations from the mean divided by 2), the “2-SD interval” (mean −2SD to mean + 2SD), and the “range interval” (minimum and maximum).
For all seven elements, the 2-SD interval for Federal bullet 1 overlaps with the 2-SD interval for Federal bullet 2. Equivalently, the difference between the means is less than twice the sum of the two SDs. For example, the 2-SD interval for Cu in bullet 1 is (270.42, 291.58), and the interval for Cu in bullet 2 is (275.50, 283.83), which is completely within the Cu 2-SD interval for bullet 1. Equivalently, the difference between the means (281.00 and 279.67) is 1.33, less than 2(5.29 + 2.08) is 14.74. Thus, the 2-SD overlap procedure would conclude that the two bullets are analytically indistinguishable (Ref. 3) on all seven elements, so the bullets would be claimed to be analytically indis-
tinguishable. The range overlap procedure would find the two bullets analytically indistinguishable on all elements except Sb because for all other elements the range interval on each element for bullet 1 overlaps with the corresponding interval for bullet 2; for example, for Cu (275, 285) overlaps with (278, 282), but for Sb, the range interval (29,000, 29,506) just fails to overlap (28,833, 28,996) by only 4 ppm. Hence, by the range-overlap procedure, the bullets would be analytically distinguishable.
2. DESCRIPTION AND ANALYSIS OF DATASETS
2.1 Description of Data Sets
This section describes three data sets made available to the authors in time for analysis. The analysis of these data sets resulted in the following observations:
-
The uncertainty in measuring the seven elements is usually 2.0–5.0%.
-
The distribution of the measurements is approximately lognormally distributed; that is, logarithms of measurements are approximately normally distributed. Because the uncertainty in the three measurements on a bullet is small (frequently less than 5%), the lognormal distribution with a small relative SD is similar to a normal distribution. For purposes of comparing the measurements on two bullets, the measurements need not be transformed with logarithms, but it is often more useful to do so.
-
The distributions of the concentrations of a given element across many different bullets from various sources are lognormally distributed with much more variability than seen from within-bullet measurement error or within-lot error. For purposes of comparing average concentrations across many different bullets, the concentrations should be transformed with logarithms first, and then means and SDs can be calculated. The results can be reported on the original scale by taking the antilogarithms for example, exp(mean of logs).
-
The errors in the measurements of the seven elements may not be uncorrelated. In particular, the errors in measuring Sb and Cu appear to be highly correlated (correlation approximately 0.7); the correlation between the errors in measuring Ag and Sb or between the errors in measuring Ag and Cu is approximately 0.3. Thus, if the 2-SD intervals for Sb on two bullets overlap, the 2-SD intervals for Cu may be more likely to overlap also.
These observations will be described during the analysis part of this section.
The three data sets that were studied by the authors are denoted here as “800-bullet data set,” “1,837-bullet data set,” and “Randich et al. data set.”
1. 800-bullet data set (Ref. 4): This data set contains triplicate measurements on 50 bullets in each of four boxes from each of four manufacturers—
CCI, Federal, Remington, and Winchester—measured as part of a careful study conducted by Peele et al. (1991). Measured elements in the bullet lead were Sb, Cu, and As, measured with neutron activation analysis (NAA), and Sb, Cu, Bi, and Ag (measured with ICP-OES). In the Federal bullet lead, As and Sn were measured with NAA and ICP-OES. This 800-bullet data set provided individual measurements on the three bullet lead samples which permitted calculation of means and SDs on the log scale and within-bullet correlations among six of the seven elements measured with ICP-OES (As, Sb, Sn, Bi, Cu, and Ag); see Section 3.2.
2. 1,837-bullet data set (Ref. 5): The bullets in this data set were extracted from a larger, historical file of 71,000+ bullets analyzed by the FBI Laboratory during the last 15 years. According to the notes that accompanied the data file, the bullets in it were selected to include one bullet (or sometimes more) that were determined to be distinct from the other bullets in the case; a few are research samples “not associated with any particular case,” and a few “were taken from the ammunition collection (again, not associated with a particular case).” The notes that accompanied this data set stated:
To assure independence of samples, the number of samples in the full data set was reduced by removing multiple bullets from a given known source in each case. To do this, evidentiary submissions were considered one case at a time. For each case, one specimen from each combination of bullet caliber, style, and nominal alloy class was selected and that data was placed into the test sample set. In instances where two or more bullets in a case had the same nominal alloy class, one sample was randomly selected from those containing the maximum number of elements measured…. The test set in this study, therefore, should represent an unbiased sample in the sense that each known production source of lead is represented by only one randomly selected specimen. [Ref. 6]
All bullets in this subset were measured three times (three fragments). Bullets from 1,005 cases between 1989 and 2002 are included; in 528 of these cases, only one bullet was selected. The numbers of cases for which different numbers of bullets were selected are given in Table K.2. The cases that had 11, 14, and 21 bullets were cases 834, 826, and 982, respectively. Due to the way in which these bullets were selected, they do not represent a random sample of bullets from any population—even the population of bullets analyzed by the laboratory. The selection probably produced a data set whose variability among bullets is higher than might be seen in the complete data set or in the population of all manufactured bullets. Only averages and SDs of the (unlogged) measurements are available, not the
TABLE K.2 Number of Cases Having b Bullets in the 1,837-Bullet Data Set
|
b = no. bullets |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
14 |
21 |
|
No. cases |
578 |
238 |
93 |
48 |
24 |
10 |
7 |
1 |
1 |
2 |
1 |
1 |
1 |
three individual measurements themselves, so a precise estimate of the measurement uncertainty (relative SD within bullets) could not be calculated, as it could in the 800-bullet data set. (One of the aspects of the nonrandomness of this dataset is that it is impossible to determine whether the “selected” bullets tended to have larger or smaller relative SDs (RSDs) compared with the RSDs on all 71,000+ bullets.) Characteristics of this data set are given in Table K.3. Only Sb and Ag were measured in all 1,837 bullets in this data set; all but three of the 980 missing Cd values occurred within the first 1,030 bullets (before 1997). In only 854 of the 1,837 bullets were all seven elements measured; in 522 bullets, six elements were measured (in all but three of the 522 bullets, the missing element is Cd); in 372 bullets, only five elements are measured (in all but 10 bullets, the missing elements are Sn and Cd); in 86 bullets, only four elements are measured (in all but eight bullets, the missing elements are As, Sn, and Cd). The data on Cd are highly discrete: of the 572 nonzero measured averages (139, 96, 40, 48, 32, and 28) showed average Cd concentrations of only (10, 20, 30, 40, 50, and 60) ppm respectively (0.00001–0.00006). The remaining 189 nonzero Cd concentrations were spread out from 70 to 47,880 ppm (0.00007 to 0.04788). This data set provided some information on distributions of averages of the various elements and some correlations between the averages.
Combining the 854 bullets in which all seven elements were measured with the 519 bullets in which all but Cd were measured yielded a subset of 1,373 bullets in which only 519 values of Cd needed to be imputed (estimated from the data). These 1,373 bullets then had measurements on all seven elements. The average Cd concentration in a bullet appeared to be uncorrelated with the average concentration of any other element, so the missing Cd concentration in 519 bullets was imputed by selecting at random one of the 854 Cd values measured in the 854 bullets in which all seven elements were measured. The 854- and 1,373-bullet subsets were used in some of the analyses below.
3. Randich et al. (2002) (Ref. 7): These data come from Table 1 of the article by Randich et al. (Ref. 7). Six elements (all but Cd) were measured in three pieces of wire from 28 lots of wire. The three pieces were selected from the beginning, middle, and end of the wire reel. The analysis of this data set confirms the homogeneity of the material in a lot within measurement error.
TABLE K.3 Characteristics of 1,837-Bullet Data Set
|
Element |
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
No. bullets with no data |
87 |
0 |
450 |
8 |
11 |
0 |
980 |
|
No. bullets with data |
1,750 |
1,837 |
1,387 |
1,829 |
1,826 |
1,837 |
857 |
|
No. bullets with nonzero data |
1,646 |
1,789 |
838 |
1,819 |
1,823 |
1,836 |
572 |
|
pooled RSD,% |
2.26 |
2.20 |
2.89 |
0.66 |
1.48 |
0.58 |
1.39 |
2.2 Lognormal Distributions
The SDs of measurements made with ICP-OES tend to be proportional to their means; hence, one typically refers to relative standard deviation, usually expressed as 100% × (SD/mean). When the measurements are transformed first via logarithms, the SD of the log(measurements) is approximately, and conveniently, equal to the RSD on the original scale. That is, the SD on the log scale will be very close to the RSD on the original scale. The mathematical details of this result are given in Appendix E. A further benefit of the transformation is that the resulting transformed measurements have distributions that are much closer to the familiar normal (Gaussian) distribution—an assumption that underlies many classical statistical procedures. The 800-bullet data set allowed calculation of the RSD by calculating the ordinary SD on the logarithms of the measurements.
The bullet means in the 1,837-bullet data set tend to be lognormally distributed, as shown by the histograms in Figures 3.1–3.4. The data on log(Sn) show two modes, and the data on Sb are split into Sb < 0.05 and Sb > 0.05. The histograms suggest that the concentrations of Sb and Sn in this data set consist of mixtures of lognormal distributions.) Carriquiry et al. (Ref. 8) also used lognormal distributions in analyzing the 800-bullet datas et.
Calculating means and SDs on the log scale was not possible with the data in the 1,837-bullet data set, because only means and SDs of the three measurements are given. However, when the RSD is very small (say, less than 5%), the difference between the lognormal and normal distributions is very small. For about 80% of the bullets in the 1,837-bullet data set that was true for the three measurements of As, Sb, Bi, Cu, and Ag.
2.3 Within-Bullet Variances and Covariances
800-Bullet Data Set
From the 800-bullet data set, which contains the three measurements in each bullet (not just the mean and SD), one can estimate the measurement SD in each set of three measurements. As mentioned above, when the RSD is small, the lognormally distributed measurement error will have a distribution that is close to normal. The within-bullet covariances shown below were calculated on the log-transformed measurements (results on the untransformed measurements were very similar).
The 800-bullet data set (200 bullets from each of four manufacturers) permits estimates of the within-bullet variances and covariances as follows:
(1)
where xijk denotes the logarithm of the ith measurement (i = 1, 2, 3; called “a, b, c” in the data file) of element j in bullet k, and ![]() is the mean of three log(measurements) of element j, bullet k. When l = j, the formula sjj reduces to a pooled within-bullet sample variance for the jth element; compare Equations E.2 and E.3 in Appendix E. Because sjj is based on within-bullet SDs from 200 bullets, the square root of sjj (called a pooled standard deviation) provides a more accurate and precise estimate of the measurement uncertainty than an SD based on only one bullet with three measurements (see Appendix F). The within-bullet
is the mean of three log(measurements) of element j, bullet k. When l = j, the formula sjj reduces to a pooled within-bullet sample variance for the jth element; compare Equations E.2 and E.3 in Appendix E. Because sjj is based on within-bullet SDs from 200 bullets, the square root of sjj (called a pooled standard deviation) provides a more accurate and precise estimate of the measurement uncertainty than an SD based on only one bullet with three measurements (see Appendix F). The within-bullet
TABLE K.4 Within-Bullet Covariances, times 105, by Manufacturer (800-Bullet Data Set)
|
CCI |
|||||
|
|
NAA-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
NAA-As |
118 |
10 |
6 |
4 |
17 |
|
ICP-Sb |
10 |
48 |
33 |
34 |
36 |
|
ICP-Cu |
6 |
33 |
46 |
31 |
36 |
|
ICP-Bi |
4 |
34 |
31 |
193 |
29 |
|
ICP-Ag |
17 |
36 |
36 |
29 |
54 |
|
Federal |
|||||
|
|
NAA-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
NAA-AS |
34 |
8 |
6 |
15 |
7 |
|
ICP-Sb |
8 |
37 |
25 |
18 |
39 |
|
ICP-Cu |
6 |
25 |
40 |
14 |
42 |
|
ICP-Bi |
15 |
18 |
14 |
90 |
44 |
|
ICP-Ag |
7 |
39 |
42 |
44 |
681 |
|
Remington |
|||||
|
|
NAA-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
NAA- |
345 |
−1 |
−3 |
13 |
3 |
|
ICP-Sb |
−1 |
32 |
21 |
16 |
18 |
|
ICP-Cu |
−3 |
21 |
35 |
15 |
12 |
|
ICP-Bi |
13 |
16 |
15 |
169 |
18 |
|
ICP-Ag |
3 |
18 |
12 |
18 |
49 |
|
Winchester |
|||||
|
|
NAA-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
NAA-As |
555 |
5 |
7 |
−5 |
16 |
|
ICP-Sb |
5 |
53 |
42 |
45 |
27 |
|
ICP-Cu |
7 |
42 |
69 |
37 |
31 |
|
ICP-Bi |
−5 |
45 |
37 |
278 |
31 |
|
ICP-Ag |
16 |
27 |
31 |
31 |
51 |
|
Average over manufacturers |
|||||
|
|
Naa-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
NAA-As |
263 |
6 |
4 |
7 |
10 |
|
ICP-Sb |
6 |
43 |
30 |
28 |
30 |
|
ICP-Cu |
4 |
30 |
47 |
24 |
30 |
|
ICP-Bi |
7 |
28 |
24 |
183 |
30 |
|
ICP-Ag |
10 |
30 |
30 |
30 |
209 |
|
Average within-bullet correlation matrix |
|||||
|
|
Naa-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
NAA-As |
1.00 |
0.05 |
0.04 |
0.03 |
0.04 |
|
ICP-Sb |
0.05 |
1.00 |
0.67 |
0.32 |
0.31 |
|
ICP-Cu |
0.04 |
0.67 |
1.00 |
0.26 |
0.30 |
|
ICP-Bi |
0.03 |
0.32 |
0.26 |
1.00 |
0.16 |
|
ICP-Ag |
0.04 |
0.31 |
0.30 |
0.16 |
1.00 |
covariance matrices were estimated separately for each manufacturer, on both the raw (untransformed) and log-transformed scales, for Sb, Cu, Bi, and Ag (measured with ICP-OES by all four manufacturers) and As (measured with NAA by all four manufacturers). Only the variances and covariances as calculated on the log scale are shown in Table K.4 because the square roots of the variances (diagonal terms) are estimates of the RSD. (These RSDs differ slightly from those cited in Table 2.2 in Chapter 2.) The within-bullet covariance matrices are pooled (averaged) across manufacturer, and the correlation matrix is derived in the usual way: correlation between elements i and j equals the covariance divided by the product of the SDs; that is, ![]() (The correlation matrix based on the untransformed data is very similar.) As and Sn were also measured with ICP-OES on only the Federal bullets, so the 6 × 6 within-bullet variances and covariances, and the within-bullet correlations among the six measurements, are given in Appendix F.
(The correlation matrix based on the untransformed data is very similar.) As and Sn were also measured with ICP-OES on only the Federal bullets, so the 6 × 6 within-bullet variances and covariances, and the within-bullet correlations among the six measurements, are given in Appendix F.
The estimated correlation matrix indicates usually small correlations between the errors in measuring elements. Four notable exceptions are the correlation between the errors in measuring Sb and Cu, estimated as 0.67, and the correlations between the errors in measuring Ag and Sb, between Ag and Cu, and between Sb and Bi, all estimated as 0.30−0.32.
Figure K.1 demonstrates that association with plots of the three Cu measurements versus the three Sb measurements centered at their mean values, so (0, 0) is roughly in the center of each plot for 20 randomly selected bullets from one of the four boxes from CCI (Ref. 2). In all 20 plots, the three points increase from left to right. A plot of three points does not show very much, but one would not expect to see all 20 plots showing consistent directions if there were no association in the measurement errors of Sb and Cu. In fact, for all four manufacturers,
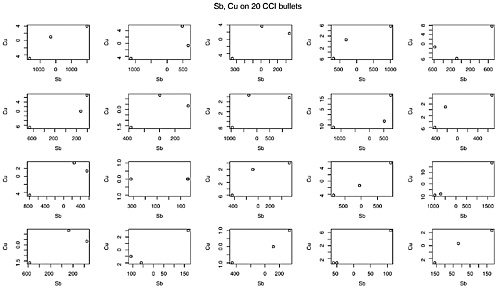
FIGURE K.1 Plots, for 20 CCI bullets, of three Cu measurements vs three Sb measurements. Each plot is centered at origin; that is, each plot shows xi,Cu−xCu vs xi,Sb−xSb. If, as was commonly believed, errors in measuring Sb and Cu were independent, one would have expected to see increasing trends in about half these plots and decreasing trends in the other half. All these plots show increasing trends; 150 of the total of 200 plots showed increasing trends.
the estimated correlation between the three measurements in each bullet was positive for over 150 of the 200 bullets; this indicates further that the errors in measuring Sb and Cu may be dependent.
It has been assumed that the errors in measuring the different elements are independent, but these data suggest that the independence assumption may not hold. The nonindependence will affect the overall false positive probability of a match based on all seven intervals.
1,837-Bullet Data Set
Estimates of correlations among all seven elements measured with ICP-OES is not possible with the 1,837-bullet data set because the three replicates have been summarized with sample means and SDs. However, this data set does provide some information on within-bullet variances (not covariances) by providing the SD of the three measurements. Pooled estimates of the RSD, from the 800-bullet data set, and the median value of the reported SD divided by the reported average from bullets in the 1,837-bullet datas ets, are given in Table K.5. (Pooled RSDs are recommended for the alternative tests described in Section.4.) Because the three fragment averages (measurements) were virtually identical for several bullets, leading to sample SDs of 0, the FBI replaced these values as indicated in the notes that accompanied this data set (Ref. 6): “for those samples for which the three replicate concentration measurements for an element were so close to the same value that a better precision was indicated than could be expected from the ICP-OES procedure, the measured precision was increased to no less than the method precision.” These values for the precision are also listed in Table K.5, in the third row labeled “Minimum SD (FBI).” The complete data set with 71,000+ bullets should be analyzed to verify the estimates of the uncertainty in the measurement errors and the correlations among them. (Note: All RSDs are based on ICP-OES measurements. RSDs for As and Sn are based on 200 Federal bullets. RSDs for Sb, Bi, Cu, and As are based on within-bullet variances averaged across four manufacturers (800 bullets); compare Table K.4. The estimated RSD for NAA-As is 5.1%.)
TABLE K.5 Pooled Estimates of Within-Bullet Relative Standard Deviations of Concentrations
|
|
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
800 bullets, % |
4.3 |
2.1 |
3.3 |
4.3 |
2.2 |
4.6 |
— |
|
1,837 bullets, 100 × med(SD/ave),% |
10.9 |
1.5 |
118.2 |
2.4 |
2.0 |
2.0 |
33.3 |
|
Minimum SD (FBI) |
0.0002 |
0.0002 |
0.0002 |
0.0001 |
0.00005 |
0.00002 |
0.00001 |
2.4 Between-Bullet Variances and Covariances
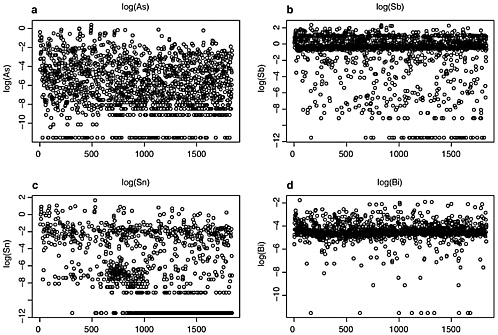
The available data averages from the 1,837-bullet data set are plotted on a log scale in Figure K.2. To distinguish better the averages reported as “0.0000,” log(0) is replaced with log(0.00001) = −11.5 for all elements except Cd, for which log(0) is replaced with log(0.000001) = −13.8. The data on Sb and Sn appear to be bimodal, and data on Cd before the 1,030th bullet (before the year 1997) are missing. The last panel (h) of the figure is a plot of the log(Ag) values only for log values between −7 (9e-4) and −5 (67e-4). This magnification shows a slight increase in Ag concentrations over time that is consistent with the findings noted by the FBI (Ref. 9).
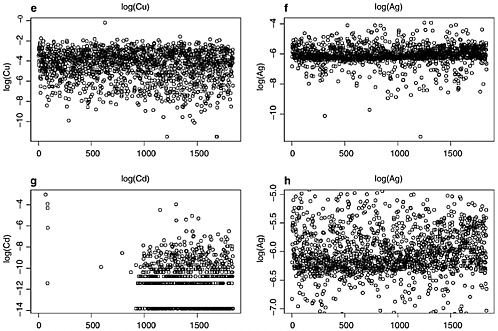
Figure K.3 shows all pairwise plots of average concentrations in the 1837-bullet data set. Each plot shows the logarithm of the average concentration of an element versus the logarithm of the average concentration of each of the other six elements (once as an ordinate and once as an abscissa). Vertical and horizontal stripes correspond to missing or zero values that were replaced with values of log(1e-6) or log(1e-7). The plots of Sn vs Ag, As vs Sn, and Ag vs Bi show that some relationships between the bullet concentrations of these pairs of elements may exist. The data on Sn fall into two categories: those whose log (mean Sn concentration) is less than or greater than −5 (Sn less than or greater than 0.0067 ppm). The data on Sb fall into perhaps four identifiable subsets: those whose log (mean Sb concentration) is less than −1 (Sb concentrations around 0.0150 ppm, from 0.0001 to 0.3491 ppm), between −1 and 0 (Sb around 0.7 ppm, from 0.35 to 1 ppm), between 0 and 1 (Sb around 1.6 ppm, from 1.00 to 2.17 ppm), and greater than 1 (Sb around 3 ppm, from 2.72 to 10.76 ppm), perhaps corresponding to “soft,” “medium,” “hard,” and “very hard” bullets.
If the 1,837-bullet data set were a random sample of the population of bullets, an estimate of the correlation (linear association) between two elements—say, Ag and Sb—is given by the Pearson sample correlation coefficient:
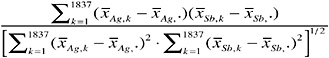
(2)
where again the x’s refer to the logarithms of the concentrations, for example, ![]() is the logarithm of the mean concentration of Ag in bullet k, and
is the logarithm of the mean concentration of Ag in bullet k, and ![]() is the average
is the average ![]() For other pairs of elements, the number 1,837 is replaced with the number of bullets in which both elements are measured. (Robust estimates of the correlations can be obtained by trimming any terms in the summation that appear highly discrepant from the others.) A nonparametric estimate of the linear association, Spearman’s rank correlation coefficient, can be computed by replacing actual measured values in the formula above with their ranks (for example, replacing the smallest Sb value with 1 and the largest with 1,837).
For other pairs of elements, the number 1,837 is replaced with the number of bullets in which both elements are measured. (Robust estimates of the correlations can be obtained by trimming any terms in the summation that appear highly discrepant from the others.) A nonparametric estimate of the linear association, Spearman’s rank correlation coefficient, can be computed by replacing actual measured values in the formula above with their ranks (for example, replacing the smallest Sb value with 1 and the largest with 1,837).
(Ref. 10). Table K.6 displays the Pearson sample correlation coefficient from the 1,837-bullet data set. The Spearman correlations on the ranks on the 1,837-bullet data set, the number of data pairs of which both elements were nonmissing, and the Spearman rank correlation coefficient on the 1,373-bullet subset (with no missing values) are given in Appendix F; the values of the Spearman rank correlation coefficients are very consistent with those shown in Table K.6. All three sets of correlation coefficients are comparable in magnitude for nearly all pairs of elements, and all are positive. However, because the 1,837-bullet data set is not a random sample, no measures of statistical significance are attributed to any correlation coefficients. The values are useful primarily for relative comparisons between correlation coefficients computed in this table.
2.5 Analysis of Randich et al. Data Set: Issues of Homogeneity
The data in Randich et al. (Ref. 7) were collected to assess the degree of inhomogeneity in lots of wires from which bullets are manufactured. Appendix H presents an analysis of those data. Here we only compare the within-replicate variances obtained on the 800-bullet data set with the within-lot variances in the Randich data. The former includes only five elements (As with NAA and Sb, Cu, Bi, and Ag with ICP), so variances on only these five elements are compared. As recommended earlier, these variances are calculated on the logarithms of the data, so they can be interpreted as the squares of the RSDs on the original scale.
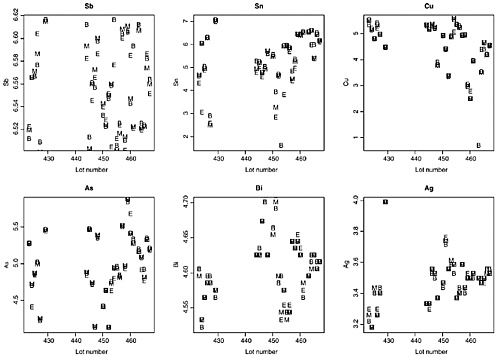
For the As and Sb concentrations, the variability of the three measurements (beginning, middle, and end, or B, M, and E) is about the same as the variability of the three measurements in the bullets in the 800-bullet data set. For Bi and Ag, the within-lot variability (B, M, and E) is much smaller than the within-bullet variability in the 800-bullet data set. The within-lot variance of the three Cu measurements is considerably larger than the within-bullet variance obtained in the 800-bullet data set because of some very unusual measurements in five lots; when these lots are excluded, the estimated within-lot variance is comparable with the within-bullet variance in the 800-bullet data set. Randich et al. do not provide replicates or precise within-replicate measurement standard errors, so one cannot determine whether the precision of one of their measurements is equivalent to the precision of one of the FBI measurements. A visual display of the relative magnitude of the lot-to-lot variability (different lots) compared with the within-lot variability (B, M, and E) is shown in Figure K.4, which plots the log(measurement) by element as a function of lot number (in three cases, the lot number was modified slightly to avoid duplicate lot numbers, solely for plotting purposes: 424A → 425; 457 → 458; 456A → 457). Lot-to-lot variability is usually 9–12 times greater than within-lot variability: separate two-way analyses of variances on the logarithms of the measurements on the six elements, with the two factors “lot” (27 degrees of freedom for 28 lots) and “position in lot” (2
TABLE K.6 Between-Element Correlationsa (1,837-Bullet Data Set)
|
|
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
As |
1.00 |
0.56 |
0.62 |
0.15 |
0.39 |
0.19 |
0.24 |
|
Sb |
0.56 |
1.00 |
0.45 |
0.16 |
0.36 |
0.18 |
0.13 |
|
Sn |
0.62 |
0.45 |
1.00 |
0.18 |
0.20 |
0.26 |
0.18 |
|
Bi |
0.15 |
0.16 |
0.18 |
1.00 |
0.12 |
0.56 |
0.03 |
|
Cu |
0.39 |
0.36 |
0.20 |
0.12 |
1.00 |
0.26 |
0.11 |
|
Ag |
0.19 |
0.18 |
0.26 |
0.56 |
0.26 |
1.00 |
0.08 |
|
Cd |
0.24 |
0.13 |
0.18 |
0.03 |
0.11 |
0.08 |
1.00 |
|
aPearson correlation; see Equation 2. Spearman rank correlations are similar; see Appendix F. |
|||||||
TABLE K.7 Comparison of Within-Bullet and Within-Lot Variancesa
|
|
ICP-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
Between lots: Randich et al. |
4,981.e-04 |
40.96e-04 |
17890e-04 |
60.62e-04 |
438.5e-04 |
|
Within-bullet: 800-bullet data |
26.32e-04b |
4.28e-04 |
4.73e-04 |
18.25e-04 |
20.88e-04 |
|
Within-lot: Randich et al. |
31.32e-04 |
3.28e-04 |
8.33e-04 |
0.72e-04 |
3.01e-04 |
|
Ratio of within-lot to within-bullet: |
1.2 |
0.8 |
1.8 |
0.04 |
0.14 |
|
aWithin-lot variance for Cu (line 3) is based on 23 of the 28 lots, excluding lots 423, 426, 454, 464, 465 (highly variable). The within-lot variance using all 28 lots is 0.0208. bBased on NAA-As. |
|||||
degrees of freedom for three positions: B, M, and E) confirm the nonsignificance of the position factor for all six elements—all except Sn—at the α level of significance. The significance for Sn results from two extreme values in this data set, both occurring at location E, on lot 424 (B = M = 414 and E = 21) and on lot 454 (B = 377, M = 367, and E = 45). Some lots also yielded three highly dispersed Cu measurements, for example, lot 465 (B = 81, M = 104, and E = 103) and lot 454 (B = 250, M = 263 and E = 156). In general, no consistent patterns (such as, B < E < M or E < M < B) are discernible for measurements within lots on any of the elements, and, except for five lots with highly dispersed Cu measurements, the within-lot variability is about the same as or smaller than the measurement uncertainty (Appendix G).
2.6 Differences in Average Concentrations
The 1,837-bullet data set and the data in Table 1 of Randich et al. (Ref. 7)
provide information on differences in average concentrations between bullets from different lots (in the case of Randich et al.) or sources (as suggested by the FBI for the 1,837-bullet data set). The difference in the average concentration relative to the measurement uncertainty is usually quite large for most pairs of bullets, but it is important to note the instances in which bullets come from different lots but the average concentrations are close. For example, lots 461 and 466 in Table 1 of Randich et al. (Ref. 7) showed average measured concentrations of five of the six elements within 3–6% of each other:
|
|
Sb |
Sn |
Cu |
As |
Bi |
Ag |
|
461 (average) |
696.3 |
673.0 |
51.3 |
199.3 |
97.0 |
33.7 |
|
466 (average) |
721.0 |
632.0 |
65.7 |
207.0 |
100.3 |
34.7 |
|
% difference |
−3.4% |
6.4% |
−21.8% |
−3.7% |
−3.3% |
−2.9% |
Those data demonstrate that two lots may differ by as little as a few percent in as many as five (or even six, including Cd also) of the elements currently being measured in CABL analysis.
Further evidence of the small differences that can occur between the average concentrations in two apparently different bullets arises in 47 pairs of bullets, among the 854 bullets in the 1837-bullet data set in which all seven elements were measured (364,231 possible pairs). The 47 pairs of bullets matched by the FBI’s 2-SD-overlap method are listed in Table K.8. For 320 of the 329 differences between elemental concentrations (47 bullet pairs × 7 elements = 329 element comparisons), the difference is within a factor of 3 of the measurement uncertainty. That is, if δ is the true difference in mean concentrations (estimated by the difference in the measured averages) and σ = measurement uncertainty (estimated by a pooled SD of the measurements in the two bullets or root mean square of the two SDs), an estimate of δ/σ ≤ 3 is obtained on 320 of the 329 element differences. Table K.8 is ordered by the maximal (over seven elements) relative mean difference, or RMD (i.e., difference in sample means, divided by the larger of the two SDs). For the first three bullet pairs listed in Table K.8, RMD ≤ 1 for all seven elements; for the next five bullet pairs, RMD ≤ 1.5 for all seven elements; for 30 bullet pairs, the maximal RMD was between 2 and 3; and for the last nine pairs in the table, RMD was between 3 and 4. So, although the mean concentrations of elements in most of these 854 bullets differ by a factor that is many times greater than the measurement uncertainty, some pairs of bullets (selected by the FBI to be different) show mean differences that can be as small as 1 or 2 times the relative measurement uncertainty. This information on apparent distances between element concentrations relative to measurement uncertainty is used later in the recommendation for the equivalence t test (see Section K.4).
TABLE K.8 Comparisons of 47 Pairs of Bullets from Among 854 of 1,837 Bullets Having Seven Measured Elements, Identified as Match by 2-SD-Overlap Method
|
(Difference in Mean Concentration)/SD |
||||||||||||
|
|
Bullet 1 |
Bullet 2 |
Elements |
|||||||||
|
|
No. |
Case |
No. |
Case |
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
FPPa |
|
1 |
1,044 |
630 |
1,788 |
982 |
0.50 |
0.50 |
0.0 |
0.67 |
0.90 |
0.71 |
0.00 |
0.85 |
|
2 |
591 |
377 |
1,148 |
679 |
0.50 |
0.79 |
0.0 |
0.20 |
0.85 |
1.00 |
0.00 |
0.85 |
|
3 |
1,607 |
895 |
1,814 |
994 |
1.00 |
0.00 |
0.0 |
0.67 |
0.60 |
0.22 |
1.00 |
0.82 |
|
4 |
1,211 |
709 |
1,412 |
808 |
0.25 |
0.09 |
0.0 |
0.17 |
0.28 |
0.53 |
1.12 |
0.88 |
|
5 |
1,133 |
671 |
1,353 |
786 |
0.00 |
0.50 |
0.0 |
1.25 |
1.20 |
0.14 |
1.00 |
0.85 |
|
6 |
1,085 |
653 |
1,180 |
697 |
0.33 |
0.50 |
0.0 |
1.00 |
1.40 |
1.20 |
0.00 |
0.85 |
|
7 |
1,138 |
674 |
1,353 |
786 |
0.50 |
0.50 |
0.0 |
0.00 |
0.83 |
1.43 |
0.00 |
0.88 |
|
8 |
1,044 |
630 |
1,785 |
982 |
0.50 |
1.50 |
0.0 |
1.00 |
0.89 |
1.25 |
0.00 |
0.72 |
|
9 |
937 |
570 |
981 |
594 |
1.00 |
2.00 |
0.5 |
2.00 |
0.41 |
1.00 |
1.00 |
0.61 |
|
10 |
954 |
578 |
1,027 |
621 |
2.00 |
0.00 |
0.5 |
0.33 |
1.00 |
0.18 |
1.00 |
0.74 |
|
11 |
1,207 |
707 |
1,339 |
778 |
1.00 |
1.83 |
0.0 |
0.50 |
1.00 |
1.20 |
2.00 |
0.61 |
|
12 |
1,237 |
724 |
1,289 |
748 |
0.00 |
0.00 |
0.0 |
0.00 |
0.80 |
2.00 |
0.00 |
0.77 |
|
13 |
1,277 |
742 |
1,353 |
786 |
0.00 |
0.50 |
0.0 |
2.00 |
1.40 |
0.43 |
0.00 |
0.77 |
|
14 |
1,286 |
746 |
1,458 |
827 |
1.00 |
0.61 |
0.5 |
1.20 |
0.78 |
0.00 |
2.00 |
0.70 |
|
15 |
1,785 |
982 |
1,788 |
982 |
0.00 |
2.00 |
0.0 |
0.00 |
0.25 |
0.00 |
0.00 |
0.79 |
|
16 |
954 |
578 |
1,793 |
982 |
2.00 |
0.00 |
0.5 |
0.33 |
1.92 |
2.18 |
1.00 |
0.55 |
|
17 |
953 |
577 |
1,823 |
997 |
2.00 |
0.84 |
0.5 |
0.60 |
2.20 |
0.94 |
2.00 |
0.52 |
|
18 |
953 |
577 |
1,075 |
648 |
2.00 |
2.23 |
0.5 |
1.80 |
1.66 |
1.71 |
1.00 |
0.40 |
|
19 |
1,220 |
715 |
1,353 |
786 |
0.00 |
0.50 |
0.0 |
2.25 |
2.17 |
0.57 |
1.00 |
0.63 |
|
20 |
1,339 |
778 |
1,353 |
786 |
1.50 |
0.00 |
0.0 |
1.75 |
0.60 |
2.29 |
2.00 |
0.47 |
|
21 |
1,202 |
703 |
1,725 |
955 |
2.00 |
2.36 |
0.0 |
0.00 |
1.73 |
2.00 |
0.00 |
0.49 |
|
22 |
953 |
577 |
1,067 |
644 |
2.00 |
0.46 |
0.5 |
0.40 |
2.41 |
1.53 |
1.00 |
0.55 |
|
23 |
1,251 |
729 |
1,314 |
760 |
0.50 |
2.41 |
0.0 |
0.71 |
1.80 |
0.76 |
0.00 |
0.63 |
|
24 |
1,550 |
871 |
1,642 |
912 |
0.50 |
0.00 |
0.0 |
2.00 |
2.07 |
2.50 |
2.00 |
0.49 |
|
25 |
1,001 |
608 |
1,276 |
742 |
0.50 |
2.65 |
0.0 |
0.00 |
2.20 |
0.50 |
1.00 |
0.48 |
|
26 |
1,207 |
707 |
1,353 |
786 |
2.00 |
1.83 |
0.0 |
1.50 |
2.67 |
1.43 |
0.00 |
0.35 |
|
27 |
1,353 |
786 |
1,749 |
968 |
0.50 |
0.50 |
0.0 |
1.00 |
2.80 |
1.71 |
0.00 |
0.48 |
|
28 |
1,226 |
719 |
1,723 |
955 |
2.00 |
0.81 |
0.0 |
2.00 |
2.91 |
0.86 |
1.00 |
0.39 |
|
29 |
953 |
577 |
1,335 |
774 |
0.50 |
0.66 |
0.0 |
0.60 |
0.22 |
1.00 |
3.00 |
0.53 |
|
30 |
954 |
578 |
1,173 |
692 |
1.50 |
0.00 |
0.5 |
3.00 |
2.62 |
0.27 |
0.00 |
0.31 |
|
31 |
1,120 |
666 |
1,315 |
761 |
2.00 |
0.00 |
0.0 |
3.00 |
0.78 |
1.00 |
2.00 |
0.40 |
|
32 |
1,133 |
671 |
1,138 |
674 |
0.50 |
0.00 |
0.0 |
1.67 |
1.83 |
3.00 |
1.00 |
0.41 |
|
33 |
1,138 |
674 |
1,207 |
707 |
1.67 |
2.00 |
0.0 |
3.00 |
1.83 |
0.00 |
0.00 |
0.36 |
|
34 |
1,244 |
725 |
1,569 |
881 |
0.00 |
1.82 |
0.0 |
2.00 |
2.27 |
3.00 |
0.00 |
0.36 |
|
35 |
1,245 |
726 |
1,305 |
757 |
0.50 |
0.86 |
0.0 |
0.50 |
2.33 |
1.43 |
3.00 |
0.47 |
|
36 |
1,245 |
726 |
1,518 |
859 |
1.00 |
0.48 |
0.0 |
3.00 |
0.67 |
0.00 |
0.00 |
0.55 |
|
37 |
1,630 |
907 |
1,826 |
998 |
2.33 |
0.87 |
0.0 |
2.00 |
2.09 |
3.00 |
1.00 |
0.34 |
|
38 |
1,709 |
947 |
1,750 |
969 |
1.00 |
0.50 |
0.0 |
3.00 |
0.79 |
2.20 |
2.00 |
0.40 |
|
39 |
921 |
563 |
1,015 |
615 |
0.50 |
3.00 |
0.0 |
1.00 |
3.13 |
3.00 |
1.00 |
0.22 |
|
40 |
1,138 |
674 |
1,749 |
968 |
0.00 |
0.00 |
0.0 |
1.33 |
3.17 |
0.67 |
0.00 |
0.55 |
|
41 |
1,277 |
742 |
1,429 |
816 |
1.67 |
1.14 |
0.0 |
0.50 |
3.20 |
1.00 |
0.00 |
0.47 |
|
42 |
1,220 |
715 |
1,277 |
742 |
0.00 |
0.00 |
0.0 |
0.50 |
3.33 |
2.33 |
1.00 |
0.48 |
|
(Difference in Mean Concentration)/SD |
||||||||||||
|
|
Bullet 1 |
Bullet 2 |
Elements |
|||||||||
|
|
No. |
Case |
No. |
Case |
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
FPPa |
|
43 |
1,305 |
757 |
1,518 |
859 |
1.50 |
0.39 |
0.0 |
2.50 |
3.00 |
3.33 |
3.00 |
0.17 |
|
44 |
1,133 |
671 |
1,207 |
707 |
2.00 |
2.00 |
0.0 |
0.33 |
3.67 |
1.80 |
1.00 |
0.21 |
|
45 |
1,133 |
671 |
1,749 |
968 |
0.50 |
0.00 |
0.0 |
3.00 |
1.60 |
3.67 |
1.00 |
0.18 |
|
46 |
1,169 |
689 |
1,725 |
955 |
0.00 |
0.40 |
0.0 |
1.00 |
0.13 |
3.75 |
1.00 |
0.33 |
|
47 |
1,689 |
934 |
1,721 |
953 |
0.33 |
2.18 |
4.0 |
3.00 |
0.68 |
0.80 |
0.00 |
0.17 |
|
NOTE: Columns 1–4 give the case number and year for the two bullets being compared; columns As through Cd give values of the relative mean difference (RMD); that is, aFPP = false-positive probability. |
||||||||||||
3. ESTIMATING FALSE-POSITIVE PROBABILITY
In this section, the false-positive probability (FPP) of the 2-SD-overlap and range-overlap procedures is estimated. The following notation will be used:
xijk = ith measurement (i=1,2,3) of jth element (j = 1,...,7) on kth CS bullet
yijk = ith measurement (i=1,2,3) of jth element (j = 1,...,7) on kth PS bullet
where “measurement” denotes an average (over triplicates) on one of the three pieces of the bullet (or bullet fragment). When the measurements are transformed with logarithms, xijk will denote the log of the measurement (more likely to be normally distributed; see Section 3.2.2). To simplify the notation, the subscript k is dropped. The mean and SD of the three measurements of a CS or PS bullet can be expressed as follows:
(min(x1j,x2j,x3j), max(x1j,x2j,x3j)) = range interval for CS bullet
(min(y1j,y2j,y3j), max(y1j,y2j,y3j)) = range interval for PS bullet
The sample means ![]() and
and ![]() are estimates of the true mean concentrations of element j in the lead source from which the CS and PS bullets were manufactured, which will be denoted by
are estimates of the true mean concentrations of element j in the lead source from which the CS and PS bullets were manufactured, which will be denoted by ![]() and
and ![]() respectively. (The difference between the two means will be denoted δj.) Likewise, the SDs
respectively. (The difference between the two means will be denoted δj.) Likewise, the SDs ![]() and
and ![]() are estimates of the measurement uncertainty, denoted by σj. We do not expect the sample means
are estimates of the measurement uncertainty, denoted by σj. We do not expect the sample means ![]() and
and ![]() to differ from the true mean concentrations
to differ from the true mean concentrations ![]() and
and ![]() by much more than the measurement uncertainty
by much more than the measurement uncertainty ![]() but it is certainly possible (probability, about 0.10) that one or both of the sample means will differ from the true mean concentrations by more than 1.15σj. Similarly, the sample mean difference,
but it is certainly possible (probability, about 0.10) that one or both of the sample means will differ from the true mean concentrations by more than 1.15σj. Similarly, the sample mean difference, ![]() is likely (probability, 1.05) to fall within
is likely (probability, 1.05) to fall within ![]() of the true difference µxj − µyj, and
of the true difference µxj − µyj, and ![]() can be expected easily to lie within 3.5448σj of the true difference (probability, 0.9996). (Those probabilities are approximately correct if the data are lognormally distributed and the measurement error is less than 5%.)
can be expected easily to lie within 3.5448σj of the true difference (probability, 0.9996). (Those probabilities are approximately correct if the data are lognormally distributed and the measurement error is less than 5%.)
The 2-SD interval (or the range interval) for the CS bullet can overlap with, or match, the 2-SD interval (or the range interval) for the PS bullet in any one of four ways—slightly left, slightly right, completely surrounds, and completely within—and can fail to overlap in one of two ways—too far left and too far right.
Because our judicial system is based on the premise that convicting an innocent person is more serious than acquitting a guilty person, we focus on the probability that two bullets match by either the 2-SD-overlap or range-overlap procedure, given that the mean concentrations of the elements are really different. We first describe the FBI’s method of estimating the probability, and then we use simulation to estimate the FPP.
3.1 FBI Calculation of False-Positive Probability
The FBI reported an apparent FPP that was based on the 1,837-bullet data set (Ref. 11). The authors repeated the method on which the FBI’s estimate was based as follows.
The 2-SD-overlap procedure is described in the analytical protocol (Ref. 11). Each bullet was compared with every other bullet by using the 2-SD-overlap criterion on all seven elements, or [(1,837)(1,836)/2] = 1,686,366 comparisons. Among these 1,837 bullets, 1,393 matched no other bullets. Recall that all seven elements were measured in only 854 bullets. In only 522 bullets, six elements were measured (Cd was missing in 519; and Sn was missing in 3). In 372 bullets, five elements were measured, and in 86 bullets, four were measured. The results showed that 240 bullets “matched” one other bullet, 97 “matched” two bullets, 40 “matched” three bullets, and 12 “matched” four bullets. Another 55 bullets “matched” anywhere from 5 to 33 bullets. (Bullet 112, from case 69 in 1990, matched 33 bullets, in part because only three elements—Sb, Ag, and Bi—were measured and were therefore eligible for comparison with only three elements in the other bullets.) A total of 1,386 bullets were found to have “matched” another bullet [240(1 bullet) + 97(2 bullets) + 40(3 bullets) + 12(4 bullets) + … = 1,386], or 693 (= 1386/2) unique pairs of bullets matched. The FBI summarized the results by claiming an apparent FPP of 693/1,686,366, or 1 in 2,433.4 (“about 1 in 2,500”).
That estimated FPP is probably too small, inasmuch as this 1,837-bullet data set is not a random sample of any population and may well contain bullets that tend to be further apart than one would expect in a random sample of bullets.
3.2 Simulating False-Positive Probability
We simulate the probability that the 2-SD interval (or range interval) for one bullet’s concentration of one element overlaps with the 2-SD interval (or range interval) for another bullet’s concentration of that element. The simulation is described below.
The CS average, ![]() , is an estimate of the true mean concentration, µx; similarly, the PS average,
, is an estimate of the true mean concentration, µx; similarly, the PS average, ![]() , is an estimate of its true mean concentration, µy. We simulate three measurements, normally distributed with mean µx = 1 and measurement uncertainty σ, to represent the measurements of the CS bullet, and three measurements, normally distributed with mean µy = µx + δ and measurement uncertainty σ to represent the measurements of the PS bullet, and determine whether the respective 2-SD intervals and range intervals overlap. We repeat this process 100,000 times, for various values of δ (0.1, 0.2, …, 7.0) and σ (0.005, 0.010, 0.015, 0.020, 0.025, and 0.030, corresponding to measurement uncertainty 0.5%, 1.0%, 1.5%, 2.0%, 2.5%, and 3.0% relative to µ = 1), and we count the proportion of the 100,000 trials in which the 2-SD intervals or range
, is an estimate of its true mean concentration, µy. We simulate three measurements, normally distributed with mean µx = 1 and measurement uncertainty σ, to represent the measurements of the CS bullet, and three measurements, normally distributed with mean µy = µx + δ and measurement uncertainty σ to represent the measurements of the PS bullet, and determine whether the respective 2-SD intervals and range intervals overlap. We repeat this process 100,000 times, for various values of δ (0.1, 0.2, …, 7.0) and σ (0.005, 0.010, 0.015, 0.020, 0.025, and 0.030, corresponding to measurement uncertainty 0.5%, 1.0%, 1.5%, 2.0%, 2.5%, and 3.0% relative to µ = 1), and we count the proportion of the 100,000 trials in which the 2-SD intervals or range
intervals overlap. In this simulation, the measurement error is normally distributed. (Because σ is small, 1.5–3.0%, the results with lognormally distributed error are virtually the same.) Unless δ = 0, the FPPs for the two procedures should be small. We denote the two FPPs by FPP2SD(δ,σ) and FPPRG(δ,σ), respectively. Appendix F shows that the FPP is a function of only the ratio δ/σ; that is, FPP2SD(1,1) = FPP2SD(2,2) = FPP2SD(3,3), and so on, and likewise for FPPRG(δ,σ).
The FPP for the 2-SD-overlap method can be written 1 – P{no overlap}, where “P{…}” denotes the probability of the event in braces. No 2-SD overlap occurs when either ![]() that is, when either
that is, when either ![]() or equivalently, when
or equivalently, when ![]() Thus, 2-SD overlap occurs whenever the difference between the two means is less than twice the sum of the two SDs on the two samples. (The average value of sx or sy, the sample SD of three normally distributed measurements with true standard deviation σ, is 0.8862σ, so on the average two bullets match in the 2-SD-overlap procedure whenever the difference in their sample means is within about 3.5448σ.)
Thus, 2-SD overlap occurs whenever the difference between the two means is less than twice the sum of the two SDs on the two samples. (The average value of sx or sy, the sample SD of three normally distributed measurements with true standard deviation σ, is 0.8862σ, so on the average two bullets match in the 2-SD-overlap procedure whenever the difference in their sample means is within about 3.5448σ.)
Likewise, no range overlap occurs when either max{x1,x2,x3}< min{y1,y2,y3} or max{y1,y2,y3} < min{x1,x2,x3}. The minimum and maximum of three measurements in a normal distribution with measurement uncertainty σ can be expected to lie within 0.8463σ of the true mean, so, very roughly, range overlap occurs on the average when the difference in the sample means lies within 0.8463 + 0.8463 = 1.6926σ of each other.
With measurement uncertainty (MU) equal to σ, the two probabilities are simulated (for only one element, so subscript j is dropped for clarity):
FPPRG(δ,σ) = 1 − P {max(y1,y2,y3) < min(x1, x2, x3)
or max(x1,x2,x3) < min(y1,y2,y3)|µy − µx = δ, MU = σ}
where P{A|S} denotes the probability that A occurs (for example, “ ![]() 2(sx + sy)” under conditions given by S (for example, “true difference in means is δ, and the measurement uncertainty is σ”). The steps in the simulation algorithm follow. Set a value of δ (0.0, 0.1, 0.2, ..., 7.0) percent to represent the true mean difference in concentrations and a value of σ (0.5, 1.0, 1.5, 2.0, 2.5, 3.0) percent to represent the true measurement uncertainty.
2(sx + sy)” under conditions given by S (for example, “true difference in means is δ, and the measurement uncertainty is σ”). The steps in the simulation algorithm follow. Set a value of δ (0.0, 0.1, 0.2, ..., 7.0) percent to represent the true mean difference in concentrations and a value of σ (0.5, 1.0, 1.5, 2.0, 2.5, 3.0) percent to represent the true measurement uncertainty.
1. Generate three values from a normal distribution with mean 1 and standard deviation σ to represent x1, x2, x3, the three measured concentrations of an element in a CS bullet. Generate three values from a normal distribution with mean 1 + δ and standard deviation σ to represent y1,y2,y3, the three measured concentrations of an element on a PS bullet.
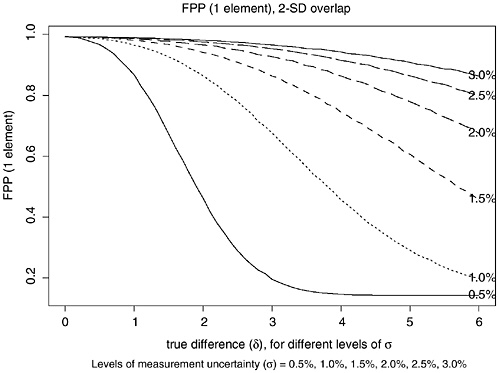
FIGURE K.5 Plot of estimated FPP for FBI 2-SD-overlap procedure as function of δ = true difference between (log)mean concentrations for single element. Each curve corresponds to different level of measurement uncertainty (MU) σ (0.5%, 1.0%, 1.5%, 2.0%, 2.5%, and 3.0%).
2. Calculate ![]() ,
, ![]() , sx, and sy, estimates of the means (µx and µy = 1 + δ) and SD (σ).
, sx, and sy, estimates of the means (µx and µy = 1 + δ) and SD (σ).
3. (a) For the 2-SD-overlap procedure:
(b) For the range-overlap procedure:
if max{x1,x2,x3} < min{y1,y2,y3} or max{y1,y2,y3} < min{x1,x2,x3},
record 0; otherwise record 1.
4. Repeat steps 1, 2, and 3 100,000 times. Estimate FPP2SD (δ,σ) and FPPRG (δ,σ) as the proportion of times that (a) and (b) record “1,” respectively, in the 100,000 trials.
That algorithm was repeated for 71 values of δ (0.0, 0.001, …, 0.070) and six values of σ (0.005, 0.010, 0.015, 0.020, 0.025, and 0.030). The resulting estimates of the FPPs are shown in Figure K.5 (FPP2SD) and Figure K.6 (FPPRG)
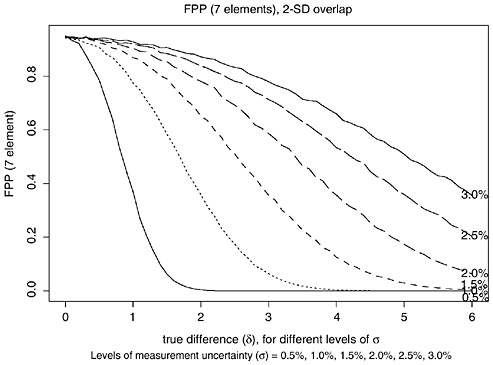
FIGURE K.6 Plot of estimated FPP for FBI 2-SD-overlap procedure as function of δ = true difference between (log)mean concentrations for seven elements, assuming independence among measurement errors. Each curve corresponds to different level of measurement uncertainty (MU) σ (0.5%, 1.0%, 1.5%, 2.0%, 2.5%, and 3.0%).
TABLE K.9 False-Positive Probabilities with 2-SD-Overlap Procedure (δ = 0−7%, σ = 0.5−3.0%)
|
σ δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.990 |
0.841 |
0.369 |
0.063 |
0.004 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.990 |
0.960 |
0.841 |
0.622 |
0.369 |
0.172 |
0.063 |
0.018 |
|
1.5 |
0.990 |
0.977 |
0.932 |
0.841 |
0.703 |
0.537 |
0.369 |
0.229 |
|
2.0 |
0.990 |
0.983 |
0.960 |
0.914 |
0.841 |
0.742 |
0.622 |
0.495 |
|
2.5 |
0.990 |
0.986 |
0.971 |
0.944 |
0.902 |
0.841 |
0.764 |
0.671 |
|
3.0 |
0.990 |
0.987 |
0.978 |
0.960 |
0.932 |
0.892 |
0.841 |
0.778 |
as a function of δ (true mean difference) for different values of σ (measurement uncertainty). Tables K.9 and K.10 provide the estimates for eight values of δ (0, 1, 2, 3, 4, 5, 6, and 7)% and six values of σ (0.5, 1.0, 1.5, 2.0, 2.5, and 3.0)%, corresponding roughly to observed measurement uncertainties of 0.5−3.0% (although some of the measurement uncertainties in both the 800-bullet data and the 1,837-bullet data were larger than 3.0%). The tables cover a wide range of values of δ/σ, ranging from 0 (true match) through 0.333 (δ = 1%, σ = 3%) to 14
TABLE K.10 False-Positive Probabilities with Range-Overlap Procedure δ = 0−7%, σ = 0.5−3.0%)
|
σ δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.900 |
0.377 |
0.018 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.900 |
0.735 |
0.377 |
0.110 |
0.018 |
0.002 |
0.000 |
0.000 |
|
1.5 |
0.900 |
0.825 |
0.626 |
0.377 |
0.178 |
0.064 |
0.018 |
0.004 |
|
2.0 |
0.900 |
0.857 |
0.735 |
0.562 |
0.377 |
0.220 |
0.110 |
0.048 |
|
2.5 |
0.900 |
0.872 |
0.792 |
0.672 |
0.524 |
0.377 |
0.246 |
0.148 |
|
3.0 |
0.900 |
0.882 |
0.825 |
0.735 |
0.626 |
0.499 |
0.377 |
0.265 |
(δ = 7%, σ = 0.5%). (Note: Only the value 0.900 for the range-overlap method when δ = 0 can be calculated explicitly without simulation. The simulation’s agreement with this number is a check on the validity of the simulation.)
For seven elements, the 2-SD-overlap and range-overlap procedures declare a false match only if the 2-SD intervals overlapped on all seven elements. If the true difference in all element concentrations were equal (for example, δ = 2.0%), the measurement uncertainty was constant for all elements (for example, 2.0%), and the measurement errors for all seven elements were independent, the FPP for seven elements would equal the product of the per-element rate, seven times (for example, for δ = σ = 2%, 0.8417 = 0.298 for the 2-SD-overlap procedure, and 0.7307 = 0.110 for the range-overlap procedure). Figures K.7 and K.8, and Tables K.11 and K.12 give the corresponding FPPs, assuming independence among the measurement errors on all seven elements and assuming that the true mean difference in concentration is 100 δ percent.
The FPPs in Tables 3.11 and 3.12 are lower bounds because the analysis in the previous section indicated that the measurement errors may not be independent. (The estimated correlation between the errors in measuring Cu and Sb is 0.7, and the correlations between Sn and Sb, between Cu and Sn, between Ag and Cu, between Ag and Sb may be about 0.3.) The actual overall FPP is likely to be higher than FPP7, probably closer to FPP6 or FPP5 [A brief simulation using the correlation matrix from the Federal bullets and assuming the Cd measurement is uncorrelated with the other 6 elements suggests that the FPP is closer to (per-element rate)5]. To demonstrate that the FPP on seven elements is likely to be higher than the values shown in Table K.11 and K.12, we conducted another simulation, this time using actual data as follows:
1. Select one bullet from among the 854 bullets in which all seven elements were measured. Let x denote the vector of seven concentrations, and let sx denote the vector of the seven SDs of the three measurements. (Note, only the mean and SD for a given bullet in this data set are given.)
2. Generate three values from a normal distribution with mean x and standard deviation sx to represent x1,x2,x3, the three measured concentrations of an
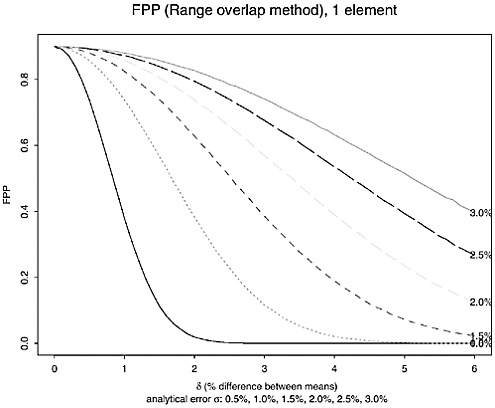
FIGURE K.7 Plot of estimated FPP for FBI range-overlap procedure as function of δ = true difference between (log)mean concentrations for single element. Each curve corresponds to different level of measurement uncertainty (MU) σ (0.5%, 1.0%, 1.5%, 2.0%, 2.5% and, 3.0%).
element in the CS bullet. Generate three values from a normal distribution with mean x(1 + δ) and SD sx to represent y1,y2,y3, the three measured concentrations of an element in the PS bullet. The three simulated x values for element j should have a mean close to the jth component of x (j = 1, …, 7) and SDs close to the jth component of sx. Similarly, the three simulated y values for element j should have a mean close to the jth component of x(1 + δ) and SDs close to the jth component of sx.
3. Calculate ![]() ,
, ![]() , sxj, and syj, for J = 1, …, 7 elements, estimates of the means x and (1 + δ)x and SD (sx).
, sxj, and syj, for J = 1, …, 7 elements, estimates of the means x and (1 + δ)x and SD (sx).
4. For the 2-SD-overlap procedure:
if ![]() for all seven elements, record 0; otherwise record 1.
for all seven elements, record 0; otherwise record 1.
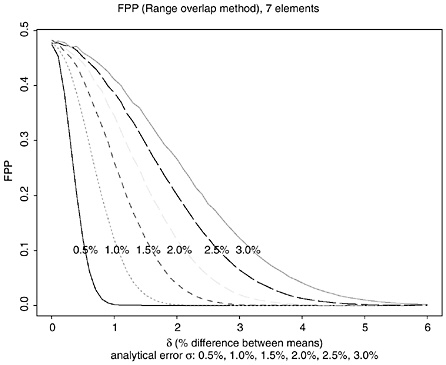
FIGURE K.8 Plot of estimated FPP for FBI range-overlap procedure as function of δ = true difference between (log)mean concentrations for seven elements, assuming independence among measurement errors. Each curve corresponds to different level of measurement uncertainty (MU) σ (0.5%, 1.0%, 1.5%, 2.0%, 2.5%, and 3.0%).
TABLE K.11 False-Positive Probabilities with 2-SD-Overlap Procedure, seven elements (assuming independence: δ = 0−7%, σ = 0.5−3.0%)
|
σ δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.931 |
0.298 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.931 |
0.749 |
0.298 |
0.036 |
0.001 |
0.000 |
0.000 |
0.000 |
|
1.5 |
0.931 |
0.849 |
0.612 |
0.303 |
0.084 |
0.013 |
0.001 |
0.000 |
|
2.0 |
0.931 |
0.883 |
0.747 |
0.535 |
0.302 |
0.125 |
0.036 |
0.007 |
|
2.5 |
0.931 |
0.903 |
0.817 |
0.669 |
0.487 |
0.302 |
0.151 |
0.062 |
|
3.0 |
0.931 |
0.911 |
0.850 |
0.748 |
0.615 |
0.450 |
0.298 |
0.175 |
TABLE K.12 False-Positive Probabilities with Range-Overlap Procedure, seven elements (assuming independence: δ = 0−7%, σ = 0.5−3.0%)
|
σ δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.478 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.478 |
0.116 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.5 |
0.478 |
0.258 |
0.037 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
|
2.0 |
0.478 |
0.340 |
0.116 |
0.018 |
0.001 |
0.000 |
0.000 |
0.000 |
|
2.5 |
0.478 |
0.383 |
0.197 |
0.062 |
0.011 |
0.001 |
0.000 |
0.000 |
|
3.0 |
0.478 |
0.415 |
0.261 |
0.116 |
0.037 |
0.008 |
0.001 |
0.000 |
For the range-overlap procedure:
if max{x1j,x2j,x3j}< min{y1j,y2j,y3j} or max{y1j,y2j,y3j} < min{x1j,x2j,x3j},
for all seven elements, record 0; otherwise record 1.
5. Repeat steps 1, 2, and 3 100,000 times. Estimate FPP2SD(δ) and FPPRG(δ) as the proportion of 1’s that occur in step 4 in the 100,000 trials.
Four values of δ were used for this simulation—0.03, 0.05, 0.07, and 0.10, corresponding to 3%, 5%, 7%, and 10% differences in the means. If the typical relative measurement uncertainty is 2.0–3.0%, the results for 3%, 5%, and 7% should correspond roughly to the values in Tables K.11 and K.12 (2-SD-overlap and range-overlap, respectively, for seven elements), under columns headed 3, 5, and 7. The results of the simulations were:
|
|
δ |
|||
|
method |
3.0% |
5.0% |
7% |
10% |
|
with 2-SD overlap |
0.404 |
0.273 |
0.190 |
0.127 |
|
with range overlap |
0.158 |
0.108 |
0.053 |
0.032 |
The FPP for the 2-SD-overlap method for all seven elements and δ = 3% is estimated in this simulation as 0.404, which falls between the two values in Table K.11 for σ = 1.5% (FPP, 0.303) and for σ 2.0% (FPP, 0.535). The FPP for the 2-SD-overlap method for all seven elements and δ = 5% is estimated in this simulation as 0.273, which falls between the two values in Table K.11 for σ = 2.0% (FPP, 0.125) and for σ = 2.5% (FPP, 0.302). The FPP for the 2-SD-overlap method for all seven elements and δ = 7% is estimated in this simulation as 0.190, which falls between the two values in Table K.11 for σ = 2.5% (FPP, 0.148) and for σ = 3.0% (FPP, 0.265). This simulation’s FPPs for the rangeoverlap method for δ = 3%, 5%, and 7% result in estimates of the FPP as 0.158, 0.108, and 0.032, all of which correspond to values of σ greater than 3.0% in Table K.12 (columns for δ = 3, 5, and 7). The simulation suggests that measurement uncertainty may exceed 2–2.5%, and/or the measurement errors may be correlated.
Note that the FPP computation would be different if the mean concentrations differed by various amounts. For example, if the mean difference in three of the concentrations was only 1% and the mean difference in four of the concentrations was 3%, the overall FPP would involve products of the FPP(δ = 1%) and FPP(δ = 3%). The overall FPP is shown in Table K.8 on the basis of the observed mean difference/MU. Because most of the values of the RMD in Table K.8 are less than 3, the FPP estimates in the final column are high. The FPP estimates are effectively zero if the RMD exceeds 20% on two or more elements.
A separate confirmation of the FPPs in Table K.9 can be seen by using the apparent matches found between 47 pairs of bullets in Table K.8. Among all possible pairs of the 854 bullets from the 1,837-bullet data set (in which all seven elements were measured), 91 pairs showed a maximal RMD (difference in averages divided by 1 SD) across all seven elements of 4.0. The 2-SD-overlap procedure did not declare a match on these other 44 bullet pairs of the 91 pairs for which the maximal difference was 4%. Thus, the FPP could be estimated here as roughly 47/91, or 0.516. Table K.9 shows, for δ = 4% and δ = 2.5%, an estimated FPP of 0.487. That is very close to the observed 0.516, although somewhat lower, possibly because of the correlation (lack of independence) that was used for the calculation from Table K.8 (0.9027 = 0.486, but 0.9026.4 = 0.517). Because homogeneous batches of lead, manufactured at different times, could by chance have the same chemical concentrations (within measurement error), the actual FPP could be even higher.
3.3 Chaining
The third method for assessing a match between bullets described in the FBI protocol [page 11, part (b)] has been called chaining. It involves the formation of “compositionally similar groups of bullets.” We illustrate the effect of chaining on one bullet from the 1,837-bullet data set. According to the notes that accompanied this data set, “it might be most appropriate to consider all samples as unrelated or independent” (Ref. 10); thus, one would not expect to see compositional groups containing large numbers of bullets.
To see the effect of chaining, the algorithm (Ref. 1, p.11, part b; quoted in Section 3.1) was programmed. Consider bullet 1,044, from case 530 in 1997 in the 1,837-bullet data set. (Bullet 1044 is selected for no reason; any bullet will show the effect described below.) The measured elemental concentrations in that bullet are given in Table K.13. (According to Ref. 6, SDs for elements whose average concentrations were zero were inflated to the FBI’s estimate of analytical uncertainty, noted in Table K.5 as “minimum SD (FBI).”)
This bullet matched 12 other bullets; that is, the 2-SD interval overlapped on all elements with the 2-SD interval for 12 other bullets. In addition, each of the 12 other bullets matched other bullets; in total, 42 unique bullets were identified. The intervals for bullet 1,044 and the other 41 bullets are shown in Figure K.9a. The variability in the averages and the SDs of the 42 bullets would call into question the reasonableness of placing them all in the same compositional group. Bullets 150, 341, 634, and 647 clearly show much wider intervals than the others; even when eliminated from the set (Figure K.9b), a substantial amount of variability among the remaining bullets exists. The overall average and SD of the 42 average concentrations of the 42 “matching” bullets are given in the third and fourth lines of Table K.13 as “avg(42 avgs)” and “SD(42 avgs).” In all cases, the SDs are at least as large as, and usually 3–5 times larger than, the SD of bullet 1,044.
TABLE K.13 Statistics on bullet 1,044, to illustrate “Chaining” (see Section 3.4 and Figure K.9)
|
|
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
Avg |
0.0000 |
0.0000 |
0.0000 |
0.0121 |
0.00199 |
0.00207 |
0.00000 |
|
SD |
0.0002 |
0.0002 |
0.0002 |
0.0002 |
0.00131 |
0.00003 |
0.00001 |
|
Avg(42 Avgs) |
0.0004 |
0.0004 |
0.0005 |
0.0110 |
0.00215 |
0.00208 |
0.00001 |
|
SD(42 Avgs) |
0.0006 |
0.0005 |
0.0009 |
0.0014 |
0.00411 |
0.00017 |
0.00001 |
Larger SDs lead to wider intervals and hence more matches. Using avg(42 avgs) ± 2SD(42 avgs) as the new 2-SD interval with which to compare the 2-SD interval from each of the 1,837 bullets results in a total of 58 matching bullets. (Even without the four bullets that have suspiciously wide 2-SD intervals, the algorithm yielded 57 matching bullets.) Although this illustration does not present a rigorous analysis of the FPP for chaining, it demonstrates that this method of assessing matches is likely to create even more false matches than either the 2-SD-overlap or the range-overlap procedure.
One of the questions presented to the committee (see Chapter 1) was, “Can known variations in compositions introduced in manufacturing processes be used to model specimen groupings and provide improved comparison criteria?” The authors of Ref. 8 (Carriquiry et al.) found considerable variability among the compositions in the 800-bullet data set; the analyses conducted here on the 1,837-bullet data set demonstrate that the variability in elemental compositions may be even greater than that seen in smaller data sets. Over 71,000 bullets have been chemically analyzed by the FBI during the last 15 years; thousands more will be analyzed, and millions more produced that will not be analyzed. In addition, thousands of statistical clustering algorithms have been proposed to identify groups in data with largely unknown success. For reasons outlined above, chaining, as one such algorithm, is unlikely to serve the desired purposes of identifying matching bullets with any degree of confidence or reliability. Because of the huge number of clustering algorithms designed for different purposes, this question on model specimen groupings posed to the committee cannot be answered at this time.
4. EQUIVALENCE TESTS
4.1 Concept of Equivalence Tests
Intuitively, the reason that the FPP could be higher than that claimed by the FBI is that the allowable range of the difference between the two sets of element concentrations is too wide. The FBI 2-SD-overlap procedure declares a match on an element if the mean difference in concentrations lies within twice the sum of the standard deviations; that is, if ![]() for all j = 1,2, …, 7
for all j = 1,2, …, 7
FIGURE K.9 Illustration of chaining. Panel (a) shows 2-SD-interval for bullet 1,044 (selected at random) as first line in each set of elements, followed by the 2-SD interval for each of 41 bullets whose 2-SD intervals overlap with that of bullet 1,044. Four of these 41 bullets had extremely wide intervals for Cu, so they are eliminated in Panel (b). Another 2-SD interval was constructed from SD of 42 (38) bullet averages on each element, resulting in a total of 58 (57) bullets that matched.
elements. The allowance used in the 2-SD interval, 2(sxj + syj) calculated for each element, is too wide for three reasons:
-
The measurement uncertainty in the difference between two sample means, each based on three observations, is
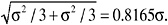 The average value of
The average value of 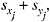 even when the measurements are known to be normally distributed, is (0.8862σ + 0.8862σ) = 1.7724σ, or roughly 2.17 times as large.
even when the measurements are known to be normally distributed, is (0.8862σ + 0.8862σ) = 1.7724σ, or roughly 2.17 times as large. -
A sample SD based on only three observations has a rather high probability (0.21) of overestimating σ by 25%, whereas a pooled SD based on 50 bullets each measured three times (compare Equation 2 in Appendix E) has a very small probability (0.00028) of overestimating σ by 25%. (That is one of the reasons that the authors urge the FBI to use pooled SDs in its statistical testing procedures.)
-
The 2 in 2(sxj + syj) is about 2–2.5 times too large, assuming that
-
The measurement uncertainty σ is estimated by using a pooled SD.
-
The procedure is designed to claim a match only if the true mean element concentrations differ by roughly the measurement uncertainty (δ ≈ σ ≈ 2–4%) or, at most, δ ≈ 1.5σ ≈ 3–6%. Measured differences in mean concentrations smaller than that amount would be considered analytically indistinguishable. Measured differences in mean concentrations larger than δ would be consistent with the hypothesis that the bullets came from different sources.
For these three reasons, the 2-SD interval claims a “match” for bullets that lie within an interval that is, on the average, about 3.5σ (σ = measurement uncertainty), or about 7–17 percent. Hence, bullets whose mean concentrations differ by less than 3.5σ (about 7–17 percent) on all seven elements, have a high probability of being called “analytically indistinguishable.”
The expected range of three normally distributed observations is 1.6926σ, so the range-overlap method tends to result in intervals that are on average, about half as wide as the intervals used in the 2-SD-overlap procedure. This fact explains the results showing that the range-overlap method had a lower rate of false matches than the 2-SD-overlap method.
4.2 Individual Equivalence t Tests
An alternative approach is to set a per-element FPP of, say, 0.30 on any one element, so that the FPP on all seven elements is small, say, 0.305 = 0.00243, or 1 in 412, to 0.306 = 0.000729, or 1 in 1,372. This approach leads to an equivalence t test, which proceeds as follows:
-
Estimate the measurement uncertainty in measuring each element using a pooled SD, that is, the root mean square of the sample SDs from 50 to 100
-
bullets, where the sample SD on each bullet is based on the logarithms of the three measurements of each bullet. (The sample SDs on bullets should be monitored with a process-monitoring chart, called an s-chart; see Ref. 12, pages 76–78.) Denote the pooled SD for element j as sj,pool.
-
Calculate the mean of the logarithms of the three measurements of each bullet. Denote the sample means on element j (j = 1, 2, ..., 7) for the CS and PS bullets as
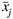 and
and 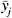 , respectively.
, respectively. -
Calculate the difference between the sample means on each element,
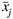 −
−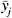 . If they differ by less than 0.63 times sj,pool (about two-thirds of the pooled standard deviation for that element), for all seven elements, then the bullets are deemed “analytically indistinguishable (match).” If the sample means differ by less than 1.07 times sj,pool (slightly more than one pooled standard deviation for that element), for all seven elements, then the bullets are deemed “analytically indistinguishable (weak match).”
. If they differ by less than 0.63 times sj,pool (about two-thirds of the pooled standard deviation for that element), for all seven elements, then the bullets are deemed “analytically indistinguishable (match).” If the sample means differ by less than 1.07 times sj,pool (slightly more than one pooled standard deviation for that element), for all seven elements, then the bullets are deemed “analytically indistinguishable (weak match).”
The limit 0.63 [or 1.07] allows for the fact that each sample mean concentration will vary slightly about its true mean (with measurement uncertainty ![]() and follows from the specification that (a) a false match on a single element has a probability of 0.30 and (b) a decision of “no match” suggests that the mean element concentrations are likely to differ by at least 1σ [or 1.5σ], the uncertainty of a single measurement. That is, assuming that the uncertainty measuring a single element is 2.5 percent and the true mean difference between two bullet concentrations on this element is at least 2.5 percent [3.8 percent], then, with a probability of 0.30, caused by the uncertainty in the measurement process and hence in the sample means
and follows from the specification that (a) a false match on a single element has a probability of 0.30 and (b) a decision of “no match” suggests that the mean element concentrations are likely to differ by at least 1σ [or 1.5σ], the uncertainty of a single measurement. That is, assuming that the uncertainty measuring a single element is 2.5 percent and the true mean difference between two bullet concentrations on this element is at least 2.5 percent [3.8 percent], then, with a probability of 0.30, caused by the uncertainty in the measurement process and hence in the sample means ![]() and
and ![]() , the two sample means will, by chance, lie within 0.63sj,pool [or 1.07] of each other, and the bullets will be judged as analytically indistinguishable on this one element (even though the mean concentrations of this element differ by 2.5%). A match occurs only if the bullets are analytically indistinguishable on all seven elements. Obviously, these limits can be changed, simply by choosing a different value for the per element false match probability, and a different value of δ (here δ = 1 for a “match” and δ = 1.5 for a “weak match.”)
, the two sample means will, by chance, lie within 0.63sj,pool [or 1.07] of each other, and the bullets will be judged as analytically indistinguishable on this one element (even though the mean concentrations of this element differ by 2.5%). A match occurs only if the bullets are analytically indistinguishable on all seven elements. Obviously, these limits can be changed, simply by choosing a different value for the per element false match probability, and a different value of δ (here δ = 1 for a “match” and δ = 1.5 for a “weak match.”)
If the measurement errors in all elements were independent, then this procedure could be expected to have an overall FPP of 0.307 = 0.00022, or about 1 in 4,572. The estimated correlation matrix in Section 3.3 suggests that the measurement errors are not all independent. A brief simulation comparing probabilities on 7 independent normal variates and 7 correlated normal variates (using the correlation matrix based on the Federal bullets given in Appendix F), indicated that the FPP is closer to 0.305.2 = 0.002, or about 1 in 500. To achieve the FBI’s stated FPP of 0.0004 (1 in 2,500), one could use a per-element error rate of 0.222 instead of 0.30, because 0.2225.2 = 0.0004. The limits for “match” and “weak match” would then change, from 0.636sj,pool and 1.07sj,pool to 0.47sj,pool (about one-half of sj,pool) and 0.88sj,pool, respectively. Table K.14 shows the calculations
involved for the equivalence t tests on Federal bullets F001 and F002, using the data in Section 3.1 (log concentrations). The calculations are based on the pooled standard deviations using 200 Federal bullets (400 degrees of freedom; see Appendix F). Not all of the relative mean differences on elements ![]() are less than 0.86 in magnitude, but they are all less than 1.05 in magnitude. Hence the bullets would be deemed “analytically indistinguishable (weak match).”
are less than 0.86 in magnitude, but they are all less than 1.05 in magnitude. Hence the bullets would be deemed “analytically indistinguishable (weak match).”
The allowance 0.86sj,pool can be written as ![]() and the value 0.645 arises from a noncentral t distribution (see Appendix F), used in an equivalence t test (Ref. 13), assuming that n = 3, that at least 100 bullets are used in the estimate sj,pool (200 bullets, or 400 degrees of freedom), and that mean concentrations with δ = σ (that is, within the measurement uncertainty) are considered analytically indistinguishable. The constant changes to
and the value 0.645 arises from a noncentral t distribution (see Appendix F), used in an equivalence t test (Ref. 13), assuming that n = 3, that at least 100 bullets are used in the estimate sj,pool (200 bullets, or 400 degrees of freedom), and that mean concentrations with δ = σ (that is, within the measurement uncertainty) are considered analytically indistinguishable. The constant changes to ![]() if one allows mean concentrations δ = 1.5σ to be considered “analytically indistinguishable.” Other values for the constant are given in Appendix F; they depend slightly on n (here, three measurements per sample mean), on the number of bullets used to estimate the pooled variance (here, assumed to be at least 100), and, most importantly, upon the per-element-FPP (here, 0.30) and on δ/σ (here, 1–1.5). The choice of δ ≈ σ used in the procedure is based on the observation that differences between mean concentrations among the seven elements (δj, j = 1,…,7) in three pairs of bullets in the 854-bullet subset of the 1,837-bullet data set (in which all seven elements were measured), which were assumed to be unrelated, can be as small as the measurement uncertainty (δj/σj ≤ 1 on all seven elements; compare Table K.8). Allowing matches between mean differences within 1.5, 2.0, or 3.0 times the measurement uncertainty increases the constant from 0.767 to 1.316, 1.925, or 3.147, respectively, and results in an increased allowance of the interval from 0.63sj,pool (“match”) to 1.07sj,pool (“weak match”), 1.57sj,pool, and 2.57sj,pool, respectively (resulting in progressively weaker matches). The FBI allowance of
if one allows mean concentrations δ = 1.5σ to be considered “analytically indistinguishable.” Other values for the constant are given in Appendix F; they depend slightly on n (here, three measurements per sample mean), on the number of bullets used to estimate the pooled variance (here, assumed to be at least 100), and, most importantly, upon the per-element-FPP (here, 0.30) and on δ/σ (here, 1–1.5). The choice of δ ≈ σ used in the procedure is based on the observation that differences between mean concentrations among the seven elements (δj, j = 1,…,7) in three pairs of bullets in the 854-bullet subset of the 1,837-bullet data set (in which all seven elements were measured), which were assumed to be unrelated, can be as small as the measurement uncertainty (δj/σj ≤ 1 on all seven elements; compare Table K.8). Allowing matches between mean differences within 1.5, 2.0, or 3.0 times the measurement uncertainty increases the constant from 0.767 to 1.316, 1.925, or 3.147, respectively, and results in an increased allowance of the interval from 0.63sj,pool (“match”) to 1.07sj,pool (“weak match”), 1.57sj,pool, and 2.57sj,pool, respectively (resulting in progressively weaker matches). The FBI allowance of ![]() for the same per-element-FPP of 0.30 corresponds to δ/σ = 4.0. That is, concentrations within roughly 4.3 times the measurement uncertainty would yield an FPP of roughly 0.30 on each element. (Because the measurement uncertainty on all 7 elements is roughly 2–5%, this corresponds to claiming that bullets are analytically indistinguishable whenever the concentrations lie within 8–20% of each other.) Those wide intervals resulted in 693 false matches among all possible pairs of the 1,837 bullets in the 1,837-bullet data set or in 47 false matches among all possible pairs of the 854 bullets in which all seven elements were measured. In contrast, using the limit 1.07sj,pool resulted in zero matches among the 854 bullets.
for the same per-element-FPP of 0.30 corresponds to δ/σ = 4.0. That is, concentrations within roughly 4.3 times the measurement uncertainty would yield an FPP of roughly 0.30 on each element. (Because the measurement uncertainty on all 7 elements is roughly 2–5%, this corresponds to claiming that bullets are analytically indistinguishable whenever the concentrations lie within 8–20% of each other.) Those wide intervals resulted in 693 false matches among all possible pairs of the 1,837 bullets in the 1,837-bullet data set or in 47 false matches among all possible pairs of the 854 bullets in which all seven elements were measured. In contrast, using the limit 1.07sj,pool resulted in zero matches among the 854 bullets.
The use of equivalence t tests for comparing two bullets depends only on a model for measurement error (lognormal distribution, or, if σ/µ is small, normal
TABLE K.14 Equivalence t-Tests on Federal Bullets F001 and F002
|
log(concentration) on F001 |
||||||
|
|
ICP-Sb |
ICP-Cu |
ICP-Ag |
ICP-Bi |
ICP-As |
ICP-Sn |
|
a |
10.28452 |
5.65249 |
4.15888 |
2.77259 |
7.25488 |
7.51861 |
|
b |
10.29235 |
5.61677 |
4.30407 |
2.77259 |
7.29980 |
7.51643 |
|
c |
10.27505 |
5.64545 |
4.18965 |
2.77259 |
7.24708 |
7.48997 |
|
mean |
10.28397 |
5.63824 |
4.21753 |
2.77259 |
7.26725 |
7.50834 |
|
SD |
0.00866 |
0.01892 |
0.07650 |
0.00000 |
0.02845 |
0.01594 |
|
log(concentration) on F002 |
||||||
|
|
ICP-Sb |
ICP-Cu |
ICP-Ag |
ICP-Bi |
ICP-As |
ICP-Sn |
|
a |
10.27491 |
5.62762 |
4.33073 |
2.77259 |
7.29506 |
7.52994 |
|
b |
10.26928 |
5.63121 |
4.20469 |
2.77259 |
7.27170 |
7.49387 |
|
c |
10.27135 |
5.64191 |
4.34381 |
2.70805 |
7.28001 |
7.47760 |
|
mean |
10.27185 |
5.63358 |
4.29308 |
2.75108 |
7.28226 |
7.50047 |
|
SD |
0.00285 |
0.00743 |
0.07682 |
0.03726 |
0.01184 |
0.02679 |
|
sj,pool |
0.0192 |
0.0200 |
0.0825 |
0.0300 |
0.0432 |
0.0326 |
|
RMD sj,pool |
0.631 |
0.233 |
−0.916 |
0.717 |
−0.347 |
0.241 |
distribution), and that a “CIVL” has been defined to be as small a volume as is needed to ensure that the variability of the elemental concentrations within this volume is much smaller than the measurement uncertainty (i.e., within-lot variability is much smaller than σ). It does not depend on any assumptions about the distribution of elemental concentrations in the general population of bullets, for which we have no valid data sets that would allow statistical inference. Probabilities such as the FBI’s claim of “1 in 2,500” are inappropriate when based on a data set such as the 1,837-bullet data set; as noted in Section 3.2, it is not a random collection of bullets from the population of all bullets, or even from the complete 71,000+ bullet data set from which it was extracted.
The use of either 0.63sj,pool or 1.07sj,pool (requiring ![]() and
and ![]() to be within 1.0 to 1.5 times the measurement uncertainty), might seem too demanding when only three pairs of bullets among 854 bullets (subset of the 1,837-bullet data set in which all seven elements were measured) showed differences of less than or equal to 1 SD on all seven elements (eight pairs of bullets had maximal RMDs of 1.5). However, as noted in the paragraph describing the data set, the 1,837 bullets were selected to be unrelated (Ref. 6), and hence do not represent, in any way, any sort of random sample from the population of bullets. We cannot say on the basis of this data set, how frequently two bullets manufactured from different sources may have concentrations within 1.0. We do know that such instances can occur. A carefully designed study representative of all bullets that might exist now or in the future may help to assess the distribution of differences
to be within 1.0 to 1.5 times the measurement uncertainty), might seem too demanding when only three pairs of bullets among 854 bullets (subset of the 1,837-bullet data set in which all seven elements were measured) showed differences of less than or equal to 1 SD on all seven elements (eight pairs of bullets had maximal RMDs of 1.5). However, as noted in the paragraph describing the data set, the 1,837 bullets were selected to be unrelated (Ref. 6), and hence do not represent, in any way, any sort of random sample from the population of bullets. We cannot say on the basis of this data set, how frequently two bullets manufactured from different sources may have concentrations within 1.0. We do know that such instances can occur. A carefully designed study representative of all bullets that might exist now or in the future may help to assess the distribution of differences
between mean concentrations of different bullets and may lead to a different choice of the constant, depending on the level of δ/σ that the procedure is designed to protect. Constants for other values of the per-element FPP (0.01, 0.05, 0.10, 0.20, 0.222 and 0.30) and δ (0.25, 0.50, 1.0, 1.5, 2.0, and 3.0), for n = 3 and n = 5, are given in Appendix F. See also Box K.1
4.3 Hotelling’s T2
A statistical test procedure that is designed for comparing two sets of 7 sample means simultaneously rather than 7 individual tests, one at a time, as in the previous section, uses the estimated covariance matrix for the measurement errors. The test statistic can be written
where:
-
n = number of measurements in each sample mean (here, n = 3).
-
p = number of elements being measured (here, p = 7).

-
s = vector of SDs in measuring the elements (length p).
-
S−1 = inverse of the estimated matrix of variances and covariances among the measurement errors (seven rows and seven columns).
-
R−1 = inverse of the estimated matrix of correlations among the measurement errors (seven rows and seven columns).
-
v = number of degrees of freedom in estimating S, the matrix of variances and covariances (here, 2 times the number of bullets if three measurements are made of each bullet).
Under the assumptions that
-
the measurements are normally distributed (for example, if lognormal, then the logarithms of the measurements are normally distributed),
-
the matrix of variances and covariances is estimated very well, using v degrees of freedom (for example, v = 200, if three measurements are made on each of 100 bullets and the variances and covariances within each set of three measurements are pooled across the 100 bullets), and
-
the bullet means truly differ by δ/σ = 1 in each element,
[v + 1 − p)/(pv)]T2 should not exceed a critical value determined by the noncentral F distribution with p and v degrees of freedom and noncentrality parameter given by n(δ/σ)R−1(δ/σ) = 3(δ/σ) times the sum of the elements in the inverse of the estimated correlation matrix (Ref. 16, pp. 541−542). When p = 7 and v = 400 degrees of freedom, and using the correlation matrix estimated from
|
BOX K.1 The recommended statistical test procedure for assessing a match will involve the calculation of the sample means from the measurements (transformed via logarithms) on the CS and PS bullets and a pooled standard deviation (as an estimate of the measurement uncertainty). If the sample means on all seven elements are “too close,” relative to the variability that is expected for a difference between two sample means, then a “match” is declared. “Too close” is determined by a constant that arises from either a non-central t distribution, if a t-test on each individual element is performed, or a non-central F distribution, if Hotelling’s T2 test is used, where the relative mean differences are combined and weighted in accordance with the correlation among the seven measurement errors. Two types of questions may be posed. The first type involves conditioning on the difference between the bullet means: Given that two bullets really did come from the same CIVL (compositionally indistinguishable volume of lead), what is the probability that the statistical test procedure correctly claims “match”? Similarly, given two bullets that are known to have come from different CIVLs, what is the probability that the test correctly claims “no match”? Stated formally, if δ represents the vector of true mean differences in the seven elemental concentrations, and if “P(A|B)” indicates the probability of A, given that B holds, then these first types of questions can be written: What are P(claim “match” | δ = 0) and P(claim “nonmatch” | δ = 0) (where these two expressions sum to 1 and the second expression is the false non-match probability), and what are P(claim “match” | δ > 0) and P(claim “nonmatch” | δ > 0) (again where these two expressions sum to 1, and the first expression is the false match probability )? In other words, one can ask about the performance of the test, given the true connection between the bullets. Using a combination of statistical theory and simulation, these probabilities can be estimated for the FBI’s current match procedures as well as for the alternative procedures recommended here. The second type of question that can be asked reverses terms and now involves conditioning on the assessment and asking about the state of the bullets. One of the two versions of this type of question is: Given that the statistical test indicates “match”, what is the probability that the two bullets came from the same CIVL? The answer to these questions depends on several factors. First, as indicated in Chapter 3, we cannot guarantee uniqueness in the mean concentrations of all seven elements simultaneously. Uniqueness seems plausible, given the characteristics of the manufacturing process and the possible changes in the industry over time (e.g., very slight increase in silver concentrations over time). But uniqueness cannot be assured. Therefore, at best, we can address only the following modified question: “If CABL analysis indicates “match,” what is the probability that these two bullets were manufactured from CIVL’s that have the same mean concentrations on all seven elements, compared with the probability that these two bullets were manufactured from CIVLs that differ in mean concentration on one or more of the seven elements?” Using the notation above, this probability can be written: P(δ = 0 | claim |
|
“match”), which is 1 − P(δ > 0 | claim “match”). Similarly, one can ask about the P(δ = 0 | claim “nonmatch”), which is 1 − P(δ > 0 | claim “nonmatch”). By applying Bayes’ rule (Ref. 8), P(δ = 0 | claim “match”) = P(claim “match” | δ = 0)P(δ = 0) / P(claim “match” ) and P(δ > 0 | claim “match”) = P(claim “match” | δ > 0)P(δ > 0) / P(claim “match” The ratio between these two probabilities, i.e. P(δ = 0 | claim “match” )/ P(δ > 0) | claim “match”) is equal to: P(claim “match” | δ = 0)P(δ = 0) / P(claim “match” | δ > 0)P(δ > 0) (*) One might reflect, “Given that the CABL analysis indicates “match,” what is the probability that the bullets came from populations with the same mean concentrations, compared to the probability that the bullets came from different populations?” A large ratio might be strong evidence that the bullets came from CIVLs with the same mean concentrations. (In practice, one might allow a small δ0 so that “δ < δ0” is effectively a “match” and “δ > δ0” is effectively a “non-match”; the choice of δ0 will be discussed later, but for now we take δ0 = 0.) The above equation shows that this ratio is actually a product of two ratios, one P(claim “match” | δ = 0) / P(claim “match” \ (δ > 0), which can be estimated as indicated above through simulation, and where a larger ratio indicates a more sensitive test, and a second ratio P(δ = 0) |P(δ > 0) which depends on the values of the mean concentrations across the entire universe of CIVLs (past, present, and future). Section 3 below estimates probabilities of the form of the first ratio and shows that this ratio exceeds 1 for all tests, but especially so for the alternative procedures recommended here. However, the second ratio is unknown, and, in fact, depends on many factors:
These factors will vary by type of bullet, by manufacturer, and perhaps by locale (i.e., more CIVLs are readily accessible to residents of a large metropolitan area than to those in a small urban town). This appendix analyzes data made available to the Committee in an attempt to estimate a frequency distribution for values of δ in the population, which is needed for the probabilities in the second ratio above. However, as will be seen, these data sets are biased, precluding unbiased inferences. In the end, one can conclude only that P(δ > 0 | claim “match”) > P(δ = 0), i.e., given the results of a test that suggests “match,” the probability that the two bullets came from the same CIVL is higher than this probability if the two bullets had not been measured at all. This, of course, is a weak statement. A stronger statement, namely, that the ratio |
|
of the probabilities in (*) exceeds 1, is possible only through a carefully designed sampling scheme, from which estimates, and corresponding confidence intervals, for the probability in question (*), can be obtained. No such unbiased information is currently available. Consequently, the recommended alternative statistical procedures (Hotelling’s T2 test and successive individual Student’s t tests on the seven elements separately) consider only the measurable component of variability in the problem, namely, the measurement error, and not the other sources of variability (within-CIVL and between-CIVL variability), which would be needed to estimate this probability. We note as a further complication to the above that the linkage between a “match” between the CS and PS bullets and the inference that these two bullets came from the same CIVL depends on how a CIVL is defined. If a CS bullet is on the boundary of a CIVL, then the likelihood of a match to bullets outside a CIVL may be much higher than if a CS bullet is in the middle of a CIVL. |
the Federal data (which measured six of the seven elements with ICP-OES; see Appendix F) and assuming that the measurement error on Cd is 5% and is uncorrelated with the others, this test procedure claims analytically indistinguishable (match) only if T2 is less than 1.9 (δ/σ = 1 for each element) and claims analytically indistinguishable (weak match) only if T2 is less than 6.0 (δ/σ = 1.5 for each element), to ensure an overall FPP of no more than 0.0004 (1 in 2,500).1 (When applied to the log(concentrations) on Federal bullets F001 and F002 in Table K.14, the value of Hotelling’s T2 statistic, using only six elements, is 2.354, which is small enough to claim “analytically indistinguishable” when δ/σ = 1.0 and the overall FPP is 0.002, or 1 in 500.)
The limit 1.9 depends on quite a large number of assumptions. It is indeed more sensitive if the correlation among the measurement errors is substantial (as it may be here for at least some pairs of elements) and if the differences in element concentrations tend to be spread out across all seven elements rather than concentrated in only one or two elements. However, the validity of Hotelling’s T2 test in the face of departures from those assumptions is not well understood. For example, the limit 1.9 was based on an estimated covariance matrix from one set of 200 bullets (Federal) from one study conducted in 1991, and the inferences from it may no longer apply to the current measurement procedure. Also, although Hotelling’s T2 test is more sensitive at detecting small differ-
ences in concentrations in all elements, it is less sensitive than the individual t tests if the main cause of the difference between two bullets arises from only one fairly large difference in one element. (That can be seen from the fact that, if the measurement errors were independent, T2/p reduces to the average of the squared two-sample t statistics on the p = 7 separate elements, so one large difference is spread out across the seven dimensions, causing [v + 1 − 7)/v]T2/p to be small and thus to declare a match when the bullets differ quite significantly in one element.) Many more studies would be needed to assess the reliability of Hotelling’s T2 (for example, types of differences typically seen between bullet concentrations, precision of estimates of the variances and covariances between measurement errors, and departures from (log)normality).
4.4 Use of T Tests in Court
One reason for the authors’ recommendation of seven individual equivalence t tests versus its multivariate analog based on Hotelling’s T2, is the familiarity of the form. Student’s t tests are in common use and familiar to many users of statistics; the only difference here is the multiplier (“0.63” for “match” or “1.07” for “weak match,” instead of “2.0” in a conventional t test, α = 0.05). The choice of FPP, and therefore the determination of δ, could appear arbitrary to a jury and could subject the examiner to a difficult cross examination. However, the choice of δ is in reality no more arbitrary than the choice of α in the conventional t test—the “convention” referred to in the name is in fact the choice α = 0.05, leading to a “2.0-sigma” confidence interval. The conventional t test has the serious disadvantage that it begins from the null hypothesis that the crime scene bullet and the suspect’s bullet match, that is, it starts from the assumption that the defendant is guilty (“bullet match”) and sets the probability of falsely assuming that the guilty person is innocent to be .05. This drawback could be overcome by computing the complement of the conventional t test Type II error rate (the rate at which the test fails to reject the null hypothesis when it is false, which in this case would be the false positive result) for a range of alternatives to the null hypothesis and expressing the results in a power curve in order to judge the power of the test. However, this is not as appealing from the statistician’s viewpoint as the equivalence t test. (It is important to note that the standard t test-based matching error rate will fluctuate by bullet manufacturer and bullet type. This is due to the fact that difference among CABLs are characteristic of manufacturer and bullet type.)
Table K.15 presents a comparison of false positive and false negative rates using the FBI’s statistical methods, and using the equivalence and conventional t-tests.
It is important to note that this appendix has considered tests of a “match” between a single CS bullet and a single PS bullet. If the CS bullet were com-
TABLE K.15 Simulated False-Positive and False-Negative Probabilities Obtained with Various Statistical Testing Procedures
|
|
Composition Identical δ = 0 |
Composition Not Identical δ = 1.5 |
|
CABL claims “match” |
||
|
|
True Positive |
False Positive |
|
FBI-2SD |
0.933 |
0.571 |
|
FBI-rg |
0.507 |
0.050 |
|
Conv t |
0.746 |
0.065 |
|
Equiv-t (1.3) |
0.272 |
0.004 |
|
HotelT2 (6.0) |
0.115 |
0.001 |
|
CABL claims “no match” |
||
|
|
False Negative |
True Negative |
|
FBI-2SD |
0.067 |
0.429 |
|
FBI-rg |
0.493 |
0.948 |
|
Conv t |
0.254 |
0.935 |
|
Equiv-t (1.3) |
0.728 |
0.996 |
|
HotelT2 (6.0) |
0.885 |
0.999 |
|
Note: Simulated false-positive and false-negative probabilities obtained with various statistical testing procedures. Simulation is based on 100,000 trials. In each trial, 3 measurements on seven elements were simulated from a normal distribution with mean vector µx, standard deviation vector σx, and within-measurement correlation matrix R, where µx is the vector of 7 mean concentrations from one of the bullets in the 854-bullet data set, σx is the vector of 7 standard deviations on this same bullet, and R is the within-measurement correlation matrix based on data from 200 Federal bullets (see Appendix F). Three further measurements on seven elements were simulated from a normal distribution with mean vector µy = µx + kσx, with the same standard deviation vector σx, and the same within-measurement correlation matrix R, where µy is the same vector of mean concentrations plus an offset equal to k times the measurement uncertainty in each element. The simulated probabilities of each test (FBI 2-SD overlap, FBI range overlap, conventional t, equivalence t) equal the proportions of the 100,000 trials in which the test claimed “match” or “no match” (i.e., the sample means on all 7 elements were within 0.63 of the pooled estimated of the measurement uncertainty in measuring that element). For the first column, the simulation was run with k = 0 (i.e., mean concentrations are the same); for the second column, the simulation was run with k = 1 (i.e., mean concentrations differ by 1.5 times the measurement uncertainty). With 100,000 trials, the uncertainties in these simulated probabilities (two standard errors) do not exceed 0.003. Note that σx is the measurement error, and we can consider this to be equal to |
||
pared with, say, 5 PS bullets, all of which came from a CIVL whose mean concentrations differed by at least 1.5 times the measurement uncertainty (δ = 1.5σ), then, using Bonferroni’s inequality, the chance that the CS bullet would match at least one of the CS bullets could be as high as five times the nominal FPP (e.g., 0.01, or 1 in 100, if the “1 in 500” rate were chosen). Multiplying the current false positive rates for the FBI 2-SD-overlap and range-overlap procedures shown in Table K.15 by the number of bullets being tested results in a very
high probability that at least one of the bullets will appear to “match,” simply by chance alone, even when the mean CIVL concentrations of the two bullets differ by 1.5 times the measurement uncertainty 3−7%). The small FPP for the equivalence t test results in a small probability that some CS bullet will match the PS bullet by chance alone, so long as the number of PS bullets is not very large.
REFERENCES
1. Laboratory Chemistry Unit. Issue date: October 11, 2002. Unpublished (2002).
2. Peele, E. R.; Havekost, D. G.; Peters, C. A.; Riley, J. P.; Halberstam, R. C.; and Koons, R. D. USDOJ (ISBN 0-932115-12-8), 1991, 57.
3. Peters, C. A. Foren. Sci. Comm. 2002, 4(3). <http://www.fbi.gov/hq/lab/fsc/backissu/july2002/peters.htm> as of Aug. 8, 2003.
4. 800-bullet data set provided by FBI in email from Robert D. Koons to Jennifer J. Jackiw, February 24, 2003.
5. 1,837-bullet data set provided by the FBI. (CD) Received by committee May 12, 2003.
6. Koons, R. D. Personal communication to committee. (CD) Received by committee May 12, 2003. Description of 1,837-bullet data set.
7. Randich, E.; Duerfeldt, W.; McLendon, W.; and Tobin, W. Foren. Sci. Int. 2002,127, 174–191.
8. Carriquiry, A.; Daniels, M.; and Stern, H. “Statistical Treatment of Case Evidence: Analysis of Bullet Lead,” Unpublished report, Dept. of Statistics, Iowa State University, 2002.
9. Grant, D. M. Personal communication to committee. April 14, 2003.
10. Koons, R. D. Personal communication to committee via email to Jennifer J. Jackiw. March 3, 2003.
11. Koons, R. D. “Bullet Lead Elemental Composition Comparison: Analytical Technique and Statistics.” Presentation to committee. February 3, 2003.
12. Vardeman, S. B. and Jobe, J. M. Statistical Quality Assurance Methods for Engineers; Wiley: New York, NY 1999.
13. Wellek, S. Testing Statistical Hypotheses of Equivalence; Chapman and Hall: New York, NY 2003.
14. Owen, D.B. “Noncentral t distribution” in Encyclopedia of Statistical Sciences, Volume 6; Kotz, S.; Johnson, N. L.; and Read, C. B.; Eds.; Wiley: New York, NY 1985, pp 286–290.
15. Tiku, M. “Noncentral F distribution” in Encyclopedia of Statistical Sciences, Volume 6; Kotz, S.; Johnson, N. L.; and Read, C. B.; Eds.; Wiley: New York, NY 1985, pp 280–284.
16. Rao, C.R., Linear Statistical Inference and Its Applications; Wiley, New York, NY 1973.