3
Statistical Analysis of Bullet Lead Data
INTRODUCTION
Assume that one has acquired samples from two bullets, one from a crime scene (the CS bullet) and one from a weapon found with a potential suspect (the PS bullet). The manufacture of bullets is, to some extent, heterogeneous by manufacturer, and by manufacturer’s production run within manufacturer. A CIVL, a “compositionally indistinguishable volume of lead”—which could be smaller than a production run (a “melt”)—is an aggregate of bullet lead that can be considered to be homogeneous. That is, a CIVL is the largest volume of lead produced in one production run at one time for which measurements of elemental composition are analytically indistinguishable (within measurement error). The chemical composition of bullets produced from different CIVLs from various manufacturers can vary much more than the composition of those produced by the same manufacturer from a single CIVL. (See Chapter 4 for details on the manufacturing process for bullets.) The fundamental issue addressed here is how to determine from the chemical compositions of the PS and the CS bullets one of the following: (1) that there is a non-match—that the compositions of the CS and PS bullets are so disparate that it is unlikely that they came from the same CIVL, (2) that there is a match—that the compositions of the CS and PS bullets are so alike that it is unlikely that they came from different CIVLs, and (possibly) (3) that the compositions of the two bullets are neither so clearly disparate as to assert that they came from different CIVLs, nor so clearly similar to assert that they came from the same CIVL. Statistical methods are needed in this context for two important purposes: (a) to find ways of making these assertions based on the evidence so that the error rates—either the chance of falsely asserting a match, or the chance of falsely asserting a non-match, are both ac-
ceptably small, and (b) to estimate the size of these error rates for a given procedure, which need to be communicated along with the assertions of a match or a non-match so that the reliability of these assertions is understood.1 Our general approach is to outline some of the possibilities and recommend specific statistical approaches for assessing matches and non-matches, leaving to others the selection of one or more critical values to separate cases 1), 2), and perhaps 3) above.2
Given the data on any two bullets (e.g., CS and PS bullets), one crucial objective of compositional analysis of bullet lead (CABL) is to provide information that bears on the question: “What is the probability that these two bullets were manufactured from the same CIVL?” While one cannot answer this question directly, CABL analysis can provide relevant evidence, the strength of that evidence depending on several factors.
First, as indicated in this chapter, we cannot guarantee uniqueness in the mean concentrations of all seven elements simultaneously. However, there is certainly variability between CIVLs given the characteristics of the manufacturing process and possible changes in the industry over time (e.g., very slight increases in silver concentrations over time). Since uniqueness cannot be assured, at best, we can address only the following modified question:
“What is the probability that the CS and PS bullets would match given that they came from the same CIVL compared with the probability that they would match if they came from different CIVLs?”
The answer to this question depends on:
1. the number of bullets that can be manufactured from a CIVL,
2. the number of CIVLs that are analytically indistinguishable from a given CIVL (in particular, the CIVL from which the CS bullet was manufactured), and
3. the number of CIVLs that are not analytically indistinguishable from a given CIVL.
The answers to these three items will depend upon the type of bullet, the manufacturer, and perhaps the locale (i.e., more CIVLs may be more readily accessible to residents of a large metropolitan area than to those in a small urban town). A carefully designed sampling scheme may provide information from
which estimates, and corresponding confidence intervals, for the probability in question can be obtained. No comprehensive information on this is currently available. Consequently, this chapter has given more attention to the only fully measurable component of variability in the problem, namely, the measurement error, and not to the other sources of variability (between-CIVL variability) which would be needed to estimate this probability.
Test statistics that measure the degree of closeness of the chemical compositions of two bullets are parameterized by critical values that define the specific ranges for the test statistics that determine which pairs of bullets are asserted to be matches and which are asserted to be non-matches. The error rates associated with false assertions of matches or non-matches are determined by these critical values. (These error rates we refer to here as the operating characteristics of a statistical test. The operating characteristics are often called the significance level or Type I error, and the power or Type II error.)
This chapter describes and critiques the statistical methods that the FBI currently uses, and proposes alternative methods that would be preferred for assessing the degree of consistency of two samples of bullet lead. In proposing improved methods, we will address the following issues:
-
General approaches to assessing the closeness of the measured chemical compositions of the PS and CS bullets,
-
Data sets that are currently available for understanding the characteristics of data on bullet lead composition,
-
Estimation of the standard deviation of measures of bullet lead composition, a crucial parameter in determining error rates, and
-
How to determine the false match and false non-match rates implied by different cut-off points (the critical values) for the statistical procedures advocated here to define ranges associated with matches, non-matches, and (possibly) an intermediate situation of no assertion of match status.
Before we address these four topics, we critique the procedures now used by the FBI. At the end, we will recommend statistical procedures for measuring the degree of consistency of two samples of bullet lead, leaving the critical values to be determined by those responsible for making the trade-offs involved.
FBI’s Statistical Procedures Currently in Use
The FBI currently uses the following three procedures to assert a “match,” that is, that a CS bullet and a PS bullet have compositions that are sufficiently similar3 for an FBI expert to assert that they were manufactured from CIVLs
with the same chemical composition. First, the FBI collects three pieces from each bullet or bullet fragment (CS and PS), and nominally each piece is measured in triplicate. (These sample sizes are reduced when there is insufficient bullet lead to make three measurements on each of three samples.) Let us denote by CSki the kth measurement of the ith fragment of the crime scene bullet, and similarly for PSki. Of late, this measurement is done using inductively coupled plasma-optical emission spectrophotometry (ICP-OES) on seven elements that are known to differ among bullets from different manufacturers and between different CIVLs from the same manufacturer. The seven elements are arsenic (As), antimony (Sb), tin (Sn), copper (Cu), bismuth (Bi), silver (Ag), and cadmium (Cd).4
The three replicates on each piece are averaged, and means, standard deviations, and ranges (minimum to maximum) for each element in each of the three pieces are calculated for all CS and PS bullets.5 Specifically, the following are computed for each of the seven elements:
the average measurement for the ith piece from the CS bullet,
the overall average over the three pieces for the CS bullet,
the within-bullet standard deviation of the fragment means for the CS bullet—essentially the square root of the average squared difference between the average measurements for each of the three pieces and the overall average across pieces (the denominator uses 2 instead of 3 for a technical statistical reason),
the spread from highest to lowest of fragment means for the three pieces for the CS bullet.
The same statistics are computed for the PS bullet.
The overall mean, avg(CS), is a measure of the concentration for a given element in a bullet. The overall mean could have differed: (1) had we used different fragments of the same bullet for measurement of the overall average, since even an individual bullet may not be completely homogeneous in its composition, and (2) because of the inherent variability of the measurement method. This variability in the overall mean can be estimated by the within-bullet standard deviation divided by √3 (since the mean is an average over 3 observations). Further, for normally distributed data, the variability in the overall mean can also be estimated by the range/3. Thus the standard deviation (divided by √3) and the range (divided by 3) can be used as approximate measures of the reliability of the sample mean concentration due to both of these sources of variation.
Since seven elements are used to measure the degree of similarity, there are seven different values of CSi and PSi, and hence seven summary statistics for each bullet. To denote this we sometimes use the notation CSi (As) to indicate the average for the ith bullet fragment for arsenic, for example, with similar notation for the other above statistics and the other elements.
Assessment of Match Status
As stated above, in a standard application the FBI would measure each of these seven elements three times in each of three samples from the CS bullet and again from the PS bullet. The FBI presented to the committee three statistical approaches to judge whether the concentrations of these seven elements in the two bullets are sufficiently close to assert that they match, or are sufficiently different to assert a non-match. The three statistical procedures are referred to as: (1) 2-SD overlap, (2) range overlap, and (3) chaining. The crucial issues that the panel examined for the three statistical procedures are their operating characteristics, i.e, how often bullets from the same CIVL are identified as not matching, and how often bullets from different CIVLs are identified as matching. We describe each of these procedures in turn. Later, the probability of falsely asserting a match or a non-match is examined directly for the first two procedures, and indirectly for the last.
2-SD Overlap First, consider one of the seven elements, say arsenic. If the absolute value of the difference between the average compositions of arsenic for the CS bullet and the PS bullet is less than twice the sum of the standard deviations for the CS and the PS bullets, that is if |avg(CS) − avg(PS)| < 2(sd(CS) + sd(PS)), then the bullets are judged as matching for arsenic. Mathematically, this is the same criterion as having the 95 percent6 confidence interval for the
overall average arsenic concentration for the CS bullet overlap the corresponding 95 percent confidence interval for the PS bullet. This computation is repeated, in turn, for each of the seven elements. If the two bullets match using this criterion for all seven elements, the bullets are deemed a match; otherwise they are deemed a non-match.7
Range Overlap The procedure for range overlap is similar to that for the 2-standard deviation overlap, except that instead of determining whether 95 percent confidence intervals overlap, one determines whether the intervals defined by the minimum and maximum measurements overlap. Formally, the two bullets are considered as matching on, say, arsenic, if both max(CS1,CS2,CS3) > min(PS1,PS2,PS3), and min(CS1,CS2,CS3) < max(PS1,PS2,PS3). Again, if the two bullets match using this criterion for each of the seven elements, the bullets are deemed a match; otherwise they are deemed a non-match.
Chaining The description of chaining as presented in the FBI Laboratory document Comparative Elemental Analysis of Firearms Projectile Lead by ICP-OES, is included here as a footnote.8 There are several different interpretations of this language that would lead to different statistical methods. We provide a
description here of a specific methodology that is consistent with the ambiguous FBI description. However, it is important that the FBI provide a rigorous definition of chaining so that it can be properly evaluated prior to use.
Chaining is defined for a situation in which one has a population of reference bullets. (Such a population should be collected through simple random sampling from the appropriate subpopulation of bullets relevant to a particular case, which to date has not been carried out, perhaps because an “appropriate” subpopulation would be very difficult to define, acquire, and test.) Chaining involves the formation of compositionally similar groups of bullets. This is done by first assuming that each bullet is distinct and forms its own initial “compositional group.” One of these bullets from the reference population is selected.9 This bullet is compared to each of the other bullets in the reference population to determine whether it is a match using the 2-SD overlap procedure.10,11 When the bullet is determined to match another bullet, their compositional groups are collapsed into a single compositional group. This process is repeated for the entire reference set. The remaining bullets are similarly compared to each other. In this way, the compositional groups grow larger and the number of such groups decreases.
This process is repeated, matching all of the bullets and groups of bullets to the other bullets and groups of bullets, until the entire reference population of bullets has been partitioned into compositional groups (some of which might still include just one bullet). Presumably, the intent is to join bullets into groups that have been produced from similar manufacturing processes. When the process is concluded, every bullet in any given compositional group matches at least one other bullet in that group, and no two bullets from different groups match.
The process to this point involves only the reference set. Once the compositional groups have been formed, let us denote the chemical composition (for one of the seven elements of interest) from the kth bullet in a given compositional group as CG(k) k =1, ..., K. Then the compositional group average and the compositional group standard deviations12 are computed for this compositional group (assuming K members) as follows, for each element:
Now, suppose that one has collected data for CS and PS bullets and one is interested in determining whether they match. If, for any compositional group, |avg(CS) − avg(CG)| ≤ 2sd(CG) for all seven elements, then the CS bullet is considered to be a match with that compositional group. (Note that the standard deviation of CS is not used.) If using the analogous computation, the PS bullet is also found to be a match with the same compositional group, then the CS and the PS bullets are considered to be a match.
This description leaves some details of implementation unclear. (Note that the 7-dimensional shapes of the compositional groups may have odd features; one could even be completely enclosed in another.) First, since sd(CG) is undefined for groups of size one, it is not clear how to test whether the CS of PS bullets matches a compositional group of one member. Second, it is not clear what happens if the CS or the PS bullet matches more than one compositional group. Third, it is not clear what happens when neither the CS nor the PS bullets match any compositional groups.
An important feature of chaining is that in forming the compositional groups with the reference population, if bullet A matches bullet B, and similarly if bullet B matches bullet C, bullet A may not match bullet C. (An example of the variety of bullets that can be matched is seen in Figure 3.1.) One could construct examples (which the panel has done using data provided by the FBI) in which large chains could be created and include bullets that have little compositionally in common with others in the same group. Further, a reference bullet with a large standard deviation across all seven chemical compositions has the potential of matching many other bullets. Having such a bullet in a compositional group could cause much of the non-transitivity13 just described.
Also, as more bullets are added to the reference set, any compositional groups that have been formed up to that point in the process may be merged if individual bullets in those compositional groups match. This merging may reduce the ability of the groups to separate new bullets into distinct groups. In an extreme case, one can imagine situations in which the whole reference set forms a single compositional group. The extent to which distinctly dissimilar bullets are assigned to the same compositional group in practice is not known, but clearly chaining can increase the rate of falsely asserting that two bullets match in comparison to the use of the 2-SD and range overlap procedures.
The predominant criticisms of all three of these procedures are that (1) the
error rates for false matching and false non-matching are not known, even if one were to assume that the measured concentrations are normally distributed, and (2) these procedures are less efficient, again assuming (log) normally distributed data, in using the bullet lead data to make inferences about matching, than competing procedures that will be proposed for use below.
Distance Functions
In trying to determine whether two bullets came from the same CIVL, one uses the “distance” between the measurements as the starting point. For a single element, the distance may be taken as the difference between the values obtained in the laboratory. Because that difference depends, at least in part, on the degree of natural variation in the measurements, it should be adjusted by expressing it in terms of a standard unit, the standard deviation of the measurement. The standard deviation is not known, but can be estimated from either the present data set or data collected in the past. The form of the distance function is then:
where s is the estimate of the standard deviation.
The situation is more complicated when there are measurements on two separate elements in the bullets, though the basic concept is the same. One needs the two-dimensional distance between the measurements and the natural variability of that distance, which depends on the standard deviations of measurements of the two elements, and also on the correlation between them. To illustrate in simple terms, if one is perfectly correlated (or perfectly negatively correlated) with the other, the second conveys no new information, and vice versa. If one measurement is independent of the other, distance measures can treat each distance separately. In intermediate cases, the analyst needs to understand how the correlation between measurements affects the assessment of distance. One possible distance function is the largest difference for either of the two elements. A second distance function is to add the differences across elements; this is equivalent to saying that the difference between two street addresses when the streets are on a grid is the sum of the north-south difference plus the east-west difference. A third is to take the distance “as the crow flies,” or as one might measure it in a straight line on a map. This last definition of distance is in accord with many of our uses and ideas about distance, but might not be appropriate for estimates of (say) the time needed to walk from one place to another along the sidewalks. Other distance functions could also be defined. Again, we only care about distance and not direction, and for mathematical convenience we often work with the square of the distance function.
The above extends to three dimensions: One needs an appropriate function of the standard deviations and correlations among the measurements, as well as a
|
Technical details on the T2 test For any number d of dimensions (including one, two, three, or seven) where X is a vector of seven average measured concentrations on the CS bullet, Y is a vector of seven average measured concentrations on the PS bullet,’ denotes matrix transposition, n=number of measurements in each sample mean (here, n =3) and S−1 = inverse of the 7 by 7 matrix of estimated variances and covariances. Under the assumptions that
then:[(ν − 6)/7ν]T2 should not exceed a critical value determined by the noncentral F distribution with p and ν degrees of freedom and noncentrality parameter, which is a function of δ, σ, and S−1. When ν = 400 degrees of freedom,and using the correlation matrix estimated from the data from one of the manufacturers of bullet lead (which measured six of the seven elements with ICP-OES; see Appendix F), and assuming that the measurement uncertainty on Cd is 5 percent and is uncorrelated with the others, the choice of the following critical values will provide a procedure with a false match |
specific way to define difference (e.g., if the measurements define two opposite corners of a box, one could use the largest single dimension of the box, the sum of the sides of the box, the distance in a straight line from one corner to the other, or some other function of the dimensions). Again, the distance is easier to use if it is squared.
These concepts extend directly to more than three measurements, though the physical realities are harder to picture. A specific, squared distance function, generally known as Hotelling’s T2, is generally preferred over other ways to define the difference between sets of measurements because it summarizes the information on all of the elements measured and provides a simple statistic that has small error under common conditions for assessing, in this application, whether the two bullets came from the same CIVL.
|
rate, due to measurement error, of no more than 0.0004 (1 in 2,500—which is equivalent to the current asserted false match rate for 2-SD overlap): assert a match when T2 is less than 1.9, assuming δ / σ = 1 for each element, and assert a match when T2 is less than 6.0, assuming δ / σ = 1.5 for each element, where δ is the true difference between each elemental concentration and σ is the true within-bullet standard deviation, i.e., the elemental measurement error assuming no within-bullet heterogeneity. The critical value 1.9 requires that several assumptions be at least approximately true. There is the assumption of (log) normality of the concentration measurements. The use of T2 is sensitive to the estimation of the inverse of the covariance matrix, and T2 assumes that the differences in element concentrations are spread out across all seven elements fairly equally rather than concentrated in only one or two elements. (The latter can be seen from the fact that, if the measurement errors were independent, T2/7 reduces to the average of squared two-sample t statistics for the p = 7 separate elements, so one moderately large difference will be spread out across the seven dimensions, causing [(v − 6) / v]T2/7 to be small and thus to declare a match when the bullets differ quite substantially in one element.) Unfortunately, the validity of Hotelling’s T2 test in the face of departures from those assumptions is not well understood. For example, the limit 1.9 is based on an estimated covariance matrix from one set of 200 bullets from one study conducted in 1991 (given in Appendix F), and the inferences from it may not apply to the current measurement procedure or to the bullets now produced. Many more studies would be needed to assess the reliability of T2 in this application, including examination of the differences typically seen between bullet concentrations, the precision of estimates of the variances and covariances between measurement errors, and sensitivity to the assumption of (log) normality. Source: Multivariate Statistics Methods, 2nd edition, Donald F. Morrison, McGraw-Hill Book Co., New York, NY, 1976. |
Statistical Power
Conclusions drawn from a statistical analysis of the distance between two sets of measurements can be wrong in either of two ways. In the case of bullet lead, if the bullets are in fact from the same CIVL, a conclusion that they are from CIVLs with different means is wrong. Conversely, if the means of the CIVL are not the same, a decision that they are the same is also an error. The latter error may occur when the two bullets from different CIVLs have different compositions but are determined to be analytically indistinguishable due to the allowance for measurement error, or when the two CIVLs in question have by coincidence the same chemical composition. The two kinds of error occur in incompatible situations, one where there is no difference and one where there is. Difficulties arise because we do not know which situation holds, so we must protect ourselves as well as possible against both types of error.
“Power” is a technical term for the probability that a null hypothesis will be rejected at a given significance level given that an alternative hypothesis is in effect. Generally, we want the power of a statistical test to be high for detecting a difference when one exists. The probabilities of the two kinds of error, the significance level—the probability of rejecting the null hypothesis when it is true, and one minus the power—the probability of failing to reject the null hypothesis when it is false, can be partly controlled through the use of efficient statistical procedures, but it is not possible to control both separately. For any given set of data, as one error is decreased, the other inevitably increases. Thus one must try to find an appropriate balance between the two types of error, which is done through the choice of critical values.
For a univariate test of the type described here, critical values are often set so that there is a 5 percent chance of asserting a non-match when the bullets actually match, i.e., 5 percent is the false non-match rate. This use of 5 percent is entirely arbitrary, and is justified by many decades of productive use in scientific studies in which data are generally fairly extensive and of good quality, and an unexpected observation can be investigated to determine whether it was a statistical fluke or represents some real, unexpected phenomenon.
If one examines a situation in which the difference between two bullets is very nearly, but not equal to zero, the probability of asserting a non-match for what are in fact non-matching bullets will remain close to 5 percent. However, as the difference between the bullets grows, the probability of asserting a nonmatch will grow to virtually 100 percent.
In the application of hypothesis testing to the issue at hand, there is an advantage in using as the null hypothesis, rather than the standard null hypothesis that the means for the two bullets are equal, the null hypothesis that the two means differ by greater than the measurement uncertainty. This has the advantage of giving priority, under the usual protocol, to the setting of the size of the test, which is then the false match probability, rather than using the standard null hypothesis, which would give priority to the false non-match probability. However, in the following we adopt a symmetric approach to the two types of errors, suggesting that both be estimated and that they be chosen to have socially acceptable levels of error.
DESCRIPTION OF DATA SETS
This section describes three data sets made available to the committee that were used to help understand the distributional properties of data on the composition of bullet lead. These three datasets are denoted here as the “800-bullet data set,” the “1837-bullet data set,” and the “Randich et al. data set.” We describe each of these data sets in turn.
TABLE 3.1 Number of Cases Having b Bullets in the 1837-Bullet Data Set
|
b = no. bullets |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
14 |
21 |
|
No. cases |
578 |
283 |
93 |
48 |
24 |
10 |
7 |
1 |
1 |
2 |
1 |
1 |
1 |
800-bullet Data Set14 This data set contains triplicate measurements on 50 bullets in 16 boxes—four boxes from each of four major manufacturers (CCI, Federal, Remington, and Winchester) measured as part of a study conducted by Peele et al. (1991). For each of the four manufacturers, antimony (Sb), copper (Cu), and arsenic (As) were measured with neutron activation analysis (NAA), and antimony (Sb), copper (Cu), bismuth (Bi), and silver (Ag) were measured with ICP-OES. In addition, for the bullets manufactured by Federal, arsenic (As) and tin (Sn) were measured using both NAA and ICP-OES. In total, this data set provided measurements on 800 bullets with Sb, Cu, Bi, and Ag, and 200 bullets with measurements on these and on As and Sn. This 800-bullet data set provides individual measurements on three bullet lead samples which permits calculation of within-bullet means, standard deviations, and correlations for six of the seven elements measured with ICP-OES (As, Sb, Sn, Bi, Cu, and Ag). In our analyses, the data are log-transformed. Although the data refer to different sets of bullets depending on the element examined, and have some possible outliers and multimodality, they are the only source of information on within-bullet correlations that the committee has been able to find.
1,837-bullet Data Set15 The bullets in this data set were extracted from a historical file of more than 71,000 bullets analyzed by the FBI laboratory. The 1,837 bullets were selected from the larger set so as to include at least one bullet from each individual case that was determined, by the FBI chemists, to be distinct from the other bullets in the case.16 (This determination involved the bullet caliber, style, and nominal alloy class.) Bullets from 1,005 different cases that occurred between 1989 and 2002 are included. The distribution of number of bullets per case (of the bullets selected for the data set) is given in Table 3.1.
While all bullets in the 1,837-bullet data set were to be measured three times using three fragments from each bullet, only the averages and standard deviations of the (unlogged) measurements are available. As a result, estimation of the measurement uncertainty (relative standard deviation within bullets) could only be estimated with bias. Further, a few of the specified measurements were not recorded, and only 854 bullets had all seven elements measured. Also, due to the way in which these bullets were selected, they do not represent a random sample of bullets from the population of bullets analyzed by the laboratory. The selection likely produced a dataset whose variability between bullets is higher than would be seen in the original complete data set, and is presumably higher than in the population of all manufactured bullets. This data set was useful for providing the committee with approximate levels of concentrations of elements that might be observed in bullet lead.17
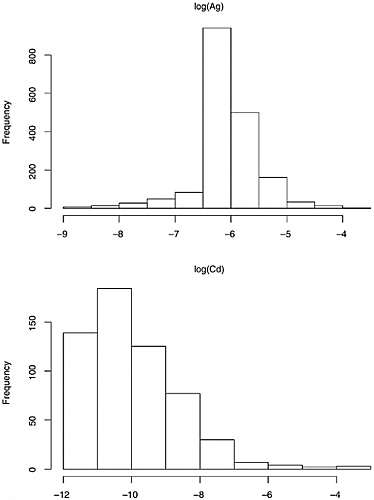
A particular feature of this data set is that the data on Cd are highly discrete: 857 measurements are available of which 285 were reported as 0, 384 of the 857 had Cd concentrations equal to one of six measurements (10, 20, 30, 40, 50, or 60 ppm), and the remaining 188 of the 857 available measurements were spread out from 70 to 47,880 ppm. (The discreteness of the measurements below 70 ppm stem from the precision of the measurement, which is limited to one significant digit due to dilutions in the analytical process.) Obviously, the assumption of log-normality is not fully supportable for this element. We at times focus our attention here on the 854-bullet subset with complete measurements, but also utilize the entire data set for additional computations.
Randich et al. (2002) These data come from Table 1 in an article by Randich et al. (2002). Six elements (all but Cd) were measured for three samples from each of 28 lead castings. The three samples were selected from the beginning, middle, and end of each lot. This data set was used to compare the degree of homogeneity of the lead composition in a lot to that between lots.
Each of these three data sets has advantages but also important limitations for use in modeling the performance of various statistical procedures to match bullet lead composition, especially with respect to determining the chances of asserting a false match or a false non-match. The 800-bullet data set has somewhat limited utility since it has data from only four manufacturers, though they are the major manufacturers in the United States and account for the majority of bullets made domestically. If those manufacturers are in any way unrepresentative of the remaining manufacturers, or if the CIVLs analyzed are for some reason not representative of what that manufacturer distributes, the data can tell us little about the composition of bullets from other manufacturers or CIVLs. However, the 800-bullet data set does provide important information on within-
|
17 |
See Appendix F for details on within-bullet correlations. |
bullet measurement variability and the correlations between various pairs of different elemental composition measurements within a bullet. The analyses in Carriquiry et al. (2002) and Appendix F show that it is reasonable to assume that these estimated parameters are not strongly heterogeneous across manufacturer. This type of analysis is important and should be continued.
The 1,837-bullet data set and the subset we have used are affected by three main problems. First, since the bullets were selected so that the FBI was relatively certain that the bullets came from different melts, the variability represented in the data set is likely to be greater than one would anticipate for bullets selected at random from different melts (which we discuss below). Therefore, two bullets chosen from different CIVLs, as represented in this data set, might coincidentally match less often than one would observe in practice when bullets come from different melts. The extent of any such bias is unknown. In addition, there is a substantial amount of missing data (some elements not measured), which sometimes forces one to restrict one’s attention to the 854 bullets for which measurements of the concentration of all seven elements are available. Finally, the panel was given the means, but not the three separate measurements (averaged over triplicates), on each bullet so that within-bullet correlations of the compositions of different elements cannot be computed.
The data of Randich et al. (2002) provide useful information on the relative degree of homogeneity in a lot in comparison to that between lots, and hence on the degree of variation within a lot in comparison to that between lots. However, as in the 800-bullet data set, these data are not representative of the remaining manufacturers, and one element, Cd, was not measured. Inhomogeneity implies that one lot may contain two or more CIVLs.
In summary, we will concentrate much of our analysis on the 1,837-bullet data set, understanding that it likely has bullets that are less alike than one would expect to see in practice. The 1,837-bullet data set was used primarily to validate the assumption of lognormality in the bullet means, and to estimate within-bullet standard deviations. However, the 1,837-bullet data set, while providing useful information, cannot be used for unbiased inferences concerning the general population of bullets, or for providing unbiased estimates of the error rates for a test procedure using as inputs bullet pairs sampled at random from the general population of bullets. The Randich and the 800-bullet data sets were utilized to address specific issues and to help confirm the findings from the 1,837 (854) bullet data set.
Properties of Data on Lead Composition
Univariate Properties
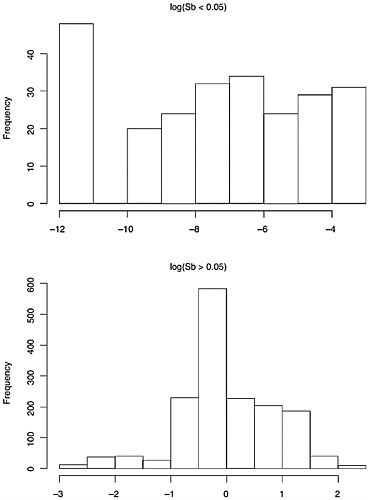
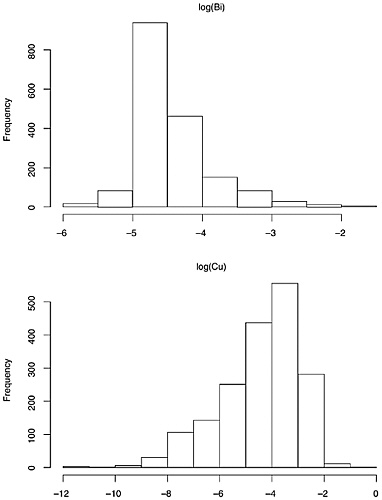
The data on composition of each of the seven elements generally, but not uniformly, appear to have a roughly lognormal distribution. (See Figures 3.2, 3.3, 3.4, and 3.5 for histograms on elemental composition.) That is, the data are
distributed so that their logarithms have an approximately normal distribution. The lognormal distribution is asymmetric, with a longer right tail to the distribution. The more familiar normal distribution that results from taking logarithms has the advantage that many classical statistical procedures are designed for, and thus perform optimally on, data with this distribution.
The 1,837-bullet data set revealed that the observed within-bullet standard deviations (as defined above for CS and PS) are roughly proportional to the measured bullet averages. In contrast, data from the normal distribution have the same variance, regardless of their actual value. For this reason, it is common in this context to refer to the relative standard deviation (RSD), which is defined as 100(stdev / mean). Taking logarithms greatly reduces this dependence of variability on level, which again results in a data set better suited to the application of many classical statistical procedures. Fortunately, standard deviations computed using data that have been log-transformed are very close approximations to the RSD, and in the following, we will equate RSD on the untransformed scale with the standard deviation on the logarithmic scale. (For details, see Appendix E.)
However, the data for the seven elements are not all lognormal, or even mixtures of lognormal data or other simple generalizations. We have already mentioned the discrete nature of the data for cadmium. In addition, the 1,837-bullet data set suggests that, for the elements Sn and Sb, the distributions of bullet lead composition either are bimodal, or are mixtures of unimodal distributions. Further, some extremely large within-bullet standard deviations for copper and tin are not consistent with the lognormal assumption, as discussed below. This is likely due either to a small number of outlying values that are the result of measurement problems, or to a distribution that has a much longer right-side tail than the lognormal. (Carriquiry et al. (2002) utilize the assumption of mixtures of lognormal distributions in their analysis of the 800-bullet data set.)
A final matter is that the data show evidence of changes over time in silver concentration in bullet lead. Most of the analysis carried out and techniques proposed for use assume that the data are from single, stable distributions of bullet-lead concentrations. Variation in concentrations over time could have a substantial impact on the operating characteristics of the statistical tests discussed here (likely making them more effective due to the added difference between bullets manufacturer at different times), resulting in estimated error rates that are higher than the true rates. However, the dynamics might be broader, e.g., making one of the seven elements less important to include in the assessment, or possibly making it useful to add other elements. This can be partially addressed by using a standard data set that was generated from bullets made at about the same time as the bullet in question. Unfortunately, one does not in general know when a CS bullet was made. This issue needs to be further examined, but one immediate step to take is to regularly measure and track element concentrations and compute within-bullet standard deviations and correlations to
ensure the stability of the measurements and the measurement process. A standard statistical construct, the control chart, can be used for this purpose. (See Vardeman and Jobe (1999) for details.)
Within-Bullet Standard Deviations and Correlations
From the 800-bullet data set of the average measurements on the logarithmic scale for each bullet fragment, one can estimate the within-bullet standard deviation for each element and the within-bullet correlations between elements. (We report results from the log-transformed data, but results using the untransformed measurements were similar).
Let us refer to the chemical composition of the jth fragment of the ith bullet from the 800-bullet data set on the log scale as ![]() and the average (log) measurement over the three fragments as
and the average (log) measurement over the three fragments as ![]() where As stands for arsenic, and where analogous measurements for other elements are represented similarly.
where As stands for arsenic, and where analogous measurements for other elements are represented similarly.
The pooled, within-bullet standard deviation, SD(As), is computed as follows:
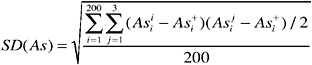
(where the 200 in the denominator is for bullets from a single manufacturer). Similarly, the pooled covariance between the measurements for two elements, such as arsenic and cadmium, is:
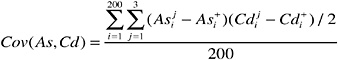
and similarly for other pairs of elements. The covariance is used to calculate the pooled, within-bullet correlation, defined as follows:
SD(As) is more accurate than the within-bullet standard deviations defined for a single bullet above since these estimates are pooled, or averaged, over 200 bullets rather than three fragments. However, the pooling utilizes an assumption of homogeneous variances across bullets, which needs to be justified. (See Appendix F for details.) One aspect of this question was examined by separately computing the within-bullet standard deviations and correlations, as shown above, for each of the four manufacturers. The results of this analysis are also
TABLE 3.2 Pooled Estimates of Within-Bullet Relative Standard Deviations of Concentrations
|
|
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
800 bullets, %a |
5.1 |
2.1 |
3.3 |
4.3 |
2.2 |
4.6 |
— |
|
1,837 bullets, 100 × med(SD/avg), % |
10.9 |
1.5 |
118.2 |
2.4 |
2.0 |
2.0 |
33.3 |
|
a Note: All RSDs based on ICP-OES measurements. RSDs for As and Sn based on 200 Federal bullets. RSDs for Sb, Bi, Cu, and As based on within-bullet variances averaged across four manufacturers (800 bullets). Estimated RSD for NAA-As is 5.1 percent. |
|||||||
given in Appendix F. There it is shown that the standard deviations are approximately equal across manufacturers.
The pooled within-bullet standard deviations on the logarithmic scale (or RSDs) for the 800-bullet and 1,837-bullet data sets are given in Table 3.2. Nearly all of the within-bullet standard deviations are between 2 and 5 (that is, between 2 and 5 percent of the mean on the original scale), a range that is narrow enough to consider the possibility that substantially more variable data might have been excluded.
The estimated (pooled) within-bullet correlations, in Table 3.3, are all positive, but many are close to zero, which indicates that for those element pairs, measurements that are high (or low) for one element are generally not predictive of high or low measurements for others. Four notable cases where the correlations are considerable are those between the measurements for Sb and Cu, estimated as 0.67, and the correlations between the measurements for Ag and Sb, Ag and Cu, and Sb and Bi, all estimated as between 0.30 and0.32. Since the full 800-bullet data set provided only five of the seven elements of interest, there are ![]() distinct correlations, with the four mentioned above higher than 0.30, two more between 0.10 and 0.30, and four less than 0.10.
distinct correlations, with the four mentioned above higher than 0.30, two more between 0.10 and 0.30, and four less than 0.10.
TABLE 3.3 Within-Bullet Correlations (800-Bullet Data Set)
|
|
Average within-bullet correlation matrix |
||||
|
NAA-As |
ICP-Sb |
ICP-Cu |
ICP-Bi |
ICP-Ag |
|
|
NAA-As |
1.00 |
0.05 |
0.04 |
0.03 |
0.04 |
|
ICP-Sb |
0.05 |
1.00 |
0.67 |
0.32 |
0.31 |
|
ICP-Cu |
0.04 |
0.67 |
1.00 |
0.26 |
0.30 |
|
ICP-Bi |
0.03 |
0.32 |
0.26 |
1.00 |
0.16 |
|
ICP-Ag |
0.04 |
0.31 |
0.30 |
0.16 |
1.00 |
It has been commonly assumed that within-bullet measurements are uncorrelated (or independent), but these data suggest that this assumption is not appropriate. These observed correlations could be due to the measurement process, or possibly different manufacturing processes used by the four suppliers for different lots of lead. Positive correlations, if real, will bias the estimated rate of false matches and false non-matches for statistical procedures that rely on the assumption of zero correlations or independence, and the bias might be substantial. The bias would likely be in the direction of increasing the probability of a false match. That is, error rates calculated under the assumption of independence would tend to be lower than the true rates if there is positive correlation. In particular, probabilities for tests, such as the 2-SD overlap procedure, that operate at the level of individual elements and then examine how many individual tests match or not, cannot be calculated by simply multiplying the individual element probabilities, since the multiplication of probabilities assumes independence of the separate tests.
Since the 1,837-bullet data set used by the committee does not include multiple measurements per bullet (only summary averages and standard deviations), it could not be used to estimate within-bullet correlations. However, the standard deviations of the three measurements that are given provide information on within-bullet standard deviations that can be compared to those from the 800-bullet data set. Medians of the bullet-specific within-bullet standard deviations from the 1,837-bullet data set (actually RSDs) can be compared to those pooled across the 800-bullet data set. The comparisons are given in Table 3.2.18 While there appears to be fairly strong agreement between the two data sets, there is a severe discrepancy for Sn, which is the result of a small number of outlying values in the 1,837-bullet data set. Again, the existence of outliers is not a property of a normal distribution (outliers are defined by not belonging to the assumed distribution), and therefore procedures that are overly reliant on the assumption of normality are potentially misleading.
We have referred to the possible bias of using a subset of the 71,000-bullet data set selected so that it was likely to be more heterogeneous than a full subset of bullets drawn from different melts. This possible bias should be investigated. Further, since the measurement of within-bullet standard deviations and correlations is central to the assessment of operating characteristics of testing procedures, it is unfortunate that the availability of multiple measurements (three measurements on three fragments) on each bullet were not reported in the 1,837-bullet data set. An analysis to verify the estimates of the within-bullet standard deviations and the within-bullet correlations should be carried out if the 71,000 bullet
data are structured in a way that makes this computation straightforward. If the data are not structured in that way, or if the data have not been retained, data for all nine measurements that are collected in the future should be saved in a format that enables these computations to be carried out.
More generally, a philosophical view of this problem is to consider bullet lead heterogeneity occurring to a lesser degree as one gets to more disaggre-gate bullet lead volumes. Understanding how this decrease occurs would help identify procedures more specific to the problem at hand. Some of this understanding would result from decomposing the variability of bullet lead into its constituent parts, i.e., within-fragment variation (standard deviations and correlations), between-fragment within-bullet variation, between-bullet withinwire reel variation, between-wire reel and within-manufacturer variation, and between-manufacturer variation. Though difficult to do comprehensively, and recognizing that data sets are not currently available to support this, partial analyses that shed light on this decomposition need to be carried out when feasible.
Between-Bullet Standard Deviations and Correlations
The previous section examined within-bullet standard deviations and correlations, that is, standard deviations and correlations concerning multiple measurements for a single bullet. These statistics are useful in modeling the types of consistency measures that one could anticipate observing from CS and PS bullets from the same CIVL. To understand how much bullets from different CIVLs differ, and the impact on consistency measures, one needs information about the standard deviations and correlations of measurements of bullets from different CIVLs.
The primary source of this information is the 1,837-bullet data set transformed to the logarithmic scale. If the 1,837-bullet data set were a random sample of the population of bullets from different CIVLs, an estimate of the standard deviation across bullets, for, say, arsenic, would be given by:
and an estimate of the correlation between two elements—say, Ag and Sb—would be given by:
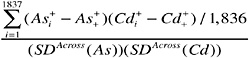
TABLE 3.4 Between-Bullet Standard Deviations (Log Scale) and Correlations (1,837-Bullet Data Set)
|
Stand. Devs: |
As 4.52 |
Sb 4.39 |
Sn 5.79 |
Bi 1.33 |
Cu 2.97 |
Ag 1.16 |
Cd 2.79 |
|
Correlations: |
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
As |
1.00 |
0.56 |
0.62 |
0.15 |
0.39 |
0.19 |
0.24 |
|
Sb |
0.56 |
1.00 |
0.45 |
0.16 |
0.36 |
0.18 |
0.13 |
|
Sn |
0.62 |
0.45 |
1.00 |
0.18 |
0.20 |
0.26 |
0.18 |
|
Bi |
0.15 |
0.16 |
0.18 |
1.00 |
0.12 |
0.56 |
0.03 |
|
Cu |
0.39 |
0.36 |
0.20 |
0.12 |
1.00 |
0.26 |
0.11 |
|
Ag |
0.19 |
0.18 |
0.26 |
0.56 |
0.26 |
1.00 |
0.08 |
|
Cd |
0.24 |
0.13 |
0.18 |
0.03 |
0.11 |
0.08 |
1.00 |
where, e.g., ![]() is the average over fragments and over bullets of the composition of arsenic in the data set (with smaller sample sizes in the case of missing observations). Acknowledging the possible impact of the non-random selection, Table 3.4 provides estimates of the between-bullet standard deviations on the logarithmic scale.
is the average over fragments and over bullets of the composition of arsenic in the data set (with smaller sample sizes in the case of missing observations). Acknowledging the possible impact of the non-random selection, Table 3.4 provides estimates of the between-bullet standard deviations on the logarithmic scale.
Table 3.4 also displays the between-bullet sample correlation coefficients from the 1,837-bullet data set. All correlations are positive and a few exceed 0.40. In particular, the correlation between Sn and As is .62. Therefore, when one has a bullet that has a high concentration of Sn relative to other bullets, there is a substantial chance that it will also have a high concentration of As.
Further Discussion of Bullet Homogeneity Using Randich data set
The data in the Randich bullet data set were collected to compare the degree of heterogeneity between and within lead casting, from which bullets are manufactured. Appendix G presents an analysis of those data. Here we focus on comparing the within-measurement standard deviations obtained using the 800-bullet data set with the within-lot standard deviations in the Randich data. The former includes five of the seven elements (As, Sb, Cu, Bi, and Ag), calculated, as before, on the logarithms of the original measurements, and so they are essentially equal to the RSDs on the original scale of measurement. The results are presented in Table 3.5.
For concentrations of the elements As and Sb, the variability of the three measurements from a lot (beginning, middle, and end; or B, M, and E) is about the same as the variability of the three measurements per bullet in the 800-bullet data set. For Bi and Ag, the within-lot variability (B, M, and E) is much smaller than the within-bullet variability in the 800-bullet data set; this finding is unexpected. Further investigation is needed to verify this finding and to determine how and why variation within a bullet could be larger than variation from end to end of a lot from which bullets are made. The within-lot standard deviation of
TABLE 3.5 Comparison of Within-Bullet and Within-Lot Standard Deviationsa
the three Cu measurements is larger than the within-bullet standard deviation obtained in the 800-bullet data set because of some very unusual measurements in five lots; when these are excluded, the estimated within-lot standard deviation is similar to the within-bullet standard deviation in the 800-bullet data set. Again, further investigation is needed to determine whether this large within-CIVL variance for copper is a general phenomenon, and if so, how it should affect interpretations of bullet lead data. Randich et al. (2002) do not provide replicates or precise within-replicate measurement standard errors, so one cannot determine whether the precision of one of their measurements is equivalent to the precision of one of the FBI measurements.
The above table can also be used to compare lot-to-lot variability to withinlot variability. For four of the five elements, the lot-to-lot variability was 9–15 times greater than within-lot variability. Finally, separate two-way analyses of variance on the logarithms of the measurements on six elements, using the two factors “lot” and “position in lot,” show that the position factor for five of the six elements (all but Sn) is not statistically significant at the α = 0.05 level. So the variability between lots greatly dominates the variability within lot. The significance for Sn results from two extreme values in this data set, both occurring at the end (namely, B = M = 414 and E = 21; and B = 377, M = 367, and E = 45). Some lots also yielded three highly dispersed Cu measurements, for example, B = 81, M = 104, and E = 103, and B = 250, M = 263, and E = 156. In general, no consistent patterns (such as, B < E < M or E < M < B) are discernible for measurements within lots on any of the elements, and, except for five lots with highly dispersed Cu, the within-lot variability is about the same as or smaller than the measurement uncertainty (see Appendix G for details).
Overall, the committee finds a need for further investigation of the variability of these measurements as a necessary tool for understanding measurement
uncertainty and between-CIVL variability, which will affect the assessment of matches between bullets.
Differences in Average Concentrations—The Relative Mean Difference
The distribution of concentrations among bullets is important for understanding the differences that need to be identified by the testing procedures, i.e., what differences exist between pairs of unrelated bullets that should result in the pair being excluded from those judged to be matches. We have already examined between-bullet standard deviations and correlations. This section is devoted to the average relative difference in chemical composition of bullets manufactured from different CIVLs. This is related to the between-bullet standard deviations, but is on a scale that is somewhat easier to interpret. There are two sources of information on this: the 1,837-bullet data set and the data in Table 1 of Randich et al. (2002). Both of these sources provide some limited information on differences in average concentrations between bullets from different lead castings (in the case of Randich et al.) or other sources (as suggested by the FBI for the 1,837-bullet data set.) The difference in the average concentration relative to the measurement uncertainty is quite large for most pairs of bullets, but it sometimes happens that bullets from different sources have differences in average concentrations that are within the measurement uncertainty, i.e., the within-bullet or within-wire reel standard deviation.
For example, lots 461 and 466 in Table 1 of Randich et al. (2002) showed average concentrations of five of the six elements roughly within 3–7 percent of each other:
|
|
Sb |
Sn |
Cu |
As |
Bi |
Ag |
|
461 (average) |
696.3 |
673.0 |
51.3 |
199.3 |
97.0 |
33.7 |
|
466 (average) |
721.0 |
632.0 |
65.7 |
207.0 |
100.3 |
34.7 |
|
% difference |
−3.4% |
6.4% |
−21.8% |
−3.7% |
−3.3% |
−2.9% |
These data demonstrate that two lots may differ by as little as a few percent in at least five of the elements currently measured in CABL analysis.
Further evidence that small differences can occur between the average concentrations in two apparently different bullets arises in the closest 47 pairs of bullets among the 854 bullets in the 1,837-bullet data set in which all seven elements were measured (364,231 possible pairs). For 320 of the 329 differences between elemental concentrations (47 bullet pairs, each with 7 elements = 329 element comparisons), the difference is within a factor of 3 of the measurement uncertainty. That is, if the measured difference in mean concentrations (estimated by the difference in the measured averages) is δ and σ = measurement uncertainty (estimated by a pooled within-bullet standard deviation), an estimate of δ/σ is less than or equal to 3 for 320 of the 329 element differences. For three of the bullet pairs, the relative mean difference (RMD), the difference in the
sample means divided by the larger of the within-bullet standard deviations, is less than 1 for all seven elements. For 30 pairs, the RMD is less than or equal to 3, again for all seven elements. So, although the mean concentrations of elements in most of the 854 bullets (selected from the 1,837-bullet data set) often differ by a factor that is many times greater than the measurement uncertainty, some of these unrelated pairs of bullets, selected by the FBI to be from distinct scenarios, show mean differences that can be as small as 1 to 3 times the measurement uncertainty.
ESTIMATING THE FALSE MATCH PROBABILITIES OF THE FBI’S TESTING PROCEDURES
We utilize the notation developed earlier, where CSi represented the average of three measurements of the ith fragment of the crime scene bullet, and similarly for PSi. We again assume that there are seven of these sets of measures, corresponding to the seven elements. These measurements are logarithmic transformations of the original data. As before, consider the following statistics:
the overall average over the three pieces for the CS bullet,
the standard deviation for the CS bullet, and the
The analogous statistics are computed for the PS bullet.
The 2-SD interval for the CS bullet is: (avg(CS) − 2sd(CS), avg(CS) + 2sd(CS)), and the 2-SD interval for the PS bullet is: (avg(PS) − 2sd(PS), avg(PS) + 2sd(PS)). The range for the CS bullet is: [min(CS1,CS2,CS3), max(CS1,CS2, CS3)] and the range for the PS bullet is: [min(PS1,PS2,PS3), max(PS1,PS2,PS3)]. We denote the unknown true concentration for the CS bullet as µ(CS), and the unknown true concentration for the PS bullet as µ(PS). We also denote the unknown true standard deviation for both CS and PS as σ.19 Finally, define δ = µ(CS) − µ(PS), the difference between the true concentrations. We do not expect avg(CS) to differ from the true concentration µ(CS) by much more than twice the standard deviation of the mean ![]() and similarly for PS, though there is a probability of about 10 percent that one or both differ by this much or more.
and similarly for PS, though there is a probability of about 10 percent that one or both differ by this much or more.
Similarly, we do not expect avg(CS) − avg(PS) to differ from the true difference in means δ by much more than ![]() though it will happen occasionally.
though it will happen occasionally.
One of the two errors that can be made in this situation is to falsely judge the CS and PS bullets to be matches when they come from distinct CIVLs. We saw in the previous section that bullets from different CIVLs can have, on occasion, very similar chemical compositions. Since in many cases a match will be incriminating, we would like to make the probability of a false match small.20 We therefore examine how large this error rate is for both of the FBI’s current procedures, and to a lesser extent, for chaining. This error rate for false matches, along with the error rate for false non-matches, will be considerations in suggesting alternative procedures. To start, we discuss the FBI’s calculation of the rate of false matching.
FBI’s Calculation of False Match Probability
The FBI reported an estimate of the false match rate through use of the 2-SD-overlap test procedure based on the 1,837-bullet data set. (Recall that this data set has a considerable amount of missing data.) The committee replicated the method on which the FBI’s estimate was based as follows. For each of the 1.686 million, i.e., ![]() pairs of bullets from this data set, the 2-SD overlap test was used to determine whether each pair matched. It was found that 1,393 bullets matched no others, 240 bullets matched one other, 97 bullets matched two others, 40 bullets matched three others, and 12 bullets matched four others. In addition, another 55 bullets matched from 5 to 33 bullets. (The maximum was achieved for a bullet that only had three chemical concentrations measured.) A total of 693 unique pairs of bullets were found to match, which gives a probability of false match of 693/1.686 million = 1/2,433 or .04 percent. As mentioned above, this estimate may be biased low because the 1,837 bullets were selected in part in an attempt to choose bullets from different CIVLs.
pairs of bullets from this data set, the 2-SD overlap test was used to determine whether each pair matched. It was found that 1,393 bullets matched no others, 240 bullets matched one other, 97 bullets matched two others, 40 bullets matched three others, and 12 bullets matched four others. In addition, another 55 bullets matched from 5 to 33 bullets. (The maximum was achieved for a bullet that only had three chemical concentrations measured.) A total of 693 unique pairs of bullets were found to match, which gives a probability of false match of 693/1.686 million = 1/2,433 or .04 percent. As mentioned above, this estimate may be biased low because the 1,837 bullets were selected in part in an attempt to choose bullets from different CIVLs.
It is important to understand the concept of a random sample of bullets in this context. Many different domestic manufacturers make bullets that are used in the United States, and a small proportion of bullets sold in the United States are from foreign manufacturers. Bullets are used in a number of activities, including sport, law enforcement, hunting, and criminal activity, and there may be differences in bullet use by manufacturer. (See Carriquiry et al., 2002, for
relevant analysis of this point.) While it may make no appreciable difference, it may be useful to consider what the correct reference population of bullets is for this problem. Once that has been established, one could then consider how to sample from that reference population or a closely related population, since it may be the case that sampling would be easier to carry out for a population that was slightly different from the reference population, and deciding to do so might appropriately trade off sampling feasibility for a very slight bias. One possible reference population is all bullets collected by the FBI in criminal investigations. However, a reference population should be carefully chosen, since the false match and non-match rates can depend on the bullet manufacturer and the bullet type. One may at times restrict one’s attention to those subpopulations.
Simulating False Match Probability
The panel carried out a simulation study to estimate the false match rate of the FBI’s procedures. Three measurements, normally distributed with mean one and standard deviation σ were randomly drawn using a standard pseudo-random number generator to represent the measurements for a CS bullet, and similarly for the PS bullet, except that the mean in the latter case was 1 + δ, so that the relative change in the mean is δ. The panel then computed both the 2-SD intervals and the range intervals and examined whether the 2-SD intervals overlapped or the range intervals overlapped, in each case indicating a match. This was independently simulated 100,000 times for various values of σ (0.005, 0.010, 0.015, 0.020, 0.025, and 0.030) and various values of δ (0.0, 0.1, 0.2, …, 7.0). The choices for σ were based on the estimated within-bullet standard deviations of less than .03, or 3.0 percent. The choices for δ were based on the data on differences in average concentrations between bullets. Clearly, except for the situations where δ equals zero, the (false) match probability should be small. (In Appendix F, it is shown that this probability is a function of only the ratio δ/σ. Also, “1” for the mean concentration in the CS bullet is chosen for simplicity and does not reduce the generality of conclusions.)
The sample standard deviation is not unbiased as an estimate of the true standard deviation; its average value (when it is calculated from three normal observations) is 0.8862σ. Therefore, when the sample means of the CS and the PS bullets lie within four times this distance, or 2(sd(CS) + sd(PS)), which is approximately 2(0.8862σ + 0.8862σ) = 3.55σ, the 2-SD intervals will overlap. Because the allowance for the difference in sample means is only 1.6σ given typical error levels for hypothesis testing (see above), the FBI allowance of approximately 3.55σ being more than twice as wide raises a concern that the resulting false match and false non-match probabilities do not represent a trade-off of these error rates that would be considered desirable. (Note that for the normal distribution, the probability drops off rapidly outside of the range of two standard deviations but not for longer-tailed distributions.) For ranges, under the
assumption of normality, a rough computation shows that the ranges will overlap when the sample means lie within 1.69σ of each other, which will result in a lower false match rate than for the 2-SD overlap procedure.
The resulting estimates of the false match rates from this simulation for eight values of δ(0, 1, 2, 3, 4, 5, 6, and 7) and for six values of σ (0.005, 0.01, 0.015, 0.020, 0,025, and 0.030) are shown in Table 3.6 and Table 3.7. Note that the column δ = 0 corresponds to the situation where there is no difference in composition between the two bullets, and is therefore presenting a true match probability, not a false match probability.
For seven elements, the 2-SD-overlap and range-overlap procedures declare a false match only if the 2-SD intervals (or ranges) overlap on all seven elements. If the true difference in all element concentrations were equal (for example, δ = 2.0 percent for all seven elements), the measurement uncertainty were constant for all elements (for example, σ = 1.0 percent), and the measurement errors for all seven elements were independent, the false match probability for seven elements would equal the product of the per-element rate seven times (for example, for δ = 2.0, σ = 1.0, .8417 = 0.298 for the 2-SD-overlap procedure, and .3777 = 0.001 for the range-overlap procedure). Tables 3.8 and 3.9 give the corresponding false match probabilities for seven elements, assuming independence among the measurement errors on all seven elements.
The false match probabilities in Tables 3.8 and 3.9 are lower bounds because the analysis in the previous section indicated that the measurement errors are likely not independent. Thus, the actual seven-element false match probabil-
TABLE 3.6 False Match Probabilities with 2-SD-Overlap Procedure, One Element (δ = 0−7%, σ = 0.5−3.0%)
|
σ/δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.990 |
0.841 |
0.369 |
0.063 |
0.004 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.990 |
0.960 |
0.841 |
0.622 |
0.369 |
0.172 |
0.063 |
0.018 |
|
1.5 |
0.990 |
0.977 |
0.932 |
0.841 |
0.703 |
0.537 |
0.369 |
0.229 |
|
2.0 |
0.990 |
0.983 |
0.960 |
0.914 |
0.841 |
0.742 |
0.622 |
0.495 |
|
2.5 |
0.990 |
0.986 |
0.971 |
0.944 |
0.902 |
0.841 |
0.764 |
0.671 |
|
3.0 |
0.990 |
0.987 |
0.978 |
0.960 |
0.932 |
0.892 |
0.841 |
0.778 |
TABLE 3.7 False Match Probabilities with Range-Overlap Procedure, One Element (δ = 0−7%, σ = 0.5−3.0%)
|
σ/δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.900 |
0.377 |
0.018 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.900 |
0.735 |
0.377 |
0.110 |
0.018 |
0.002 |
0.000 |
0.000 |
|
1.5 |
0.900 |
0.825 |
0.626 |
0.377 |
0.178 |
0.064 |
0.018 |
0.004 |
|
2.0 |
0.900 |
0.857 |
0.735 |
0.562 |
0.377 |
0.220 |
0.110 |
0.048 |
|
2.5 |
0.900 |
0.872 |
0.792 |
0.672 |
0.524 |
0.377 |
0.246 |
0.148 |
|
3.0 |
0.900 |
0.882 |
0.825 |
0.735 |
0.626 |
0.499 |
0.377 |
0.265 |
TABLE 3.8 False Match Probabilities with 2-SD-Overlap Procedure, Seven Elements (Assuming Independence: δ = 0−7%, σ = 0.5−3.0%)
|
σ/δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.931 |
0.298 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.931 |
0.749 |
0.298 |
0.036 |
0.001 |
0.000 |
0.000 |
0.000 |
|
1.5 |
0.931 |
0.849 |
0.612 |
0.303 |
0.084 |
0.013 |
0.001 |
0.000 |
|
2.0 |
0.931 |
0.883 |
0.747 |
0.535 |
0.302 |
0.125 |
0.036 |
0.007 |
|
2.5 |
0.931 |
0.903 |
0.817 |
0.669 |
0.487 |
0.302 |
0.151 |
0.062 |
|
3.0 |
0.931 |
0.911 |
0.850 |
0.748 |
0.615 |
0.450 |
0.298 |
0.175 |
TABLE 3.9 False Match Probabilities with Range-Overlap Procedure, Seven Elements (Assuming Independence: δ = 0−7%, σ = 0.5−3.0%)
|
σ/δ |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.5 |
0.478 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.0 |
0.478 |
0.116 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
0.000 |
|
1.5 |
0.478 |
0.258 |
0.037 |
0.001 |
0.000 |
0.000 |
0.000 |
0.000 |
|
2.0 |
0.478 |
0.340 |
0.116 |
0.018 |
0.001 |
0.000 |
0.000 |
0.000 |
|
2.5 |
0.478 |
0.383 |
0.197 |
0.062 |
0.011 |
0.001 |
0.000 |
0.000 |
|
3.0 |
0.478 |
0.415 |
0.261 |
0.116 |
0.037 |
0.008 |
0.001 |
0.000 |
ity is likely to be higher than the false match probabilities for a single element raised to the seventh power, which are what are displayed. As shown below, the panel has determined that for most cases the correct false match probability will be closer to the one element probability raised to the fifth or sixth power.
Table 3.8 for the 2-SD-overlap procedure for seven elements is rather disturbing in that for values of δ around 3.0, indicating fairly sizeable differences in concentrations, and for reasonable values of σ, the false match probabilities can be quite substantial. (A subset of the 1,837-bullet data set showed only a few pairs of bullets where δ/σ might be as small as 3 for all seven elements. However, the 1837-bullet data set was constructed to contain bullets selected to be as distinct as possible, so the actual frequency is likely higher.)
A simulation study using the within-bullet correlations from the Federal bullets and assuming the Cd measurement is uncorrelated with the other six elements suggests that the false match probability is close to the single element rate raised to the fifth power. An additional simulation study carried out by the panel, based on actual data, further demonstrated that the false match probabilities on seven elements are likely to be higher than the values shown in Table 3.8 and 3.9. The study was conducted as follows:
-
Select a bullet at random from among the 854 bullets (of the 1,837 bullet data set) in which all seven elements were measured.
TABLE 3.10 Simulated False Match Probabilities Based on Real Dataa
-
Start with seven independent standard normal variates. Transform these seven numbers so that they have the same correlations as the estimated within-bullet correlations. Multiply the individual transformed values by the within-bullet standard deviations to produce a multivariate normal vector of bullet lead concentrations with the same covariance structure as estimated using the 200 Federal bullets in the 800-bullet data set. Add these values to the values for the randomly selected bullet. Repeat this three times to produce the three observations for the CS bullet. Repeat this for the PS bullet, except add δ to the values at the end.
-
For each bullet calculate the within-bullet means and standard deviations, and carry out the 2-SD-overlap and range-overlap procedures.
-
Repeat 100,000 times, calculating the overall false match probabilities for four values of δ, 0.03, 0.05, 0.07, and 0.10.
The results of this simulation are given in Table 3.10.
Generally speaking, the false match probabilities from this simulation were somewhat higher than those given in Tables 3.8 and 3.9. This may be due to either a larger than anticipated measurement error in the 854 bullet data set, the correlations among the measurement errors, or both. (This simulation does not include false matches arising from the possibility of two CIVLs having the same composition.)
This discussion has focused on situations in which the means for the CS and PS bullets were constant across elements. For the more general case, the results are more complicated, though the above methods could be used in those situations.
False Match Probability for Chaining
To examine the false match probability for chaining, the panel carried out a limited analysis. The FBI, in its description of chaining, states that one should avoid having a situation in which bullets in the reference population form compositional groups that contain large numbers of bullets. (It is not clear how the algorithm should be adjusted to prevent this from happening.) This is because
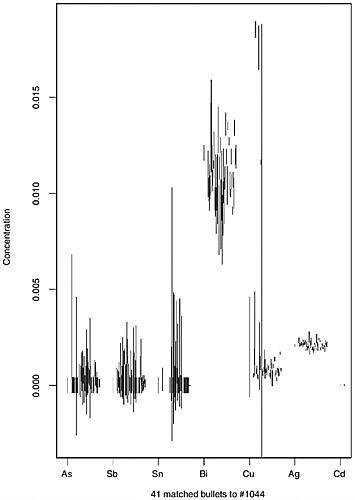
large groups will tend to have a number of bullets that as pairs may have concentrations that are substantially different.
To see the effect of chaining, consider bullet 1,044, selected at random from the 1,837-bullet data set. The data for these bullets are given in the first two lines of Table 3.11.
Bullet 1,044 matched 12 other bullets; that is, the 2-SD interval overlapped on all elements with the 2-SD interval for 12 other bullets. In addition, each of the 12 other bullets in turn matched other bullets; in total, 42 unique bullets were identified. The variability in the averages and the standard deviations of the 42 bullets would call into question the reasonableness of placing them all in the same compositional group. The overall average and average standard deviation of the 42 average concentrations of the 42 “matching” bullets are given in the third and fourth lines of Table 3.11. In all cases, the average standard deviations are at least as large as, and usually 3–5 times larger than, the standard deviation of bullet 1,044, and larger standard deviations are associated with wider intervals and hence more false matches. Although this illustration does not present a comprehensive analysis of the false match probability for chaining, it demonstrates that this method of assessing matches could possibly create more false matches than either the 2-SD-overlap or the range-overlap procedures.
One of the questions presented to the committee (see Chapter 1) was, “Can known variations in compositions introduced in manufacturing processes be used to model specimen groupings and provide improved comparison criteria?” Bullets from the major manufacturers at a specific point in time might be able to be partitioned based on the elemental compositions of bullets produced. However, there are variations in the manufacturing process by hour and by day, there are a large number of smaller manufacturers, and there may be broader trends in composition over time. These three factors will erode the boundaries between these partitions. Given this and the reasons outlined above, chaining is unlikely to serve the desired purposes of identifying matching bullets with any degree of reliability. In part due to the many diverse methods that could be applied, the panel has not examined other algorithms for partitioning or clustering bullets to determine whether they might overcome the deficiencies of chaining. FBI support for such a study may provide useful information and a more appropriate partitioning algorithm that has a lower false match rate than chaining appears to have.
TABLE 3.11 Elemental Concentrations for Bullet 1,044
|
|
As |
Sb |
Sn |
Bi |
Cu |
Ag |
Cd |
|
Average |
0.0000 |
0.0000 |
0.0000 |
0.0121 |
0.00199 |
0.00207 |
0.00000 |
|
SD |
0.0002 |
0.0002 |
0.0002 |
0.0002 |
0.00131 |
0.00003 |
0.00001 |
|
Avg of 42 Avgs |
0.0004 |
0.0004 |
0.0005 |
0.0110 |
0.00215 |
0.00208 |
0.00001 |
|
SD of 42 Avgs |
0.0006 |
0.0005 |
0.0009 |
0.0014 |
0.00411 |
0.00017 |
0.00001 |
Alternative Testing Strategies
We have discussed the strategies used by the FBI to assess match status. An important issue is the substantial false match rate that occurs when using the 2-SD overlap procedure for bullets with elemental compositions that differ by amounts moderately larger than the within-bullet standard deviation. (This concern arises to a somewhat lesser degree for the range overlap procedure.) In addition, all three of the FBI’s procedures fail to represent current statistical practice, and as a result the data are not used as efficiently as they would be if the FBI were to adopt one of the alternative test strategies proposed for use here. A result of this inefficiency is either false match rates, false non-match rates, or both, that are larger than they could otherwise be.
This section describes alternative approaches to assessing the match status for two bullets, CS and PS, in a manner that makes effective and efficient use of the data collected, so that neither the false match nor the false non-match rates can be made smaller without an increase in the other, and so that estimates of these error rates can be calculated and the reliability of the assessment of match status can be determined.
The basic problem is to judge whether 21 numbers (each an average of three measurements), measuring seven elemental concentrations for each of three bullet fragments from the CS bullet, are either far enough away from the analogous 21 numbers from the PS bullet to be consistent with the hypothesis that the mean concentrations of the CIVLs from which the bullets came are different, or whether they are too close together, and hence more consistent with the hypothesis that the CIVLs means are the same. There are also other data available with information about the standard deviations and correlations of these measurements, and the use of this information is an important issue.
Let us consider one element to start. Again, we denote the three measurements on the CS and PS bullets CS1,CS2,CS3 and PS1,PS2,PS3, respectively. The basic question is whether three measurements of the concentrations of one of the seven elements from two bullets are sufficently different to be consistent with the following hypothesis, or are sufficiently close to be inconsistent with that hypothesis: that the mean values for the elemental concentrations for the bullets manufactured from the same CIVL with given elemental concentrations, of which the PS bullet is a member, are different from the mean values for the elemental concentrations for the bullets manufactured from a different CIVL of which the CS bullet is a member.
Assuming that the measurements of any one element come from a distribution that is well-behaved (in the sense that wildly discrepant observations are extremely unlikely to occur), and assuming that the standard deviation of the CS measurements is the same as the standard deviation of the PS measurements, the standard statistic used to measure the closeness of the six numbers for this single
element is the two sample t-test: 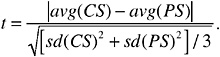 When additional data on the within-bullet standard deviation is available, whose use we strongly recommend here, the denominator is replaced with a pooled estimate of the assumed common standard deviation sp, resulting in the t-statistic
When additional data on the within-bullet standard deviation is available, whose use we strongly recommend here, the denominator is replaced with a pooled estimate of the assumed common standard deviation sp, resulting in the t-statistic ![]() To use t, one sets a critical value tα so that when t is smaller than tα the averages are considered so close that the hypothesis of a “non-match” must be rejected, and the bullets are judged to match, and when t is larger than tα the averages are considered to be so far apart that the bullets are judged to not match.
To use t, one sets a critical value tα so that when t is smaller than tα the averages are considered so close that the hypothesis of a “non-match” must be rejected, and the bullets are judged to match, and when t is larger than tα the averages are considered to be so far apart that the bullets are judged to not match.
Setting a critical value simultaneously determines a power function. For any given difference in the true mean concentrations for the CS and the PS bullets, δ, there is an associated probability of being judged a match and a probability of being judged a non-match. If δ equals 0, the probability of having t exceed the critical value tα is the probability of a false non-match. If δ is larger than 0, the probability of having t smaller than the critical value tα is the probability of a false match (as a function of δ).
As mentioned early in this chapter, one may also set two critical values to define three regions; match, no decision, and no match. Doing this may have important advantages in helping to achieve error rates that are more acceptable, at the expense of having situations for which no judgment on matching is made. When the assumptions given above obtain (assuming use of the logarithmic transformation), the two-sample t-test has several useful properties, given normal data, for study of a single element, and is clearly the procedure of choice. In practice we can check to see how close to normality we believe the bullet data or transformed bullet data are, and if they appear to be close to normality with no outliers we can have confidence that our procedure will behave reasonably.
The spirit of the 2-SD overlap procedure is similar to the two-sample t-test for one element, but results in an effectively much larger critical value than would ordinarily be used because the “SD” is the sum of two standard deviations (SD(CS) + SD(PS)), rather than ![]() which substantially overestimates the standard deviation of the difference between the two sample means. This reduces the false non-match rate when the bullets are identical, and simultaneously increases false match rates when they are different.
which substantially overestimates the standard deviation of the difference between the two sample means. This reduces the false non-match rate when the bullets are identical, and simultaneously increases false match rates when they are different.
To apply the two-sample t-test, the only remaining questions are: (a) how to choose tα, and (b) how to estimate the common standard deviation of the measurement error. To estimate the common standard deviation using pooling, it would be necessary to carry out analysis of reference bullets to determine what factors were associated with heterogeneity in within-bullet standard deviations.
Having done that, all reference bullets that could be safely assumed to have equal within-bullet standard deviations could be pooled using the following formula:
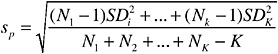
where Ni is the number of replications for the ith bullet used in the computation (typically 3 here), and K is the total number of bullets used for pooling. When Ni is the same for all bullets, (in this application likely N1 = N2 = … = NK = 3, then sp is just the square root of the mean of the squared deviations.
Assuming that the measurements (after transforming using logarithms) are roughly normally distributed, tables exist that, given tα and δ, provide the false match and false non-match rates. (These are tables of the central and non-central t distribution.) Under the assumption of normality, the two-sample t-test has operating characteristics—the error rates corresponding to different values of δ—that are as small as possible. That is, given a specific δ, one cannot find a test statistic that has a simultaneously lower false match rate, given a specific δ, and lower false non-match rate.
The setting of tα, which determines both error rates, is not a matter to be decided here, since it is not a statistical question. One can make the argument that the false match rate should be controlled to a level at which society is comfortable. In that case, one would take a particular value of δ, the difference between the CS and PS bullet concentrations that one finds important to discriminate between, and determine tα to obtain that false match rate, at the same time accepting the associated false non-match rate. Appropriate values of δ to use will depend on the situation, the manufacturer, and the type of bullet. Having an acceptable false match rate for values where the within-bullet standard deviation becomes unlikely to be a reasonably full explanation for a difference in means would be very beneficial. However, in this case it would still be essential to compute and communicate the false non-match rate, since greatly reducing the false match rate by making tα extremely small may result in an undesirable trade-off of one error rate versus the other.21 Further, if one cannot make both error rates as small as would be acceptable, then there may be non-standard steps that can be taken to decrease both error rates, such as taking more readings per bullet or decreasing the measurement error in the laboratory analysis. (This assumes that the main part of within-bullet variability is due to measurement error and not due to within-bullet heterogeneity, which has yet to be confirmed.)
Now we add the complication that seven elements are used to make the judgment of match status. The 2-SD overlap procedure uses a unanimous vote for matching based on the seven individual assessments by element of match or non-match status. A problem is that several of the differences for the seven elements may each be close to, but smaller than, the 2-SD overlap criterion, yet in some collective sense, the differences are too large to be compatible with a match. The 2-SD overlap procedure provides no opportunity to accumulate these differences to reach a conclusion of “no match.”
To address this, assume first that the within-bullet correlations between elemental concentrations are all equal to zero. In that case, the theoretically optimal procedure, assuming multivariate normality, is to add the squares of the separate t-statistics for the seven elements and to use the sum as the test statistic. The distribution of this test statistic is well-known, and false match rates and false non-match rates can be determined for a range of possible critical values and vectors of separation, δ. (There is a separation vector, since with seven elements, to determine a false match rate, one must specify the true distances between the means for the bullets for each of the seven elements.) Again, under the assumptions given, this procedure is theoretically optimal statistically in the sense that no test statistic can have a simultaneously lower false non-match rate and lower false match rate, given a specific separation vector.
However, as seen from the 800-bullet data set, it is apparently not the case that the within-bullet measurements of elemental composition are uncorrelated. If the standard deviations and correlations could be well estimated, the theoretically optimal procedure, assuming multivariate normality, to judge the closeness of the 21 numbers from the CS and the PS bullets would be to use Hotelling’s T2 statistic. However, there are three complications regarding the use of T2. First, the within-bullet correlations and standard deviations have not, to date, been estimated accurately. Second, the T2 statistic has best power against alternative hypotheses for which all of the mean elemental concentrations are different between the CS and the PS bullets. If this is not the case, T2 averages the impact of the differences that exist over seven anticipated differences, thus reducing their impact. Given situations where only three or four of the elements exhibit differences, T2 will have a relatively high false match error rate relative to procedures, like 2-SD overlap, that can key on one or two large differences. Third, T2 is somewhat sensitive to large deviations from normality, and the bullet lead data do seem to have frequent outlying observations, whether from heterogeneity within bullets or inadequately controlled measurement methods.
Even given these concerns, once the needed within-bullet correlations have been well-estimated, and the non-(log) normality has been addressed, the use of T2 should be preferred to the use of either the 2-SD overlap or the range overlap procedures. This is because T2 retains the theoretical optimality properties of the simpler tests described above. (It is the direct analogue of the two-sample t-test in more than one dimension.) One way to describe the theoretical optimality,
|
Theoretical Optimality of T2 Procedure Hotelling’s T2 uses the observations to calculate the following statistic: T2 = n(X − Y)′S−1(X − Y), without which the n is known as the Mahalanobis distance. This statistic, whether it is used in a formal test or not, has a theoretical optimality property. The same distance between the center (mean) and contours appears in the mathematical formulation of the multivariate normal distribution (in the exponent). This statistic defines “contours” of equal probability around the center of the distribution, and the contours are at lower and lower levels of probability as the statistic increases. This means that, if the observations are multivariate normal, as seems to be approximately the case for the logged concentrations in bullet lead, the probability is most highly concentrated within such a contour. No other function of the data can have this property. The practical result is that the T2 statistic and the chosen value of |
given data that are multivariate normal, of T2 is that, for different critical values, say ![]() T2 defines a region of observed separation vectors that are the most probable if there were no difference between the means of the concentrations of the CS and the PS bullets.
T2 defines a region of observed separation vectors that are the most probable if there were no difference between the means of the concentrations of the CS and the PS bullets.
The panel has identified an alternative to the use of the T2 test statistic that retains some of the benefits of being derived from the univariate t-test statistic, but also has the advantage of being able to reject a match based on one moderately substantial difference in one dimension, which is an advantage of the 2-SD overlap procedure. This approach, which we will denote the “successive t-test approach” test statistics, is as follows:
-
estimate the within-bullet standard deviations for each element using a pooled within-bullet standard deviation sp from a large number of bullets, as shown above.
-
calculate the difference between the means of the (log-transformed) measurements of the CS and the PS bullets,
-
If all the differences are less than kαsp for each of the seven elements for some constant kα, then the bullets are deemed a match, otherwise they are a nonmatch.
Unfortunately, the estimation of false match rates and false non-match rates for the successive t-test statistic is complicated by the lack of independence of within-bullet measurements between the different elements. The panel carried
out a number of simulations that support estimating the false match rate by raising the probability of a match for a single element to the fifth power (rather than the seventh power, which would be correct if the within-bullet measurements were independent). That is, raising the individual probabilities to the fifth power provides a reasonable approximation to the true error rates. This is somewhat ad hoc, but further analysis may show that for the modest within-bullet correlations in use, this is a reasonable approximation.22 In any event, for a specific separation vector, simulation studies can always be used to assess, to some degree of approximation, the false match and false non-match probabilities of this procedure. The advantage of the successive t-test statistics are that the approach has the ability to notice single large differences, but also retains the use of efficient measures of variability.
Similar to the above, choices of kα form a parametric family of test procedures, each of which trades off one of the two error rates against the other. The choice of kα is again a policy matter that we will not discuss except to stress that whatever the choice of kα is, if the FBI adopts this suggested procedure, both the false match and the false non-match probabilities must be estimated and communicated in conjunction with the use of this evidence in court.
In summary, the two alternatives to the FBI’s test statistics advocated by the panel are the T2 test statistic and the successive t-test statistics procedure. If the underlying data are approximately (log) normally distributed, and if pooled estimates, over an appropriate reference set of bullets, are available to estimate within-bullet standard deviations and within-bullet correlations, and finally, if all seven elements are relatively active in discriminating between the CS and the PS bullets, then T2 is an excellent statistic for assessing match status. The successive t-test statistics procedure is somewhat less dependent on normality and can be used in situations in which a relatively small number of elements are active. However, quick assessment of error rates involves an approximation. Given the different strengths of these two procedures, there are good reasons to report both results. In addition, the FBI should examine the 71,000, bullet data set for recent data to see whether all seven elements now in use are routinely active, or whether there may be advantages from reducing the elements considered. This would be an extension of the panel’s work described above on the 1,837-bullet data set.
In the meantime, both of the recommended approaches have advantages over the use of the current FBI procedures. They are both based on more efficient univariate statistical tests, and they both allow direct estimation (in one case, approximate estimation) of the false match and false non-match rates. One
procedure, successive t-test statistics, is better at identifying non-matching situations in which there are a few larger discrepancies for a subset of the seven elements, and the other, T2, is better at identifying non-matching situations in which there are modest differences for all seven elements. In addition, if T2 is to be used, given the small amount of data collected on the PS and the CS bullets, pooling across a reference data set of bullets to estimate the within-bullet standard deviations and correlations is vital to support this approach.23
If both of these procedures are adopted, the FBI must guard against the temptation to compute both statistics and report only the one showing the more favorable result.
We have stressed in several places that prior to use of these test procedures, the operating characteristics, i.e., the false match rate and false non-match rates, be calculated and communicated along with the results of the specific match. (Even though non-matches are unlikely to be presented as evidence in court, knowing the false non-match error rate protects against setting critical values that too strongly favor one error rate against the other.) A different false match rate is associated with each non-zero separation vector δ (in seven dimensions). It is difficult to prescribe a specific set of separation vectors to use for this communication purpose. However, as in the univariate case, having an acceptable false match rate for separation vectors where the within-bullet standard deviations become unlikely to be a reasonably full explanation for differences in means would be very beneficial. It would also be useful to include a separation vector that demonstrated the performance of the procedure when not all mean concentrations for elements differ.
In addition, for any procedure that the FBI adopts, a much more comprehensive study of the procedure’s false non-match and false match rates should be carried out than can be summarized in a small number of false match rates.
In discussing the calculation of false match rates, the panel is devoting its attention to cases that are at least somewhat unclear, since those are the cases for which the choice of procedure is most important. However, for a large majority of bullet pairs that are clearly dissimilar, there would be strong agreement between the procedures that the FBI is using today and the two procedures recommended here as preferred alternatives.
Finally, the 2-SD and range overlap procedures, the T2 test statistic, and to a lesser extent, the successive t-test statistics procedure, are all sensitive to the assumption of normality. By sensitive, we mean that the error rates computed under the assumption of (log) normality may be unrealistic if the assumption
does not hold. Specifically, the presence of outlying values is likely to inflate the estimates of variability more than the differences in concentrations, so that more widely disparate bullet pairs will be found to match using these test statistics. (See Eaton and Efron, 1970; Holloway and Dunn, 1967; Chase and Bulgren, 1971; and Everit, 1979, for the non-robustness of T2.) The FBI could take two actions to address this sensitivity. First, if the non-normality is not a function of laboratory error or contamination or other sources that can be reduced over time, the FBI should use, in addition to the two procedures recommended here, a “robust” test procedure such as a permutation test, to see if there is agreement with the normal-theory based procedure. If there is agreement between the robust and non-robust procedures, one may safely report the results from the standard procedure. If, on the other hand, there is disagreement, the source of the disagreement would need to be investigated to see if outliers or other data problems were at fault. If the non-normality may be a function of human error, the data should be examined prior to use to identify any discrepant measurements so that they can be repeated in order to replace the outlying observation. Identifying outliers from a sample of size three is not easy, but over time, procedures (such as control charts) could be identified that would be effective at determining when additional measurements would be valuable to take.
RECOMMENDATIONS
The largest source of error in the use of CABL is the unknown variability within the population of bullets in the United States due to variations within and across manufacturing processes. (The manufacturing process and its effect on the interpretation of CABL evidence is discussed in detail in Chapter 4.) This variability is not sufficiently taken into account by the statistical methods currently in use in the analysis of CABL data. In addition, the FBI’s methods are not representative of current statistical practice. Several steps can be taken to remedy these problems. A key need is the identification of statistical tests that have acceptable levels of rates of false matches and false non-matches. The committee has proposed a variety of analyses to increase understanding of the variability in the composition of bullet lead, and how to make better use of statistical methods in analyzing this information.
The discussion above supports the following recommendations.
Recommendation: The committee recommends that the FBI estimate within-bullet standard deviations on separate elements and correlations for element pairs, when used for comparisons among bullets, through use of pooling over bullets that have been analyzed with the same ICP-OES measurement technique. The use of pooled within-bullet standard deviations and correlations is strongly preferable to the use of within-bullet standard deviations that are calculated from the two bullets being compared. Further, estimated standard deviations should be charted regularly to
ensure the stability of the measurement process; only standard deviations within control-chart limits are eligible for use in pooled estimates.
In choosing a statistical test to apply when determining a “match,” the goal was to choose a test that had good performance properties as measured by (1) its rate of false non-matches and (2) its rates of false matches, evaluated at a variety of separations between the concentrations of the CS and the PS bullets. The latter corresponds to the probability of providing false evidence of guilt, which our society views as important to keep extremely low.
Given arguments of statistical efficiency that translate into lower error rates, it is attractive to consider either the T2 test statistic, or the successive t-test statistics procedure, since they are more representative of current statistical practice. The application of both procedures is illustrated using some sample data in Appendix K.
Recommendation: The committee recommends that the FBI use either the T2 test statistic or the successive t-test statistics procedure in place of the 2-SD overlap, range overlap, and chaining procedures. The tests should use pooled standard deviations and correlations, which can be calculated from the relevant bullets that have been analyzed by the FBI Laboratory. Changes in the analytical method (protocol, instrumentation, and technique) will be reflected in the standard deviations and correlations, so it is important to monitor these statistics for trends and, if necessary, to recalculate the pooled statistics.
The committee recognizes that some work remains in order to provide additional rigor for the use of this testing methodology in criminal cases. Further exploration of the several issues raised in this chapter should be carried out. As part of this effort, it will be necessary to further mine the extant data resources on lead bullet composition to establish an empirical base for the methodology’s use. In addition, this analysis may discover deficiencies in the extant data resources, thereby identifying additional data collection that is needed.
Recommendation: To confirm the accuracy of the values used to assess the measurement uncertainty (within-bullet standard deviation) in each element, the committee recommends that a detailed statistical investigation using the FBI’s historical data set of over 71,000 bullets be conducted. To confirm the relative accuracy of the committee’s recommended approaches to those used by the FBI, the cases that match using the committee’s recommended approaches should be compared with those obtained with the FBI approaches, and causes of discrepancies between the two approaches—such as excessively wide intervals from larger-than-expected estimates of the standard deviation, data from specific time periods, or examiners—should be identified. As the FBI adds new bullet data to its
71,000+ data set, it should note matches for future review in the data set, and the statistical procedures used to assess match status.
No matter which statistical test is utilized by examiners, it is imperative that the same statistical protocol be applied in all investigations to provide a replicable procedure that can be evaluated.
Recommendation: The FBI’s statistical protocol should be properly documented and followed by all examiners in every case.
REFERENCES
Carriquiry, A.; Daniels, M.; and Stern, H. “Statistical Treatment of Case Evidence: Analysis of Bullet Lead,” Unpublished report, Dept. of Statistics, Iowa State University, 2002.
Chase, G.R., and Bulgren, W.G., “A Monte Carlo Investigation of the Robustness of T2,” Journal of the American Statistical Association, 1971, 66, pp 499–502.
Eaton, M.L. and Efron, B., “Hotelling’s T2 Test Under Symmetry Conditions,” Journal of the American Statistical Association, 1970, 65, pp. 702–711.
Everitt, B.S., “A Monte Carlo Investigation of the Robustness of Hotelling’s One- and Two-Sample T2 Tests,” Journal of the American Statistical Association, 1979, 74, pp 48–51.
Holloway, L.N. and Dunn, O.L., “The Robustness of Hotelling’s T2,” American Statistical Association Journal, 1967, pp 124–136.
Owen, D.B. “Noncentral t distribution” in Encyclopedia of Statistical Sciences, Volume 6; Kotz, S.; Johnson, N. L.; and Read, C.B.; Eds.; Wiley: New York, NY 1985, pp 286–290.
Peele, E. R.; Havekost, D. G.; Peters, C. A.; Riley, J. P.; Halberstam, R. C.; and Koons, R. D. USDOJ, (ISBN 0-932115-12-8), 1991, 57.
Peters, C. A. Comparative Elemental Analysis of Firearms Projectile Lead by ICP-OES, FBI Laboratory Chemistry Unit. Issue date: Oct. 11, 2002. Unpublished (2002).
Peters, C. A. Foren. Sci. Comm. 2002, 4(3). <http://www.fbi.gov/hq/lab/fsc/backissu/july2002/peters.htm> as of Aug. 8, 2003.
Randich, E.; Duerfeldt, W.; McLendon, W.; and Tobin, W. Foren. Sci. Int. 2002, 127, 174–191.
Rao, C.R., Linear Statistical Inference and Its Applications: Wiley, New York, NY 1973.
Tiku, M. “Noncentral F distribution” in Encyclopedia of Statistical Sciences, Volume 6; Kotz, S.; Johnson, N. L.; and Read, C.B.; Eds.; Wiley: New York, NY 1985, pp 280–284.
Vardeman, S. B. and Jobe, J. M. Statistical Quality Assurance Methods for Engineers, Wiley: New York, NY 1999.
Wellek, S. Testing Statistical Hypotheses of Equivalence; Chapman and Hall: New York, NY 2003.