6
Energetic Particle Acceleration
As a consequence of the release of energy in a cosmic plasma, some portion of the background charged particle population is accelerated to very high—in some cases, relativistic—energies. Particle acceleration occurs throughout the universe, and the heliosphere provides the quintessential laboratory within which to investigate in situ the detailed character of different acceleration processes. Lessons learned here can often be translated to more exotic locations. Detailed models for particle acceleration have been developed by astrophysicists and space physicists for environments ranging from supernova remnant shock waves to flares on the Sun and stars to the magnetospheres of planets and pulsars. The development of these models provides one of the best examples of the cross-fertilization that can occur between space physics and astrophysics. For example, the theory of shock acceleration was originally developed in an astrophysical context. Its most refined development, however, has taken place in space physics owing to the availability of data from in situ observations of shocks in various solar system settings.
Cosmic acceleration processes can be grouped into three broad classes: (1) shock acceleration, (2) coherent electric field acceleration, and (3) stochastic acceleration. Both coherent and stochastic electric field acceleration can also occur as a part of the shock acceleration process. This chapter outlines the basic physical principles underlying each class of acceleration process and describes certain solar system plasma phenomena illustrative of the various processes.
SHOCK ACCELERATION
Shock Acceleration Mechanisms
One basic particle acceleration mechanism operating at shocks is known as diffusive shock acceleration or Fermi acceleration.1 The workings of this mechanism are illustrated by the example of an elastic ball bouncing between two walls that are moving toward each other. In each collision with a wall, the ball not only changes direction but also increases its speed by a small increment proportional to the speed of the wall that it hits. No matter which wall the ball hits, its speed increases each time. This process will
continue as long as the walls are moving together. Within a collisionless plasma, the reflecting “walls” are waves upstream and downstream from a shock wave. The waves are typically generated by the accelerated particles themselves. Particles may scatter off the upstream and downstream waves and bounce back and forth across the shock. If, as is usually the case, there is compression of the wave velocities at the shock, then the particles traversing the shock are accelerated, like the elastic ball between the approaching walls.
Diffusive shock acceleration occurs at both quasi-parallel and quasi-perpendicular shocks. (“Quasi-parallel” and “quasi-perpendicular” refer to the angle between the magnetic field and the shock normal. See the discussion of quasi-parallel and quasi-perpendicular shocks in Chapter 3.) At quasi-perpendicular shocks, in the absence of particle collisions with turbulence or waves, the compressed magnetic field downstream of a shock causes particles to drift along the shock face and to be accelerated in the upstream motional electric field. This coherent mechanism is referred to as shock drift acceleration.2
Heliospheric Shock Acceleration Sites
The solar wind flow speed is highly supersonic, and therefore shock waves will form ahead of any obstacle to the flow, or regions where high-speed plasma collides with low-speed plasma. The primary obstacles within the heliosphere are magnetic structures within the solar wind flow itself. The size of these obstacles, and the length of time during which particles can interact with them, determine the overall effectiveness of particle energization at these shocks. For example, at Earth’s quasi-parallel bow shock, about 1 percent of the solar wind is accelerated from an initial energy of about 1 keV/e to energies of tens of keV/e. Shock acceleration at Jupiter’s bow shock is proportionally larger because the interaction region is larger. The extreme example of this scaling (at least in the solar system) is at the heliospheric termination shock (the interface between the solar wind and the interplanetary medium where the solar wind is slowed to subsonic speeds). At this enormous shock, it is now thought that particles acquire energies of up to several hundred MeV/nucleon and become the anomalous cosmic-ray population. An additional consideration is the original seed population of ions that is accelerated, since this population is of varying character at different heliospheric sites. Below are enumerated the primary shock types in the heliosphere, each of which has an associated energetic particle population. The review starts at the Sun and moves outward to the heliosphere’s termination shock.
Coronal Mass Ejections As the name implies, coronal mass ejections are events on the Sun wherein material from the corona (ranging from 1014 to a few times 1016 g) is ejected within a magnetic structure that moves out from the Sun at speeds of 10 to 2500 km/s. At solar maximum they occur as frequently as four to five times per day, and the fastest ones are associated with energetic particles. At solar minimum they rarely occur. At a typical speed of 600 km/s, a CME will reach the orbit of Earth about 3 days after it is launched from the Sun. As it moves out, it grows in size so that by the time it reaches Earth’s orbit, it may be close to 1 AU across.3
CME-driven shocks can accelerate particles over basically the entire region from the Sun to Earth orbit and beyond. The shocks are shaped like quasi-spherical shells moving radially outward. They are broad and comparatively uniform so that the acceleration process, acting on particles moving along the shock front, can work maximally to completion before the shock finally fades away. Scientists know that significant acceleration occurs at the Sun itself because energetic particles propagate promptly to Earth well in advance of the arrival of the CME shock. Processes such as solar flares and coronal shocks often take place in association with CME eruptions. As the CME itself passes Earth, a further increase in energetic particles is often observed, and in this case is clearly associated with interplanetary acceleration near the CME. The seed population of particles available for acceleration by these CME shocks includes solar wind ions and
other ions that may be present in the inner heliosphere; it may even include energized particles from earlier events. The range of speeds is larger for CME shocks than for any of the other heliospheric shocks, leading to a wide range of possible energies for the accelerated particles.
Corotating Interaction Regions The solar wind has a low-speed (~400 km/s) component, which originates from regions above closed magnetic loops, and a high-speed (~750 km/s) component, which originates from regions essentially free from overlying magnetic fields (coronal holes). Owing to the Sun’s rotation, the solar wind streams move out into the interplanetary medium in a manner similar to water escaping from a rotating lawn sprinkler. The high-speed streams eventually overtake the low-speed streams, forming a compression region that is bounded by shock waves in the region beyond Earth’s orbit. Because the solar wind streams corotate with the Sun, the regions of this fast/slow stream interaction are called corotating interaction regions (CIRs). Particles can interact with the CIR shocks for an extended period of time since the structure can be long-lived; in addition, the shock size is large, of the order of several astronomical units. Recent observational and theoretical studies have shown that, in addition to acceleration at the shocks bounding the compression region, particles are also accelerated by a Fermi-type process within the compression region itself.4 CIR particles can achieve energies up to 10 to 20 MeV.
Planetary and Cometary Bow Shocks Planets with magnetic fields, such as Earth, Jupiter, Saturn, Uranus, and Neptune, have large standing shocks on the sunward side where the solar wind impacts the planet’s magnetic field. Upstream of these shocks, energetic particle bursts are routinely observed.5 In the case of Earth, the solar wind convects past the shock on a time scale of ~1 hour. Thus, even though the shock itself is a permanent feature, the actual lifetime of particle interactions with the shock is limited, resulting in the acceleration of particles to only modest energies.
Planets without magnetic fields (Mars, Venus) and comets also have bow shocks, which are produced by the interaction between the solar wind and the planetary or cometary ion populations. Cometary and planetary neutral atoms are ionized by sunlight and then picked up by the solar wind. The pickup ions mass load and slow the solar wind, eventually resulting in the formation of a bow shock. The pickup ions also generate intense wave activity. These waves on both sides of the shock appear to accelerate ions to higher energies, in a manner similar to that seen at other solar system shocks. The in situ plasma and energetic particle measurements acquired during the Giotto spacecraft’s close encounter with comets Halley and Grigg-Skellerup and the ICE spacecraft’s close encounter with comet Giacobini-Zinner clearly showed that ions are accelerated to energies of hundreds of keV in the cometary environment.
Termination Shock of the Solar Wind As the solar wind moves out of the inner heliosphere, the density of the plasma and the pressure that it exerts greatly exceed the pressure and density of the dilute, cold plasma in the local interstellar medium, and so the solar wind blows aside the interstellar plasma to form a cavity called the heliosphere (see Figure 3.5). The solar wind density decreases as the square of the distance from the Sun. Eventually, when the solar wind is roughly 10,000 times less dense than at Earth orbit, its pressure is so low that it cannot push aside the thin interstellar plasma, and it slows abruptly, creating a shock that marks the termination of the solar wind beyond which the shocked solar wind is diverted to form a heliosheath.6 The solar wind plasma of the heliosheath is separated from the interstellar plasma by a discontinuity known as the heliopause, which is the heliosphere’s outer boundary.
The actual size of the termination shock is unknown. The distance to the shock is estimated to be around 100 AU. In this distant region, the low-energy particle population most easily accelerated consists of interstellar neutral atoms that have penetrated deep into the heliosphere and come close enough to the Sun to lose one of their orbital electrons as a result of photoionization by solar ultraviolet radiation or
through charge exchange with the solar wind. They are then picked up by the solar wind and transported outward, taking a year or more to reach the termination shock. Some of these ions then interact with the shock and move along its length for scores of astronomical units, eventually escaping from the shock with energies of up to tens of MeV/nucleon.7
The origin of the energetic particles from this so-far-unseen shock has been deduced from their highly unusual elemental composition, which led to their being called anomalous cosmic rays (ACRs). The main ACR source population consists of neutral atoms with a relatively high first ionization potential that allows them to enter the heliosphere as neutrals, become ionized, and then participate in the acceleration process when they reach the termination shock.
Virtually all of the heliospheric energetic particle populations observed outside magnetospheres and not associated with coronal active regions are associated with shocks. Where the shock is directly observable, the energetic particles are generally observed to have maximum intensity at the shock. The basic acceleration mechanism is essentially Fermi acceleration at either a quasi-parallel or a quasi-perpendicular shock wave. Coherent shock-drift acceleration also plays an important role.
Outstanding Questions About Shock Acceleration
-
What are the seed populations for shock-accelerated particles and the injection mechanism?
-
What are the sources and composition of pickup ions?
-
What mechanism accelerates ions to energies greater than 1 GeV at the Sun?
-
What causes the apparent plateau in the solar energetic particle intensity?
-
What causes the universal spectra of solar energetic particle events at late times?
-
What are the scalings that allow for detailed models developed, tested, and constrained in the heliosphere to be extended to remote cosmic environments such as supernova remnant shocks and the termination shocks of stellar winds?
COHERENT ELECTRIC FIELD ACCELERATION
Particles can be accelerated by means of large-scale, coherent (nonstochastic) electric fields. Conceptually, such acceleration is easy to understand when it occurs in the direction parallel to strong magnetic fields (as along magnetic field lines connected to Earth’s auroral ionosphere) or in regions where the magnetic field strength is very weak (as perhaps near the center of the neutral sheet that separates the northern and southern magnetic lobes of Earth’s magnetotail). When charged particles are placed in a vector electric field E, they experience a vector force (F), which has magnitude F = qE. A charged particle will accelerate or decelerate as long as this force is present, or as long as the particle is not diverted out of the acceleration region by the cumulative action of weak magnetic fields. For convenience this conceptually simple process of acceleration by parallel electric fields is referred to here as direct electric field acceleration.
Strong particle acceleration also occurs when coherent electric fields are applied in directions perpendicular to relatively strong magnetic fields, a process referred to here as indirect electric field acceleration. Indirect acceleration is either adiabatic or nonadiabatic. It is adiabatic when the temporal and spatial scales of the acceleration are large compared with the temporal and spatial scales associated with the gyrating and bouncing motions of the particles around and along the magnetic field lines (Figure 6.1). It is nonadiabatic when the temporal and spatial scales of the acceleration approach (or are smaller than) the scales of the gyration and bouncing motions of the particles.
In the adiabatic case, the acceleration of the particles is relatively easy to calculate. Within the complex geometry of a realistic magnetic field configuration (as found, for example, within a planetary
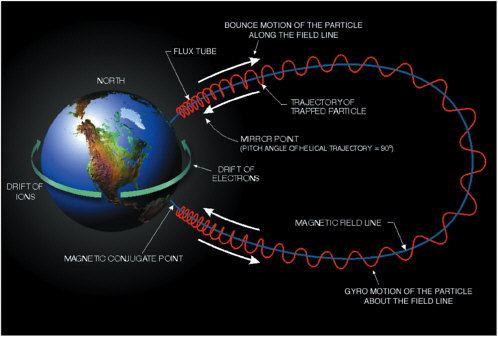
FIGURE 6.1 The three basic motions of a charged particle in a magnetic field are gryo, bounce, and drift. The “bouncing” occurs in closed magnetic geometries where particles bounce back and forth between regions along the magnetic field lines where the magnetic field strength is strong. Adapted from W.N. Spjeldvik and P.L. Rothwell, The radiation belts, Handbook of Geophysics and the Space Environment, A.S. Jursa, ed., Air Force Geophysics Laboratory, Air Force Systems Command, USAF, Hanscom AFB, Mass., 1985.
magnetosphere), there are “guiding center” drifts (with vector velocities VD) that arise strictly from the effect of the nonuniformities within the magnetic field. The acceleration of such particles engendered by a coherently applied electric field E is simply the vector dot product: qE · VD. The process results in acceleration parallel to the background magnetic field (betatron acceleration) and perpendicular to it (Fermi acceleration, a variant of the Fermi acceleration discussed in the context of shocks).
Nonadiabatic acceleration can produce even stronger particle energization than adiabatic acceleration can. If the electric field increases in a period of time that is commensurate with the time period associated with the bounce motions of the particles, or even faster and commensurate with the gyromotions of particles around the magnetic field, then the acceleration parallel or perpendicular to the background magnetic field can be much larger than that achieved by adiabatic betatron acceleration or Fermi accelera-
tion. If the electric field turn-on is “instantaneous,” then the perpendicular energization is similar to the so-called pickup energization that occurs when an atom is suddenly ionized in the presence of an electric field.
In space plasmas, the electric fields invoked in the preceding paragraphs can be produced either by a separation of positive and negative charges (as in the case of parallel auroral acceleration) or by the action of time-varying magnetic fields through Faraday’s law of magnetic induction (as is the case when the magnetic tail of Earth’s magnetosphere partially collapses and becomes more dipolar in configuration). The coherent electric field acceleration processes described above will occur in various manifestations in all dynamic magnetized plasma systems. As mentioned previously, direct electric field acceleration produces the energetic electrons that create auroras at Earth. Various combinations of direct and indirect electric field acceleration also operate at sites of magnetic reconnection such as in planetary magnetotails and other current-sheet structures, and in solar flares. In magnetospheres, coherent electric field acceleration helps create the pressure-bearing plasma that supports magnetotails against collapse, and helps create planetary radiation belts. The pickup energization mentioned above occurs, in the presence of the solar wind’s motional electric field, to ions newly created by the ionization of neutral atoms from planetary or cometary atmospheres (cf. Chapter 4). The pickup process also accelerates those ions that enter the heliosphere originally as neutrals from the local interstellar medium. The subsections that follow expand on some of the most interesting examples of coherent electric field acceleration.
Radiation Belt Particles
Earth’s Radiation Belts The acceleration of trapped particle populations in magnetospheres is facilitated by the residence time of particles in regions where energy can be extracted from time-varying fields. Particles that originate in the distant magnetic tail of a magnetosphere and the solar wind are often moved abruptly toward Earth as a result of bursty reconnection. Inductive electric fields produced by the abruptly changing magnetic fields in these flows accelerate electrons and ions prior to their entry into the radiation belts. These injected particles, associated with geomagnetic storms and substorms, constitute a source of the planetary radiation belts, but the quantitative contribution of this pre-acceleration process to the overall energization of radiation belt particles during storms is still not known. In Earth’s magnetosphere, an extreme example of impulsive acceleration occurred March 24, 1991, when a high-speed interplanetary shock launched by a CME compressed the boundary of the magnetosphere well inside the orbit of geosynchronous spacecraft.8 The event produced >10-MeV electron and proton radiation belts within a normally benign region called the electron slot (Figure 6.2). Trapping and energization to ~10 MeV occurred on a particle drift time scale of minutes as a result of the induction electric field launched by rapid magnetopause compression. The new >10-MeV electron and proton belts persisted for years.
The March 1991 event was unusual. The more usual process for generating or enhancing radiation belts is described here. Near solar maximum, large geomagnetic storms are often initiated by CME-driven interplanetary shocks that compress the magnetosphere, causing what is called a storm sudden commencement. After an initial compression by the shock and during an extended interval when the southward orientation of the interplanetary magnetic field results in the efficient transfer of energy from the solar wind to the magnetosphere, magnetospheric plasma is transported radially inward from the plasma sheet (Figure 6.3) to a region of stronger magnetic field, where the radial gradient in the magnetic field causes a westward drift of energetic (tens to hundreds of keV) ions and an eastward drift of electrons (VD in the preceding section) producing the so-called ring current (Figure 6.3). When such drifting particles experience a variation in the magnetic field at a frequency comparable to that of its drift period, they will diffuse
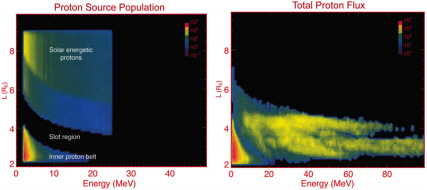
FIGURE 6.2 Computer simulation of the formation of a new proton belt during the magnetic storm of March 24, 1991. The panel on the left shows the seed population of solar energetic protons, while the panel on the right shows the new proton belt formed in the slot region as a result of the interaction of the CME-driven interplanetary shock with Earth’s magnetosphere. Image courtesy of M.K. Hudson (Dartmouth University). Modified and reprinted, with permission, from M.K. Hudson, Simulations of radiation belt formations during storm sudden commencements, Journal of Geophysical Research 102(A7), 14087-14102, 1997. Copyright 1997, American Geophysical Union.
radially from one drift shell to another. Recently, ultralow-frequency waves have been shown to play a key role in the inward diffusion of particles. When the particles diffuse planetward, where the magnetic field increases in strength, their energies increase.
Coherent electric field acceleration cannot explain all aspects of radiation belt enhancement. Satellite measurements of particle velocity distributions suggest that additional heating due to waves with frequencies comparable to the electron gyrofrequency is taking place.
Other Planetary Magnetospheres Planetary probes have identified trapped relativistic electrons and energetic ions in the magnetospheres of Jupiter, Saturn, Uranus, and Neptune. Processes both similar to and distinct from those occurring at Earth energize these particle populations. Jupiter’s radiation belts are the most intense in the solar system, as much as a factor of 1000 more intense than Earth’s. The combination of that intensity and the strength of Jupiter’s magnetic field (with a magnetic moment 20,000 times that of Earth’s) results in the emission of observable synchrotron radiation in the decimetric wavelength range, a unique characteristic of Jupiter’s magnetosphere (Figure 6.4). Jovian radiation belts derive their high energies (1000 MeV) and flux levels from the planet’s rotational kinetic energy and are largely shielded from the buffeting by the interplanetary environment that plays such a critical role in generating the terrestrial radiation belts. Data acquired during the 8-year orbital tour of the Jupiter system by the Galileo spacecraft has revolutionized our knowledge of many aspects of the behavior of the jovian magnetosphere. However, how Jupiter, utilizing steady rotational energies rather than the dynamic solar wind, generates such powerful and energetic radiation regions remains obscure. Detailed information about the radiation belt environment of another giant outer planet will become available when the Cassini orbiter begins its
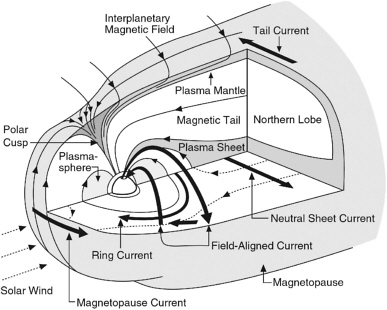
FIGURE 6.3 Schematic of the magnetosphere showing the principal plasma populations and current systems. Courtesy of C.T. Russell, University of California, Los Angeles.
tour of the Saturn system in mid-2004. The data provided by Cassini on the energetic particle populations in Saturn’s inner magnetosphere will be an invaluable contribution to comparative studies of the acceleration, transport, and loss of radiation belt particles in different planetary environments.
Solar Flares
Hard x-ray/gamma-ray continuum and gamma-ray line observations show that solar flares, as well as fast CMEs, can accelerate ions up to tens of GeV and electrons to hundreds of MeV. Flares release up to 1032 to 1033 ergs in 102 to 103 s, with the accelerated 10- to 100-keV electrons (and probably ≥ 1 MeV/ nucleon ions) containing a significant fraction, ~10 to 50 percent, of this energy. How the Sun releases this energy, presumably stored in the magnetic fields of the corona, and how it rapidly accelerates electrons and ions with such high efficiency, and to such high energies, are currently not known. Hard x-ray spectra obtained with high spectral resolution show a break at ~20 to 100 keV, suggesting that the accelerated electrons have a sharp feature in that energy range.9 Similar features in electron spectra observed in Earth’s auroral zone are the result of acceleration by a quasi-stationary (DC) electric field parallel to B, with the peak energy corresponding to the total potential drop. Coherent, and perhaps direct, electric field accelera-
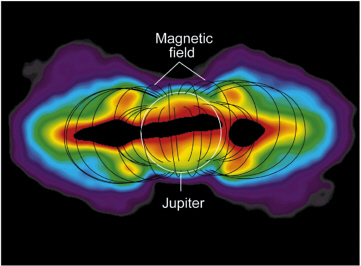
FIGURE 6.4 Energetic electrons accelerated to velocities near the speed of light are responsible for the synchrotron emission from Jupiter’s powerful radiation belts. The false color indicates the intensity of the emission, with red being the most intense. Courtesy of Imke de Pater (University of California, Berkeley), NRAO/VLA, and Sky Publishing Co.
tion is thus believed to play a role in particle acceleration associated with solar flares, although other processes (shock acceleration and stochastic acceleration by magnetohydrodynamic (MHD) turbulence) are also thought to be involved.
The Auroral Magnetosphere
Electric fields parallel to the background magnetic field have long been thought to play a role in producing Earth’s aurora. A field-aligned potential drop was first proposed in the mid-1970s by David Evans to explain the monoenergetic electron beams observed in association with auroral arcs.10 Evidence for the existence of such structures has been provided by double probe measurements, chemical release experiments, and particle data.
Prior to these measurements, debate focused on the implied violation of the frozen-in magnetic field condition of ideal magnetohydrodynamics, which requires that in a collisionless plasma any electric field E must be perpendicular to B. It was understood that at the lowest altitudes in the ionosphere, this condition is violated by collisions with neutrals, which permit ions to flow parallel to E and carry a current, while electrons flow perpendicular and in the E × B direction. The new understanding is that the ideal MHD conditions are violated well above the ionosphere where the plasmas are collisionless. In the ionosphere, the transverse currents allow closure of magnetic field-aligned currents imposed from the magnetosphere.
It has been shown recently that large-amplitude, coherent MHD (Alfvén) waves in the boundary layer between the central plasma sheet and tail lobes (see Figure 6.3), mapping to the auroral ionosphere, carry a downward wave energy flux that is consistent with the energy associated with the auroral emissions. Also, on large transverse scales compared to the ion gyroradius, perpendicular electric fields map along auroral field lines, while at smaller transverse scales a parallel potential drop can be inferred. The distribution of that potential drop along B continues to be debated, as does the quasi-static versus electromagnetic nature of the potential drop. Localized structures appear to provide an anomalous resistivity that modifies the reflection properties of Alfvén waves, carrying a parallel electric field component on transverse scales comparable to those of auroral arcs.
Outstanding Questions About Coherent Electric Field Acceleration
-
What is the relative contribution to radiation belt acceleration and loss of magnetic-moment-conserving ultralow-frequency (MHz range) waves and other adiabatic transport processes versus nonconserving influences such as very low frequency (up to kHz) waves?
-
How probable are extreme radiation belt flux enhancements such as that on March 24, 1991, which produced new MeV electron and trapped solar proton belts on a drift time scale of minutes?
-
Why did outer zone electron fluxes essentially disappear for 2 months following the May 11, 1999, period in which solar wind density dropped to less than 0.1 cm−1?
-
How does Jupiter generate its incomparably powerful radiation belt in the absence of solar wind buffeting effects?
-
What is the distribution of parallel electric field along B within the auroral acceleration region and how is it maintained?
STOCHASTIC PARTICLE ACCELERATION
In his original model for the acceleration of cosmic rays in the interstellar medium, Fermi suggested that the random movement of magnetic scattering centers or clouds could further energize fast-moving particles since they would experience more head-on (energy-gaining) than overtaking (energy-losing) collisions. In the interplanetary or interstellar medium, particles experiencing scattering by a random ensemble of waves or turbulence can effectively experience head-on and overtaking collisions. In this case, the process is a little more subtle. Consider for simplicity Alfvén waves only. One can introduce a frame of reference in which the motional electric field is transformed away so that a particle experiences pitch-angle scattering by the Alfvén waves and experiences diffusion in momentum space. Back in the laboratory frame of reference, researchers recover the motional electric field and find that the particles will have gained or lost energy in a somewhat random “stochastic” sense. The physical content of stochastic acceleration amounts to a particle being either accelerated or decelerated in randomly oriented electric field perturbations associated with the ensemble of Alfvén (or other) waves or turbulence.
One can show that the rate of energy gain is proportional to the square of the ratio of Alfvén speed to particle speed (a small number for energetic particles) and hence is often referred to as second-order Fermi acceleration. By contrast, the presence of a shock wave ensures that all particle “collisions” are effectively head-on. The energy gain in this case is proportional to the ratio of the shock speed to the particle speed rather than the square of the Alfvén to particle speed. Consequently, shock acceleration is referred to as first-order Fermi acceleration and is generally much more efficient than stochastic acceleration.
The most detailed studies of stochastic acceleration have been based on assuming either Alfvénic or slab turbulence or low-frequency MHD waves. The relatively simple relationships between velocity and
magnetic field fluctuations allow tractable forms of the momentum diffusion coefficient to be derived and included in models of particle transport in the solar wind, for example. Such models have addressed the origin and transport of solar energetic particles and interstellar pickup ions. However, the characteristics of energetic particles observed in situ, while admitting a partial explanation in terms of stochastic acceleration, continue to defy simple theoretical explanation. For example, accelerated pickup He+ spectra as observed at 1 AU reveal the existence of (1) a knee connecting the pickup ion “core” with the accelerated “tail” and (2) an accelerated tail with a rather flat slope. The accelerated tail closely resembles that which might be expected from diffusive shock acceleration. However, the observations are integrated over relatively long periods when the solar wind was especially quiet and free of interplanetary shocks. Simple stochastic acceleration models based on slab turbulence have considerable difficulty explaining such observations.
Alternative approaches based on a much more sophisticated description of interplanetary or interstellar turbulence are now under consideration for stochastic acceleration models. Observations, theory, and simulations all suggest that MHD turbulence in the solar wind is quasi-two-dimensional, which is superimposed on a large-scale interplanetary magnetic field. One interesting feature of two-dimensional turbulence is that random convective motions of MHD vortices lead to nonlinear interactions of neighboring magnetic islands. Turbulent reconnection between neighboring magnetic islands of opposite magnetic polarity creates turbulent electric fields. Very strong turbulent intermediate-scale electric fields have been observed in the solar wind at low helio-latitudes, and simulations of particles in a two-dimensional turbulence field demonstrate that turbulent electric fields can efficiently accelerate charged particles. Turbulent electric fields associated with two-dimensional turbulence could explain the acceleration of pickup and solar wind ions in the quiet low-latitude solar wind, i.e., in the absence of nearby shocks. Clearly, to understand stochastic acceleration in realistic physical environments requires an intimate understanding of local turbulence.
Outstanding Questions About Stochastic Particle Acceleration
-
What is the origin of the power law-like accelerated ion tail in the quiet solar wind?
-
Can a stochastic acceleration process provide the seed particles for diffusive shock acceleration?
-
What is the effect of different turbulence characteristics on stochastic particle acceleration?
-
In what plasma regimes is stochastic particle acceleration effective compared to alternative acceleration processes?
SUMMARY
In situ access to energetic particle acceleration mechanisms in the solar system provides a unique opportunity to make direct measurements of processes that can be scaled up to astrophysical counterparts.
The rapid acceleration of energetic particles in solar flares and substorms is still not well understood. Undoubtedly, reconnection processes discussed in Chapter 2 lead to explosive energy conversion, discussed in Chapter 5, and a substantial fraction of that energy is carried away by energetic particles.
Slower acceleration by interplanetary shocks, typically initiated by CMEs inside 1 AU, is better understood at the level of local shock acceleration, but the current level of understanding does not yet provide a macroscopic model for solar energetic particle events, nor explain quantitatively the observed plateau in maximum flux. We do not yet have a quantitative predictive capability for solar energetic particle fluxes in the magnetosphere, nor of their trapping lifetimes, which requires a better understanding of trapping and loss processes.
The relative importance of various radial transport processes and of localized acceleration in radiation belt enhancements is not well understood. An improved understanding of these processes is needed so that researchers can better characterize the harsh and highly time-variable radiation environment of the inner magnetosphere, where many important spacecraft operate, and so that potentially hazardous conditions can eventually be predicted. We do not know, for example, how probable an extreme event such as the March 24, 1991, enhancement is, which produced fluxes still measurable a decade later in a generally benign region of the radiation belts (the so-called slot region for its usual absence of flux).
Direct acceleration by parallel electric fields is important at the Sun and in auroral acceleration regions. While much progress has been made in understanding microphysical processes of parallel electric field acceleration, there is still much uncharted territory. So, for example, it was learned only recently how structured and time-variable the auroral return current region is, and particle acceleration theory has not yet caught up with the recent observations from the FAST satellite. How such fields are modulated on the macroscale is not yet well understood.
Finally, it is important to note the universality of the particle acceleration mechanisms described here. Particle acceleration provides one of the most outstanding examples of cross-fertilization between the space physics and astrophysics communities. Mechanisms developed in one community have almost inevitably migrated to the other community, the quintessential example being diffusive shock acceleration. The virtue of the heliosphere is that it allows for detailed in situ investigation of acceleration processes, whereas the universe allows us to consider (and possibly test remotely on the basis of photons—synchrotron radiation emitted by energized electrons, for example) much more extreme environments and to explore the possible scalings from heliosphere to galaxy. In a general sense, the development of such scalings remains as one of the outstanding questions related to particle acceleration and one that emphasizes the universality of particle acceleration throughout the cosmos.












