2
Elements of Detection: Concepts, Threats, and Devices
Detection of explosives involves collecting a sample, processing the sample, and ultimately deciding whether explosives are present or not. In order to provide a common vocabulary for subsequent discussion of the properties and potential of various detection methodologies, the committee first reviews basic concepts relating to performance assessment, sample collection, the elements of a potential threat, and the related composition of explosive devices that may be exploited for detection.
SENSITIVITY, SPECIFICITY, AND ROC CURVES
The basic statistical and probabilistic elements of assessing performance of any detection methodology include sensitivity, specificity, and receiver operating characteristic (ROC) curves. The following contains a brief review of basic definitions of these measures and links them to notions of “false positives,” “false negatives,” “false-alarm rates,” and the expected field performance of any detection method.
To start, suppose we have a detector with binary output (“yes” or “no”), and we have a binary measure of “truth” reflecting the actual presence or absence of an explosive. Also suppose we run a number of tests, recording for each test the true status and the detector reading. Consider the following 2 × 2 table reflecting the performance of the detector:
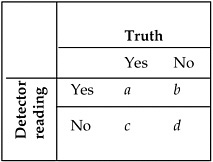
where a, b, c, and d reflect the number of times (out of a + b + c + d total tests) that a particular combination of detector reading and true presence or absence occurs.
The column totals are set by the experimental design (i.e., we know there are a + c tests run with explosives present and b + d tests run with explosives absent). We typically treat the detector response as a random variable and are interested in the following conditional probabilities (letting D denote the status of the detector and T denote the status of the true presence or absence):
True positive rate (sensitivity): Pr(D = Yes | T = Yes) = a/(a + c),
False positive rate: Pr(D = Yes | T = No) = b/(b + d),
Specificity: Pr(D = No|T = No) = d/(b + d).
Note that specificity is defined as (1 minus the false-positive rate). Verbally, sensitivity reflects the ability of the detector to identify explosives if an explosive is present (i.e., the detector “alarms” when it should), and specificity reflects the ability of the detector to identify explosives only if an explosive is present (i.e., the detector does not alarm when it should not).
Many detection systems are based on measurements of some quantity that has one range of values expected in the absence of explosives and another range of values expected in the presence of explosives. Suppose the ranges of measurement values in the presence and absence of explosives can be expressed as probability densities as in Figure 2.1. In this example, higher measurement values are more likely in the presence of an explosive, so we typically choose a cutoff value m and the detector alarms (D = Yes) when the observed measurement exceeds this value. Analogous conclusions follow when lower values indicate the presence of an explosive. When the distributions of values in the presence and absence of explosives overlap (as in Figure 2.1), we can have false positives (measure-
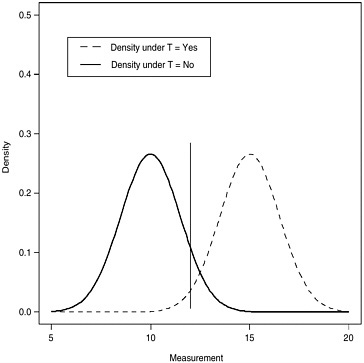
FIGURE 2.1 Probability density functions of test measurement in the absence (solid curve) and presence (dashed curve) of explosives. Setting the detection cutoff value at m = 12, sensitivity (Pr(M > m|T = Yes)) corresponds to the area under the dashed curve to the right of the vertical line, and specificity (1 − Pr(M > m|T = No)) corresponds to the area under the solid curve to the left of the vertical line.
ment greater than m in the absence of explosives [T = No]) and true positives (measurement greater than m in the presence of explosives [T = Yes]). If M denotes a random variable representing the measurement, then the event D = Yes is equivalent to the event M > m, so
Sensitivity = Pr[M > m|T = Yes], and
Specificity = 1 − Pr[M > m|T = No].
The choice of the cutoff m influences both the sensitivity and the specificity of the detector as shown in Figure 2.2.
To summarize a detector’s performance across all possible choices for m, we may use the ROC curve. The ROC curve sees application in a wide variety of fields including (but not limited to) medical diagnosis and signal processing. The ROC curve is defined to be a plot of sensitivity versus
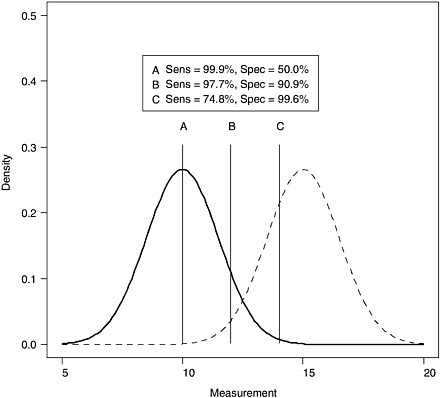
FIGURE 2.2 Impact of choice of cutoff value (m = 10, 12, and 14 for points labeled A, B, and C, respectively) on sensitivity and specificity, assuming normal distributions with means 10 and 15 and standard deviation of 1.5 for measurements in the absence and presence of explosives, respectively.
(1 − specificity) over a range of choices for m. Figure 2.3 illustrates the ROC curve associated with the simple example from Figures 2.1 and 2.2.
ROC curves by definition begin at the point (0,0) for cutoff values far to the left of the densities in Figures 2.1 and 2.2, and end at the point (1,1) for cutoff values far to the right. These points correspond to the extremes of 100% sensitivity and 0% specificity (every observation sets off the alarm) and 0% sensitivity and 100% specificity (no observation sets off the alarm), respectively. The ideal test corresponds to an ROC curve beginning at point (0,0) then immediately jumping to 100% sensitivity and 100% specificity, corresponding to no overlap in the probability densities of the measurement in the presence and absence of explosives. The “worst-case scenario” results when the density of the measurement remains identical
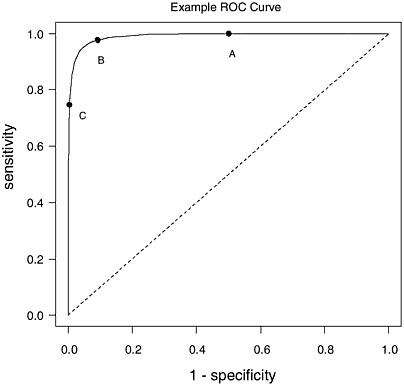
regardless of the presence of explosives (i.e., the test has no diagnostic value), yielding sensitivity identical to (1 − specificity) and an ROC curve falling along the line joining points (0,0) and (1,1).
ROC curves provide a means to compare two competing detection techniques. The technique with an ROC curve closer to the ideal (i.e., closer to the upper left-hand corner of the plot) will have better performance in terms of both sensitivity and specificity. Examination of Figure 2.2 suggests that densities with less overlap result in better detectors. Therefore, two ways to improve a detector are either to use measurements where the mean observation is very different depending on the presence or absence of explosives or to reduce measurement error (e.g., perhaps through increased sample size or longer observation time) so that the densities are more tightly defined around the mean measurement. While Figures 2.1 through 2.3 use normal densities to define ideas, any probability
density for measurements provides the necessary information for ROC curves.
Estimation and inference for comparing ROC curves remain active topics in the statistical, medical imaging, and signal processing literature, although developments usually occur separately within disciplines with little cross-fertilization.
FIELD PERFORMANCE OF DETECTORS
Sensitivity, specificity (equivalently true or false positive rates), and ROC curves reflect commonly reported performance measures for any proposed detector, but one should keep in mind that even a detector with strong sensitivity and specificity can have unacceptable performance in the field, where a performance probability of interest is
Pr(T = Yes|D = Yes)
(i.e., the probability of the true presence of explosives), given an alarm occurs. Note that this probability (which corresponds to the notion of “positive predictive value” in the medical diagnostic testing literature) reverses the conditioning from the false positive/false negative rates defined above. The probability that no explosives are present given an alarm occurs, i.e.,
Pr(T = No|D = Yes) = 1 − Pr(T = Yes|D = Yes),
differs from the “false positive rate” Pr(D = Yes|T = No), again through a reversal of conditioning. This probability (the proportion of observed alarms that are false) differs from the standard use of the phrase “false alarm rate” (the number of tests with no explosives that result in an alarm, synonymous with “false positive rate” defined above) in the literature. The primary difference is in the denominator, the false positive rate is the proportion of “alarms” among tests with no explosives, while the probability that no explosives are present given an alarm occurs is the proportion of “false alarms” among all alarms in the field.
The conditional probability Pr(T = Yes|D = Yes) (the probability that an observe alarm is “true”) depends on the sensitivity and specificity of the test and on the background frequency of both explosives (expected to be very low), via Bayes’ Theorem
Pr(T = Yes|D = Yes) = [Pr(D = Yes| T = Yes) Pr(T = Yes)]/Pr(D = Yes).
Typically, we do not have an estimate of Pr(D = Yes) (the probability
that the detector sets the alarm during use, averaged over settings with and without explosives) from the test results in the 2 × 2 table above, but we may express this probability in terms of known values through the law of total probability, that is,
Pr(D = Yes) = Pr(D = Yes|T = Yes)Pr(T = Yes) + Pr(D = Yes|T = No)Pr(T = No), = (Sensitivity) Pr(T = Yes) + (1 − Specificity)[1 − Pr(T = Yes)].
We will require an outside estimate of Pr(T = “Yes”), the unconditional probability of the presence of explosives, since the quantity (a + c)/ (a + b + c + d) from the assessments of the test reflects the experimental design and not the true marginal probability of explosive presence among screened objects or locations in the field. We may obtain estimates of Pr(T = Yes) under certain scenarios from Federal Bureau of Investigation or Bureau of Alcohol, Tobacco, Firearms and Explosives statistics.
The equations above indicate that the probability of no explosives given an alarm for a particular detector is a function of the detectors’ sensitivity, specificity, and the underlying probability of the true presence of explosives (regardless of detection). For a very low probability of explosives presence in the field, even tests with very high sensitivity and specificity can have unacceptably high probabilities that any observed alarm is false. That is, even a test with a low “false alarm rate” (high specificity) can have a high probability of no explosives for any given alarm if the presence of explosives is rare enough. To illustrate, suppose we have a detector with 99% sensitivity and 99% specificity. Figure 2.4 plots the probability of no explosives given an observed alarm as a function of Pr(T = Yes), and illustrates how this probability increases nonlinearly as the probability of the true presence of explosives decreases. Conceptually, the proportion of alarms that are false nears 100% as the presence of true explosives nears 0% since all alarms will be false if there is no chance of explosives in the system under surveillance. Figure 2.4 also illustrates Pr(D = Yes), the marginal probability of an alarm, decreases linearly with Pr(T = Yes) as suggested in the equations above. While this probability decreases, it does not go to zero (except in a “perfect” detector), and if the detector is applied to a very large number of individuals the number of false alarms can still be large (e.g., 1% of 500,000 people attending a sporting event).
Figure 2.4 illustrates the impact of wide application of a detection system in a situation where the event to be detected is extremely rare. While sobering, the public may be willing to accept a fairly high proportion of alarms that prove to be false if the general perception is that detec-
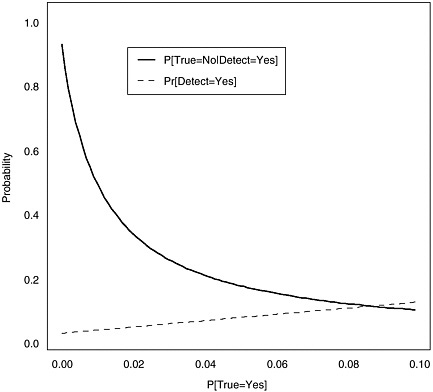
FIGURE 2.4 Probability of no explosives given an observed alarm as a function of the probability of the presence of explosives for fixed specificity and sensitivity (both 99%).
tion reduces the probability of an explosive-based event. For example, consider the performance of airport metal detectors as “weapons detectors.” Most alarms occurring during screening are false with respect to weapons (i.e., the detectors detect metal, but not weapons), but most passengers accept such false alarms since there are many non-weapon reasons for an alarm to go off. This said, such a perception may not exist for explosives detectors.
SYSTEM EFFECTIVENESS
In the literature, the phrase “receiver operating characteristic” is commonly used in conjunction with individual device performance to identify the effectiveness of the device. To avoid ambiguity and to accommo-
date the assessment of a system built on multiple technologies, a measure called system effectiveness (SE) is used to characterize the overall system performance in the presence of environmental, threat, and other potential confusions. This SE is a function of threat characterization, technology, environment, and other factors. SE is quantified by combining quantitative measures of system, threat, and environmental attributes.
In addition, the concept of SE also allows us to broaden the scope of detection beyond the performance of particular sensors (via sensitivity and specificity) and incorporate additional concerns, e.g., the mass of the explosive, and the available sampling time. Also, SE allows us to move from assessments of detection to assessments of system performance, including additional factors such as human intervention (how do security forces effectively respond to an alarm from the detector, and how much time do they have to do it?). Finally, SE allows us to consider “false alarms” based on sensor unreliability (as considered via sensitivity and specificity above) as well as situations involving the legitimate presence of explosives that present no actual “threat” (e.g., a munitions delivery through a military checkpoint).
There are many definitions of system effectiveness, depending on the application. In this application, system effectiveness is defined as “a measure of the degree to which an item can be expected to achieve a set of specific mission requirements and which may be expressed as a function of availability, dependability and capability.”1 For standoff explosives detection, system effectiveness could include detection system availability, maintainability, system ROC, and the probability of avoiding defeat.
THREAT SCENARIOS
In considering any situation involving standoff detection of explosives, one must have some general understanding both of the overall scenario and of the parameters that describe the explosive device and the surrounding environment. This section discusses these topics, with particular attention to specific scenarios that the committee has been asked to consider. Since there is no single explosives detection technology that is applicable under all circumstances, it is important to understand the situation in as much detail as possible. Details that are not relevant to a specific detection technology may be important for other technologies, and an understanding of all potentially important parameters is thus a first
critical step in the development of a system solution that may involve two or more orthogonal detection technologies (see Chapter 3).
In principle, there are an infinite number of situations in which standoff explosives detection might be utilized. Two scenarios (see Appendix B for a definition of scenario) that are of primary concern to the committee are the suicide bomber and wide-area surveillance.
Suicide bombings have occurred with increasing frequency in recent years, particularly in the Middle East. These bombings normally involve an individual who carries a concealed high explosive (HE) charge hidden either on his person or in a vehicle. This individual (the bomber) transports the explosive to his intended target—often a crowded public area where a large number of deaths will result, or perhaps a military checkpoint manned by forces he wishes to attack—and detonates the charge, killing himself along with his intended victims. Since the bomber does not have to plant the device and make his escape prior to its detonation, there is less time and opportunity to find the bomb prior to detonation than in scenarios involving a nonsuicidal bomber. Clearly, the ability to detect such an individual by any means before he reaches the intended target is an important goal that could be realized by the development of appropriate standoff explosives detection techniques.
Wide-area surveillance refers to monitoring a large area for the presence of explosives. The area under surveillance can be of almost any type: a military base, a secure government facility, a public building or event, and so forth. The goal in this situation is to prevent the illicit introduction of HE into the area being monitored and/or to pinpoint the location of any HE that has been brought into the area. The bomber in such a scenario may be either suicidal or nonsuicidal, and depending upon access to the area, the HE may be conveyed either on a person, in a vehicle, in a handcarried item such as a brief case, or via mailing or shipping. Within the category of wide-area surveillance, two subcategories can be identified, which may be referred to as open and closed situations. A closed situation is one in which public access to the location or event is limited, and all persons present must pass through certain checkpoints before being admitted.2 An example would be a Super Bowl, where all attending persons enter via stadium gates, or a military base, with a limited number of entrances manned by military security personnel. In such situations, the entry of HE into the area can be controlled in principle through applying appropriate detection technologies at the controlled checkpoints. An open
situation is one such as a large public event—for example, Mardi Gras or the Rose Parade—where public access is essentially unlimited, and there are thus no fixed checkpoints at which all incoming persons or vehicles can be screened. In this type of scenario, standoff detection of explosives within the wider area can be of vital importance.
Threat Parameters
Having outlined the above scenarios in broad terms, it is necessary to next consider those parameters that define the situation, collectively referred to here as threat parameters. These parameters can be broken down into three categories: (1) those relating to the local environment, (2) those describing the explosive device, and (3) those that characterize the bomber.
Threat Parameters Related to the Local Environment
Among threat parameters relating to the local environment, perhaps the most important is the intended target of the HE detonation. The target represents the motivation for the attack; thus, by understanding what the target is (or might be), one can begin to develop ideas about the likelihood of attacks involving HE detonation in different areas. In other words, an understanding of potential targets helps prioritize the areas that have to be monitored and protected. Broadly speaking, the target is usually either people or infrastructure. Within the former category, the goal can be either to kill and injure a large number of people or to kill a single important person such as a political leader. In the second category, the target could be a building or landmark that is of great symbolic import (i.e., the White House, Statue of Liberty, etc.) or one that might cause great economic or environmental damage if destroyed (dam, nuclear power plant). The timing of the detonation is clearly much more critical if people are the intended target. A bombing in a crowded sports stadium will have a much greater impact than a bombing in an empty sports stadium, whereas blowing up a dam will likely have the same impact regardless of when the explosion occurs. Some agencies and organizations interested in standoff explosives detection have specific areas, facilities, or people that they are tasked with protecting, while others (e.g., police) have responsibilities that span very large areas without specific, well-defined targets.
Another important threat parameter relating to the environment is the presence or absence of a background of trace explosives materials or potential interferents. Many explosive detection technologies rely on collection and identification of minute amounts of explosive vapor or particulate material to make detections (Chapter 4). Such technologies will
tend to give frequent alarms when a background of trace explosive material is present; if these alarms are too frequent, they can render the technique unusable. An explosives background could be present in a number of situations—for example, in a battlefield setting or on a military base where large amounts of explosives are routinely stored or handled. Interferents are nonexplosive chemicals that lead to false alarms for explosives with certain types of chemical sensors,3 and a background containing one or more of these chemicals thus can also inhibit the use of these detection technologies. Knowledge of the chemical background, which may change significantly over time, can therefore be essential in determining how best to perform explosives detection within a given area.
Other important environmental threat parameters are those relating to the ambient meteorology. Temperature is clearly important since it affects the amount of vapor that will be emitted by an HE charge (Chapter 3); this in turn may determine what vapor-based detection techniques are applicable. Atmospheric pressure can affect the calibration of some vapor sensors such as ion mobility spectrometers and must therefore also be taken into account. Humidity can be a factor, both because some explosive vapors may form clusters with water molecules and because interactions of the probing radiation with water vapor in air can limit the application of techniques such as terahertz spectroscopy. Dust particles in air can adsorb explosive vapors, interfering with some types of vapor detection but possibly also leading to improved sampling strategies based on collection of the particles. Wind conditions are obviously significant if one is attempting any type of vapor detection, since whatever plume of explosive vapor is present will be entrained in the prevailing air currents. All of the prevailing weather conditions will influence the concentration of explosive vapor that is available for sampling, and this concentration—which often will be extremely small—places constraints on the detection strategies that can be employed.
A final factor relating to the environment is the nature of the society in which the detection scheme is to be applied. This will often place constraints on the types of technology that can be utilized. For example, screening people by using low-dose backscatter X-ray systems to image beneath clothing has generally been judged too great an invasion of privacy for widespread use in the United States. The same technology would probably be considered acceptable in Israel, where a higher incidence of bombings has led to greater public tolerance for more invasive detection technologies. Technologies that are not widely accepted by the general
public, or that may violate constitutional or other legal rights when applied too broadly, are severely limited in their applicability to standoff explosives detection. However, consideration of this issue is beyond the scope of this study.
Threat Parameters That Describe the Device
Several key threat parameters characterize any explosive device. These include the type of explosive used, the mass of explosive, and several other factors relating to the device construction. Different detection strategies may or may not be appropriate, depending on the nature of the device.
Many types of explosives can be used as the main charge in a device, as will be revealed by perusal of any survey book on explosives and their properties.4 Traditionally, some of the most widely used and studied explosives have been nitro-based compounds such as 2,4,6-trinitrotoluene (TNT), cyclotrimethylenetrinitramine (RDX), pentaerythritol tetranitrate (PETN), and nitroglycerin (NG). TNT is widely used in land mines, NG in the manufacture of dynamites, and RDX and PETN in the manufacture of plastic explosives such as C-4, detasheet, and semtex. Black powder is widely used in the construction of pipe bombs, while the favorite explosive for large vehicle bombs has been ammonium nitrate fuel oil (ANFO). Some more novel explosives that are being used increasingly, such as TATP, are fundamentally different because they lack nitrogen altogether. The choice of explosive in a device is of importance for two reasons. First, different explosives have different explosive energies per unit mass (kilojoules per gram). Since TNT is widely available and most explosives fall within a factor of two of TNT in energy per unit mass, it is common to express explosive masses in terms of a TNT equivalent mass (the mass of TNT that would produce an explosion of the same energy if detonated). Second, as discussed in Chapter 3, different explosives have different properties that make them more or less susceptible to various detection technologies. Perhaps the most obvious of these properties is vapor pressure, which varies over more than eight orders of magnitude for common high explosives. Other important properties that can influence detection schemes include density and atomic composition.
Given that explosives are characterized by specific energy content per unit mass, the mass of explosive in a device is of paramount importance. The greater the mass of explosive, the greater is the potential damage that
can be done. At the same time, a larger explosive mass in a device tends to make detection easier, so an adversary is usually faced with a trade-off between the amount of damage that a bomb can inflict and the probability that the device will be detected prior to detonation. Expressing the mass as a TNT equivalent mass provides a convenient basis for comparing the destructive power of different bombs. Note that the maximum possible explosive mass of a bomb will depend to a large degree on the means of conveyance. If there is no vehicular access to the target location and the bomb must be concealed on a person, no more than a few tens of pounds can be involved. On the other hand, if a vehicle can be used, the detonation may involve thousands of pounds of explosive. In addition to the explosive mass, the destructiveness of a bomb is also greatly influenced by the distance from the device to its intended target. A rule of thumb is that the mass of explosive required to inflict equivalent damage increases as the cube of the bomb-to-target distance.5 This means that increasing the distance to the target by a factor of two increases the required explosive mass by a factor of eight. It can thus be seen that forcing the bomb to be detonated further from the target is one of the most effective forms of protecting a target. Standoff detection can, of course, be an important first step in preventing a bomb from being detonated in close proximity to its intended target, especially if the sensor and target are not collocated.
Besides the explosive material, other important device components include the casing or shielding around the main charge, the detonator, and any associated wiring. Very often, some or all of these components will be made of metal, and metal detection thus becomes one possible means of detecting the explosive device in some circumstances. Metal detection is probably most useful in scenarios involving checkpoint screening of personnel, where all persons can be passed through a standard metal detection portal such as those currently used in airports. This assumes that detonation at the screening point, although undesirable, would be less destructive than detonation at some points within the area being protected. Metal detection is not useful when vehicles are being screened for explosives, since the vehicles are themselves made of metal and the metal in an explosive device would not be distinguishable. There may be other methods that can be applied to the detection of detonators besides metal detection (Chapter 7), and such methods might also be used for detection of the explosive device, which in some cases may even involve remote detonation.
The casing or shielding around the explosive charge is important be-
cause it may tend to mask the explosive from certain types of detection. An example would be a main charge inside a hermetically sealed container. In such a case, there would be no explosive vapor on the outside of the container, so any attempts to use a vapor detection technology to sense the chemical plume would be in vain. There are other examples involving non-vapor detection technologies. For example, nuclear quadrupole resonance (NQR) is susceptible to metal shielding. These examples emphasize the point that no single detection technology is adequate under all circumstances; hence an effective detection system may well involve two or more largely orthogonal detection technologies (Chapter 3).
An explosive device may cause damage not only due to the power released by the detonation, but also due to small flying objects that are propelled through the air. This is especially true when many people are present: such flying objects—whether metal, plastic, or shards of glass—can actually kill and injure more people that the explosion itself. Many devices intentionally have objects such as nails, thumb tacks, or sharp pieces of metal attached to their surfaces; when the device is detonated these objects—collectively referred to as “shrapnel”—become “bullets,” any one of which might kill a person. In buildings with large windows, the glass fragments produced in the blast can serve the same purpose. The presence or absence of shrapnel on the device, along with the size and number of windows near the detonation, is thus of great importance in evaluating the possible injury the detonation may cause to humans.
An explosive detonation can cause additional harm to both humans and the environment if the detonation is used to disperse radioactive materials or biological or chemical agents. Scenarios involving such dispersal are outside the scope of the present study. Clearly, detecting a device prior to detonation is the best and most cost-effective means of dealing with such a threat.
Threat Parameters That Characterize the Bomber
A psychological profiling of individuals who carry out bombings is beyond the scope of the present study. Nevertheless, bombers may display certain characteristics that aid in their detection in some cases. A device concealed under clothing may weigh tens of pounds and thus add significantly to a person’s weight. This increase would likely be useful for detection only in specialized cases where the perpetrator must pass through a man-trap portal, the weight may cause the individual to walk in an odd manner or have some other effect that might arouse suspicion. Nervous behavior might also be an indicator that could lead to detection. Exposure to large amounts of explosive material could even lead to physiological changes such as alterations in the chemical composition of a
person’s sweat. Some of these possibilities are explored further in Chapters 6 and 7.
ORTHOGONALITY
Two or more explosive detection technologies are completely orthogonal if the detection methods are mutually independent. That is, they detect independent characteristics of the explosive device. This definition allows for the possibility of partially independent (partially orthogonal) methods as well. For example, detecting the exact chemical compound by sniffing and spectroscopy of the vapor plume would be partially independent.
To employ two or more orthogonal detection technologies implies “system” of detectors. Successful standoff detection of an explosive when an explosive is present—and very few indications of an explosive when there is no explosive—is the intent of a system of orthogonal detectors.
Detection technologies may be orthogonal in method, but not in characteristic. For example, two hypothetical standoff detection technologies, one based on schlieren photography and the other on olfactory analysis of vapors, are orthogonal in method. Schlieren photography techniques would detect an image of the vapor plume from the explosive formed by refraction and scattering from areas of varying refractive index. Olfactory analysis of the vapors from the explosive would detect the aroma signature of the molecules in the vapor plume to determine the potential chemical composition of the explosive. Both methods depend, to some extent, on the existence and behavior of the vapor plume. So although the two hypothetical detection technologies would be orthogonal in method, they would be only partially orthogonal in practice. However, if the olfactory analysis also included a remote vapor sampling capability to concentrate the vapor, the independence between the two would be stronger.
A more orthogonal (i.e., independent) combination of detection technologies would be olfactory analysis and an imaging technology. The imaging technology would detect the shape, mass, or density of the explosive device and any potential detonators and shrapnel. These characteristics are strongly independent of the chemical composition of the device. However, the density of the explosive material would be related to its chemical composition.
The three potential significant advantages of a system of orthogonal detection technologies over a system dependent on one technology are the following:
-
It has a higher probability of detecting the presence of an explosive device over a range of potential threats.
-
It is more difficult for a potential bomber to avoid, confuse, or defeat the system.
-
It can be more effective in detecting explosive devices than any single technology.
However, the use of orthogonal detection technologies presents a significant challenge to implementation. That challenge is how to process the information from two orthogonal technologies when one is indicating positive for the presence of an explosive device and the other negative. This challenge is compounded when additional orthogonal or partially orthogonal technologies are employed.

















