Appendix C
ROC Analysis: Key Statistical Tool for Evaluating Detection Technologies
ROC analysis provides a systematic tool for quantifying the impact of variability among individuals’ decision thresholds. The term receiver operating characteristic (ROC) originates from the use of radar during World War II. Just as American soldiers deciphered a blip on the radar screen as a German bomber, a friendly plane, or just noise, radiologists face the task of identifying abnormal tissue against a complicated background. As radar technology advanced during the war, the need for a standard system to evaluate detection accuracy became apparent. ROC analysis was developed as a standard methodology to quantify a signal receiver’s ability to correctly distinguish objects of interest from the background noise in the system.
For instance, each radiologist has his or her own visual clues guiding them to a clinical decision as whether the pattern variation of a mammogram indicates tissue abnormalities or just normal variation. The varying decisions make up a range of decision thresholds.
SENSITIVITY AND SPECIFICITY DEPEND ON INDIVIDUAL READER’S DECISION THRESHOLDS
Sensitivity and specificity are the most commonly used measures of detection accuracy. Both depend upon the decision threshold used by individual readers, and thus vary with each reader’s determination of what to call a positive test and what to call a negative test. Measures of sensitivity and specificity alone are insufficient to determine the true performance of a diagnostic technology in clinical practice.
For example, cases are classified as normal or abnormal according to a specific reader’s interpretation bias. As the decision point for identifying an abnormal result is shifted to the left or right, the proportions of true positives and true negatives change. Thus, the relationship reveals the tradeoff between sensitivity and specificity. For instance, using an enriched set of data with 100 exams that includes 10 true cancers, if a reader correctly identifies 8 cancers while missing 2 cancers (a sensitivity rating of 0.8 or 80 percent) of the 90 true negatives, the reader only correctly identified only 72 as normal (a specificity of 0.8 or 80 percent). However, a reader with more stringent criteria for an abnormal test may have a higher false-negative rate, increasing the number of missed cancers and decreasing the number of false alarms. For example, using the same distribution of 100 cases, the reader would correctly identify 6 cancers (a sensitivity of 0.7 or 70 percent). However, the reader would now correctly identify 85 true negatives as normal (a specificity of 0.94 or 94 percent). The opposite effect could also be obtained for a reader with less stringent criteria. Such a reader would have a higher false-positive rate but would find more cancers. Therefore, this example shows that these measures that depend on the true-positive rate and true-negative rate respectively are reader specific. In the case of interpreting mammograms, different radiologists with different decision thresholds can affect the clinical outcome in the assessment of non-obvious mammograms.
ROC CURVES ARE NECESSARY TO CHARACTERIZE DIAGNOSTIC PERFORMANCE
The ROC curve maps the effects of varying decision thresholds, accounting for all possible combinations of various correct and incorrect decisions.4 A ROC curve is a graph of the relationship between the true-positive rate (sensitivity) and the false-positive rate (1-specificity) (see Figure C-1). For example, a ROC curve for mammography would plot the fraction of confirmed breast cancer cases (true positives) that were detected against the fraction of false alarms (false positives). Each point on the curve might represent another test, for instance each point would be the result of a different radiologist reading the same set of 20 mammograms. Alternatively, each point might represent the results of the same radiologist reading a different set of 20 mammograms.
The ROC curve describes the overall performance of the diagnostic modality across varying conditions. Sources of variation for these conditions can include different radiologist’s decision thresholds, different amounts of time between interpreting mammograms, or variation within cases due to the inherent imprecision of breast compression. ROC analysis allows one to average the effect of different conditions on accuracy. There-
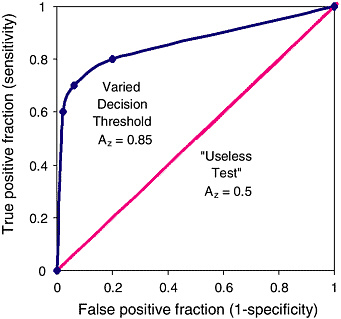
FIGURE C-1 Receiver operating characteristic (ROC) graph of a varying decision threshold compared with a “useless test.” The three decision thresholds discussed in the previous section are represented on this graph. The best-fit curve drawn through these points is the ROC curve, which represents the overall performance of the diagnostic test across all possible interpretations (decision thresholds). The overall accuracy of this test under varying conditions is determined by the area under the complete curve, 0.85.
The leftmost point shows low sensitivity and high specificity. The middle point shows moderate sensitivity and specificity. The rightmost point shows high sensitivity and low specificity. Yet because they all lie on the same curve they have the same overall statistical accuracy, which is quantified by AZ.
The 45-degree-angle line represents a series of guesses between two choices, as in a coin toss. This would be considered a “useless test” if the outcome of the test was dichotomous (for example cancer vs. no cancer) for diagnostic purposes. For instance, radiologists reading mammograms with their eyes closed would tend to fall on this line. The number of true positives would approach the number of false negatives.
The area under such a curve, 0.5, represents 50 percent accuracy of the test. In contrast, the ROC curve for a test with 100 percent accuracy will trace the Y-axis up at a false-positive fraction of zero and follow along the top of the graph at a true-positive fraction of one. The area under such a curve would be 1.0 and represent a perfect test.
fore, the area under the ROC curve can be viewed as the diagnostic accuracy of the technology.
There is often ambiguity in comparing diagnostic modalities when one has only a single sensitivity-specificity pair measure on one modality and a single sensitivity-specificity pair measured on a competing modality.5
Since there is no unique decision threshold used by radiologists, there is no reason to single out specificity and sensitivity values. Radiologists adjust their decision thresholds as a function of context and available information, such as whether a patient is known to be at high risk for breast cancer, the presence of signs or symptoms, or the likelihood of being sued for a missed cancer.
There are many situations in which relying on single estimates of specificity and sensitivity would distort the ranking of competing systems. Different sensitivity-specificity pairs on the ROC curve can arise from many ambiguities beyond variability among radiologists, such as patient variation, use of different machines, and different image processing software.
The ROC approach can be used to accurately compare breast cancer diagnostic tests. The ROC plot provides a visual representation of the accuracy of a detection test, incorporating not only the intrinsic features of the test, but also reader variability.
Figure C-2 shows an example of how ROC curves were used to analyze
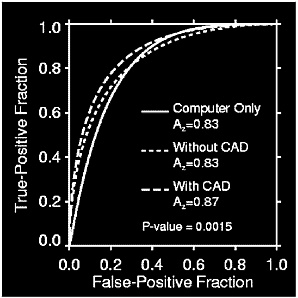
FIGURE C-2 Example of ROC curve analysis for computer-assisted detection. A comparison of the ROC curves for computer only, without CAD, and with CAD, show the value of ROC curves in evaluating diagnostic technologies. The area under the curves, corresponding to overall diagnostic accuracy, illustrates that a radiologist “with CAD” will maximize sensitivity and specificity as compared with the other two approaches. In addition, comparison of the computer alone with the unassisted radiologist shows the same overall accuracy; however, the curve for the radiologist alone is shifted to the left indicating a slightly higher specificity. Yet, if ROC curves cross and the areas are the same the result would suggest that one test provides the optimal strategy for certain cases and the other test may be better with another set of cases.
the value of a computer-assisted detection (CAD) system.3 The curves represent the accuracy, in terms of sensitivity and specificity, of a modality across the varying conditions of the study. At a true-positive fraction of 80 percent, radiologists who used CAD outperformed those who did not use CAD in terms of sensitivity and specificity. Nevertheless, data based on a single decision threshold are insufficient to rank competing systems, because they fail to account for the various decision thresholds that will be applied using the modality. The area under the ROC curve is the best way to rank competing systems, because it integrates the essential measures of sensitivity, specificity, and decision threshold. Figures C-3 and C-4 demonstrate the ability of ROC curves to differentiate the benefits and limitations of two tests over a range of conditions that may occur in clinical practice. The greater area under the ROC curve in the example indicates that computer-assisted mammography increases a radiologist’s ability to correctly identify neoplastic breast tissue, as well as to avoid false alarms.
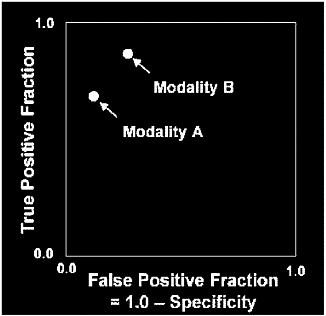
FIGURE C-3 Comparison of two diagnostic modalities without ROC curves. Without the help of ROC curves it is difficult to reach a conclusion as to which modality is more accurate.
SOURCE: Adapted from Metz C. Methodologic Issues. Fourth National Forum on Biomedical Imagining in Oncology. Bethesda, MD. February 6, 2003.
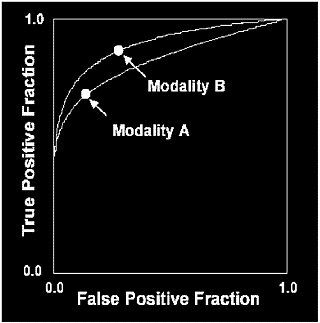
FIGURE C-4 Comparison of two diagnostic modalities utilizing ROC curves. After drawing ROC curves it is easy to see that modality B is better. Modality B achieves a higher true-positive fraction at the same false-positive fraction as modality A. Modality B also results in a lower false-positive fraction with the same true-positive fraction as modality A.
SOURCE: Adapted from Metz C. Methodologic Issues. Fourth National Forum on Biomedical Imagining in Oncology. Bethesda, MD. February 6, 2003.
MULTIPLE-READER MULTIPLE-CASE ROC
The findings of clinical studies are insignificant unless the results can be applied to some sort of clinical use. Therefore, in the case of breast cancer diagnostic modalities, the reader in the study must represent all radiologists and the case set must also closely resemble all mammograms that can be generated in the clinic. It may be impossible to exactly replicate the full variability of mammography findings in clinics nationwide. However, clinical studies that incorporate more case variation to measure the diagnostic accuracy of a modality will have significantly more clinical value than studies based on little case variation.
Variability in cancer detection tests has two main components, reader variability and case-sample variability. The first was described in the discussion of ROC analysis. The latter results from subtle differences in mammograms that, when spanning the continuum from definitely revealing
cancer to definitely not revealing cancer, may influence a reader’s decision. Methodological solutions to account for these sources of variability can maximize the amount of information that can be gathered from data sets.
The combination of ROC analysis and a study design with multiple readers and multiple cases provides a possible solution to the components of variance. In multiple-reader multiple-case (MRMC) ROC analysis, all readers interpret every mammogram in the case set. The readers in a study represent the diverse readership that might use a specific technology. The representative case-set population allows one to generalize the findings to the diverse breast cancer cases that may appear in nationwide clinics. This allows for significant findings to be generalized to widespread clinical practice.
The MRMC study design has several advantages over the collection of single-reader ROC analyses because MRMC analysis provides a quantitative measure of the performance of a diagnostic test across a population of readers with varying degrees of skill. Even though having more than one reader increases variability in the measurement, MRMC studies can be designed so that the statistical power of differences between competing modalities will be greater than if only one reader’s interpretation is used.1 When using MRMC methodology, statistical models can be used to account for both case variability and reader variability. The results of a study in which readers interpret different mammogram case sets cannot account for case-sample variation. Therefore, single-reader studies can only be generalized to the cases that each reader interpreted. Conversely, the results of an MRMC study can be generalized to all radiologists as well as all mammograms.6
The practical result of MRMC methodology is saving time and money. The concept of design of pivotal studies using results from pilot MRMC studies offers an opportunity for the development of imaging technology assessment with some degree of coherence and continuity. MRMC studies during the research phase of imaging system development can provide the information to design and size studies for the demonstration of safety and effectiveness required for Food and Drug Administration (FDA) approval.6 MRMC methods yield more information per case, which translates into smaller sample sizes for trials. Reducing the size of trials makes it easier to recruit patients. Smaller trials also require less money. This procedure can also be used to help design clinical trials by estimating the size of future studies. For instance, the FDA approval of the first digital mammography technology was based on only 44 breast cancers across 5 readers in a pilot study using the MRMC paradigm. The results of this study can be generalized to a pivotal trial of 200 cancers and 6 readers, or 78 cancers with 100 readers.7 According to the 2001 FDA guidance on digital mammography systems, ROC estimates that take into account uncertainties are an essential
part of a clinical study. The FDA also presents several methodologies that have been used in the past to measure uncertainties in ROC estimates; however, it is noted that MRMC methodology is the only approach that accounts for reader and case variability.2 As a result, through November 2002, all successful submissions to the FDA of a system for digital mammography utilized the MRMC ROC paradigm.
REFERENCES
1. Beiden SV, Wagner RF, Doi K, Nishikawa RM, Freedman M, Lo SC, Xu XW. 2002. Independent versus sequential reading in ROC studies of computer-assist modalities: analysis of components of variance. Acad Radiol 9(9):1036-1043.
2. Center for Devices and Radiological Health. 2001. Premarket Applications for Digital Mammography Systems; Final Guidance for Industry and FDA. Washington, DC: Food and Drug Administration.
3. Giger M. 2003. Computer Assisted Diagnosis. Workshop on New Technologies for the Early Detection and Diagnosis of Breast Cancer. Washington, DC: Institute of Medicine of the National Academies.
4. Metz CE. 1978. Basic principles of ROC analysis. Semin Nucl Med 8(4):283-298.
5. Wagner RF, Beiden SV. 2003. Independent versus sequential reading in ROC studies of computer-assist modalities: analysis of components of variance. Acad Radiol 10(2):211-212; author reply 212.
6. Wagner RF, Beiden SV, Campbell G, Metz CE, Sacks WM. 2002. Assessment of medical imaging and computer-assist systems: lessons from recent experience. Acad Radiol 9(11):1264-1277.
7. Wagner R. 2003. CDRH Research Perspectives. Fourth National Forum on Biomedical Imaging in Oncology. Bethesda, MD: National Cancer Institute.








