1
Introduction
1.1 THE CHALLENGE TO LEARN
Of the many contributions that Jerome Bruner made to the scientific study of education, perhaps none is more important than his insistence that we must challenge students to learn and to think and that we must support their doing so. In 1959, Bruner offered a classic example of how to foster thinking, using only the simplest of tools. The work grew out of his concern with the “passivity of knowledge-getting,” an approach he saw as depriving students of the thinking that is the reward for learning.
Fifth-grade students learned about the geography of the north central states in the United States in one of two ways:
One group learned geography as a set of rational acts of induction—that cities spring up where there is water, where there are natural resources, where there are things to be processed and shipped. The other group learned passively that there were arbitrary cities at arbitrary places by arbitrary bodies of water and arbitrary sources of supply. One learned geography as a form of activity. The other stored some names and positions as a passive form of registration. (Bruner, 1959, p. 188)
Bruner’s description of the work of the first group captures the power and excitement of thinking:
We hit upon the happy idea of presenting this chunk of geography not as a set of knowns, but as a set of unknowns. One class was presented blank maps, containing only tracings of the rivers and lakes of the area as well as the natural resources. They were asked as a first exercise to indicate where the principal cities would be located, where the railroads, and where the main highways. Books and maps were not permitted and “looking up the facts” was cast in a sinful light. Upon completing this exercise, a class discussion was begun in which children attempted to justify why the major city would be here, a large city there, a railroad on this line, etc.
The discussion was a hot one. After an hour, and much pleading, permission was given to consult the rolled up wall map. I will never forget one young student, as he pointed his finger at the foot of Lake Michigan, shouting, “Yipee, Chicago is at the end of the pointing-down lake.” And another replying, “Well, OK: but Chicago’s no good for the rivers and it should be here where there
is a big city (St. Louis).” These children were thinking, and learning was an instrument for checking and improving the process. To at least a half dozen children in the class it is not a matter of indifference that no big city is to be found at the junction of Lake Huron, Lake Michigan, and Lake Superior. They were slightly shaken up transportation theorists when the facts were in. (Bruner, 1959, pp. 187–188)
The first group of children was practicing a vital form of thinking—spatial thinking—and their work was supported by a simple outline map. Hidden behind many of the daily operations of everyday life, the workplace, and science, spatial thinking is integral to successful problem solving. Section 1.2 defines spatial thinking and presents two examples of spatial thinking in epidemiology. Section 1.3 discusses the committee’s charge. The first group of children in Bruner’s study was successful in spatial thinking, and the purpose of this report (Section 1.4) is to foster a generation of students who are spatially literate, who can match the accepted norms for what should be known about space, representation, and reasoning. Fostering spatial literacy can be achieved only by systemic educational reform, and central to the reform process are members of the four audiences of this report (Section 1.5). Section 1.6 describes the structure of the report.
1.2 SPATIAL THINKING
There are many forms of thinking: verbal, logical, metaphorical, hypothetical, mathematical, statistical, and so forth. They can be distinguished in terms of their representational system (e.g., verbal, using linguistic symbols; mathematical, using mathematical symbols) or their reasoning system (e.g., logic, metaphor). In any domain of knowledge, multiple forms of thinking are used: science, for example, uses linguistic, hypothetical, mathematical, logical, and many other thinking processes.
Spatial thinking, one form of thinking, is a collection of cognitive skills. The skills consist of declarative and perceptual forms of knowledge and some cognitive operations that can be used to transform, combine, or otherwise operate on this knowledge. The key to spatial thinking is a constructive amalgam of three elements: concepts of space, tools of representation, and processes of reasoning. It is the concept of space that makes spatial thinking a distinctive form of thinking. By understanding the meanings of space, we can use its properties (e.g., dimensionality, continuity, proximity, separation) as a vehicle for structuring problems, finding answers, and expressing and communicating solutions. By expressing relationships within spatial structures (e.g., maps, multidimensional scaling models, computer-assisted design [CAD] renderings), we can perceive, remember, and analyze the static and, via transformations, the dynamic properties of objects and the relationships between objects. We can use representations in a variety of modes and media (graphic [text, image, and video], tactile, auditory, kinesthetic, and olfactory) to describe, explain, and communicate about the structure, operation, and function of objects and their relationships. Spatial thinking is not restricted to any domain of knowledge, although it may be more characteristic, for example, of architecture, medicine, physics, and biology than of philosophy, business administration, linguistics, and comparative literature.
To think spatially entails knowing about (1) space—for example, the relationships among units of measurement (e.g., kilometers versus miles), different ways of calculating distance (e.g., miles, travel time, travel cost), the basis of coordinate systems (e.g., Cartesian versus polar coordinates), the nature of spaces (e.g., number of dimensions [two- versus three-dimensional]); (2) representation—for example, the relationships among views (e.g., plans versus elevations of buildings, or orthogonal versus perspective maps), the effect of projections (e.g., Mercator versus equal-area map projections), the principles of graphic design (e.g., the roles of legibility, visual contrast, and figure-ground organization in the readability of graphs and maps); and (3) reasoning—for example,
the different ways of thinking about shortest distances (e.g., as the crow flies versus route distance in a rectangular street grid), the ability to extrapolate and interpolate (e.g., projecting a functional relationship on a graph into the future or estimating the slope of a hillside from a map of contour lines), and making decisions (e.g., given traffic reports on a radio, selecting an alternative detour).
Boxes 1.1 and 1.2 illustrate the process and power of spatial thinking. While both deal with waterborne threats to public health, the key parallels lie in their imaginative treatments of epidemiological data. Mapped patterns of spatial variability in levels of cholera incidence and dissolved arsenic can be understood in terms of the source of drinking water—in the first case as a function of the differential surface location of the wells and, in the second case, the differential depth of the wells. Both cases depend on visualization in three dimensions, with the differential contamination levels within the spatial structure of subsurface aquifers providing the explanation for the patterns of spatial variability in health impacts. In the first case, the technology of data acquisition and graphic production is relatively simple; in the second case, it depends on sophisticated technologies that produce remarkable levels of locational accuracy. In both cases, the technology enables an exploratory and explanatory approach to problem solving that draws on the scientific knowledge, intuition, and experience of researchers.
1.3 CHARGE TO THE COMMITTEE
The title of the proposal for this report was Support for Thinking Spatially: The Incorporation of Geographic Information Science Across the K–12 Curriculum. Given the need for increased scientific and technological literacy in the workforce and in everyday life, we must equip K–12 graduates with skills that will enable them to think spatially and to take advantage of tools and technologies—such as GIS (geographic information systems) (see Box 1.3)—for supporting spatial thinking. Therefore, the charge contained two questions, the first of which was intended to generate recommendations for levels of technology (hardware and software), system supports (e.g., teaching materials), curriculum scope and sequence (e.g., the role of necessary precursors), and pre-service and in-service training, while the second was intended to generate recommendations based on an assessment of theoretical and empirical approaches, in psychology and education, relevant to the development of knowledge and skills that underpin the use of GIS.
However, the committee recognized that the charge could not be met without first addressing the educational role of spatial thinking itself. New and better support tools for education—such as GIS—may well be necessary and appropriate, but to what purpose and in what contexts? The answer might seem obvious from the proposal title: to support spatial thinking across the K–12 curriculum. However, such a response points to a fundamental question: Why—and where—do we need to support spatial thinking across the K–12 curriculum? Why should we invest in better GIS or other support tools? What is the role of spatial thinking in everyday life, the workplace, and science?
After learning to appreciate the fundamental importance of spatial thinking, the committee came to a new understanding of the charge. Questions about the current role and future development of GIS as a support system could be answered satisfactorily only after the societal and therefore educational need for spatial thinking, and the ways in which we learn to think spatially, were understood.
Therefore, the committee developed an understanding of two additional questions: (1) What are the nature and character of spatial thinking? (2) How does the capacity for spatial thinking develop and how might it be fostered systematically by education and training? This revision to the committee charge was approved by the National Research Council (NRC) and met with consent from the project sponsors.
|
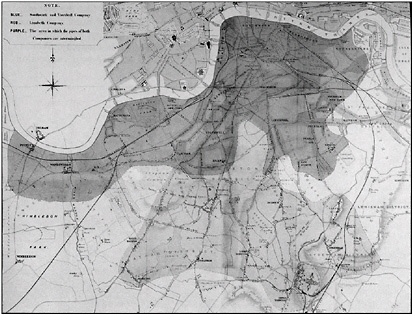
BOX 1.1 Dr. John Snow (1813–1858), an English medical health officer, is celebrated for his now-famous and often-reproduced map of the relationship between cholera deaths and water pumps in central London, depicting what he called “the topography of the outbreak” of cholera in the late summer of 1854. On the basis of this map, he recommended the removal of the handle of a water pump that proved to be a source of contaminated drinking water. For that feat alone, he merits the soubriquet of the “father of epidemiology.” However, in a less well-known section of his book On the Mode of Communication of Cholera (1855), Snow is responsible for an even more remarkable exercise in spatial thinking. (This analysis is based on Robinson, 1982, pp. 175–180.) After establishing to his satisfaction the link between contaminated water and the incidence of cholera, Snow undertook an exercise in data collection, representation, and interpretation that captures the essence of spatial thinking. He knew that there were differential death rates from cholera throughout London. He also knew that at least two major water companies, the Southwark & Vauxhall Company and the Lambeth Company, provided water to more than 300,000 Londoners. He did not know, however, the service area of each water supply company because the data either did not exist or were not available to him. Knowing that Southwark & Vauxhall Company drew its water from the River Thames and the Lambeth Company from inland wells, Snow developed a simple test for water salinity to differentiate water derived from the two sources. Based on tests of the salinity of samples gathered by collaborators from locations throughout the city, he mapped the distribution of salinity values, and from this map, he inferred the service areas of the two companies. Interestingly, there was an area of spatial overlap in the pattern of water distribution (Figure 1.1). Snow also had a map of the rates of cholera deaths per 1,000 houses. He correlated data from the water distribution and cholera death maps. Interestingly again, the two “sole-service” areas and the “both-providers” service area had different death rates. The South & Vauxhall Company sole-service area experienced a death rate of 71 per 1,000 and the Lambeth Company sole-service area experienced a death rate of 5 per 1,000. Crucial to his reasoning, the area with both providers experienced an intermediate cholera death rate. Death rates were, therefore, correlated with water source. The resultant explanation for the variation in death rates was simple: the Southwark & Vauxhall Company drew its water from a river that also served as a depository for untreated sewage, whereas the Lambeth Company had switched from the river source to less-polluted inland wells in 1852. Snow’s approach exemplifies spatial thinking. After collecting data, he used maps to integrate the data. From these maps, he identified spatial patterns (service areas and differential death rates). He correlated the two patterns and reasoned about the spatial variation in one (death rates) as a function |
This report, therefore, answers four questions:
-
What are the nature and character of spatial thinking: what is it, why do we need to know about it, and what do we need to know about it?
-
How does the capacity for spatial thinking develop and how might it be fostered systematically by education and training?
-
How might current versions of GIS be incorporated into existing standards-based instruction in all knowledge domains across the school curriculum?
-
How can cognitive developmental and educational theory be used to develop new versions of GIS that are age appropriate in their design and to implement new GIS curricula that are age appropriate in their scope and sequence?
The committee came to believe that spatial thinking is pervasive: it is vital across a wide range of domains of practical and scientific knowledge; yet it is underrecognized, undervalued,
underappreciated, and therefore, underinstructed. Despite the practical importance of spatial thinking—historical and contemporary—the committee recognized that scientists and educators have not yet clearly identified and described the operations of spatial thinking. Without a clear understanding of the nature and character of spatial thinking, it is impossible to design instructional systems and technologies to support it.
1.4 AN OUTCOME OF THE REPORT: FOSTERING SPATIAL LITERACY
The committee was charged with exploring ways of supporting the process of thinking spatially. If this charge is met successfully, then American students will become more spatially literate. Section 1.4.1 defines the components of spatial literacy, and Section 1.4.2 presents the characteristics of a student who is spatially literate.
|
BOX 1.2 In many areas of the world, arsenicosis—arsenic poisoning that leads to cancers and other debilitating diseases—is an increasing problem. In Bangladesh, the cause of the problem is arsenic from groundwater that is pumped from wells, the source of drinking water for 97 percent of the population. van Geen et al. (2003) analyzed the spatial variability of arsenic in tube wells in a 25 km2 area in Araihazar Upazilla (an administrative unit). The parallels to the work of Snow are obvious: a public health crisis, a waterborne agent, the use of wells, the need for mapping, and the ideas of spatial patterns and variability. The differences are equally obvious: access to sophisticated technologies, knowledge of the causative agent, and the deployment of teams of well-equipped scientific researchers. The challenge in the case of arsenic in the watertable in Bangladesh is one of understanding what the authors refer to as “… the bewildering degree of spatial variability of groundwater arsenic contaminations” (van Geen et al., 2003, p. 3-1). The variability in arsenic levels over very short distances is remarkable (where levels of ≤10 μg/L meet the World Health Organization guidelines for safe drinking water and levels of ≤50 μg/L meet the U.S. Environmental Protection Agency guidelines). The researchers sampled water from 5,971 wells, recording arsenic levels, the position of the well (via a global positioning system [GPS]), and well characteristics (e.g., date of installation, depth). Data were mapped onto an IKONOS satellite image. Figure 1.2 shows the spatial pattern of variability. Each color-coded circle on the map (right) corresponds to a well whose location was determined by students using a hand-held GPS receiver. The wells are clustered in two villages. Water from each well was sampled and analyzed for arsenic. The safer wells are color-coded in green, and the more dangerous wells are color-coded as red or red-brown dots. (Interestingly, public health authorities in parts of Bangladesh paint the handles of the safer wells green and those of the high-arsenic-level wells red, matching the universal symbols for stop and go, safe and dangerous). The background is an IKONOS satellite image showing rectangular patches corresponding to rice fields that separate the villages. The parallel section (left) shows the same information as a function of depth. Well owners know the depth of their wells, the majority of which were installed in the past 10 years, because they paid for each 15-foot PVC (polyvinyl chloride) pipe section that went into the well construction. The map shows that most households in the northern village have access to low-arsenic water, whereas only some households in the southern village do. The explanation is that in the northern village, a shallow clay layer has forced villagers to install wells that tap into a deeper, but low-arsenic, sandy aquifer. A shallower aquifer with highly variable arsenic levels was available in the southern village, and therefore, many (but not all) villagers chose to install their wells as inexpensively as possible by minimizing well depth. Now that villagers and local well drillers are aware of the depth distribution of arsenic in this area, most new wells are being installed to tap into the deeper aquifer. This analysis is an equally brilliant exercise in spatial thinking that follows the same steps as those of Snow: from data to maps to patterns to causal explanations. Apart from the technical sophistication, the major difference is the spatial complexity. van Geen and his colleagues are looking at arsenic levels in a three-dimensional context: two surface coordinates and a depth coordinate. The complexity of the surface patterns of safer versus less safe wells can be understood only in terms of subsurface structures that vary in all three dimensions. |
1.4.1 Components of Spatial Literacy
Bruner refers to his students as being “slightly shaken up transportation theorists.” He points out that “… [t]hese children were thinking, and learning was an instrument for checking and improving the process.” Although the committee does not necessarily want fifth-grade students to become better transportation theorists, it does want all students to learn to be better spatial thinkers.
Learning to think is a key educational goal. Achieving this goal leads to literacy, where literacy is a normative statement of what members of a culture should know and be able to do with that
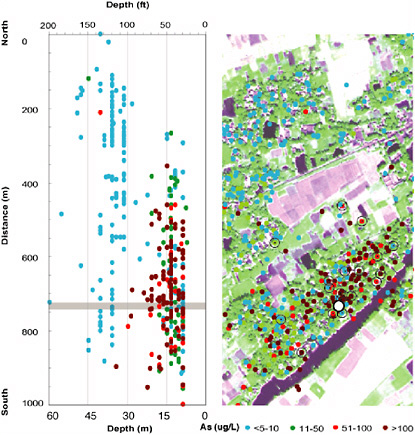 FIGURE 1.2 Spatial distribution of arsenic levels in wells in Arailhazar Upazilla, Bangladesh. SOURCE: van Geen et al., 2003, p. 3-11. Reproduced by permission of American Geophysical Union. |
knowledge. The Workforce Investment Act of 1998 (Public Law 105-220) stated that “… [t]he term ‘literacy’ means an individual’s ability to read, write, and speak in English, compute, and solve problems, at levels of proficiency necessary to function on the job, in the family of the individual, and in society” (Title II, Section 203, Number 12). The committee would add spatial thinking to this list of necessary abilities. A person proficient in spatial thinking is spatially literate and can match the norms for what should be known about space, representation, and reasoning.
These norms are set within a framework derived from Technically Speaking: Why All Americans Need to Know More About Technology (NRC, 2002c). That NRC report saw a technologically
|
BOX 1.3 A geographic information system mirrors many of the functions and operations of spatial thinking. A GIS can serve as one means of support for spatial thinking and as a model for exemplifying the challenges and ways of incorporating spatial thinking into K–12 education. A GIS is an integrated system of hardware, software, and procedures designed to support the collection, management, manipulation, analysis, modeling, and display of spatially referenced data about Earth’s surface in order to solve complex planning and management problems.The power of a GIS is that it allows us to ask questions of data and to perform spatial operations on spatial databases. A GIS can answer five generic questions:
SOURCE: Geography Education Standards Project, 1994, p. 256. |
||||||||||||||||||
literate person as displaying three characteristics: knowledge of concepts, command over ways of thinking and acting, and development of capabilities. “Like literacy in reading, mathematics, science, or history, the goal of technological literacy is to provide people with the tools to participate intelligently and thoughtfully in the world around them” (NRCc, 2002, p. 3).
Given the resonances between this view of technological literacy and the committee’s view of spatial literacy, and given the shared emphasis on the importance of tools for thought, the committee offers a parallel characterization of spatial literacy as constituting proficiency in terms of spatial knowledge, spatial ways of thinking and acting, and spatial capabilities.
Spatial Knowledge
Students need to know the concepts that are the building blocks for spatial thinking. There are general spatial concepts that are found in many disciplines, such as symmetry, isomorphism, reflection, orientation, rotation, and function, and spatial concepts that are tailored to a particular discipline, such as relative versus absolute distance, small versus large scale, and distance decay in geography.
Students learn the meanings and uses of concepts relevant to spatial thinking in the context of specific disciplines or school subjects. Thus, in mathematics, students learn about general concepts, such as minima and maxima, and their specific forms, such as hyperbolas and parabolas. In geometry, they learn about conic sections: hyperbola, parabola, ellipse, and circle. They learn to distinguish among a torus, Mobius strip, and Klein bottle. In physics, they learn that the equilibrium position of a fixed chain is a catenary curve (or hyperbolic cosine).
Even this cursory listing of concepts by discipline illustrates two fundamental educational challenges. First, there is a rich, complex, conceptual structure to the description and explanation of space to be learned within each discipline. Second, rather than coming up with an omnibus list of concepts for spatial thinking, students—and especially teachers—should identify concepts relevant to specific disciplines but should also look for common themes. They should reflect on how
concepts of one discipline might inform or interfere with learning about concepts in another discipline. For example, in algebra, geometry, and science, the concept of function has different meanings. Similarly, in geometry, a point is a dimensionless location, whereas in geography, a point in space is a specific place with a small but definite area.
Spatial Ways of Thinking and Acting
People draw upon strategies that emphasize the use of spatial thinking to carry out projects. They set ideas into spatial contexts, seeing similar things as being close together and dissimilar things as far apart. They draw diagrams and graphs. They look for patterns and note outliers (anomalies) from the patterns. They look for clusters. They use statistical analyses to test for spatial relationships. They look for relationships among different spatial patterns. They disentangle change over space from change over time. Some representations are sketches used only during the thinking process, whereas others are created for an audience. In each case, there is an interplay between thinking and acting, between ideas and their representation, between expression for one’s self and communication and dissemination to others.
The educational challenge is to teach students strategies for spatial thinking; to teach how, where, and when to use them; and to convey a critical awareness of the strengths and limitations of each strategy.
Spatial Capabilities
Skills in spatial thinking are learned within a specific context. Skills can be supported by tools and technologies (see Chapter 6 for the concept of support systems and Chapter 7 for a range of high-tech spatial support systems). Disciplines adapt particular supporting tools and technologies: in mathematics, students learn to use graphing calculators; in design, students learn to use CAD programs; and in geography, students learn to use GIS. As a result of the human genome project, students must learn new representational schemes and develop sophistication in spatial thinking.
Tools and technologies support different tasks: concept maps are used for structuring ideas, CAD for design, GIS for geospatial data analysis, and so forth. For each task category, there are often competing versions of tools: for GIS, there are low-tech approaches, such as traditional techniques for overlaying paper or mylar maps at the same scale on a light table; for high-tech approaches, there are software programs by Environmental Systems Research Institute (ESRI), Intergraph, Idrisi, etc. (see Chapters 7 and 8). Moreover, new categories of tools and technologies emerge as fields advance. For example, developing a robust spatial representation of the brain has become feasible as magnetic resonance imaging (MRI), functional magnetic resonance imaging (fMRI), and other techniques become available.
The educational challenge is threefold: (1) to provide students with experience using low-tech tools (paper, pencils, protractors, compasses, etc.); (2) to provide students with opportunities to learn several, general-purpose, high-tech applications that support spatial thinking (e.g., Excel, Powerpoint, Photoshop); and (3) to develop the skills that will allow them to learn new low- but especially new high-tech applications. When students specialize in a discipline, they often need to learn a complex application relatively quickly. However, expert use of many high-tech support systems requires a lengthy investment of time. Often students have difficulty determining how support systems work. Moreover, teachers question the value of investing in the instruction time necessary for students to attain a level of proficiency that allows them to solve interesting problems with the tools.
Taken together, the educational challenges for teachers and students are complex. On the one hand, students need to learn how to use a relatively small number of discipline-specific tools as
quickly as possible. On the other hand, in the longer run, students also need to learn how to learn new supporting tools as they emerge. Each tool is costly to learn in terms of time. New tools become available and old tools are revised or discarded (e.g., the slide rule). Focused tools—such as CAD—are very powerful, but they do not necessarily offer opportunities across disciplines and therefore across the curriculum.
If these educational challenges are met, we can also meet the goal of fostering a new generation of spatially literate students. To do so, we need to invest in a systematic educational program to enhance levels of spatial thinking in all K–12 students.
1.4.2 Three Characteristics of a Spatially Literate Student
Spatially literate students who have developed appropriate levels of spatial knowledge and skills in spatial ways of thinking and acting, together with sets of spatial capabilities,
-
have the habit of mind of thinking spatially—they know where, when, how, and why to think spatially;
-
practice spatial thinking in an informed way—they have a broad and deep knowledge of spatial concepts and spatial representations, a command over spatial reasoning using a variety of spatial ways of thinking and acting, have well-developed spatial capabilities for using supporting tools and technologies; and
-
adopt a critical stance to spatial thinking—they can evaluate the quality of spatial data based on their source, likely accuracy, and reliability; they can use spatial data to construct, articulate, and defend a line of reasoning or point of view in solving problems and answering questions; and they can evaluate the validity of arguments based on spatial information.
The committee believes that students can derive pleasure from thinking spatially. The children in Jerome Bruner’s first group of active, engaged, and excited spatial thinkers should represent the rule, not the exception.
1.5 AUDIENCES FOR LEARNING TO THINK SPATIALLY
Fostering a new generation of spatial thinkers requires systemic educational reform. Such reform cannot be achieved without the long-term participation, cooperation, and commitment of many individuals. Therefore, this report is aimed at four groups of people, often overlapping in composition, who are central to educational reform.
Its first audience is the educational establishment—those federal, state, and local officials who are charged with establishing educational policy and practice. These officials establish content and performance standards for what students should know and be able to do; they adopt assessment programs to measure levels of student performance; they establish criteria for teacher preparation and certification; they provide the supplies and equipment necessary for instruction; and they provide instructional programs for pre- and in-service teachers. The educational establishment can mandate or encourage systemic change. However, the successful implementation of change is possible only with the active participation and cooperation of the second audience—members of the educational infrastructure. This audience ranges from the leadership of teachers’ unions to pre-service trainers to curriculum developers, textbook writers, educational publishers, courseware developers, and test and assessment developers. The precise direction of change and reform will depend on members of the third audience—researchers in education and psychology. As argued earlier, without a clear understanding of the nature and character of spatial thinking it is impossible to design instructional systems and technologies to support spatial thinking. The de-
sign of one such instructional system, GIS, falls under the aegis of the fourth audience—the developers of GIS software.
Some of the recommendations in Chapter 10 are aimed specifically at particular audiences (e.g., members of the educational establishment or GIS software developers). Other recommendations require the collaboration of members of all four audiences. The committee believes that the set of recommendations provides the basis for actions to ensure that the next generation of American students is spatially literate.
Spatial thinking can be learned; it should be taught at all levels in the education system. With advances in the tools and technologies of computation (hardware and software), spatial thinking can be supported in ways that enhance the speed, accuracy, capacity (to manage large amounts of data), and flexibility of its operation and open up the process to increasing numbers of people, working collaboratively and at higher levels of performance. Because of newly available computational technologies, support for spatial thinking is more readily possible today, but concomitantly, more challenging cognitive skills are necessary to take advantage of rapidly changing support systems. Given the rapid change in supporting tools and technologies, therefore, spatially literate students must be lifelong learners.
1.6 STRUCTURE OF THIS REPORT
In Part I, “The Nature and Function of Spatial Thinking” (Chapters 2 through 6), the committee focuses on the first pair of questions of the charge about spatial thinking and its support: its definition, character, and operations (Chapter 2); its roles in everyday life, work, and science (Chapter 3); its incorporation into instruction in the K–12 curriculum (Chapter 4); and its central role in workforce needs, and its implicit, unacknowledged role in standards-based K–12 education (Chapter 5). The nature and characteristics of a support system for spatial thinking are defined in the K–12 context (Chapter 6).
The committee sees spatial thinking as a basic and essential skill that can be learned, that can be taught formally to all students, and that can be supported by appropriately designed tools and technologies. With appropriate instruction and support, spatial thinking can become a lifelong habit of mind. The committee presents a set of educational guidelines for developing instructional systems and curricula that can foster spatial literacy in American students. Therefore, Part I generates one recommendation.
On the basis of this understanding, Part II, “Support for Spatial Thinking” (Chapters 7 through 9), focuses on questions three and four of the charge. The committee reviews a range of high-tech systems for supporting spatial thinking (Chapter 7), evaluates the design and implementation of GIS as a system for supporting spatial thinking in the K–12 context (Chapter 8), and assesses the current status and potential of GIS as a support system in the K–12 context (Chapter 9).
The committee believes that although GIS can make a significant impact on teaching and learning about spatial thinking, it must be situated in a context wherein there is a systematic, standards-based approach to teaching spatial thinking, along with a suite of supporting tools available to do so. Taken alone, GIS is not the answer to the problem of teaching spatial thinking in American schools; however, it can play a significant role in an answer. Therefore, Part II generates five recommendations.
In Part III, “Supporting Spatial Thinking in the Future” (Chapters 10 and 11), the committee addresses the role of spatial thinking in general, and in K–12 education in particular, and illustrates the role of GIS in supporting spatial thinking. Chapter 10 presents the committee’s conclusions and a set of six recommendations, and Chapter 11 describes students who are spatially literate and who are using GIS to solve interesting and important problems.