6
Tools for Thought: The Concept of a Support System
6.1 INTRODUCTION
A support system provides tools and technologies to leverage the power of the human capacity to think and to solve problems (Figure 6.1). In so doing, a support system augments and enhances selected mental capacities involving memory, computation, analysis, visualization, representation, reasoning, and evaluation. Levels of technology can range from simple pencil-and-paper tools to high-performance digital computing systems with scanners, printers, flat screens, voice and gesture interfaces, and projection systems. In the K–12 context, a support system comprises multiple elements: materials and technology, logistics, teachers, and curricula.
The chapter consists of nine sections. Section 6.2, using two detailed examples, establishes the two roles of a support system and emphasizes that its role is as a support, not as a substitute for human thought. Section 6.3, specifies the five principal functions of a support system in general. Section 6.4 identifies major problems in the design of a high-tech support system Section 6.5 focuses on criteria for the design of a high-tech support system in the context of K–12 education. Building from this base, Section 6.6 makes the case for a support system for spatial thinking, and Section 6.7 establishes requirements for the design of a support system for spatial thinking. Section 6.8 presents the need for a suite of tools, both high tech and low tech, for the support of spatial thinking in the K–12 context. Section 6.9 identifies five interlocking components essential for the implementation of a support system in the K–12 context.
6.2 THE NATURE OF A SUPPORT SYSTEM
The key to a support system is not technology as such. This is best illustrated by looking at a ubiquitous human spatial task, navigation, and drawing a contrast between two case studies. The first case (Box 6.1) is a description of the now famous navigational prowess of the Puluwatan islanders of the southern Pacific Ocean. The second case (Box 6.2) is an analysis of the typical vehicle navigation systems that are available in cars in the United States.

FIGURE 6.1 Using a calculator to solve a mathematical problem. SOURCE: http://pics.tech4learning.com/details.php?img=calculator1.jpg. Reprinted by permission from Tech4Learning, Inc.
The parallels between Puluwatan voyagers and car drivers are striking: navigation is a function of knowledge structures and databases to which are applied rules and heuristics for selecting and following routes under a variety of environmental conditions. The differences are equally striking: in one case, most of the work is done “in the head” by a skilled navigator, whereas in the other a computer and a GPS unit do most of the work. The technological supports are minimal in one case and extensive in the other. But in both cases, it is the mind of the navigator or driver that determines the success of the operation. Navigators and drivers have learned how to navigate in a continuously changing and somewhat unpredictable environment. The Puluwatans have learned enormous amounts of highly specific information on land (from models and sketches drawn in the sand) and have practiced and mastered their skills at sea. Drivers have learned to operate the navigation system from the manual provided and then practiced and mastered their skills on the highway. It is the human power to think that is crucial: to the extent that the knowledge structures and display screens are functional (that is, user friendly and reliable), the in-vehicle navigation system (IVNS) works. In this way, support systems augment and leverage human problem solving.
Support systems play two principal roles, one practical and one conceptual. First, they enable us to do things more efficiently and more effectively in contexts ranging from everyday life to careers in all domains of knowledge: support systems are tools for thought and for lifelong learning. Second, they can change the process of education in fundamental ways for both students and teachers. In the case of spatial thinking, students can learn to understand and use the underlying thinking processes and they can learn to understand content areas whose concepts and data can be made more accessible through the application of spatial thinking. From a teacher’s perspective,
|
BOX 6.1 One of the classics of social science is Thomas Gladwin’s (1970) East Is a Big Bird. The subtitle, Navigation and Logic on Puluwat Atoll, captures the thrust of this work. It is spatial thinking in its purest and perhaps most remarkable form. The culture of this group of Micronesian islanders values ocean navigation in outrigger canoes (Figure 6.2). Voyages are undertaken over hundreds of miles and many days, but they use none of the navigational equipment that is common to Western culture. There are no maps, compasses, sextants, or GPS units, at least in the classic form of this way of life. The voyages are guided by highly trained and skilled navigators who have mastered a system of knowledge that is rich, complex, efficient, and non-Western in organization and principle. It is complete, in that every conceivable situation at sea is accounted for; it is strategic, built on a vast amount of detailed information and employing a series of heuristics; it is specific, tailored to the environment in the  FIGURE 6.2 A Puluwatan canoe. SOURCE: The Pacific Trust Territory of the Pacific Islands. Reprinted with permission of the Trust Territory Archives, Pacific Collection, University of Hawaii Library. |
|
immediate locality. The training takes years, linking on-land instruction to apprenticeship at sea. The on-land portion makes use of diagrams, drawn in the sand with shells as symbols, and the mattang or stick charts, depicting typical patterns of waves and currents (Figure 6.3). The core of the system is an intricate and highly detailed knowledge of the physical environment: stars and their seasonal appearances in rising and setting positions; clouds and water color and their relationships to land; and birds and their typical foraging distances from land. The navigational process links star courses, sequences of rising and setting stars, with a system of dead reckoning. The canoes are steered by the “shape of the sky” as it relates to rigging of the canoe. The dead reckoning system depends on the continuous integration and updating of a mass of information, itself a remarkable feat of spatial thinking. Star courses are memorized lists of sailing directions between islands, a list that must accommodate the rising and setting positions of stars at different times of the year. Because no single set of phenomena is sufficient to guide the canoe under all conditions, the system relies on backup procedures that vary in their ease of use and their accuracy and reliability. For people without clocks or compasses, it is much less accurate to sail using the constantly changing position of the Sun than it is to follow a sequence of stars, each for a short period of time. 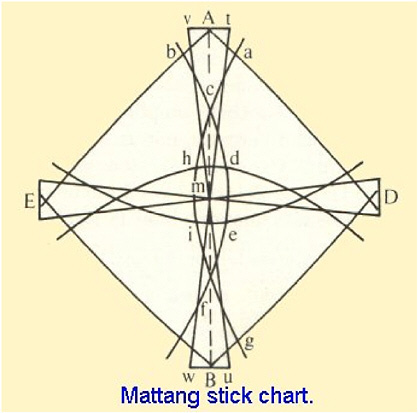 FIGURE 6.3 A mattang stick chart. SOURCE: http://www.janesoceania.com/micronesian_stick_chart/. Reprinted with permission from Dr. Jane Resture. |
|
Nothing captures the power of spatial thinking better than one component of the dead reckoning system, known as etak. Gladwin (1970, p. 181) describes etak as an abstraction: … of a rather high order. The concept in etak of a specific but invisible island moving under often invisible navigation stars is not only an abstraction. It is also a purposefully devised logical construct by the use of which data inputs (rate and time) can be processed to yield a useful output, proportion of the journey completed. While that description is analytical and framed to meet our technical understanding of cognitive processes, the remarkable nature of etak is best captured by these passages from Gladwin’s book: Picture yourself on a Puluwat canoe at night…. On either side of the canoe water streams past, a line of turbulence and bubbles merging into a wake and disappearing in the darkness. Overhead there are stars, immovable, immutable. They swing in their paths across and out of the sky but invariably come up again in the same places. You may travel for days on the canoe but the stars will not go away or change their positions aside from their nightly trajectories from horizon to horizon. Hours go by, miles of water have flowed past. Yet the canoe is still underneath and the stars are still above. Back along the wake, however, the island you left falls farther and farther behind, while the one toward which you are heading is hopefully drawing closer. You can see neither of them, but you know this is happening. You know too that there are islands on either side of you, some near, some far, some ahead, some behind. The ones that are ahead will in due course fall behind. Everything passes by the little canoe—everything except the stars by night and the Sun in the day. (Gladwin, 1970, p. 182) Thus, the canoe and the sky are seen as fixed in relation to each other: the world is seen as moving or flowing past the canoe. To track the canoe’s position in this moving world requires an etak island (Figure 6.4). 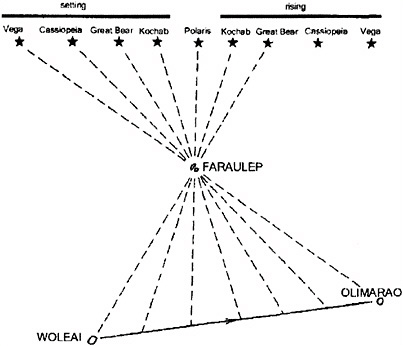 FIGURE 6.4 Representation of the Etak method, a system for tracking position at sea. SOURCE: Rainbird, 2004, p. 54. Reprinted with the permission of Cambridge University Press. |
|
It is the passage of the islands under the stars which is used for etak, the reckoning of distance traveled on a voyage. More specifically, one island is selected for each seaway and used throughout every voyage as a reference…. Ideally this island is fifty or so miles to one side of the line of travel and roughly opposite the midpoint of the seaway which stretches between the islands of origin and destination. The star bearings of the reference island from both the starting and ending points of the trip are known, since on another occasion the reference island may become a destination. In between there are other navigation star positions under which the reference island will pass as it “moves” backward. Its passage under each of these stars marks the end of one etak and the beginning of another. Thus the number of star positions which lie between the bearing of the reference island as seen from the island of origin and its bearing as seen from the island of destination determines the number of etak, which can here be called segments, into which the voyage is conceptually divided. When the navigator envisions in his mind’s eye that the reference island is passing under a particular star he notes that a certain number of segments have been completed and a certain proportion of the voyage has therefore been accomplished. (Gladwin, 1970, p. 184) This mental structure integrates speed and distance: In sum, the contribution of etak is not to generate new primary information, but to provide a framework into which the navigator’s knowledge of rate, time, geography, and astronomy can be integrated to provide a conveniently expressed and comprehended statement of distance traveled…. It is a useful and deliberate logical tool for bringing together raw information and converting it into the solution of an essential navigational question: “How far away is our destination?” (Gladwin, 1970, p. 186) While we advocate the development and use of tools and technologies to support spatial thinking, the Puluwatan navigators illustrate the remarkable power of spatial thinking without modern technology. They show the way in which spatial thinking is woven into the culture of a group of people. They also show the remarkable ingenuity and inventiveness of those predecessors who “invented” the system. Although the regular use of the system does not generate new primary information, those sailors who developed the suite of strategies were indeed generators of new, primary knowledge. |
support systems allow for the orderly and sequenced introduction of basic concepts and skills and for the guidance of the inquiry process.
Support systems cannot and should not substitute for thought. Therefore, a support system does not replace the human process of thinking, automating it by means of a “machine.” It cannot provide a substitute for an understanding of what to do, when, how, and why. Instead, a support system provides an interactive environment within which thinking can take place. It is supportive in a variety of ways: it performs tasks that would otherwise be time-consuming and demanding in terms of effort and attention; it offers guidance in terms of options and alternatives; it provides checks and feedback; and it manages the flow of work. It is enhancing in that it allows access to a range of problem-solving strategies (heuristics and algorithms) that might otherwise be inaccessible, it fosters collaborative work by externalizing otherwise “private” processes, and it generates a range of possible answers to a question.
6.3 THE FUNCTIONS OF A SUPPORT SYSTEM
A support system for thinking in any domain of knowledge performs some or all of five functions:
-
Database construction and management: provides a capacity for data acquisition, entry, formatting, storage, and management (the functional equivalent of long-term memory)
-
Data analysis: performs operations and functions for data manipulation, analysis, interpretation, representation, and evaluation
-
Memory: provides working memory for tracking the flow of computations and the storage
-
of working and final results (the functional equivalent of short-term memory)
-
Assistance: provides prompts, feedback, hints, and suggestions to guide the choice of data analysis steps and to manage the flow of work
-
Display: provides a flexible display system for the representation of working and final results to oneself and to others—in physical form (e.g., a graph on paper, a three-dimensional model of molecular structure) or in virtual form (e.g., on-screen, for hard-copy printing, for export to other software packages)
For example, throughout history, we have developed, taught, and used a suite of tools—abacuses, compasses, Cuisenaire rods, protractors, graph paper, measuring and slide rules, and mechanical and electronic calculators—to facilitate calculations in the process of mathematical problem solving. Today, with the advent of sophisticated computer technologies, we are beginning to teach students to use software such as spreadsheets, database management programs, computer programming languages, and statistical analysis programs to perform calculations and to solve mathematical problems.
By routinizing basic mathematical operations (simple—such as addition, subtraction, multiplication, and division, complex—such as percentages, square roots, exponentiation, or generating trigonometric functions), tools and technologies provide ways of performing calculations and tracking the flow of sequences of chained operations. They can speed up the process of problem solving and increase the chances of arriving at a correct answer. They also provide ways of representing the working and final results to oneself and to others. Similar suites of tools and technologies can support spatial thinking in other knowledge domains (e.g., in architecture: pencil sketches, colored perspective drawings, sections [plans, elevations, etc.], balsa wood and cardboard models, CAD systems, virtual reality displays; in sea navigation; portolan charts, astrolabes, compasses, sextants, modified Mercator projection maps, chronometers, celestial tables, Loran, GPS).
In any knowledge domain, the components of a suite of support systems serve different functions in different contexts, for example, trading off speed and simplicity (in terms of data needs and the execution of operations) for depth and complexity. The elements of a suite of tools are not necessarily built in a coordinated fashion, either in terms of a division of functions or in terms of common design principles: they are assembled over time, with new tools adding to or replacing existing ones. However, their alignment along a low- to high-technology continuum is not necessarily synonymous with worse to better. Because of their simplicity, transparency, and intuitive nature, low-technology tools are often taught and used as precursors for understanding the complex, nontransparent, and non-intuitive operations of high-technology tools. Indeed, in many instances, the “back-of-the-envelope” answers generated by low-technology tools are perfectly adequate to the task at hand. However, with the increasing link between workforce demands and digital information technology, familiarity with and indeed mastery over high-technology tools is increasingly important.
6.4 TOOLS FOR THOUGHT: THE LIMITS TO POWER
Support systems, especially those that are computer based, are the cognitive equivalent of power tools. With the promise of access to such power comes costs and challenges. These include the time and committed effort it takes to learn to use a support system (and continuously upgrade to new versions), the need to understand the system’s range of appropriate and inappropriate uses, and the need to appreciate the system’s characteristic limits and idiosyncrasies.
There is a wide range of support systems available in science, mathematics, and design (see Box 7.1 for a description of hi-tech support systems for spatial thinking). These support systems can be a boon or a bane to the learner. Experts in a knowledge domain start with an understanding
|
BOX 6.2 Becoming “lost” implies disorientation, a consequence of the failure to recognize one’s current location, the failure to recognize local or distant landmarks, the failure to understand (or interpret) local signage, the inability to retrace the current path, the breakdown of cognitive processing (such as path integration or ability to define a homing vector), and the resultant emotional stress. Not only do some drivers in the United States get lost when departing from a habitual travel route, but they cannot recover from the error. They have not developed the spatial thinking skills (including map reading) to be able to recover positional and orientational information from memory or from examining their proximate environment. Obviously this situation is not universal, and many highly skilled wayfinders and navigators are also present in the general population. However, a thriving technology, in-vehicle navigation systems (IVNS), has been developed to
Drivers have the luxury of choosing to be a navigator or a wayfinder. To navigate implies following a pre-planned route without departure except for unexpected emergencies (e.g., congestion, accidents, construction.). Wayfinding involves searching out a path rather than exactly following a pre-planned route. In the former case, the navigator has to recognize the presence of defined choice points where actions such as changing direction are involved. It is often referred to as “piloting,” where the driver proceeds from landmark to landmark in a prescribed sequence. Wayfinders often choose their own routes, incorporating local knowledge of road systems plus select path segments by using their spatial skills (e.g., general orientational, directional, and distance knowledge or knowledge of environmental layout and its geometry). Strategies such as shortcutting through familiar or unfamiliar areas can be incorporated into the wayfinding strategy on both the outward and return journey. Research on human navigation and wayfinding indicates that females often prefer the “piloting” system for local navigation, using a landmark to landmark (or choice point to choice point) decision support system. Males prefer to use their understanding of the geometry of layouts as a primary support system, enabling tactics such as shortcutting and minimizing travel time or travel distance (described as a “homing vector” or “path integration” procedure) (Montello et al., 1999; Saucier et al., 2002). The in-vehicle support system to accommodate this activity can be visual (map based), minimally verbally descriptive, or reliant only on a simple device such as a dashboard compass (Battista, 1990; Beatty and Tröster, 1987; Ferguson and Hegarty, 1993; Lawton, 1994; Loomis et. al., 1999; O’Laughlin and Brubaker, 1998). In-vehicle navigation support systems can be low tech in design: a dashboard compass, a handheld cartographic road map (e.g., topographic sheet), or a simplified and linearized route map (as in an AAA Trip-Tik). Because the bulk of daily travel is regularly episodic and habitual, relying on people’s cognitive maps (or environmental knowledge stored in long-term memory), drivers in most situations have little need for an in-vehicle navigation support system. Exceptions occur when (1) a well-known route is obstructed, requiring a change of travel plans to bypass the obstruction; (2) one is required to travel to an unfamiliar destination; (3) one is exploring new places for, say, recreational or aesthetic purposes; and (4) one has become lost. In most of these cases, a low-tech system can be replaced by (or supplemented with) a high-tech IVNS. |
of the nature of the data, the ways of thinking, and the problems characteristic of the field within which the system could be used. They develop a working understanding of the tool—especially its glitches and quirks—as they use it. In using systems for calculating, for example, they appreciate the difference between truncating and rounding, the necessity for appreciating the number of significant digits, the differences in the effects of error on addition and subtraction versus multipli-
|
When a driver becomes lost, a navigation system could perform a range of functions: (1) automatically call for help if an airbag is deployed; (2) if the vehicle is stolen, give the authorities the vehicle’s current location from GPS tracking; (3) summon emergency services on request; and (4) provide concierge services such as making restaurant reservations. This system is both a navigation and a communication aid and is based on speech interaction with a home base. Vehicle location and tracking is done via a GPS, which uses radio signals from a selection of satellites orbiting at 10,900 nautical miles above Earth. Location is defined by the time taken for a satellite signal to reach a vehicle receiver. Input from four or more satellites enables triangulation of vehicle location in a georeferenced frame (latitude and longitude), which is downloaded and matched with the coordinate frame used in the vehicle’s base map. A more advanced IVNS might have all or most of the basic features in addition to an in-vehicle heads-up display of the travel environment. Early versions displayed only a screen-based two-dimensional road map with the current location identified and with a bird’s-eye view of the travel environment, including destination location and perhaps a navigable route overlain on the road system. Current versions provide bird’s-eye views of the total environment for “you are here” fixing, then enable zooming of scale and visualization from an eye-level perspective that obviates the need for abstract map reading, replacing this process with a more common local visual experience in which three-dimensional presentations of buildings and landmarks replace the two-dimensional flat maps that require abstract map reading skills. An IVNS consists of (1) a computer; (2) a detailed, geocoded electronic base map covering road and/or highway systems; (3) a GPS for determining current location and/or for vehicle tracking; (4) a spatial (geocoded) supporting database (a GIS) that contains the locations of landmarks and other features such as commercial entities and a set of analytical tools that can use current location and a given destination to develop a route plan or to provide location-based services such as details of the location and types of restaurants; and (5) an appropriate in-vehicle interface that does not distract the driver’s attention away from road and traffic conditions for any appreciable time. The latter implies using a simplified rather than a cluttered or complex visualization (e.g., a strip road map rather than a more complex land-use map), auditory description and instructions, or a combination of visual and auditory inputs. The design of an IVNS should take account of the properties of spatial thinking including (1) the level of detail given in any visual or auditory portrayal of a relevant environmental representation; (2) the degree to which an IVNS distracts perceptual attention away from the primary task of driving safely; (3) the modality chosen to provide necessary information, usually sight or speech; (4) the nature of a visualization, particularly in terms of scale, continuous zooming capacity, use of color, feature simplification, information complexity, and time taken to interpret information; and (5) determining optimal in-vehicle location of an IVNS (e.g., on the ceiling, above the steering wheel, on the dashboard, on the console between the front seats) such that it requires minimal head-turning and optical scanning away from the road and traffic. IVNS are important for commercial vehicles such as taxis, delivery systems such as FedEx or UPS, and mail delivery. Via GPS tracking, fleet vehicle locations can be monitored (e.g., for sending the closest taxi, police car, or emergency vehicle to a specific destination or for knowing current locations of members of a local or interstate trucking fleet). IVNS are still considered to be a luxury item in all but high-end private vehicles. However their use and acceptance are growing. IVNS reduce the cognitive load for drivers by substituting information from a spatial support system for the cognitive process of navigation while simultaneously providing a spatial support system for wayfinders, explorers, and independent and skillful spatial thinkers. |
cation and division versus exponentiation, the problems of estimating rather than reporting a divide by zero as an error, and the difference between statistical significance and meaningful difference. Even for experts, there can be negative transfer in going, for example, from one word processing software system to another, with function keys having different meanings, identical patterns of keystrokes activating different operations, and identical operations being given different names.
Naive users, those who are not expert in a knowledge domain, face a dual problem: that of learning to use the support system in the context of an underdeveloped understanding of the knowledge domain. Appreciating the nature of data, understanding the characteristic ways of thinking (i.e., doing things), and sharing the sense of characteristic problems are skills that are, at best, partially and incompletely developed or, at worst, based on intuitive and often erroneous understandings of the knowledge domain.
In the case of someone engaged in the process of mathematical thinking, tools for thought provide support and challenges by (1) decreasing or increasing the cognitive demands (e.g., in terms of the performance of specific calculating tasks that might or might not be the most appropriate given the nature of the data); (2) decreasing or increasing the memory demands (in the use of short- and long-term memory capacity to recall how specific subroutines work or the meaning of conventions chosen by the system designer); (3) increasing or decreasing flexibility (by providing access to alternative sets of operations or making some apparently simple operations difficult to access or perform); (4) increasing or decreasing problem-solving skills (by offering access to model analysis sequences that could be illuminating or obscure); and (5) increasing or decreasing applicability (by enabling the person to make generalizations in the application of mathematical thinking across different problem domains that might or might not be appropriate).
Therefore, in the design of a support system, the implementation and instruction process, and the use of a support system, there are inevitably tensions that can lead to significant problems for learners and teachers. For each issue, there is no simple resolution.
-
The end-means issue: learning about the nature of a support system as an end in itself versus learning to use a support system as a means of solving problems. The more complex a system, the greater are the time and effort that must be invested in learning about the system. That investment, while necessary, does not of itself entail success in a particular domain of thinking. Tools are means, not ends, and the goal is successful problem solving. There is a significant risk of a disconnect between students learning about a support tool and students learning how to apply that tool in a variety of contexts. Support systems must be presented as working tools in the context of domain knowledge and domain problems.
The educational challenge is to ensure that there is a balance between learning about and learning to use the support system to solve problems.
-
The opacity-transparency issue: learning to perform operations that remain opaque versus having those operations become transparent through understanding what happens, how, and why. The so-called calculator wars in mathematics education exemplify this tension (Alkhateeb, 2002; Alkhateeb and Taha, 2002; NRC, 1991). In the absence of a support system, individuals must perform all of the steps in the process “by hand,” as it were; thus, they are more likely to understand the meaning of the calculations. In a computer-based support system, most of the individual steps not only are hidden from view but often are inaccessible to the user.
The educational challenge is to ensure that a student has a good grasp of the fundamentals of problem solving in a domain before learning about and then using a support system that necessarily presumes an understanding of the fundamentals.
-
The rote learning-comprehension issue: learning the right sequence of buttons to push (the concept of “buttonology” in the e-domain) or the right sequence of things to do versus understanding what to do and why to do those things in that particular way in this particular problem context. This issue is an extension of the opacity-transparency issue. Learning to use a tool for thought is not the same as learning to think. It is relatively easy to reinforce a facile but inflexible command of, say, sequences of key strokes or the rote learning of a series of actions that lead to correct results if and only if the problem context remains the same. Problem solving can be reduced to
-
stereotypical and reflexive patterns of “this is how you do it.” There is no transfer to other domains of knowledge.
The educational challenge is to ensure that a student understands why particular ways of doing things are appropriate for particular problem contexts. Problem solving must be reflective.
-
The power-limitations issue: learning and understanding what the system is versus is not capable of doing or what the system can versus should be used to do. Of necessity, any system privileges some ways of doing things at the expense of others. To the extent that the system design reflects best practices in a particular knowledge domain, especially as reflected in the thinking processes of domain experts, then the support system can be very powerful.
However, in the hands of an unwary user, support systems can do things that may be misleading, counterproductive, and wrong (Figure 6.5). Thus, cartographic mapping packages can generate a remarkable range of maps, based on different projections. Selection of the wrong projection can lead a user to make comparisons between data values plotted on a map that does not preserve area, thus resulting in inappropriate inferences (as exemplified by the so-called Greenland versus South America effect seen on an inappropriately used modified Mercator projection). Support systems have defaults, pre-set ways of operating that are taken as standard in a domain, but whose implications and use must be understood before they are applied automatically.
This general problem is compounded in the K–12 context because as the concepts of developmental and educational appropriateness make clear, data management, data analysis, and display functions must be matched to the student’s cognitive capacities. Expert practices may not match the capacities and needs of beginning or even intermediate students.
The educational challenge is to build and deploy support systems that are educationally and developmentally appropriate. The committee believes: (1) that a successful support system should be a means to an end, that of problem solving, helping to frame problems and providing ways of responding to them; (2) that components of the system should be transparent wherever possible; and (3) that the system should be comprehensible to the full range of students. The ultimate goal in learning to use a support system is understanding and flexibility in problem solving, not necessarily enhancing speed and efficiency by minimizing error and increasing accuracy, desirable though those characteristics might be.
Therefore, a support system should be viewed not as a prosthesis that substitutes for and replaces thought but as an enabling device that facilitates and enhances the process of thinking. It should enable students to engage in thinking more consciously, more willingly, more effectively, more reflectively, and with more confidence in as wide a range of contexts as possible (i.e., integrating across the curriculum).
6.5 GENERAL CRITERIA FOR THE DESIGN OF A SUPPORT SYSTEM IN THE K–12 EDUCATIONAL CONTEXT
The design of a support system should (a) meet specific educational goals, (b) be appropriate to student needs, and (c) match the educational context. Given its analyses in Chapters 2 through 5, the committee has identified 10 general criteria for the design of a support system in K–12 education.
Meeting Educational Goals
-
Be supportive of the inquiry process in at least five basic ways:
-
providing prompts, feedback, and helpful hints to guide the flow of work and to encourage critical reflection;
-
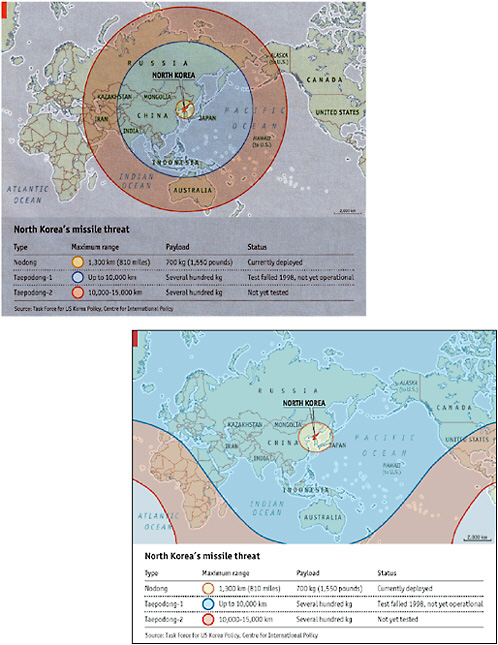
FIGURE 6.5 The dangers of an inappropriate map projection: (a) In this map, published in the Economist on May 3, 2003, concentric circles are erroneously superimposed on a Mercator map. As a result, the map incorrectly identifies regions that could be reached by missiles of various ranges launched from North Korea. (b) In the corrected map, published in the Economist on May 17, 2003, all of the United States and Canada are within range of the Taepodong-1 or Taepodong-2 missile. Reproduced with permission from Task Force on U.S. Korea Policy, Center for International Policy.
-
-
keeping track of the flow of work;
-
modeling ways of performing operations and analyses;
-
finding an exact or correct answer to a problem or presenting a range of alternate problem-solving scenarios (as in a decision support system for community planning); and
-
providing ways of representing data and results to oneself and to others.
-
-
Be useful in solving problems in a wide range of real-world contexts
-
Facilitate learning transfer across a range of school subjects
-
Provide a rich, generative, inviting, and challenging problem-solving environment for the users of the support system
Being Appropriate to Student Needs
-
Be developmentally and educationally appropriate, tailored for use by novice learners, not expert users, and graded to support increasing levels of skill and experience
-
Be accessible to and supportive of the full range of learners (i.e., including those who are differently abled)
-
Be customizable to meet the needs of specific groups of learners working on particular tasks in specific contexts
Matching the Educational Context
-
Be flexible enough to be effective in a variety of school contexts (e.g., infused versus subject-based curricula; elementary versus high school) and to enable a range of modes of use (e.g., individual and stand-alone; collaborative and networked, locally and globally)
-
Be quick and intuitive for students and teachers to learn to use
-
Be robust and realistic in terms of the expectations placed on teachers and the demands on school infrastructure (in terms of hardware and software)
These 10 criteria are desiderata rather than immediately attainable goals. No support system can be expected to meet all of the criteria simultaneously and to the maximum extent. Indeed, systems can be successful without necessarily fulfilling all 10 criteria. In some contexts, criteria may pose contradictory demands. Thus, something that satisfies criterion 6 (ease of learning) may indeed meet criterion 8 (utility across a range of contexts) but do so only because it meets criterion 1 (support inquiry) and criterion 4 (a rich environment) in relatively superficial and shallow ways. Nevertheless, these 10 criteria provide working guidelines for the design and implementation of a support system.
6.6 THE NEED FOR SUPPORT SYSTEMS FOR SPATIAL THINKING (SSST)
The committee advocates the design, development, testing, and implementation of systems—low tech and high tech—for the support of spatial thinking. These systems can facilitate the inquiry approach (hypothesis generating and testing) to problem solving in real-world contexts. They can be fine-tuned to accommodate the needs of different disciplinary traditions and problem-solving contexts, and they can be structured to reflect individual performance differences as a function of age and ability (the concepts of developmental and educational appropriateness).
Support systems for spatial thinking are necessary for two reasons:
-
Spatial thinking is a complex and challenging process. Support systems can help to manage this complexity by
-
storing and handling multiple and often large data sets;
-
routinizing repetitious and laborious elemental parts of the process (akin to the development of macros in word processing programs);
-
keeping track of the results of chained sequences of operations;
-
providing in-process feedback and assistance; and
-
providing a means for the display and communication of results, working and final, for oneself and for others.
-
Spatial thinking is a powerful process. Support systems can help to ensure the appropriate use of this power by
-
making its roles clear;
-
making its practice accessible to a wide range of users;
-
making its instruction and application successful in a wide range of contexts;
-
drawing on the experiences of as broad a range of disciplines as possible and on the expertise of members of those disciplines (the idea of best practices);
-
providing multiple, alternative formats for representing data and results;
-
providing access to key activities (in terms of transformations, operations, and analyses); and
-
recognizing the roles of incompleteness and error in data, uncertainty in analysis, and therefore ambiguity in results.
Given the different forms that spatial thinking can take and the diverse range of contexts within which it can be applied, there is no single system that can be a universal support for spatial thinking. Chapters 8 and 9 analyze one exemplar system, GIS, in terms of its design and implementation in the K–12 context, and Chapter 10 presents recommendations for improving its design and implementation.
However, it is the committee’s belief that a mix of support systems must be brought to bear on the teaching of spatial thinking. Although GIS is evaluated in detail as one such system, the committee recognizes that the fundamental challenge is first and foremost to appreciate the practical power and educational importance of spatial thinking. The problem that we face in American schools today is not one of inadequate tools as such but the need to appreciate and understand the process of spatial thinking. We can only teach people to do what we recognize, understand, and value.
6.7 THE REQUIREMENTS OF A SUPPORT SYSTEM FOR SPATIAL THINKING
Spatial thinking is built on a constructive amalgam of an understanding of space, representation, and reasoning (see Chapters 1 and 2). These three elements shape the specific characteristics of a support system for spatial thinking that must have the capacity to do the following:
1. Spatialize data sets by providing spatial data structures and coding systems (see Chapter 2) for spatial and nonspatial data.
Data sets that are spatial in form (e.g., containing positional data expressed in terms of latitude and longitude coordinates) must be registered and projected into a geographic space (e.g., on a map projection using the State Plane Coordinate System [SPCS]). With numerous ways of expressing spatial data, a support system must be able to integrate heterogeneous data sets by registering and projecting them onto a common framework for analysis and display.
Data sets that are not necessarily spatial in their original form can be spatialized by adding geoor spatial coordinates. Temporal and attribute data can be spatialized. For a single data set, identities of objects can become locations in one or more spaces; pairwise relationships between objects located in that space (based on the degrees of similarity, difference, and connection, where those relationships can reflect function, genesis, history, appearance, properties, etc.) can become distances; sets of multiple relationships between the locations of objects can become patterns (permitting the identification of spatial structures, deviations, and exceptions); and patterns can be explained in terms of the processes that generated them. Multiple spatialized data sets can be overlain and combined in different spaces. All spaces can be restructured along different axes with different distance metrics and different dimensionalities.
The capacity to spatialize is what motivates the process of spatial thinking.
2. Visualize working and final results by creating representations that capture the structure of spaces and the locations, relationships, and patterns of objects depicted in them.
There are numerous general classes of representations—maps, graphs, diagrams, charts, cross sections, drawings, photographs, animations, models, remotely sensed images, etc.—that can be adapted to meet the needs characteristic of a particular knowledge domain (see Chapter 3).
Similarly, there are numerous forms for representations. Representations can be static or dynamic (either cross-sectional or continuous); they can be still images or animations; they can be visual-graphic or expressed in a variety of sensory modes (e.g., three-dimensional tabletop models, globes, plastic maps with raised relief, braille maps); they can be in black and white or in color; they can be presented via a range of media (e.g., video, sound, vibrotactile) that can be converted to other media forms (e.g., voice-recognition and text-to-speech software).
The capacity to represent is integral to the process of spatial thinking.
3. Perform functions that manipulate the structural relations of spatialized data sets. These functions include the following:
Transformations
-
Symbolizing (use of graphic markers [point, lines, and areas] and sensory media-appropriate variables [e.g., in the visual graphic case: size, shape, orientation, hue, value, chroma] to capture the identity of objects; similar variables can be created for sensory media such as touch [force feedback, tactile, and vibrotactile mapping symbols] and sound)
-
Scale change (zooming in [magnification] and zooming out [minification] in either a continuous or a discrete stepwise manner)
-
Replotting into different frames of reference (from projections using one coordinate system to another [e.g., abstract as in azimuthal versus Cartesian or specific as in cartographic mapping systems such as latitude and longitude, the universal transverse Mercator zones, the SPCS])
-
Reprojecting (within families of map projections that preserve properties such as area, shape, direction, and distance [e.g., the Molleweide equal area, which is used for world statistical maps where the areas of particular interest are in the midlatitudes])
-
Rescaling (converting from one distance metric to another [e.g., Euclidean versus Manhattan])
-
Perspective change (adopting different viewing azimuths [from 0° to 360° around an arbitrary reference] and viewing angles [from 0° to 90°, eye-level to orthogonal])
-
Spatial transformations (movements of objects in terms of translations and rotations in the plane, etc.)
-
Dimensional change (e.g., converting three-dimensional to two-dimensional depictions)
Operations
-
Set theoretic relations between data sets (union, intersection, etc.) leading to aggregation and disaggregation
-
Interpolation and extrapolation
-
Abstraction (e.g., converting numerical point data to a surface with contour lines)
-
Generalization (e.g., classification, smoothing, simplification, exaggeration [as in different scales for horizontal versus vertical distances on a map])
Analyses
-
Descriptions of the properties of spatial distributions in terms of density, dispersion, centroids, regions, outliers
-
Pattern analysis (e.g., differentiating random patterns from systematic patterns; classifying systematic patterns in terms of regularity [as in grids or other tessellations] or clustering; identifying deviations; identifying relations between patterns [positive and negative correlations])
-
Structural analysis (e.g., for patterns, calculation of nearest neighbors, or spatial autocorrelation; for networks, calculations of centrality, connectivity, and various paths [shortest, the traveling salesman route, etc.]; for hierarchies, calculation of tree structures)
-
Process modeling (e.g., developing explanations of spatial patterns as a function of time and/or distance [Boxes 1.1 and 1.2])
The capacity to manipulate structural relationships is the essence of spatial thinking.
6.8 SUPPORT SYSTEMS FOR SPATIAL THINKING IN THE K–12 CONTEXT
With the increasing availability of powerful IT systems, it is tempting to see the development of support systems for spatial thinking as necessarily being computer based and, therefore, high tech in nature. This is not the case.
Spatial thinking can also be supported with low-tech systems, essentially involving paper-and-pencil systems allied to the use of simple graphic representations (as in the case of Jerome Bruner’s work using simple outline maps, cited in Chapter 1). Such low-tech systems are important for the following reasons:
-
Despite the increasing penetration of IT into American schools, access to hardware and software remains limited. To build supports for spatial thinking only around IT would be a mistake; it would restrict the opportunities for both teachers and students to learn about and use spatial thinking across the curriculum.
-
Understanding many of the fundamental building blocks of spatial thinking can be more readily achieved through simple, low-tech systems (see Box 6.3). These place fewer demands on teachers, students, and schools. They are easily adapted for use across the curriculum. They have immediacy and face validity that permit students to understand the basic components of spatial thinking. Specific skills can be isolated and practiced. For example, students can use simple transparencies to overlay maps and to understand correlations between patterns of data. They can use graph paper to learn about rescaling and transformations of data.
|
BOX 6.3 As an example of a very effective and imaginative low-tech system for supporting spatial thinking, a class of 9-year-olds was presented with a box. The contents were unknown to them: their challenge was to find out what was inside the box through an ingenious adaptation of spatial sampling. The top of the box was perforated with 100 holes, arranged in a 10 × 10 grid. The two axes were labeled from 1 to 10 and from A to J, thus ensuring that each hole could be given a unique spatial identifier. Next to the box was a sheet of paper, also laid out with an identical 10 × 10 grid with the same axis identifiers. The children were given knitting needles and first had to calibrate them to provide “depth” readings below the surface of the box when the needle was inserted into a hole and it touched whatever object was in the box. They created summary tables of their data (in effect, x-y-z coordinates) and then transferred the coordinate data onto the paper using Lego blocks for the Z coordinate. When they finished creating a Lego shape and surface, they were allowed to open the box. Inside was a three-dimensional model of a mountain range which they had, much to their excitement, recreated through a classic example of spatial thinking. |
6.9 THE IMPLEMENTATION OF A SUPPORT SYSTEM FOR SPATIAL THINKING IN THE K–12 EDUCATIONAL CONTEXT
In the K–12 educational context, the implementation of a support system for spatial thinking entails an awareness of a series of five interlocking components, all of which must be addressed for the system to be implemented successfully. There should be programs to provide
-
material support in the form of computer hardware, software, high-speed network access, tools, and supplies (e.g., disks, paper, pencils);
-
logistical support in the form of technical support for the installation, maintenance, and upgrading of hardware and software;
-
instructional support in the form of pre-service and in-service training programs for teachers;
-
curriculum support in the form of educational goals, knowledge and performance standards, assessment procedures, unit and lesson plans, and supporting materials; and
-
community support in the form of the recognition of the educational value of the support system and, therefore, the collaboration by stakeholders in providing students with opportunities for problem solving in real-world contexts (e.g., requests for assistance, internships, access to data).
Designed and implemented appropriately, systems for supporting spatial thinking can have three major effects in the K–12 education context. First, they can change how things are taught, which is important in itself, but more importantly, they can change what can be taught. Second, they can offer students a critical awareness of a crucial thought process that is either unknown or poorly understood because it is largely hidden from view and insufficiently appreciated at present. Third, they can be mind-enhancing: students can learn to use a powerful way of thinking, one that can have lifelong implications for problem solving in life and career contexts. If we are successful in the design and implementation of support systems, we can help to foster a generation of students who will become spatially literate (see Chapter 11).
A support system facilitates the process of spatial thinking: it empowers students. However, we have to distinguish clearly between two goals: (1) that of learning to think spatially and (2) that of learning to use a support system for spatial thinking per se.
In Part 1 of this report, the committee has presented the case for teaching spatial thinking to all students. It is important to understand what spatial thinking is and how it works. It is equally important to understand how expertise in spatial thinking develops in general and differently among different people. Both sets of understandings are necessary precursors for developing systematic educational programs to teach American students how to think spatially. In Part II of this report, the committee shows how support systems, particularly those that are technologically based, can facilitate the teaching and practice of spatial thinking. Chapter 7 reviews a series of high-tech support systems for spatial thinking, providing a context for the detailed analysis of GIS. Chapter 8 presents a critical analysis of the design, implementation, and use of GIS. The current use and potential development of GIS are evaluated in terms of the ten general criteria for the design of a support system and in terms of the three specific characteristics of a support system for spatial thinking. Chapter 9 summarizes the findings of the analysis of GIS. In Chapter 10, the committee presents recommendations directed at the goal of fostering spatial thinking in general and at the specific goal of enhancing the design and implementation of one support system, GIS.


















