2
The Nature of Spatial Thinking
2.1 INTRODUCTION
In Chapter 1, the committee defines spatial thinking as a constructive amalgam of three elements: concepts of space, tools of representation, and processes of reasoning. Space provides the conceptual and analytical framework within which data can be integrated, related, and structured into a whole. Representations—either internal and cognitive or external and graphic, linguistic, physical, and so forth—provide the forms within which structured information can be stored, analyzed, comprehended, and communicated to others. Reasoning processes provide the means of manipulating, interpreting, and explaining the structured information.
In this chapter, the committee describes and explains spatial thinking in more detail. It begins in Section 2.2 by looking at the current understanding of spatial thinking, distinguishing it from narrower concepts such as spatial ability, and viewing it as a means of problem solving. Section 2.3 explores the use of space as a framework for understanding, identifying the three contexts in which spatial thinking operates and pointing to the key role of spatialization. Section 2.4 turns to the three functions of spatial thinking: description, analysis, and inference. The basis for spatial thinking is the structure of space and the operations that can be performed on and in that structure. Section 2.5 builds a four-part structure of space based on primitives, languages of space, spatial concepts, and operations. The chapter ends in Section 2.6 with a psychological analysis of the cognitive processes underlying spatial thinking.
2.2 APPROACHES TO SPATIAL THINKING
2.2.1 Forms of Thinking About Space
In terms of its power and pervasiveness, spatial thinking is on a par with, although perhaps not yet as well recognized and certainly not as well formalized as, mathematical or verbal thinking. It can be contrasted with verbal thinking. Language allows us to express the output of direct sensory perceptions of the world; it allows us to develop metaphors; and it can support abstractions such as
meanings that are counterfactual or hypothetical, or do not rely on direct sense perceptions. Another quality of verbal thinking is that it can be and most often is public and external. After millennia of talking and writing, there are well-established, formal conventions of meaning and pragmatics that ensure considerable consensus across people within a language community. We have a good understanding of what it means to be articulate and literate in the verbal domain. We can assess performance in spoken and written forms, and we focus on the teaching and learning of verbal thinking.
By contrast, there is as yet no clear consensus about spatial thinking and, therefore, spatial literacy. Thus, there are many related concepts in use: we speak about spatial ability, spatial reasoning, spatial cognition, spatial concepts, spatial intelligence, environmental cognition, cognitive mapping, and mental maps (see for example, Eliot, 1987; Gardner, 1983; Golledge and Stimson, 1997; Gould and White, 1974; Kitchin, 1994; Kitchin and Freundschuh, 2000; Newcombe and Huttenlocher, 2000; Portugali, 1996; Tversky, 2000a,b).
Perhaps the most familiar of these terms is spatial ability. Spatial ability is conceptualized as a trait that a person has and as a way of characterizing a person’s ability to perform mentally such operations as rotation, perspective change, and so forth. The concept derives in part from the psychometric tradition of intelligence measurement and testing with, for example, the French (French et al., 1963) reference test kit identifying types of spatial ability such as spatial orientation and visualization. By classifying the cognitive processes used to solve tasks thought to measure spatial ability, Linn and Petersen (1986) identified three categories of spatial ability: spatial perception, mental rotation, and spatial visualization. For example, spatial visualization is measured by tests such as the paper folding test (in which respondents are presented with drawings of folded pieces of paper that have hole(s) punched in them and are asked to select which drawing indicates how the paper would look when unfolded), and the embedded figures test (in which respondents are asked to find a simple shape within a complex one) (see Figure 2.1). Spatial ability has been studied in terms of group and individual performance differences (see Eliot, 1987; Golledge et al., 1983; Linn and Petersen, 1985).
Spatial ability is clearly related to but much more restricted in its scope than spatial thinking, as are all of the competing concepts. It is the links among space, representation, and reasoning that give the process of spatial thinking its power, versatility, and applicability. Spatial thinking is multifaceted in its operation: just as there is no single recipe for how to think verbally or mathematically, there is no single way to think spatially. Instead, the process of spatial thinking comprises broad sets of interconnected competencies that can be taught and learned.
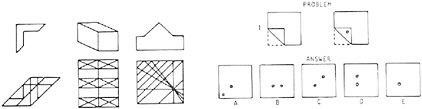
FIGURE 2.1 Spatial visualization items. Left, embedded figures: respondents are asked to find the simple shape shown on the top in the complex shape shown on the bottom. Right, paper folding: respondents are asked to indicate how the paper would look when folded. SOURCE: Linn and Petersen, 1985. Reprinted with permission of the Society for Research in Child Development.
At one level, we can learn to read the pressure and temperature axes of a phase diagram in physics, to understand the relations between elements in the atomic chart in chemistry, to recognize the particular shapes and locations that are indicative of tumors in an MRI, to understand the spatial properties that are preserved by a modified Mercator projection in cartography, and to visualize the three-dimensional spatial relations between different air masses and the associated types of fronts in meteorology. In each case, we can identify a particular set of spatial concepts that must be known and understood and the interpretive skills, parts of spatial ways of thinking and acting, that must be mastered. Taken together, the set of concepts and skills forms a cognitive spatial tool kit that is tuned to the practice of a particular discipline (for example, see Chapter 3.6.1). The tool kit mixes domain-specific spatial knowledge (concepts, models, and theories) with the use of generic representational forms and spatial structures (e.g., Cartesian coordinate systems, linear and nonlinear relations, scale transformations, rotations and perspective change). To the extent that there are tools and technologies to be learned (e.g., how to take an MRI reading or to create a map projection using a computer algorithm), we learn the spatial capabilities that make us proficient in a domain of knowledge.
At another level, as we become spatially literate, we develop a general spatial attitude. This entails a willingness and ability to frame problems in spatial terms, to use the language of space to express the elements of a problem, to think about relations between objects in terms of distances or directions or patterns, to imagine alternative graphical representations, to change viewing perspective or viewing angle, to zoom in or out, to hypothesize and visualize the effects of different rates of change, to predict what might happen to spatial patterns or structures or relations if … By linking spatial knowledge, spatial ways of thinking and acting, and spatial capabilities with this general spatial attitude, we have a flexible and powerful way of thinking that is transferable to and applicable in a wide range of contexts in everyday life, the workplace, and science.
2.2.2 Spatial Thinking as Problem Solving
Our concept of spatial thinking is broader than spatial ability and related concepts in that it approaches the process of problem solving via the coordinated use of space, representation, and reasoning. Scientists in general and educators in particular have not paid sufficient attention to identifying and articulating the nature, characteristics, and operation of what is arguably a defining characteristic of the scientific approach.
Spatial thinking uses representations to help us remember, understand, reason, and communicate about the properties of and relations between objects represented in space, whether or not those objects themselves are inherently spatial. Objects can be concrete things (as in a cognitive map of roads and neighborhoods in a city) or abstract concepts (as in a two-dimensional graphic plot from a multidimensional scaling model of the love-hate relationships between characters in a Shakespeare play). In the first case, there is an objective geographic space within which the objects exist and from which, on the basis of experience, we can calculate distances and directions. The subjective cognitive map is a mental representation that may transform and systematically distort objective distances and directions between places. In the second case, the number and types of words exchanged between characters are converted into similarity measures and then distances between characters. The graphic plot locates characters in a space in which one dimension is hate and the other love. Location in space can be used to understand the relationships between characters.
Representations can be internal, a mental image of the workings of a pulley system, or external, a printed cross section of a geological structure or an immersive virtual reality display of the interior of a new building. The forms of representation can range from a schematic diagram of a pulley system to a photograph or movie of actual pulleys, lines, and weights. The cross-sectional diagram can be two dimensional, showing depth and extent, or a pseudo-perspectival diagram
showing depth and two horizontal dimensions. It could be a geological cross section in which time replaces depth as the vertical axis. Instead of an immersive space, the representation of the building could be a plan and elevation, an architect’s three-dimensional physical model, or an ordered series of architectural renderings, viewing the interior from different places in the building with a near-photographic appearance. Representations can capture what is (e.g., a map of a city), what might be (e.g., a sketch of an addition to a house on a lunchroom napkin), and what should be (e.g., a score for a piece of music or dance).
Reasoning processes can ask: What happens if we add weight to one part of the pulley system, if we remove weight from another part, or if the string breaks in a particular place? We can ask which parts move, how far, and what the equilibrium position is. In the other cases, we can ask how the thickness of the rock layers varies with depth, or what the “sense” of space is that we “feel” as we move through the lobby of the building. The questions can capture either the results of change or the process of change. They can deal with possible or hypothetical (“what would it look like if”) situations (e.g., a fly’s-eye view of the atrium of the building or David Macaulay’s images of parts of the urban infrastructure “floating” in three-dimensional space without the surrounding and supporting physical ground) (Figure 2.2).
Spatial thinking occurs in private and in public. On the one hand, spatial thinking encompasses a range of cognitive processes that support exploration and discovery: we can visualize relations, imagine transformations from one scale to another, rotate an object to look at its other sides, create novel viewing angles or perspectives, evoke images of places and spaces, and so forth (see Hanson and Hanson, 1993). On the other hand, spatial thinking allows us to externalize these operations by creating spatial representations in a range of media, forms, and sensory modalities: tactile maps or graphs, auditory maps, vibrotactile surfaces, traditional cartographic maps, two-dimensional graphs, link or flow diagrams, tree diagrams of hierarchical relations, three-dimensional (3-D) scale models, exploded views of a structure, and so on. The representations can be created as part of a personal working dialogue. They can be shared with others, thus exposing the representational and reasoning processes of spatial thinking to public scrutiny. The representations are simultaneously ways of expressing personal understanding and rhetorical acts of communication and persuasion that can establish a public consensus.
2.3 THE USE OF SPACE AS A FRAMEWORK FOR UNDERSTANDING
2.3.1 Spaces for Interpreting Data
Crucial to the power of spatial thinking is our ability to use space as a framework for understanding. The process of interpretation begins with data:
Data consists of numbers, text, or symbols which are in some sense neutral and almost context-free. Raw geographic facts, such as the temperature at a specific time and location, are examples of data. When data are transmitted, they are treated as a stream of bits; and the internal meaning of the data is irrelevant to the transfer process.
Information is differentiated from data by implying some degree of selection, organization, and preparation for a particular purpose—information is data serving some purpose, or data that have been given some interpretation. (Longley et al., 2001, p. 6)
There are three spatial contexts within which we can make the data-to-information transition: those of life spaces, physical spaces, and intellectual spaces. In each case, space provides the essential interpretive context that gives meaning to the data.

FIGURE 2.2 Underneath a typical urban street corner. SOURCE: Illustration from Underground by David Macaulay. Copyright 1976 by David Macaulay. Used by permission of Houghton Mifflin Company. All rights reserved.
2.3.2 The Three Contexts for Spatial Thinking
The first context is that of the everyday or physical geographic world of four-dimensional space-time. Variously called spatial perception, environmental cognition, cognitive mapping, and so forth, in this context spatial thinking is a means of coming to grips with the static and dynamic spatial relations between and among self and other objects in the physical environment. The domain of concern is locations defined on the surface and near-surface of Earth, at resolutions between millimeters and hundreds of kilometers.
This is cognition in space and involves thinking about the world in which we live. It is exemplified by wayfinding and navigation, actions that we perform in space. It extends to other everyday activities: assembling a child’s toy from a set of parts using printed instructions; packing the trunk of a car to maximize carrying capacity; and building a dog kennel using tools, a pile of lumber, and a general model of what dog kennels typically look like. We might call this context the geography of our life spaces (see Chapter 3.2).
The second context is built on the four-dimensional world of space-time, but in this case the focus is on a scientific understanding of the nature, structure, and function of phenomena that range from the microscopic to the astronomical scales. It is the world of the structure of the atom, the structure of Earth, and the structure of the universe (as expressed, for example, in Figure 2.3, see also http://www.falstad.com/scale and Chapter 3.5). This is cognition about space and involves thinking about the ways in which the “world” works. We might call this the geography of our physical spaces.
The third context is in relationship to concepts and objects—the focus of our thoughts—that are not in and of themselves necessarily spatial but can be assigned locations via space-time coordinates and therefore can be spatialized. The key premise is the conversion of some data relationship between objects—for example, similarity or dissimilarity, order or sequence, time of appearance—into locations and therefore arrangements of the objects in a space. The domain of concern and therefore the nature of the space is defined by the particular problem. It could be the space of compact versus midsized cars that might be purchased, the familial relations between European languages, or the newspaper article space representing the thematic content of two issues of the New York Times (Skupin and Buttenfeld, 1996, 1997).
This is cognition with space and involves thinking with or through the medium of space in the abstract. It is exemplified by the conversion of linguistic statements into spatially ordered sequences to answer questions, and therefore the process depends on representations that we develop of concepts in space. Thus, we can take two linguistic propositions, Mary is nicer than Jane and Jane is nicer than Sally; interrelate them by converting them into an ordered left-to-right or top-to-bottom sequence image or diagram of Mary, Jane, and Sally; and then, by using visual inspection, answer the transitive question: Who is nicer, Mary or Sally? We might call this context the geography of our intellectual spaces.
A classic example of the geography of an intellectual space is a concept map. A concept map treats concepts within a domain of discourse as features to be mapped, and it defines their position and ordering in space using similarity measures. The similarity can be in terms of function, genesis, structure, or appearance. The underlying data are not inherently spatial in the geographic sense, lacking positional coordinates, but geographic space and representations provide a useful canvas—a familiar two-dimensional (2-D) space on which ideas can be represented—and a metaphor for similarity—in that near things are more alike than distant things. This approach has taken on new significance in the form of tools for visually exploring complex data sets, where software converts data into spatial forms, calculates distance metrics, displays the outcomes graphically, and supports the exploration of data sets using visualization methods. Figure 2.4 shows a concept map of the utility of data sources for constructing a map of gravitational anomalies that can be used to understand the deep geological structure of Earth.
Figure 2.5 uses another geographic metaphor, the idea of a landscape, where surface morphology, as well as planar distance, contribute to the perception of similarity between places. Familiarity with interpreting landscape structures such as mountains and valleys is leveraged to provide insight into a more complex, but hidden, high-dimensional structure. Figure 2.5 shows an information landscape produced from year 2000 Census demographics. States with a similar demographic profile appear clustered together. Height is used to show the absolute difference between two states, so that the presence of “hills” between states indicates that they are in fact quite different.

FIGURE 2.3 Units of length arrayed in a scalar progression from the micro to the macro. SOURCE: Morrison et al., 1982, p. 122.
2.3.3 Spatialization
These contexts for thinking spatially—life spaces, physical spaces, and intellectual spaces—are not independent of one another. The ability to spatialize is built on the understanding of space that comes initially from our interactions with the everyday world of four-dimensional space-time. The processes of spatial thinking (e.g., perspective change, scale change, transformation, rotation,
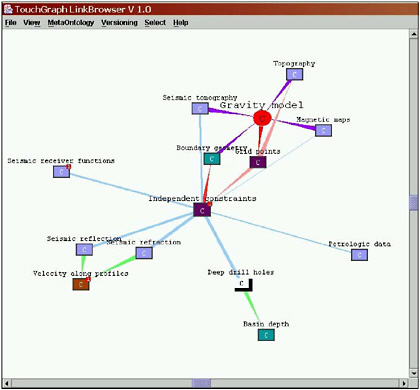
FIGURE 2.4 A concept map depicting how various information sources are used to synthesize a geophysical gravity model (represented by the red, circular node). The concepts are spatialized around this node according to their importance, so closer concepts represent the more useful data sources. SOURCE: Concept graph courtesy of Dr. Randy Keller, University of Texas, software developed by the GeoVISTA Center, Penn State. Reproduced by permission from Dr. Randy Keller.
pattern searching) are identical in the life and physical space contexts. Many forms of representation are derived from our interactions with the everyday world (e.g., images, graphs, maps). These representations support visualization whereby we convert information into a spatial form that can be perused by sight.
While the initial and intuitive roots of spatial thinking are grounded, literally, in the geographies of our life and physical spaces, a major part of its scientific and therefore educational importance lies in the process of spatialization that creates intellectual spaces. With the advent of computers and scientific instrumentation, we have gone from a problem-rich, data-poor world to one that is both data-rich and problem-rich, but is currently lacking the capacity to bring data to bear on solving problems. The solution to problems will depend on the capacity to process, analyze, and represent the vast quantities of data that we can gather and store. Some of these data are already geospatial in nature, as in the case of pixel or raster data derived from remote-sensing platforms. Much of the remainder of the data, although nonspatial in its original manifestation, can be spatialized. By embedding and representing these data in spaces, we can bring powerful spatial reasoning procedures to bear and therefore solve problems (see Box 2.1).
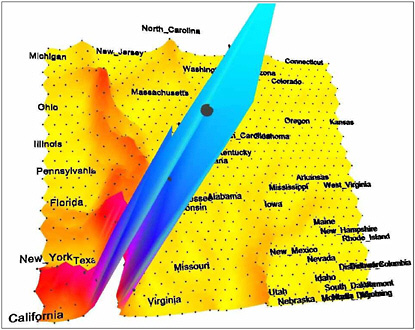
FIGURE 2.5 An information landscape depicting demographic similarities and differences between the 50 states. The high peak at the front represents California, which is very different from all other states. Image produced using a self-organizing map (neural network) and data from the 2000 Census.
2.4 THE THREE FUNCTIONS OF SPATIAL THINKING
Spatial thinking serves three purposes. It has (1) a descriptive function, capturing, preserving, and conveying the appearances of and relations among objects; (2) an analytic function, enabling an understanding of the structure of objects; and (3) an inferential function, generating answers to questions about the evolution and function of objects.
The power of spatial thinking resides in its capacity to provide an understanding of structure and of function. By an understanding of structure is meant a description of how something is organized—what part is where in relation to other parts. We can capture the arrangement of objects in space and speak about order, relation, and pattern. By function is meant an understanding of how and why something works. It can express how something changes with time (kinematics) and allow us to explain the reasons for the changing arrangements of time-varying spatial patterns (dynamics). Therefore, spatial thinking is not static. It is a dynamic process that allows us to describe, explain, and predict the structure and functions of objects and their relationships in real and imagined spatial worlds. It allows us to generate hypotheses, to make predictions, and to test their consequences.
The archetypal case of a spatial representation is a cartographic map, and we can see the three functions of spatial thinking at work in map reading and interpretation. The most commonly available map form, a road map, provides a two-dimensional picture of part of the world, depicting places and the roads that connect them. Spatial thinking is the analytical and inferential process that allows us to select a route connecting two places subject to criteria such that the route is easy to follow (e.g., contains a minimum number of decision points [intersections, turns, etc.]) and that it
|
BOX 2.1 At present, the capacity to store digital information far exceeds the capacity to retrieve desired information. There is a premium on methods for knowledge discovery in databases, using exploratory techniques and data mining. Spatialization and visualization are central to information retrieval processes. Spatialization provides structures for organizing information, and visualization displays the results of searches. Fabrikant (2000, p. 69) provides a classic statement of the power of spatial thinking: “Spatialization, which combines powerful visualization techniques with spatial metaphors, has a great potential to overcome current impediments in information access and retrieval. Spatialization is utilised to create lower-dimensional digital representations of higher-dimensional data sets, whose characteristics are often quite complex. These digital data sets may not be spatial in nature. Common spatial concepts such as distance, direction, scale, and arrangement which are part of the human’s experience in everyday life are applied to construct abstract information spaces.” She applies these ideas to the information about places stored in the Alexandria Digital Library (ADL) collection (http://www.alexandria.ucsb.edu). Fabrikant (2000, p. 69) begins with a model of the visual information-gathering process, based on what she describes as “… the visual-information-seeking mantra. The mantra includes three parts: ‘Overview first, zoom and filter, then details-on-demand.’” Figure 2.6 is an abstract model of the information-gathering process that is implemented into an experimental query interface allowing a user to visually browse through the ADL data-type catalog. 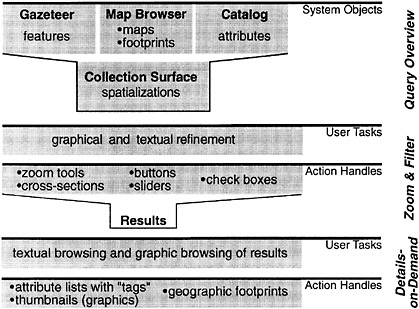 FIGURE 2.6 Visual browsing query process. SOURCE: Fabrikant and Buttenfield, 1997, p. 688. Reproduced by permission from Blackwell Publishing. |
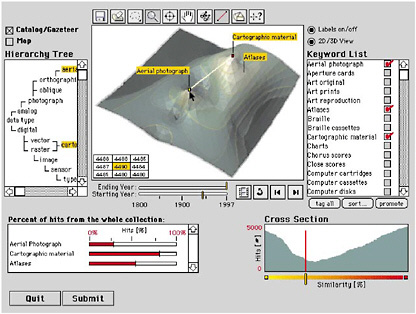 FIGURE 2.7 Spatialized query user interface. SOURCE: Modified from Fabrikant and Buttenfield, 1997, p. 689. Reproduced by permission from Blackwell Publishing. “The design of this direct manipulation interface is based on three spatial concepts, including distance (similarity), scale (level of detail), and arrangement (dispersion and concentration)” (Fabrikant, 2000, p. 72). The interface applies the visual-information-seeking mantra to a landscape of keywords from the catalog entries (Figure 2.7). The landscape is based on the similarities between lists of key words, with proximity reflecting high degrees of similarity. As Fabrikant (2000, p. 74) notes: This landscape affords a user to:
The interface contains other spatial thinking approaches: level of detail is available through a zoom function; there is a “looking glass” tool that allows detailed inspection of the surface of the landscape; and the cross-section window shows the magnitude of related documents to be found under the white line of the landscape. The physical act of browsing on library shelves has been replaced by spatial search through a document keyword landscape, a model that exemplifies both spatialization as a way of structuring information and spatial thinking as a way of developing an understanding of a nonspatial domain, library items. |
minimizes travel time (e.g., trades off travel time for distance by maximizing the distance traveled on limited-access, higher-speed highways). Spatial thinking allows us to follow the selected route, to anticipate junctions and turns, and to make a detour, working from memory or from the map itself, if traffic and road conditions necessitate it. The travel time calculation can account for levels of congestion according to time of day, day of week, and even weather conditions. Spatial thinking is also powerfully evocative. By interpreting the shaded relief symbols on the map, we can visualize the texture of the topography over which we are passing. By interpreting symbols for urban areas and forests, we can conjure up images of typical built-up or natural landscapes through which we might pass. The place names may remind us of other places that we have known and visited.
However, it is crucial to recognize that spatial thinking is not limited to graphic representations of the visual world. We access the world through multiple senses, and each sensory modality can provide a basis for spatial thinking. We can locate a crying child or an approaching car by estimating its position from the ways that sound arrives differentially at each ear. Smells can characterize places. A dressmaker can use touch to match the nap of fabric pieces by running a hand up and down the fabric. Neither spaces nor representations are necessarily sense specific. In scientific visualization, for example, spatial information can be presented visually and auditorally at the same time. Virtual reality systems can mix visual, auditory, and kinesthetic modalities in the presentation of information. For visually impaired people, tactile, kinesthetic, and auditory systems support and enable spatial thinking (see Box 2.2). Although vision dominates the process and language of spatial thinking for most people, spatial thinking is not restricted to the visual modality: it is multimodal. Whatever the sense modality of the representation, its contents can be scanned (to gain an overview), disaggregated into parts, reassembled into wholes, transformed in scale, analyzed in terms of patterns, and interpreted in terms of processes. Some operations may be easier, faster, and more precise in one particular modality as a function of channel capacity and “bandwidth.” Nevertheless, part of the power of spatial thinking lies in the access to multiple sensory modalities, with the opportunities for backup, redundancy, and parallel processing.
2.5 SPACE AS THE BASIS FOR SPATIAL THINKING
The basis for spatial thinking is the structure of space and the operations that we can perform on and in that structure. We can think about spatial structure and spatial operations from a number of perspectives, each of which is built from a root metaphor. For example, geography and cartography give us the map as a way of describing, representing, and understanding spatial relations. Mathematics gives us the analytic power of geometry and topology. Each root metaphor can be expressed in a form that is inherently spatial. For example, the concepts of maps and mappings exist in cartography and mathematics, and they can lead to a remarkable range of representational forms: cartographic maps, tree diagrams, graphs of phase spaces, cross tabulations, flow charts, networks, nonplanar graphs, etc.
To illustrate the basis for spatial thinking, we use a combination of the map, geometry, topology, and graphics metaphors. The idea of spatial structure can be understood in terms of sets of primitives and the concepts that can be derived from them. The idea of spatial operations can be understood in terms of the transformations that are possible within the space and the interpretations that can be generated from the spatial structures.
Spatial thinking can be decomposed into competencies that allow us to understand four ideas: (1) we can start with a set of primitives, (2) to which we can add some languages of space, (3) from which we can derive spatial concepts, and (4) on the basis of which we can perform operations.
1. The set of primitives is a way of capturing our encounters with a world full of objects (occurrences of phenomena): objects are the things that we are trying to understand (Golledge,
1995, 2002). For each domain of scientific knowledge, there are different sets of objects: in biology they might include genes, cells, proteins, biota, and so forth, and in sociology they might include neighborhoods, stereotypes, organizations, etc. In any domain, we can specify at least four fundamental properties of objects that allow us to reason and think about features of objects such as their (a) identity or name, (b) location in space, (c) magnitude, and (d) temporal specificity and duration. These properties allow for the identification of an object.
In the case of geographic location, for example, identification requires a coordinate system that can be globally applied and understood, as in the latitude-longitude system, or can be locally contingent, as in terms of street names and numbers. Georeferencing ensures that each object has an unambiguous location specification, and thus the entire set of objects can be located in a space (e.g., the set of georeferenced place names in an atlas gazetteer, the set of nine-digit zip codes for addresses in the United States).
2. The languages of space allow us to capture the fundamental properties of objects. One language is based on dimensionality and uses a geometric (and graphic) dimensional series: by limiting ourselves to objects in three-space for the moment, we can think about objects as instances of a point, a line, an area, or a volume. As is clear from looking at a large- and a small-scale map of an area of Earth’s surface, a point on a large-scale map can become an area on a small-scale map. (To geographers, a large-scale map encompasses a small area of Earth’s surface and vice versa. This is an instance of the tuning of spatial thinking by means of a disciplinary convention that is perhaps counter-intuitive.) The language is a flexible way of capturing the spatial properties of objects. However, we must be careful in using this language across knowledge domains: a point in geometry is a dimensionless location, whereas a point on a map is an area, perhaps very small, on the surface of Earth.
A second language is based on scale and uses scalar relations between objects to arrive at a sense of context (Montello, 1993). Context can be established by means of the terminal values that encompass the scale sequence, the lower bound of which often acts as a datum. The choice of terminal values can reflect extremes in our understanding of the phenomena studied. Thus, the stunning realization of the span of contemporary knowledge in Powers of Ten (Morrison et al., 1982) offers a visual model of the world that ranges from 1025 to 10-16, encompassing 42 powers of ten arranged around the datum of 1 meter, roughly the world at arm’s length (see Figure 2.3). Thus:
The pages offer a reference frame, a marker for exploration of experience in the domain of astronomy, or of geography, or of biology, or of chemistry. Any physical object can be sought out in its proper place along the journey, and so given an appropriate context. (Morrison et al., 1982, p. 190)
The choice of bounds reflects a convention about the phenomenal range of the particular domain of knowledge (see also Packard, 1994). We can consider other properties related to scale: the limit of resolution, the units of measurement and the calibration of a scale, the conversion between different scales, and the standard benchmarks against which objects are compared. Other languages of space deal with frames of reference and directions.
3. The third step allows us to derive a series of spatial concepts from the (spatial or temporal) location properties of sets of objects. In two-space representations, we can specify distance, angle, and direction (relative to a given frame of reference), sequence and order, connection and linkage. We can understand the structural properties of sets of objects in terms of boundaries, density, dispersion, shape, pattern, and region. In three-space, we can also consider the properties of slope or gradient, peaks, and valleys.
4. The fourth—and crucial—step captures the operations that allow us to manipulate and transform the space that we have created and to interpret the relations among objects in the set. We could, for example, translate or rotate sets of objects within the space or change the spatial scale at
|
BOX 2.2 The University of California Santa Barbara Personal Guidance System (PGS) is a support system for travelers developed from an innovative 1985 conceptualization by Loomis (Loomis, 1985). A group under Loomis, Klatzky, and Golledge, graduate students, and technicians have cooperated in undertaking basic research, technical development, and laboratory and field experimentation to build a series of testbed PGSs. The goal of this research is to determine how to develop a means of spatial information processing about real-world environments without the use of vision, the spatial sense par excellence. To achieve this goal requires convincing evidence that human wayfinding in a complex real-world context can be undertaken systematically and successfully without the use of sight. This has required
To achieve these goals, Loomis conceptualized three interconnected modules (Figure 2.8). The first module—the localization and tracking component—focused on using the U.S. Navstar global positioning system (GPS) of 24 geosynchronous satellites to fix the current spatial position in real time. The GPS used satellite triangulation to determine a traveler’s starting position and to track movement by recording a location fix about every second. The GPS unit consisted of a receiver with liquid crystal display (LCD) to display latitude-longitude coordinates (and height above sea level if needed); the locating signals were received via an antenna, and the system was battery operated and portable. Because latitude and longitude coordinates are not well understood by most people, the coordinate information is converted to a local coordinate system. The second module consists of a laptop computer with GIS software that includes a digitized spatial database, a routine for locating the GPS coordinate on the local base map, and a set of 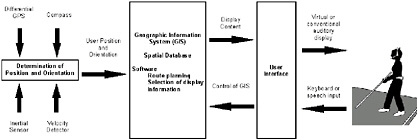 FIGURE 2.8 Three modules of the Personal Guidance System. SOURCE: Loomis, 1985. |
 FIGURE 2.9 Representations can be brought into direct contact with the real world using wearable computers. functionalities that perform spatial manipulations on digitized data sets. In particular, the GIS (1) calculated shortest paths through the local network between the traveler’s current location and a given destination, (2) identified local environmental features that fell within a given radius of the traveler (called buffering), (3) defined a corridor of specific width along the chosen path to allow for local veering without departing too far from the line of travel, and (4) defined waypoints, places en route where a spatial choice must be made (e.g., turn left, turn right, go straight ahead). The third module is a unique creation by Loomis—an interface consisting of a virtual auditory display. As the traveler moves from choice point to choice point along a route, the GPS and GIS combine to provide simultaneous tracking of the traveler’s position along the path in the spatial database (digitized maps). A buffer centered on the traveler moves simultaneously. Any database feature (e.g., buildings, bus stops, roads) that falls within the range of the buffer identifies itself (by speech) to the traveler. Although the identification is heard through stereophonic headphones, the Loomis virtual system makes it seem as if the spoken label emanates from the real-world location of the object (i.e., sound appears to be projected from outside the traveler’s head, emanating from a specific location so that the traveler can accurately point to the direction and estimate the distance to a real-world feature). This allows blind travelers to develop a “mental map” of the area through which they are traveling, thus providing them with a system that gives information about their local setting similar to what would be obtained by visual processing. With repeated experience of a route and with changes in the buffer size, the traveler can build up an increasingly detailed mental map of the environment (Figure 2.9). Ongoing research is exploring the basis for wayfinding instruction. Choices range from spatial language instructions (e.g., go left, go right, go straight ahead), orienting and directional styles (e.g., using clock face directions such as “2 o’clock, 150 yards”), angular advice (e.g., “veer 50 degrees”), or geographic advice (e.g., “turn northeast”). The question is which type of instruction is clearest and most easily interpreted by the traveler. |
which we are operating (by zooming in or out) or change the distance metric (e.g., using a Manhattan or city-block metric versus a Euclidean or as-the-crow-flies metric) or change the dimensionality of the space (collapsing from three to two dimensions).
Through processes of simplification, generalization, and classification, we can identify patterns in distributions of objects (see Chapter 3.8). We could describe patterns as random versus systematic, recognizing that these descriptions suggest something about the processes that may have given rise to the patterns, thus linking space and time. Systematic patterns can be clustered or uniform; uniform patterns in two-space can be built on either a rectangular or a triangular lattice. Shapes and patterns can display symmetry or be asymmetrical. We can look for outliers to patterns, breaks or discontinuities, and distortions in portions of the pattern.
We could identify higher-order structures in the spatial structure such as systems, networks, or hierarchies based on concepts of sequence, linkage, dominance, and subordination. We can overlay sets of objects in the same space, looking for associations and correlations, or disaggregate complex spatial patterns into separate layers. We look for correlations (positive or negative) between layers. We can identify—and try to interpret—outliers or exceptions that do not conform to a pattern. We can interpolate between or extrapolate from objects. We can bring to bear interpretive axioms: for example, nearby objects are likely to be similar, but closer objects are likely to be more similar. From this we can consider nearest neighbors, distance decay effects, spatial autocorrelation, and so forth. (All of these operations can be performed on a GIS working with geospatial data; see Chapters 7 and 8.)
At this point, the basis for the power of spatial thinking is clear: it lies in the range of operations that we can bring to bear on the description and explanation of spatial structures and the range of representations that we can use to capture those spatial structures. We can appreciate that power in another way, as well. This discussion of three sets of ideas—the language of space, spatial concepts, and operations—is based on only one member of the set of four primitives—spatial location. Each of the other three primitives—identity, magnitude, and temporal specificity and duration—can be approached spatially. Thus, identity gives rise to taxonomies and a range of spatial representations can be used to express the structure of classifications (trees, Venn diagrams, etc.). We can capture branching relations and ordination (super- and subordinates) and think about families, hierarchies, etc. The property of time gives rise to ideas such as growth, change, and development, all of which can be spatialized and represented. Magnitude can be considered an ordered series and therefore easily spatialized.
2.6 THE PROCESS OF SPATIAL THINKING
Spatial thinking is not unitary in character and operation (as demonstrated in Section 2.2.2). It can appear in many flavors and varieties—some appropriate for one task, some for another. For example, mental rotation is involved in describing the world as it appears from another’s point of view, while distinguishing figure from ground is involved in finding a face in a crowd. Individuals may excel at some aspects of spatial thinking and not at others. Facility in using the components increases with experience, most obviously expressed in expertise in a knowledge domain, such as finding tumors in X-rays, inferring the presence of oil-bearing strata in a geological cross section, or imagining three-dimensional shapes from two-dimensional architectural drawings (see Chapter 3).
What follows is a framework for organizing the components of spatial thinking (Tversky, 2005). Any complex spatial reasoning task, such as comprehending a weather map or planning a route, will use several components in concert. To characterize the nature and varieties of spatial thinking, we have to make a distinction about thinking in general.
In analyzing any kind of thought, it is useful to distinguish representations from transformations—that is, data from manipulations performed on data or information from operations applied to the information. The distinction is not hard and fast; it is easy to argue that representations and transformations can be decomposed into finer levels of representations and transformations (Rumelhart, 1980). Spatial thinking rests on the interplay between mental representations that capture spatial features of the world and the transformations that can be applied to those representations. The transformations are similar to the perceptual transformations that are applied to the visuospatial world (Podgorny and Shepard, 1978). However, this statement, too, must be qualified because people can use spatialization to think about abstract concepts that are metaphorically spatial, a powerful feature of spatial thinking. Such uses are reflected in language; we say that someone is on top of the world or has fallen into a depression or become closer.
The committee proposes an organized catalog of elements of spatial thinking, beginning simply with the properties of representations, first static and then dynamic. It continues by describing the properties of transformations that can be performed on either external stimuli or mental representations. Then the committee turns to issues such as the process of complex spatial reasoning, the role of distortions in spatial thinking, using spatial thinking in abstract domains, and spatial thinking using external diagrammatic representations as opposed to internal mental representations. Finally, links between levels of expertise and the process of spatial thinking are discussed.
Representations: The Properties of Entities Representations, whether in the mind or external, map elements and their relations in the world to elements and their relations in the represented world. Thus, representations consist of elements and the spatial or conceptual relations among the elements with respect to a reference frame. An important component of spatial thinking, then, is encoding of the attributes of the spatial world. What follows is a partial list of the kinds of attributes that can be encoded and the processes that encode them. Saying that these attributes can be encoded does not say that they are encoded faithfully; indeed, there are systematic distortions in at least some of the encoding operations, distortions that appear to function to ease information-processing demands. For example, the location of an entity is encoded with respect to the locations of other entities or to a reference frame, and normalized to the reference frame so that entities are remembered as more aligned with the reference frame. Which attributes of entities are encoded will depend on the task and on the experience of the perceiver. Recognizing patterns, for example, may entail evaluating the shapes and sizes of the parts of the pattern.
Spatial thinking can be said to begin with distinguishing and encoding spatial features of the world (Hochberg, 1978). First, figures must be distinguished; then their features and their relations to each other and to their context can be encoded into mental representations. A partial list of encoding operations that establish mental representations follows; it is suggestive of the sorts of perceptual features that people encode, and it is ordered in terms of the importance of the process in terms of spatial thinking. Encoding processes are not atomistic in themselves; they result from prior information processing and, in turn, serve as components for more complex spatial judgments and inferences. Encoding processes include
-
distinguishing figures from ground;
-
recognizing patterns, both outline shapes and internal configurations;
-
evaluating size;
-
discerning texture;
-
recognizing color; and
-
determining other attributes.
For example, the process of distinguishing figures from ground occurs early in information processing, so early that we are rarely aware of it. However, on dark, foggy nights, it is sometimes
difficult to discern what is a figure—an object, vehicle, or building—and what is shadow or fog. Novices have that experience when looking at X-rays: what is bone, what is tissue, what is tumor?
Pattern recognition is of special significance in everyday life and in specialized knowledge domains. In everyday life, it underlies recognition of faces and places. For recognizing that something is a face, the outside contour is important; for recognizing that a face is that of a particular individual, the inside configuration is critical (Farah et al., 1998). In specialized knowledge domains, pattern recognition underlies recognition of a multitude of spatial categories from flight paths on radar screens and interactions in graphs to fault lines in aerial photographs. For shapes, it underlies object and letter recognition in everyday life, as well as recognition of rare subspecies in biology, protein molecules in chemistry, rock types in geology, and symbols in mathematics. Learning to correctly distinguish one pattern from another can take considerable experience and often depends on first discerning figure from ground. Expertise in many domains requires recognition of specific patterns, but the principles are the same as those for recognizing the objects and patterns in the world around us. For everyday and expert situations, recognizing patterns entails discerning relevant features and their appropriate spatial relations.
In everyday life, evaluating size is essential for navigation, packing, and rearranging furniture. In scientific thinking, size evaluation is used in thinking about structures in geology, biology, and many aspects of engineering. Size evaluations are subject to many perceptual illusions, so learning to overcome them is important.
Texture is one important clue to depth and distance, so evaluating texture is important in navigating the world (Gibson, 1979). It is also a clue to object recognition: the furriness of a cat, the sleekness of an automobile, and the coarseness of freshly sawed wood. Texture is also a clue to how something should be handled and interpreted. In science, texture can distinguish one kind of rock from another (see Chapter 3.6), one kind of tissue from another, or one kind of vegetation from another in a remotely sensed image.
Color evaluation is a clue to object recognition. Small round things that are orange are more likely to be apricots than plums. Similarly, in science, color distinguishes one chemical, rock, or tissue from another.
Representations: The Relations Between Static Entities Often spatial judgments, such as size, shape, distance, or direction comparisons, are not evaluations of properties of entities but rather evaluations that depend on relating an entity to a reference frame (e.g., determining whether something is upright), or relating one entity to another (e.g., deciding whether one glass is closer than another or filled higher than another). Important spatial evaluations and comparisons that depend on relating an entity to a reference frame or comparing two entities are
-
determining orientation,
-
determining location,
-
assessing distance,
-
comparing size,
-
comparing color,
-
comparing shape,
-
comparing texture,
-
comparing location,
-
comparing direction, and
-
comparing other attributes.
Thus, in the case of determining orientation, we can ask: Is the picture on the wall upright or tilted? Evaluating orientation requires comparing the intrinsic frame of reference of an object—in this case, the picture—to the extrinsic frame of reference—in this case, the room. Determining
orientation is often critical to identifying what something is, for example, distinguishing a letter M from a W, a b from a d, or a diamond from a square. Similarly in science and engineering, ascertaining orientation is an essential spatial judgment: in chemistry, for identifying molecules and predicting their behavior; in geology, for identifying rock strata and inferring the conditions that produced them; in building design, for identifying sources of light and predicting their seasonal and daily changes.
Representations: The Relations Between Dynamic Entities The world is not static, and the mind finds ways to encode, interpret, and represent moving objects. Evaluating characteristics of a dynamic entity is also done with respect to other entities or to a frame of reference. Dynamic features that can be evaluated include the following:
-
direction of movement,
-
manner of motion,
-
speed or acceleration, and
-
intersection or collision.
Evaluating direction of movement can be critical for survival: Is an object headed toward me? Is that beast turning around? Note that encoding change in size can underlie perception of direction of movement; thus, if something is growing larger, it is likely to be coming closer. The direction in which something animate is going is a clue to the organism’s intent: Is the motion toward a restaurant or a movie theater? Evaluating direction of movement underlies scientific reasoning as well, for example, the directions of tectonic plates or weather fronts.
Evaluating manner of motion is important for understanding the world; manner of motion distinguishes one animal from another—indeed, one individual human being from another. Running, swaggering, stumbling are all clues to the state of another person. Differences in manner of motion distinguish different physical entities, the weight and shape of rocks for example. Manner of motion can diagnose an unhealthy heart or, on a more abstract level, an irregular electroencephalogram (EEG).
Each of these judgments about relations among dynamic entities plays a role in everyday interactions in the world, in walking along crowded streets and in driving on the highway; in avoiding flying objects or trying to catch them in baseball (McBeath et al., 1995) or return them in tennis. These judgments underlie scientific inferences as well, in understanding the operations of a machine, anticipating weather conditions, or predicting traffic flows and bottlenecks.
Transformations of Representations of Entities These encoding operations establish mental representations of the spatial world. A powerful feature of spatial thinking is transforming, manipulating, and operating on representations. By mentally extrapolating a path of movement, we can predict time and place of arrival. By mentally rotating an object, we can determine whether it will fit into a room, a dishwasher, or a suitcase. By mentally extending a line in a graph, we can detect a trend.
According to the dominant theory of mental imagery, the mental operations that we perform on actual and mental representations are internalizations of the physical changes that we perceive as we interact in the world (Finke and Shepard, 1986). In the world, things move in different manners and directions; they change shape, color, and texture in regular and predictable ways. For this reason, many mental transformations parallel the changes encoded in forming mental representations of changing entities. Anticipating these changes is critical to interacting with the world. Anticipating changes entails mentally enacting those changes. The extraordinary flexibility of the human mind then allows these mental spatial operations to be applied to imagined stimuli as well as to perceived ones, providing the means not only to anticipate states and processes in the world, but
also to create new states and processes in the imagination. That said, not all the changes we observe in the world are faithfully reflected in mental transformations.
Manipulations of spatial representations are the bases of inference, prediction, and creativity. We have already mentioned the cases of catching fly balls and predicting trends from graphs. Transforming spatial representations is elementary to scientific reasoning, from comprehending new situations to creating and testing new ideas. Surgeons use spatial transformations to envisage a new surgical procedure; geologists use spatial transformations to understand how earthquakes could have produced the rock formations they observe; microbiologists use spatial transformations to test whether vaccines may fit large molecules (Shepard, 1984). Some of the spatial transformations that people can apply include
-
changing perspective (reference frame),
-
changing orientation (mental rotation),
-
transforming shapes,
-
changing size,
-
moving wholes,
-
reconfiguring parts,
-
zooming in or out,
-
enacting, and
-
panning.
Changing perspective entails imagining a new point of view in an environment or taking a new point of view on an object. Whenever we shake hands, we have to mentally change reference frame, though this piece of spatial behavior has become automatized for most adults. However, we become aware of the difficulties of mentally changing reference frame when we give directions to strangers who have lost their way. In scientific spatial thinking, surgeons need to mentally change perspective to plan and perform an operation, and geologists need to mentally change perspective to go from frontal views to cross sections.
Changing perspective is closely related to changing orientation (mental rotation). People can imagine an object changing its position in an environment. For example, people can imagine rotating a picture on a wall to determine if it would look better in another orientation. Mental rotation is useful for geometricians in determining properties of triangles and squares and for chemists in determining whether molecules will fit or bind.
Several transformations are of special significance because skill in performing them correlates with performance on complex spatial reasoning tasks. Notably, mental rotation or changing orientation (Shepard and Cooper, 1982), changing perspective or reference frames (Franklin and Tversky, 1990), and reconfiguring parts or detecting embedded figures (Suwa and Tversky, 2001) seem to be involved in a large number of spatial tasks: mental rotation in catching or manipulating objects, changing perspective in navigating the world, reconfiguring parts in rearranging the spatial world, and detecting embedded figures in recognizing people in crowds. (These skills are also addressed in the discussion of individual differences in Appendix C.)
Enacting is a special case of spatial transformation that combines spatial thinking with motoric thinking (Schwartz, 1999). Just as spatial thinking is based on perceptual processing, motor thinking has action as its foundation. Action is accomplished by the interaction of the space of the body in the space of the world. Enacting underlies the mental practice techniques used by athletes, musicians, orators, and others to rehearse performances. Enactions can be coopted to understand forces as well as the mechanics and sequences of actions. For example, enaction is involved in imagining steering a boat or car or bicycle, and in understanding the forces of wind on all three, and the effects of ocean currents on the boat and gravity on the car or bicycle. There is a famous story
about Einstein, well-known for his prodigious powers of spatial thinking, that in developing the theory of relativity, he imagined himself hurtling in space at the speed of light. Enactions can underlie the ordering of spatial transformations when several transformations are applied in sequence to the same representation. Thus, when people have to apply several transformations to the same figure in order to solve geometric analogies, they first move the figure, then change its orientation, then determine its size, and finally add parts to the figure. This order corresponds exactly to the order in which people draw figures; they first decide where to begin drawing, then what direction to draw in, and then how far to draw (Novick and Tversky, 1987). Thus, the order of performing the mental transformations in this complex reasoning task corresponds to the order of executing the analogous external task, suggesting that the enactment of drawing is internalized and applied to other mental tasks.
The Process of Complex Spatial Reasoning Representations and transformations are the components that enter into complex spatial reasoning. Combining components enables complex spatial reasoning, such as solving geometric analogies or developing relativity theory. In actual practice, spatial reasoning often uses several representations, several comparisons, and multiple transformations. For example, planning a route requires determining a location, then a direction of movement to the next location, then reorientation at each successive location. Deciding which route is the most efficient entails constructing, then comparing several possible routes on several spatial attributes: distance, complexity (number of turns), and type of path, city street or highway. Determining whether two independent variables interact requires making successive magnitude estimations, first on each variable, then between variables. Imagining chemical bondings requires moving elements into an array, then rearranging them as a consequence of the bonding. For some spatial inferences, the spatial-temporal information may be suggestive but not sufficient, for example, for determining force and mass.
Role of Distortions in Spatial Thinking The processes that establish representations and execute transformations are schematic. That is, they delete some information and add or emphasize other information. The schematization is systematic and not random, driven by perceptual organizing principles and leading to predictable distortions in memory and judgment. For example, one way in which perception is organized is with respect to the frame of reference the world provides, one vertical and two horizontal axes. We localize objects in the world with respect to those axes, in an approximate fashion. Organization with respect to a reference frame carries over to the north-south-east-west canonical axes of geographic space and to the axes provided by a diagram in graphic space. One result is that when an entity’s location is coded relative to the surrounding frame of reference, it is remembered as more aligned with the reference frame than it actually is. Thus, people remember “tilted” entities, such as South America, as more “upright,” or aligned north-south, than they actually are (Tversky, 1981). Motion paths are similarly schematized and hence distorted; slightly oblique motion is coded as vertical or horizontal (Pani et al., 1996; Shiffrar and Shepard, 1991).
Role of Abstract Spatial Thinking People use spatial thinking metaphorically in everyday life as well as in science. We say that we feel “close” to one person, that another has “fallen out” of favor, that a third is “on top of the world,” and that yet another has “lost his center” (Lakoff and Johnson, 1980). The periodic table, flow diagrams in heat transfer and computer programs, and the “solar system” model of atoms are but some of the spatial representations used to summarize and organize abstract information. They have multiple effects on ways that scientists think about these concepts and teach them to their students. They enable spatial reasoning to be applied to complex causal phenomena. Because people have had a lifetime of experience in reasoning spatially (indeed, survival depends on it), they come to science with a spatial toolbox that can be applied to abstract concepts. Applying these spatial thinking tools is by no means automatic; in fact, one of the great challenges of education is facilitating transfer of tools acquired in one domain to another (see
Chapter 4.4). The key to effective transfer of skills, such as spatial ones, from one domain to another is going from concrete content to the abstractions that cut across domains. (Ways to facilitate transfer are discussed in Chapter 4.5.)
Role of External Spatial Representations in Spatial Thinking Note that many of the previous examples (e.g., the periodic table, flow diagrams, molecular models) are external spatial representations. That is, they are visible on paper or some other physical medium, though they do exist in some form in the mind as well. People have been creating external representations since before recorded history, from maps in the sand to bent trees as trail markers to notches on wood to record heads of cattle. The advantages of externalizing spatial representations are multiple (Tversky, 2001). They provide a semipermanent record that can be examined by a community, unlike mental representations that may be forgotten and are accessible only to an individual. For science and engineering, external representations have the advantage of being visible to other members of a community. They can be referred to by gesture as well as language in explaining, inferring, and discovery. They relieve the burden of limited working memory to maintain a representation, freeing it to perform transformations and operations on an external representation. Thus, one important function of external spatial representations is to augment working memory. Another is to focus attention on critical aspects of the conceptions. Like internal spatial representations, external spatial representations schematize; they omit irrelevant information and highlight the relevant. External representations may also be supplemented with diagrammatic devices that focus attention, such as arrows, guidelines, boxes, brackets, and boldface large type. Many external representations are pictorial. All other things equal, pictures are easier to remember than comparable words, so spatial representations also facilitate long-term memory for the concepts they convey.
Effective External Representations We have already mentioned the key to creating effective external representations: they must convey the essential conceptual information and eliminate the irrelevant information that can clutter and distract. This is harder than it sounds. For example, what information should be included in a tourist map? Which facilities of use to tourists—historic buildings, museums, restaurants, hotels, and so on—should be included, without cluttering the map with so much information that none of it is legible? Similar problems arise in scientific visualizations. Another issue in designing effective visualizations is deciding how to depict elements and mapping spatial relations. Ideally elements should be easy to recognize and decipher, associated in some way with what they represent. Spatial relations among elements, especially distance, should reflect conceptual relations in the abstract domain (Tversky, 2001). Animated diagrams have their appeal, yet they turn out to be no more effective than comparable still diagrams across a broad range of content areas in conveying conceptual information. This is partly because animations are typically complex and fleeting, so learners have trouble knowing what to attend to. Perhaps more important is that animations are continuous but people think about continuous processes as discrete steps. A well-designed sequence of still diagrams can convey the information essential to each step (Tversky et al., 2002).
Role of Expertise in Spatial Thinking As with all cognitive competencies, there are significant differences among people as to how, how quickly, and how well they do something. Spatial thinking is no exception. Within domains of knowledge, there are experts and novices. Differences between experts and novices can be accounted for by training and experience. Across domains of knowledge, there are disciplines within which spatial thinking is emphasized and taught and those within which it plays a hidden and relatively minor role. Across groups, there are also significant variations in how people approach spatial thinking. Across age, for example, children and adults do not think spatially in the same way. Those differences can be accounted for by maturation, education, and experience. All of these issues are addressed in Chapter 4 and Appendix C.
If, for the moment, the effects of domain are ignored, the expert-novice distinction can be used to understand some of the major differences in the ways in which people think spatially. A key goal,
especially in science, is to learn to extract functional information from spatial structures and to understand how and why something works. In learning to do this, we can order component tasks of spatial thinking in terms of relative difficulty.
The first and easiest step is extracting spatial structures. This process of pattern description involves identifying relations between the components of a spatial representation and understanding them in terms of the parts and wholes that give rise to patterns and coherent wholes. The second step, performing spatial transformations, is harder. Translations in space or scale transformations (changes in viewing distance) are easier than rotations or changes of perspective (changes in viewing angle or azimuth). Imagining the motions of different parts in relation to each other—running the object—can be very difficult. The third step, drawing functional inferences, is the most difficult and yet the most central to the process of scientific thinking. It requires establishing temporal sequences and cause-and-effect relations.
The difficulty of each of these three steps increases with increasing dimensionality: spatial structures in two-space are easier to understand than those in three-space. In scientific applications, difficulty also increases as a function of data quality and quantity. Missing data require extrapolation and interpolation. Data error leads to uncertainty and increasing difficulty. Partial and incomplete data require an even more skilled use of extrapolation and interpolation and more complex inference processes.
People use representations, whether in the mind or external, to comprehend and remember a set of concepts as well as to make inferences and discoveries about those concepts. Understanding the spatial relations and structure of a diagrammed system is relatively straightforward for most learners, because a diagram shows the parts in their spatial relations, using diagrammatic space to map real space. Most people can grasp the essential parts and their spatial relations from a diagram, such as a bicycle pump or a heart. What is much harder to understand is the meaning, interpretation, function, and causal chain that the diagram is meant to convey. While a novice can understand the spatial structure of a bicycle pump or heart from a diagram, only those with some expertise can grasp the functional and causal relations among the parts, that is, understand how the pump or the heart works (Heiser and Tversky, 2002).
For most scientific and engineering contexts, diagrams are meant to convey not just the structure of a system but also its behavior or the causal chain of its parts or the function of its operations. These are exactly the aspects of diagrams that students of all ages find difficult. Diagrams show structure, but they do not show function or behavior or causal relations. Language can compensate by stating this information directly. However, diagrams can also be enriched with extrapictorial devices, notably lines, arrows, boxes, and brackets, to convey abstract information. For example, when asked to describe a diagram of a bicycle pump, students describe the structural relations among the parts. When arrows are added to the diagram that denote the sequence of actions of the pump, students describe the causal, functional actions of the pump (Heiser and Tversky, 2002). Even the addition of arrows may not be sufficient to convey the functional information. For understanding bicycle pumps and car brakes, diagrams were sufficient for undergraduates of high mechanical ability but not for those of low ability; for those of low mechanical ability, language compensated (Heiser and Tversky, 2002).
In many educational settings, diagrams are taken for granted. These studies suggest that teaching how to reason from diagrams could reap great benefits. Such teaching would be needed in a number of domains: geography, arithmetic and mathematics, biology, geology, chemistry, physics, and engineering. Diagrams are common in history and the humanities as well. Across the curriculum, what is needed is exercises in interpreting the spatial entities and spatial relations of diagrams, making inferences as well as making discoveries. Constructing diagrams is an integral part of this instruction, especially in groups. Junior high school dyads working together produced diagrams of,
for example, plant ecology that were more abstract and contained less irrelevant, pictorial information than those produced by individuals.
2.7 CONCLUSION
Spatial thinking is a powerful tool. It is fundamental to problem solving in a variety of contexts: in life spaces, physical spaces, and intellectual spaces. In each case, it can offer increasingly powerful understandings, moving from description through analysis to inference. In each case, it depends upon a level of spatial knowledge, skills in spatial ways of thinking and acting, and the development of spatial capabilities. All of the component skills can, to some significant degree, be learned and this points to the crucial need for education in spatial thinking.
In Chapter 3, the committee shows how spatial thinking plays a fundamental role in everyday life, the workplace, and science. In everyday life, the necessary skills are rarely learned in formal contexts: we learn by informal means and by doing. In the workplace and scientific contexts, there are increasing demands in terms of levels of spatial knowledge, spatial ways of thinking and acting, and spatial capabilities: those demands are often met by formal instruction. Chapter 3 shows how demands have changed over time (in, for example, astronomy), how they are met by learning within a domain of knowledge (in, for example, the geosciences), and how some people become particularly skilled at spatial thinking (in the cases of Marie Tharp and Walter Christaller). People use spatial thinking daily, to find the things they need at home and their ways in the world. Spatial tools that everyone possesses can be articulated and refined to turn learners into powerful scientific thinkers.


























