Appendix C
Measures of Performance
This appendix defines the standard measures of performance that were used by the committee to assess and compare power and energy source technologies. It describes thermodynamic limits of performance and derives weight limit criteria for fuel cell and small engine systems based on the system efficiencies of fuel and conversion systems.
DEFINITIONS OF TERMS
Power is the rate of doing work—or, alternatively, the energy or work produced or consumed per unit time—and is quantified in this report in watts (W). In the meter-kilogram-seconds (MKS) system of units, 1 W is equal to 1 joule (J) of energy per second (1 J/s or 1 kg−m2/s2), and in the British engineering system, 1 W is equal to 0.0013 horsepower (hp) (or, 746 W = 1 hp). Conveniently, 1 W is also equal to the electrical power dissipated when 1 ampere (A) of electrical current is carried through a 1-ohm resistive load, producing a voltage drop of 1 volt (V).
Power can take many forms, including electrical power, mechanical power, photonic power (electromagnetic radiation, such as radio waves or light), acoustic power, and thermal power. Electrical power, Pelec, in watts is simply the product of current, I, in amperes multiplied by the potential drop across the load, V, in volts:
Pelec = I × V
The heat generation rate, Pheat, is also expressed in watts as the time rate of change (derivative) of heat, Q, in joules, over time, t, in seconds:
Pheat = dQ/dt
Energy is the amount of work done and can be calculated from the time integral of the power:
E=∫P(t)dt
The amount of energy can be quantified with the watt-hour (Wh), with 1 Wh of energy being equal to 1 W of average power integrated over a 1-hr period; it is equal to 3,600 J in the MKS system of units.
Capacity defines quantity of charge and is measured in units of ampere-hours or amp-hours (Ah). By definition, an ampere has units of 1 coulomb (C) of charge per second, so that 1 Ah is equal to 3,600 C. Capacity can be used to determine the coulombic efficiency of charging and discharging in batteries and the amount of fuel utilized by a fuel cell or engine.
Fuel consumption is quantified by the amount of fuel, in grams, used to produce a kilowatt-hour (kWh) of energy by a fuel conversion device. Grams per kilowatt-hour (g/kWh) is a standard and convenient metric for the fuel consumption of engines.
Wh is a measure of energy, but because the discharge voltage of the battery or operating voltage of the fuel cell is usually not constant, Wh, or energy from the power source, is not an accurate measure of the charge remaining in a battery or the fuel consumed by a fuel cell. The efficiency of batteries and fuel cells varies with current, so higher current (higher power) from a portable power source results in lower voltages. This point is illustrated by the curves in Figure C-1. Three discharge rates are shown, with each curve displaying voltages corresponding to the nominal capacity of the cell (in Ah) multiplied by the discharge factor (e.g., 0.2), the result being in units of amperes. Notice that the higher rates of discharge result in lower cell voltages and slightly lower capacities. These same features are present for the other charging curves, with higher recharge voltages being required at higher charging rates.
Specific power and power density are power per unit weight or volume of the system and are usually expressed with units of W/kg and W/L, respectively. Military systems
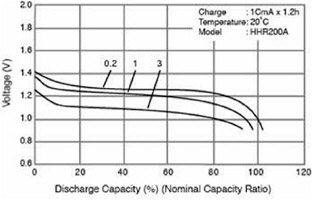
FIGURE C-1 The capacity of a battery changes with the rate of discharge. SOURCE: Panasonic, 2003.
typically focus on specific power, but the power density can be as important or more important for portable electronics, especially when a certain form factor is required. Because power is a function of the current drawn from the system, the power is often defined as the maximum power that can be delivered by the system. Alternatively, power can be specified at the practical operating current of the source. The specific power and power density of batteries are typically measured with respect to their full, packaged system. Fuel cells and engines can be defined by the power and weight of their conversion system only or of the conversion system and fuel combination.
Specific energy and energy density are the energy per unit weight or volume of the system. The most common units for portable power devices are Wh/kg and Wh/L. The amount of energy that is generated by a system is affected by operating conditions, as discussed above, so there is often a practical range in the reported values of the specific energy and energy density of battery chemistries. For clarity, the specific energy of systems is often reported as a single value, but it should be understood that, in practice, a variation should be expected.
The weight and volume term for batteries is measured for the full packaged system, and that for fuel cells and batteries includes the conversion system, plus the fuel and fuel tank, and relevant auxiliary components. Note that a fuel cell or engine with no fuel has no energy, so to accurately estimate these terms the amount of fuel consumed over a period of time must be known. Furthermore, when determining the specific energy and energy density of a developmental power source, care should be taken to qualify exactly what is included in the weight and volume terms, as the developer will not want to be saddled in the future with unforeseen components that add to the weight and volume of the system and make it less attractive. Additional weight might also be necessary for ruggedizing systems for military use.
Classes of energy storage/conversion systems are frequently compared by plotting the log of specific power as a function of the log of specific energy—such a plot is referred to as a Ragone plot (pronounced rah-GO-knee). The technique is used to compare classes of technologies and chemistries and can also be used to show how specific power and energy interrelate for a given battery or energy converter/ fuel solution as it is discharged at different rates. Ragone plots are useful when trying to select a power source for high energy or high power. Figure C-2 shows an example of such a plot for several rechargeable batteries and an internal combustion engine. Note that the energy of a battery is inversely proportional to the power, so draining a battery quickly (at high current and, thus, high power) tends to lower the specific energy and draining it slowly (at low power) leads to higher energy densities. Care should be taken when evaluating batteries to discern whether the specific power and energy were determined at the same current, or whether they are the best-case scenario on the Ragone plot.
Efficiency
The efficiency, η, of an energy conversion or storage device is a function of both thermodynamics and engineering and determines the system energy and thermal signature. Systems can be described by either their thermal or electrical efficiency. The thermal efficiency, ηth, of an energy conversion device is defined as the amount of useful energy
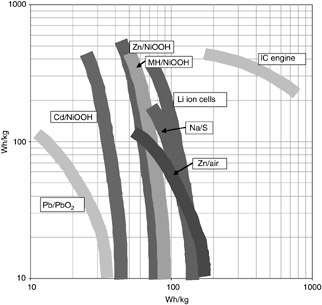
FIGURE C-2 Ragone plot comparing the specific energy vs. specific power of various batteries and of an internal combustion engine.
SOURCE: Cairns, 2004.
produced relative to the change in the amount of stored chemical energy.
Fuel Cells
For a fuel cell, these parameters are described by the Gibbs free energy, G, and the enthalpy, H, of the system and fuel. The maximum thermal efficiency for such an electrochemical system is the ratio of the Gibbs free energy for the reaction to the enthalpy change for the reaction:
ηth(max) = ∆G/∆H
The standard free energy change of a hydrogen-fueled system is typically calculated from the reaction of gaseous hydrogen to form liquid water:
H2 (g) + 1⁄2O2 → H2O (l)
At room temperature, this chemical energy of the system, ∆H, is 285.8 kJ/mole and the free energy for useful work, ∆G, is 237.1 kJ/mol, so the thermal efficiency of an ideal fuel cell operating reversibly on pure hydrogen and oxygen at standard conditions would be
ηth = ∆G/∆H = 237.1/285.8 = 0.83
The values needed to calculate enthalpy and free energy of fuel cells reactions can be easily obtained from sources such as the JANAF Thermochemical Tables (Chase, 1986).
The efficiency of a real operating fuel cell is calculated from the actual vs. ideal voltage of the cell. The ideal (reversible) voltage of an H2/O2 fuel cell under no load at room temperature and pressure is 1.229 V when the product is liquid water (with a higher heating value [HHV]) and 1.18 V when the product is gaseous water (with a lower heating value [LHV]). Thus, the thermal efficiency of a fuel cell operating at voltage Va at room temperature and utilizing all of the fuel, according to the last reaction above, is calculated from the equation
ηth = 0.83 × Va/1.229
Therefore, a fuel cell that produces liquid water operating at 0.8 V has an ideal thermal efficiency of 54 percent, while a fuel cell operating at 0.6 V has one of 40 percent. Of course, practical fuel cells do not usually consume all of the fuel supplied, and some leaves the system unreacted. This unreacted fuel needs to be taken into account in the effi-
ciency calculation. The overall thermal efficiency would then be
ηth = Va/1.229 × U × ∆G/∆H
where U is the fraction of the fuel utilized electrochemically.
For solid oxide fuel cells (SOFCs) running on a hydrocarbon fuel, the parameters must be adjusted for temperature and the reactions for hydrocarbon oxidation. The ideal cell voltage of SOFCs is lower than that of proton exchange membrane (PEM) systems because voltage decreases with increasing temperature, but the LHV of gaseous water (1.18 V) improves the theoretical cell efficiency. Fuel cells do not achieve their theoretical efficiency because of ohmic losses within the cell due to materials resistance and polarization losses of the electrochemical reactions.
Small Engines
For engines, thermal efficiency is the ratio of the net work done, Wnet, to the heat absorbed during a cycle. The amount of work is given by the net amount of heat converted into work by the engine, or the difference between the heat absorbed from the hot zone, Qh, and rejected to the cool zone, Qc, or sink:
ηth = W/Qh = (Qh − Qc)/Qh = 1 − Qc/Qh
For a Carnot cycle, the ratio of heat absorbed/rejected is equal to the ratio of temperature absorbed/rejected, resulting in the following equation:
ηth(Carnot) = 1 − Tc/Th
Batteries
The same concepts apply to batteries, but here, thermal efficiency is not normally used. The efficiency of a rechargeable battery is simply the ratio of the energy obtained during discharge to the energy used for recharge. The ratio of all reactants that participate in electrochemical (faradaic) reaction to all the reactants present within a storage battery is referred to as the “utilization.”
A rechargeable lithium battery operating at a nominal 3.7 V at rated power is operating with an efficiency of 88 percent, assuming an average charging voltage of 4.2 V. The high energy conversion efficiency of batteries adds to their value because it significantly reduces their thermal signature. The thermal energy released during operation of a battery is the difference between the enthalpy change for the cell reaction and the electrical energy produced by the battery. The thermal energy effect can be either a release of heat or the absorption of heat. The latter is rather unusual.
System Efficiency
The overall system efficiency, ηS, is a function of the thermal or electric efficiency of the power source and the balance-of-plant (BOP) efficiency, ηBOP, and fuel utilization, μf.
-
For a fuel cell, overall system efficiency is given by ηS = μf × ηBOP × ηec
-
And for a heat engine, system efficiency is given by ηS = μf × ηBOP × ηhe
-
For a rechargeable battery, the overall efficiency is described as
ηS = Energy delivered during discharge/ Energy used during recharge
The BOP efficiency includes the electrical and thermal penalties for the system, among them the electrical power needed to run air and fuel pumps and the thermal losses or cooling requirements. For low-temperature hydrogen PEM fuel cell systems, BOP efficiency is typically assumed to be better than 95 percent.
Fuel reformers must also be factored into the efficiency of systems operating on logistics fuel (JP-8). The fuel utilization factor for the reformer is written as follows:
μf = LHV of fuel products out/LHV of fuel in
Because all reformers operate above the boiling point of water, the LHV of the fuels is always used.
The fuel utilization, μf, in fuel cells and engines can be calculated from the ratio of the fuel converted to electricity by electrochemical oxidation to the fuel provided. For heat-producing engines, μf can be defined as the ratio of oxidized fuel producing heat (for potential conversion to work) to the total fuel content input to the engine.
In fuel cells, fuel is not fully utilized for several reasons. The greatest loss comes from incomplete electrochemical oxidation of the fuel at the anode. In closed systems, such as direct methanol fuel cells (DMFCs), where the fuel is recycled, the unreacted fuel can be passed back over the anode, but even then the fuel cell can never convert all of its fuel to electricity because some of it is vented with the exhaust from the anode (H2O and CO2) and there must be some extra fuel carried. Low-temperature fuel cells with polymer electrolytes (PEM fuel cells and DMFCs) also experience crossover of fuel from the anode through the electrolyte to the cathode, where the fuel is oxidized to heat and reaction products and no useful electrons (see Appendix D). In some designs, the fuel can also be oxidized by internal currents within the cell stack or by shunt currents, which effectively short circuit the external load and therefore produce no energy. Fuel can also be lost by mechanical means, such as purging or evaporation.
All of the factors above can have a significant impact on overall system efficiency. For a low-temperature PEM fuel cell system that produces liquid water, that is run at 0.8 V, and that has a 95 percent efficient BOP, the overall thermodynamic system efficiency can approach 49 percent. DMFCs are typically on the order of 30 percent efficient. They have lower overall efficiencies relative to PEM/H2/air systems owing to a combination of lower cell voltages (0.5 V/1.25 V), reduced fuel utilization (μf <90 percent), and perhaps a higher BOP burden (ηBOP <90 percent). The efficiency parameters also vary with cell power or cell voltage, as shown in Figure C-3 for a nominally 20-W DMFC.
To simplify the characterization, fuel cell systems are also defined by their overall thermal efficiency, which is calculated from the following equation:
ηel = Electrical energy output/Heating value of fuel in
The efficiency values for fuel cells used in Chapter 2 are the overall thermal efficiency.
COMPARING PROSPECTIVE MILITARY SYSTEMS
Technology readiness levels (TRLs) are used by the Army and other government agencies to measure the relative maturity of system developments. Definitions for the nine levels used by the committee to compare prospective power systems are shown in Table C-1. TRL 6 is the level at which a power source model or prototype has been demonstrated in a relevant environment.
Once new power systems such as fuel cells and engines are developed, the efficiency of the overall system can be used to verify the validity of the system by predicting the maximum allowable weight of the hardware components, as described below.
First, the calculated weights are given in Tables C-2 and C-3 for 24- and 72-hr missions, respectively, for complete power sources operating at average levels of 2, 20, 100, and 3,000 W at specific energies of 200, 600, 1,000, 2,000, and 3,000 Wh/kg. For example, a 24-hr mission at 20 W has a net energy, Enet, of 480 Wh, and the power source would have a total weight of 2.4 kg (including system mass and fuel) if it has a specific energy of 200 Wh/kg and 0.48 kg if it has 1,000 Wh/kg. A 1,440-Wh mission, or 72 hr at 20 W, would require a 200-Wh/kg power source weighing 7.2 kg or a 1,000-Wh/kg power source weighing 1.44 kg. For fueled systems, such as fuel cells and engines, a portion of the total weight, Wtotal, is due to the system, Wsystem (including the fuel conversion system and associated balance of plant), and the remaining weight is due to fuel, Wfuel. Wsystem can be calculated from the system electrical efficiency, ηel; the net energy of the mission, Enet; the specific energy of the system, Esp; and the heating value of the fuel, HV, by solving two equations:
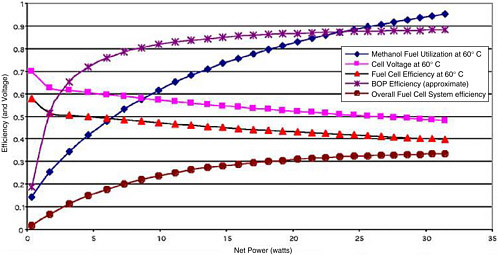
FIGURE C-3 Variation in efficiency parameters of a 20-W-rated DMFC with variations in the load (net power).
TABLE C-1 Criteria for Technology Readiness Levels
|
TRL |
Task Accomplished |
Description |
|
1 |
Basic principals observed and reported |
Lowest level of technology readiness. Scientific research begins to be translated into applied research and development. Examples might include paper studies of a technology’s basic properties. |
|
2 |
Technology concept or application formulated |
Invention begins. Once basic principles are observed, practical applications can be invented. The application is speculative and there is no proof or detailed analysis to support the assumption. Examples are still limited to paper studies. |
|
3 |
Analytical and experimental critical function or characteristics proof of concept |
Active research and development are initiated. These include analytical studies and laboratory studies to physically validate analytical predictions of separate elements of the technology. Examples include components that are not yet integrated or representative. |
|
4 |
Component or breadboard validation in laboratory environment |
Basic technology components are integrated to establish that the pieces will work together. This is relatively “low fidelity” compared with the eventual system. Examples include integration of ad hoc hardware in a laboratory. |
|
5 |
Component or breadboard validation in relevant environment |
Fidelity of breadboard technology increases significantly. The basic technological components are integrated with reasonably realistic supporting elements so that the technology can be tested in a simulated environment. Examples include high-fidelity laboratory integration of components. |
|
6 |
System/subsystem model or prototype demonstration in a relevant environment |
Representative model or prototype system, which is well beyond the breadboard tested for TRL 5, is tested in a relevant environment. Represents a major step up in a technology’s demonstrated readiness. Examples include testing a prototype in a high-fidelity laboratory environment or in a simulated operational environment. |
|
7 |
System prototype demonstration in an operational environment |
Prototype near or at planned operational system. Represents a major step up from TRL 6, requiring the demonstration of an actual system prototype in an operational environment, such as in an aircraft, vehicle or space. Examples include testing the prototype in a testbed aircraft. |
|
8 |
Actual system completed and flight qualified through test and demonstration |
Technology has been proven to work in its final form and under expected conditions. In almost all cases, this TR represents the end of true system development. Examples include developmental test and evaluation of the system in its intended weapon system to determine if it meets design specifications. |
|
9 |
Actual system flight proven through successful mission operations |
Actual application of the technology in its final form and under mission conditions, such as those encountered in operational test and evaluation. In almost all cases, this is the end of the last bug fixing aspects of true system development. Examples include using the system under operational mission conditions. |
|
SOURCE: NRC, 2003. |
||
Esp = Enet/Wtotal = Enet/(Wsystem + Wfuel)
Wsystem = Enet/Esp − Wfuel
(1)
and
ηel × HV = Enet/Wfuel
Wfuel = Enet/ηel × HV
(2)
Substitute equation 2 into equation 1 to get the final equation:
Wsystem = (Enet/Esp) − [Enet/(ηel × HV)]
Alternatively, if the dry system mass is known, its specific energy can be calculated as a function of its efficiency using the equation
Esp = Enet × ηel × HV/(Wsystem × ηel × HV + Enet)
These equations can be used to calculate the maximum allowable dry weight of a system (i.e., weight of the system without fuel) or the maximum allowable specific energy of a system with a known dry mass. The results of the equations are shown graphically in Figures C-4 and C-5 for 24-hr and 72-hr 20-W missions (net energy = 1,440 Wh) on methanol (HHV = 6,088 Wh/kg) and JP-8 (LHV = 12,000 Wh/kg) for devices having specific energies from 200 to 3,000 Wh/kg.
TABLE C-2 Energy and Total System Weights for 24-Hour Missions
|
|
|
Weight of Total System (kg)a |
||||
|
Power of Mission (W) |
Energy of 24-hr Mission (Wh) |
200 Wh/kg Device |
600 Wh/kg Device |
1,000 Wh/kg Device |
2,000 Wh/kg Device |
3,000 Wh/kg Device |
|
2 |
48 |
0.24 |
0.08 |
0.048 |
0.024 |
0.016 |
|
20 |
480 |
2.4 |
0.8 |
0.48 |
0.24 |
0.16 |
|
100 |
2,400 |
12 |
4 |
2.4 |
1.2 |
0.8 |
|
3,000 |
72,000 |
360 |
120 |
72 |
36 |
24 |
|
NOTE: Calculated weights of devices having specific energies of 200, 600, 1,000, 2,000, and 3,000 Wh/kg at power levels of 2, 20, 100, and 3,000 W. aSystem weight includes dry system plus fuel. |
||||||
TABLE C-3 Energy and Total System Weights for 72-Hour Missions
|
|
|
Weight of Total System (kg)a |
||||
|
Power of Mission (W) |
Energy of 72 hr Mission (Wh) |
200 Wh/kg Device |
600 Wh/kg Device |
1,000 Wh/kg Device |
2,000 Wh/kg Device |
3,000 Wh/kg Device |
|
2 |
144 |
0.72 |
0.24 |
0.144 |
0.072 |
0.048 |
|
20 |
1,440 |
7.2 |
2.4 |
1.44 |
0.72 |
0.48 |
|
100 |
7,200 |
36 |
12 |
7.2 |
3.6 |
2.4 |
|
3,000 |
216,000 |
1,080 |
360 |
216 |
108 |
72 |
|
NOTE: Calculated weights of devices having specific energies of 200, 600, 1,000, 2,000, and 3,000 Wh/kg at power levels of 2, 20, 100, and 3,000 W. aSystem weight includes dry system plus fuel. |
||||||
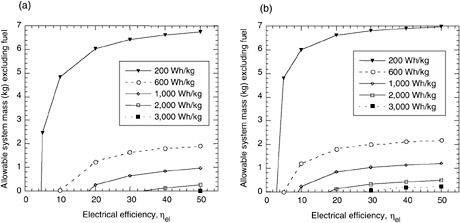
FIGURE C-4 The maximum allowable system mass (excluding fuel) calculated for (a) energy conversion systems operating below 100°C on methanol (HHV = 6,088 Wh/kg) or (b) high-temperature conversion systems (>100°C) operating on JP-8 (LHV = 12,000 Wh/kg). The energy density of the systems is varied from 200 to 3,000 Wh/kg. The data are derived from the equations in this appendix.
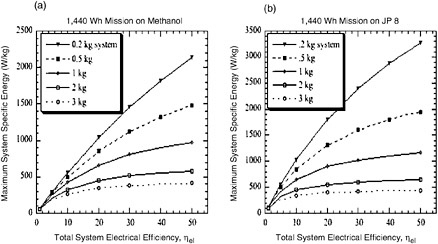
FIGURE C-5 The maximum allowable system specific energy calculated for (a) energy conversion systems operating below 100°C on methanol (HHV = 6,088 Wh/kg) or (b) high-temperature conversion systems (>100°C) operating on JP-8 (LHV = 12,000 Wh/kg). The dry weight of the systems is varied from 0.2 to 3 kg. The data are derived from the equations in this appendix.
The calculations for Figure C-5 are made with a simple equation, given below for a 2,000-Wh/kg system with a 1,440-Wh mission on methanol (6,088 Wh/kg):
System mass (kg) =
(1,440/2,000) − [1,440)/(efficiency/100) x 6,088]
A similar equation is used to generate the data plotted in Figure C-5 for a 2-kg dry system:
The plots in Figures C-4 and C-5 show that for a 20-W system used for 72 hr (1,440 Wh), a greater dry system mass can be tolerated by a fuel cell or engine that operates on JP-8 rather than methanol. A 30 percent efficient DMFC must weigh 1.6 kg to operate at 600 Wh/kg, but a SOFC running on JP-8 can weigh 2 kg. This discrepancy is simply due to the energy content of the fuels. One can infer from the plots that system efficiency and system weight are the key factors affecting the specific energy of the system. Also, systems with efficiencies below 10 percent are limited in their specific energy—for instance, a 1,000-Wh/kg system can never be achieved by a methanol-fueled system with 10 percent efficiency (Figure C-5)
The equations can be used to estimate the viability of certain systems for various missions. For a 480-Wh mission (20 W for 24 hr), any JP-8 fueled system with a target specific energy of 1,000 Wh/kg would have to weigh less than 400 g; the task of integrating the device, the insulation, the fuel tank, and so forth would be a challenging one. However, when the mission duration is extended to 4,800 Wh (10 days at 20 W), the fueled systems become highly attractive.
REFERENCES
Cairns, Elton J. 2004. Battery overview. Chapter B. Encyclopedia of Energy, Vol. 1. C.J. Cleveland, ed. New York: Elsevier, 124.
Chase, M.W. 1986. JANAF Thermochemical Tables, 3rd ed., vols. 1 and 2. American Chemical Society.
NRC (National Research Council). 2003. Science and Technology for Army Homeland Security: Report 1 . Washington, D.C.: The National Academies Press.
Panasonic. 2003. Panasonic Nickel Metal Hydride Handbook. Available at http://www.panasonic.com/industrial/battery/oem/chem/nicmet/index.html. Last accessed on December 23, 2003.








