6
Judgment, Uncertainty, and Valuation
INTRODUCTION
Some aspects of the economic valuation of aquatic and related terrestrial ecosystem services inevitably involve investigator judgments, and some are unavoidably uncertain. This chapter aims to identify the needs for investigator judgments and how they arise, how such judgments should be made, and how they should be presented to environmental decision-makers. It also seeks to describe the sources and types of uncertainty, indicate which are most significant, and suggest how analysts and decision-makers can and should respond. More specifically, this chapter provides a review of issues related to framing, methodological judgments, and peer review; the sources and management of uncertainty and how these relate to valuation and policymaking considerations; and a summary of the chapter and its conclusions and recommendations. Although unavoidable, uncertainty and the need to exercise professional judgment are not debilitating to ecosystem services valuation. It is important to be clear, however, when such judgments are made, to explain why they are needed, and to indicate the alternative ways in which judgment could have been exercised. It is also important that the sources of uncertainty be minimized and accounted for in ways that ensure that one’s conclusions and resulting decisions regarding ecosystem valuation are not systematically biased and do not convey a false sense of precision.
PROFESSIONAL JUDGMENTS
The following sections describe cases in which investigators had to use professional judgments in ecosystem valuation regarding issues of: (1) how to frame a valuation study; (2) how to address the methodological judgments that have to be made during the study (such as the choice of a discount rate); and (3) how to use peer review to identify and evaluate these judgments.
Framing
Perhaps the most important choice in any ecosystem services valuation study is the selection of the question to be asked and addressed. This report has previously described the importance of a careful selection of the question in several case studies including the Catskills watershed and the Exxon Valdez oil
spill (see Chapter 5). In the Catskills study (see also NRC, 2000), a critical decision was made early on to not attempt to value the entire suite of services provided by the watershed but rather to focus on the service of water purification. More specifically, the issue was whether the restoration of the Catskills watershed would be more cost-effective than constructing a new drinking water filtration system as a way of addressing New York City’s drinking water quality problems. This definition of the issue was determined by policymakers, not by the analysts.
This very specific and policy-oriented focus meant that it was not necessary to identify and attempt to value all of the services provided by the watershed, but rather to ascertain whether the cost of restoring its water purification services exceeded or was less than the known cost of a replacement for them. As discussed in Chapter 5, this focus greatly simplified the valuation task because a full economic valuation of the services of the watershed would have required the following: (1) that all sources of value be identified, such as water purification, tourism, support of biodiversity, esthetic values, recreational fishing, streamflow stabilization, and so on; (2) that each of these services be quantified; and (3) that each service be valued. It was not even necessary to establish the restoration cost exactly, but only to compare it to the cost of the alternative (i.e., construction of a drinking water filtration system). Since the outcome of this comparison was that the cost of restoration was less than that of the alternative, New York City decided to spend more than one billion dollars on increased protection and restoration of the watershed (NRC, 2000). It is worth emphasizing that no aspects of the services of the Catskills ecosystems were valued to reach this conclusion; watershed restoration costs were compared to those of an alternative source of the desired service. If this answer had been different—if, for example, the cost of restoration had exceeded the cost of a new water filtration system—it might still have been appropriate to restore the watershed. However, in that case, a complete economic justification of such a decision would have required the valuation of a sufficient number of services of the Catskills watershed to show that the total economic value exceeded the costs of restoration, and offered New York City an attractive return on its investment. Such a valuation exercise would have been an order of magnitude more complex. Thus, not only was the question framed in a way that simplified the analysis, but the existing data were conducive to supporting the simplest possible outcome. The decision tree in Figure 6-1 illustrates this point—investigation of the New York City watershed followed the upper part of this decision tree, leading to a conclusion that avoided two complex steps that would otherwise have been required.
The Exxon Valdez case presents a different situation (Carson et al., 2003; Hanemann, 1994; Portney, 1994) as legal liability issues required estimates of damages to natural resources. A complete economic valuation of the costs of the massive oil spill would have required the following: (1) identification of all of the categories of impacts of the spill such as loss of fish catch, loss of tourist revenues, deaths of many species of birds, fish, mammals, and invertebrates; (2) quantification of all of these types of impacts (e.g., how much revenue from
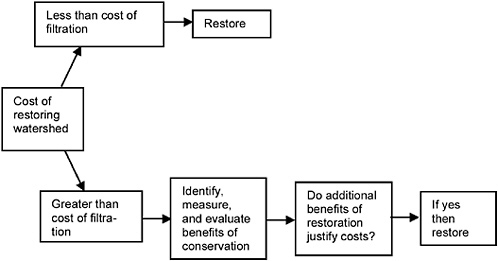
FIGURE 6-1 Decision tree for Catskills watershed study.
fishing and tourism was lost, how many animals of each type were killed); and (3) valuation of each of these losses. Clearly, completing all three stages of such an ecosystem valuation study presents a massive and challenging task.1 Although numerous studies were commissioned by Exxon, the State of Alaska, the federal government, and other interested parties, a clear answer to the question of the dollar value of damages to ecosystem services caused by the oil spill was not produced (Portney, 1994). As noted in Chapter 5, there are difficulties in quantifying the link between the oil spill and changes in ecosystem services as well as difficulties in valuing such changes—especially when considering nonuse values such as existence value. There was no obvious and simple way of framing this issue in the Exxon Valdez case because all aspects of the damages were relevant to disputes about compensation.
These two cases illustrate the importance of how a valuation study is framed, and how the frame used derives from the specific context within which an ecosystem valuation issue is raised. They also illustrate that the way an issue is posed may make a huge difference in the complexity of the valuation problem to be addressed.
In addition to determining the question to be asked and the complexity of the analysis required, psychologists have shown that how an issue is framed frequently affects the way in which people make judgments about that issue and
the subsequent answers they give to questions about the issue (Kahneman and Tversky, 2000; Machina, 1987). One classic illustration concerns the difference between the way people react to a policy that can alternatively be described as either saving lives or losing lives. Suppose that 100 people are threatened by a fatal disease but a policy intervention may save half of them. This situation could be described by stating that if this policy is followed, 50 of 100 people will die. Alternatively, one could also accurately state that this policy will save the lives of 50 of the 100 people who would otherwise die. Not surprisingly, the latter description is usually found to elicit a much more positive response and a higher “willingness to pay” (see more below) that is due entirely to the differences in the way the issue is framed. In one case, the emphasis is on saving lives, while the other is on losing lives.
A similar phenomenon has been noted in the description and interpretation of event probabilities (Kunreuther et al., 2001). Suppose that a natural disaster has a 1 in 100 chance of occurring each year. One could accurately state that over a 20-year period there is a 1 in 5 chance of such an event occurring. However, the latter way of presenting the same event probability almost always produces a stronger negative reaction. For example, people are typically willing to pay more for disaster insurance if the data is presented in the second way than in the first.
In the context of valuing aquatic ecosystems and their services, framing effects could matter in the choice between whether to emphasize what will be lost or what will be preserved. If an environmental policy will result in half of an existing wetland being lost, should this be presented as half being lost or half being saved? Should an analyst emphasize the number of birds or fish saved as the result of a policy measure or the number that will die in spite (or because) of the measure? One might be tempted to answer that the correct solution is to present all relevant information and allow individuals to select based on what is important to them. Although in some cases this might be possible, in many cases the volume of relevant data will be so large that it is virtually impossible to present it all in a completely even-handed way. In such cases, some element of selection and framing will be unavoidable.
The choice between willingness to pay (WTP) and willingness to accept (WTA) as measures of the value of an ecosystem good or service (see Chapters 2 and 4 for further information) is also a choice about how an issue is framed. This choice is normally thought of as depending on where the property rights lie (Hanemann, 1991). If the recipients of an ecosystem service have a right to that service, then the loss from removing it or allowing it to be lost is what they would be willing to accept as compensation. Unlike WTP, this measure is not bounded by their wealth. If on the other hand there is no inherent right to an ecosystem good or service, then its value to people is better measured by their willingness to pay for it. Certainly, there are situations in which the underlying ownership rights are not clear and it is therefore not obvious as to which measure is the better one. For example, do polluters have a right to pollute water, or do individuals have a right to clean water? The answers to such questions de-
termine whether clean water is most appropriately valued by WTP or WTA compensation for its loss. These are likely to result in very different valuation estimates, and unfortunately the methods of eliciting them are also rather different (see Chapter 4).
In fact, methods of eliciting WTP are better developed than those for eliciting WTA. Indeed the experience of some investigators in this area is that subjects in contingent valuation studies are more comfortable with questions about what they are WTP than with questions about WTA, as deciding what to pay for a good or service is an everyday human activity whereas one is rarely called upon to decide what to accept.2 In such cases, the analyst should ideally report both sets of estimates in a form of sensitivity analysis. However, the committee recognizes that in some cases this may effectively double the work and in such situations a second best alterative is to carefully document the ultimate choice made and state clearly that the answer would probably have been higher or lower had the alternative measure been chosen.
The previously described Catskills watershed example (NRC, 2000) provides a good illustration of the possible ambiguity of property rights and the consequent ambivalence about whether willingness to pay or to accept is the more appropriate measure of value. Did the upstream communities have the right to pollute, at least within some limits, or did New York City have the right to clean drinking water? The answers were governed by the legislative framework, in particular the federal Clean Water Act (see footnote 1, Chapter 1), which makes a sharp distinction between point source pollution and nonpoint source pollution—the former being strictly regulated, the latter less so. It also became clear during the discussions about conserving the Catskills watershed that the answer could change as a part of the ongoing negotiations. This was made clear when the State of New York introduced the possibility of using eminent domain legislation to compulsorily allow the purchase of areas of land deemed critical. The cost to New York City of restoring the watershed was affected by these considerations because they determined how much had to be paid to landowners in the watershed to help persuade them to reduce polluting activities. These payments would obviously be higher, given better-established landowners’ “rights to pollute.”
There are cases in which the ability to present an environmental policy recommendation in several different frames may be important to decision-makers because it allows them to seek and obtain support from different constituencies. For example, a recommendation to use tradable air emission permits to limit emission of a pollutant can be presented as an extension of the use of market mechanisms to those who may be predisposed to support such measure because of their belief in the market mechanism. It can also be presented as a limitation on pollution to “environmentalists,” who may be disposed to support such a measure because it results in a net reduction in air pollution. The fact that a particular environmental policy appeals to several different constituencies often
stems from the ability to frame it in different ways. Cross-constituency support for a measure may mean that there is widespread agreement on the measure; it may also indicate that it can be seen from several different perspectives and is framed differently to appeal to different groups.
These preceding examples suggest that framing unavoidably affects both the question that is asked in an ecosystem valuation study, and therefore the type and level of analysis needed to answer it, and the way in which people respond to any given issue. Framing in the second of these senses introduces an element of subjectivity into an ecosystem valuation analysis. Rarely, if ever, will a completely objective presentation of the issues be attainable. Analysts must be aware of this and sensitive to the different ways of presenting data and issues and make a serious attempt to address all perspectives in their presentations. Failure to do so could undermine the legitimacy of an ecosystem valuation study.
Framing in the first sense—that is, determining the question to be asked in a valuation study such as the Catskills and Exxon Valdez studies—represents a legitimate and appropriate attempt to fit the analysis conducted to the precise decision to be made. In the Catskills case, it was appropriate and logical to ask whether watershed restoration could meet the same needs at a lower cost. In the Exxon Valdez case, investigators used the information available from the impact and injury studies being conducted by the State of Alaska to present the issues to respondents and so to frame the issues. The investigators attempted to be conservative in summarizing the conclusions of these studies and were constrained by the fact that the economic and ecological studies were being conducted somewhat in parallel. Because they did not desire the survey respondents to rely on information they had individually gleaned from the media, the investigators went out of their way to describe the effects of the spill, albeit in a succinct manner. Furthermore, the investigators chose to avoid duplicating the impact and injury studies that had already been completed. Instead they relied on the presentation and discussion of these studies in the media and other public fora to have created an informed public who could use this discussion to place values on the avoidance of a similar event. Such an approach does raise questions about how informed the sample used in the Exxon Valdez contingent valuation study was, about the soundness of their understanding of the impact of the oil spill on the local ecosystem, and about the sensitivity of the values people placed on preventing ecosystem damage to possible further information about the issues.
Additional Methodological Judgments
In most ecosystem valuation studies, the analyst will be called on not only to frame the study but also to make additional judgments about how the study should be designed and conducted. Typically, these will address issues such as whether, and at what rate, future benefits and costs should be discounted (see
Chapter 2 for further information); whether to value goods and services by what people are willing to pay or what they would be willing to accept if these goods and services were reduced or lost; and how to account for and present distributional issues arising from possible policy measures. In many cases, different choices regarding some of these issues will make a substantial difference to the final valuation. For example, many environmental restoration projects have projected lives of a century or more, and over such long periods, even small differences in discount rates can result in order-of-magnitude differences to the present value of a stream of net benefits (Heal and Kriström, 2002). In such cases, the appropriate response is undoubtedly for the analyst to present figures on the sensitivity of the results to alternative choices.
In the case of choice of discount rate, it is a straightforward matter to present a table of results showing how valuation varies with the discount rate selected. For cases in which a measure has significant distributional impacts, it is incumbent on the analyst to identify and describe these impacts, providing details of the groups that gain and lose from the policy, and the extents of these gains and losses. The analyst may also provide an estimate for the aggregate value of an environmental policy if benefits and costs to all recipients are weighted equally and then indicate how this would change if different distributional weights were used (see Layard and Walters, 1994).
Another illustration of the importance of methodological judgments comes in the choice of an objective in an economic project evaluation. There are usually several possibilities in making this selection. The conventional approach is to follow the utilitarian route of choosing the project that generates the greatest net total benefit. In this approach, the analyst calculates all of the gains and losses to the different groups in society and then totals them, with the project having the highest total gains deemed the best. In the process of adding benefits over different groups, the analyst might apply different weights: for example, weighting gains and losses to indigent groups more than those to the affluent. Of course, in adding up gains and losses that occur at different dates, the analyst may weigh by discount factors (see Chapter 2 for further information).
An alternative approach is to follow the Rawlsian route;3 in this case the analyst focuses exclusively on the impact of the policy measure on one social group, the poorest group in society. In such cases, the “best” policy is defined as the one that does best by this poorest group. These two different approaches, the utilitarian and the Rawlsian, often lead to significantly different outcomes (Heal, 1998). The ultimate choice depends, among other things, on which approach the analyst believes best reflects the values of the group for whom the study is being undertaken. If the client is society as a whole, are its values better reflected by utilitarian or Rawlsian goals? Similar to situations in which WTP or WTA is used in ecosystem valuation study, ideally the analyst will present the
results of both approaches and explain how and why they differ. However, the reality is that this may greatly increase the complexity of the ecosystem valuation study. If time and resources allow only one approach, then it is reasonable to expect a clear explanation of how the choice was made and some discussion of alternatives.
Peer Review
The unavoidable need to make professional judgments in ecosystem valuation activities through choices of framing and methods suggests that there is a strong case for peer review to provide input on these methodological issues before study design is complete and relatively unchangeable. Although most significant ecosystem valuation studies will be reviewed by external reviewers on completion and/or publication, the committee believes that external review by peers and stakeholders could also be particularly valuable at a much earlier stage, when key judgments for the study have tentatively been chosen but there remains a legitimate opportunity for revision. Outside review at these earlier stages can make the difference between a valuation study that is widely accepted and one that is regarded as controversial or misleading (NRC, 1996).
UNCERTAINTY
The following sections discuss the major sources of uncertainty in the economic valuation of aquatic ecosystem services and how policymakers and analysts should respond.
Levels of Uncertainty: Risk and Ambiguity
The almost inevitable uncertainty facing analysts involved in ecosystem valuation can be more or less severe depending on the availability of good probabilistic information. A favorable case would be one in which, although there is uncertainty about the magnitudes of various parameters, the analyst nevertheless has good probabilistic information. That is, there is a distribution of possible magnitudes—with means, standard deviations, and other aspects of the distributions available—and these distributions are based on statistical data that are sufficiently extensive to allow some confidence in their predictions. An illustration of such a case is provided by insurance companies, which typically have many years of actuarial data on the death rates of people with different characteristics and thus can calculate the expected number of deaths in a population with some confidence.
An alternative and common scenario in ecosystem valuation is one in which there is really no good probabilistic information about the likely magnitudes of
some variables and what is available is based only on expert judgment. To continue the insurance analogy, this would likely be the position of an insurance company trying to assess the risk it faces if it provides terrorist insurance for owners of prominent buildings in major cities. There is no database of events on which the company can draw, and important decisions will have to be based solely on experts’ assessments of the risks. Environmental policymakers find themselves in this situation when making decisions about climate changes because there is no database that allows an estimation of the consequences of increasing concentrations of greenhouse gases. Thus, such decisions should be based on the analyses of expert groups such as the Intergovernmental Panel on Climate Change (IPCC).4 Analysts are in a similar position when evaluating changes designed to restore functionality in complex ecosystems such as the Florida Everglades.5
Situations such as the first of these, where there are reliable probabilities describing the unknown magnitudes, are described as characterized by risk—and the word “risk” in this context refers to situations in which reliable estimates of the probabilities are available. In contrast, the term ambiguity describes situations in which there are no data-based probabilities. Obviously, making good decisions is harder under conditions of ambiguity than under conditions of risk (Machina, 1987).
One way in which decision-makers can attempt to bridge the gap between risk and ambiguity is to assign subjective probabilities to the different possible outcomes. A subjective probability is one that is not based on repeated trials and observed occurrence frequencies, which is the classical interpretation of a probability, but rather on strength of belief in the likelihood of an outcome. So, in situations where there are no objective frequency-based probabilities, such as the consequences of the accumulation of greenhouse gases in the atmosphere, one could ask experts to present their best judgments about the likelihood of different outcomes by probability distribution. These would be subjective probabilities. Such judgments provide probability-like numbers to use in situations in which there are no data to provide frequency-based probabilities. One might, of course, end up with as many different subjective probabilities as there are different experts (Nordhaus, 1994; Roughgarden and Schneider, 1999.)
Model Uncertainty
Model uncertainty arises for the obvious reason that in many cases the relationships between certain key variables are not known with certainty (i.e., the “true model” of an important phenomenon or process will not be known). To
|
4 |
The IPCC was organized by the United Nations to provide scientific, technical, and socioeconomic data on the impacts and options for adaptation and mitigation in climate change. Further information is available on-line at http://www.ipcc.ch, accessed June 14, 2004. |
|
5 |
Such groups include, for example, the South Florida Ecosystem Task Force (see http://www.sfrestore.org for further information). |
use a biogeochemical example, the relationship between the nature of riparian tree cover in a watershed and the purification of water by that watershed may never be known. How do the amount and extent of water purification depend on the types of plant communities in a watershed and the successional stage of those communities? This is an example of the relationships discussed in Chapter 3 between ecological structure and function and the provision of ecosystem goods and services to the community. This relationship is often poorly understood and inevitably a source of uncertainty in ecosystem valuation efforts. In fact, in most studies of the value of aquatic ecosystems, this will be the largest single source of uncertainty because our understanding of how the structure of an ecosystem is affected by human activities and of how these effects translate into changes in ecosystem services is often rudimentary (see, for example, the Columbia River case study in Chapter 5 for further information).
On the economic side, an analyst might not know how society’s WTP for an ecosystem service depends on the way in which that service is provided. For example, how does the degree of visible cleanliness, or the degree of development and crowding, affect the value that is placed on a particular waterbody? What are the functional forms that relate the value that people place on a body of water to the parameters describing the state of that waterbody? In economic terms, what is clear is that investigators often do not know the form of the demand function for an ecosystem service. Difficulties in estimating societal values of an ecosystem’s services are especially acute for nonuse values such as the existence value that individuals may have for preserving species or intact ecosystems.
As discussed in Chapter 3, a particularly important issue in evaluating environmental policies designed to change the functioning of ecosystems is the existence of thresholds at which the qualitative behavior of an ecosystem changes. There is, for example, some evidence that many streams can absorb nitrate pollution up to a certain level with little or no effect on their biochemistry, but that beyond a certain level of nitrate input, their capacity to neutralize nitrates is exhausted and their biochemistry changes sharply (Lovett et al., 2001). The discussion of Lake Mendota in Chapter 5 also illustrates this effect. In such a situation, assuming a linear or even smooth response of the behavior of the system to outside influences could lead to massive errors in forecasts of the impacts of these influences. Model uncertainties about qualitative changes in ecosystem behavior are particularly important in ecosystem valuation. These should always be of concern to analysts who should establish a range for the main sources of uncertainty whenever possible.
It is clear from the preceding examples that given the imperfect knowledge of the way people value natural ecosystems and their goods and services, and our limited understanding of the underlying ecology and biogeochemistry of aquatic ecosystems, calculations of the value of the changes resulting from a policy intervention will always be approximate.
Parameter Uncertainty
Parameter uncertainty is one level below model uncertainty in the logical hierarchy of uncertainty in the valuation of ecosystem services. Even if the mathematical form of a relationship between important variables were known, one could—and in all probability would—still be uncertain about the values of the parameters in this functional form. For example, assume that an analyst knew with certainty that the value individuals place on a lake take the form V = AxByCz, where A, B, and C are characteristics of the lake such as water clarity, fish populations, and cleanliness; x, y, and z are parameters; and V is the value placed on the lake. Even if the functional form were known, the exact values of the parameters x, y, and z of the function would still not be known. At best, statistical estimates of these could be obtained, giving expected values of the parameters and distributions of possible errors about these parameters.
Most commonly, an analyst seeking to value the service or services of a particular ecosystem is subject to both model, and parameter uncertainty in that he or she is not sure of the true model and, conditional on the choice of model, faces further uncertainty about the values of parameters in the model.
Reducing Uncertainty: (Quasi) Option Values and Adaptive Management
Although there is considerable uncertainty regarding the value of ecosystem services, there is often the possibility of reducing this uncertainty over time through learning. Learning can be either active (the result of actions such as research designed to generate new knowledge), or passive (the byproduct of actions taken for other purposes or simply of the passage of time). Regardless of its source, the possibility of reducing uncertainty in the future through learning can affect current decisions, particularly when the impacts of these decisions are irreversible (Arrow and Fisher, 1974; Demers, 1991; Epstein, 1980; Henry, 1974). With learning, a “quasi-option value” has to be incorporated into the analysis, beyond the inclusion of expected net benefits that reflects the value of the additional flexibility. (From now on, this is collectively referred to simply as just “option value”; see also Chapter 2.) This flexibility allows future decisions to respond to new information as it becomes available.6
If the destruction of a natural system is irreversible, and if its value is currently unclear but may become better known in the future, then preserving it now allows the “destroy or conserve” issue to be revisited at a time when decision-makers are better informed; whereas destroying the ecosystem forces a permanent choice without the benefit of better knowledge. It follows that with
the possibility of learning, in a cost-benefit analysis the measurement of the benefits of ecosystem protection through ecosystem valuation should consider the possibility of learning and, in consequence, making a better decision at a later date (i.e., it should incorporate the option value; Arrow and Fisher, 1974; Hanemann, 1989; Henry, 1974).7
The incorporation of option value in cost-benefit analysis still entails a balancing. Although the flexibility created by preservation and by the opportunity to revisit the decision adds to the benefits of preservation, this balancing does not necessarily imply that preservation will in all cases be justified by this criterion. The benefits of ecosystem preservation (including the value of retaining the flexibility to respond to new information) will not necessarily exceed the associated costs. At present, there is little guidance about the importance of option values in ecosystem valuation. Similarly, only a limited amount of empirical work has been done to date on estimating the magnitude of option value. There is a need for further research in both of these areas in the context of ecosystem valuation.
Adaptive Management
A natural extension of the observation that better decisions can be made if one waits for additional information is the use of adaptive management, which is a relatively new paradigm for confronting the inevitable uncertainty arising among management policy alternatives for large complex ecosystems or ecosystems in which functional relationships are poorly known. Although advanced in the late 1970s and 1980s (Holling, 1978; Walters, 1986), adaptive management has recently only been applied by natural resource managers.8 A key component of adaptive management is active learning by introducing new management policies to learn more about the system’s behavior and thereby reduce uncertainty. Typically, there may be an effort to implement environmental management actions as “experiments” in order to “learn by doing,” with the experiments designed to reduce critical uncertainties about the ecosystem’s behavior. The usual goal of ecosystem management is to manage for resiliency (i.e., capacity for self-renewal) while optimizing benefits to society. Possible economic
benefits are often a part of the mix of information that stakeholders or government officials use to select management actions. Actually implementing potentially beneficial policies thus winnows the uncertainty in system response, albeit in a reversible and experimental sense. Adaptive management therefore provides a mechanism for learning systematically about the links between human societies and ecosystems. In contrast, the learning that occurs in economic models with option values is purely passive—information about the value of an environmental system is acquired with the passage of time. If one believes that additional information could be influential in selecting the best environmental policy option, then adaptive management is a natural step from the passive concept of an option value associated with gaining information to the concept of managing the ecosystem to learn and so reduce uncertainty. When an adaptive management approach is possible, which will not always be the case, the option value associated with conservation is likely to be increased because of the enhanced rate of information acquisition.
Adaptive management often uses explicit dynamic modeling or conceptual models of large complex ecosystems. These computer models are useful for two purposes. First, building an explicit numerical model requires a clear statement of what is known and what is assumed, which helps to expose broad gaps in data and understanding that are easily overlooked in verbal and qualitative assessments. Second, even crude models can help “screen” policy options and eliminate those that are simply too small in scale to be important or would be unacceptably risky given uncertainty about directions of response in key policy indicators (Walters et al., 2000). Proponents of adaptive management have long emphasized the importance of such modeling (Holling, 1978; Walters, 1986). Adaptive management is not a tool for ecosystem valuation or a method of valuation per se, nor does it require valuation. Rather, by reducing uncertainty and illuminating relationships within the ecosystem and between the ecosystem and human actions, it aids management and decision-making and may make economic valuation easier and more accurate.
DECISION-MAKING AND DECISION CRITERIA UNDER UNCERTAINTY
Decision Criteria
Just as there are different types of uncertainty, there are also different ways in which an analyst can allow for uncertainty in the support of environmental decision-making. A central issue is how to account for the range of possible outcomes (the variability of outcomes) that is an inevitable result of uncertainty. A widely used criterion for decision-making is to choose the alternative that yields the greatest expected value of benefits. This rates as equal all distributions of outcomes that have the same mean even if they have very different higher moments and so ignores information about variability. However, this
approach can be adopted only if the possible values of the relevant variables are known and associated probabilities can be assigned; otherwise, expected values cannot be computed. Thus, in order to adopt the objective of maximizing expected net benefits in ecosystem valuation, one has to be able to assign probabilities, either objective probabilities from past experience or subjective probabilities (for a general discussion, see Machina, 1987).
The unpredictability of the outcome of an environmental policy under uncertainty means that while the outcome could be excellent, it also has a chance of being poor. In general, faced with the choice between policies that generate the same expected value but with different ranges of outcomes, most people would choose the policy with the lowest variability, implying that they are “risk averse.” The extent of their risk aversion determines what they would be willing to pay to avoid a risk and replace it by a certain outcome. If people are very risk averse, an environmental policy that delivers a modest outcome with some certainty might be preferred to one that may deliver a truly outstanding outcome but may also deliver a very poor result. In such situations, an analyst has to decide whether to build some measure of risk aversion into the analysis and, if so, how much. There are studies of the degree of risk aversion displayed by individuals in financial markets (see Chetty, 2003, and references therein), but because risk aversion for a given person may vary with the magnitude of the risk and because it varies across people, these are not necessarily the appropriate values to use in environmental studies. In a heterogeneous population the analyst will have to make an assumption about the level of risk aversion that is appropriate for the group as a whole. In general, this is a matter in which the best solution is to state clearly that the assumption about the degree of risk aversion will affect the outcome and to conduct sensitivity analyses to indicate how this assumption impacts the outcome of the study (Heal and Kriström, 2002). If contingent valuation methods are used, it may be possible to inform subjects of the uncertainties associated with estimates presented in the study, so that their valuations reflect their own degrees of risk aversion.
A key assumption in ecosystem valuation models is that individuals seek to maximize their utility and that they will be indifferent to changes that leave their utility unchanged. Under uncertainty, the assumption is that they maximize their expected utility, which is simply the expected value of the utilities they would realize under the possible outcomes. Although widely used in economic analyses, the expected utility assumption has been controversial since in some contexts its predictions are not consistent with observed behavior (Machina, 1987). Alternative theories of behavior under uncertainty have been proposed, including prospect theory (Kahnemann and Tversky, 2000).9 These alternatives introduce psychological responses (such as feelings of loss aversion and regret)
into models of choice. This modifies the arguments and structure of the individual’s utility or payoff function, but maintains the assumption that there is a payoff function that individuals seek to maximize. Thus, these alternative theories retain the basic assumption that individual behavior is based on self-interest.
Under the assumption that individuals seek to maximize their expected utility, the value of ecosystem protection is typically defined as the amount an individual would be willing to pay to ensure that protection occurs, which is then a measure of the dollar value or benefit of protection. The ecosystem valuation process is designed to provide an estimate of this measure. In the context of uncertainty, both WTP and WTA have to be interpreted as expressing preferences over uncertain outcomes and, in particular, as reflecting individuals’ aversions to the risks they perceive to be associated with the options available. To the extent that valuations reflect individuals’ attitudes toward risk and those individuals are accurately informed of the uncertainties associated with a project, there is no need for the analyst to make further allowance for risk aversion.
If society is extremely risk averse, the objective of maximizing the expected value of the aggregate utility can be replaced by an objective known as “maximin.” The intent in such cases is to focus on the worst possible outcome, the minimum, and then seek the policy option that makes this as favorable as possible, or maximum (hence, the name; for a discussion, see Arrow and Hurwicz, 1972; Maskin, 1979). By way of illustration, consider an aquatic ecosystem that, among other services, provides flood control to a residential area. It is possible that decision-makers believe that the loss of human life through floods is the worst possible outcome and must be prevented at all costs. Such a belief would be appropriately represented by maximin preferences, which would lead the analyst to select the project that minimizes the loss of life from flooding. Focusing exclusively on the worst possible outcome is justified only if there are good reasons to suppose that society is really risk averse and is willing to sacrifice considerable possible benefit from a policy to avoid any chance of a bad outcome. Technically, the maximin objective can be seen as a limiting case of the expected utility objective as the degree of risk aversion increases without limit. There are also arguments that suggest that the maximin may be an appropriate choice of objective in some cases of ambiguity—that is, cases in which there are no objective or subjective probabilities (Arrow and Hurwicz, 1972; Maskin, 1979). Implementing the maximin criterion does not require probabilities; it requires only that the worst possible outcome be identified, so it is particularly suited to problems for which no probabilities are available.
Recent literature on this topic (e.g., Ghirardato et al., 2002) has extended this concept to a broader analysis of decision-making with ambiguity and suggests, in outline, that under quite general conditions a decision-maker faced with ambiguity should look for the worst possible outcome, then for the best possible outcome, and then rank projects and policies by a weighted average of these. Obviously, using the maximin criterion in ecosystem services valuation is a special case because all of the weight in the weighted average is placed on the worst case. A logical extension of this line of thinking leads to concepts such as the
precautionary principle and the idea of a safe minimum standard, which are discussed next.
The Precautionary Principle and Safe Minimum Standard
Another approach to environmental decision-making under uncertainty is embodied by the precautionary principle. Notably, the 1992 Rio Declaration (Article 15) (see Gollier et al., 2000) stated: “Where there are threats of serious and irreversible damage, lack of full scientific certainty shall not be used as a reason for postponing cost-effective measures to prevent environmental degradation.” Alhough the precautionary principle has been attacked as a vague concept lacking a precise definition, the essence of the precautionary principle is clear and is that the burden of proof should be to demonstrate that changes do not cause irreversible environmental damage, rather than proving that a change is dangerous. Most economists, if asked to think of a justification for the precautionary principle in decision-making, would probably couch it in terms of learning, especially about the validity of a scientific model, irreversibilities, and option values. The option value linked to conserving an ecosystem whose change is irreversible is in effect a reward for cautious behavior, although it certainly does not imply that conservation is always appropriate. Gollier et al. (2000) note that the precautionary principle can also be given a formal justification in environmental decision-making without invoking irreversibilities, just by assuming that there is cumulative damage from a stock of pollutant and possible learning over time about the consequences of the pollutant.
There has been extensive discussion of irreversibility, learning, option values, and the precautionary principle in the context of policy toward climate change. Since the basic decision framework is similar to that in ecosystem conservation and valuation, it is useful to review briefly some of the more relevant conclusions from this literature. Notable references include Fisher and Narain (2002), Gollier et al. (2000), Kolstad (1996a,b), Pindyck (2000), among others.
One of the conclusions to emerge from this discussion is that while there may be an option value associated with ecosystem conservation, it is also possible that there is a value associated with not adopting conservation policy measures that require significant investments. The point is that if an environmental policy requires investment in fixed capital and there is some uncertainty about the appropriateness of the policy, and so about the value of the associated investment, there may be a benefit from delaying its adoption so as to benefit from learning about the value of the investment. Thus, if one is unsure of how effective a policy measure is and it requires a long-term and unchangeable commitment, it may be appropriate to wait to implement it until there is more information and the value is clear.
This implies that in discussions of the conservation of an ecosystem whose destruction would be irreversible and whose conservation would require an investment in fixed capital, there is an option value argument for conserving the
ecosystem and also an option value argument for delaying implementation of the conservation policy until it is clear whether the associated investment in fixed capital is in fact appropriate. In such a case, there are two opposing option values and which is larger is an empirical question. An example of an effectively irreversible policy would be the construction or removal of a dam or of a system of canals, which cannot readily be undone once implemented.
One recommendation that emerges from this discussion is that under conditions of uncertainty and learning, there should be a preference for environmental policy measures that are flexible and minimize the commitments of fixed capital or that can be implemented on a small scale on a pilot or trial basis. In effect, this is adaptive management and the option value stays on one side of the equation.
In their study of Lake Mendota, Carpenter et al. (1999; see also Chapter 5) set out a quite different approach. In an intensive agricultural region, such as the Midwest of the United States, phosphorus is often applied as a fertilizer to the land and some runs off into nearby streams and lakes, including Lake Mendota. In sufficient concentrations, phosphorus can cause a change in the normal biological state of the lake that results in a potentially locally stable state of eutrophication in which the lake is unproductive for most human uses. Eutrophication of a lake can be reversed, albeit slowly. The response of a lake to phosphorus concentration is highly nonlinear and the concentration depends not only on the runoff but also on temperature and rainfall. How should the runoff of phosphorus over time be managed in order to maximize the expected discounted value of benefits net of the costs of phosphorus mitigation? In this regard, Carpenter et al. (1999) modeled the dynamics of the interacting lake and surrounding agricultural systems as a nonlinear dynamical system with several different locally stable states, one of which (eutrophication) is highly undesirable. Avoiding this state in agriculturally intensive regions is costly, so there are trade-offs to be made. Further, the stochasticity of the weather means that the problem has to be viewed in probabilistic terms. A particularly relevant conclusion that these authors (Carpenter et al., 1999) reached follows:
An important lesson from this analysis is a precautionary principle. If phosphorus inputs are stochastic, lags occur in implementing phosphorus input policy, or decision makers are uncertain about lake response to altered phosphorus inputs, then phosphorus input targets should be reduced. In reality, all of these factors—stochasticity, lags, uncertainty—occur to some degree. Therefore, if maximum economic benefit is the goal of lake management, phosphorus input levels should be reduced below levels derived from traditional limnological models. The reduction in phosphorus input targets represents the cost a decision maker should be willing to pay as insurance against the risk that the lake will recover slowly or not at all from eutrophication. This general result resembles those derived in the case of harvest policies for living resources subject to catastrophic collapse… We believe that the precautionary principle that emerges from our model applies to a wide range of scenarios in which maximum benefit is sought from an ecosystem subject to hysteretic or irreversible changes.
Although Carpenter et al. (1999) mention the precautionary principle, they do not define it or state it in an operational way in the context of managing Lake Mendota. Rather, the precautionary principle is implied to be a recommendation that phosphorus levels should be below that recommended by traditional limnological models, this being a cost that decision-makers must shoulder to avoid the risk of eutrophication. Thus, this is not a concept that can be made operational without further work, and indeed it seems possible that much of what is at issue in this case is captured in economists’ concepts of risk aversion and option value, which were not explicitly developed in the model of Carpenter et al.
The precautionary principle is widely cited by the environmental community as a justification for erring on the side of conservation in situations of uncertainty. However, it is not clear that the precautionary principle brings anything new to the decision criteria frameworks usually used by economists. As stated above, many of the concerns that drive people to articulate the precautionary principle are addressed by existing economic approaches to environmental decision-making but under different names. With learning and irreversibility, option values may tilt decisions in the direction of environmental conservation, more so if learning can be actively pursued through an adaptive management approach, and especially if there is a chance of a significantly negative outcome from environmental impacts. In such cases, risk aversion will normally move decisions in the same direction.
Related in some ways to the precautionary principle is the concept of a “safe minimum standard,” which introduces a class of choices in which decision-makers seek to maintain populations or ecosystems at levels deemed necessary to ensure their continued existence. The most striking example in the United States is the Endangered Species Act (ESA). As originally passed, the ESA explicitly prohibited actions that would reduce the survival chances of an endangered species, whatever the economic costs of this prohibition.10 Thus, the ESA mandated conservation irrespective of economic costs when the very existence of a species was threatened. The intent of the ESA was clearly to take species survival decisions out of the realm of economics, asserting the primacy of an ethical imperative to prevent extinction over any cost-benefit calculations. The ESA was subsequently amended to include a provision for balancing extinction against the economic costs of its prevention.11 As amended, the ESA is consistent with the safe-minimum standard approach, under which a minimum population is protected unless it is too costly to do so. However, the consideration of costs can only be invoked in extreme cases. As a result of the ESA, when the survival of a species is at stake, one does not have to place an eco-
|
10 |
In Tennessee Valley Authority vs. Hill, the Supreme Court upheld that the Endangered Species Act of 1973 was intended by Congress to “…halt and reverse the trend toward species extinction at whatever the cost.” |
|
11 |
In 1978, the ESA was amended to “take into consideration economic impact, and other relevant impact” of listing and designation of critical habitats. See http://endangered.fws.gov for further information about the ESA. |
nomic value on its continuation because legislators have determined that this is infinite and outweighs any possible costs. The Clean Water Act also contains provisions that explicitly set the attainment of public health-related standards outside the range of economic valuation, mandating that they be met whatever the cost.
These preceding examples illustrate situations in which U.S. society reacts to uncertainty about ecosystem services by specifying safe minimum standards (i.e., not causing conditions that would drive a species to extinction, not damaging human health) for impacts on or changes in these systems. Rather than calculate the expected costs and benefits of different levels of impacts and choosing the best, society specifies a bound on the permissible impacts. Of course, with ambiguity rather than risk, and thus no probabilities with which to work, it may be impossible to calculate expected costs and benefits so that standard cost-benefit analysis in such cases is hardly applicable.
Choosing one bound or safe minimum standard over another requires some justification and supporting analysis. One possible line of argument relates to thresholds in ecosystem behavior in response to stress (see Chapter 3). If stresses above a certain level are believed to lead to sharp deterioration in an ecosystem, this may provide a strong case for restricting impacts below this critical level. Yet even this argument relies implicitly on the idea that the costs of ecosystem stress rise sharply and are therefore likely to exceed benefits at some threshold—an argument that cannot be made plausibly without some idea of the magnitudes of the costs and benefits and of the associated margins of error. Once a safe minimum standard is chosen, however, valuation is not needed, but valuation may be needed in setting the safe minimum standard (Berrens, 1996; Berrens et al., 1998; Bishop, 1978; Ciriacy-Wantrup, 1952; Farmer and Randall, 1998; Palmini, 1999; Randall and Farmer, 1995; Ready and Bishop, 1991).
ILLUSTRATIONS OF THE TREATMENT OF UNCERTAINTY
This section briefly illustrates how uncertainty could be treated in ecosystem services valuation studies, with reference to the Catskills watershed in New York (also discussed earlier in this chapter) and the Edwards Aquifer case studies provided in Chapter 5. The section begins with an introduction to evaluating and assessing uncertainty through “Monte Carlo”12 simulations and indicates
|
12 |
Monte Carlo methods have been practiced for centuries, but under more generic names such as “statistical sampling.” The "Monte Carlo" designation was popularized by early pioneers in the field during World War II because of the similarity of statistical simulation to games of chance and because Monte Carlo (the capital of Monaco) was a well known center for gambling and similar pursuits. For further information about the history, development, and use of Monte Carlo simulation methods, see http://csep1.phy.ornl.gov/mc/node1.html. |
how this approach could be applied to provide a more complete description of the consequences of uncertainty regarding the inputs to the valuation process.
Monte Carlo Simulation
A sophisticated way of incorporating uncertainty in the output of an ecosystem services valuation study is to use Monte Carlo simulation. This method can provide an estimate of the probability distribution of possible values that is derived from uncertainty about the underlying parameters and relationships. A prerequisite for such an analysis is some probabilistic information about the elements of the valuation.
By way of illustration, assume that a policy intervention is being evaluated that would conserve an ecosystem at some cost in terms of forgone residential development, which was a relevant issue in the Catskills watershed in New York. Assume further that there are two elements to the benefits, (1) the quantity of clean water assured because of the policy intervention and (2) the price at which this water should be valued. Call these Q and P respectively, where both are uncertain. On the cost side there is a present cost of Cp and a continuing cost of Cf per year in the future while the benefits continue into the future. If all values were known with certainty, then the net present value of the project would be represented by the following formula if the time horizon is fifty years and the discount rate is r:
If the parameters of this expression are known only with some degree of uncertainty, then NV is a random quantity and an analyst would desire data on its distribution. Suppose that the uncertainty is about P, Q, and Cf with r and Cp being known, and that the analyst possesses probability distributions over these uncertain variables. That is, for each of the uncertain variables there is a density function that provides the probability that the variable is within any interval. An analyst can then conduct a Monte Carlo simulation by picking a series of values for the uncertain variables as random numbers chosen according to their density function and for each set values for P, Q, and Cf computing the value of NV. This simulation is repeated many times with a different set of randomly-chosen values of P, Q, and Cf each time. The result will be a set of values for NV. As the number of repetitions of this process increases, the distribution of this set will approach that of the uncertain value of NV. An analyst can therefore obtain from this process approximations to the mean and standard deviation of the values of NV that are compatible with what is known about the uncertain parameters P, Q, and Cf.
In practice an analyst will use computer programs written for Monte Carlo simulation for this process and will need only to input information about the
distributions of the uncertain parameters and a formula indicating how these are used to compute the value. Of course, and as has been emphasized previously, obtaining probabilistic information about parameter values is often not straightforward and on many occasions it will be necessary to use subjective probabilities for this purpose. A potential complication is that in some cases the distributions of the various parameters will not be independent but will be drawn from a joint distribution. For example, in the illustration above, price P and quantity Q will not be independent—high prices will tend to be associated with low quantities and vice versa. In such cases the analyst will have to specify joint rather than independent distributions, which is a somewhat more demanding task.
There is little doubt that if resources and sufficient information are available for a Monte Carlo approach, and if the analyst is able to supply the required probabilistic information, this approach provides decision-makers a better appreciation of the range of possible outcomes that are consistent with what is known or believed to be known concerning ecosystem services valuation. EPA has already applied Monte Carlo methods to some studies (EPA, 1997), and Jaffe and Stavins (2004) have reviewed these and conducted their own analyses. Although these previous applications were not in the context of ecosystem services valuation, they illustrate the feasibility of using Monte Carlo analysis to evaluate environmental policies and suggest that this approach could be applied in ecosystem valuation studies as well.
Catskills Watershed and Edwards Aquifer Cases Studies
In the Catskills case, and as noted previously, the key issue was to compare the cost of watershed restoration with the cost of the alternative to provide the service of water purification (NRC, 2000). While the costs of the alternative—construction of a drinking water filtration system) are relatively certain, the cost of increased watershed protection and restoration is uncertain, as is the effectiveness of a given level of restoration in restoring ecosystem services. The poorly understood link from ecosystem structure and function to services is again the cause of the problem. Uncertainty about the effectiveness of watershed restoration, however, can in this case be subsumed into uncertainty about costs, so that the main issue can be treated as uncertainty about the cost of restoring the ecosystem service of water purification to a level needed by New York City.
The first step in dealing with uncertainty in this case will be to obtain information about the possible costs of watershed restoration. Ideally, a probability distribution over possible costs can be obtained. It may be that the analyst feels able to provide this information without further research, but in many cases this will require modeling the restoration process and then using ecological models to link the final state of the system post-restoration to the levels of ecosystem services provided. This will provide an estimate of the cost of restoring a given level of ecosystem services. Because the parameters of the restoration
process will typically be uncertain, as will those of the ecological models, it would therefore be desirable to use Monte Carlo simulation to study the distribution of restoration costs and service levels. In doing this, the uncertainty associated with the links between ecosystem structure and function on the one hand and ecosystem services on the other are central. At issue is how far one must restore the watershed, in terms of area, land use, and vegetation, in order to provide water purification services at the level required by New York City. There are no existing models that can be readily enlisted to answer this question in a routine way. Monte Carlo simulation will provide a probability distribution over the costs of restoration to an appropriate level. Then, if the decision-maker is risk neutral, the next step is to compare the expected cost of the restoration with the cost of the alternative (i.e., construction of a water filtration system). If some degree of risk aversion is appropriate, then to the expected cost of restoration should be added a risk premium that depends on the degree of risk aversion of the decision-maker and the standard deviation and higher moments of the probability distribution of possible restoration costs, and this total is to be compared with the cost of the alternative.
In the absence of a probability distribution for the restoration costs, the best approach is probably to construct three scenarios for restoration costs: a best case, worst case, and expected case. These might, for example, amount to $1 billion, $2.2 billion, and $1.6 billion. If the restoration cost is less than the replacement cost for each cost value, the choice is simple—restoration is preferable to the alternative. This would be the case provided that the worst case restoration cost is less than the cost of a new filtration system (i.e., less than about $8 billion; NRC, 2000).
A more complex case would arise when the range of restoration costs crosses the cost of replacement—for example, when the three restoration cost estimates are $1.5 billion, $9 billion, and $2.5 billion with a replacement cost of $8 billion. If probabilities were available to attach to these numbers, then an expected cost could be calculated and adjusted to allow for risk aversion, and the risk-adjusted expected restoration cost could be compared with the replacement cost.
In the case of the Edwards Aquifer, which provides water to San Antonio, Texas, uncertainty arises from several sources—one of which is our inability to forecast recharge rates for the aquifer. The dynamics of the aquifer can be written as:
Here, St is the stock of water in the aquifer at date t and Rt and Ct are the recharge and consumption rates, respectively. The consumption rate is relatively predictable and indeed can be controlled to some degree by limitations on water use, whereas the recharge rate depends on weather, which is inherently stochastic. There may also be a trend in the recharge rate associated with changing patterns of rainfall as a result of climate change and another resulting from land
development in the intake region of the aquifer, which by increasing the amount of impervious surface can reduce the amount of water collected in the aquifer for any given level of rainfall. There are several other factors that aquifer managers have to take into account, including whether the structure of the aquifer may be damaged if water stocks are drawn down too low, and whether there are any endangered species that live in the aquifer and can be harmed by low water levels. The lowest level to which the water stock has fallen to date is an important variable because this can affect the health of aquifer-specific species. The precise ways in which the structure of the aquifer and the prospects of any endangered species depend on the minimum water level is far from clear, so this relationship is an additional source of uncertainty.
How should these considerations affect the value that resource managers place on water in the aquifer? If managers are risk averse, the recognition of uncertainty will tend to increase the value of water stocks in the aquifer. The fact that in a stochastic world there is a chance of little or no rainfall in the coming years and therefore of little or no replenishment of the water stock in the aquifer means that current stocks might possibly have to last through a long dry period, which adds to the value of having a slightly higher stock. Thus, the marginal value of a unit of water will be higher because of the risk. Likewise, the possibility of damage to endangered species or to the structure of the aquifer because of low water levels increases the value of existing water stocks, because in addition to providing more water for consumption, a higher stock will lower the risk of damage from a future low stock level.
The value of the aquifer considering uncertainty about future replenishment can be approximated by Monte Carlo simulation, using the equation for the dynamics of the aquifer with alternative future replenishment patterns that draw probabilistically from a distribution of future replenishment rates. It is also worth noting that if the structure of an aquifer can be damaged irreversibly by allowing the water level fall too low, then there may be an option value associated with the preservation of water levels above a minimum. This is the type of context in which such values are applicable—there is a possible irreversible change, as well as the opportunity to learn more about the aquifer system’s responses over time.
These two cases indicate that it is conceptually straightforward to see how the analyst should allow for uncertainty in valuation studies. Application of the concepts requires that the uncertainty be characterized to some extent and that the analyst understands decision-makers’ attitudes toward uncertainty. Even if a characterization of the uncertainty is not available, it will often be possible, as in the case of the Edwards Aquifer, to state clearly what the qualitative impact of uncertainty will be—whether it will raise or lower a value—even though it may not be possible to measure the extent of this change.
SUMMARY: CONCLUSIONS AND RECOMMENDATIONS
The valuation of aquatic and related terrestrial ecosystem services inevitably involves investigator judgments and some amount of uncertainty. Although unavoidable, uncertainty and the need to exercise professional judgment are not debilitating to ecosystem valuation. It is important to be clear however when such judgments are made, to explain why they are needed, and to indicate the alternative ways in which judgment could have been exercised. It is also important that the sources of uncertainty be acknowledged, minimized, and accounted for in ways that ensure that a study’s results and related decisions regarding ecosystem valuation are not systematically biased and do not convey a false sense of precision.
There are several cases in which investigators have to use professional judgment in ecosystem valuation regarding how to frame a valuation study, how to address the methodological judgments that must be made during the study, and how to use peer review to identify and evaluate these judgments. Of these, perhaps the most important choice in any ecosystem services valuation study is the selection of the question to be asked and addressed (i.e., framing the valuation study). The case studies discussed in this chapter illustrate the fact that the policy context unavoidably affects the framing of an ecosystem valuation study and therefore the type and level of analysis needed to answer it. Framing also affects the way in which people respond to any given issue. Analysts need to be aware of this and sensitive to the different ways of presenting data and issues and make a serious attempt to address all perspectives in their presentations because failure to do so could undermine the legitimacy of an ecosystem services valuation study.
In most ecosystem valuation studies, an analyst will be called on to make various methodological judgments about how the study should be designed and conducted. Typically, these will address issues such as whether, and at what rate, future benefits and costs should be discounted; whether to value goods and services by what people are willing to pay or what they would be willing to accept if these goods and services were reduced or lost; and how to account for and present distributional issues arising from possible policy measures. In many cases, different choices regarding some of these issues will make a substantial difference to the final valuation.
The unavoidable need to make professional judgments in ecosystem valuation activities through choices of framing and methods suggests that there is a strong case for peer review to provide input on these issues before study design is complete and relatively unchangeable. There are several major sources of uncertainty in the valuation of aquatic ecosystem services and options for the way policymakers and analysts can and should respond. Model uncertainty arises for the obvious reason that in many cases the relationships between certain key variables are not known with certainty (i.e., the “true model” will not be known). Chapter 3 discusses the relationship between ecological structure and function and the provision of aquatic ecosystem goods and services to the com-
munity; however, this relationship is often poorly understood and will be the greatest single source of uncertainty in many studies of the value of aquatic ecosystems. On the economic side, an analyst might not know the extent to which society’s willingness to pay for an ecosystem service depends on the way in which that service is provided. Parameter uncertainty is one level below model uncertainty in the logical hierarchy of uncertainty in the valuation of ecosystem services.
The almost inevitable uncertainty facing analysts involved in ecosystem valuation can be more or less severe depending on the availability of good probabilistic information and the amount of ambiguity. A favorable case would be one in which, although there is uncertainty about some key magnitudes of various parameters, the analyst nevertheless has good probabilistic information. An alternative and common scenario in ecosystem valuation is one in which there is really no good probabilistic information about the likely magnitudes of some variables, and what is available is based only on expert judgment.
Just as there are different types of uncertainty in ecosystem valuation, there are also different ways and decision criteria that an analyst can use to allow for uncertainty in the support of environmental decision-making. One of these is the use of Monte Carlo simulations as a method of estimating the range of possible outcomes and the parameters of its probability distribution. A key assumption in ecosystem valuation models is that individuals seek to maximize their utility and that they will be indifferent to changes that leave their utility unchanged. Under uncertainty, this implies they maximize their expected utility. Although widely used in economic analyses, the expected utility assumption has been controversial, since in some contexts its predictions are not consistent with observed behavior. Alternative theories of behavior under uncertainty have been proposed, including prospect theory and regret theory.
The outcome of an environmental policy choice under uncertainty is necessarily unpredictable, and risk aversion is a measure of what a person is willing to pay to avoid an uncertain outcome. In a heterogeneous population, the analyst will have to make an assumption about the level of risk aversion that is appropriate for the group as a whole. If society is extremely risk averse, then the objective of maximizing the value of the aggregate expected utility can be replaced by an objective known as maximin. Focusing exclusively on the worst possible outcome is justified, however, only if there are good reasons to suppose that society is really risk averse and is willing to sacrifice considerable potential gain from a policy to avoid any chance of a bad outcome. Implementing the maximin criterion does not require probabilities; it requires only that the worst possible outcome be identified, so it is particularly suited to valuation conditions for which no probabilities are available. A logical extension of this line of thinking leads to concepts such as the precautionary principle and the idea of a safe minimum standard, which are summarized below.
Although there is considerable uncertainty regarding the value of ecosystem services, there is often the possibility of reducing this uncertainty over time through passive and/or active learning. Regardless of its source, the possibility
of reducing uncertainty in the future through learning can affect current decisions, particularly when the impacts of these decisions are (effectively) irreversible, such as the construction or removal of a dam. With learning, an option value needs to be incorporated into the analysis as part of the expected net benefits that reflects the value of the additional flexibility. This flexibility allows future decisions to respond to new information as it becomes available. It follows that with the possibility of learning, in a cost-benefit analysis the measurement of the benefits of ecosystem protection through ecosystem valuation should consider the possibility of learning (i.e., should incorporate the option value). At present, only a limited amount of empirical work has been done on estimating the magnitude of option value. A natural extension of the observation that better decisions can be made if one waits for additional information is through the use of adaptive management. Adaptive management provides a mechanism for learning systematically about the links between human societies and ecosystems, although it is not a tool for ecosystem valuation or a method of valuation per se.
Another approach to environmental decision-making under uncertainty is embodied by the precautionary principle as articulated in the 1992 Rio Declaration (Article 15). The precautionary principle is widely cited by the environmental community as a justification for erring on the side of conservation in situations of uncertainty. However, it is not clear that the precautionary principle brings anything new to the decision criteria frameworks usually used by economists. With learning and under conditions of irreversibility, option values may similarly move environmental policy decisions in the direction of environmental conservation, more so if learning can be actively pursued through an adaptive management approach and especially if there is the chance of a significantly negative outcome from environmental impacts. In such cases, risk aversion will normally move environmental decisions in the same direction. While there may be an option value associated with ecosystem conservation, there may also be an option value associated with not adopting conservation policy measures that require significant investments.
Related in some ways to the precautionary principle is the concept of a safe minimum standard, which introduces a class of choices in which decision-makers seek to maintain population or ecosystem levels sufficient for survival. Under this approach, the presumption is that the necessary population size should be maintained, unless the costs of doing so are prohibitively high. The most striking example of this in the United States is the ESA.13 Choosing one bound or safe minimum standard over another requires some justification and supporting analysis. Once a safe minimum standard is chosen however, valuation is not needed, but valuation may be needed in setting the safe minimum standard.
Based on these conclusions, the committee makes the following recommendations regarding judgment and uncertainty in ecosystem valuation activities and methods and approaches to effectively and proactively respond to them:
-
Analysts must be aware of the importance of framing in designing and conducting ecosystem valuation studies so that the study is tailored to address the major questions at issue. Analysts should also be sensitive to the different ways of presenting study data, issues, and results and make a concerted attempt to address all relevant perspectives in their presentations.
-
The decision to use WTP or WTA as a measure of the value of an ecosystem good or service is a choice about how an issue is framed. If the good or service being valued is unique and not easily substitutable with other goods or services, then these two measures are likely to result in very different valuation estimates. In such cases the analyst should ideally report both sets of estimates in a form of sensitivity analysis. However, the committee recognizes that in some cases this may effectively double the work and in such situations a second best alternative is to document carefully the ultimate choice made and clearly state that the answer would probably have been higher or lower had the alternative measure been selected and used.
-
Because even small differences in a discount rate for a long-term environmental restoration project can result in order-of-magnitude differences to the present value of net benefits, in such cases, analysts should present figures on the sensitivity of the results to alternative choices for discount rates.
-
Ecosystem valuation studies should undergo external review by peers and stakeholders early in their development when there remains a legitimate opportunity for revision of the study’s key judgments.
-
Analysts should establish a range for the major sources of uncertainty in an ecosystem valuation study whenever possible.
-
Analysts will often need to make an assumption about the level of risk aversion that is appropriate for use in an ecosystem valuation study. In such cases, the best solution is to state clearly that the assumption about risk aversion will affect the outcome and conduct sensitivity analyses to indicate how this assumption impacts the outcome of the study.
-
There is a need for further research about the relative importance of, and estimating the magnitude of, option value in ecosystem valuation.
-
Under conditions of uncertainty, irreversibility, and learning, there should be a clear preference for environmental policy measures that are flexible and minimize the commitment of fixed capital or that can be implemented on a small scale on a pilot or trial basis.
REFERENCES
Arrow, K., and L. Hurwicz. 1972. An optimality criterion for decision-making under ignorance. In Uncertainty and Expectations in Economics, C.F. Carter and J.L. Ford (eds.). Oxford, U.K.: Basil Blackwell.
Arrow, K., and A. Fisher. 1974. Environmental preservation, uncertainty, and irreversibility. Quarterly Journal of Economics 98:85-106.
Berrens, R.P. 1996. The safe minimum standard approach: An alternative to measuring non-use values for environmental assets? Pp. 195-211 in Forestry, Economics and the Environment, W.L. Adamowicz, P. Boxall, M.K. Luckert, W.E. Phillips, and W.A. White (eds.). Wallingford, U.K.: CAB International.
Berrens, R., D. Brookshire, M. McKee, and C. Schmidt. 1998. Implementing the safe minimum standard. Land Economics 74:147-161.
Bingham, G., R. Bishop, M. Brody, D. Bromley, E. Clark, W. Cooper, R. Costanza, T. Hale, G. Hayden, S. Keller, R. Norgaard, B. Norton, J. Payne, C. Russell, and G. Suter. 1995. Issues in ecosystem valuation: Improving information for decision making. Ecological Economics 14(2):73-90.
Bishop, R.C. 1978. Endangered species and uncertainty: The economics of a safe minimum standard. American Journal of Agricultural Economics 60(1):10-18.
Carpenter, S.R., D. Ludwig, and W.A. Brock. 1999. Management and eutrophication for lakes subject to potentially irreversible change. Ecological Applications 9:751-771.
Carson R., R. Mitchell, M. Hanemann, R.J. Kopp, S. Presser, and P.A. Ruud. 2003. A contingent valuation and lost passive use: Damages from the Exxon Valdez oil spill. Environmental and Resource Economics 25:257-286.
Chetty, R. 2003. A new method of estimating risk aversion. NBER Working Paper 9988. Available on-line at http://www.nber.org/papers/w9988. Accessed June 15, 2004.
Chichilnisky, G. 1997. The costs and benefits of benefit-cost analysis. Environment and Development Economics 2:202-5.
Ciriacy-Wantrup, S.V. 1952. Resource Conservation: Economics and Policies. First Edition. Berkeley, Calif.: University of California Press.
Claude, H., and M. Henry. 2002. Formalization and Applications of the Precautionary Princicple. Ecole Polytechnique. Available on-line at http://www.columbia.edu/itc/economics/henry/G6426/pdfs/Pp_aer.pdf. Accessed January 24, 2005.
Demers, M. 1991. Investment under uncertainty, irreversibility, and the arrival of information over time. Review of Economic Studies 58:333-350.
EPA (U.S. Environmental Protection Agency). 1997. Guiding Principles for Monte Carlo Analysis. EPA/630/R-97/001. Washington, D.C.: Risk Assessment Forum.
Epstein, L. 1980. Decision making and the temporal resolution of uncertainty. International Economic Review 21:264-83.
Farmer, M.C., and A. Randall. 1998. The rationality of a safe minimum standard. Land Economics 74(3):287-302.
Fisher, A., and M.W. Hanemann. 1986. Option value and the extinction of species. Volume 4 in Advances in Applied Microeconomics, V.K. Smith (ed.). Greenwich, Conn.: JAI Press.
Fisher, A.C., and U. Narain. 2000. Global warming, endogenous risk, and irreversibility. CUDARE Working Paper Series No. 908. Berkeley, Calif.: University of California at Berkeley, Department of Agricultural and Resource Economics and Policy.
Freixas, Z., and J.J. Laffont. 1984. On the irreversibility effect. In Bayesian Models in Economic Theory, M. Boyer and R. Kihlstrom (eds.). Amsterdam: Elsevier.
Ghirardato, P., F. Maccheroni, and M. Marinacci. 2002. Ambiguity from the differential viewpoint. Working Paper no. 17/2002, April 2002, Applied Mathematics Working Paper Series, International Centre for Economic Research. Available on-line at http://www.icer.it. Accessed June 15, 2004.
Gollier, C., B. Jullien, and N. Treich. 2000. Scientific progress and irreversibility: An economic interpretation of the “precautionary principle.” Journal of Public Economics 75:229-253.
Graham-Tomasi, T. 1995. Quasi-option value. In Handbook of Environmental Economics, D.W. Bromley (ed.). Oxford, U.K.: Blackwell.
Gunderson, L.H., C.S. Holling, and S.S. Light. 1995. Barriers and Bridges to the Renewal of Ecosystems and Institutions. New York: Columbia University Press.
Hanemann, M.W. 1991. Willingness to pay and willingness to accept: How much can they differ? American Economic Review 81(3):635-47
Hanemann, M.W. 1994. Valuing the environment through contingent valuation. Journal of Economic Perspectives 8(4):19-43.
Hanemann, M.W., and I.E. Strand. 1993. Natural resource damage assessment: Economic implications for fisheries management. American Journal of Agricultural Economics 75:1188-1193.
Hanemann, M.W. 1989. Information and the concept of option value. Journal of Environmental Economics and Management 16:23-7.
Heal, G.M. 1998. Valuing the Future. New York: Columbia University Press.
Heal, G.M, and B. Kriström. 2002. Uncertainty and climate change. Environmental Resource Economics 23:3-25.
Henry, C. 1974. Option values in the economics of irreplaceable assets. Review of Economic Studies 41:89-104.
Holling, C.S. 1973. Resilience and stability of ecological systems. Annual Review of Ecological Systems 4:1-23.
Jaffe, J., and R. Stavins. 2004. The Value of Formal Quantitative Assessment of Uncertainty in Regulatory Analysis. Available on-line at http://www.aei-brookings.org/admin/authorpdfs/page.php?id=1045. Accessed October 6, 2004.
Kahneman, D., amd A. Tversky. 1979. Prospect theory: An analysis of decisions under risk. Econometrica 47:313-327.
Kahneman, D, and A. Tversky (eds.). 2000. Choices, Values and Frames. New York: Cambridge University Press and the Russell Sage Foundation.
Kolstad, C.D. 1996a. Fundamental irreversibilities in stock externalities. Journal of Public Economics 60(2):221-233.
Kolstad, C.D. 1996b. Learning and stock effects in environmental regulation: The case of greenhouse gas emissions. Journal of Environmental Economics and Management 31(1):1-18.
Kunreuther, H., N. Novemsky, and D. Kahneman. 2001. Making low probabilities useful. Journal of Risk and Uncertainty 23:103-120.
Layard, R., and A.A. Walters. 1994. Income distribution. In R. Layard and S. Glaister (eds) Cost-Benefit Analysis, Second Edition. Cambridge, U.K.: Cambridge University Press.
Lee, K.N. 1993. Compass and Gyroscope: Integrating Science and Politics of the Environment. Washington, D.C.: Island Press.
Lovett, G.M., K.C. Weathers, and M.A. Arthur. 2001. Is nitrate in stream water an indicator of forest ecosystem health in the Catskills. Pp. 23-30 in Catskill Ecosystem Health. M.S. Adams (ed.). New York: Purple Mountain Press.
Machina, M.J. 1987. Choice under uncertainty: Problems solved and unsolved. Journal
of Economic Perspective 1(1):121-157.
Maskin, E. 1979. Decision-making under ignorance with implications for social choice. Theory and Decision 11:319-37.
Nordhaus, W.D. 1994. Expert opinion on climatic change. American Scientist 82:45-52.
NRC (National Research Council). 1996. Understanding Risk in a Democratic Society. Washington, D.C.: National Academy Press.
NRC. 2000. Watershed Management for Potable Water Supply: Assessing the New York City Strategy. Washington, D.C.: National Academy Press.
Palmini, D. 1999. Uncertainty, risk aversion, and the game theoretic foundations of the safe minimum standard: A reassessment. Ecological Economics 29:463-472.
Pindyck, R.S. 2000. Irreversibilities and the timing of environmental policy. Resource and Energy Economics 22(3):233-259.
Portney, P.R. 1994. The contingent valuation debate: Why economists should care. Journal of Economic Perspectives 8(4):3-17.
Randall, A., and M.C. Farmer. 1995. Benefits, costs, and the safe minimum standard of conservation. In The Handbook of Environmental Economics, D.W. Bromley (ed.). Oxford, U.K.: Blackwell.
Rawls, J. 1971. A Theory of Justice. Cambridge, Mass.: The Belknap Press of Harvard University Press
Ready, R., and R.C. Bishop. 1991. Endangered species and the safe minimum standard. American Journal of Agricultural Economics 72(2):309-312.
Ready, R. 1995. Environmental valuation under uncertainty. In Handbook of Environmental Economics, D.W. Bromley (ed.). Oxford, U.K.: Blackwell.
Roughgarden, T., and S.H. Schneider. 1999. Climate change policy: Quantifying uncertainties for damages and optimal carbon taxes. Energy Policy 27(7):415-429.
Walters, C.J. 1986. Adaptive Management of Renewable Resources. New York: McGraw-Hill.
Walters, C., J. Korman, L.E. Stevens, and B. Gold. 2000. Ecosystem modeling for evaluation of adaptive management policies in the Grand Canyon. Conservation Ecology 4(2):1. Available on-line at http://www.consecol.org/vol4/iss2/art1. Accessed March 2, 2005.






























