Appendix B
Household Production Function Models
This appendix discusses in more detail the modeling of household production methods of valuing aquatic ecosystem services discussed in Chapter 4.
Household production function (HPF) approaches involve some form of modeling of household behavior, based on the assumption of either a substitute or a complementary relationship between the environmental good or service and one or more marketed commodities consumed by the household. Examples of these models include allocation of time models for recreation or other activities involving household labor allocation, averting behavior models that account for the health and welfare impacts of pollution, and hedonic price models that account for the impacts of environmental quality on choice of housing.
The underlying assumption in most HPF models is that a household allocates some of its available labor time, and possibly its income, for an activity that is affected in some way by “environmental quality” (i.e., the state of the environment or the goods and services it provides). The household therefore combines its labor, environmental quality, and other goods to “produce” a good or service, but only for its own consumption and welfare (i.e., household utility). By determining how changes in environmental quality influence this household production function and thus the welfare of the household, it is possible to value these changes.
TRAVEL-COST MODELS
Assume a representative household that allocates some of its labor time l for an “environmentally” based activity from which the household derives utility. In this example, assume that this activity is recreational fishing from a mountain lake. The household could be located near the mountains, or it could be traveling from other regions or even different countries to fish in this location.
To capture the effects that this fishing activity has on the household’s welfare, one assumes that the household maximizes a utility function U, representing its welfare level and consisting of
(1)
where x represents all market-purchased consumption goods, lu is the time the household spends on leisure, and z is the number of visits the household makes
to the mountain lake for fishing. The utility function is assumed to have the normal properties of being concave with respect to its individual arguments.
The number of visits by the household is its internal “production function” for recreational fishing at the mountain lake. These visits may depend on the total time l that the household spends traveling to and fishing at the site, the various goods and services v (e.g., mode of travel, expenditures during traveling, and lodging, fishing gear) that the household uses in these activities, and the overall environmental quality of the lake q that makes it particularly suitable for fishing. Thus, the household’s “production” of the number of fishing visits z to the mountain lake is
(2)
Production of z is concave with respect to l and v and will shift with changes in environmental quality of the lake q.
Finally, one assumes that the household has an income based on wage earnings and uses that income to purchase all of its expenditures, including money spent on traveling to and from the lake. Given market prices px and pv for commodities x and v, respectively, and representing the market wage rate earned by the household as w, the household’s budget constraint is expressed as
(3)
with L being the total labor time available to the household and M representing any nonlabor income of the household (e.g., property rents, interest income, dividends). Equation (3) indicates that the total expenditures of the household must equal its total income.
By assuming that the household maximizes its utility from Equation (1) subject to Equations (2) and (3), one can derive the optimal demands for the time and purchased inputs, l* and v*, respectively, that the household spends on recreational fishing. These input demands will depend on the prices faced by the household px, pv, and w, its nonlabor income level M; and the environmental quality of the lake q. By substituting l* and v* into Equation (2), the household’s demand for the optimal number of visits z* to the lake for recreational fishing can be expressed as
(4)
Since the number of visits for recreational fishing is observable for all households that engage in this activity, the demand function in Equation (4) can be estimated empirically across households. Moreover, it is a common practice in many travel-cost models to determine whether households would vary their number of visits if any fees for recreational fishing f also changed. As a result,
the aggregate recreational visit function in Equation (4) estimated across all households would represent the willingness to pay, or demand, of these households for recreational fishing visits to the lake in response to changes in the fee rate f. Changes in environmental quality of the lake would therefore cause this demand curve to “shift,” and the welfare consequences, or value, of this change in environmental quality would be measured by changes in consumer surplus from this shift in the demand for fishing visits.
AVERTING BEHAVIOR MODEL
Instead of z being a desirable commodity such as recreational visits, it could alternatively be “bad,” such as the incidence of waterborne disease from use of a microbially polluted aquatic system as a source of domestic water supply. This implies that ∂U / ∂z < 0 in the utility function from Equation (1). The household may not be able to allocate its labor time to affect the incidence of the disease, but it may be able to allocate expenditures pvv that would mitigate the adverse effects of z or reduce its occurrence. For example, these could be purchases of marketed goods (e.g., bottled water, water filters, medical treatment) or payment for access to public services (e.g., improved sewage treatment or water supply). In addition, any improvements in water quality q may also mitigate the incidence of disease. As a result, Equation (2) is now modified to
(5)
where ∂z/v∂ < 0 and ∂z/∂q < 0. By assuming that the household’s allocation of its labor time is not relevant to this simplified problem, the budget constraint in Equation (3) is now
(6)
where M is total household income, including any labor income. Maximizing the utility function of Equation (1) with respect to Equations (5) and (6) yields the optimal demand for any mitigating good or service purchased v*, as a function of prices px and pv; household income M; and water quality q. By substituting latter demand for v* into the disease incidence function of Equation (5), totally differentiating, and rearranging, one can obtain an estimable reduced form relationship between disease incidence z* and levels of water quality q.
HEDONIC PRICE MODELS
Another possibility is that z is a desirable characteristic of certain residential property (e.g., “good” neighborhood, beautiful scenery or views, beachfront), which is in turn influenced by the services of an aquatic ecosystem (e.g., pristine environment, unpolluted water, good beaches, protected coastline). As a consequence, the market equilibrium for this residential property, and in turn its price P, will be affected by the desirable characteristic and, thus, the ecological services and environmental quality q that influences this characteristic
(7)
For a household purchasing this property, the budget constraint is likely to be
(8)
where M is again total household income and P is the property purchase. Substituting Equation (8) and z(q) into the utility function of Equation (1) for x and z, respectively; totally differentiating with respect to P and q; and rearranging yield the following condition for optimal choice of any ecological service q that affects the value of the residential property:
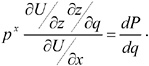
(9)
That is, the marginal willingness to pay for an improvement in environmental quality q must equal its marginal implicit price in terms of the impact of q on property values. Estimation of the hedonic price function in Equation (7) will allow this implicit price to be calculated.




