1
Introduction
The climate of the Earth over its history has varied from “snowball” conditions with global ice cover to “hothouse” conditions when glaciers all but disappeared. Over the past 10,000 years (current interglacial, called the Holocene), the climate has been remarkably stable and favorable for human civilizations to flourish. Even during this stable period there have been notable regional climatic fluctuations such as the so-called Little Ice Age (A.D. 1600-1800), when Europe experienced unusually cold conditions. Increasing evidence points to a large human impact on global climate over the past decades through emissions of greenhouse gases and aerosols and through widespread changes in land cover (IPCC, 2001; NRC, 2001).
Climate change is driven by perturbations to the energy balance of the Earth system. These perturbations are called “climate forcings” and have been the subject of considerable scientific inquiry both for understanding Earth’s history and for projecting future change. Indeed, further enhancing knowledge of climate forcings is critical for improving projections of future climate change. It is in that context that the U.S. Climate Change Science Program asked the National Academies to examine the current state of knowledge regarding the climate forcings associated with gases, aerosols, land use, and solar variability and to identify relevant research needs (see Appendix B for full statement of task). In response, the Committee on Radiative Forcing Effects on Climate was formed (see Appendix A for biographies of committee members). This report provides the committee’s consensus views on the current understanding of different climate forcings, considers alternatives for quantifying and comparing different forcing
agents, and recommends research priorities for attaining a more complete understanding of climate forcing.
EARTH’S CLIMATE SYSTEM
Climate is conventionally defined as the long-term statistics of the weather (e.g., temperature, cloudiness, precipitation). This definition emphasizes the atmospheric and physical components of the climate system. These physical processes within the atmosphere are affected by ocean circulation, the reflectivity of the Earth’s surface, the chemical composition of the atmosphere, and vegetation patterns, among other factors. Improved understanding of how the atmosphere interacts with the oceans, the cryosphere (ice-covered regions of the world), and the terrestrial and marine biospheres has led scientists to expand the definition of climate to encompass the oceanic and terrestrial spheres as well as chemical components of the atmosphere (Figure 1-1). This expanded definition promotes an Earth system approach to studying how and why climate changes.
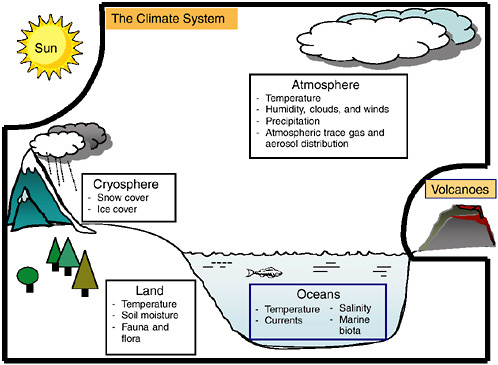
FIGURE 1-1 The climate system, consisting of the atmosphere, oceans, land, and cryosphere. Important state variables for each sphere of the climate system are listed in the boxes. For the purposes of this report, the Sun, volcanic emissions, and human-caused emissions of greenhouse gases and changes to the land surface are considered external to the climate system.
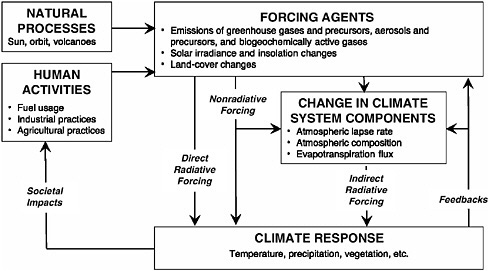
FIGURE 1-2 Conceptual framework of climate forcing, response, and feedbacks under present-day climate conditions. Examples of human activities, forcing agents, climate system components, and variables that can be involved in climate response are provided in the lists in each box.
Factors that affect climate change are usefully separated into forcings and feedbacks. The conceptual diagram of Figure 1-2 illustrates the connections between climate forcings, responses, and feedbacks as defined in this report. A climate forcing is an energy imbalance imposed on the climate system either externally or by human activities. Examples include changes in solar energy output, volcanic emissions, deliberate land modification, or anthropogenic emissions of greenhouse gases, aerosols, and their precursors. A climate feedback is an internal climate process that amplifies or dampens the climate response to an initial forcing. An example is the increase in atmospheric water vapor that is triggered by an initial warming due to rising carbon dioxide (CO2) concentrations, which then acts to amplify the warming through the greenhouse properties of water vapor. Climate change feedbacks are the subject of a recent report of the National Research Council (NRC, 2003).
Climate forcings can be classified as radiative (direct or indirect) or nonradiative. Direct radiative forcings affect the radiative budget of the Earth directly; for example, added CO2 absorbs and emits infrared (IR) radiation. Indirect radiative forcings create a radiative imbalance by first
altering climate system components, which then almost immediately lead to changes in radiative fluxes; an example is the effect of aerosols on the precipitation efficiency of clouds. Nonradiative forcings create an energy imbalance that does not involve radiation directly; an example is the increasing evapotranspiration flux resulting from agricultural irrigation. This report focuses on the forcing agents and the ways in which they act to create a climate response (i.e., downward arrows in Figure 1-2). Although they are not the primary focus of this report, it is necessary at times to address climate responses because of what they tell us about climate forcings. See Box 1-1 and Appendix C for definitions of important terms.
Some times the climate system is defined more broadly by including the Sun, the lithosphere (the Earth’s crust), or even humans as part of the climate system (e.g., Claussen, 2004; Steffen et al., 2004). For the purposes of this report, however, those elements that impact climate but are not affected by it are considered external to the climate system. Changes in solar output are viewed as a natural external forcing because the Earth does not affect the Sun. Volcanic aerosols are also considered a natural external forcing because Earth’s climate does not impact volcanic activity, except on very long timescales. Increases in CO2 and other greenhouse gases due to human activities are assumed to be an external anthropogenic forcing. Defining the climate system in this way allows separation between external climate forcings and internal climate responses to those forcings. This definition is consistent with that adopted in the recent NRC report on climate change feedbacks (NRC, 2003).
The definition of climate forcing and climate response may vary depending on the timescale under consideration. On the timescale of billions of years, greenhouse gas concentrations may both influence climate, through their radiative properties, and be influenced by climatic variations in weathering rates. On the timescale of millions of years, on the other hand, greenhouse gas concentrations are determined largely by slowly evolving tectonic boundary conditions. In this case, greenhouse gas concentrations can be treated as a forcing, and changes in global mean temperature can be considered a response. Over the past 1000 years, CO2 concentrations appear to have varied in response to surface temperature changes prior to large-scale fossil fuel burning during the nineteenth and twentieth centuries, while during the latter period they can be considered primarily as a forcing of surface temperature changes (Gerber et al., 2003).
Given the conventional focus of climatologists on temperature as well as the clear link between greenhouse gases and surface temperature, studies of long-term changes in climate have emphasized temperature as the primary index for climate change. The concept of “radiative forcing” provides a way to quantify and compare the contributions of different agents that affect surface temperature by modifying the balance between incoming and
|
BOX 1-1 Climate system: The system consisting of the atmosphere, hydrosphere, lithosphere, and biosphere, determining the Earth’s climate as the result of mutual interactions and responses to external influences (forcing). Physical, chemical, and biological processes are involved in the interactions among the components of the climate system. Climate forcing: An energy imbalance imposed on the climate system either externally or by human activities.
Climate response: Change in the climate system resulting from a climate forcing. Climate feedback: An amplification or dampening of the climate response to a specific forcing due to changes in the atmosphere, oceans, land, or continental glaciers. NOTE: Additional definitions are provided in Appendix C. |
outgoing radiative energy fluxes. Global radiative forcing at the top of the atmosphere (TOA), as used in assessments by the Intergovernmental Panel on Climate Change (IPCC), is relatively easy to compute in climate models and has straightforward policy applications. However, it has important limitations when applied to radiative forcing agents not conventionally considered as such (e.g., aerosols, land-use change) or when used to measure climatic implications other than global mean temperature (e.g., regional precipitation). To address these limitations, the concept of radiative forcing needs to be expanded; that expansion is a major theme of this report.
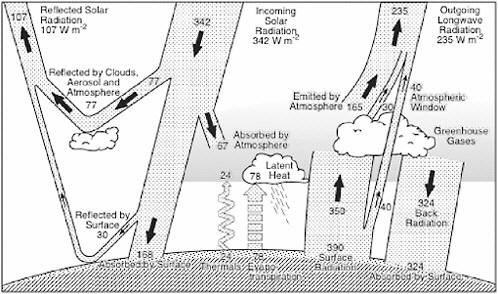
FIGURE 1-3 Energy budget for the atmospheric components of the climate system. SOURCE: Kiehl and Trenberth (1997).
RADIATIVE FORCING: PERTURBATION TO EARTH’S ENERGY BUDGET
The various physical processes that contribute to Earth’s global annual mean energy budget are shown in Figure 1-3. The Earth receives a continuous influx of energy from the Sun. About 69 percent of this energy is absorbed at the Earth’s surface or by the atmosphere, while the rest is reflected back to space. At the same time, the Earth and its atmosphere emit energy to space, resulting in an approximate balance between energy received and energy lost. The so-called greenhouse gases, such as water vapor, CO2, methane (CH4), nitrous oxide (N2O), halocarbons, and ozone (O3), modify this balance by absorbing and then re-emitting some of the outgoing radiation.1 Small particles in the atmosphere (aerosols) also ab-
sorb and scatter some of the outgoing radiation. Changes in the Sun or in the reflective characteristics of the Earth’s surface represent additional perturbations. Knowledge of the natural and anthropogenic processes that affect Earth’s energy balance is critical for understanding how Earth’s climate has changed in the past and will change in the future
The energy budget in Figure 1-3 assumes an exact balance in energy fluxes. In reality, the solar flux, the chemical composition of Earth’s atmosphere, and surface conditions maintain a perpetual state of slight imbalance. For example, solar flux is affected by variability in Earth’s orbit around the Sun and by changes in the intensity of solar output. Radiative forcing provides a conceptual framework for thinking about how Earth’s energy budget can be modified and for quantifying the modifications and their potential impact in terms of surface temperature response. Radiative forcing has traditionally been defined as a change in energy flux at the tropopause resulting from a change in a component external to the physical climate system (see Box 1-2). This definition was used initially in radiative transfer models, in which its application is straightforward (Manabe and Strickler, 1964; Manabe and Wetherald, 1967). In these models, the internal climate state (e.g., thermal structure, clouds, water vapor) is held fixed and the only change made to the model is in a single atmospheric constituent (e.g., CO2 mixing ratio). This constitutes a change in radiative flux with all internal variables held fixed or, in mathematical terms, the partial derivative of the radiative flux with respect to a single constituent.
Initial applications of radiative forcing focused on the immediate change in the radiative flux at the top of the atmosphere. It was soon realized that the stratosphere, the layer of the atmosphere extending from about 10 to 50 km altitude, returns rapidly (in about a year) to radiative equilibrium and is largely decoupled from the surface. In contrast, the surface and the troposphere (the lowest layer of the atmosphere) are strongly coupled through vertical motions. The definition of TOA radiative forcing was thus modified to allow the stratosphere to return to local thermal equilibrium. Such “adjusted radiative forcing” values are the standard reported in the literature today. They are sometimes referred to as the radiative forcing at the tropopause (boundary between the troposphere and the stratosphere), although with a stratosphere in radiative equilibrium this is equivalent to TOA radiative forcing. Stratospheric adjustment is most important for forcings that affect the stratospheric thermal structure, such as well-mixed greenhouse gases. For nonuniform perturbations near the tropopause the adjustment can be quite sensitive to the vertical profile of forcing.
The original estimation of radiative forcing was carried out in terms of a change in the globally averaged radiative flux. For well-mixed gases this provides a reasonable estimate of forcing, but even for these types of gases there is still considerable latitudinal variation in radiative forcing from pole
|
BOX 1-2 A steady state climate system exists when the amount of energy entering the system equals the amount of energy leaving the system. For Earth this means that the amount of solar energy absorbed by the surface-troposphere system equals the amount of longwave energy emitted to space. A simple analogy is that of a bucket with a hole in it. Imagine water flowing into the bucket at some fixed rate. The water will flow out of the bucket at a rate dependent on the size of the hole in the bucket and the depth of the water. The water in the bucket will reach a fixed level once the amount of water leaving the bucket equals the amount entering the bucket. The water flowing into the bucket is analogous to the solar energy flowing into Earth’s system. The amount of water flowing out of the bucket is analogous to the longwave energy leaving Earth’s system. The level of water in the bucket is analogous to Earth’s global heat content (which is determined to a first order by mean temperature and water vapor pressure). The concept of radiative forcing is analogous to a change in either the amount of water flowing into the bucket or the amount of water leaving the bucket. For example, if the hole in the bucket was made smaller, less water would flow out initially and the water level would rise until there was a new balance between what flows into and out of the bucket. This is analogous to increasing a greenhouse gas in Earth’s atmosphere, impeding the escape of longwave radiation to space. An increase in the flow of water into the bucket will also result in an increase in the water level, which is analogous to an increase in solar energy. Both changes lead to increased global heat content, all other factors remaining constant. Radiative forcing is a change in the amount of energy per unit time flowing into or out of Earth’s climate system. |
to equator, which is due mainly to variation in temperature and specific humidity (e.g., Kiehl and Ramanathan, 1982). For tropospheric ozone, tropospheric aerosols, and land surface changes, there is considerable spatial variability in radiative forcing (e.g., Kiehl and Briegleb, 1993; Kiehl et al., 1998; Pielke et al., 2002). Some have argued that spatial variation in forcing is dampened in the climate response because of the homogenization effect from atmospheric transport of heat. However, it is becoming apparent that spatial variations in forcing are important to understanding observed climate signals (e.g., Karl et al., 1995; Hegerl et al., 2003).
Until five years ago the focus in radiative forcing was on changes in tropopause or TOA fluxes. However, early studies on absorbing aerosols (e.g., Ogren and Charlson, 1983) recognized that these aerosols would require a focus on radiative forcing at the Earth’s surface. Recent observations and consequent modeling studies from the Indian Ocean Experiment (INDOEX) found that the presence of absorbing aerosols led to significantly different changes in shortwave radiative flux between the surface and the tropopause because a significant amount of energy is absorbed
within the atmosphere (Ramanathan et al., 2001a). As shown in Chapter 4 (see Box 4-1) the TOA forcing observed during INDOEX over the Indian subcontinent was close to zero, but the surface forcing was −14 W m−2 and tropospheric forcing was about +14 W m−2. As shown by several general circulation model (GCM) sensitivity studies (Ramanathan et al., 2001b; Chung and Ramanathan, 2003; Menon et al., 2002b), in spite of the near-zero TOA forcing, the introduction of absorbing aerosols results in a large surface cooling (−0.5 to −1 K) of the North Indian Ocean and South Asia, a large lower tropospheric warming (0.5 to 1 K), and large changes in regional precipitation. This means that in addition to calculating radiative forcing at the tropopause, one must also quantify radiative forcing at the surface and its atmospheric distribution.
THEORETICAL DEVELOPMENT OF THE RADIATIVE FORCING CONCEPT
The concept of radiative forcing is based on the hypothesis that the change in global annual mean surface temperature is proportional to the imposed global annual mean forcing, independent of the nature of the applied forcing. The fundamental assumption underlying the radiative forcing concept is that the surface and the troposphere are strongly coupled by convective heat transfer processes; that is, the earth-troposphere system is in a state of radiative-convective equilibrium (RCE; see Box 1-3). In the present context, the term “convective heat transfer” refers to heat transport by all types of vertical motions ranging from small (few meters) to planetary scales. The net result of radiative-convective equilibrium is that the vertical temperature profile within the troposphere (the so-called lapse rate) is largely determined by convective heat transport, while the vertically averaged surface-troposphere temperature is regulated by radiative flux equilibrium at the tropopause. RCE models were initially used to determine the vertical temperature profile of stellar (Chandrasekhar, 1947; Ambartsumyan, 1958) and planetary atmospheres (e.g., Chamberlain, 1960; Gierasch and Goody, 1968; Cess, 1972). Its first application to the Earth’s atmosphere with a proper treatment of convective heat transport and the radiative transfer effects of infrared active gases and clouds was published by Manabe and Strickler (1964) and Manabe and Wetherald (1967).
According to the radiative-convective equilibrium concept, the equation for determining global average surface temperature of the planet is
(1-1)
|
BOX 1-3 According to the RCE concept, radiative processes cool the troposphere and warm the ground. As shown in the figure below, the primary source of tropospheric cooling is infrared emission (or radiative cooling) by water vapor and clouds, while the ground warming is due to solar heating and back radiation from atmospheric water vapor and clouds. Such a pattern of atmospheric cooling and surface warming leads to superadiabatic lapse rates (temperature decreasing by more than 9.8 K km−1) and triggers atmospheric convection. The ensuing vertical motions transport heat from the surface to the atmosphere and restore the lapse rate to neutral (adiabatic). The heat is released in the form of latent heating during condensation or as sensible heat from turbulent eddies originating in the boundary layer. 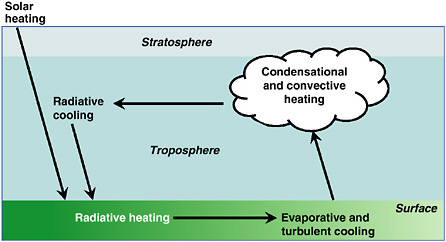 Schematic illustration of the balance between radiative and nonradiative processes under RCE. Arrows indicate direction of energy transfer. Within the troposphere, longwave radiative cooling far exceeds solar heating, resulting in a net radiative cooling. This cooling is balanced by release of latent heating by condensation and precipitation and convective transport of sensible heat transfer from the surface. At the surface, solar heating far exceeds longwave cooling, and this radiative heating is balanced by convective transport of latent and sensible heat from the surface to the atmosphere. In addition, the sum of surface radiative heating and tropospheric radiative cooling is zero, thus maintaining radiation energy balance for the whole surface-troposphere column, and it is this radiation balance that is perturbed by the addition of greenhouse gases and aerosols. Likewise, the sum of convective cooling of the surface and convective heating of the troposphere balance each other, and this balance is perturbed by land surface changes. SOURCE: Adapted from Ramanathan et al. (1989). |
where
(1-2)
is the heat content of the land-ocean-atmosphere system with ρ the density, Cp the specific heat, T the temperature, and zb the depth to which the heating penetrates. Equation 1-1 describes the change in the heat content where f is the radiative forcing at the tropopause, T′ is the change in surface temperature in response to a change in heat content, and λ is the climate feedback parameter (Schneider and Dickinson, 1974), also known as the climate sensitivity parameter, which denotes the rate at which the climate system returns the added forcing to space as infrared radiation or as reflected solar radiation (by changes in clouds, ice and snow, etc.). In essence, λ accounts for how feedbacks modify the surface temperature response to the forcing. In principle, T′ should account for changes in the temperature of the surface and the troposphere, and since the lapse rate is assumed to be known or is assumed to be a function of surface temperature, T′ can be approximated by the surface temperature. For steady state, the solution yields
(1-3)
Studies from one-dimensional radiative convective models initially indicated that λ was a nearly invariant parameter for a variety of forcings (Ramanathan et al., 1985). This finding has generally been supported by three-dimensional modeling studies of climate sensitivity, which indicate that λ varies by only about 25 percent within a particular model, although there can be much greater differences between models (Manabe and Wetherald, 1975; Hansen et al., 1997; IPCC, 2001).
The implication of Equation 1-3 with fixed λ is that surface temperature change is uniquely determined by the radiative forcing at the tropopause (or at the top of the atmosphere if the stratosphere is adjusted for radiative equilibrium). The primary validity for this concept was provided by a series of sensitivity studies by Manabe and Wetherald (1975), who used a three-dimensional GCM to calculate the global mean surface temperature change due to a doubling of CO2 and a 2 percent change in solar insolation. They found that surface temperature estimated by the GCM can be scaled with the initial forcing as in Equation 1-3. Since then, similar sensitivity studies have been performed by other GCMs and basically confirmed Manabe and Wetherald’s result, with most success for perturbations due to uniformly mixed greenhouse gases, changes in incoming solar irradiance, and homogeneously distributed scattering aerosols in the troposphere and the stratosphere (e.g., Cess and Potter, 1988; Hansen et al., 1997).
Highly inhomogeneous perturbations do not show as good a scaling. In addition, successful scaling for global mean surface temperature does not necessarily imply similar success for other climate variables such as precipitation (e.g., Chen and Ramaswamy, 1996).
The RCE concept and the formulation of Equation 1-3 for radiative forcing and feedback have thus been used since the 1960s, implicitly (Budyko, 1969; Kellogg and Schneider, 1974) as well as explicitly (Moller, 1963; Yamamoto and Tanaka, 1972; Schneider and Mass, 1975; Cess, 1976; and hundreds of studies since then). The term radiative forcing was not in vogue until the 1980s, although the climate forcing, feedback, and response framework was implicit in the 1979 “Charney Report,” the NRC’s first report addressing the potential for human-caused climate change (NRC, 1979). Early references introducing this terminology for anthropogenic changes are seen in Ramanathan et al. (1985) and the World Meteorological Organization report on atmospheric ozone (WMO, 1985; republished as Ramanathan et al., 1987), which also gives a detailed and still-accepted definition of radiative forcing. Early use of the term radiative forcing also can be found in the NRC report Toward an Understanding of Global Change (NRC, 1988) and the IPCC reports published in 1990, 1992, and 1996 (IPCC, 1990, 1992, 1996). During the early phases of its use, radiative forcing was not restricted to changes external to the climate system but was used in a more general sense. For example, the radiative effects of clouds were referred to as “cloud-radiative forcing” (Charlock and Ramanathan, 1985) because clouds introduce spatial and temporal gradients in radiative heating. After the IPCC Second Assessment Report (IPCC, 1996), the term radiative forcing came to imply climate forcing (i.e., a term that forces climate changes).
An important construct in the formulation of the concept of forcing is that the equilibrium of the Earth system must have matching incoming and outgoing energy fluxes. Over long time periods the proposition that the Earth is in thermal equilibrium with its surroundings must hold, but the timescale for relaxation of the entire system to this equilibrium may be as long as 2000-3000 years2 for some forcings and the associated feedbacks. Current understanding of the climate response to radiative forcing relies heavily on climate equilibrium simulations rather than on transient responses. The uncertainty and variability of the predicted short-term (i.e., less than a couple of years) climate changes are high since many of the important processes parameterized in climate models have been tuned to
match climate statistics over decadal timescales. Simulating short-term regional climate change requires methods of downscaling large-scale information. Currently this is accomplished either through statistical approaches or by forcing a regional model with boundary conditions from a global climate model.
THE RADIATIVE FORCING CONCEPT AND CLIMATE POLICY
The concept of radiative forcing has provided a clear mechanism for conceptualizing the Earth’s climate as a closed system with a detectable metric of change: global mean surface temperature. The metric is easily understandable and readily correlated to global-scale geological, oceanographic, and biological changes (e.g., ice caps melting, sea level rising, ecosystems changing). The projected changes in climate have been translated into economic costs (with varying uncertainty), providing a direct relationship between radiative forcing and economic impacts. This relationship enables policy makers to consider the relative benefits of investments in new technologies, emissions regulations, carbon taxes, sequestration and offsetting, and emissions trading. This conceptual framework is illustrated in Figure 1-4.
For most policy applications, the relationship between radiative forcing and surface temperature is assumed to be linear, thereby making it possible to add different forcings to assess the overall climate impact. As discussed above, the linearity of response in several GCM experiments using the radiative forcing of homogeneously distributed greenhouse gases supports this approach as do summary diagrams compiled to compare different radiative forcings, such as those presented in the IPCC reports (see Figure 2-1 of this report). In these diagrams, it is often assumed that the bars from different sources may be added to give an overall effect although this is not entirely correct.
The simplification of complex, mechanistically disparate processes to the same radiative forcing metric, with the implication that positive forcings may cancel negative forcings, provides a way of easily communicating climate forcing factors and their relative importance to general audiences. However, a net zero global mean radiative forcing may be associated with large regional or nonradiative (e.g., precipitation) changes. Further, when forcings are added, uncertainties in individual forcings must be propagated, resulting in large uncertainties in the total forcing. Adding forcings also belies the complexity of the underlying chemistry, physics, and biology. It suggests that all effects on climate can be quantified by a similar metric without knowing, or needing to know, the details of the climate response as captured in feedback effects. Yet there are many aspects of climate change—including rainfall, biodiversity, and sea level—that are currently not related quantitatively, much less linearly, to radiative forcings.
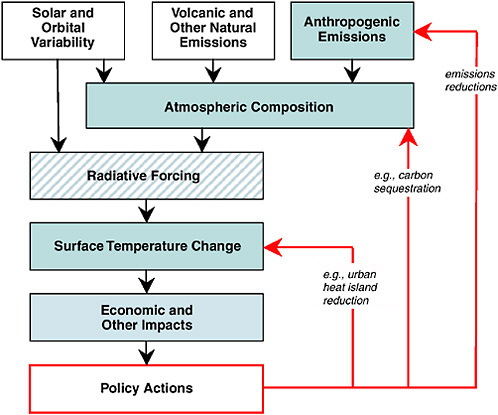
FIGURE 1-4 Conceptual framework for how radiative forcing fits into the climate policy framework. Blue-shaded boxes indicate quantities that have been considered as policy targets in international negotiations and other policy analyses. Radiative forcing (striped box) has not been treated as a policy target in the same explicit way that limiting emissions (e.g., Kyoto Protocol), limiting concentrations (e.g., greenhouse gas stabilization scenarios), and limiting temperature changes and impacts (e.g., environmental scenarios) have. That is, an explicit cap on anthropogenic radiative forcing levels has not been proposed analogous, for example, to the Kyoto Protocol cap on emissions. Note that land-use change has not received much attention as a forcing agent and is not included here, though this report recommends that it should be.
Simple Climate Models
The radiative forcing concept has been employed in simple climate models that rely on the assumption that climate sensitivity is constant. These models often use formulas for the radiative forcing for individual greenhouse gases, such as those published by the IPCC. A well-known
example is the formula for the forcing f(t) for CO2 expressed in units of watts per square meter with a coefficient from IPCC (2001):
(1-4)
where CO2(t) is the atmospheric concentration of CO2 for year t. Such models can relate greenhouse gas emissions to the equilibrium global averaged temperature changes and, using transient oceanic heat uptake models, to transient temperature changes and impacts. For short-lived species, such as aerosols, expressions of the type of Equation 1-4 are not available due to the great spatial variability in concentrations and optical properties.
When linked to socioeconomic models, simple climate models have become a powerful tool for policy analysis, often referred to as “integrated assessment” models (Manne et al., 1995; de Vries et al., 2000; Nordhaus and Boyer, 2000; Roehrl and Riahi, 2000; Matsuoka et al., 2001). They can be linked to an economic “damage” function that simulates the economic impacts and damages of global warming. The system may be further coupled to an optimization scheme to determine optimal investment rates in reductions of greenhouse gas emissions. In these optimization schemes the damage function is dependent on the global averaged surface temperature, while the cost function depends on the level of greenhouse gas emissions abatement (Nordhaus and Boyer, 2000). The simplified “box” approach to climate modeling used in most integrated assessment models is subject to criticism for ignoring regional temperature changes. The current dearth of regionally specific data on damages and their economic costs is a key limitation as well.
Integrated assessment models have been used to evaluate many climate policy questions. Most recently they have been part of the burgeoning suite of studies that evaluated the Kyoto Protocol treaty for greenhouse gas emissions targets for the years 2010-2015 (Kyoto Protocol, 1997). Various emissions pathways were studied in terms of their overall cost-benefit ratios (Nordhaus and Boyer, 2000). The policy targets can be limits on emissions rates as in the Kyoto Protocol; limits on greenhouse gas concentrations, which is the approach for stabilization studies; or limits on the rate of global warming as in the case of environmentally oriented scenarios. These possible policy targets are shown by the shaded boxes in Figure 1-4. Although radiative forcing is inherent to integrated assessment models, radiative forcing per se has not been treated as a climate policy target.
Global Warming Potentials and Greenhouse Gas Equivalence Models
Many climate policy questions require comparing the climate change effects of different greenhouse gases, aerosols, and other forcings. Such comparisons are integral to the formulation of climate treaties and the assessment of progress toward greenhouse gas emissions reductions. For example, if one party to a climate target achieves emissions reductions in CO2, and another party focuses on CH4, some metric is needed to compare these reductions in order to assess overall progress toward the target.
Policy analysts have sought a simple basis for quantitatively comparing the radiative consequences of emissions of different gases. The concept of global warming potential (GWP) was developed to address this need. GWPs compare the integrated radiative impact of a one time-unit of emissions of greenhouse gas X to the integrated radiative forcing impact of a one time-unit of CO2 emissions (IPCC, 2001). Mathematically, GWP is expressed as
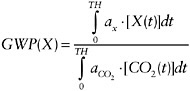
(1-5)
where TH is the time horizon over which the calculation is considered and ax is the radiative efficiency of gas X, or the increase in radiative forcing for a unit increase in the atmospheric abundance of the substance. This radiative efficiency is typically expressed in units of W m−2 kg−1. The parameter X(t) is the time decay profile for the gas following its release into the atmosphere. The corresponding factors for CO2, the reference gas, are in the denominator. Scaling the radiative impact of other forcings by that of CO2 makes it easier to compare forcings quantitatively to each other, but this approach has been criticized because it depends on how well the radiative impact of CO2 is understood. A change in the denominator of Equation 1-5 requires that the whole set of GWPs be revised, potentially introducing confusion.
The radiative forcing formulas (e.g., Equation 1-4) are used in the calculation of the efficiency term ax. The marginal increase in radiative forcing can be calculated as the first derivative of the radiative forcing with respect to concentration. For low-concentration gases, such as chlorofluorocarbons (CFCs), whose radiative forcing increases linearly with concentration, this derivative is a constant. For more abundant gases such as CO2, the derivative—and marginal radiative forcing response—depends on the background atmospheric concentration at the time of the hypothetical pulse
release of the gas. The IPCC calculates GWPs for the well-mixed gases for three discrete time horizons of 20, 100, and 500 years. The Kyoto Protocol recommends that parties to the treaty use the 100-year value for comparing emissions reductions of different gases toward meeting targeted greenhouse emissions reductions for the first commitment period of 2008-2012 (Kyoto Protocol, 1997).
Application of the GWP concept has mainly been restricted to the long-lived greenhouse gases. In principle, it could be applied to short-lived forcing agents such as ozone and aerosols or, more specifically, to the emissions of their precursors (e.g., Schwartz, 1993), but there are a number of complicating factors including (1) the often poorly defined relationship between the precursor and the radiative forcing agent; (2) the inhomogeneity of the forcing; and (3) the much shorter time horizons (decades or less) relevant to the radiative forcing from these short-lived agents. In addition, the current concept is not useful for evaluating how the rate of technical transformation, which depends on economic and policy drivers, affects the trade-off between two greenhouse gases. At present, integrated assessment models are used to consider the combined scientific and economic factors that contribute to the global warming impacts of different forcings (e.g., Manne and Richels, 2001).
Many criticisms of the oversimplicity of the GWP approach have been published (Lashof, 2000; O’Neill, 2000; Smith and Wigley, 2000a,b). More complex equivalence calculations, such as the “forcing equivalence index” of Wigley (1998), have been developed to address its shortcomings. The essence of the forcing equivalence index is that a time series of emissions of a greenhouse gas produces a time series of radiative forcings. By inverting this temporal profile of radiative forcing in terms of the atmospheric properties of another greenhouse gas, the “equivalent” emissions of the alternative gas are estimated. This calculation, like the GWP, does not fully treat the complexities of the long-term behavior of the two gases (O’Neill, 2000).

















