5
Education
This chapter explores the possibility of constructing a satellite account for education within a framework that is compatible with the national accounts. During their younger years, individuals spend a large percentage of their nonmarket time engaged in school-related activities. The focus then tends to shift from formal to informal education and from school-based learning to work-related training as individuals become adults—but education continues. Because its benefits are realized over an extended period, education should be thought of as an investment in human capital. Early economists such as Adam Smith and John Stuart Mill recognized this fact.1 Although the nation’s gross domestic product (GDP) includes expenditures for education, it fails to capture fully the contribution of nonmarket time spent in education to future economic growth, the well-being of individuals, and society in general. Individuals with a higher level of education tend to earn higher incomes; have higher productivity in the workplace and elsewhere; be better informed about and more involved in community activities; and generally report that they are happier.
Satellite accounts for education would be useful to researchers and policy makers in at least three ways. First, nonmarket inputs such as time—including the
time of students, parents, and others—and social capital are important aspects of investment in education, and they are missed in the traditional National Income and Product Accounts (NIPAs). Looking at all education inputs, and their related outputs, would form a more complete picture. Second, human capital, particularly that arising from education, is large relative to the nonhuman capital stock measured by the Bureau of Economic Analysis (BEA). By one estimate, more than two-thirds of national income in recent years is a return to past investments in schooling and to work experience (Krueger, 1999). Separate education accounts would contain data essential for improving our understanding of how investment and the capital stock, defined more broadly to include both human and nonhuman capital, affect economic growth. Third, the education sector is large and important in its own right. Understanding trends in output and productivity in the education sector, both public and private, therefore is of interest.
CONCEPTUAL FRAMEWORK
In this chapter we discuss the components of an education satellite account, including inputs and outputs, focusing primarily on formal education and the significant measurement issues it involves. There are difficulties on both the input and the output side: How does one value time that is not transacted in an explicit market? How does one define and value the output of education, given that it is not directly traded and not directly observed? Regardless of the methodology employed, a goal is to have independent estimates of inputs and outputs—both market and nonmarket—in nominal and constant dollars, to allow for the estimation of productivity.
The emphasis of this chapter is on formal education, in part because data on informal education and training are limited.2 This is not to imply that the role of families in preparing young children for school early in life or on-the-job-training and other sources of informal education later in life are unimportant. Rather, we do not discuss these less formal investments only because their magnitude and effects are difficult or impossible to measure at present. The scope of the chapter also excludes other factors, such as health and the role of social capital, that may enhance or impinge on education.3 By looking at formal education, the chapter highlights approaches that could be used to produce more comprehensive education accounts and measurement issues that would arise in the construction of such accounts.
The National Center for Education Statistics, the Bureau of Labor Statistics (BLS), and the Census Bureau, as well as the National Education Association and
|
2 |
Schools and their staffs also provide child care services, which are valued by parents, but these services can be considered a separate joint product of having children attend school, rather than an output of education itself. |
|
3 |
Social capital is defined in Chapter 1; see Chapter 6 for a discussion of accounting for health. |
other private organizations and researchers, have compiled a wealth of data on education. These sources are used by the BEA in constructing its education-related estimates. The BEA estimates expenditures for both government-provided and privately provided education. In general, only expenditures for market inputs are included, although an imputation is made for capital services from fixed assets (e.g., equipment, structures, and computer software).4 Expenditures for meals, rooms, and entertainment are excluded. Quantities at the category level are generally estimated as nominal expenditures deflated by a weighted input cost index. Aggregates are then created with cost weights for government-provided education and revenue weights for privately provided education.5 The prices of inputs to education generally are not adjusted for changes in quality, but there is an adjustment for changes in teaching staff composition.6 The BEA index of public school teaching staff composition is based on an index of the number of teachers weighted with salaries cross-classified by years of experience and highest degree obtained. As the existing accounts do not measure output independently of inputs, it is impossible to estimate productivity in either the public or the private education sector. The BEA is now studying the feasibility of constructing output measures independently from input measures for public education (Fraumeni et al., 2004).
Information is available on market inputs to education, such as teachers, buildings, and books, but not on nonmarket inputs, such as social capital and time, including the time of students, parents, and others. Outputs cannot be measured easily. Counting numbers of students enrolled is not the same as measuring the amount of education received, although years of schooling is a strong predictor of earnings and other economic outcomes.
The value of nonmarket inputs to education could well be larger than market and government expenditures for education, estimated to be approximately $628 billion in 2001, though without specific estimates for the value of nonmarket inputs it is difficult to know for sure.7 To begin conceptualizing how a satellite account might be structured to give a more comprehensive picture of education, it is useful to identify the relevant inputs and outputs, as is done in Table 5-1.
Market inputs include paid labor, materials, and fixed capital; nonmarket inputs include volunteer labor, students’ and parents’ time, and social capital.
|
4 |
The capital services from these assets are set equal to consumption of fixed capital (depreciation). These imputed capital services are allocated to consumption. |
|
5 |
Estimates for education are included in the NIPAs and in the BEA’s GDP by industry accounts. Some real estimates depend on indexes from sources other than the BEA, but these are input based measures. |
|
6 |
Quality adjustments are made for some inputs that are not specific to education, the most notable being the quality adjustments made to the price index for computers. |
|
7 |
See the discussion of the value of time that primary and secondary students devote to their education in Chapter 1. All BEA data in this chapter are of a pre-December 2003 comprehensive revision vintage. |
TABLE 5-1 Education Inputs and Outputs, Market and Nonmarket
|
Inputs |
Outputs |
|
Paid labor |
Educated individuals |
|
Teachers and support staff |
Higher income from being more educated, higher workplace and nonmarket productivity |
|
Volunteer labor |
|
|
Parent Time |
Intangibles |
|
Student Time |
Better informed citizens, improved individual and societal well-being |
|
Materials |
|
|
Books and other |
|
|
Fixed capital |
|
|
School buildings and other structures, equipment, and computer software |
|
|
Social capital |
Students learn more with teachers, books, facilities, and help from others than without these inputs. Volunteer labor is listed separately as an input to capture the unpaid time spent by people other than students and their parents (see the discussion of volunteer labor in Chapter 7). Students bring to the learning process aptitude and attitude, the latter of which can be strongly influenced by the social environment in which they live. Family, community, and peer attitudes all clearly can influence a student’s attitude toward learning.
The output of education is educated individuals who are more productive and thus earn higher incomes and also contribute to society in other, less tangible, ways. A possible measurement methodology is to estimate the value of education by the amount that an increase in education raises an individual’s earnings. Higher productivity is also an output of education. If the time of more educated individuals is treated as a more valuable input than the time of less educated individuals, estimates of productivity will not rise as the workforce becomes more educated. But if labor inputs are not quality adjusted in this way, one of the effects of an increase in education levels would be an increase in estimated productivity in the sectors that employ more educated workers. It would be incorrect, however, to count both this increase in productivity and the higher earnings of more educated workers in determining the return to education. Intangible outputs, especially those that may accrue to society as a whole rather than to the individual receiving an education, are apt to be particularly difficult to measure.
An education satellite account can incorporate nonmarket inputs and outputs. In addition, there may be more flexibility to experiment with alternative measures of market inputs and outputs in a satellite account. Education occurs in a complex environment in which many elements may influence both the quantity
and the quality of education received, and the benefits of that education for the recipients and for society. Accordingly, both conceptual and measurement issues must be confronted.
Recommendation 5.1: An education satellite account, presented in nominal and real dollars, should be produced by the Bureau of Economic Analysis in collaboration with the National Center for Education Statistics (NCES).
MEASURING AND VALUING INPUTS
Market and government inputs to education can be estimated relatively easily, but estimating nonmarket inputs (other than those originating from the government) is difficult. A variety of data on market and government inputs to education are available, but data on nonmarket inputs are harder to find and much less complete.
Market and Government Inputs
Market and government inputs to education account for a substantial share of GDP: Table 5-2 gives a snapshot of the sources and uses of expenditures on education in 2001, and Table 5-3 gives a historical perspective. From the mid-1960s onward, education expenditures as a percentage of GDP hovered in the 5-6 percent range; this percentage was lower in earlier years. Spending for elementary and secondary education dominates other expenditures, accounting for approximately 70 percent of spending included in GDP. Not surprisingly, state and local spending is primarily for elementary and secondary education although, since 1970, about 20 percent of state and local expenditures are for higher education. Spending by state and local governments includes federal grants-in-aid to
TABLE 5-2 The Nation’s Education Dollar, 2001 (percent of expenditures)
|
Sources |
Uses |
||
|
Federal government |
1 |
Primary and secondary education |
71 |
|
State and local government |
86 |
Higher education |
22 |
|
Private education services |
13 |
Other |
7 |
|
NOTES: State and local government expenditures include grants-in-aid from the federal government that account for 4 percent of education spending. Shares were constructed with data from the National Income and Product Accounts (Tables 3.15 and 3.17) and GDP by industry data, available on the BEA website (www.bea.gov). Intermediate inputs to the private educational services industry, such as books and supplies, are excluded from GDP, while government expenditures for intermediate inputs are included in GDP. |
|||
TABLE 5-3 Education Expenditures, 1952-2000
|
Year |
GDP (billions) |
Total education expenditures as a percentage of GDPa |
Expenditures as a Percentage of Total Education Expenditures |
||||||
|
Sources |
Uses |
||||||||
|
Federal government |
State and local government |
Within state and local, federal grants-in-aid |
Private education services |
Elementary and secondary education |
Higher education |
Other |
|||
|
1952 |
358.6 |
3 |
1 |
88 |
3 |
11 |
|
||
|
1960 |
527.4 |
4 |
1 |
88 |
2 |
10 |
|||
|
1970 |
1039.7 |
6 |
1 |
87 |
7 |
12 |
|||
|
1980 |
2795.6 |
6 |
1 |
89 |
6 |
11 |
70 |
24 |
6 |
|
1990 |
5803.2 |
5 |
1 |
87 |
4 |
12 |
70 |
24 |
6 |
|
2000 |
9824.6 |
6 |
1 |
86 |
4 |
13 |
71 |
22 |
7 |
|
aIncludes only expenditures reflected in GDP. |
|||||||||
state and local governments. These grants-in-aid accounted for no more than 3 percent of education spending by state and local governments from the 1950s through the mid-1960s. This percentage at least doubled through the early 1970s, then dropped to at most 5 percent during the 1990s. Spending on higher education in the last quarter of the twentieth century accounted for 50-60 percent of the total private educational services spending included in GDP; the share of vocational schools and other “not elsewhere classified” spending increased to about 25 percent, and the share of elementary and secondary schools decreased to 20 percent over the last few years.
None of the BEA’s GDP-by-industry estimates include all of the capital input costs associated with the provision of education. Information on a portion of the relevant investment and capital stocks, which could be used to estimate full capital costs, is available from BEA. It includes investment and capital stocks of the private educational services industry and educational structures held either by the federal or by state and local governments. The full capital service flow corresponding to these stocks, and others, could be estimated by making assumptions regarding the net return to capital; the depreciation component of the capital service flow is already included in GDP (see National Research Council, 1998). We do not detail the methodology that could be used, except to note that capital input to education is probably understated in GDP.8 To allow for comparisons across time and for productivity estimation, a measure of the real inputs to education is needed. Such a measure could be readily constructed for market inputs using data from the BEA that are available as of the fall of 2004.
Since public education is an obvious near-market activity, it makes sense to measure inputs and outputs in the same way for public and private schooling. It would be useful to have consistent methodology and coverage for the government-provided and privately provided education categories in the national accounts. In addition, it would be helpful if estimates of GDP for private educational services were available by subcategory, disaggregated at least for primary, secondary, higher, and other education. Such disaggregation would allow for analysis of public and private education by level (primary, secondary, and higher education), as well as for all levels combined.
Another way to summarize direct monetary inputs to education is by type of expenditure—that is, salaries, capital costs, operation, and other. As already noted, public elementary and secondary schools make up the largest part of spending on education; Garrison and Krueger (2004) provide estimates for this category, broken down by expenditures on instruction, administration, plant maintenance and operation, fixed charges and other school services, and capital outlays. The largest expenditure is for salaries—the main component of the instruction and administration categories.
Nonmarket Time Inputs
In this section we focus on educational activities directly related to formal schooling. These include students’ time spent in school and doing homework, as well as parents’ time spent in school-related activities, such as parent-teacher meetings and assisting their children with homework. Other types of educational activities, such as attending plays, reading books for leisure, or on-the-job training, are not considered.
Time Estimates
The most promising sources of information on time spent in educational activities are time-use surveys, as only limited information is available from other sources. Eisner (1989) used the Michigan surveys of 1965, 1975, and 1981 for that purpose (see, for example, Juster, 1978), but does not report the actual time estimates. Gates and Murphy (1982) and Jorgenson and Fraumeni (1989) both relied on the Coleman report (Coleman et al., 1966) for estimates of time spent in school and homework. Jorgenson and Fraumeni assumed that all enrolled students spent 1,300 hours per year on these activities over the 1948-1986 period they studied. Gates and Murphy (1982) do not report their assumption about hours per student. Garrison and Krueger (2004) estimate the time spent in public elementary or secondary school as 6.5 hours per day times the term length. They vary the term length from 175 days in 1939-1940 to 180 days in 1999-2000. It should be noted that, unfortunately, BLS’s new American Time Use Survey does not provide data on the allocation of time for children under the age of fifteen, and thus cannot be used to estimate the time they devote to education.
Eisner (1989, p. 66) estimates average minutes per week by adults in child education at home, by sex and employment categories. Data are available from the Michigan time-use surveys for selected years; these data are extrapolated to cover the whole period of interest. Minutes per week vary from a low of 5 minutes for nonemployed males in 1981 to a high of 116 minutes for nonemployed females in 1946-1975. Neither Gates (1984) nor Jorgenson and Fraumeni (1989) separate out time spent by parents in school-related activities, and Garrison and Krueger (2004) do not include parent time devoted to child education in their estimates. More and more up-to-date information on student and parent time inputs to education clearly is needed.
Recommendation 5.2: Information on time-use patterns from statistical agencies and other sources, together with a consistent set of demographic data, should be used to estimate the amount of time spent in school and in educational-related activities by students and their parents. New sources of information will be needed for these estimates.
Time Valuations
Several different approaches have been developed to value the time spent in educational activities; they generally use an opportunity cost concept to estimate the value of students’ time inputs to education and a replacement cost concept to estimate the value of parents’ time inputs to education. The size of the estimates for the value of time inputs varies significantly as currently there is no consensus on best methodologies.
Kendrick (1974), Eisner (1989), Garrison and Krueger (2004), and Gates (1984) estimate students’ time cost as the compensation pupils could have earned in a market job. Kendrick assumes that only students aged 14 and older could perform market work; accordingly, the opportunity cost for younger students is zero. Eisner uses an updated version of the Kendrick data. Gates assumes the opportunity cost for students to be positive only for those aged 16 and older. All of these studies use estimates of actual wages paid to measure opportunity cost. Garrison and Krueger demarcate the positive and zero opportunity cost groups by grade level. For students attending grades 9 through 12, the opportunity cost is assumed to equal the minimum wage; for students in lower public school grades it is assumed to be zero. One relevant consideration in assigning these valuations is that child labor laws prevent young children from working. Accordingly, it seems reasonable to assume as an approximation that young children face an opportunity cost of zero for the time they spend in school, even though children younger than 14 could perform some useful work and did so to a much greater extent in earlier time periods (e.g., farm work and household tasks).
Jorgenson and Fraumeni (1992) argue that a positive value should be placed on the time of younger students because enrollment in higher grades is predicated on completion of lower grades, but they value this time based on the future earnings stream it produces rather than the current earnings foregone.9 More specifically, Jorgenson and Fraumeni calculate the value of students’ time input to education as a residual—the difference between the estimated value of investment in education and the value of market inputs. Because the value of investment is so large and the value of market inputs is relatively small, the residually determined value of students’ time input to education is very large.
Opportunity cost approaches have also been explored for valuing parents’ time. Gates (1984) and Murphy (1978) estimate such values for parents’ time inputs to child care and instruction. Jorgenson and Fraumeni (1989) use an opportunity cost approach to value parents’ time inputs to education. Alternatively, parent’s time inputs to education could be treated as an investment by parents in their children, using an approach similar to the one they took for valuing investment in education by the students themselves.
For valuing parental time inputs to education (e.g., the time parents spend helping students with homework), valuations based on replacement options are more common than those based on opportunity cost. Some researchers (e.g., Eisner, 1989; Landefeld and McCulla, 2000) have used a generalist wage, while others have used a specialist wage. Murphy (1982) uses the average wage paid to domestic workers to value hours spent in child care and instruction, but also offers alternative estimates of the value of parents’ time inputs using a specialist wage. His specialist wage is a weighted average over five occupational categories: child care provider in private household, child care provider outside household, welfare service aide, school monitor, and teacher aide. Presumably, only the last two categories would be included in the weighted wage average for valuing parents’ time input to instruction on its own. Although Murphy’s parent time estimates are available only for 1976, they are of particular interest because he also presents estimates for three variants of the opportunity cost approach (gross compensation, after-tax compensation, and net compensation) to value time inputs. The generalist and specialist approaches both produce lower estimates for the value of parents’ time than the opportunity cost approach, reflecting the lower-than-average wage rate paid to housekeepers, child care providers, and teacher aides. Garrison and Krueger (2004) offer an alternative perspective: they estimate the amount that parents of public school children would pay to have their children cared for during school hours if the children were not enrolled in school, but not the time cost of providing instruction to their children at home. They make use of cost figures for child care from the Census Bureau.
One criticism of all three approaches to valuing parents’ time—the generalist (sometimes labeled housekeeper), specialist, and opportunity cost approaches—is that, in practice, average market wages, not marginal wages, are used to construct estimates. Using a replacement cost approach and valuing the parents’ time at the specialist wage is sensible if one believes that parents’ expertise is roughly equivalent to that of the average specialist. A preferable option, however, would be to use a productivity-equivalent replacement wage that accurately reflected the relative skill of a parent relative to that of the specialist in providing educational services. An opportunity cost measure may overvalue the parent’s time spent in providing educational services, particularly for a high-wage parent. The difference between a specialist (or generalist) wage and the productivity-equivalent replacement wage is probably less on average than the difference between the opportunity cost of parent time and the productivity-equivalent replacement wage.
There are other questions about whether a market wage adequately reflects the value of the services being performed. First, the wages of the relatively few specialists who are paid to perform activities primarily carried on outside of the marketplace arguably would be higher if all of these activities were market activities, as the demand for them would be higher (Murphy, 1978). Second, the market wage may not reflect the full value of these activities because of nonpecuniary returns enjoyed by those who perform them or other factors. It is difficult to know
how one should adjust the market wage to adjust for these last two considerations. The panel believes that productivity-equivalent replacement cost provides the best conceptual basis for valuing parent time spent in child education; in practice, it would be extremely difficult to adjust candidate replacement wages for productivity differences between parents and market providers.
Most researchers calculate the total cost of nonmarket time devoted to education—students’ and parents’—as the sum of two positive costs. In Garrison and Krueger (2004), however, parents’ time costs can be negative because they include the potential savings of child care for parents while students are in school. Specifically, they count the amount parents save on child care when a child is in kindergarten through grade 6. The time they (or someone else) otherwise would have had to spend caring for the child is valued at the average cost of child care, using a specialist approach. In this sense, it makes no difference whether the child would have been cared for by a parent or by someone else, such as a child care professional. The cost savings for young students offset the non-negative opportunity costs incurred by older students enrolled in school; accordingly, the nonmarket time costs of education may be negative, depending on the age distribution of the students by grade.
As shown in Table 5-4, it is clear that the magnitudes of the estimates of time costs can be significantly different, even when the same general approach is used. Both Gates and Eisner use an opportunity cost to value students’ time, but the Eisner estimate for 1979 is more than 50 percent larger than the Gates estimate. This difference is due in part to the range of years for which opportunity cost is estimated: Gates calculates the cost for students aged 16 through 24, while Eisner calculates it for students aged 14 through over 35. The largest differences shown are those between the Jorgenson and Fraumeni estimate and all of the others. As described more fully below, Jorgenson and Fraumeni impute the value of student time as a function of the incremental addition to future lifetime income from completing another year of school. Garrison and Krueger’s estimates of the value of student plus parent time inputs to education are the smallest. This result certainly reflects the coverage of their study (K-12), but it also reflects their counting parents’ time not spent on child care for young children during the school hours as an offset to the cost of the investment. As would be expected, adding college education to the Garrison and Krueger calculations significantly increases their estimate of input costs (see the last column of the table). Regardless of the specific methodology used, it is important to recognize that education normally requires commitments of time from both students and parents.
Recommendation 5.3: The value of the time that students and parents spend in educational activities should be estimated and included in satellite accounts. In principle, the time cost for students should be estimated using a modified opportunity cost approach. Parents’ time should be valued as the productivity-equivalent replacement cost of providing comparable educational services.
TABLE 5-4 Value of Time Inputs to Education in Selected Studies (billions of nominal dollars)
|
Yeara |
Gatesb (Students) |
Eisner (Students) |
Eisner (Students and Parents) |
Jorgenson-Fraumeni (Students) |
Garrison-Krueger (K-12 Students) |
Garrison-Krueger (K-12 Students and Parents) |
Garrison-Krueger (K-16 Students and Parents)c |
|
1940 |
|
2.083 |
−1.176 |
|
|||
|
1950 |
|
16.420 |
20.577 |
255.353 |
3.703 |
−2.243 |
|
|
1960 |
33.320 |
40.721 |
644.510 |
9.872 |
.191 |
7.664 |
|
|
1970 |
103.857 |
117.933 |
1365.691 |
24.673 |
9.218 |
36.039 |
|
|
1980 |
161.5c |
259.918 |
285.911 |
2289.584 |
45.156 |
19.684 |
92.240 |
|
1990 |
|
3686.547 |
45.525 |
−1.906 |
125.227 |
||
|
2000 |
|
79.332 |
8.808 |
203.112 |
|||
|
aCalendar year, except for Garrison-Krueger entries, for which it is the school year that ends in the indicated year. bFor the year 1979. cIncludes public elementary and secondary school students and their parents, and all college students. The opportunity cost of college students’ time is valued at the average wage of production, nonsupervisory workers on nonfarm payrolls. NOTE: See text for citations. |
|||||||
Schools and their staffs can be viewed as producing two outputs: education and child care services. In the framework recommended here, the value of investment in education would not include the value of child care services provided to young children while they are in school. Both education and child care services are investments in human capital. For the account being considered in this chapter, however, we are concerned with activities directly linked to the production of educated individuals. Accordingly, while a satellite account for human capital (broadly defined) would estimate the value of the child care services schools provide as well as the value of the education they offer, an education satellite account would include only the latter as output.
MEASURING AND VALUING OUTPUT
Researchers do not typically attempt to produce direct measures of the output of the education sector. Frequently, the value of educational output is set equal to the cost of educational inputs, and no price is estimated for output or inputs. Accordingly, little is known about growth, quality improvements, or productivity in the education sector.
Educational output has been or could be directly estimated using any of three general approaches—the indicator approach, the incremental earnings approach, or the housing value approach—each of which we discuss in turn. Regardless of the approach used, it should be recognized that a significant component of education is an investment in human capital. In the NIPAs, education expenditures other than those for structures and equipment are treated as consumption or intermediate inputs, rather than as investment. The output of the education sector is the flow of improved capabilities that result from schooling each year. That accumulation of skills adds to the stock of human capital.
Recommendation 5.4: Education should be recognized as an investment in human capital in a nonmarket satellite account.
The human capital created through education can have both private and social benefits. Human capital is a broad term meant to capture the skills, attitudes, and abilities that are valuable because they raise productivity in market and/or nonmarket activities. Human capital can lead both to private benefits that accrue only to those who acquire the education and to external benefits that accrue to others. In addition to yielding higher individual earnings, for example, education might increase voter participation, lead to voters being more informed, and result in reduced crime.10 Any of these positive externalities is a potential source of social benefits from education. Nelson and Phelps (1966) and Romer (1990) are
among the many researchers who have argued that the social return to investment in education exceeds the private earnings return. Others argue that the private return to education exceeds the social return because of signaling. In this view, education is seen as a costly mechanism that serves to sort workers in terms of productivity without necessarily enhancing their skills.11
The available empirical evidence points strongly to sizable private benefits from education. Extensive research documents that individuals with more education tend to have higher earnings (see Card, 1999, for a survey). Each additional year of schooling is associated with roughly a 10 percent increase in earnings. It is possible that those with a high level of education tend to have more inherent ability or higher motivation, which would have led to their having higher earnings, on average, even without their high level of education. If this were the case, the observed education-earnings gradient would be an upwardly biased estimate of the causal impact of education on earnings. Much of the available evidence suggests, however, that the higher earnings associated with higher education result from increased cognitive and noncognitive skills due to the education per se, not from other unmeasured factors that are correlated with education.
A number of studies address the possible effect of selection on estimated returns to education by exploiting exogenous variation in educational attainment due to differences in compulsory schooling requirements or geographic proximity to a college (see Card, 1999). Other studies look at the differences in earnings between identical twins with different levels of education to net out unobserved family and individual factors. Ashenfelter et al. (1999) compiled estimates from 27 studies representing 9 different countries, and found that, if anything, omitted variables tend to lead researchers to understate the private return to education.
The evidence on the magnitude of externalities from education—either positive or negative—is less clear cut. In practice, the importance of externalities has been very difficult to assess. Many implications of the sorting model are similar to those of the human capital model, so it has proved difficult to distinguish between the two perspectives, although studies of the effects of changes in compulsory schooling requirements provide some support for the human capital model. In principle, the strongest evidence regarding the existence of educational externalities could come from studies that estimate how differences in educational attainment across countries relate to GDP or how increases in education over long periods of time relate to GDP growth. If education has a larger (smaller) effect on GDP growth than would be expected based on estimates of the private return to education, this could be taken as evidence of positive (negative) externalities from education. Cross-country evidence is always difficult to interpret because there are only a relatively small number of countries and many potential
influences on GDP and because there are difficulties with comparing educational attainment across countries. Nonetheless, we interpret the bulk of the evidence as indicating that increases in education are associated with higher living standards because education raises individuals’ productive capacities (see Krueger and Lindahl, 2001; Cohen and Soto, 2002; Heckman and Klenow, 1997; Acemoglu and Angrist, 2001; for a different view see Benahabib and Spiegel, 1994).
Indicator Approach
The simplest indicator approach to measuring the output of education makes no adjustment for changes in the quality of education or for changes in the productivity of the educational sector over time.12 Often it takes the total number of students or (better) the total number of hours spent by all students in educational activities as the output index. A problem with the simplest indicator approach is illustrated by considering the impact on output estimates of a reduction of a given percentage in class size with a corresponding decline in the total number of pupils in the system and no change in the teaching staff or facilities used. The output of the education sector, and possibly productivity, will be estimated to have decreased by the same percentage, even though the quality of education provided (as measured by the skill level achieved) probably will have increased.
More sophisticated indicator approaches use student test scores, subjective ratings of the overall quality of instruction, degrees granted, the number of students advanced from one grade to the next, or other indicators. Hoxby (2003), Garrison and Krueger (2004), and others use test scores as a measure of performance for the U.S. education system. Test scores have not been adopted into the U.S. national accounts,13 though some researchers working on foreign national accounts have used test scores and other indicators.14
In the remainder of this section, we outline an example of the output indicator approach that incorporates performance measures. This example could be extended to more accurately assess the “value” of output as proxied by test scores by looking at the relationship between scores and earnings or scores and housing values; at this point, however, this next step has not yet been taken.
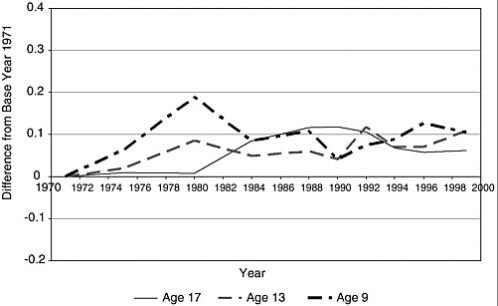
FIGURE 5-1 NAEP reading scores, 1971-1999.
NOTE: Difference is calculated as a percentage of cross-sectional standard deviation (1996).
SOURCES: NAEP 1999 Report, Trends in Academic Progress, Table B1. NAEP 1996 Trends in Academic Progress, Tables C16-C18.
The most commonly used measure of school performance in the United States is the National Assessment of Educational Progress (NAEP). NAEP is a nationwide test administered to 9-, 13-, and 17-year-olds that provides time-series data on reading, mathematics, and science achievement. Hoxby (2003), for example, uses NAEP points per dollar spent as a measure of school productivity. Whether NAEP scores map linearly into output is an open question.
Garrison and Krueger (2004) look at trends in NAEP subject scores to study changes in the quality of education output. Figures 5-1 and 5-2 show trends in average NAEP scores for two of the three subject areas (reading and mathematics).15 Scores have been normalized into units of standard deviation changes from the initial year in which data are available. The standard deviation is from a single cross-section.
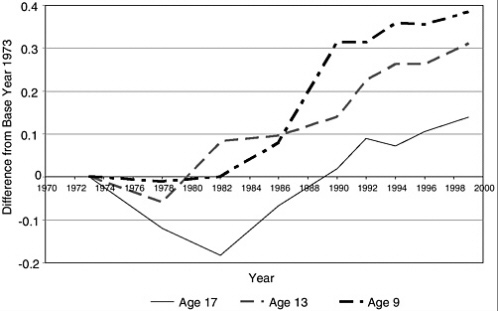
FIGURE 5-2 NAEP mathematics scores, 1973-1999.
NOTE: Difference is calculated as a percentage of cross-sectional standard deviation (1996).
SOURCES: NAEP 1999 Report, Trends in Academic Progress, Table B1. NAEP 1996 Report, Trends in Academic Progress, Tables B16-B18.
Using NAEP scores as a measure of performance has several limitations. First, NAEP data are available for only a relatively short period of time. In addition, NAEP scores do not account for post-high-school gains (e.g., improvements in cognitive skills due to higher education, on-the-job training, etc.) and do not assess skill retention. Therefore, NAEP scores do not reflect the current cognitive skill of tested cohorts. And, the separate NAEP scores would have to be assigned weights to produce a single output indicator series. Test score growth rates then could be calculated and applied to the nominal dollar input expenditure in the base year to form a quality-adjusted output indicator suitable for a dollar denominated satellite account.16
Data from the International Adult Literacy Survey (IALS) could be used to supplement the NAEP scores. Designed for cross-country comparisons, this household-based survey of adults (aged 16-65) was performed in 22 countries between 1994 and 1998. The survey collected demographic data and work history information and assessed literacy by administering a standardized test. For each respondent, the IALS provides three estimates of literacy—prose, document, and quantitative—scored on a scale of 0 to 500. The IALS data can be used to create cohort-level trends in test scores.
The IALS scores reflect the current cognitive skill of adults in the participating countries. Since all three literacy measures are very highly correlated (see Blau and Kahn, 2001), it is reasonable to focus on a single measure. Figure 5-3 shows the mean IALS prose score by year of birth (5-year moving average) for the United States (natives only), United Kingdom, and Sweden.
Garrison and Krueger use IALS scores by birth cohort to make inferences about how the output of the education system has changed over time. Drawing inferences about cohort trends from a single cross-section is complicated because aging can affect the cohort scores independently. Additionally, IALS results provide a broader measure of human capital than that associated with formal education alone. To construct meaningful time-series flow data from these results,
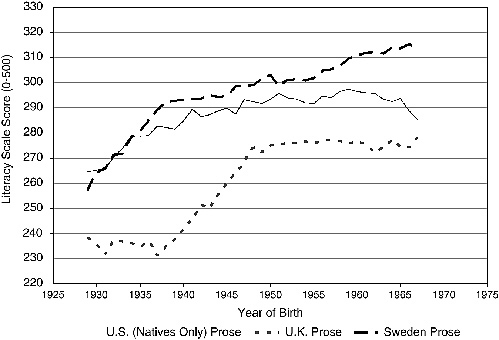
FIGURE 5-3 IALS prose scores by year of birth for the United States, United Kingdom, and Sweden (5-year moving average).
SOURCE: Organisation for Economic Co-operation and Development, 2000.
the effects of aging and other human capital enhancing factors would need to be accounted for. Nevertheless, repeated cross-sections of the IALS could be used to compute measures of the stock of human capital for the working-age population, at least for literacy.
Incremental Earnings Approach
The output of the education sector can be valued using information on how education affects earnings, either by looking at incremental earnings as a function of additional years of school completed or by looking at incremental earnings as a function of improvements in test scores. The prime example of the former approach, also called the present value or lifetime income approach in the literature, is the work of Jorgenson and Fraumeni (1989, 1992). Studies that have estimated the relationship between test scores and earnings include Murnane et al. (1995); Currie and Thomas (1999); and Neal and Johnson (1996).
The Jorgenson and Fraumeni approach to education accounts treats the output of the education sector—years of schooling—as an investment in human capital that is analogous to investments in physical capital such as plant and equipment. Education is regarded as an investment because benefits accrue to an educated individual over a lifetime of activities in the same way that income is generated from the use of physical capital over the lifetime of an asset. This approach explicitly recognizes the gestation period between the application of educational inputs and the realization of benefits. Investment in education is valued as the additional lifetime income from completing another year of school. The theory of investment hypothesizes that the amount that someone will be willing to pay for an investment good is determined by the present discounted value of the future flow of income he or she garners from that good. Accordingly, assuming no externalities, the value of an increment to education will reflect the present discounted value of the additional lifetime income associated with that education. The method used by Jorgenson and Fraumeni (1992) is to compare pairs of demographic groups of the same sex, age, and completed years of schooling, one group enrolled in school and the other not. The present discounted value of the flow of current and expected future income for each pair of groups is compared. The additional lifetime income earned by the group enrolled in school is assumed to arise from the additional year of schooling about to be completed and is used as a measure of the value of the investment in education.17
In the Jorgenson and Fraumeni approach, lifetime income includes both market and nonmarket components. Given the substantial amount of time that individuals spend outside of the market, even excluding sleep, the value of nonmarket activities can be several times larger than the value of market activities. Jorgenson and Fraumeni make the strong assumption that education increases productivity in all nonmarket activities, except for the ten hours a day assumed to be devoted to self-maintenance, by the same amount that it increases market productivity. They refer to the assigned value of the time spent in nonmarket activities as nonmarket income. Assigning a uniform increase in value to a full fourteen hours per day of educated individuals’ time is somewhat controversial. An alternative would be to assume that, beyond its effect on market productivity, education raises the value only of nonmarket time in which individuals are engaged in productive activity, thereby excluding time devoted to leisure. One also might want to allow for the possibility that the effect of education on nonmarket productivity varies depending on the task involved; as discussed elsewhere in this report, there are certain tasks for which the productivity advantage enjoyed by more educated individuals seems likely to be relatively small. Other researchers who have estimated the nonmarket return to education report substantially smaller figures than do Jorgenson and Fraumeni.18
The studies that have estimated incremental earnings as a function of improvements in test scores focus on annual market earnings, rather than lifetime market and nonmarket income. Murnane et al. (1995), for example, estimate that male high school seniors who scored one standard deviation higher on the basic math achievement test in 1980 earned 7.7 percent higher earnings 6 years later, based on data from the High School and Beyond Survey; the comparable figure for females was 10.9 percent. Because this study also controls for students’ eventual educational attainment, any effect of cognitive ability as measured by test scores on educational attainment is not counted as a gain from higher test scores.
Currie and Thomas (1999) use the British National Child Development Study to examine the relationship between math and reading test scores at age 7 and earnings at age 33. Estimating a multiple regression of earnings on both test score variables, they find that students who score in the upper quartile of the reading exam earn 20 percent more than students who score in the lower quartile of that exam; similarly, students in the top quartile of the math exam earn another 19 percent more than those in the bottom quartile of that exam. Assuming normality, the average student in the top quartile scores about 2.5 standard deviations higher than the average student in the bottom quartile, so their results imply that a 1.0 standard deviation increase in reading test performance is associated with 8.0
percent higher earnings, while a 1.0 percent standard deviation increase in the math test is associated with 7.6 percent higher earnings. Neal and Johnson (1996) use the National Longitudinal Survey of Youth to estimate the effect of students’ scores on the Armed Forces Qualification Test (AFQT) taken at age 15-18 (adjusted for age when the test was taken) on their earnings at age 26-29. They find that a 1.0 standard deviation increase in scores is associated with about 20 percent higher earnings for both men and women. Based on these three studies, a plausible assumption is that a 1.0 standard deviation increase in either math or reading scores is associated with about 8 percent higher earnings.
Of course, noncognitive skills imparted through schooling are also an important component of human capital (see Heckman and Rubinstein, 2001). Unfortunately, measures of noncognitive abilities lag behind available measures of cognitive abilities. In principle, however, the Garrison and Krueger approach could be extended to include noncognitive abilities. If cognitive and noncognitive abilities are correlated, then to some extent the cognitive test measures will reflect noncognitive skills.19
Jorgenson and Fraumeni essentially look at the earnings gains due to additional years of schooling, whereas the other researchers discussed above look at earnings gains due to achievement test score gains. Hansen et al. (2004) provide something of a potential bridge between the Jorgenson and Fraumeni method and this approach, as they estimate the effects of additional years of schooling on cognitive test scores. They find that a 1-year increase in schooling is associated with a 0.17 standard deviation increase in the average person’s score on the Armed Forces Qualifying Test.
Housing Value Approach
Hedonic housing price models provide another possible technique for estimating the output of the education sector, or at least the output of public primary and secondary education. This approach uses differences in housing prices across areas to estimate the value that parents place on school quality, as indicated by test scores. An often-cited study in this genre, Black (1999) exploits the natural experiment created by different school catchment areas, looking at differences in the values of otherwise similar houses on either side of the border between school zones with different test scores. This approach provides an estimate of the latent price placed on student achievement in the housing market. The close proximity of the houses helps to control for unobserved variables. Her results indicate that parents are willing to pay 2.5 percent more for a house in a district with test scores that are 5 percent higher. Unfortunately, she does not have data on the
inter-student standard deviation of scores, which would be needed as a bridge to scale the results comparably to the NAEP or IALS data.
Kane et al. (2003) follow Black’s regression discontinuity design to examine the effect of school test scores on property values in Mecklenberg County (which includes Charlotte), North Carolina, an area encompassing 304,000 real estate parcels and 640,000 people. They have access to data on both the school-level and student-level standard deviation of test scores. In this study, housing prices increase by 18-25 percent for a 1.0 standard deviation increase in test scores (where the standard deviation refers to student-level test score data). At the school level (i.e., using the school-average test score), a 1.0 standard deviation increase in test scores implies a 4-5 percent increase in housing prices. Kane et al. conclude that their estimate of the value parents place on educational attainment is slightly greater than Black’s, if put on comparable footing. Other work by Bogart and Cromwell (1997) and Weimer and Wolkoff (2001) also documents a positive relationship between housing prices and school performance.
Estimates such as these could be used to identify the implicit market value of improvements in test scores. One potential advantage of estimates derived from the hedonic housing market literature vis-à-vis the earnings literature is that housing prices presumably take into account the nonwork value of improvements in human capital, or at least that portion of the nonwork value for which parents are willing to pay on behalf of their children (in grades K-12). For example, acquisition of human capital could help individuals to become better parents or better consumers, and these characteristics might be things for which parents would be willing to pay, meaning that their value would be reflected in higher house prices in school districts that produced more of those attributes.
Use of the hedonic approach in an education account should proceed with caution and, certainly, more basic research is needed (the experimental context of satellite accounting should facilitate this). In this literature, which relies on data sources that are fairly limited, unobserved variables appear to be a significant concern. Specification of the functional form and variables to be included in the hedonic regression also may raise questions.20 As a result, it is difficult to judge how reliable estimates from such studies are relative to, say, those from the incremental earnings studies.
As noted above, the standardized test scores used to measure school district quality reflect only a subset of the valuable attributes fostered by schools. To the extent that different schools have different emphases, test scores may capture their students’ relative accomplishments imperfectly. To illustrate, students at a vocational high school might score relatively poorly on standardized tests, but
still leave school with highly marketable practical skills that have considerable market value. In addition, the increasing use of test scores to evaluate schools and school administrators could change their meaning in the future. To the extent that schools respond to legislated performance standards by focusing on those areas of learning covered by the tests used in their implementation, at the expense of other important areas that are not covered, the historical association between test scores and human capital may well be altered.
Even accepting test scores as valid measures of human capital, there may be problems with the way that test score information has been used in housing value studies. Parents should be interested in the value added by the school system—in this context, the schools’ ability to raise their children’s test scores above what they would have been. In practice, researchers have used differences in average test scores across districts as the measure of school district quality. But if average test scores depend on factors such as the education of parents in the district, and these factors are not adequately controlled for, then the estimates could be biased. Neighborhoods with better schools also may have other desirable attributes that contribute to students’ accomplishments. At the individual family level, parents who are willing to pay the higher prices associated with homes in higher-test-score school district may spend more time in at-home child education and transmit to their children a greater sense of the importance of education. Black (1999) was particularly concerned about this issue, but her approach of looking at houses very close to school district boundaries where there is discrete variation in school quality should overcome much of the omitted variable problem.
We have argued that, in any experimental satellite account, output should be measured independently of inputs, if at all possible. As we note above, without this independent measurement, productivity in the production of the outputs covered by the account cannot be estimated. As productivity is an important source of economic growth, good estimates of productivity trends are important. There are several possible incremental earnings approaches to valuing the output of education, including the lifetime income approach and approaches that estimate the relationship between test scores and earnings. The implicit valuation of test scores (e.g., NAEP and IALS) using differences in house prices across school districts provides an attractive alternative approach for measuring the value of the output of schools, when the output is measured by performance on standardized tests. On the input side, information on market inputs usually can be found, but obtaining information on nonmarket time inputs and estimating an appropriate wage for valuing those time inputs may be difficult. Once measures of the relevant inputs have been constructed, it is straightforward to create an aggregate input index. In principle, the value of noncognitive skills to which education may contribute could be measured similarly to the value of cognitive skills, although we are not aware of attempts to do so.
Recommendation 5.5: The value of education output should be measured independently of the cost of inputs. Output should be measured using an incremental earnings approach or a housing value approach.
OTHER ISSUES
In the framework outlined in this chapter, there likely will be a substantial “profit” in the education account. This is in part because investment in education may, in fact, deliver a high private return compared with other investments and in part because some of the costs of education are unlikely to be fully accounted for in the education account.
Concerning the former, education may generate a high return because capital constraints prevent workers from investing sufficiently in education (see Ellwood and Kane, 2000; Carneiro and Heckman, 2002), because devoting time to education is viewed as difficult or unpleasant by a substantial number of potential students, or because, for any individual, education is a risky investment and part of the return is a return to risk.21 In addition, the return could be high because students apply high personal discount rates or underestimate the return to education. And it is possible for the market for human capital to be in temporary disequilibrium because supply can adjust only slowly over time to demand shocks. These concerns, of course, apply to many kinds of markets.
Concerning the latter, investment in children of preschool age is, to some extent, a part of the cost of education that is not measured by the education accounts. In addition, home production necessary to students’ school attendance—including activities that range from nurturing and psychological support to preparing school lunches—is another input that is not fully reflected in the education accounts. As with other accounts, it is important to be aware of the reasons for a surplus (or deficit) of output over inputs before making decisions based on the accounts.
























