5
PAVE PAWS Exposure Conditions
EXPOSURE CHARACTERISTICS
The Radar and Its Signal
To briefly review the radar description provided in Chapter 4, the PAVE PAWS radar is pulsed; it transmits a pulse sequence, and then is quiescent while the radar echoes return. Then another pulse sequence is transmitted and the process is repeated. Pulse widths vary from 250 microseconds to 16 milliseconds, and the listening period is at least 38 milliseconds. Some pulses vary in carrier frequency during the pulse, using a technique called “chirping” to improve range resolution. The carrier frequency varies from 420 MHz to 450 MHz. Signal bandwidths at the input to the final amplifiers range from 8 kHz for the narrowest pulse to 125 Hz for the widest pulse. The “chirp” bandwidth is 2 MHz.
The antenna is comprised of two phased arrays, each located on a planar face, tilted back 20 degrees from vertical. The elements are located on a regular hexagonal lattice, and there are 1792 active elements per face and 885 passive elements. The elements are deployed in quadrantal symmetry to allow precise monopulse tracking of targets. The diameter of each array is approximately 72.5 ft. Each array face will support many more elements, but that expansion has not occurred, and the committee has been informed that there are no plans to expand the number of elements on the array. The elements are bent dipoles, each supported by a two-post balun. Bending down the arms avoids blind angles produced by dipole-balun mode interference. Crossed dipoles are used, thus providing both vertical and horizontal polarization. Both arms are hot; the two conductors supporting the dipole arms constitute a balun, which transforms the balanced dipole arm connection to an unbalanced coax; the latter connects to the module contain-
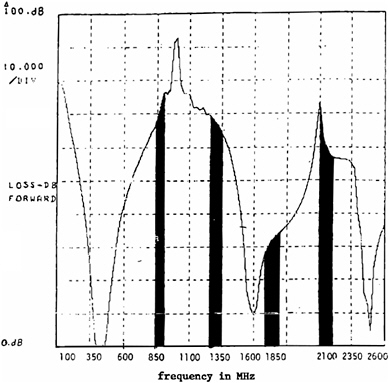
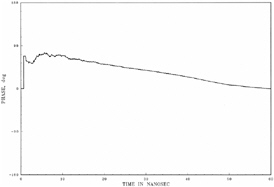
FIGURE 5-1 Measured module filter response. The filter minimizes the interference of PAVE PAWS to services such as cell phones, GPS, and other communications systems. Filter bandwidth is 115 MHz at 10 dB points. This figure shows the pass band (low attenuation for the radar frequencies [425-450 MHz], and high attenuation for harmonics; attenuation of 70 dB for second harmonic at 850 MHz; 68 dB for third harmonic at 1350 MHz; 31 dB for 4th harmonic at 1800 MHz; and 59 dB for fifth harmonic at 2100 MHz). This filter insures that the PAVE PAWS signal has very small harmonic content. Figure is reproduced with permission from Raytheon Company.
ing the amplifier. This is a well known and widely used technology. Each quadrant has 14 subarrays, and each subarray has 32 transmit-receive (TR) modules and 32 active elements. The array main beam is steered by applying phase shift to each TR module. All modules are excited simultaneously; beam scan is provided by phase shift. Sidelobe levels are held 20 dB below the main beam by tapering: the inner subarrays have all active elements, while middle subarrays have some passive elements, and outer subarrays have more passive elements. Thus an amplitude taper is produced over the array (see Figure 5-4). Each TR module includes a bandpass filter to minimize interference caused by the radar. Filter bandwidth is 115 MHz at 10 dB points; the measured filter response is shown in Figure 5-1. Note that the filter skirts around 420 and 450 MHz are quite steep. This filter affects the pulse buildup and decay.
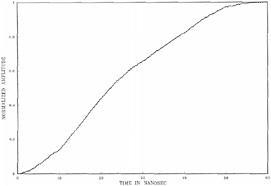
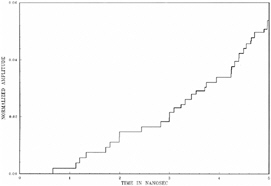
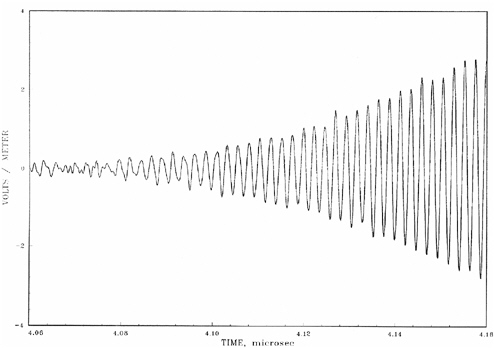
Measurements of the exciter output RF waveform are shown in Figures 5-2a, 5-2b, and 5-2c. Note that these appear inverted, due to the measuring equipment using negative detection. In Figure 5-2b the rise time is approximately 1 microsecond, with a gradual rise and gradual leveling off. Finally Figure 5-2c shows fall time, which is much slower, roughly 12 microseconds, and therefore no abrupt changes are evident. Note that the rise-time bandwidth is narrow (roughly 2 MHz).
WAVEFORM DECAY
Each PAVE PAWS dual polarized element is driven by a Class C (highly non-linear) amplifier; a second Class C amplifier drives all 64 element amplifiers in a sub-array; a third Class C amplifier drives all 56 sub-arrays. All of these amplifiers are “on” all the time; the radar exciter unit applies the waveform (pulse) to the amplifier driving the sub-arrays. Beam steering is provided by a phaser at each element module. Class C amplifiers tend to sharpen up transients, so the exciter buildup and decay times of roughly 1 and 12 microsec (Figures 5.2b and 5.2c) become typically 200 and 1000 nsec for the radiated signal.
An examination of Phase IV buildup and decay pairs shows that these times are roughly equal, about 200 nsec (see Figures 5-6 and 5-11, which are expansions of Figures 3-48e and 3-53e in the AFRL (2003) Phase IV Time-Domain Waveform Characterization report. In a number of cases, a trailing-edge spike is larger than the main waveform. All of these are at wide angles from the main beam, where the sidelobe envelope is much lower. These spikes are probably due to two factors working together. First, the individual Class C amplifiers do not turn off alike, due to different resonant circuit Q (ratio of stored energy to dissipated energy), different gain, and other factors. Second, when all element contributions add in phase, the main beam is produced. Sidelobes and nulls are produced when the element contributions partly cancel, producing sidelobe levels away from the main beam 30-40 dB down (in power down to 0.001-0.0001 from 1). If amplifiers have typical gain variation of ±1 dB or even more, field-strength levels well above the steady-state sidelobe level are possible as the elements variously shut down. This is substantiated by calculations made by Tomlin for the PPPHSG.1 It should be noted that the discrete delay is not a possible cause here.
Signal Propagation
The radar signal power decays as 1/R2 in free space, but multipath signals are usually a problem at UHF. Multipath is caused by diffraction and reflection. For example, if a hill or slope blocks the direct radar signal, the signal can be re-
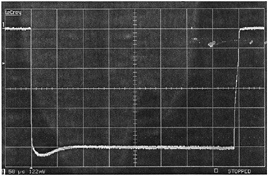
FIGURE 5-2a Entire exciter waveform pulse (negative direction) taken from RF monitor example in T.O. 31P6-2FPS115-51, Chapter 6.
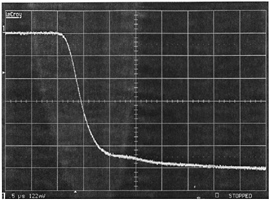
FIGURE 5-2b Exciter output pulse (negative direction) rise time taken from RF monitor example in T.O. 31P6-2FPS115-51, Chapter 6.

FIGURE 5-2c Exciter output pulse fall time (negative direction) taken from RF monitor example in T.O. 31P6-2FPS115-51, Chapter 6.
flected or diffracted by towers, buildings, power lines, or other obstacles and can reach areas that are not line-of-sight from the radar. These multipath signals need not be in the direction of the observer; they may arrive sideways. Reflected multipath is provided by many types of metallic structures: metal lighting poles; fence poles and wire; rebars in concrete; and telephone cable and power wires, to mention a few. These multipath signals are well known, and can easily disrupt the 1/R2 energy falloff. Almost certainly the anomalous Phase IV measurements are due to multipath.
The question of surface waves has been raised by concerned Cape Cod citizens. However, it has been accepted for 50 years that the longitudinal field component that may exist at HF, VHF, and UHF is not a surface wave. Sommerfeld in his classic 1909 work (Sommerfeld 1914) made a sign error, according to Norton (1937) and others in several papers. There is recent evidence by Collin (2004) that the original sign was correct, but in either case the earth does not support a surface wave. The waves are now called “ground waves”; the vertical electric field tilts just enough to satisfy the lossy boundary conditions in the ground. The term “surface wave” has for at least 40 years referred to slow waves, waves with velocity less than that of light, and usually supported by reactive surfaces. At 435 MHz, ground waves attenuate rapidly. Using sandy soil (epsilon = 10, σ = .002 S/ m), the radiation is attenuated 40 dB (0.0001 in power, 0.01 in field) over a distance of 120 m (400 ft) . Outside the safety fence, the ground wave should be too small to measure. Use of the formulas of Baños, as suggested, is not recommended. They are excellent for dipoles in earth, or dipoles very close to earth, but are error prone for separations of a wavelength or more.
Although it has been implied that the measured radial fields (radial waves) represent a new and unexpected phenomenon, they are just the result of multipath and simple geometry. As sketched in Figure 5-3a, the line of sight during the Phase IV measurements was not horizontal, but was inclined down about 2 degrees. Since the electric field at the measurement point is perpendicular to the line of sight, it can be resolved into a large vertical component and a small horizontal or longitudinal component. For many points on Cape Cod, the line of sight angle is larger, leading to a larger longitudinal component. At UHF frequencies multipath is a well known and serious problem. Metallic structures including towers, power lines, and rebars in concrete, that are inclined or curved, will convert vertically polarized fields into horizontally polarized fields. Even curved earth hills can produce polarization conversion. It is difficult if not impossible to compute the combined multipath effects in a given environment. The multipath contributions and the horizontal field due to line of sight tilt combine to produce a longitudinal E field. (See Figure 5-3b taken from 3-92c, and Figure 5-3c taken from 3-96c of the Phase IV report.) Because this field is parallel to ground, and the sensor is roughly two wavelengths above it, there are also ground reflection effects. The derivative sensors used in the measurements have very broad pat-
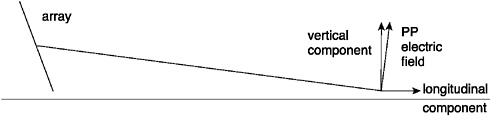
FIGURE 5-3a Vector resolution of PP electric field into vertical and longitudinal component. NOTE: This figure has been changed since the original prepublication version to correct an error.
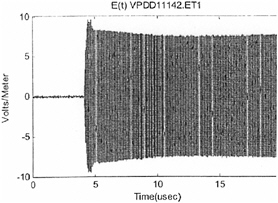
FIGURE 5-3b Vertical field amplitude (from 3-92.c of the waveform report).
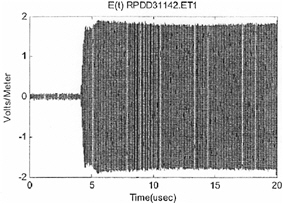
FIGURE 5-3c Radial field amplitude (from 3-96.c of the waveform report).
terns, and pickup signals from many directions. It would be better physics to call the field a “longitudinal component.”
Time Delay in Large Antennas
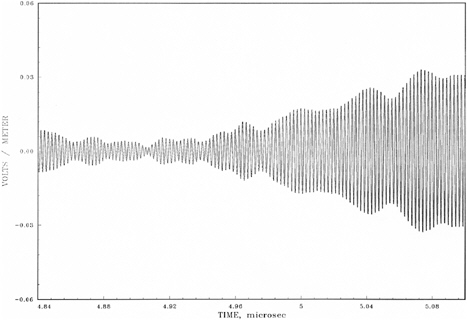
It was suggested by Dr. Albanese2 that phased-array radars are different from other radars due to their discrete time delay. This is one of the key issues relating to PAVE PAWS effects and it is examined thoroughly here. In the far-field of a large phased array or reflector antenna, the contributions from all parts of the antenna arrive at the main beam peak simultaneously (broadside beam for a phased array). At other angles, there is a differential delay as the energy from the closest part of the array or reflector arrives first, while that from the farthest part arrives last. Of course this applies primarily to pulsed signals. For the reflector, the pattern buildup starts at 90 degrees from the axis due to the currents on the reflector edge (see Hansen 1987; Hansen and Kramer 1992) and the pattern builds up slowly and continuously. With a phased array, the pattern builds up slowly but in a discrete stair-step fashion. Due to the large number of elements, the stair has many very small steps. As expected, the effect of those small steps does not appear in the waveform measurement (see Figure 5-6).
In the near-field region (distance generally less than 2000 ft), there are delays also in forming the main beam. For the phased array, the near-field stair-step buildup of the waveform is expected to be very close to a continuous buildup. For a reflector antenna, the near-field buildup is more complex.
At angles away from the normal to the face of the array, there is a time delay between energy arriving from the closest element and that arriving from the farthest element, since all elements are turned on simultaneously. This delay, in amplitude and phase, has been computed for the PAVE PAWS radar. The active array is 72.5 feet wide. A worst case scenario is postulated: the beam is scanned to the farthest left position of 60 degrees azimuth, and to the lowest elevation position −17 degrees (3 degrees above the horizon). The observation point is 60 degrees right azimuth, and −20 degrees elevation (on the horizon). A computer program was written to calculate the waveform buildup. The x-y coordinates of the 1792 excited elements were provided on a disk by Mitre. Figure 5-4 shows the positions of the active elements. They are closely spaced around the center but space tapering is used in the outer portion, to control the sidelobe level.
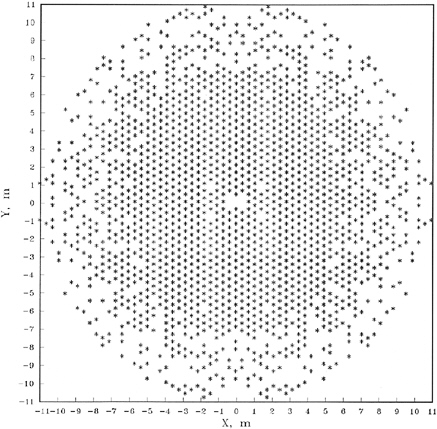
FIGURE 5-4 Positions of the active PAVE PAWS elements.
Using the observation direction, the projected distance from each element to the first element (center row, right side) is calculated for the 1792 elements. The projected distances are calculated using direction cosines, where the polar angle θ is measured from the normal to the array face, and the azimuth angle Φ is measured in a horizontal plane from normal to the surface. Since those with the smallest projected separation contribute first, the array of projected separations is ordered in ascending order by a well-known subroutine called HEAPSORT. Because the excitation phases associated with the main beam position affect the phase of the buildup, the x and y coordinates are sorted in consonance with the projected separations. The delay time across the array is roughly 74 nanoseconds; the delay for the worst case mentioned above is 60 nanoseconds. In order to get a fine-grain picture of how the elements contribute, the time line is divided into 12,000 steps of roughly 5 picoseconds each. The time stepping starts at 0 at the right-most reference element and proceeds on. When it has encompassed the next closest element, the contribution of that element with the appropriate scan phase
and unity amplitude is added in. As the time step proceeds, more and more elements are added until the opposite side of the array is reached. Since the phase and amplitude are both a result of stair-step contributions, no smoothing or interpolation has been used in the plots. Figure 5-5a shows the amplitude buildup for the extreme case mentioned above.
This curve is made of 1790 stair steps, although they are not visible due to the scale. But a portion of the delay time is expanded in Figure 5-5b, where the steps are clearly visible.
The delays range from 5 psec (or less, as this is the least count) to roughly 100 psec. Note that the height of the large steps is roughly 4 × 10−3 times the final height, and that is the level of a far-out sidelobe, perhaps 1 × 10−4 times the main beam power. So a typical step represents a power step of the order of 4 × 10−7 times the main beam power. Figure 5-5c gives the phase buildup; the first step is an artifact due to the plotting program starting at zero phase. Note that the calculations were made along one of the four directions (axes) of symmetry, which is a worst case. If a slightly different azimuth angle had been used, the distance steps would be less regular, and the buildup would be even smoother. These incremental delays, as radiation from antenna elements appear, are very much smaller by comparison to the rise times (less than a factor of a thousand) produced by the TR modules, as discussed below.
Total phase change during buildup is very modest. Thus the phased-array delay is expected to produce a negligible effect; the waveform rise time is very gradual. Buildup is similar to that of a large parabolic dish antenna system.
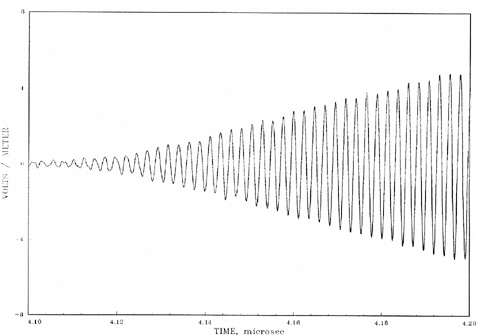
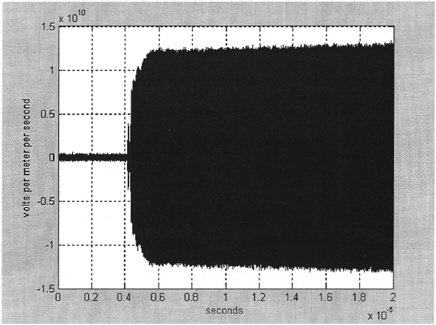
The PAVE PAWS Phase IV measurement program produced data that are relevant to the effects of time delay, both in arrays, and in reflectors. All of the graphs presented below are excerpts of the digital data provided to the committee by AFRL. First, the PP waveform buildup at 60 degrees from the array normal (from Figure 3-48e of the waveform report) (AFRL 2003) is shown in Figure 5-6.
The PP waveform buildup near normal (from Figure 3-46b in the waveform report) is shown in Figure 5-7. At center frequency of 435 MHz the maximum delay in Figure 5-6 is 63.8 nsec, or 28 carrier cycles. The time-delay period extends over roughly one-third of the rise time in Figure 5-6. As expected from the buildup calculations just discussed, there is no apparent indication in Figure 5-6 that the discrete delay has any effect. Figure 5-7, near normal, incurs negligible delay; the slight irregularities in amplitude occur equally in both. Before buildup starts, the data show noise and interference; this probably accounts for the later small irregularities.
The committee notes that the Air Force Phase IV report revisions incorrectly assume time-delay beam steering, instead of phase beam steering.
For comparison Figure 5-8 shows buildup for a single PP element. The envelope is smoother, but the pre-buildup noise is smaller than in Figures 5-6 and 5-7. Similarly, the Phase IV measurements on two PP elements, with an introduced 50 nsec delay, are indistinguishable from those of a single element.
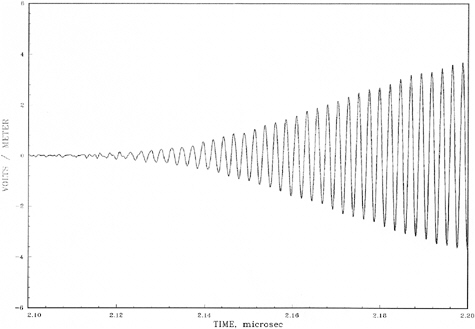
FIGURE 5-8 Single element buildup.
From these data, several conclusions may be drawn. First, none of the buildup or decay plots show anything that can be related to the time delay. Second, the buildup time is very much longer than the maximum delay time, for both array and reflector. Third, noise and interference were much worse for the D-dot measurements; all measurements discussed here were made with the TEM horn. Fourth, these results agree with the buildup calculations of Figures 5-7a and 5-7c, of the Air Force Phase IV waveform report; the discrete nature of the buildup can only be glimpsed at the very beginning, when the waveform has very small amplitude, and is heavily corrupted by noise and interference.
Next, delay in reflector antennas will be examined. Delay occurs in a reflector as a transmitted pulse appears first at the center of the reflector, then spreads out. The delay period continues until the farthest edge is excited, and the wave has reached a given angle off-axis (Hansen 1987; Hansen 1992) This delay for angle θ off-axis is:
Here D is reflector diameter, λ is wavelength, F is frequency, and f is focal length. For the SRI dish, D = 150 ft and f/D = 0.42. At center frequency of 435 MHz, and at an angle off-axis of 46 degrees, the maximum time delay is 70 nsec. This
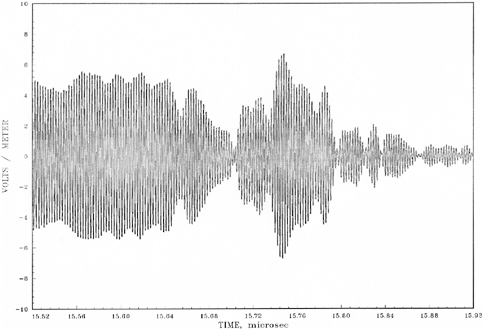
represents roughly 31 carrier cycles. Two transmitters were available for the SRI measurements. The wideband source had a rise time of 100 nsec; the narrow-band source had a rise time of 500 nsec. Figure 5-9, wideband data, is extracted from Figure 3-73c of the waveform report; only a small part of the buildup is shown.
Note the significant noise and interference before start of buildup, and its effect after buildup. Although the delay is 71 nsec, its effects are not discernable. Figure 5-10, from Figure 3-63e in the waveform report, shows buildup for the narrow-band dish.
Note that both interference and its effect on the rising waveform are reduced from Figure 5-9. It was stated by the measurement team that the interference at the SRI site was appreciable, and these graphs show this. In comparing Figure 5-6, PAVE PAWS buildup off-axis, with SRI buildup off-axis, the clear conclusion is that in neither can the delay effects be observed.
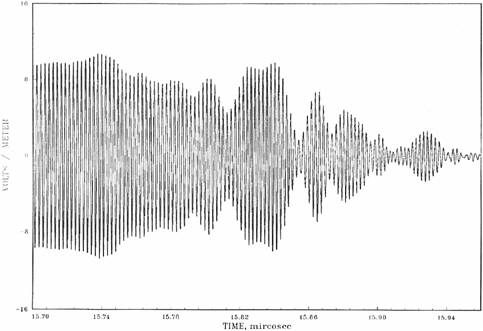
Turning now to the waveform decay, Figure 5-11 (from Figure 3-56b in the Air Force Phase IV wave form report) shows the array at wide angle.
Figure 5-12 (from Figure 3-53e in the Air Force Phase IV wave form report) shows the array near normal, where there are negligible time delays. Both show erratic decay; that at normal to the array face is probably less well behaved. In both cases the effects of interference are visible. Nothing in Figure 5-10 can be traced to an array discrete time delay.
For the reflector antenna, Figure 5-13 (from Figure 3-76c in the Air Force
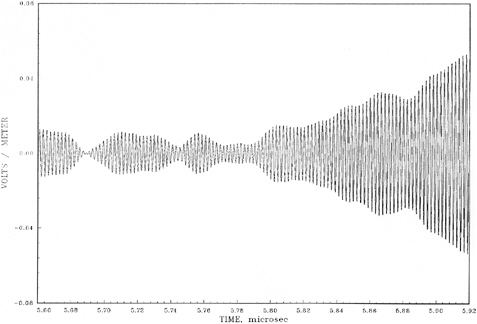
FIGURE 5-9 Dish buildup; 46 degrees off normal wide band.
Phase IV wave form report) shows the wideband decay. Again the effects of interference are apparent during the decay, and after. Note that for this case, the source rise time is 100 nsec. Again no effects of the reflector delay are visible. The narrow-band source decay graph is not shown; it decays much more slowly, due to the 0.5 µsec rise time, and the interference is correspondingly reduced.
PRECURSORS
Radar Electromagnetics
Another key argument by Dr. Albanese regarding PAVE PAWS was that precursors might be formed. If so, their deeper penetration into cellular material might be a factor to consider in the evaluation of possible health effects. In communications with the committee, Dr. Albanese recommended that the PAVE PAWS committee take advantage of the extensive technical literature on measurement and calculation of precursors. Accordingly, all available measurements are discussed; several Annexes are devoted to calculations.
The committee has identified the following questions regarding PAVE PAWS, biological tissues, and precursors. These questions are (1) does the radar radiation produce precursors in biological tissue or equivalent media; (2) does precursor formation depend upon signal bandwidth; (3) if precursors are produced, how do they decay with penetration distance? Definitive and reasonable answers to these questions have been developed, and are discussed below.
Central to all of these questions is bandwidth, which is critical here, as it is in all electronic and computer systems. Signal bandwidth is affected by both waveform rise time and pulse width. For PAVE PAWS the pulses are long (shortest pulse is 250 µsec); the bandwidth is primarily due to rise time. A continuous-wave (CW) signal may have a rapid rise time (roughly 1/4 of a cycle), but the CW signal has zero bandwidth. Conversely, phase-modulated signals such as QPSK may have wide bandwidth, but the signal is always on. It is wide bandwidth that is of concern for precursor formation.
Central to all of these questions are the electrical properties of the material the radar signal is traveling through. Precursors occur in anomalous dispersive media, that is, where there is a decrease in the permittivity (dielectric constant) with increasing frequency and where one or more absorption bands exist in the frequency range of the signal. See Annex 5-1 for data on dispersion in biological tissues.
A precursor is a modification of the incident waveform that arrives at a given depth in the dispersive medium before or during the incident waveform. Sommerfeld precursors arrive before, and tend to contain frequencies higher than the signal carrier frequency. Brillouin precursors arrive next, and tend to contain lower frequencies. In the medium, the incident waveform travels with the group velocity. The wave front of the Sommerfeld precursor travels with the speed of light in a vacuum; but this wave front is extremely small. The signal velocity,
based on energy transport, is slower. However this signal velocity is larger than the group velocity, which is that of the incident waveform, accounting for the early apperance. In contrast, the Brillouin precursor has a signal velocity below the group velocity. Phase velocity has no meaning except for a monochromatic (single frequency) signal (Oughstun and Sherman, 1994).
Precursors may exist in a dispersive medium (dielectric constant/permittivity) and/or loss varying with frequency. Whether they are excited depends also upon the bandwidth of the incident signal. Wideband signals can produce precursors in highly dispersive media. But the variation in material parameters with frequency over a narrow-band signal does not allow observable precursors to form. This is substantiated by the Sandia National Laboratory calculations (see Annex 5-3).
The PAVE PAWS instantaneous bandwidth is never more than 5 MHz, although the carrier frequency changes as the beam moves between 420 MHz and 450 MHz. Thus this narrow bandwidth will not produce measurable precursors.
When precursors are created, the decay is a function of bandwidth of the applied waveform. Roberts (see Annex 5-3) has shown that a wideband signal will have significant spectral energy below the frequency of the carrier. Each of these spectral components decays exponentially in a linear lossy medium; if the wideband applied waveform has sufficient lower frequency energy, the resulting precursor will decay more slowly than the exponential decay of the carrier. Because the spectral components of lower frequencies decay more slowly with penetration distance, the mix (spectrum) changes with distance, resulting in a decay rate for the Brillouin precursor of approximately ![]() (papers by Oughstun and by Roberts; see Annex 5-3). Note that all examples computed by Oughstun and colleagues utilize very wideband waveforms, typically bandwidths of 10 to 20 GHz or more, at optical (laser) frequencies. For PAVE PAWS with its very narrow bandwidth, the carrier frequency predominates, and all decay in a lossy media will be exponential at this frequency.
(papers by Oughstun and by Roberts; see Annex 5-3). Note that all examples computed by Oughstun and colleagues utilize very wideband waveforms, typically bandwidths of 10 to 20 GHz or more, at optical (laser) frequencies. For PAVE PAWS with its very narrow bandwidth, the carrier frequency predominates, and all decay in a lossy media will be exponential at this frequency.
Waveform Slopes
Slope is the rate at which electric field is changing. Thus it may be measured in volts/meter per nanosecond. This is not to be confused with rise time, in nanoseconds, which is independent of field strength. At the September 16, 2003, PAVE PAWS committee meeting, Dr. Albanese presented charts on phase and slope estimation. The zero crossings of waveforms were examined to determine slopes. The slope between adjacent zero crossings changes at rates greater than 1 volt per meter per nanosecond have been postulated to be biologically significant by some individuals. However at the zero crossings, the PP signal is approaching zero; Jim Tomlin has shown in detail3 that noise and interference, although small, can sig-
FIGURE 5-14 PAVE PAWS spatial variation at 500 meters. Used with permission from Richard Albanese.
FIGURE 5-15 Leading edge 540 meters from PAVE PAWS.
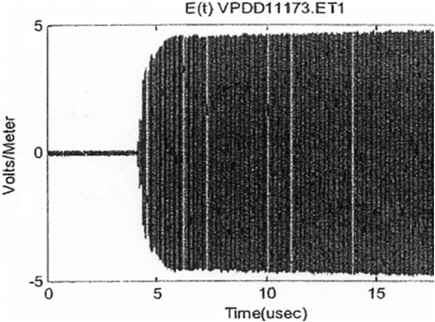
A similar match occurs in FIGURE 5-16 (vpdd 11173.ed1) and FIGURE 5-17 (Figure 3-106h from the waveform report).
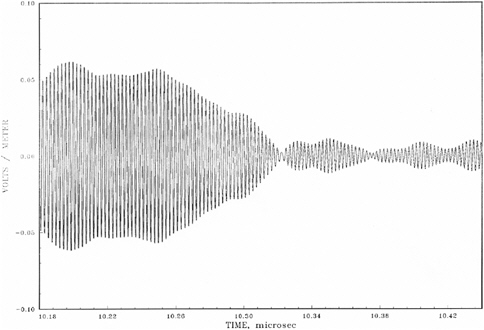
nificantly change the slopes because in the vicinity of a zero crossing the PP signal is smaller than the noise. As a result, the slopes and slope changes (delta slopes) calculated by Dr. Albanese are corrupted by interference. The spatial variation in Figure 5-14 matches almost exactly the leading edge of the related Phase IV waveform in Figure 5-15; Figure 5-14 should be volts/meter, as in Figure 5-15.
The “wiggles” in the Phase IV waveform envelopes are caused by interference, and these same wiggles are added to the PP carrier slope of 2.7 V/m/nsec (for a 1 V/m signal at 425 MHz). Slopes in Figure 5-18 (provided by Dr. Albanese as figure parl11090.ed1) are shown over a 400 nsec time, representing about 170 carrier cycles. The granularity maximum delay is 60 nsec; the waveform buildup is completely covered by Figure 5-18 but nothing attributable to the discrete delay is visible.
Jim Tomlin, for the PPHSG, has smoothed the waveform data, and has calculated and plotted delta slopes (see Figure 5-19). The upper curve, with right scale, shows the smoothed (two-point running average) of the noise and interference derivative for a record segment just prior to the arrival of the indicated PAVE PAWS pulse. The lower curve, with left scale, shows the delta slopes that would have been recorded due to this noise and interference had a pure 434.8 MHz non-phased sine wave signal been present. It is clear that the variations in delta slope are due to interference. All high-power radiating systems (TV, FM, radars) have
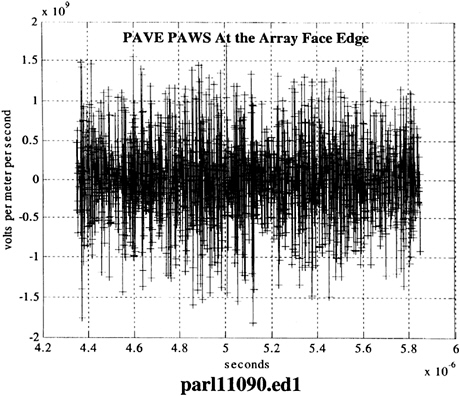
FIGURE 5-18 Slope differentials at adjacent zero points. Used by permission from Richard Albanese.
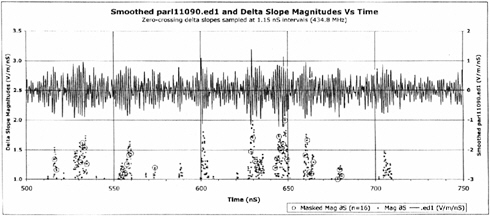
FIGURE 5-19 Smoothed waveform data and delta slope magnitudes vs time. Used with permission from Jim Tomlin.
slopes of several V/m/nsec, plus delta slopes induced by interferers. There is no reason to believe that PAVE PAWS effects are different. Tomlin has suggested additional measurements; the committee concludes the variations are due to interference and that further measurements are not needed.
Relation of Waveform Slopes to Precursers
As part of the committee’s information-gathering effort, Dr. Albanese was asked by the committee what, in his opinion, the relationship was between slope (V/m/nsec) and precursor formation. He responded that the association was indicated in the paper by Albanese, Penn, and Medina (see Annex 5-3). A careful reading of this paper shows that Brillouin precursors occur when the medium is sufficiently dispersive, and when the bandwidth is wide. Their calculations used a convenient applied field of 1 V/m, and the precursor levels were related to this. The system is linear; it is clear that a hypothetical applied field of 1 mV/m would produce a precursor with amplitude 1/1000 of the precursor in the paper. This paper shows indirectly the association between signal rise time (in nsec) and precursor formation. Slope (V/m/nsec) is not associated therein. It is important to distinguish between rise time, in nsec, and slope, in V/m/nsec.
Discussion of Extant Measurements
The committee has located only three measurements that showed precursors. First, circa 1967, as thesis work at NYU-Bronx; second, circa 1986, at Physics International; third, calculations and measurements made at the Naval Surface Warfare Center in the 1990s, but published in 2001. In addition, circa 1990, cal-
culations and measurements were made at the University of Michigan but not published, and later briefly extracted. Further measurements were made by AFRL-DED contractors on water, sand, and concrete. The Michigan and AFRL measurements did not show precursors.
Pleshko (see Annex 5-2)
Graduate student Peter Pleshko, under the supervision of Professor Istvan Palocz, designed experiments to produce precursors in the microwave region, and took measurements accordingly, all as a Ph.D. project at New York University-Bronx. Their paper describes and discusses the three experiments they designed to demonstrate precursors.
Precursors were observed, but in all three experiments the bandwidths were wide: the smallest bandwidth was roughly 500 MHz. Thus, there is minimal relevance to PAVE PAWS.
Physics International Report “Dispersive Pulse Propagation” (see Annex 5-2)
Physics International (PI) experiments replicated one of the Pleshko experiments, using a coaxial test fixture for additional measurements and also open-tank measurements. Measuring and test equipment for short-pulse wideband were somewhat primitive (circa 1987) compared with current capabilities. The source signals were of poor quality: the source pulse had high pre- and post-pulses. The coaxial test cell was designed for a 50 ohm match with air; the water, salt, and sugar solutions produced major mismatches resulting in quite apparent ringing. All of the measurements were wideband, and had frequency spectra centered above 1000 MHz, where dielectric constant ε and conductivity σ changes with frequency are significant. Precursors were observed only in those few wideband experiments that were designed to create strong dispersion (waveguide and Goubau line). No discernable precursors were observed in test cell and liquid tank experiments, even though bandwidths were wide and frequency spectra were in the region of changing dielectric properties.
Stoudt, Peterkin, and Hankla, NSWC report “Transient RF and Microwave Pulse Propagation in a Debye Medium (Water)” (see Annex 5-2)
The measurements utilized a coaxial line test cell filled with re-circulating deionized water. Waveforms were wideband; low-frequency precursors were measured. Agreement with calculated data was excellent. These measurements used well-designed equipment with realistic media, and were of high quality.
Mourou and Williamson (see Barrett in Annex 5-2)
The paper by Barrett reproduces a small set of the measurements made at the University of Michigan by Mourou and Williamson. The Mourou and Williamson work has not been published. Measurements were made using microwave stripline with beta-alumina dielectric. A wideband waveform at 8 GHz was used, but the apparatus introduced significant reflections. Nonetheless, no signals that could be identified as precursors were observed.
Farr and Frost, Measurement Notes 49 and 52, AFRL-DED (see Annex 5-2)
The purpose of the measurements was determination of dielectric properties of water, sand, and concrete. A coaxial transmission line was used, with an impulse waveform with spectral content from DC to over 20 GHz. Significant pulse broadening and attenuation were observed, but no overt precursors appeared.
Discussion of Calculations
Extensive calculations have been published by Oughstun and colleagues, in a book and numerous papers (see Annexes 5-3 and 5-5). All of these use wideband waveforms, typically at laser (infrared) frequencies. Classic precursor waveforms are produced, but the vital contribution of bandwidth is not discussed.
Sandia Report “Calculations of Precursor Propagation in Dispersive Dielectries” (see Annex 5-3)
Bacon calculated propagation of waveforms into pure water at 435 MHz, for two bandwidths: 200 MHz, and 10 MHz. The 200 MHz bandwidth waveforms showed precursors, while the 10 MHz bandwidth waveforms did not. The narrow-band signal also showed a slow buildup (and presumably decay). The wideband waveforms decay at the carrier rate for several meters, then more slowly. However the band-limited signal decays at the carrier rate at all penetration distances. PAVE PAWS has band-limiting filters in the exciter units, so these 10 MHz results are expected to represent the radar (see annex 3).
These calculations were buttressed by Roberts, who showed that decay slower than carrier exponential requires significant spectral energy below the carrier frequency, i.e., wideband. As mentioned in Radar Electromagnetics, the spread of spectral energy allows the precursors to decay as ![]() at distances where the main signal is negligible.
at distances where the main signal is negligible.
Moten and Others (see Annex 5-3)
Moten and colleagues calculated that a wideband waveform produces pre-
cursors, but stated that narrow band systems would not generate precursors (see Annex 5-3).
In several papers, Albanese and colleagues calculated precursors, but all for wideband signals. No attempt was made to correlate precursor generation with either bandwidth, or dispersive characteristics of the medium with frequency.
Mokole and Samaddar (see Annex 5-3)
Mokole and Samaddar calculated the behavior of a laser pulse (very wideband) propagating into a semi-infinite medium. Strong precursors were predicted.
Dvorak (see Annex 5-3)
Dvorak, using exotic functions, calculated propagation in a waveguide, thus verifying the prior experimental work of Pleshko.
Discussion of Annexes
The annexes contain a citation and review of each journal paper that appears relevant. They are grouped into precursor measurements, precursor calculations, related papers on precursors, pulse propagation in lossy media, and publications by Professors Oughstun and others.
SUMMARY
The PAVE PAWS phased array contains a large number of elements per face (1792), all of which are turned on simultaneously. Bandwidth is very narrow, 5 MHz at most; the signal is heavily filtered to reduce interference. Waveform buildup is slow (about 200 nsec) due to the signal bandwidth and to the amplifier characteristics. Waveform slopes, in V/m/nsec, are as expected, except in the vicinity of zero crossings; there, noise and interfering signals control slopes, and the PAVE PAWS signals are negligible. Radial fields as such are not present; the longitudinal field components observed were produced by the dipole 20 degree tilt, and multipath fields.
At angles away from the array axis, time delay exists between the signal from the closest dipole and the farthest dipole. It is a maximum of about 60 nsec. Reflector (dish) antennas have a similar delay at wide angles; the same-size array and reflector have roughly the same delay. For PAVE PAWS the peak delay is roughly 1/3 of the buildup time. Due to the large number of active elements per face, and due to the pseudo-random distances from each element to an observer, the signal buildup is smooth as shown by detailed calculations. In none of the Phase IV measured data is it possible to discern the delay effects. The committee’s
conclusion is that narrow-band phased-array radiation is just like narrow-band reflector radiation.
At wide angles from the array axis and from the radar beam, the sidelobe level is extremely low. This low sidelobe level results from the destructive summation of 1792 contributions. Turnoff and decay of the Class C amplifiers is somewhat irregular, which sometimes results in decay transients above the normal low sidelobe level. Amplitude of these spikes is still much below the allowable power density; this, with their short duration, indicates a negligible effect.
Precursors are transient signals that may appear before, during, and after the signal, in a dispersive medium such as water or cells. None propagate faster than light. Those that have been considered as possibly important have significant low-frequency spectral energy, that is, important frequency components below the carrier frequency. There are extensive calculations, and several measurements, that show that wideband signals produce observable precursors. Typical precursor wide bandwidth is 10,000 MHz, a factor of 2000 times the PAVE PAWS bandwidth. Each frequency component of the wideband waveform decays exponentially in the medium. After the signal has experienced a large attenuation, the precursor waveform may decay algebraically. Precursor formation is related to signal bandwidth (buildup time) but not to signal level (V/m). The criterion of 1 V/m/nsec has no meaning for precursor formation. As discussed under Precursors: Radar Electromagnetics, rise time and bandwidth are independent of field strength in V/m.
For the PAVE PAWS bandwidth no measurable precursors were found in the several experiments. All calculations and measurements conclude that narrow-band phased-array radiation effects are not distinguishable from those of reflector antennas. This may also be true for wideband phased arrays, but no relevant data are available.
REFERENCES
AFRL (Air Force Research Laboratory). 2003. Phase IV—Time-Domain Waveform Characterization Measurements of the PAVE PAWS Radar. Kirtland Air Force Base, Albuquerque, NM.
Baños, A. 1966. Dipole Radiation in the Presence of a Conducting Halfspace. New York: Pergamon Press.
Brillouin, L. 1962. Wave Propagation and Group Velocity. St. Louis, MO: Academic Press.
Collin, R.E. 2004. Hertzian dipole radiating over a lossy or sea: Some early and late 20th century controversies. IEEE Antennas and Propagation Magazine 46:64-79.
Hansen, R.C. 1987. Short pulse excitation of reflector antennas. P IEEE 134: 557-559.
Hansen, R.C. and E. Kramer. 1992. Correction to short-pulse excitation of reflector antennas. P IEEE 139:119-120.
Norton, K.A. 1937. Space and surface waves in radio propagation. Phys Rev 132-133.
Jordan, E.C. and Balmain, K.G. 1968. Electromagnetic Waves and Radiating Systems. Prentice Hall.
Oughstun, K.E. and G.C. Sherman. 1994. Electromagnetic Pulse Propagation in Causal Dielectrics, Springer Series on Wave Phenomena, vol. 16. Berlin-Heidelberg: Springer-Verlag.
Somerfeld, A. 1914. Above the propagation of light in dispersive media. Ann Physik 44:177-202.
ANNEX 5-1: DISPERSION IN BIOLOGICAL TISSUES
In biological tissues, three distinct dispersion regimes have been defined. The lowest frequency dispersion, referred to as the α dispersion, is very large, and occurs near 10 Hz to 100 Hz, and is believed to be associated with large biological structures such as cell bodies. The second dispersion (referred to as the β dispersion) occurs over the range of approximately 100 kHz to 100 MHz. It reflects the dipolar characteristics of the molecular constituents of the tissue, and terminates at the permittivity of water (approximately 80 farads/meter). The third dispersion (γ), is associated with the relaxation time of water and occurs in the low GHz range. Correspondingly, in the frequency range of the PAVE PAWS signal, the dielectric permittivity of biological tissue is very near to that of water, and the dispersion is very low. While the dispersion (δε/δf) depends on both the specific tissue and frequency range, dispersions in biological tissues near 500 MHz are in the range of only 1 to 10 farad/meter per 100 MHz. This is a very small dispersion. Nonetheless, whenever the frequency spectrum of an applied waveform encompasses a region of anomalous dispersion, precursors may be formed. If the bandwidth is narrow, and the material parameters change little if at all over the frequency range of interest, precursors will have negligible amplitude. An examination of the dielectric properties of the white matter of brain tissue, for example, shows that the permittivity changes at a relatively constant rate of 0.5 decade of permittivity/decade of frequency, from a value of 10,000 at 10 KHz, to a value of 30 at 1 GHz. The PAVE PAWS instantaneous bandwidth is never more than 5 MHz, although the carrier frequency changes as the beam moves between 420 MHz and 450 MHz. Thus this narrow bandwidth signal is not expected to produce measurable precursors.
ANNEX 5-2: PAPERS ON PRECURSOR MEASUREMENTS
1. P. Pleshko and I. Palocz, “Experimental Observations of Sommerfeld and Brillouin Precursors in the Microwave Domain,” Phys. Rev. Letters, Vol. 22, 2 June 1967, 1201-1204
Graduate student Peter Pleshko, under the supervision of Professor Istvan Palocz, designed experiments to produce precursors in the microwave region, and took measurements accordingly, all as a Ph.D. project at New York University-Bronx. This paper describes and discusses the experiments they designed to demonstrate precursors.
The first experiment utilized a coaxial transmission line filled with ferrite material, which was magnetized by an applied external magnetic field. This simulated the first branch of the dispersion curve. A pulse of sine waves at a carrier frequency of 625 MHz was applied at one end of a long coax, and the waveform was observed at the other end. With an applied magnetic field of 100 gauss (earth field 0.3 to 0.6 gauss), the Brillouin precursor was visible but the main signal was
not. With a 200 gauss field the Brillouin precursor, which looks like one cycle with a slightly lower frequency than the carrier, was followed by the pulse train. The precursor amplitude was nearly twice that of the pulse train.
The second experiment was aimed at simulating the second branch of the dispersion curve. A waveguide with a cutoff frequency of 4290 MHz was used; the guide length was 6 ft. A pulser source producing a 100 picosecond single pulse with fast rise time was used. A Sommerfeld precursor with a frequency of roughly 15,000 MHz was observed, but the amplitude was small compared to the main signal; these precursors are of higher frequency.
The third experiment was also second branch, and used a Goubau surface-wave transmission line consisting of RG-8 coaxial cable with the outer braid removed. It was then a wire with a dielectric sheath. Horn feeds were used. Again the 100 picosecond pulser with 30 picosecond rise time was the source. The Brillouin (low frequency) precursor was observed; the pulse was not shown.
In all three experiments described above the bandwidths were large: in experiment one, 350 Mhz or 315%; experiments two and three, 350 MHz. These large bandwidth[s] are critical, as signals occupying large bandwidth can experience significant dispersion (dispersion is a change of parameters with frequency), and have major energy at low frequencies. In spite of the deliberately introduced large dispersion, the high frequency (Sommerfeld) precursor was very small. The amplitude of the low frequency (Brillouin) precursor was not compared to the pulse amplitude. The large precursors calculated for the optical region by Oughstun did not develop, but the optical bandwidth and dispersion are much larger, and the wavelength is very much shorter than at microwave frequencies.
2. R.R. Smith, Dispersive Pulse Propagation, report PITR 3341, Physics International Co., prepared for USAFSAM/RZM, Dec. 1988
The principal investigator performed three experiments to determine if precursors could be generated by microwave frequencies.
The first PI experiment replicated the Goubau surface-wave transmission-line experiment of Pleshko and Palocz. A step-input function was used, with a rise time of roughly 300 picoseconds. The Brillouin precursor was observed as an overshoot of roughly 100% with rapid decay. Signal bandwidth was approximately 6700 MHz.
The next experiment simulated muscle tissue in a coaxial test fixture filled with distilled water. A single-step function with a rise time of roughly 500 picoseconds was the applied signal. For the frequency spectrum of the waveform, roughly 4000 MHz wide, distilled water, if sufficiently pure, has dielectric constant and conductivity similar to those of muscle tissue. The results showed severe waveform distortion and ringing (steps) as illustrated in trace 906D of Figure 8 of the report. Unfortunately the coaxial line was designed for 50 ohms impedance (industry standard for test equipment) when air filled. When water or
ionic solution fills the test cell, the impedance is badly mismatched, resulting in the serious ringing observed.
Another experiment used a pulse generator that supplied a bipolar pulse (a positive pulse followed by a negative pulse), again into distilled water. This pulse was of poor quality, having itself a small precursor and a small postcursor, along with a negative pulse much lower in amplitude and wider in time, than the positive pulse. Results from the test cell showed considerable ringing, no doubt due to the impedance mismatch, but no evidence of Sommerfeld or Brillouin precursors. Measurements next used water with 1.4% salt, with the step-function signal source. Results showed severe waveform distortion but no evidence of precursors. With the bipolar-pulse signal, again results were distorted but no precursors were present. Use of a sugar/salt mixture with water produced essentially the same results: distortion but no precursors. Coaxial test fixture measurements were contaminated by ringing due to impedance mismatch, and by poor quality source signals. No Sommerfeld or Brillouin precursors were observed.
Open-tank measurements used a waveguide as an illuminator, with Set One with cut-off at 910 MHz and Set Two with cutoff at 1320 MHz. The signal was tripolar (−,+,−) but was of poor quality with ringing. Results did not show any precursors for several salt and sugar solutions. Finally, as the signal propagates into the lossy solution, the higher frequency components are attenuated more, as expected. The source signal was of very poor quality, and there were internal and external reflections, resulting in extraneous signals (ringing). No precursors were observed.
Short-pulse, wideband measuring and test equipment was somewhat primitive (circa 1987) compared with current capabilities. The source signals were of poor quality. The coaxial test cell was designed for a 50 ohm match with air; the water, salt, and sugar solutions produced major mismatches with resulting quite apparent ringing. These reflections tended to mask the changes in waveform produced by the medium. All of the measurements were wideband and had frequency spectra centered above 1000 MHz, where dielectric constant and conductivity ? changes with frequency are significant. Precursors were observed only in those few experiments that used wide bandwidth and deliberately created strong dispersion (waveguide and Goubau line). No discernible precursors were observed in test-cell and liquid-tank experiments, even though bandwidths were wide and frequency spectra were in the area of changing dielectric properties.
3. T.W. Barrett, “Energy Transfer and Propagation and the Dielectrics of Materials: Transient Versus Steady State Effects,” Proc. Ultra-wideband Radar Symp., Los Alamos, CRC Press, 1990, 1-20
In this paper, the author gives a brief review of the saddle-point approximations used in calculating transient response of dispersive materials. A much more thorough account is given by Oughstun and Sherman. The paper reproduces some
of the unpublished measurements made circa 1990 at the Ultrafast Science Laboratory of the University of Michigan by Professor Mourou and Dr. Williamson. A more extensive set of the raw measured data has been made available by Dr. Whittaker of the University of Michigan. The relevant measurements utilized strip line with either air or beta-alumina as the dielectric. The frequency was 8 GHz, and waveforms of one to eight cycles were used. Unfortunately, the waveform generator and the detector/receiver together produced several significant reflections (echoes) in the reference air line results. Reflected waveforms appeared at roughly four and eight cycles. Using a length of dielectric of 1 inch, both single-cycle and eight-cycle incident waveforms showed a distorted waveform due to the echoes, but no precursors. With a dielectric length of 4 inches, the carrier waveform was absent due to attenuation, but the transmitted waveform did not look like any calculated precursors. In all of these experiments, the bandwidths were large, and extended to frequencies well below the carrier frequency.
4. D.C. Stoudt, F.E. Peterkin, and B.J. Hankla, “Transient RF and Microwave Pulse Propagation in a Debye Medium (Water),” NSWC report JPOSTC-CRF-005-03, Dahlgreen, VA, Sept. 2001
The test cell was a 1.4 m-long coaxial transmission line with recirculated deionized water. A tapered dielectric plug matched the 33 ohm line (when filled) to the 50 ohm test equipment. A short was placed at the far end of the line, so that the signal would be reflected. At the feed end, a tee junction separated out the return signal. Round trip delay was 82 nanoseconds. Equipment included a Gigatronics 7100 signal generator and an HP 54720A Digitizing Oscilloscope.
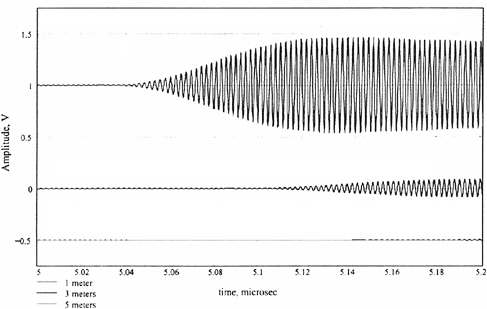
A 10-cycle pulse at 1 GHz was the test signal. This signal showed two small amplitude residual cycles at the end of the signal, but the input signal quality was good. The output signal, after 2.76 m of water travel, showed only two precursors, no main signal. The fore and aft precursors were of opposite polarity, and closely matched the calculated values. A 10.5-cycle 1 GHz waveform showed similar results, and again agreed with calculations. In this case, because of the half cycle, both precursors are of the same polarity.
Two 6-cycle 400 MHz waveforms were used as exciters. The square-wave modulated pulse, after 2.76 m of water, showed precursor amplitude roughly twice the main signal amplitude. Again, calculations and measurements agree very closely. It is worth noting that the calculations for this waveform after 1.5 m of water showed only very slight precursor effects. Trapezoidal modulations of the 10 cycles of carrier were also tested. Only small precursor effects appeared after 2.76 m of water.
These measurements were carefully designed and conducted, with attention paid to impedance matching, use of time delays to separate input and output signals, and data recording. Thus these are the definitive measurements utilizing representative media.
5. E.G. Farr and C.A. Frost, “Time Domain Measurement of the Dielectric Properties of Water in a Coaxial Test Fixture,” Measurement Notes 49, Dec. 1996; “Impulse Propagation Measurements of the Dielectric Properties of Water, Dry Sand, Moist Sand and Concrete, “Measurement Notes 52, AFRL Directed Energy Directorate, Albuquerque, NM.
An oversized coaxial transmission line, with the sample occupying part of the line length, was used. The signal was a wideband impulse (short pulse), with major spectral energy from DC to over 10 GHz. The line was used in both the transmission and the reflection modes. Unfortunately, the line was matched with air for 50 ohms, which produced significant mismatch at the sample interfaces. Thus, the results were contaminated with significant ringing. In passing through the distilled water sample, the impulse waveform was significantly attenuated and broadened. The resulting waveforms did not show any of the typical oscillations commonly seen in precursor waveforms. Although the time domain instrumentation was up to date and of high quality, the results were degraded by the design of the coaxial test chamber.
ANNEX 5-3: PAPERS ON PRECURSOR CALCULATIONS
1. L. Brillouin, Wave Propagation and Group Velocity, Academic Press, 1960
This most interesting, but hard to find, book is a retrospective of the work by Sommerfeld and Brillouin on wave velocities and precursors. A translation (from German) of the classic 1914 paper by Sommerfeld is included, along with a translation (from French) of the classic 1914 paper by Brillouin; both concern propagation in dispersive media and saddle-point asymptotics. In the other chapters, Brillouin discusses several waveform velocities: group velocity, signal velocity, and energy-transfer velocity. His calculations of precursors are less useful, due to errors, as observed by Oughstun and others. Both Sommerfeld and Brillouin used the term “forerunners” rather than precursors; use of “precursors” apparently found favor relatively recently.
2. K.E. Oughstun and G.C. Sherman, Electromagnetic Pulse Propagation in Causal Dielectric, Springer, 1997
This treatise shows in detail the difficulties in obtaining approximate solutions to wave propagation in dispersive media. Crudely, the signal is represented in the complex phase plane by a pole, and the precursors by branch points. Elaborate asymptotics are used to obtain the propagated waveforms. Unfortunately (for PAVE PAWS relevancy), all calculations are at infrared wavelengths, where the frequency is roughly 10,000,000 times higher than that of PAVE PAWS. All waveforms are either single cycle or a few cycles. For these very wideband signals, precursor formation is calculated. Further, the work is mathematically oriented, and has little physics interpretation. In particular, there is no discussion of the crucial effect of bandwidth.
Oughstun and colleagues have published many informative papers; almost all concern laser (IR) waveforms. Even their papers in Radio Science are on optical (IR) waveforms.
3. T.M. Roberts, “Radiated Pulses Decay Exponentially in Materials in the Far Fields of Antennas,” Electronics Ltrs., Vol. 38, 4 July 2002, 679-680
This salient paper shows that low-frequency spectral components of a waveform can produce a decay rate in dispersive material that is lower than that of the carrier frequency. In a linear medium, and at low power levels, tissue is linear and all spectral components decay exponentially. See also:
4. T.M. Roberts and P.G. Petropoulos, “Asymptotics and Energy Estimates for Electromagnetic Pulses in Dispersive Media,” J. Opt. Soc. Amer. A, Vol. 13, June 1996, 1204-1217 and “Addendum,” J. Opt. Soc. Amer. A, Vol. 16, 1999, 2799-2800
5. T.M. Roberts, “Measured and Predicted Behavior of Pulses in Debye-and Lorenz-Type Materials.” Trans. IEEE AP-52 Jan. 2004. 310-314.
Asymptotic calculations are shown to validate precursor measurements made using liquid-filled coax cables by AFRL contractors (see Annex 2). Results show algebraic decay after significant attenuation has occurred. Signal bandwidth was approximately 10 GHz; the widest PAVE PAWS bandwidth is 5 MHz, or 2000 times smaller. PAVE PAWS precursors will be too small to be measurable.
6. L.D. Bacon, “Calculations of Precursor Propagation in Dispersive Dielectries,” SAND 2003-3040, Aug. 2003, Sandia National Laboratories
Dr. Larry Bacon of Sandia National Laboratories has calculated waveform propagation in lossy dispersive media. These cases utilized a carrier frequency of 435 MHz, which is in the middle of the PAVE PAWS band. Pure water was the medium.
He used a narrow-band (1 microsecond) pulse train, and a wideband (10 nanosecond) pulse train. Note that the narrow-band pulse has about the same bandwidth as the widest PAVE PAWS waveform. Each pulse train was utilized without, and with, a filter. The 1 microsecond waveform used a 10 MHz wide filter, while the 10 nanosecond waveform used a 200 MHz wide filter. The two filter bandwidths are shown in Figure 5-A3.1.
The wideband unfiltered waveform displayed at 1meter depth in the medium a precursor, small compared to the main signal; at 5-meter depth, the precursor was larger than the signal but very small compared to the signal at 1 meter. When the wideband filter was applied, no precursors were visible.
The narrow-band unfiltered waveform displayed at 1-meter depth in the medium a very small precursor; at 5-meter depth the precursor was again larger than the signal but very small compared to that at 1 meter. With the filter applied,
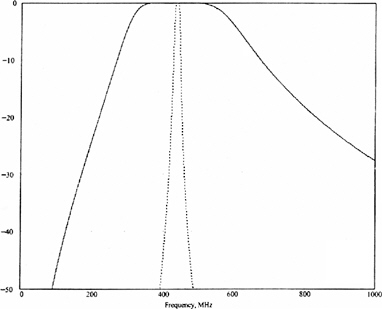
FIGURE 5-A3.1 10 MHz (dotted) and 200 MHz (solid) bandpass filter frequency responses.
which represents the PAVE PAWS radar, a slow buildup was observed at all depths, as seen in Figure 5-A3.2. No precursors were evident. However, at great depth in the medium, a precursor is visible but its amplitude is below the incident amplitude by a factor of roughly 100 million. Such small values are way below the natural noise level, hence are not measurable. Because of the narrow bandwidth of the 1 microsecond waveform, all spectral (Fourier) components decay essentially exponentially, producing the classic “skin depth.”
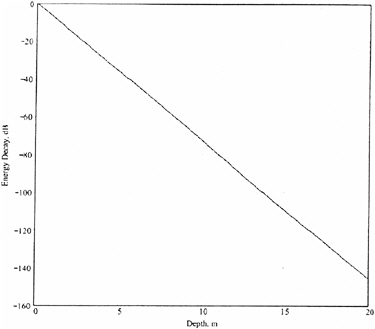
Figure 5-A3.3 shows waveform decay over a 20-meter depth; this waveform decays exponentially just like all narrow-band waveforms. Exponential decay is linear on a logarithmic scale (decibels).
In summary, wideband waveforms do produce observable precursors. Narrowband waveforms, such as those of PAVE PAWS, do not produce measurable precursors.
7. D.C. Stoudt, F.E. Peterkin, and B.J. Hankla, “Transient RF and Microwave Pulse Propagation in a Debye Medium (Water),” NSWC report JPSTC CRF-005-03, Dahlgren, VA, Sept. 2001
This work concerns frequencies below 2 GHz, where water shows a nearly constant permittivity but a varying conductivity with frequency. Accordingly, group and signal velocity dispersion can be neglected, and the Debye dispersion model is adequate. The propagation of waveform is analyzed using Fourier Trans-
forms; the resulting frequency spectra are propagated through the lossy media, then inverse transformed into a waveform. Waveforms used include an ideal 10-cycle, 1 GHz pulse, a 6-cycle, 400 MHz pulse, and these two with a more practical trapezoidal envelope on the 1 GHz waveform. These calculations agree with those of Albanese (see reference 13, this section).
For the square-wave modulated 1 GHz signal, at a depth of 75 cm (2.5 ft.), the fore and aft precursors are much larger than the main 10-cycle waveform. At the much shorter depths representative of humans, the waveform would be much larger than the precursor. When the modulation is trapezoidal, the precursors are only slightly larger than the main signal, at the same 75 cm depth. Bandwidth of both signals is roughly 200 MHz. For depths so large that the main signal has disappeared due to strong attenuation, the precursor decays approximately as ![]() , thus validating the one-term series approximation of Oughstun.
, thus validating the one-term series approximation of Oughstun.
The 6-cycle, 400 MHz signal, with ideal square-wave modulation (instant turn on), shows only a precursor slightly larger than the main signal, at a depth of 1.5 m (4.9 ft). Bandwidth is roughly 130 MHz.
These calculations show that for 400 MHz, even with the large bandwidth associated with the 6-cycle waveform, precursors are negligible at the limited tissue depth available in humans.
8. K. Moten, C.H. Durney, and T.G. Stockham, “Electromagnetic Pulse Propagation in Dispersive Planar Dielectrics,” Bioelectromagnetics, Vol. 10, 1989, 35-49
This paper investigates a plane-wave pulse-train incident on a lossy dispersive slab, using Fast Fourier Transform techniques. Calculations show that wideband pulses can produce significant precursors. However, “the narrower the bandwidth of the pulse train, the less the difference between the pulse response and CW response.” And, “only very broadband pulsed systems could be expected to produce results that differ significantly from those of CW systems.” Pulse penetration depends on the dispersive nature of the dielectric medium and the Fourier coefficients (bandwidth) of the waveform.
9. R. Albanese, J. Penn, and R. Medina, “Ultrashort Pulse Response in Nonlinear Dispersive Media,” in Ultra-Wideband, Short-Pulse Electromagnetics, H.L. Bertoni, L. Carin, and L.B. Felsen, Eds., Plenum, 1993, 259-265
see also:
10. R. Albanese, J. Penn, and R. Medina, “Short-Rise-Time Microwave Pulse Propagation through Dispersive Biological Media,” J. Opt. Soc. Amer. A, Vol. 6, Sept. 1989, 1441-1446
These papers use Fourier series (of the waveform) as an analysis tool. Their
calculations used a waveform with 10 carrier cycles with a carrier frequency of 1 GHz. The waveform buildup was instantaneous; the envelope was a square wave. At 1.5 m distance the rise time affected the precursor amplitude, with longer rise time reducing the amplitude. However, at this distance the main signal is very small and the precursors are also small.
11. R. Albanese, J. Blaschak, R. Medina, and J. Penn, “Ultrashort Electromagnetic Signals: Biophysical Questions, Safety Issues, and Medical Opportunities,” Aviation, Space, and Environmental Medicine, May 1994, A116-A120
This paper shows a 1 nanosecond wideband pulse of 10 carrier cycles, carrier frequency 10 GHz. Both Sommerfeld- and Brillouin-calculated precursors appear after propagating 1 cm in pure water. Also shows precursors produced by laser (IR) radiation. Possible cellular effects of very high electric fields (hundreds or thousands of kW/m) are discussed.
12. R.A. Albanese, “An Electromagnetic Inverse Problem in Medical Science,” Chapter 2 of Invariant Imbedding and Inverse Problems, SIAM, 1992. 30-41
Using a square-wave modulation containing 5 carrier cycles, with a 3 GHz carrier frequency, a waveform with Brillouin precursors was calculated at 10 cm. depth. With no noise, partial results were obtained, but with very weak added noise there were no results.
13. R.A. Albanese, R.L. Medina, and J.W. Penn, “Mathematics, Medicine, and Microwaves,” Inverse Problems, Vol. 10, 1994, 995-1007
This paper shows a 1 nanosecond wideband pulse of 10 carrier cycles, carrier frequency 10 GHz. Both Sommerfeld-and Brillouin-calculated precursors appear after propagating 1 cm in pure water. Most of the paper concerns the inverse problem: given the response, find the dielectric and loss properties of the material.
14. E.L. Mokole and S.N. Samaddar, “Transmission and Reflection of Normally Incident, Pulsed Electromagnetic Plane Waves upon a Lorentz Half-Space,” J. Opt. Soc. Amer. B, Vol. 16, May 1999, 812-831
Both reflected and transmitted fields are calculated for a semi-infinite medium; the incident waveform is a single laser pulse at IR (frequency ~2 THz). As expected, this extremely wideband waveform produces strong Sommerfeld precursors.
15. S.L. Dvorak, “Exact, Closed-Form Expressions for Transient Fields in Homogeneously Filled Waveguides,” Trans. IEEE, Vol. MTT-42, Nov. 1984. 2164-2170
see also:
16. S.L. Dvorak and D.G. Dudley, “Propagation of Ultra-Wide-Band Electromagnetic Pulses through Dispersive Media,” Trans. IEEE, Vol. EMC-37, May 1995, 192-200
Using the Incomplete Lipschitz-Hankel Integrals (ILHI), waveform propagation in a waveguide is studied. Waveguides provide dispersion. The waveform used is a single cycle of a sine wave. Calculations show significant precursors; the waveform bandwidth is very wide. Prior experimental work of Pleshko is not mentioned, but the precursor increases in frequency as it propagates, just as measured by Pleshko.
ANNEX 5-4: RELATED PAPERS ON PRECURSORS
1. Albanese, R.A. and E.L. Bell, Radiofrequency Radiation and Living Tissue: Theoretical Studies, report SAM-TR-79-41, Dec. 1979
This interim report models possible interactions of RF energy and cells. No distinction is made between thermal effects and pulsed effects.
2. Albanese, R.A. and E.L. Bell, “Radiofrequency Radiation and Chemical Reaction Dynamics,” in Nonlinear Electrodynamics in Biological Systems, W. R. Adey and A. F. Lawrence, Eds., Plenum, 1984, 277-285
Treated in this paper are high field strengths (100 to 2000 V/m) where the media are non-linear. There is no relevance to PAVE PAWS, where the field strengths are low, and the media are linear.
3. Albanese, R.A., R. Medina, and J. Penn, “Mathematics and Electromagnetic Theory,” unpublished and undated paper, circa 2001
The statement “frequency dependence in the frequency domain implies local tissue memory in the time domain” is too general to have meaning. Certainly, frequency spectrum and time waveform are related. But this does not necessarily imply tissue memory. The entire paper is not concerned with pulses.
4. Papazoglou, T.M., “Transmission of a Transient Electromagnetic Plane Wave into a Lossy Half-Space,” J. Appl. Phys., Vol. 46, Aug. 1975, 3333-3341
see also:
5. Dudley, D.G., T.M. Papazoglou, and R.C. White, “On the Interaction of a Transient Electromagnetic Plane Wave and a Lossy Half-Space,” J. Appl. Phys., Vol. 45, March 1974, 1171-1175
Propagation of a single Gaussian type pulse (slow rise time and fall time) into a lossy medium is considered. One case of interest uses a lossy and disper-
sive medium (earth). Waveforms with and without dispersion are very much the same, probably due to the narrow bandwidth of the incident pulse. No precursors were evident.
6. Devaney, A.J., “Linearized Inverse Scattering in Attenuating Media,” Inverse Problems, Vol. 3, 1987. 389-397
Dr. Devaney has extended this work to dispersive media, but it has not been published. The aim was to see if precursors could help in the inverse problem. Note, the inverse problem is: given the response, find the details of the scatterer or the details of the medium.
Pulse Propagation in Lossy Media
Researchers from Harvard have published papers on pulse propagation in sea water, a highly lossy medium. Single pulses and a pulse of carrier oscillations have been considered. These papers utilize a dipole as source, unlike the plane-wave source of Oughstun and colleagues. The dipole near-field greatly complicates the analysis. The papers show that the rise and fall times each produce a transient, with the carrier oscillations in between. When the rise and fall times are slow, two things occur. First, the lower frequencies in the transient allow them to decay more slowly than does the carrier. So after some distance, the carrier may be smaller than the transient waveform. These are probably not precursors in the Brillouin sense. Second, the amplitude of the transient is reduced by f2rs/(f2 + f2rs), where f is the carrier frequency and frs is the principal frequency of the rise time. Thus, if the rise time equals 20 carrier cycles, the rise-time transient amplitude is reduced by 0.0025, or 52 dB.
1. King, R.W.P. and T.T. Wu, “The Propagation of a Radar Pulse in Sea Water,” J. Appl. Phys., Vol. 73, 15 Feb. 1993, 1581-1590
see also:
2. King, R.W.P. and T.T. Wu, Erratum: “The Propagation of a Radar Pulse in Sea Water,” J. Appl. Phys., Vol. 77, 1 April 1995, 3586-3687
3. King, R.W.P., “The Propagation of a Gaussian Pulse in Sea Water and Its Application to Remote Sensing,” Trans. IEEE, Vol. GRS-31, May 1993, 595-605
4. King, R.W.P., “Propagation of a Low-Frequency Rectangular Pulse in Seawater,” Radio Science, Vol. 28, May-June 1993, 299-307
5. Margetis, D., “Pulse Propagation in Sea Water,” J. Appl. Phys., Vol. 77, 1 April 1995, 2884-2888
6. Margetis, D., “Pulse Propagation in Sea Water: The Modulated Pulse,” Progress in Electromagnetics Research, Vol. 26, 2000, 89-110
The prediction by Song and Chen that early arrival and late arrival parts of a waveform in lossy media decay algebraically (as 1/R3 or 1/R5) has been shown to be incorrect by Margetis and King:
7. Song, J. and K-M Chen, “Propagation of EM Pulses Excited by an Electric Dipole in a Conducting Medium,” Trans. IEEE, Vol. AP-41, 1993, 1414-1421
8. Margetis, D. and R.W.P. King, “Comments on ‘Propagation of EM Pulses Excited by an Electric Dipole in a Conducting Medium,’” Trans. IEEE, Vol. AP-43, Jan 1995, 119-120
9. Wait, J.R., “Electromagnetic Fields of Sources in Lossy Media,” Chapter 24 in Antenna Theory, Part II, R.E. Collin and F.J. Zucker, Eds., McGraw-Hill, 1969
This paper treats single-pulse propagation in lossy (non-dispersive) media. Extensive references are provided.
ANNEX 5-5: PAPERS BY PROFESSOR OUGHSTUN AND COLLEAGUES
These papers are concerned with wideband optical (laser) short pulses in media that are lossy and dispersive. No discussions of the effects of waveform bandwidth are given. These papers are listed because they are often cited for PAVE PAWS. However the very narrow-band nature of the PAVE PAWS signal makes all of these papers irrelevant to the PAVE PAWS problem. And the laser frequency is roughly 10,000,000 times higher than that of PAVE PAWS.
1. Oughstun, K.E. and G.C. Sherman, “Propagation of Electromagnetic Pulses in a Linear Dispersive Medium with Absorption (the Lorentz Medium),” J. Opt. Soc. of Am. B, Vol. 5, April 1988, 817-849
2. Oughstun, K.E. and S. Shen, “Velocity of Energy Transport for a Time Harmonic Field in a Multiple-Resonance Lorentz Medium,” J. Opt. Soc. of Am. B, Vol. 5, Nov. 1988, 2395-2398
3. Shen, S. and K.E. Oughstun, “Dispersive Pulse Propagation in a Double-Resonance Lorentz Medium,” J. Opt. Soc. of Am. B, Vol. 6, May 1989, 948-963
4. Wyns, P., D.P. Foty, and K.E. Oughstun, “Numerical Analysis of the Precursor Fields in Linear Dispersive Pulse Propagation,” J. Opt. Soc. of Am. A, Vol. 6, Sept. 1989, 1421-1429
5. Oughstun, K.E. and J.E.K. Laurens, “Asymptotic Description of Ultrashort Electromagnetic Pulse Propagation in a Linear, Causally Dispersive Medium,” Radio Science, Vol. 26, Jan.-Feb. 1991, 245-258
6. Oughstun, K.E., “Pulse Propagation in a Linear, Causally Dispersive Medium,” Proc. IEEE, Vol. 79, Oct. 1991, 1379-1390
7. Oughstun, K.E. and J.E.K. Laurens, “Asymptotic Description of Electromagnetic Pulse Propagation in a Linear Dispersive Medium,” in Ultra-Wideband, Short-Pulse Electromagnetics, H. Bertoni et al,. Eds., Plenum Press, 1993, 223-240
8. Balictsis, C.M. and K.E. Oughstun, “Uniform Asymptotic Description of Ultrashort Gaussian Pulse Propagation in a Causal, Dispersive Dielectric,” Phys. Rev. E, Vol. 47, 1993, 3645-3669
9. Balictsis, C.M. and K.E. Oughstun, “Uniform Asymptotic Description of Gaussian Pulse Propagation of Arbitrary Initial Pulse Width in a Linear, Causally Dispersive Medium,” in Ultra-Wideband, Short-Pulse Electromagnetics 2, L. Carin and L.B. Felsen, Eds., Plenum Press, 1994, 273-283
10. Smith, P.D. and K.E. Oughstun, “Electromagnetic Energy Dissipation of Ultrawideband Plane Wave Pulses, in a Causal, Dispersive Dielectric,” in Ultra-Wideband, Short-Pulse Electromagnetics 2, L. Carin and L.B. Felsen, Eds., Plenum Press, 1994, 285-295
11. Oughstun, K.E., “Transient in Chiral Media with Single Resonance Dispersion: Comments, Jour. Opt. Soc. of Am. A, Vol. 12, 1995, 626-628
12. Sherman, G.C. and K.E. Oughstun, “Energy-Velocity Description of Pulse Propagation in Absorbing, Dispersive Dielectrics,” J. Opt. Soc. of Am. B, Vol. 12 Feb. 1995, 229-247
13. Oughstun, K.E., “Dynamical Structure of the Precursor Fields in Linear Dispersive Pulse Propagation in Lossy Dielectrics,” in Ultra-Wideband, Short-Pulse Electromagnetics 2, L. Carin and L.B. Felsen, Eds., Plenum Press, 1995, 257-272
14. Oughstun, K.E., “Noninstantaneous, Finite Rise-Time Effects on the Precursor Field Formation in Linear Dispersive Pulse Propagation,” J. Opt. Soc. of Am. A, Vol. 12, Aug. 1995, 1715-1729
15. Marozas, J.A. and K.E. Oughstun, “Electromagnetic Pulse Propagation Across a Planar Interface Separating Two Lossy, Dispersive Dielectrics,” in Ultra-Wideband, Short-Pulse Electromagnetics 3, C. Baum, L. Carin, and A. P. Stone, Eds., Plenum Press, 1996, 217-230
16. Oughstun, K.E. and C.M. Balictsis, “Gaussian Pulse Propagation in a Dispersive, Absorbing Dielectric, “Phys. Rev Ltrs., Vol. 77, 9 Sept. 1996, 2210-2213
17. Oughstun, K.E. and Hong Xiao, “Failure of the Quasimonochromatic Approximation for Ultrashort Pulse Propagation in a Dispersive, Attenuative Medium,” Phys. Rev. Ltrs., Vol. 78, 27 Jan. 1997, 642-645
18. Balictsis, C.M. and K.E. Oughstun, “Generalized Asymptotic Description of the Propagated Field Dynamics in Gaussian Pulse Propagation in a Linear, Causally Dispersive Medium,” Phys. Rev. Ltrs. E, Vol. 55, Feb 1997, 1910-1921
19. Xiao, H. and K.E. Oughstun, “Hybrid Numerical-Asymptotic Code for Dispersive Pulse Propagation Calculations, Jour. Optical Society of America A, Vol. 15, 1998, 1256-1267
20. Solhaug, J.A., K.E. Oughstun, J.J. Stamnes, and P.D. Smith, “Uniform Asymptotic Description of the Brillouin Precursor in a Lorentz Model Dielectric,” Jour. European Opt. Soc. A., Pure and Applied Optics, Vol. 7, 1998, 575-602
21. Oughstun, K.E., “The Angular Spectrum Representation and the Sherman Expansion of Pulsed Electromagnetic Beam Fields in Dispersive, Attenuative Media,” Jour. European Opt. Soc. A., Pure and Applied Optics, Vol. 7, 1998, 1059-1078
22. Solhau, J.A., J.J. Stamnes, and K.E. Oughstun, “Diffraction of Electromagnetic Pulses in a Single-Resonance Lorentz Model Dielectric,” Jour. European Optical Soc. A., Pure and Applied Optics, Vol. 7, 1998, 1079-1101
23. Smith, P.D. and K.E. Oughstun, “Electromagnetic Energy Dissipation and Propagation of an Ultrawideband Plane Wave Pulse in a Causally Dispersive Dielectric,” Radio Science, Vol. 33, 1998, 1489-1504
24. Xiao, H. and K.E. Oughstun, “Failure of the Group-Velocity Description for Ultrawideband Pulse Propagation in a Causally Dispersive, Absorptive Dielectric,” J. Opt. Soc. Am. B, Vol. 16, Oct. 1999, 1773-1785
25. Laurens, J.E.K. and K.E. Oughstun, “Electromagnetic Impulse Response of Triply-Distilled Water,” Ultra-Wideband, Short-Pulse Electromagnetics 4,” Heyman et al,. Eds., Kluwer Academic/Plenum Publ., 1999, 243-264
26. Smith, P.D. and K.E. Oughstun, “Ultrawideband Electromagnetic Pulse Propagation in Triply Distilled Water,” Ultra-Wideband, Short-Pulse Electromagnetics 4,” Heyman et al, Eds., Kluwer Academic/Plenum Publ., 1999, 265-276
27. Oughstun, K.E. and H. Xiao, “Influence of Precursor Fields on Ultrashort Pulse Autocorrelation Measurements and Pulse Width Evolution,” Optics Express, Vol. 8, 9 April 2001, 481-491
28. Oughstun, K.E. and H. Xiao, “Influence of the Precursor Fields on Ultrashort Pulse Measurements,” in Ultra-Wideband, Short-Pulse Electromagnetics 5, P.D. Smith and S.R. Cloude, Eds., Kluwer Academic/Plenum Publ., 2002, 569-576
29. Oughstun, K.E. “Asymptotic Description of Ultrawideband, Ultrashort Pulsed Electromagnetic Beam Field Propagation in a Dispersive, Attenuative Medium,” in Ultra-Wideband, Short-Pulse Electromagnetics 5, P.D. Smith and S.R. Cloude, Kluwer Academic/Plenum Publi, 2002, 687-696