Modeling the Stuff of the Material World: Do We Need All of the Atoms?
ROB PHILLIPS
Division of Engineering and Applied Science
California Institute of Technology
Pasadena, California
The advent of computers ushered in a new way of doing science and engineering in which a host of complex problems ranging from weather prediction to the microstructural evolution of multiphase alloys to the DNA/protein interactions that mediate gene regulation could be explored explicitly using computer simulation. Indeed, some say that the physical sciences are now based on a triumvirate of experiment, theory, and simulation, with simulation complementing more traditional techniques for understanding problems involving many interacting degrees of freedom. One class of problems for which simulation is increasingly important is associated with the understanding and control of materials. When we speak of materials, we mean “stuff” as diverse as the materials of which man is made (soft, squishy stuff) and technologies (stuff with desirable properties, such as strength or conductivity) (Amato, 1997).
Clearly, the use of computation to understand and even design complex materials is one of the major challenges that will make it possible to replace the enlightened empiricism that gave rise to the great material ages (e.g., the Iron Age, Bronze Age, and silicon-based Information Age) with rational design. Similar roles are anticipated for simulation in many other fields as well. One of the flagship techniques for examining problems involving complex materials is molecular dynamics in which the microscopic trajectories of each and every atom are followed explicitly. Despite their promise, however, these simulations sometimes generate enormous quantities of information (i.e., terabyte data sets) without necessarily delivering the promised concomitant increase in understanding.
Terabyte data sets engendered by simulations represent a staggering quantity of information. A simple estimate reveals that the entire 10 floors worth of books in the Caltech Millikan Library corresponds roughly to a terabyte of information. More impressively, the genomes of many viruses have an information content that can be stored comfortably on a 256-megabyte memory stick alongside the genomes of even more complex organisms from bacteria to yeast. Indeed, even organisms as complex as humans have genomes that are much smaller than a terabyte. And yet our computers are overflowing with terabyte data sets, and worse yet, discussions of petabyte data sets are becoming routine. For example, a molecular dynamics calculation on a 100,000-atom system run for only 10 nanoseconds, woefully inadequate for accessing most materials processes, already generates a terabyte worth of data. Clearly, there is a mismatch between the quality of information generated in our simulations and the information present in genomes and libraries.
The question of how to build quantitative models of complex systems with many interacting degrees of freedom is not new. Indeed, one of the threads through the history of physics, the development of continuum theories, resulted in two compelling examples of this kind of theory—elasticity and hydrodynamics. These theories share the idea of smearing out the underlying discreteness of matter with continuum field variables. In addition, with both theories, material properties are captured in simple parameters, such as elastic moduli or viscosity, which reflect the underlying atomic-level interactions without specifically mentioning atoms.
One lesson of these examples is that “multiscale modeling” is neither the exclusive domain of computational model building nor a fundamentally new idea. Indeed, in the deepest sense, the sentiment that animates all efforts at model building, whether analytical or computational, is of finding a minimal but predictive description of the problem of interest.
One feature that makes problems like those described here especially prickly is that they often involve multiple scales in space or time or both. An intriguing response to the unbridled proliferation of simulated data has been a search for streamlined models in which there is variable resolution. Many of the most interesting problems currently being tackled in arenas ranging from molecular biology to atmospheric science are those in which structures or processes at one scale influence the physics at another scale. As a response to these challenges, modelers have begun to figure out how to construct models in which the microscopic physics is maintained only where needed. One benefit of these approaches is that they not only reduce the computational burden associated with simulations of complex systems, but they also provide a framework for figuring out which features of a given problem dictate the way the “stuff” of interest behaves. Several examples of this type of thinking are described below.
Before embarking on a discussion of case studies, it is worth discussing the metrics that might be used in deciding whether or not a particular coarse-grained
model should be viewed as a success. From the most fundamental point of view, the job of theoretical models is to provide a predictive framework for tying together a range of different phenomena. For example, in the case of elasticity described above, there are vast numbers of seemingly unrelated problems (from flying buttresses to the mechanical response of ion channels) that may be brought under the same intellectual roof through reference to Hooke’s law. With elasticity theory, we can predict how the cantilever of an atomic-force microscope will deflect when tugging on a protein tethered to a surface. In this sense, elasticity theory has to be viewed as an unqualified success in the coarse-grained modeling of materials and shows just how high the bar has been raised for multiscale models worthy of the name.
A CASE STUDY IN MULTISCALE MODELING
The Quasicontinuum Method
One of the computational responses to problems involving multiple scales is multiresolution models that attempt to capture several scales at the same time. There has been great progress along these lines in recent years from a number of different quarters, and presently we will consider one example, namely the quasicontinuum method that permits the treatment of defects in crystalline solids.1 The main idea of the quasicontinuum method is to allow for atomic-level detail in regions where interesting physical processes, such as dislocation nucleation, dislocation intersections, and crack propagation are occurring, while exploiting a more coarse-grained description away from the key action. The motivation for the method is based on a recognition that when treating defects in solids there are both long-range elastic interactions between these defects and atomic-scale processes involving the arrangements of individual atoms. What makes these problems so difficult is that both the short-range and long-range effects can serve as equal partners in dictating material response.
The numerical engine that permits a response to problems of this type is finite elements that allow for nonuniform meshes and introduce geometric constraints on atomic positions through the presence of interpolation functions (so-called finite-element shape functions). Just as those of us who learned how to interpolate on logarithm or trigonometric tables remember, the key idea of the finite-element procedure is to characterize the geometric state of the system by keeping track of the positions of a few key atoms that serve as nodes on the finite-element mesh. The positions of all other atoms in the system can be found, if needed, by appealing to simple interpolation.
|
1 |
There are many articles on the quasicontinuum method, but the interested reader is invited to consult www.qcmethod.com, which has an extensive list of papers dealing with this method. |
To simulate material response, geometry is not enough. We not only have to know where the nodes are, but also what forces act on them. To that end, the quasicontinuum method posits that the forces on the nodes can be obtained by appealing to interatomic potentials that describe interactions between individual atoms. Using the interpolated atomic positions, a neighborhood of atoms around each node is constructed, and the energies and forces are then computed using standard atomistic techniques. This is an elegant prescription because it ensures that the material response is strictly determined by the underlying microscopic physics without any ad hoc material assumptions. Once the geometric mesh has been constructed and the forces on the nodes computed, the simulation itself can take place by either minimizing the energy with respect to nodal coordinates or by using F = ma physics to compute the trajectories of the system over time.
For a concrete example, consider a crystalline solid subjected to external loading in the form of an indenter like the one shown in Figure 1. The quasicontinuum philosophy is to discretize the system in such a way that there is full atomic resolution where the action is (such as beneath the indenter) and a select, representative subset of atoms that serve as nodes of the finite-element regions where all-atom resolution is surrendered. For the particular case of two-dimensional dynamical nanoindentation considered here, the calculation involves a total of 5,000 nodes as opposed to the 107 atoms that would be needed in a full atomistic calculation. This point is driven home in an even more compelling fashion in the case of a fully three-dimensional calculation for which the full atomistic calculation would have implicated in excess of 1011 atoms (Knap and Ortiz, 2003).
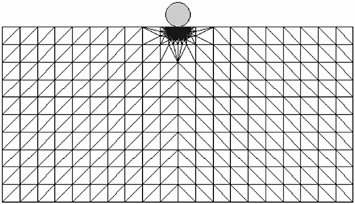
FIGURE 1 Schematic illustration of a multiresolution mesh used to describe nanoindentation of a crystalline solid. In the region just beneath the indenter, the mesh has full atomic resolution. In the “far fields,” the mesh is much coarser.
The main point of this example is to reveal the kind of thinking now being used to address complex problems, such as material deformation. As exemplified by the quasicontinuum method, the underlying microscopic physics of bond stretching and bond breaking is treated explicitly where needed, and only approximately elsewhere.
THE PROBLEM OF LIVING MATERIALS
Understanding the workings of living materials presents even more compelling multiscale challenges than those encountered in the traditional materials setting. Indeed, we are now realizing that almost no individual macromolecule in the living world acts alone. Rather, the cell can be viewed as “a collection of protein machines,” assemblies of individual macromolecules (Alberts, 1998). One of the pressing challenges to have arisen from the stunning successes of structural biology is the study of assemblies, such as viruses and the many “SOMES” (i.e., macromolecular assemblies that work in concert to maintain the mass and energy budget of the cell), such as nucleosomes, ribosomes, proteosomes, and assemblies that mediate gene expression, such as replisomes, spliceosomes, and so on.
Models of the function of assemblies such as “SOMES,” will remain out of reach of traditional atomic-level techniques for the foreseeable future. Consider the process of translation mediated by the ribosome. Even if we very generously assume that a new amino acid is added only once every millisecond, a molecular dynamics simulation of translation would have to be run for 1012 time steps for the addition of even a single amino acid to the nascent polypeptide. The number of atoms (including the surrounding water) engaged in this process is well in excess of 100,000, implying a whopping 1017 positions corresponding to all of the atoms during the entire molecular dynamics trajectory.
Similar estimates can be made for the workings of many other macromolecular assemblies that mediate the processes of a cell. All of these estimates lead to the same general conclusion—that even as we continue to pursue atomic-level calculations, we must redouble our efforts to understand the workings of “SOMES” from a coarse-grained perspective.
So the hunt is on to find methods of modeling processes of biological relevance involving assemblies of diverse molecular actors, such as proteins, lipids, and DNA, without having to pay the price in excessive data of all-atom simulation. One way to guarantee a rich interplay between experiment and models is through the choice of case studies that are well developed from the standpoint of molecular biology and for which we have compelling quantitative data.
One example of great importance is the lac operon, which has served as the “hydrogen atom” of gene regulation. This gene regulatory network, which controls the digestion of the sugar lactose in bacteria, has been the cornerstone of the development of our modern picture of gene regulation. An intriguing history of
this episode in the history of molecular biology can be found in the books of Judson (1996) and Echols (2001).
The basic idea is that only when a bacterium is deprived of glucose and has a supply of lactose does the bacterium synthesize the enzymes needed to digest lactose. The “decisions” made by the bacterium are mediated by molecules, such as lac repressor, a protein that sits on the DNA and prevents the genes responsible for lactose digestion from being expressed. Lac repressor binds to several sites in the vicinity of the promoter for the genes responsible for lactose digestion and prohibits expression of those genes while simultaneously creating a loop of DNA between the two repressor binding sites.
From a modeling perspective, a minimal description of this system involves the DNA molecule itself, RNA polymerase, lac repressor, and an activator molecule called CAP. The kinds of questions that are of interest from a quantitative modeling perspective include the extent of gene expression as a function of the number of copies of each molecular actor in this drama, as well as the distance between the DNA binding sites for lac repressor and other features.
One recent multiscale attempt to simulate the interaction between DNA and lac repressor uses a mixed atomistic/continuum scheme, in which the lac repressor and the surrounding complement of water molecules are treated in full atomistic detail while the looped DNA region is treated using elasticity theory (Villa et al., 2004). The advantage of this approach is that it permits the DNA to present an appropriate boundary condition to the lac repressor simulation without having to do a full atomistic simulation of both DNA and the protein. Figure 2 shows an example of the simulation box and the elastic rod treatment of DNA. The key point of this example is not to illustrate what can be learned about the lac operon using mixed atomistic-continuum methods, but to illustrate how multiscale methods have begun to take root in the biological setting, just as they have in the conventional materials setting.
A second scheme, even more coarse-grained than the multiscale simulations of the lac repressor, is a statistical mechanics treatment of molecular decision makers, such as the repressor and its activator counterpart CAP. The relevant point is that all of the atomic-level specificity is captured by simple binding energies that reflect the affinity of these molecules for DNA and for each other.
This statistical mechanics perspective is a natural quantitative counterpart to the cartoons describing gene regulation used in classic texts of molecular biology. As shown in Figure 3, these cartoons depict various states of occupancy of the DNA in the neighborhood of the site where RNA polymerase binds. The statistical mechanics perspective adds the ability to reckon explicitly the statistical weights of each distinct state of occupancy of the DNA. From these statistical weights, a quantitative prediction can be made of the probability that a given gene will be expressed as a function of the number of molecules of each species.
Ultimately, one of the primary ways of judging a model must be by its ability to make predictions about as-yet undone experiments. The outcome of the

FIGURE 2 Illustration of a mixed atomistic/continuum description of the interaction of lac repressor protein with DNA. The lac repressor molecule is shown in dark gray, the part of the DNA treated explicitly is shown in medium gray, and the part of the DNA treated via continuum mechanics is shown as a ribbon. Water molecules surrounding the protein are shown in light gray. Source: Courtesy of Klaus Schulten and Elizabeth Villa.
so-called “thermodynamic models” (Ackers et al., 1982) described above is a predictive framework that characterizes the extent to which genes are expressed as a function of concentrations of the relevant decision-maker molecules (i.e., the transcription factors), the distance between the looping sites on the DNA, etc. Paradoxically, as a result of the great successes of structural biologists in determining the atomic-level structures of important complexes, such as DNA and its binding partners, we are now faced with the challenge of eliminating molecular details in models of their function.
SUMMARY
The critical question for building models of the material world is the extent to which we can suppress an atom-by-atom description of the function of materials. As emergence of “multiscale modeling” reveals, even with increasing

FIGURE 3 a. Schematic illustration showing the relation between cartoon models of various states of the genetic network and their corresponding weights in the statistical mechanics framework. b. Graph showing activation as a function of the number of activator molecules. The three curves correspond to different strengths for the interaction between the RNA polymerase and the activator.
computational power, a host of important problems remain out of reach of strictly brute-force approaches. In the analysis of the material world, whether of the complex, rigid metallic structures used to construct cities or the soft, squishy materials that make up the organisms that populate them, the key action often takes place at the level of individual atoms—whether of a bond breaking at a crack tip or the active site of an enzyme. Many of the atoms that are part of these processes are interlopers, however, that seem to be little more than passive observers that provide boundary conditions for the atoms actively involved in the process of interest.
From a model-building perspective, the goal is to “make things as simple as possible, but no simpler” (i.e., to eliminate as many molecular details as possible). In my opinion, this is one of the key design criteria for multiscale models. Although multiscale computational models are receiving most of the effort and attention right now, I believe the hunt should continue for analytic models that can capture the key features of complex materials and lead to the kind of insight that can be discussed at a blackboard.
ACKNOWLEDGMENTS
I am grateful to Jané Kondev, Michael Ortiz, Ellad Tadmor, Ron Miller, Vijay Shenoy, Vivek Shenoy, David Rodney, Klaus Schulten, Darren Segall, and Laurent Dupuy for collaboration and conversation. All of them played a key role in the development of my understanding of multiscale modeling. Farid Abraham first illustrated the meaning of a terabyte to me by comparing it to the informational content of a library.
REFERENCES
Ackers, G.K., A.D. Johnson, and M.A. Shea. 1982. Quantitative model for gene regulation by l phage repressor. Proceedings of the National Academy of Sciences 79(4): 1129–1133.
Alberts, B. 1998. The cell as a collection of protein machines: preparing the next generation of molecular biologists. Cell 92(3): 291–294.
Amato, I. 1997. Stuff: The Materials the World Is Made Of. New York: Basic Books.
Echols, H. 2001. Operators and Promoters. Berkeley: University of California Press.
Judson, H.F. 1996. The Eighth Day of Creation. Plainview, N.Y.: Cold Spring Harbor Laboratory Press.
Knap, J., and M. Ortiz. 2003. Effect of indenter-radius size on Au(001) nanoindentation. Physical Review Letter 90(22). Article No. 226102.
Villa, E., A. Balaeff, L. Mahadevan, and K. Schulten. 2004. Multi-scale method for simulating protein-DNA complexes. Multiscale Modeling and Simulation 2(4): 527–553.










